Mahesh

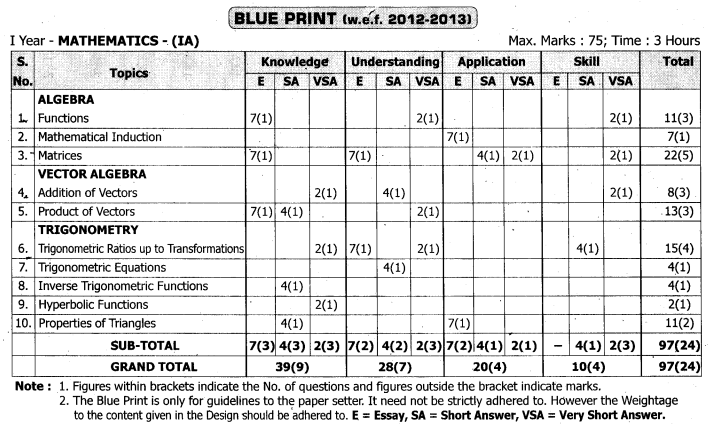
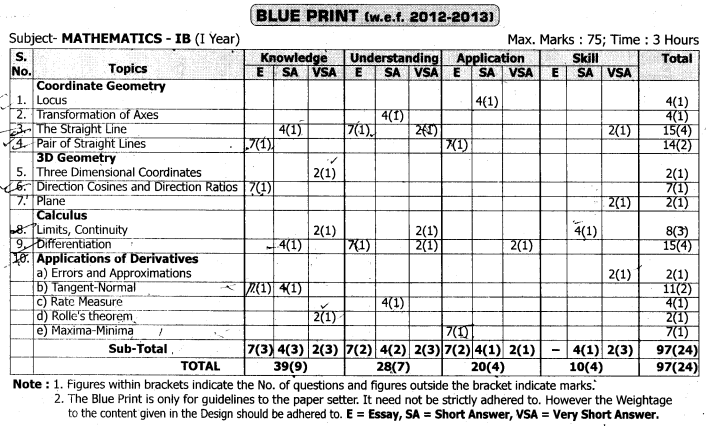
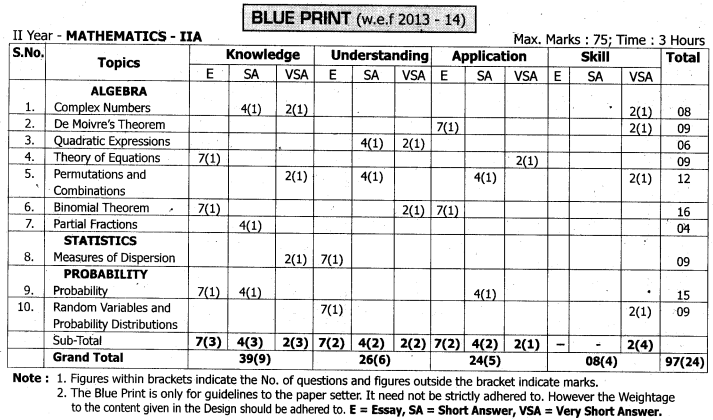
Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Matrices Solutions Exercise 3(a) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Matrices Solutions Exercise 3(a)

I.

Question 1.
Write the following as a single matrix.
(i) \(\left[\begin{array}{lll}
2 & 1 & 3
\end{array}\right]+\left[\begin{array}{lll}
1 & 0 & 0
\end{array}\right]\)
(ii) \(\left[\begin{array}{ccc}
3 & 9 & 0 \\
1 & 8 & -2
\end{array}\right]+\left[\begin{array}{ccc}
4 & 0 & 2 \\
7 & 1 & 4
\end{array}\right]\)
(iii) \(\left[\begin{array}{c}
0 \\
1 \\
-1
\end{array}\right]+\left[\begin{array}{l}
1 \\
1 \\
1
\end{array}\right]\)
(iv) \(\left[\begin{array}{cc}
-1 & 2 \\
2 & -2 \\
3 & 1
\end{array}\right]-\left[\begin{array}{cc}
0 & 1 \\
-1 & 0 \\
-2 & 1
\end{array}\right]\)
Solution:

Question 2.
If A = \(\left[\begin{array}{cc}
-1 & 3 \\
4 & 2
\end{array}\right]\), B = \(\left[\begin{array}{cc}
2 & 1 \\
3 & -5
\end{array}\right]\), X = \(\left[\begin{array}{ll}
x_{1} & x_{2} \\
x_{3} & x_{4}
\end{array}\right]\) and A + B = X, then find the values of x₁, x₂, x₃ and x₄.
Solution:
A + B = X

∴ x₁ = 1, x₂ = 4, x₃ = 7, x₄ = -3

Question 3.
If A = \(\left[\begin{array}{ccc}
-1 & -2 & 3 \\
1 & 2 & 4 \\
2 & -1 & 3
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
1 & -2 & 5 \\
0 & -2 & 2 \\
1 & 2 & -3
\end{array}\right]\) and C = \(\left[\begin{array}{ccc}
-2 & 1 & 2 \\
1 & 1 & 2 \\
2 & 0 & 1
\end{array}\right]\) then find A + B + C.
Solution:

Question 4.
If A = \(\left[\begin{array}{ccc}
3 & 2 & -1 \\
2 & -2 & 0 \\
1 & 3 & 1
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
-3 & -1 & 0 \\
2 & 1 & 3 \\
4 & -1 & 2
\end{array}\right]\) and X = A + B then find X.
Solution:

Question 5.
If \(\left[\begin{array}{cc}
x-3 & 2 y-8 \\
z+2 & 6
\end{array}\right]=\left[\begin{array}{cc}
5 & 2 \\
-2 & a-4
\end{array}\right]\) then find the values of x, y, z and a.
Solution:
Given \(\left[\begin{array}{cc}
x-3 & 2 y-8 \\
z+2 & 6
\end{array}\right]=\left[\begin{array}{cc}
5 & 2 \\
-2 & a-4
\end{array}\right]\)
∴ x – 3 = 5 ⇒ x = 3 + 5 = 8
2y – 8 = 2 ⇒ 2y = 8 + 2 = 10 ⇒ y = 5
z + 2 = -2 ⇒ z = -2 – 2 = -4
a – 4 = 6 ⇒ a = 4 + 6 = 10

II.

Question 1.
If \(\left[\begin{array}{ccc}
x-1 & 2 & 5-y \\
0 & z-1 & 7 \\
1 & 0 & a-5
\end{array}\right]=\left[\begin{array}{ccc}
1 & 2 & 3 \\
0 & 4 & 7 \\
1 & 0 & 0
\end{array}\right]\) then find the values of x, y, z and a.
Solution:
Given \(\left[\begin{array}{ccc}
x-1 & 2 & 5-y \\
0 & z-1 & 7 \\
1 & 0 & a-5
\end{array}\right]=\left[\begin{array}{ccc}
1 & 2 & 3 \\
0 & 4 & 7 \\
1 & 0 & 0
\end{array}\right]\)
∴ x – 1 = 1 ⇒ x = 1 + 1 = 2
5 – y = 3 ⇒ y = 5 – 3 = 2
z – 1 = 4 ⇒ z = 4 + 1 = 5
a – 5 = 0 ⇒ a = 5

Question 2.
Find the trace of \(\left[\begin{array}{ccc}
1 & 3 & -5 \\
2 & -1 & 5 \\
1 & 0 & 1
\end{array}\right]\)
Solution:
Trace of \(\left[\begin{array}{ccc}
1 & 3 & -5 \\
2 & -1 & 5 \\
1 & 0 & 1
\end{array}\right]\) = Sum of the diagonal elements
= 1 – 1 + 1
= 1

Question 3.
If A = \(\left[\begin{array}{rrr}
0 & 1 & 2 \\
2 & 3 & 4 \\
4 & 5 & -6
\end{array}\right]\) and B = \(\left[\begin{array}{ccc}
-1 & 2 & 3 \\
0 & 1 & 0 \\
0 & 0 & -1
\end{array}\right]\) find B – A and 4A – 5B.
Solution:

Question 4.
If A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
3 & 2 & 1
\end{array}\right]\) and B = \(\left[\begin{array}{lll}
3 & 2 & 1 \\
1 & 2 & 3
\end{array}\right]\) find 3B – 2A.
Solution:

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Mathematical Induction Solutions Exercise 2(a) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Mathematical Induction Solutions Exercise 2(a)

Using mathematical induction, prove each of the following statements for all n ∈ N.

Question 1.
1² + 2² + 3² + …… + n² = \(\frac{n(n+1)(2 n+1)}{6}\)
Solution:
Let p(n) be the given statement:
1² + 2² + 3² + ….. + n² = \(\frac{n(n+1)(2 n+1)}{6}\)
Since 1² = \(\frac{(1)(1+1)(2 \times 1+1)}{6}\)
⇒ 1 = 1 the formula is true for n = 1
i.e., p(1) is true.
Assume the statement p(n) is true for n = k
i.e., 1² + 2² + 3² + …… + 1k² = \(\frac{k(k+1)(2 k+1)}{6}\)
We show that the formula is true for n = k + 1
i.e., We show that p(k + 1) = \(\frac{(k+1)(k+2)(2 k+3)}{6}\)
(Where p(k) = 1² + 2² + 3² + … + k²)
We observe that
p(k + 1) = 1² + 2² + 3² + …… + (k)² + (k + 1)² = p(k) + (k + 1)²
Since p(k) = \(\frac{k(k+1)(2 k+1)}{6}\)
We have p(k + 1) = p(k) + (k + 1)²

∴ The formula holds for n = k + 1
∴ By the principle of mathematical induction, p(n) is true for all n ∈ N
i.e., the formula 1² + 2² + 3² + ……. + n² = \(\frac{n(n+1)(2 n+1)}{6}\) for all n ∈ N

Question 2.
2.3 + 3.4 + 4.5 + …… up to n terms = \(\frac{n\left(n^{2}+6 n+11\right)}{3}\)
Solution:
The nth term in the given series is (n + 1) (n + 2)
Let p(n) be the statement:
2.3 + 3.4 + 4.5 + …… + (n + 1) (n + 2) = \(\frac{n\left(n^{2}+6 n+11\right)}{3}\)
and let S(n) be the sum on the left-hand side.
Since S(1) = 2.3 = \(\frac{(1)(1+6+11)}{3}\) = 6
∴ The statement is true for n = 1
Assume that the statement p(n) is true for n = k
i.e., S(k) = 2.3 + 3.4 + …… + (k + 1) (k + 2) = \(\frac{k\left(k^{2}+6 k+11\right)}{3}\)
We show that the statement is true for n = k + 1
i.e., We show that S(k + 1) = \((k+1)\left[\frac{(k+1)^{2}+6(k+1)+11}{3}\right]\)
We observe that
S(k + 1) = 2.3 + 3.4 + 4.5 + + (k + 1) (k + 2) + (k + 2) (k + 3)
= S(k) + (k + 2) (k + 3)

∴ The statement holds for n = k + 1
∴ By the principle of mathematical induction,
p(n) is true for all n ∈ N
i.e., 2.3 + 3.4 + 4.5 + ……. + (n + 1) (n + 2) = \(\frac{n\left(n^{2}+6 n+11\right)}{3}\)

Question 3.
\(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\ldots+\frac{1}{(2 n-1)(2 n+1)}=\frac{n}{2 n+1}\)
Solution:
Let p(n) be the statement:
\(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\ldots+\frac{1}{(2 n-1)(2 n+1)}=\frac{n}{2 n+1}\)
and let S(n) be the sum on the L.H.S.
Since S(1) = \(\frac{1}{1.3}=\frac{1}{1(2+1)}=\frac{1}{1.3}\)
∴ P(1) is true.
Assume that the statement p(n) is true for n = k
i.e., S(k) = \(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\ldots+\frac{1}{(2 k-1)(2 k+1)}\) = \(\frac{k}{2 k+1}\)
We show that the statement p(n) is true for n = k + 1
i.e., we show that s(k + 1) = \(\frac{k+1}{2(k+1)+1}\)
We observe that

∴ The statement holds for n = k + 1
∴ By the principle of mathematical induction,
p(n) is true for all n ∈ N
i.e., \(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\ldots+\frac{1}{(2 n-1)(2 n+1)}=\frac{n}{2 n+1}\)

Question 4.
4³ + 8³ + 12³ + …… up to n terms = 16n²(n + 1)².
Solution:
4, 8, 12,….. are in A.P., whose nth term is (4n)
Let p(n) be the statement:
4³ + 8³ + 12³ + ………. + (4n)³ = 16n²(n + 1)²
and S(n) be the sum on the L.H.S.
S(1) = 4³ = 16(1²) (1 + 1)² = 16(4) = 64 = 4³
∴ p(1) is true
Assume that the statement p(n) is true for n = k
i.e., S(k) = 4³ + 8³ + (12)³ + …… + (4k)³ = 16k²(k + 1)²
We show that the statement is true for n = k + 1
i.e., We show that S(k + 1) = 16(k + 1)² (k + 2)²
We observe that
S(k + 1) = 4³ + 8³ + 12³ + …… + (4k)³ + [4(k + 1)]³
= S(k) + [4(k + 1)]³
= 16k² (k + 1)² + 4³ (k + 1)³
= 16(k + 1)² [k² + 4(k + 1)]
= 16(k + 1)² [k² + 4k + 4]
= 16(k + 1)² (k + 2)²
= 16(k + 1)² \((\overline{k+1}+1)^{2}\)
∴ The formula holds for n = k + 1
∴ By the principle of mathematical induction,
p(n) is true for all n ∈ N
(i.e.,) 4³ + 8³ + 12³ + …… + (4n)³ = 16n²(n + 1)²

Question 5.
a + (a + d) + (a + 2d) + ……. up to n terms = \(\frac{n}{2}\) [2a + (n – 1)d]
Solution:
Let p(n) be the statement:
a + (a + d) + (a + 2d) + …… + [a + (n – 1)d] = \(\frac{n}{2}\) [2a + (n – 1)d]
and let the sum on the L.H.S. is denoted by S(n)
Since S(1) = a = \(\frac{1}{2}\) [2a + (1 – 1)d] = a
∴ p(1) is true.
Assume that the statement is true for n = k
(i.e.,) S(k) = a + (a + d) + (a + 2d) + ……. + [a + (k – 1)d] = \(\frac{k}{2}\) [2a + (k – 1 )d]
We show that the statement is true for n = k + 1
(i.e.,) we show that S(k + 1) = \(\left(\frac{k+1}{2}\right)[2 a+k d]\)
We observe that
S(k + 1) = a + (a + d) + (a + 2d) + …… + [a + (k – 1)d] + (a + kd)
= S(k) + (a + kd)
= \(\frac{k}{2}\) [2a + (k – 1)d] + (a + kd)
= \(\frac{k[2 a+(k-1) d]+2(a+k d)}{2}\)
= \(\frac{1}{2}\) [2ak + k(k – 1)d + 2a + 2kd]
= \(\frac{1}{2}\) [2a(k + 1) + k(k – 1 + 2)d]
= \(\frac{1}{2}\) (k + 1)(2a + kd)
∴ The statement holds for n = k + 1
∴ By the principle of mathematical inductions,
p(n) is true for all n ∈ N
(i.e.,) a + (a + d) + (a + 2d) + …… + [a + (n – 1)d] = \(\frac{n}{2}\) [2a + (n – 1)d]

Question 6.
a + ar + ar² + ……… up to n terms = \(\frac{a\left(r^{n}-1\right)}{r-1}\); r ≠ 1
Solution:
Let p(n) be the statement:
a + ar + a.r² + …… + a. r^n-1 = \(\frac{a\left(r^{n}-1\right)}{r-1}\), r ≠ 1
and let S(n) be the sum on the L.H.S
Since S(1) = a = \(\frac{a\left(r^{1}-1\right)}{r-1}\) = a
∴ p(1) is true
Assume that the statement is true for n = k
(i.e) S(k) = a + ar + ar² + ……… + a . r^k-1 = \(\frac{a\left(r^{k}-1\right)}{r-1}\)
We show that the statement is true for n = k + 1
(i.e) S(k + 1) = \(\frac{a\left(r^{k+1}-1\right)}{r-1}\)
Now S(k + 1) = a + ar + ar² + ……. + a r^k-1 + ar^k
= S(k) + a . r^k

∴ The statement holds for n = k + 1
∴ By the principle of mathematical induction,
p(n) is true for all n ∈ N
(i.e) a + ar + ar² + ……. + a.r^n-1 = \(\frac{a\left(r^{n}-1\right)}{r-1}\), r ≠ 1

Question 7.
2 + 7 + 12 + ……. + (5n – 3) = \(\frac{n(5 n-1)}{2}\)
Solution:
Let p(n) be the statement:
2 + 7 + 12 + ……. + (5n – 3) = \(\frac{n(5 n-1)}{2}\)
and let S(n) be the sum on the L.H.S
Since S(1) = 2 = \(\frac{1(5 \times 1-1)}{2}=\frac{4}{2}\) = 2
∴ p(1) is true
Assume that the statement is true for n = k
(i.e) S(k) = 2 + 7 + 12 + …….. + (5k – 3) = \(\frac{k(5 k-1)}{2}\)
We have to show that S(k + 1) = \(\frac{(k+1)(5 k+4)}{2}\)
We observe that S(k + 1) = 2 + 7 + 12 + ……. + (5k – 3) + (5k + 2)
= S(k) + (5k + 2)
= \(\frac{k(5 k-1)}{2}\) + (5k + 2)
= \(\frac{5 k^{2}-k+2(5 k+2)}{2}\)
= \(\frac{1}{2}\) [5k² + 9k + 4]
= \(\frac{1}{2}\) (k + 1) (5k + 4)
= \(\frac{1}{2}\) (k + 1) [5(k + 1) – 1]
∴ p(k + 1) is true
∴ By the principle of mathematical induction,
p(n) is true for all n ∈ N.
(i.e.,) 2 + 7 + 12 + …… + (5n – 3) = \(\frac{n(5 n-1)}{2}\)

Question 8.
\(\left(1+\frac{3}{1}\right)\left(1+\frac{5}{4}\right)\left(1+\frac{7}{9}\right) \ldots \ldots\left(1+\frac{2 n+1}{n^{2}}\right)\) = (n + 1)²
Solution:
Let p(n) be the statement:
\(\left(1+\frac{3}{1}\right)\left(1+\frac{5}{4}\right)\left(1+\frac{7}{9}\right) \ldots \ldots\left(1+\frac{2 n+1}{n^{2}}\right)\) = (n + 1)²
and let S(n) be the product on the LHS
since S(1) = 1 + 3 = 4 = (1 + 1)² = 4
∴ P(a) 4 time for n = 1
Assume that p(n) is true for n = k

= (k + 1)² + 2k + 3
= k² + 2k + 1 + 2k + 3
= k² + 4k + 4
= (k + 2)²
= (k + 1 + 1)²
∴ P(n) is true for n = k + 1
By the principle of Mathematical Induction,
p(n) is true & n ∈ N

Question 9.
(2n + 7) < (n + 3)²
Solution:
Let p (n) be the statement
When n = 1, 9 < 16
∴ p(n) is true for n = 1
Assume p (n) is true for n = k
(2k + 7) < (k + 3)²
We show that p(n) is true for n = k + 1
2(k + 1) + 7 = 2k + 7 + 2
< (k + 3)² + 2
< k² + 6k + 9 + 2 + 2k + 5 – 2k – 5
< (k + 4)² – (2k + 5)
< (k + 4)²
< (k + 1 + 3)²
∴ p(n) is true for n = k + 1
By the principle of Mathematical Induction
p(n) is true ∀ n ∈ N

Question 10.
1² + 2² + …… + n² > \(\frac{n^{3}}{3}\)
Solution:
Let P(n) by the statement
when n = 1, 1 > \(\frac{1}{3}\)
∴ p(n) is true for n = 1
Assume p (n) is true for n = k
1² + 2² + …… + k² > \(\frac{k^{3}}{3}\)
We show that p(n) is true for n = k + 1

∴ p(n) is true for n = k + 1
By the principle of Mathematical Induction,
p(n) is true ∀ n ∈ N

Question 11.
4ⁿ – 3n – 1 is divisible by 9.
Solution:
Let p(n) be the statement:
4ⁿ – 3n – 1 is divisible by 9
Since 4¹ – 3(1) – 1 = 0 is divisible by 9.
The statement is true for n = 1
Assume that p(n) is true for n = k
(i.e) 4^k – 3k – 1 is divisible by 9
Then 4^k – 3k – 1 = 9t, for some t ∈ N ……..(1)
Show that the statement p(n) is true for n = k + 1
(i.e.,) we show that S(k + 1) = 4^k+1 – 3(k+1) – 1 is divisible by 9
From (1), we have
4^k = 9t + 3k + 1
∴ S(k + 1) = 4 . 4^k – 3(k + 1) – 1
= 4(9t + 3k + 1) – 3k – 3 – 1
= 4(9t) + 9k
= 9[4t + k]
Hence s(k + 1) is divisible by 9
Since 4t + k is an integer
∴ 4^k+1 – 3(k+1) – 1 is divisible by 9
∴ The statement is true for n = k + 1
∴ By the principle of mathematical induction,
p(n) is true for all n ∈ k
(i.e.,) 4ⁿ – 3n – 1 is divisible by 9

Question 12.
3 . 5²ⁿ⁺¹ + 2³ⁿ⁺¹ is divisible by 17.
Solution:
Let p(n) be the statement:
3. 5²ⁿ⁺¹ + 2³ⁿ⁺¹ is divisible by 17
Since 3 . 5²⁽¹⁾⁺¹ + 2³⁽¹⁾⁺¹
= 3 . 5³ + 2⁴
= 3(125) + 16
= 375 + 16
= 391
= 17(23) is divisible by 17
∴ The statement is true for n = 1
Assume that the statement is true for n = k
(i.e) 3 . 5^2k+1 + 2^3k+1 is divisible by 17
Then 3 . 5^2k+1 + 2^3k+1 = 17t, for some t ∈ N ……..(1)
Show that the statement p(n) is true for n = k + 1
(i.e.,) We have to show that
\(\text { 3. } 5^{2(k+1)+1}+2^{3(k+1)+1}\) is divisible by 17
From (1) we have

Here 25t + 2^3k+1 is an integer
∴ \(\text { 3. } 5^{2(k+1)+1}+2^{3(k+1)+1}\) is divisible by 17
∴ The statement is true for n = k + 1
∴ By the principle of mathematical induction,
p(n) is true for all n ∈ N
(i.e.,) 3 . 5²ⁿ⁺¹ + 2³ⁿ⁺¹ is divisible by 17.

Question 13.
1.2.3 + 2.3.4 + 3.4.5 + ……. upto n terms = \(\frac{n(n+1)(n+2)(n+3)}{4}\)
Solution:
The nth term of the given series is (n) (n + 1) (n + 2)
Let p(n) be the statement:
1.2.3 + 2.3.4 + 3.4.5 +……. + (n) (n+1) (n+2) = \(\frac{n(n+1)(n+2)(n+3)}{4}\)
and S(n) be the sum on the L.H.S.
∵ S(1) = 1.2.3 = \(\frac{(1)(1+1)(1+2)(1+3)}{4}\) = 1.2.3
∴ p(1) is true
Assume that the statement p(n) is true for n = k
(i.e) S(k) = 1.2.3 + 2.3.4 + 3.4.5 + ……. + k(k + 1) (k + 2) = \(\frac{k(k+1)(k+2)(k+3)}{4}\)
We show that the statement is true for n = k + 1
(i.e) We show that S(k + 1) = \(\frac{(k+1)(k+2)(k+3)(k+4)}{4}\)
We observe that
S(k + 1) = 1.2.3 + 2.3.4 + …… + k(k + 1) (k + 2) + (k + 1) (k + 2) (k + 3)
= S(k) + (k + 1) (k + 2) (k + 3)
= \(\frac{k(k+1)(k+2)(k+3)}{4}\) + (k + 1)(k + 2)(k + 3)
= (k + 1)(k + 2)(k + 3) \(\left(\frac{k}{4}+1\right)\)
= \(\frac{(k+1)(k+2)(k+3)(k+4)}{4}\)
∴ The statement holds for n = k + 1
∴ By the principle of mathematical induction,
p(n) is true for all n ∈ N
(i.e.,) 1.2.3 + 2.3.4 + 3.4.5 + ……. + (n)(n + 1)(n + 2) = \(\frac{n(n+1)(n+2)(n+3)}{4}\)

Question 14.
\(\frac{1^{3}}{1}+\frac{1^{3}+2^{3}}{1+3}+\frac{1^{3}+2^{3}+3^{3}}{1+3+5}\) + …. up to n terms = \(\frac{n}{24}\) [2n² + 9n + 13]
Solution:
The nth term of the given series is \(\frac{1^{3}+2^{3}+3^{3}+\ldots .+n^{3}}{1+3+5+\ldots+(2 n-1)}\)
Let p(n) be the statement :

and let S(n) be the sum on the L.H.S.
∵ S(1) = \(\frac{1^{3}}{1}=\frac{1}{24}(2+9+13)=1=\frac{1^{3}}{1}\)
∴ p(1) is true
Assume that p(k) is true
(i.e.,) S(k) = \(\frac{1^{3}}{1}+\frac{1^{3}+2^{3}}{1+3}+\ldots+\frac{1^{3}+2^{3}+\ldots \pm k^{3}}{1+3+\ldots+(2 k-1)}\) = \(\frac{k}{24}\) [2k² + 9k + 13]
We show that p(k + 1) is true
(i.e,) we show that


∴ The statement holds for n = k + 1
∴ By the principle of mathematical induction,
p(n) is true for all n
(i.e.,) \(\frac{1^{3}}{1}+\frac{1^{3}+2^{3}}{1+3}+\ldots+\frac{1^{3}+2^{3}+\ldots \ldots+n^{3}}{1+3+\ldots+(2 n-1)}\) = \(\frac{n}{24}\) [2n² + 9n + 13]

Question 15.
1² + (1² + 2²) + (1² + 2² + 3²) + ……. up to n terms = \(\frac{n(n+1)^{2}(n+2)}{12}\)
Solution:
The nth term of the given series is (1² + 2² + 3² + …… + n²)
Let p(n) be the statement:
1² + (1² + 2²) + (1² + 2² + 3²) + ……. + (1² + 2² + …… + n²) = \(\frac{\mathrm{n}(\mathrm{n}+1)^{2}(\mathrm{n}+2)}{12}\)
and the sum on the LH.S. is denoted by S(n).
Since S(1) = 1² = \(\frac{1(1+1)^{2}(1+2)}{12}\) = 1 = 1²
∴ p(1) is true.
Assume that the statement is true for n = k
(i.e.,) S(k) = 1² + (1² + 2²) + ……. + (1² + 2² + ……. + k²)
= \(\frac{k(k+1)^{2}(k+2)}{12}\)
We show that S(k + 1) = \(\frac{(k+1)(k+2)^{2}(k+3)}{12}\)
We observe that


∴ The statement holds for n = k + 1.
∴ By the principle of mathematical induction,
p(n) is true for all n ∈ N.
(i.e.,) 1² + (1² + 2²) + (1² + 2² + 3²) + …….. (1² + 2² + ………. + n²) = \(\frac{n(n+1)^{2}(n+2)}{12}\)

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Functions Solutions Exercise 1(c) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Functions Solutions Exercise 1(c)

I.

Question 1.
Find the domains of the following real-valued functions.
(i) f(x) = \(\frac{1}{\left(x^{2}-1\right)(x+3)}\)
Solution:
f(x) = \(\frac{1}{\left(x^{2}-1\right)(x+3)}\) ∈ R
⇔ (x² – 1) (x + 3) ≠ 0
⇔ (x + 1) (x – 1) (x + 3) ≠ 0
⇔ x ≠ -1, 1, -3
∴ Domain of f is R – {-1, 1, -3}

(ii) f(x) = \(\frac{2 x^{2}-5 x+7}{(x-1)(x-2)(x-3)}\)
⇔ (x – 1) (x – 2) (x – 3) ≠ 0
⇔ x ≠ 1, x ≠ 2, x ≠ 3
∴ Domain of f is R – {1, 2, 3}

(iii) f(x) = \(\frac{1}{\log (2-x)}\)
Solution:
f(x) = \(\frac{1}{\log (2-x)}\)
⇔ log (2 – x) ≠ 0 and 2 – x > 0
⇔ (2 – x) ≠ 1 and 2 > x
⇔ x ≠ 1 and x < 2
x ∈ (-∞, 1) ∪ (1, 2) (or) x ∈ (-∞, 2) – {1}
∴ Domain of f is {(-∞, 2) – {1}}

(iv) f(x) = |x – 3|
Solution:
f(x) = |x – 3| ∈ R
⇔ x ∈ R
∴ The domain of f is R

(v) f(x) = \(\sqrt{4 x-x^{2}}\)
Solution:
f(x) = \(\sqrt{4 x-x^{2}}\) ∈ R
⇔ 4x – x² ≥ 0
⇔ x(4 – x) ≥ 0
⇔ x ∈ [0, 4]
∴ Domain of f is [0, 4]

(vi) f(x) = \(\frac{1}{\sqrt{1-x^{2}}}\)
Solution:
f(x) = \(\frac{1}{\sqrt{1-x^{2}}}\) ∈ R
⇔ 1 – x² > 0
⇔ (1 + x) (1 – x) > 0
⇔ x ∈ (-1, 1)
∴ Domain of f is {x/x ∈ (-1, 1)}

(vii) f(x) = \(\frac{3^{x}}{x+1}\)
Solution:
f(x) = \(\frac{3^{x}}{x+1}\) ∈ R
⇔ 3^x ∈ R, ∀ x ∈ R and x + 1 ≠ 0
⇔ x ≠ -1
∴ Domain of f is R – {-1}

(viii) f(x) = \(\sqrt{x^{2}-25}\)
Solution:
f(x) = \(\sqrt{x^{2}-25}\) ∈ R
⇔ x² – 25 ≥ 0
⇔ (x + 5) (x – 5) ≥ 0
⇔ x ∈ (-∞, -5] ∪ [5, ∞)
⇔ x ∈ R – (-5, 5)
∴ Domain of f is R – (- 5, 5)

(ix) f(x) = \(\sqrt{x-[x]}\)
Solution:
f(x) = \(\sqrt{x-[x]}\) ∈ R
⇔ x – [x] ≥ 0
⇔ x ≥ [x]
⇔ x ∈ R
∴ Domain of f is R.

(x) f(x) = \(\sqrt{[x]-x}\)
Solution:
f(x) = \(\sqrt{[x]-x}\) ∈ R
⇔ [x] – x ≥ 0
⇔ [x] ≥ x
⇔ x ≤ [x]
⇔ x ∈ Z
∴ The domain of f is z (Where z denotes a set of integers)

Question 2.
Find the ranges of the following real-valued functions.
(i) log|4 – x²|
Solution:
Let y = f(x) = log|4 – x²|
f(x) ∈ R
⇔ 4 – x² ≠ 0
⇔ x ≠ ±2
∵ y = log|4 – x²|
⇒ |4 – x²| = e^y
∵ e^y > 0 ∀ y ∈ R
∴ The range of f is R.

(ii) \(\sqrt{[x]-x}\)
Solution:
Let y = f(x) = \(\sqrt{[x]-x}\)
f(x) ∈ R
⇔ [x] – x ≥ 0
⇔ x ≤ [x]
⇔ x ∈ z
∴ Domain of f is z. Then range of f is {0}

(iii) \(\frac{\sin \pi[x]}{1+[x]^{2}}\)
Solution:
Let f(x) = \(\frac{\sin \pi[x]}{1+[x]^{2}}\) ∈ R
⇔ x ∈ R
∴ The domain of f is R
For x ∈ R, [x] is an integer,
sin π[x] = 0, ∀ x ∈ R [∵ sin nπ = 0, ∀ n ∈ z]
∴ Range of f is {0}

(iv) \(\frac{x^{2}-4}{x-2}\)
Solution:
Let y = f(x) = \(\frac{x^{2}-4}{x-2}\) ∈ R
⇔ y = \(\frac{(x+2)(x-2)}{x-2}\)
⇔ x ≠ 2
∴ The domain of f is R – {2}
Then y = x + 2, [∵ x ≠ 2 ⇒ y ≠ 4]
Then its range R – {4}

(v) \(\sqrt{9+x^{2}}\)
Solution:
Let y = f(x) = \(\sqrt{9+x^{2}}\) ∈ R
The domain of f is R
When x = 0, f(0) = √9 = 3
For all values of x ∈ R – {0}, f(x) > 3
∴ The range of f is [3, ∞)

Question 3.
If f and g are real-valued functions defined by f(x) = 2x – 1 and g(x) = x² then find
(i) (3f – 2g)(x)
(ii) (fg) (x)
(iii) \(\left(\frac{\sqrt{f}}{g}\right)(x)\)
(iv) (f + g + 2) (x)
Solution:
(i) (3f – 2g)(x)
f(x) = 2x – 1, g(x) = x²
(3f – 2g) (x) = 3f(x) – 2g(x)
= 3(2x – 1) – 2x²
= -2x² + 6x – 3

(ii) (fg) (x)
= f(x) . g(x)
= (2x – 1) (x²)
= 2x³ – x²

(iii) \(\left(\frac{\sqrt{f}}{g}\right)(x)\)
\(\frac{\sqrt{f(x)}}{g(x)}=\frac{\sqrt{2 x-1}}{x^{2}}\)

(iv) (f + g + 2) (x)
= f(x) + g(x) + 2
= (2x – 1) + x² + 2
= x² + 2x + 1
= (x + 1)²

Question 4.
If f = {(1, 2), (2, -3), (3, -1)} then find
(i) 2f
(ii) 2 + f
(iii) f²
(iv) √f
Solution:
Given f = {(1, 2), (2, -3), (3, -1)}
(i) 2f = {(1, 2 × 2), (2, 2(-3), (3, 2(-1))}
= {(1, 4), (2, -6), (3, -2)}

(ii) 2 + f = {(1, 2 + 2), (2, 2 + (-3)), (3, 2 + (-1)}
= {(1, 4), (2, -1), (3, 1)}

(iii) f² = {(1, 22), (2, (-3)2), (3, (-1)2)}
= {(1, 4), (2, 9), (3, 1)}

(iv) √f = {(1, √2)}
∵ √-3 and √-1 are not real

II.

Question 1.
Find the domains of the following real-valued functions.
(i) f(x) = \(\sqrt{x^{2}-3 x+2}\)
Solution:
f(x) = \(\sqrt{x^{2}-3 x+2}\) ∈ R
⇔ x² – 3x + 2 ≥ 0
⇔ (x- 1) (x – 2) ≥ 0
⇔ x ∈ (-∞, 1 ] ∪ [2, ∞]
∴ The domain of f is R – (1, 2)

(ii) f(x) = log(x² – 4x + 3)
Solution:
f(x) = log(x² – 4x + 3) ∈ R
⇔ x² – 4x + 3 > 0
⇔ (x – 1) (x – 3) > 0
⇔ x ∈ (-∞, 1) ∪ (3, ∞)
∴ Domain of f is R – [1, 3]

(iii) f(x) = \(\frac{\sqrt{2+x}+\sqrt{2-x}}{x}\)
Solution:
f(x) = \(\frac{\sqrt{2+x}+\sqrt{2-x}}{x}\) ∈ R
⇔ 2 + x ≥ 0, 2 – x ≥ 0, x ≠ 0
⇔ x ≥ -2, x ≤ 2, x ≠ 0
⇔ -2 ≤ x ≤ 2, x ≠ 0
⇔ x ∈ [-2, 2] – {0}
Domain of f is [-2, 2] – {0}

(iv) f(x) = \(\frac{1}{\sqrt[3]{(x-2)} \log _{(4-x)} 10}\)
Solution:
f(x) = \(\frac{1}{\sqrt[3]{(x-2)} \log _{(4-x)} 10}\) ∈ R
⇔ 4 – x > 0, 4 – x ≠ 1 and x – 2 ≠ 0
⇔ x < 4, x ≠ 3, x ≠ 2
∴ Domain of f is (-∞, 4) – {2, 3}

(v) f(x) = \(\sqrt{\frac{4-x^{2}}{[x]+2}}\)
Solution:
f(x) = \(\sqrt{\frac{4-x^{2}}{[x]+2}}\) ∈ R
Case (i) 4 – x² ≥ 0 and [x] + 2 > 0 (or) Case (ii) 4 – x² ≤ 0 and [x] + 2 < 0
Case (i): 4 – x² ≥ 0 and [x] + 2 > 0
⇔ (2 – x) (2 + x) ≥ 0 and [x] > -2
⇔ x ∈ [-2, 2] and x ∈ [-1, ∞]
⇔ x ∈ [-1, 2] ……..(1)
Case (ii): 4 – x² ≤ 0 and [x] + 2 < 0
⇔ (2 + x) (2 – x) ≤ 0 and [x] < – 2
⇔ x ∈ (-∞, -2] ∪ [2, ∞] and x ∈ (-∞, -2)
⇔ x ∈ (-∞, -2) ……(2)
from (1) and (2),
Domain of f is (-∞, -2) ∪ [-1, 2]

(vi) f(x) = \(\sqrt{\log _{0.3}\left(x-x^{2}\right)}\)
Solution:
f(x) = \(\sqrt{\log _{0.3}\left(x-x^{2}\right)}\) ∈ R
Then log_0.3(x – x²) ≥ 0
⇒ x – x² ≤ (0.3)⁰
⇒ x – x² ≤ 1
⇒ -x² + x – 1 ≤ 0
⇒ x² – x + 1 ≥ 0
This is true for all x ∈ R ……..(1)
and x – x² ≥ 0
⇒ x² – x ≤ 0
⇒ x(x – 1) ≤ 0
⇒ x ∈ (0, 1) …….(2)
From (1) and (2)
Domain of f is R ^ (0, 1) = (0, 1)
∴ The domain of f is (0, 1)

(vii) f(x) = \(\frac{1}{x+|x|}\)
Solution:
f(x) = \(\frac{1}{x+|x|}\) ∈ R
⇔ x + |x| ≠ 0
⇔ x ∈ (0, ∞)
∵ |x| = x, if x ≥ 0
|x| = -x, if x < 0
∴ The domain of f is (0, ∞)

Question 2.
Prove that the real valued function f(x) = \(\frac{x}{e^{x}-1}+\frac{x}{2}+1\) is an even function on R \ {0}.
Solution:
f(x) ∈ R, e^x – 1 ≠ 0
⇒ e^x ≠ 1
⇒ x ≠ 0

⇒ f(x) is an even function on R – {0}

Question 3.
Find the domain and range of the following functions.
(i) f(x) = \(\frac{\tan \pi[x]}{1+\sin \pi[x]+\left[x^{2}\right]}\)
Solution:
f(x) = \(\frac{\tan \pi[x]}{1+\sin \pi[x]+\left[x^{2}\right]}\) ∈ R
⇔ x ∈ R, since [x] is an integer tan π[x] and sin π[x] each is zero for ∀ x ∈ R and f(x) ∈ R
Domain of f is R
Its range = {0}

(ii) f(x) = \(\frac{x}{2-3 x}\)
Solution:

(iii) f(x) = |x| + |1 + x|
Solution:
f(x) = |x| + |1 + x| ∈ R
⇔ x ∈ R
∴ Domain of f is R
∵ |x| = x, if x ≥ 0
= -x, if x < 0
|1 + x| = 1 + x, if x ≥ -1
= -(1 + x) if x < -1
For x = 0, f(0) = |0| + |1 + 0| = 1
x = 1, f(1) = |1| + |1 + 1| = 1 + 2 = 3
x = 2, f(2) = |2| + |1 + 2| = 2 + 3 = 5
x = -2, f(-2) = |-2| + |1 + (-2)| = 2 + 1 = 3
x = -1, f(-1) = |-1| + |1 +(-1)| = 1 + 0 = 1
∴ The range of f is [1, ∞]

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Functions Solutions Exercise 1(b) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Functions Solutions Exercise 1(b)

I.

Question 1.
If f(x) = e^x and g(x) = log_ex, then show that f o g = g o f and find f^-1 and g^-1.
Solution:
Given f(x) = e^x and g(x) = log_ex
Now (f o g) (x) = f(g(x))
= f(log_ex) [∵ g(x) = \(\log _{e} x\)]
= \(e^{\left(\log _{e} x\right)}\)
= x
∴ (fog) (x) = x ………(1)
and (g o f) (x) = g(f(x))
= g(e^x) [∵ f(x) = e^x]
= log_e (e^x) [∵ g(x) = log_ex]
= x log_e (e)
= x(1)
= x
∴ (g o f) (x) = x …….(2)
From (1) and (2)
f o g = g o f
Given f(x) = e^x
Let y = f(x) = e^x ⇒ x = f^-1(y)
and y = e^x ⇒ x = log_e (y)
∴ f^-1(y) = log_e (y) ⇒ f^-1(x) = log_e (x)
Let y = g(x) = log_e (x)
∵ y = g(x) ⇒ x = g^-1(y)
∵ y = log_e (x) ⇒ x = e^y
∴ g^-1(y) = e^y ⇒ g^-1(x) = e^x
∴ f^-1(x) = log_e (x) and g^-1(x) = e^x

Question 2.
If f(y) = \(\frac{y}{\sqrt{1-y^{2}}}\), g(y) = \(\frac{y}{\sqrt{1+y^{2}}}\) then show that (fog) (y) = y
Solution:
f(y) = \(\frac{y}{\sqrt{1-y^{2}}}\) and g(y) = \(\frac{y}{\sqrt{1+y^{2}}}\)
Now, (fog) (y) = f(g(y))

∴ (fog) (y) = y

Question 3.
If f : R → R, g : R → R are defined by f(x) = 2x² + 3 and g(x) = 3x – 2, then find
(i) (fog)(x)
(ii) (gof) (x)
(iii) (fof) (0)
(iv) go(fof) (3)
Solution:
f : R → R, g : R → R and f(x) = 2x² + 3; g(x) = 3x – 2
(i) (f o g) (x) = f(g(x))
= f(3x – 2) [∵ g(x) = 3x – 2]
= 2(3x- 2)² + 3 [∵ f(x) = 2x² + 3]
= 2(9x² – 12x + 4) + 3
= 18x² – 24x + 8 + 3
= 18x² – 24x + 11

(ii) (gof) (x) = g(f(x))
= g(2x² + 3) [∵ f(x) = 2x² + 3]
= 3(2x² + 3) – 2 [∵ g(x) = 3x – 2]
= 6x² + 9 – 2
= 6x² + 7

(iii) (fof) (0) = f(f(0))
= f(2(0) + 3) [∵ f(x) = 2x² + 3]
= f(3)
= 2(3)² + 3
= 18 + 3
= 21

(iv) g o (f o f) (3)
= g o (f (f(3)))
= g o (f (2(3)² + 3)) [∵ f(x) = 2x² + 3]
= g o (f(21))
= g(f(21))
= g(2(21)² + 3)
= g(885)
= 3(885) – 2 [∵ g(x) = 3x – 2]
= 2653

Question 4.
If f : R → R, g : R → R are defined by f(x) = 3x – 1, g(x) = x² + 1, then find
(i) (f o f) (x² + 1)
(ii) f o g (2)
(iii) g o f (2a – 3)
Solution:
f : R → R, g : R → R and f(x) = 3x – 1 ; g(x) = x² + 1
(i) (f o f) (x² + 1)
= f(f(x² + 1))
= f[3(x² + 1) – 1] [∵ f(x) = 3x – 1]
= f(3x² + 2)
= 3(3x² + 2) – 1
= 9x² + 5

(ii) (f o g) (2)
= f(g(2))
= f(2² + 1) [∵ g(x) = x² + 1]
= f(5)
= 3(5) – 1
= 14 [∵ f(x) = 3x – 1]

(iii) (g o f) (2a – 3)
= g(f(2a – 3))
= g[3(2a – 3) – 1] [∵ f(x) = 3x – 1]
= g(6a – 10)
= (6a – 10)² + 1 [∵ g(x) = x² + 1]
= 36a² – 120a + 100 + 1
= 36a² – 120a + 101

Question 5.
If f(x) = \(\frac{1}{x}\), g(x) = √x for all x ∈ (0, ∞) then find (g o f) (x).
Solution:
f(x) = \(\frac{1}{x}\), g(x) = √x, ∀ x ∈ (0, ∞)
(g o f) (x) = g(f(x))
= g(\(\frac{1}{x}\)) [∵ f(x) = \(\frac{1}{x}\)]
= \(\sqrt{\frac{1}{x}}\)
= \(\frac{1}{\sqrt{x}}\) [∵ g(x) = √x]
∴ (gof) (x) = \(\frac{1}{\sqrt{x}}\)

Question 6.
f(x) = 2x – 1, g(x) = \(\frac{x+1}{2}\) for all x ∈ R, find (g o f) (x).
Solution:
f(x) = 2x – 1, g(x) = \(\frac{x+1}{2}\) ∀ x ∈ R
(g o f) (x) = g(f(x))
= g(2x – 1) [∵ f(x) = 2x – 1]
= \(\frac{(2 x-1)+1}{2}\)
= x [∵ g(x) = \(\frac{x+1}{2}\)]
∴ (g o f) (x) = x

Question 7.
If f(x) = 2, g(x) = x², h(x) = 2x for all x ∈ R, then find (f o (g o h)) (x).
Solution:
f(x) = 2, g(x) = x², h(x) = 2x, ∀ x ∈ R
[f o (g o h) (x)]
= [f o g (h(x))]
= f o g (2x) [∵ h(x) = 2x]
= f[g(2x)]
= f((2x)²) [∵ g(x) = x²]
= f(4x²) = 2 [∵ f(x) = 2]
∴ [f o (g o h) (x)] = 2

Question 8.
Find the inverse of the following functions.
(i) a, b ∈ R, f : R → R defined by f(x) = ax + b, (a ≠ 0).
Solution:
a, b ∈ R, f : R → R and f(x) = ax + b, a ≠ 0
Let y = f(x) = ax + b
⇒ y = f(x)
⇒ x = f^-1(y) ……..(i)
and y = ax + b
⇒ x = \(\frac{y-b}{a}\) ……..(ii)
From (i) and (ii)
f^-1(y) = \(\frac{y-b}{a}\)
⇒ f^-1(x) = \(\frac{x-b}{a}\)

(ii) f : R → (0, ∞) defined by f(x) = 5^x
Solution:
f : R → (0, ∞) and f(x) = 5^x
Let y = f (x) = 5^x
y = f(x) ⇒ x = f^-1(y) ……(i)
and y = 5^x ⇒ log₅ (y) = x ……..(ii)
From (i) and (ii)
f^-1(y) = log₅(y) ⇒ f^-1(x) = log5 (x)

(iii) f : (0, ∞) → R defined by f(x) = log₂ (x).
Solution:
f : (0, ∞) → R and f(x) = log₂ (x)
Let y = f(x) = log₂ (x)
∵ y = f(x) ⇒ x = f^-1(y) ……..(i)
and y = log₂(x) ⇒ x = 2y
From (i) and (ii)
f^-1(y) = 2y ⇒ f^-1(x) = 2x

Question 9.
If f(x) = 1 + x + x² + …… for |x| < 1 then show that f^-1(x) = \(\frac{x-1}{x}\)
Solution:
f(x) = 1 + x + x² + ……..

Question 10.
If f : [1, ∞) ⇒ [1, ∞) defined by f(x) = \(2^{x(x-1)}\) then find f^-1(x).
Solution:

II.

Question 1.
If f(x) = \(\frac{x-1}{x+1}\), x ≠ ±1, then verify (f o f^-1) (x) = x.
Solution:
Given f(x) = \(\frac{x-1}{x+1}\), x ≠ ±1
Let y = f(x) = \(\frac{x-1}{x+1}\)
∵ y = f(x) ⇒ x = f^-1(y) ……(i)
and y = \(\frac{x-1}{x+1}\)

Question 2.
If A = {1, 2, 3}, B = {α, β, γ}, C = {p, q, r} and f : A → B, g : B → C are defined by f = {(1, α), (2, γ), (3, β)}, g = {(α, q), (β, r), (γ, p)}, then show that f and g are bijective functions and (gof)^-1 = f^-1 o g^-1.
Solution:
A = {1, 2, 3}, B = {α, β, γ},
f : A → B and f = {(1, α), (2, γ), (3, β)}
⇒ f(1) = α, f(2) = γ, f(3) = β
∵ Distinct elements of A have distinct f – images in B, f: A → B is an injective function.
Range of f = {α, γ, β} = B(co-domain)
∴ f : A → B is a surjective function.
Hence f : A → B is a bijective function.
B = {α, β, γ}, C = {p, q, r}, g : B → C and g : {(α, q), (β, r), (γ, p)}
⇒ g(α) = q, g(β) = r, g(γ) = p
∴ Distinct elements of B have distinct g – images in C, g : B → C is an injective function.
Range of g = {q, r, p} = C, (co-domain)
∴ g : B → C is a surjective function
Hence g : B → C is a bijective function
Now f = {(1, α), (2, γ), (3, β)}
g = {(α, q), (β, r), (γ, p)}
g o f = {(1, q), (2, p), (3, r)}
∴ (g o f)^-1 = {(q, 1), (r, 3), (p, 2)} ………(1)
g^-1 = {(q, α), (r, β), (p, γ)}
f^-1 = {(α, 1), (γ, 2),(β, 3)}
Now f^-1 o g^-1 = {(q, 1), (r, 3), (p, 2)} …….(2)
From eq’s (1) and (2)
(gof)^-1 = f^-1 o g^-1

Question 3.
If f : R → R, g : R → R defined by f(x) = 3x – 2, g(x) = x² + 1, then find
(i) (g o f^-1) (2)
(ii) (g o f)(x – 1)
Solution:
f : R → R, g : R → R and f(x) = 3x – 2
f is a bijective function ⇒ its inverse exists
Let y = f(x) = 3x – 2
∵ y = f(x) ⇒ x = f^-1(y) …….(i)
and y = 3x – 2
⇒ x = \(\frac{y+2}{3}\) ……..(ii)
From (i) and (ii)
f^-1(y) = \(\frac{y+2}{3}\)
⇒ f^-1(x) = \(\frac{x+2}{3}\)
Now (gof^-1) (2)
= g(f^-1(2))

∴ (g o f^-1) (2) = \(\frac{25}{9}\)

(ii) (g o f) (x -1)
= g(f(x – 1))
= g(3(x – 1) – 2) [∵ f(x) = 3x – 2]
= g(3x – 5)
= (3x – 5)² + 1 [∵ g(x) = x² + 1]
= 9x² – 30x + 26
∴ (g o f) (x – 1) = 9x² – 30x + 26

Question 4.
Let f = {(1, a), (2, c), (4, d), (3, b)} and g^-1 = {(2, a), (4, b), (1, c), (3, d)} then show that (gof)^-1 = f^-1 o g^-1
Solution:
f = {(1, a), (2, c), (4, d), (3, b)}
∴ f^-1 = {(a, 1), (c, 2), (d, 4), (b, 3)}
g^-1 = {(2, a), (4, b), (1, c), (3, d)}
∴ g = {(a, 2), (b, 4), (c, 1), (d, 3)}
(g o f) = {(1, 2), (2, 1), (4, 3), (3, 4)}
∴ (gof)^-1 = {(2, 1), (1, 2), (3, 4), (4, 3)} ……….(1)
f^-1 o g^-1 = {(2, 1), (4, 3), (1, 2), (3, 4)} ……..(2)
From eq’s (1) and (2), we observe (gof)^-1 = f^-1 o g^-1

Question 5.
Let f : R → R, g : R → R be defined by f(x) = 2x – 3, g(x) = x³ + 5 then find (f o g)^-1 (x).
Solution:
f : R → R, g : R → R and f(x) = 2x – 3 and g(x) = x³ + 5
Now (fog) (x) = f(g(x))
= f(x³ + 5) [∵ g(x) = x² + 5]
= 2(x³ + 5) – 3 [∵ f(x) = 2x – 3]
= 2x³ + 7
∴ (f o g) (x) = 2x³ + 7
Let y = (f o g) (x) = 2x³ + 7
∵ y = (fog)(x)
⇒ x = (fog)^-1 (y) …….(1)
and y = 2x³ + 7
⇒ x³ = \(\frac{y-7}{2}\)
⇒ x = \(\left(\frac{y-7}{2}\right)^{\frac{1}{3}}\) …..(2)
From eq’s (1) and (2),
(f o g)^-1 (y) = \(\left(\frac{y-7}{2}\right)^{\frac{1}{3}}\)
∴ (f o g)^-1 (x) = \(\left(\frac{x-7}{2}\right)^{\frac{1}{3}}\)

Question 6.
Let f(x) = x², g(x) = 2^x. Then solve the equation (f o g) (x) = (g o f) (x)
Solution:
Given f(x) = x² and g(x) = 2^x
Now (f o g) (x) = f(g(x))
= f(2^x) [∵ g(x) = 2^x]
= (2^x)²
= 2^2x [∵ f(x) = x²]
∴ (f o g) (x) = 2^2x ……(1)
and (g o f) (x) = g(f(x))
= g(x²) [∵ f(x) = x²]
= \((2)^{x^{2}}\) [∵ g(x) = 2^x]
∴ (g o f) (x) = \((2)^{x^{2}}\)
∵ (f o g) (x) = (g o f) (x)
⇒ 2^2x = \((2)^{x^{2}}\)
⇒ 2^x = x²
⇒ x² – 2x = 0
⇒ x(x – 2) = 0
⇒ x = 0, x = 2
∴ x = 0, 2

Question 7.
If f(x) = \(\frac{x+1}{x-1}\), (x ≠ ±1) then find (fofof) (x) and (fofofof) (x).
Solution:
f(x) = \(\frac{x+1}{x-1}\), (x ≠ ±1)
(i) (fofof) (x) = (fof) [f(x)]
= (fof) \(\left(\frac{x+1}{x-1}\right)\) [∵ f(x) = \(\left(\frac{x+1}{x-1}\right)\)]

(ii) (fofofof) (x) = f[(f o f o f) (x)]
= f [f(x)] {from (1)}

In the above problem if a number of f is even its answer is x and if a number of f is odd its answer is f(x).

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Functions Solutions Exercise 1(a) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Functions Solutions Exercise 1(a)

I.

Question 1.
If the function f is defined by

then find the values of
(i) f(3)
(ii) f(0)
(iii) f(-1.5)
(iv) f(2) + f(-2)
(v) f(-5)
Solution:
(i) f(3)
For x > 1, f(x) = x + 2
∴ f(3) = 3 + 2 = 5

(ii) f(0)
For -1 ≤ x ≤ 1, f(x) = 2
∴ f(0) = 2

(iii) f(-1.5)
For -3 < x < -1, f(x) = x – 1
∴ f(-1.5) = -1.5 – 1 = -2.5

(iv) f(2) + f(-2) For x > 1, f(x) = x + 2
∴ f(2) = 2 + 2 = 4
For -3 < x < -1, f(x) = x – 1
∴ f(-2)= -2 – 1 = -3
f(2) + f(-2) = 4 + (-3) = 1

(v) f(-5) is not defined, since domain of x is {X/X ∈ (-3, ∞)}

Question 2.
If f: R{0}R is defined by f(x) = \(x^{3}-\frac{1}{x^{3}}\); then show that f(x) + \(f\left(\frac{1}{x}\right)\) = 0.
Solution:
Given f(x) = \(x^{3}-\frac{1}{x^{3}}\) ……(i)
Now \(f\left(\frac{1}{x}\right)=\left(\frac{1}{x}\right)^{3}-\frac{1}{\left(\frac{1}{x}\right)^{3}}=\frac{1}{x^{3}}-x^{3}\) ……(2)
Add (1) and (2)
\(f(x)+f\left(\frac{1}{x}\right)=\left(x^{3}-\frac{1}{x^{3}}\right)+\left(\frac{1}{x^{3}}-x^{3}\right)\) = 0
∴ f(x) + \(f\left(\frac{1}{x}\right)\) = 0

Question 3.
If f : R → R is defined by f(x) = \(\frac{1-x^{2}}{1+x^{2}}\), then show that f(tan θ) = cos 2θ.
Solution:
Given f(x) = \(\frac{1-x^{2}}{1+x^{2}}\)

∴ f(tan θ) = cos 2θ

Question 4.
If f : R\{±1} → R is defined by f(x) = \(\log \left|\frac{1+x}{1-x}\right|\), then show that \(f\left(\frac{2 x}{1+x^{2}}\right)\) = 2f(x)
Solution:
f : R\{±1} → R and f(x) = \(\log \left|\frac{1+x}{1-x}\right|\)

∴ \(f\left(\frac{2 x}{1+x^{2}}\right)\) = 2f(x)

Question 5.
If A = {-2, -1, 0, 1, 2} and f : A → B is a surjection defined by f(x) = x² + x + 1, then find B.
Solution:
A = {-2, -1, 0, 1, 2} and f : A → B, f(x) = x² + x + 1
f : A → B is a surjection
f(-2) = (-2)² + (-2) + 1
= 4 – 2 + 1
= 3
f(-1) = (-1)² + (-1) + 1
= 1 – 1 + 1
= 1
f(0) = 0² + 0 + 1
= 0 + 0 + 1
= 1
f(1) = 1² + 1 + 1
= 1 + 1 + 1
= 3
f(2) = 2² + 2 + 1
= 4 + 2 + 1
= 7
∴ B = f(A) = {3, 1, 7}

Question 6.
If A = {1, 2, 3, 4} and f : A → R is a function defined by f(x) = \(\frac{x^{2}-x+1}{x+1}\), then find the range of f.
Solution:
A= {1, 2, 3, 4}

∴ Range of f = f(A) = \(\left\{\frac{1}{2}, 1, \frac{7}{4}, \frac{13}{5}\right\}\)

Question 7.
If f(x + y) = f(xy) ∀ x, y ∈ R then prove that f is a constant function.
Solution:
Given f(x + y) = f(x y), x, y ∈ R
take x = y = 0
⇒ f(0) = f(0) ………(1)
Let x = 1, y = 0
⇒ f(1) = f(0) ……..(2)
Let x = 1, y = 1
⇒ f(2) = f(1) ………(3)
from (1), (2), (3)
f(0) = f(1) = f(2)
⇒ f(0) = f(2)
Similarly f(3) = f(0)
f(4) = f(0)
and so on
f(n) = f(0)
∴ f is a constant function

II.

Question 1.
If A = {x | -1 ≤ x ≤ 1}, f(x) = x², g(x) = x³, which of the following are surjections?
(i) f : A → A
(ii) g : A → A
Solution:
(i) ∵ A = {x | -1 ≤ x ≤ 1} and f(x) = x²
This implies f(x) is a function from A to A
(i.e.,) f : A → A
Now let y ∈ A
If f(x) = y then x² = y
x = √y
So, if y = -1 then x = √-1 ∉ A
∴ f : A → A is not a surjection.

(ii) ∵ A = {x | -1 ≤ x ≤ 1} and g(x) = x³
⇒ g : A → A
Let y ∈ A. Then g(x) = y
⇒ x³ = y
⇒ x = \((y)^{1 / 3}\) ∈ A
So if y = -1 then x = -1 ∈ A
y = 0, then x = 0 ∈ A
y = 1, then x = 1 ∈ A
∴ g : A → A is a surjections.

Question 2.
Which of the following are injections or surjections or bijections? Justify your answers.
(i) f : R → R defined by f(x) = \(\frac{2 x+1}{3}\)
Solution:
f(x) = \(\frac{2 x+1}{3}\)
Let x₁, x₂ ∈ R
∵ f(x₁) = f(x₂)
⇒ \(\frac{2 x_{1}+1}{3}=\frac{2 x_{2}+1}{3}\)
⇒ 2x₁ + 1 = 2x₂ + 1
⇒ 2x₁ = 2x₂
⇒ x₁ = x₂
∵ f(x₁) = f(x₂) ⇒ x₁ = x₂, ∀ x₁, x₂ ∈ R
So f(x) = \(\frac{2 x+1}{3}\), f : R → R is an injection
If y ∈ R (co-domain) then y = \(\frac{2 x+1}{3}\)
⇒ x = \(\frac{3 y-1}{2}\)
Then f(x) = \(\frac{2 x+1}{3}=\frac{2\left(\frac{3 y-1}{2}\right)+1}{3}=y\)
∴ f is a surjection
∴ f : R → R defined by f(x) = \(\frac{2 x+1}{3}\) is a bijection

(ii) f : R → (0, ∞) defined by f(x) = 2x
Solution:
Let x₁, x₂ ∈ R
∵ f(x₁) = f(x₂)
⇒ \(2^{x_{1}}=2^{x_{2}}\)
⇒ x₁ = x₂
∴ f(x₁) = f(x₂) ⇒ x₁ = x₂ ∀ x₁, x₂ ∈ R
∴ f(x) = 2x, f : R → (0, ∞) is injection
If y ∈ (0, ∞) and y = 2x ⇒ x = log₂ (y)
Then f(x) = 2x
= \(2^{\log _{2}(y)}\)
= y
∴ f is a surjection
Hence f is a bijection.

(iii) f : (0, ∞) → R defined by f(x) = log_ex
Solution:
Let x₁, x₂ e (0, ∞)
f(x₁) = f(x₂)
⇒ \(\log _{e}\left(x_{1}\right)=\log _{e}\left(x_{2}\right)\)
⇒ x₁ = x₂
∵ f(x₁) = f(x₂)
⇒ x₁ = x₂ ∀ x₁, x₂ ∈ (0, ∞)
∴ f(x) is injection.
Let y ∈ R.
y = log_ex ⇒ x = e^y
Then f(x) = log_ex
= log_e(e^y)
= y . log_ee
= y(1)
= y
∴ f is a surjection.
∴ f is a bijection.

(iv) f : [0, ∞) → [0, ∞) defined by f(x) = x².
Solution:
Let x₁, x₂ ∈ [0, ∞) (i.e.,) domain of f.
Now f(x₁) = f(x₂)
⇒ \(x_{1}^{2}=x_{2}^{2}\)
⇒ x₁ = x₂
∵ x₁, x₂ ≥ 0
∴ f(x) = x², f : {0, ∞) → {0, ∞) is injection
Let y ∈ (0, ∞), co-domain of f
Let y = x² ⇒ x = √y, ∵ y ≥ 0
Then f(x) = x²
= \((\sqrt{y})^{2}\)
= y
∴ f is surjection.
Hence f is a bijection.

(v) f : R → [0, ∞) defined by f(x) = x².
Solution:
Let x₁, x₂ ∈ R.
f(x₁) = f(x₂)
⇒ \(x_{1}^{2}=x_{2}^{2}\)
⇒ x₁ = ±x₂, ∵ x₁, x₂ ∈ R
Hence f is not injection
Let y ∈ [0, ∞)
y = x²
⇒ x = ±√y, where y ∈ [0, ∞)
Then f(x) = x²
= \((\sqrt{y})^{2}\)
= y
∴ f is surjection
Hence f is not a bijection

(vi) f : R → R defined by f(x) = x².
Solution:
Let x₁, x₂ ∈ R, (domain of f)
∴ f(x₁) = f(x₂)
⇒ \(x_{1}^{2}=x_{2}^{2}\)
⇒ x₁ = ±x₂, ∵ x₁, x₂ ∈ R
∴ f(x) is not injection
For elements that belong to (-∞, 0) codomain of f has no pre-image in f.
∴ f is not a surjection
Hence f is neither injection nor surjection.

Question 3.
Is g = {(1, 1) (2, 3) (3, 5) (4, 7)} is a function from A = {1, 2, 3, 4} to B = {1, 3, 5, 7}. If this is given by the formula g(x) = ax + b, then find a and b.
Solution:
A = {1, 2, 3, 4}; B = {1, 3, 5, 7}
g : {(1, 1), (2, 3), (3, 5), (4, 7)}
∵ g(1) = 1, g(2) = 3, g(3) = 5, g(4) = 7
So for each element a ∈ A, there exists a unique b ∈ B such (a, b) ∈ g
∴ g : A → B is a function
Given g(x) = ax + b, ∀ x ∈ A
g(1) = (a) + b = 1
⇒ a + b = 1 ……..(1)
g(2) = 2a + b = 3
⇒ 2a + b = 3 …….(2)
Solve (1) and (2)
a = 2, b = -1

Question 4.
If the function f : R → R defined by f(x) = \(\frac{3^{x}+3^{-x}}{2}\), then show that f(x + y) + f(x – y) = 2f(x) f(y).
Solution:
f : R → R and f(x) = \(\frac{3^{x}+3^{-x}}{2}\)

∴ f(x + y) + f(x – y) = 2 f(x).f(y)

Question 5.
If the function f : R → R defined by f(x) = \(\frac{4^{x}}{4^{x}+2}\), then show that f(1 – x) = 1 – f(x) and hence reduce the value of \(f\left(\frac{1}{4}\right)+2 f\left(\frac{1}{2}\right)+f\left(\frac{3}{4}\right)\)
Solution:


∴ f(1 – x) = 1 – f(x)

Question 6.
If the function f : {-1, 1} → {0, 2), defined by f(x) = ax + b is a surjection, then find a and b.
Solution:
f : {-1, 1} → {0, 2} and f(x) = ax + b is a surjection
Given f(-1) = 0 and f(1) = 2 (or) f(-1) = 2, f(1) = 0
Case (i):
f(-1) = 0 and f(1) = 2
a(-1) + b = 0 ⇒ -a + b = 0 ……..(1)
a(1) + b = 2 ⇒ a + b = 2 ……(2)
Solve eq’s (1) and (2), we get a = 1, b = 1
Case (ii):
f(-1) = 2 and f(1) = 0
a(-1) + b = 2 ⇒ -a + b = 2 ……(3)
a(1) + b = 0 ⇒ a + b = 0 ……….(4)
Solve eq’s (3) and (4), we get a = -1, b = 1
Hence a = ±1 and b = 1

Question 7.
If f(x) = cos (log x), then show that \(f\left(\frac{1}{x}\right) \cdot f\left(\frac{1}{y}\right)-\frac{1}{2}\left[f\left(\frac{x}{y}\right)+f(x y)\right]=0\)
Solution:
Given f(x) = cos(log x)
\(f\left(\frac{1}{x}\right)=\cos \left(\log \left(\frac{1}{x}\right)\right)\)
= cos(log 1 – log x)
= cos(-log x)
= cos (log x) (∵ log 1 = 0)
Similarly
\(f\left(\frac{1}{y}\right)\) = cos (log y)
\(f\left(\frac{x}{y}\right)=\cos \log \left(\frac{x}{y}\right)\)
= cos (log x – log y)
and f(x y) = cos log (x y) = cos (log x + log y)
\(f\left(\frac{x}{y}\right)\) + f(x y) = cos (log x – log y) + cos (log x + log y)
= 2 cos (log x) cos (log y)
[∵ cos (A – B) + cos (A + B) = 2 cos A . cos B]
LHS = \(f\left(\frac{1}{x}\right) \cdot f\left(\frac{1}{y}\right)-\frac{1}{2}\left[f\left(\frac{x}{y}\right)+f(x y)\right]\)
= cos (log x) cos (log y) – \(\frac{1}{2}\) [2 cos (log x) cos (log y)]
= 0

Inter 1st Year Maths 1A Formulas PDF: Here we have created a list of Telangana & Andhra Pradesh BIEAP TS AP Intermediate Inter 1st Year Maths 1A Formulas PDF Download just for you. To solve mathematical problems easily, students should learn and remember the basic formulas based on certain fundamentals such as algebra, arithmetic, and geometry.

Get a unique way of solving the maths problem, which will make you learn how the equation came into existence. This is the better way of memorizing and applying the Intermediate 1st Year Maths 1A Formulas PDF. Math formulas are expressions that have been created after several decades of research that help to solve questions quickly.

Students can also go through Intermediate 1st Year Maths 1A Textbook Solutions and Inter 1st Year Maths 1A Important Questions for exam preparation.

Intermediate 1st Year Maths 1A Formulas PDF Download

We present you with Inter 1st Year Maths 1A Formulas PDF for your reference to solve all important mathematical operations and questions. Also, each formula here is given with solved examples.

1. Inter 1st Year Maths 1A Functions Formulas
2. Inter 1st Year Maths 1A Mathematical Induction Formulas
3. Inter 1st Year Maths 1A Matrices Formulas
4. Inter 1st Year Maths 1A Addition of Vectors Formulas
5. Inter 1st Year Maths 1A Products of Vectors Formulas
6. Inter 1st Year Maths 1A Trigonometric Ratios up to Transformations Formulas
7. Inter 1st Year Maths 1A Trigonometric Equations Formulas
8. Inter 1st Year Maths 1A Inverse Trigonometric Functions Formulas
9. Inter 1st Year Maths 1A Hyperbolic Functions Formulas
10. Inter 1st Year Maths 1A Properties of Triangles Formulas

Here students will find Intermediate 1st Year Maths 1A Formulas for each and every topic and also get an idea of how that equation was developed. Thus, you will not have to memorize formulas, as you understand the concept behind them. Use these Inter 1st Year Maths 1A Formulas to solve problems creatively and you will automatically see an improvement in your mathematical skills.

Jr Inter Maths 1A Important Questions: Here we have created a list of Telangana & Andhra Pradesh BIEAP TS AP Intermediate Jr Inter 1st Year Maths 1A Important Questions Chapter Wise with Answers Solutions Pdf 2022-2023 Download just for you. Those who are preparing for Inter exams should practice Inter Maths 1A Important Questions and do so will clear their doubts instantly. These Inter 1st Year Maths 1A Important Questions Chapterwise Pdf enhances your conceptual knowledge and prepares you to solve different types of questions in the exam.

Students must practice these Intermediate Maths 1A Important Questions to boost their preparation for the Maths paper. These Jr Inter Maths 1A Important Questions with Answers are prepared as per the latest exam pattern. Each of these chapters contains a set of solved questions and additional questions for practice.

Students can also go through Inter 1st Year Maths 1A Formulas to understand and remember the concepts easily. Students can also read Intermediate 1st Year Maths 1A Textbook Solutions for exam preparation.

Intermediate Maths 1A Important Questions | Maths 1A Important Questions Chapter Wise with Solutions Pdf 2022

To access the Jr Inter 1st Year Maths 1A Important Questions Chapter Wise with Solutions Pdf 2022, click on the links below.

AP Inter 1st Year Maths 1A Important Questions in English Medium

Jr Inter Maths 1A Important Questions with Answers

1. Inter 1st Year Maths 1A Functions Important Questions
2. Inter 1st Year Maths 1A Mathematical Induction Important Questions
3. Inter 1st Year Maths 1A Matrices Important Questions
4. Inter 1st Year Maths 1A Addition of Vectors Important Questions
5. Inter 1st Year Maths 1A Products of Vectors Important Questions
6. Inter 1st Year Maths 1A Trigonometric Ratios up to Transformations Important Questions
7. Inter 1st Year Maths 1A Trigonometric Equations Important Questions
8. Inter 1st Year Maths 1A Inverse Trigonometric Functions Important Questions
9. Inter 1st Year Maths 1A Hyperbolic Functions Important Questions
10. Inter 1st Year Maths 1A Properties of Triangles Important Questions

AP Inter 1st Year Maths 1A Important Questions in Telugu Medium

• Chapter 1 ప్రమేయాలు Important Questions
• Chapter 2 గణితానుగమనం Important Questions
• Chapter 3 మాత్రికలు Important Questions
• Chapter 4 సదిశల సంకలనం Important Questions
• Chapter 5 సదిశల గుణనం Important Questions
• Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Important Questions
• Chapter 7 త్రికోణమితీయ సమీకరణాలు Important Questions
• Chapter 8 విలోమ త్రికోణమితీయ ప్రమేయాలు Important Questions
• Chapter 9 అతిపరావలయ ప్రమేయాలు Important Questions
• Chapter 10 త్రిభుజ ధర్మాలు Important Questions

The questions given in the Intermediate Maths 1A Important Questions are designed and laid out chronologically and as per the syllabus. Practice daily these Intermediate Jr Inter 1st Year Maths 1A Important Questions Chapter Wise with Answers Solutions Pdf 2022-2023 Download to build a better understanding of the concepts for the Mathematics subject.

Inter 1st Year Maths 1B Formulas PDF: Here we have created a list of Telangana & Andhra Pradesh BIEAP TS AP Intermediate Inter 1st Year Maths 1B Formulas PDF Download just for you. To solve mathematical problems easily, students should learn and remember the basic formulas based on certain fundamentals such as algebra, arithmetic, and geometry.

Get a unique way of solving the maths problem, which will make you learn how the equation came into existence. This is the better way of memorizing and applying the Intermediate 1st Year Maths 1B Formulas PDF. Math formulas are expressions that have been created after several decades of research that help to solve questions quickly.

Students can also go through Intermediate 1st Year Maths 1B Textbook Solutions and Inter 1st Year Maths 1B Important Questions for exam preparation.

Intermediate 1st Year Maths 1B Formulas PDF Download

We present you with Inter 1st Year Maths 1B Formulas PDF for your reference to solve all important mathematical operations and questions. Also, each formula here is given with solved examples.

1. Inter 1st Year Maths 1B Locus Formulas
2. Inter 1st Year Maths 1B Transformation of Axes Formulas
3. Inter 1st Year Maths 1B The Straight Line Formulas
4. Inter 1st Year Maths 1B Pair of Straight Lines Formulas
5. Inter 1st Year Maths 1B Three Dimensional Coordinates Formulas
6. Inter 1st Year Maths 1B Direction Cosines and Direction Ratios Formulas
7. Inter 1st Year Maths 1B The Plane Formulas
8. Inter 1st Year Maths 1B Limits and Continuity Formulas
9. Inter 1st Year Maths 1B Differentiation Formulas
10. Inter 1st Year Maths 1B Applications of Derivatives Formulas

Here students will find Intermediate 1st Year Maths 1B Formulas for each and every topic and also get an idea of how that equation was developed. Thus, you will not have to memorize formulas, as you understand the concept behind them. Use these Inter 1st Year Maths 1B Formulas to solve problems creatively and you will automatically see an improvement in your mathematical skills.

Jr Inter Maths 1B Important Questions: Here we have created a list of Telangana & Andhra Pradesh BIEAP TS AP Intermediate Jr Inter 1st Year Maths 1B Important Questions Chapter Wise with Answers Solutions Pdf 2022-2023 Download just for you. Those who are preparing for Inter exams should practice Inter Maths 1B Important Questions and do so will clear their doubts instantly. These Inter 1st Year Maths 1B Important Questions Chapterwise Pdf enhances your conceptual knowledge and prepares you to solve different types of questions in the exam.

Students must practice these Intermediate Maths 1B Important Questions to boost their preparation for the Maths paper. These Jr Inter Maths 1B Important Questions with Answers are prepared as per the latest exam pattern. Each of these chapters contains a set of solved questions and additional questions for practice.

Students can also go through Inter 1st Year Maths 1B Formulas to understand and remember the concepts easily. Students can also read Intermediate 1st Year Maths 1B Textbook Solutions for exam preparation.

Intermediate Maths 1B Important Questions | Maths 1B Important Questions Chapter Wise with Solutions Pdf 2022

To access the Jr Inter 1st Year Maths 1B Important Questions Chapter Wise with Solutions Pdf 2022, click on the links below.

AP Inter 1st Year Maths 1B Important Questions in English Medium

Jr Inter Maths 1B Important Questions with Answers

1. Inter 1st Year Maths 1B Locus Important Questions
2. Inter 1st Year Maths 1B Transformation of Axes Important Questions
3. Inter 1st Year Maths 1B The Straight Line Important Questions
4. Inter 1st Year Maths 1B Pair of Straight Lines Important Questions
5. Inter 1st Year Maths 1B Three Dimensional Coordinates Important Questions
6. Inter 1st Year Maths 1B Direction Cosines and Direction Ratios Important Questions
7. Inter 1st Year Maths 1B The Plane Important Questions
8. Inter 1st Year Maths 1B Limits and Continuity Important Questions
9. Inter 1st Year Maths 1B Differentiation Important Questions
10. Inter 1st Year Maths 1B Applications of Derivatives Important Questions

AP Inter 1st Year Maths 1B Important Questions in Telugu Medium

• Chapter 1 బిందుపథం Important Questions
• Chapter 2 అక్ష పరివర్తనం Important Questions
• Chapter 3 సరళరేఖ Important Questions
• Chapter 4 సరళరేఖాయుగ్మాలు Important Questions
• Chapter 5 త్రిపరిమాణ నిరూపకాలు Important Questions
• Chapter 6 దిక్ కొసైన్లు, దిక్ సంఖ్యలు Important Questions
• Chapter 7 సమతలం Important Questions
• Chapter 8 అవధులు, అవిచ్ఛిన్నత Important Questions
• Chapter 9 అవకలనం Important Questions
• Chapter 10 అవకలజాల అనువర్తనాలు Important Questions

The questions given in the Intermediate Maths 1B Important Questions are designed and laid out chronologically and as per the syllabus. Practice daily these Intermediate Jr Inter 1st Year Maths 1B Important Questions Chapter Wise with Answers Solutions Pdf 2022-2023 Download to build a better understanding of the concepts for the Mathematics subject.