Students get through Maths 1A Important Questions Inter 1st Year Maths 1A Matrices Important Questions which are most likely to be asked in the exam.
Intermediate 1st Year Maths 1A Matrices Important Questions
Question 1.
If A = \(\left[\begin{array}{ccc}
2 & 3 & -1 \\
7 & 8 & 5
\end{array}\right]\) and B = \(\left[\begin{array}{ccc}
1 & 0 & 1 \\
2 & -4 & -1
\end{array}\right]\) then find A + B.
Solution:
The matrices A and B both are of the same order 2 × 3. Hence A + B is defined. Now

Question 2.
If \(\left[\begin{array}{ccc}
x-1 & 2 & y-5 \\
z & 0 & 2 \\
1 & -1 & 1+a
\end{array}\right]\) = \(\left[\begin{array}{ccc}
1-x & 2 & -y \\
2 & 0 & 2 \\
1 & -1 & 1
\end{array}\right]\) then find the values of x, y, z and a.
Solution:
From the equality of matrices
x – 1 = 1 – x ⇒ 2x = 2 ⇒ x = 1
y – 5 = -y ⇒ 2y = 5 ⇒ y = \(\frac{5}{2}\) ⇒ z = 2
z = 2
1 + a = 1 ⇒ a = 1 – 1 ⇒ a = 0
![]()
Question 3.
Find the trace of A if A = \(\left[\begin{array}{ccc}
1 & 2 & -\frac{1}{2} \\
0 & -1 & 2 \\
-\frac{1}{2} & 2 & 1
\end{array}\right]\) (Mar. ’04)
Solution:
The elements of the principal diagonal of A are 1,-1, 1.
Hence the trace of A is 1 + (-1) + 1 =1
Question 4.
If A = \(\left[\begin{array}{cc}
4 & -5 \\
-2 & 3
\end{array}\right]\) then find -5A.
Solution:
-5A = -5\(\left[\begin{array}{cc}
4 & -5 \\
-2 & 3
\end{array}\right]\) = \(\left[\begin{array}{cc}
-20 & 25 \\
10 & -15
\end{array}\right]\)
Question 5.
Find the additive inverse of A, where
A = \(\left[\begin{array}{ccc}
i & 0 & 1 \\
0 & -i & 2 \\
-1 & 1 & 5
\end{array}\right]\)
Solution:
The additive inverse of A is -A = (-1)A
∴ Additive inverse of A
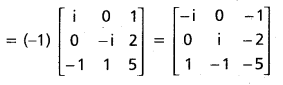
Question 6.
If A = \(\left[\begin{array}{ccc}
2 & 3 & 1 \\
6 & -1 & 5
\end{array}\right]\) and B = \(\left[\begin{array}{ccc}
1 & 2 & -1 \\
0 & -1 & 3
\end{array}\right]\) then find the matrix X such that A + B – X = 0. What is the order of the matrix X ?
Solution:
Given, A + B – X = 0 ⇒ X = A + B
= \(\left[\begin{array}{ccc}
2 & 3 & 1 \\
6 & -1 & 5
\end{array}\right]\) + \(\left[\begin{array}{ccc}
1 & 2 & -1 \\
0 & -1 & 3
\end{array}\right]\)
∴ X = \(\left[\begin{array}{ccc}
3 & 5 & 0 \\
6 & -2 & 8
\end{array}\right]\) ∴ Order of X is 2 × 3.
![]()
Question 7.
If A = \(\left[\begin{array}{lll}
0 & 1 & 2 \\
2 & 3 & 4 \\
4 & 5 & 6
\end{array}\right]\) and B = \(\left[\begin{array}{ccc}
1 & -2 & 0 \\
0 & 1 & -1 \\
-1 & 0 & 3
\end{array}\right]\) then find A – B and 4B – 3A.
Solution:

Question 8.
If A = \(\left[\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right]\), B = \(\left[\begin{array}{ll}
3 & 8 \\
7 & 2
\end{array}\right]\) and 2X + A = B then find ‘X’. (A.P.) (Mar. ’15, ’11)
Solution:
2X + A = B ⇒ 2X = B – A

Question 9.
Two factories I and II produce three varieties of pens namely. Gel, Ball and Ink pens. The sale in rupees of these varieties of pens by both the factories in the month of September and October in a year are given by the following matrices A and B.
September sales (in Rupees)
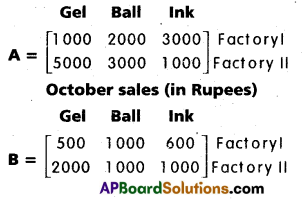
i) Find the combined sales in September and October for each factory in each variety.
ii) Find the decrease in sales from September to October.
Solution:
i) Combined sales in September and October for each factory in each variety is given by

ii) Decrease in sales from September to October is given by

Question 10.
Construct a 3 × 2 matrix whose elements are defined by aij = \(\frac{1}{2}|\mathbf{i}-3 \mathbf{j}|\). (T.S) (Mar. ’15)
Solution:
In general 3 × 2 matrix is given by

Question 11.
If A = \(\left[\begin{array}{lll}
0 & 1 & 2 \\
1 & 2 & 3 \\
2 & 3 & 4
\end{array}\right]\) and B = \(\left[\begin{array}{cc}
1 & -2 \\
-1 & 0 \\
2 & -1
\end{array}\right]\) then find AB and BA.
Solution:
The number of columns of A = 3 = the number of rows of B.
Hence AB is defined and
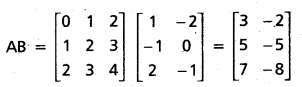
Since the number of columns of B = 2 ≠ 3 = the number of rows of A.
∴ BA is not defined.
![]()
Question 12.
If A = \(\left[\begin{array}{ccc}
1 & -2 & 3 \\
2 & 3 & -1 \\
-3 & 1 & 2
\end{array}\right]\) and B = \(\left[\begin{array}{lll}
1 & 0 & 2 \\
0 & 1 & 2 \\
1 & 2 & 0
\end{array}\right]\) then examine whether A and B commute with respect to multiplication of matrices.
Solution:
Both A and B are square matrices of order 3. Hence both AB and BA are define and are matrices of order 3.

which shows that AB ≠ BA
Therefore A and B do not commute with respect to multiplication of matrices.
Question 13.
If A = \(\left[\begin{array}{cc}
\mathbf{i} & 0 \\
\mathbf{0} & -\mathbf{i}
\end{array}\right]\) then show that A2 = -I where i2 = -1.
Solution:
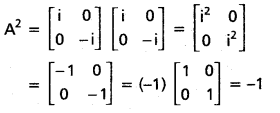
Question 14.
If A = \(\left[\begin{array}{cc}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta
\end{array}\right]\) then show that A2 – 4A – 5I = 0 then show that for all the positive integers n.
An = \(\left[\begin{array}{cc}
\cos n \theta & \sin n \theta \\
-\sin n \theta & \cos n \theta
\end{array}\right]\)
Solution:
We solve this problem by using the principle of mathematical induction consider the statement P(n) : An = \(\left[\begin{array}{cc}
\cos n \theta & -\sin n \theta \\
-\sin n \theta & \cos n \theta
\end{array}\right]\)
Since A = \(\left[\begin{array}{cc}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{array}\right]\)
⇒ A1 = \(\left[\begin{array}{cc}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta
\end{array}\right]\), P(n) is true for n = 1
Suppose that the given statement P(n) is true for n = k, k ≥ 1.
∴ Then Ak = \(\left[\begin{array}{cc}
\cos k \theta & \sin k \theta \\
-\sin k \theta & \cos k \theta
\end{array}\right]\) .
Consider Ak+1 = Ak.A
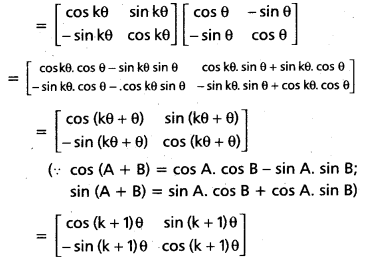
∴ Therefore P (n) is true for n = k + 1.
Hence, by mathematical induction, P(n) is true for all positive integral values of n.
![]()
Question 15.
If A = \(\left[\begin{array}{lll}
1 & 2 & 2 \\
2 & 1 & 2 \\
2 & 2 & 1
\end{array}\right]\) then show that A2 – 4A – 5I = 0. (A.P.) (Mar. ’16)
Solution:
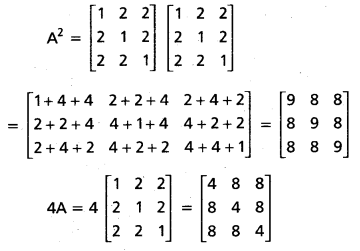

Question 16.
If A = \(\left[\begin{array}{ccc}
-2 & 1 & 0 \\
3 & 4 & -5
\end{array}\right]\) and B = \(\left[\begin{array}{cc}
1 & 2 \\
4 & 3 \\
-1 & 5
\end{array}\right]\) then find A + B.
Solution:
A + B = \(\left[\begin{array}{ccc}
-2 & 1 & 0 \\
3 & 4 & -5
\end{array}\right]\) + \(\left[\begin{array}{ccc}
1 & 4 & -1 \\
2 & 3 & 5
\end{array}\right]\)
= \(\left[\begin{array}{ccc}
-1 & 5 & -1 \\
5 & 7 & 0
\end{array}\right]\)
Question 17.
If A = \(\left[\begin{array}{cc}
-1 & 2 \\
0 & 1
\end{array}\right]\) then find AA’. Do A and A’ commute with respect to multiplication of matrices ?
Solution:

Since AA’ ≠ A’A, A and A’ do not commute with respect to multiplication of matrices.
Question 18.
If A = \(\left[\begin{array}{ccc}
0 & 4 & -2 \\
-4 & 0 & 8 \\
2 & -8 & x
\end{array}\right]\) is a skew symmetric matrix, find the value of x.
Solution:
A is a skew symmetric matrix and x is an element of the diagonal. Hence x = 0.
![]()
Question 19.
For any n × n matrix A, prove that A can be uniquely expressed as a sum of a symmetric matrix and a skew symmetric matrix.
Solution:
For A square matrix of order n, A + A’ is symmetric and A – A’ is a skew symmetric matrix and
A = \(\frac{1}{2}\)(A + A’) + \(\frac{1}{2}\)(A – A’)
To prove uniqueness, let B be a symmetric matrix and C be a skew-symmetric matrix, such that
A = B + C
Then A’ = (B + C)’ = B’ + C’
= B + (-C) = B – C
and hence B = \(\frac{1}{2}\)(A + A’)
C = \(\frac{1}{2}\)(A – A’)
Question 20.
Show that
 (Mar. ’05)
(Mar. ’05)
Solution:

Question 21.
Without expanding the determinant show that (AP) (Mar. ’15)
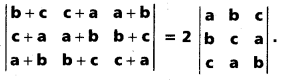
Solution:

Question 22.
Show that \(\left|\begin{array}{lll}
1 & a^{2} & a^{3} \\
1 & b^{2} & b^{3} \\
1 & c^{2} & c^{3}
\end{array}\right|\) = (a – b)(b – c)(c – a)(ab + bc + ca)
Solution:

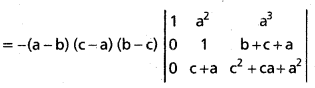
= -(a – b)(b – c)(c – a) [(c2 + ca + a2) – (b + c + a) (c + a)]
= -(a – b)(b – c)(c – a)[c2 + ca + a2 – b(c + a) — (c + a)2]
= -(a – b)(b – c)(c – a)[c2 + ca + a2 – bc – ab – c2 – 2ca – a2]
= -(a – b) (b – c) (c – a) [-ab – bc – ca]
= (a – b)(b – c)(c – a) (ab + bc + ca)
∴ \(\left|\begin{array}{lll}
1 & a^{2} & a^{3} \\
1 & b^{2} & b^{3} \\
1 & c^{2} & c^{3}
\end{array}\right|\) = (a – b)(b – c)(c – a)(ab + bc + ca)
Question 23.
If ω is complex (non real) cube root of 1 then show that \(\left|\begin{array}{ccc}
1 & \omega & \omega^{2} \\
\omega & \omega^{2} & 1 \\
\omega^{2} & 1 & \omega
\end{array}\right|\) = 0 (Mar. ’14, ’11)
Solution:

![]()
Question 24.
Show that
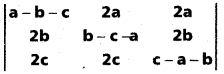
= (a + b + c)3. (May. ’11)
Solution:
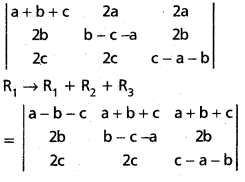

Question 25.
Show that the determinant of a skew-symmetric matrix of order three is always zero.
Solution:
Let us consider a skew-symmetric matrix of order 3 × 3, say

Question 26.
Find the value of x if
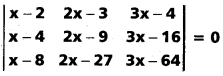
(T.S) (Mar. ’15
Mar. ’06)
Solution:
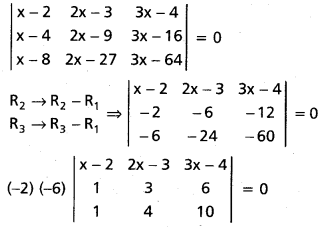
⇒ (x – 2)(30 – 24) – (2x – 3)(10 – 6) + (3x – 4)(4 – 3) = 0
⇒ 6x – 12 – 8x + 12 + 3x – 4 = 0
x – 4 = 0 ∴ x = 4
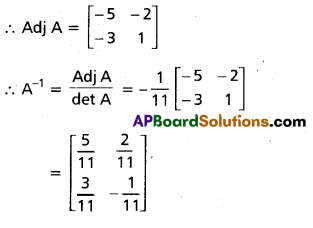
Question 27.
Find the adjoint and the inverse of the matrix A = \(\left[\begin{array}{cc}
1 & 2 \\
3 & -5
\end{array}\right]\).
Solution:
|A| = \(\left|\begin{array}{cc}
1 & 2 \\
3 & -5
\end{array}\right|\) = -5 – 6 = -11 ≠ 0
Hence A is invertible.
The cofactor matrix of A = \(\left[\begin{array}{cc}
-5 & -3 \\
-2 & 1
\end{array}\right]\)
Question 28.
Find the adjoint and the inverse of the matrix A = \(\left[\begin{array}{lll}
1 & 3 & 3 \\
1 & 4 & 3 \\
1 & 3 & 4
\end{array}\right]\)
Solution:
|A| = \(\left[\begin{array}{lll}
1 & 3 & 3 \\
1 & 4 & 3 \\
1 & 3 & 4
\end{array}\right]\)
= 1(16 – 9) – 3(4 – 3) + 3(3 – 4)
= 7 – 3 – 3
= 1 ≠ 0
∴ A is invertible.
The factor of A is B = \(\left[\begin{array}{ccc}
7 & -1 & -1 \\
-3 & 1 & 0 \\
-3 & 0 & 1
\end{array}\right]\)
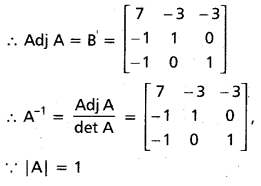
![]()
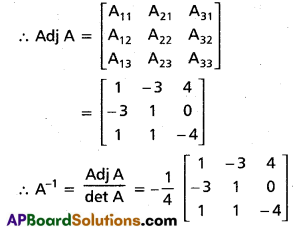
Question 29.
Show that A = \(\left[\begin{array}{lll}
1 & 2 & 1 \\
3 & 2 & 3 \\
1 & 1 & 2
\end{array}\right]\) is non singular and find A-1
Solution:
Let A = \(\left[\begin{array}{lll}
1 & 2 & 1 \\
3 & 2 & 3 \\
1 & 1 & 2
\end{array}\right]\)
det A = 1(4 – 3) – 2(6 – 3) + 1(3 – 2)
= 1 – 6 + 1 – 4
The cofactors of elements of A are
A11 = +(4 – 3) = 1,
A12 = -(6 – 3) = -3,
A13 = +(3 – 2) = 1,
A21 = -(4 – 1) = -3,
A22 = +(2 -1) = 1,
A23 = -(1 – 2) = 1,
A31 = + (6 – 2) = 4,
A32 = -(3 – 3) = 0,
A33 = +(2 – 6) = -4
Question 30.
Find the rank of A = \(\left[\begin{array}{lll}
0 & 1 & 2 \\
1 & 2 & 3 \\
3 & 2 & 1
\end{array}\right]\) using elementary transformations.
Solution:

The last matrix is singular and \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\) is a non singular submatrix of it. Hence its rank is 2.
∴ Rank (A) = 2.
Question 31.
Find the rank A = \(\left[\begin{array}{cccc}
1 & 2 & 0 & -1 \\
3 & 4 & 1 & 2 \\
-2 & 3 & 2 & 5
\end{array}\right]\) using elementary transformations.
Solution:

Question 32.
Apply the test of rank to examine whether the following equations are consistent.
2x – y + 3z = 8, —x + 2y + z = 4, 3x + y – 4z = 0 and, ¡f consistent, find the complete solution.
Solution:
The augmented matrix is


Hence rank (A) = rank [AD] = 3
The system has a unique solution.
We write the equivalent system of the equations from (F) : i.e.,
-x + 2y + z = 4
3y + 5z = 16
-38z = -76
∴ z = 2, y = 2, x = 2 is the solution.
![]()
Question 33.
Show that the following system of equations is consistent and solve it completely x + y + z = 3, 2x + 2y – z = 3, x + y – z = 1.
Solution:
Let A = \(\left[\begin{array}{ccc}
1 & 1 & 1 \\
2 & 2 & -1 \\
1 & 1 & -1
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and D = \(\left[\begin{array}{l}
3 \\
3 \\
1
\end{array}\right]\)
Then the given equations can be written as
AX = D
Augmented Matrix
[AD] = \(\left[\begin{array}{cccc}
1 & 1 & 1 & 3 \\
2 & 2 & -1 & 3 \\
1 & 1 & -1 & 1
\end{array}\right]\)
Applying R2 → R2 – 2R1, R3 → R3 – R1,
~ \(\left[\begin{array}{cccc}
1 & 1 & 1 & 3 \\
0 & 0 & -3 & -3 \\
0 & 0 & -2 & -2
\end{array}\right]\)
Applying R3 → 3R3 – 2R2
~ \(\left[\begin{array}{cccc}
1 & 1 & 1 & 3 \\
0 & 0 & -3 & -3 \\
0 & 0 & 0 & 0
\end{array}\right]\)
Clearly all the submatrices of order 3 × 3 of the above matrix are singular.
Hence rank of A ≠ 3, and rank of [AD] ≠ 3
Now consider the submatrix \(\left[\begin{array}{cc}
1 & 1 \\
0 & -3
\end{array}\right]\) of both
A and AD is non-singular.
Hence Rank (A) = 2 = Rank [AD]
∴ The system of equations is consistent and has infinitely many solutions.
From the above [AD] matrix
x + y + z = 3
-3z = -3 ⇒ z = 1
and x + y = 2
Hence x = k, y = 2 – k, z = 1, k ∈ R is a solution set.
Question 34.
Solve the following simultaneous linear equations by using ‘Cramers rule.
3x + 4y + 5z = 18
2x – y + 8z = 13
5x – 2y + 7z = 20
Solution:
Let A = \(\left[\begin{array}{ccc}
3 & 4 & 5 \\
2 & -1 & 8 \\
5 & -2 & 7
\end{array}\right]\) ; X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\), D = \(\left[\begin{array}{l}
18 \\
13 \\
20
\end{array}\right]\)
i.e., AX = D
Δ = det A = \(\left|\begin{array}{ccc}
3 & 4 & 5 \\
2 & -1 & 8 \\
5 & -2 & 7
\end{array}\right|\)
= 3(-7 + 16) – 4(14 – 40) + 5(-4 + 5)
= 27 + 104 + 5
= 136 ≠ 0

Hence by Cramer’s rule
x = \(\frac{\Delta_{1}}{\Delta}\) = \(\frac{408}{136}\) = 3
y = \(\frac{\Delta_{2}}{\Delta}\) = \(\frac{136}{136}\) = 1
z = \(\frac{\Delta_{3}}{\Delta}\) = \(\frac{136}{136}\) = 1
∴ The solution of the given system of equation is x = 3, y = z = 1.
![]()
Question 35.
Solve 3x + 4y + 5z = 18; 2x – y + 8z = 13 and 5x – 2y + 7z = 20 by using ‘Matrix inversion method’. (A.P) (Mar. ‘15, ’08)
Solution:
Let A = \(\left[\begin{array}{ccc}
3 & 4 & 5 \\
2 & -1 & 8 \\
5 & -2 & 7
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\), B = \(\left[\begin{array}{l}
18 \\
13 \\
20
\end{array}\right]\)
Given equations can be written as AX = B
By matrix inversion method X = A-1B is the solution.
det A = 3(-7 + 16) – 4(14 – 40) + 5(-4 + 5)
= 27 + 104 + 5
= 136
The cofactors of elements of A are
A11 = +(-7 + 16) = 9,
A12 = -(-14 – 40) = 26,
A13 = +(-4 + 5) = 1,
A21 = -(28 + 10) = -38,
A22 = +(21 – 25) = -4,
A23 = -(-6 – 20) = 26,
A31 = +(32 + 5) = 37,
A32 = -(24 – 10) = -14,
A33 = (-3 – 8) = -11

∴ x = 3, y = 1, z = 1 is the solution.
Question 36.
Solve the following equations by Gauss-Jordan method.
3x + 4y + 5z = 18,
2x – y + 8z = 13,
5x – 2y + 7z = 20.
Solution:
The augmented matrix is

Hence the solution is x = 3, y = 1, z = 1
Question 37.
Solve the following system of equations by Gauss-Jordan method,
x + y + z = 3,
2x + 2y – z = 3,
x + y – z = 1.
Solution:
The matrix equation is AX = D, where
A = \(\left[\begin{array}{ccc}
1 & 1 & 1 \\
2 & 2 & -1 \\
1 & 1 & -1
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\), D = \(\left[\begin{array}{l}
3 \\
3 \\
1
\end{array}\right]\)
The augmented matrix is
[AD] = \(\left[\begin{array}{cccc}
1 & 1 & 1 & 3 \\
2 & 2 & -1 & 3 \\
1 & 1 & -1 & 1
\end{array}\right]\)
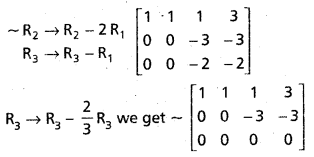
Hence the following is the system of equations equivalent to the given system of equation: x + y + z = 3, -3z = -3
Hence z = 1, x + y = 2
∴ The solution set is
x = k, y = 2 – k, z = 1 where k ∈ R.
Question 38.
By using Gauss-Jordan method, show that the following system has no solution 2x + 4y – z = 0, x + 2y + 2z = 5,
3x + 6y – 7z = 2.
Solution:

Hence the given system of equations is equivalent to the following system of equations 2x + 4y – z = 0, 5z = 10 ⇒ z = 2 and 0(x) + 0(y) + 0(z) = 130.
Clearly no x, y, z satisfy the last equation.
∴ Given system of equations has no solution.
Question 39.
Find the non-trivial solutions, If any, for the following system of equations
2x + 5y + 6z = 0, x – 3y + 8z = 0, 3x + y -4z = 0.
Solution:
The coefficient matrix A = \(\left[\begin{array}{ccc}
2 & 5 & 6 \\
1 & -3 & -8 \\
3 & 1 & -4
\end{array}\right]\)
On interchanging R1 and R2, we get
A ~ \(\left[\begin{array}{ccc}
1 & -3 & 8 \\
2 & 5 & 6 \\
3 & 1 & -4
\end{array}\right]\)
R2 → R2 – 2R1, R3 → R3 – 3R1 we get

det A = 0 as R2 and R3 are identical. Clearly rank (A) = 2, as the sub-matrix
\(\left[\begin{array}{cc}
1 & -3 \\
0 & 1
\end{array}\right]\) is non-singular.
Hence the system has non-trivial solution. The following system of equations is equivalent to the given system of equations
x – 3y – 8z = 0
y + 2z = 0
On giving an arbitrary value k to z, we obtain the solution set is ‘
x = 2k, y = -2k, z = k, k ∈ R, for k ≠ 0.
We obtain non-trivial solutions.
![]()
Question 40.
Find whether the following system of linear homogeneous equations has a non-trivial solution. (T.S) (Mar. ’16)
x – y + z = 0,
x + 2y – z = 0,
2x + y + 3z = 0
Solution:
The coefficient matrix is \(\left[\begin{array}{ccc}
1 & -1 & 1 \\
1 & 2 & -1 \\
2 & 1 & 3
\end{array}\right]\)
Its determinant is 9 ≠ 0.
Hence the system has the trivial solution
x = y = z = 0 only.
Question 41.
Theorem : Matrix multiplication is associative. i.e., If conformability is assured for the matrices A, B and C, then
(AB)C = A(BC). (July ‘01, Inst. ’93, Oct.’83)
Solution:
Proof : Let A = (aij)m × n, B = (bjk)n × p’
C = (Ckl)p × q
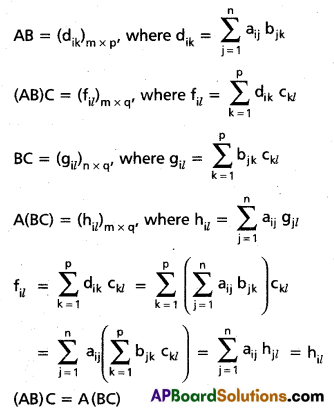
Question 42.
Theorem : Matrix multiplication is distri-butive over matrix addition i.e., If con-formability is assured for the matrices A, B and C, then. (Oct. ’99, inst. ’98)
i) A(B + C) = AB + AC
ii) (B + C)A = BA + CA
Proof:

Similarly we cna prove that
(B + C)A = BA + CA.
Question 43.
Theorem : If A is any matrix, then (AT)T = A. (Nov. ’80)
Solution:
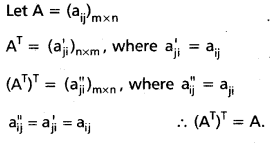
Question 44.
Theorem: If A and B are two matrices of same type, then (A + B)T = AT + BT. (July ‘01)
Proof:

Question 45.
Theorem: If A and B are two matrices for which conformability for multiplication is assured, then (AB)T = BTAT.
Solution:
Proof:
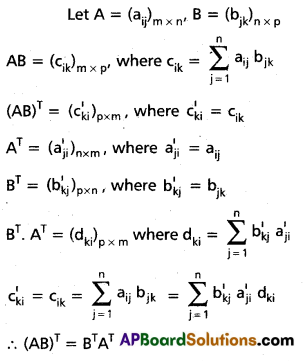
![]()
Question 46.
Theorem : If A and B are two invertible matrices of same type then AB is also invertible and (AB)-1 = B-1A-1.
Solution:
Proof:
A is invertible matrix ⇒ A-1 exists and AA-1 = A-1A = I
B is an invertible matrix ⇒ B-1 exists and
BB-1 = B-1B = I
Now (AB)(B-1A-1) = A(BB-1) A-1
= AIA-1 = AA-1 = 1
(B-1A-1)(AB) = B-1(A-1A)B = B-1IB
= B-1B = I
∴ (AB) (B-1A-1) = (B-1A-1) (AB) = I
∴ AB is invertible and (AB)-1 = B-1A-1.
Question 47.
Theorem : If A is an invertible matrix then A’ is also invertible and (AT)-1 = (A-1). (Nov. ’98)
Solution:
Proof : A is an invertible matrix ⇒ A-1 exists
and AA-1 = A-1A = I
(AA-1)’ = (A-1A)’ = I’
⇒ (A-1)’A’ = A’. (A-1) = I .
⇒ By def. (A’)-1 = (A-1)’.
Question 48.
Theorem: If A \(\left[\begin{array}{lll}
a_{1} & b_{1} & c_{1} \\
a_{2} & b_{2} & c_{2} \\
a_{3} & b_{3} & c_{3}
\end{array}\right]\) is a non-singular matrix then A is invertible and
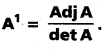 .
.
Proof:
Let A = \(\left[\begin{array}{lll}
a_{1} & b_{1} & c_{1} \\
a_{2} & b_{2} & c_{2} \\
a_{3} & b_{3} & c_{3}
\end{array}\right]\) be a non-singular matrix.
∴ det A ≠ 0
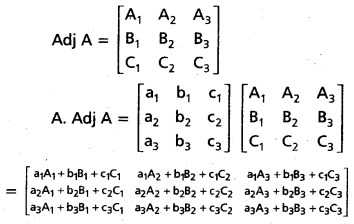

Question 49.
A certain bookshop has 10 dozen chemistry books, 8 dozen physics books, 10 dozen economics books. Their selling prices are Rs. 80, Rs. 60 and Rs. 40 each respectively. Using matrix algebra, find the total value of the books in the shop.
Solution:
Number of books
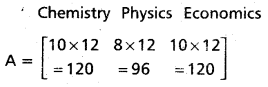
Selling price (in rupees)
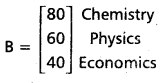
Total value of the books in the shop.

= [120 × 80 + 96 × 60 + 120 × 40]
= [9600 + 5760 + 4800]
= [20160] (in rupees)