AP State Syllabus AP Board 8th Class Maths Solutions Chapter 2 Linear Equations in One Variable Ex 2.2 Textbook Questions and Answers.
AP State Syllabus 8th Class Maths Solutions 2nd Lesson Linear Equations in One Variable Exercise 2.2
![]()
Question 1.
Find ‘x’ in the following figures?
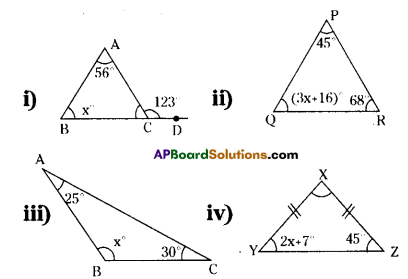
Solution:
1) In a triangle the exterior angle is equal to the sum of its opposite interior angles.
∴ ∠ACD = ∠B + ∠A
⇒ 123°= x + 56°
⇒ x = 123°- 56° = 67°
∴ x = 67°
ii) Sum of three angles of a triangle = 180°
∠P + ∠Q +∠R = 180°
⇒ 45° + 3x + 16°+ 68° = 180°
⇒ 3x + 129° = 180°
3x = 180 – 129 = 51
∴ x = \(\frac{51}{3}\)
∴ x = 17°
![]()
iii) ∠A + ∠B + ∠C = 180°
⇒ 25° + x + 30° = 180°
x + 55°= 180°
x = 180 – 55 = 125°
∴ x = 125°
iv) In ΔXYZ, \(\overline{\mathrm{XY}}=\overline{\mathrm{XZ}}\) then ∠Y = ∠Z
∴ 2x + 7° = 45°
⇒ 2x = 45 – 7
⇒ 2x = 38
⇒ x = \(\frac{38}{2}\)
∴ x = 19°
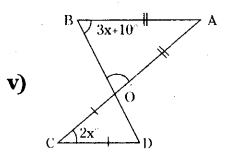
v) From ΔBOA
\(\overline{\mathrm{AB}}=\overline{\mathrm{OA}} \) ⇒ ∠B = ∠O = 3x + 10° ………(1)
From ΔCOD
\(\overline{\mathrm{OC}}=\overline{\mathrm{CD}} \) ⇒ ∠O = ∠D …………………(2)
[∵ The angles which are opposite to the equal sides are equal].
from (1) & (2)
∠BOA = ∠COD
[∵ Vertically opposite angles are equal.]
But ∠COD = 90 – x
(∵ 2x + ∠O + ∠D = 180
⇒ 2x + ∠O + ∠O = 180 (∵∠O = ∠D)
⇒ 2∠O = 180 – 2x
∠O = \(\frac{180-2 x}{2}\) = 90 – x]
∴ From ∠BOA = ∠COD
⇒ 3x + 10 = 90 – x
⇒ 3x + x = 90 – 10
⇒ 4x = 80
∴ x = 20°
![]()
Question 2.
The difference between two numbers is 8. if 2 is added to the bigger number the result will be three times the smaller number. Find the numbers.
Solution:
Let the bigger number be x.
The difference between two numbers 8
∴ Smaller number = x – 8
If 2 is added to the bigger number the result will be three times the smaller
number.
So x + 2 = 3(x – 8)
x + 2 = 3x – 24
x – 3x = -24 – 2
– 2x = -26
∴ x = \(\frac{26}{2}\) = 13
∴ Bigger number = 13
Smaller number = 13 – 8 = 5
Question 3.
What are those two numbers whose sum is 58 and difference is 28’?
Solution:
Let the bigger number be ‘x’.
The sum of two numbers = 58
∴ Smaller number = 58 – x
The difference of two numbers = 28
∴ x – (58 – x) = 28
x – 58 + x = 28
2x = 28 + 58 = 86
∴ x = \(\frac{86}{2}\) = 43
∴ Bigger number or one number = 43
Smaller number or second number = 58 – 43 = 15
![]()
Question 4.
The sum of two consecutive odd numbers is 56. Find the numbers.
Solution:
Let the two consecutive odd numbers
be 2x 1, 2x + 3 say.
Sum of the odd numbers
=(2x + 1) + (2x + 3) = 56
= 4x + 4 = 56
⇒ 4x = 56 – 4 = 52
x = \(\frac{52}{4}\) = 13
∴ x = 13
∴ 2x + 1 = 2 × 13 + 1
= 26 + 1 = 27
2x + 3 = 2 × 13 + 3
= 26 + 3 = 29
∴ The required two consecutive odd numbers be 27, 29.
![]()
Question 5.
The sum of three consecutive multiples of 7 is 777. Find these multiples.
(Hint: Three consecutive multiples of 7 are ‘x’, ‘x+ 7’, ‘x+ 14’)
Solution:
Let the three consecutive multiples of 7 be x, x + 7, x + 14 say.
According to the sum,
The sum of three consecutive multiples of 7 is 777.
⇒ x + (x + 7) + (x + 14)= 777
⇒ 3x + 21 = 777
⇒ 3x = 777 – 21 = 756
x = \(\frac { 756 }{ 3 }\) = 252
x+ 7 = 252 + 7 = 259
x + 14 252 + 14 = 266
∴ The required three consecutive multiples of 7 are 252, 259, 266
Question 6.
A man walks 10 km, then travels a certain distance by train and then by bus as far as twice by the train. 1f the whole journey is of 70km, how far did he travel by train?
Solution:
The distance travelled by walk = 10 km
Let the distance travelled by train = x km say.
The distance travelled by bus
= 2 × x = 2x km
∴ 10 + x + 2x = 70
⇒ 3x = 70 – 10
⇒ 3x = 60
⇒ x = \(\frac { 60 }{ 3 }\) = 20
⇒ x = 20
∴ The distance travelled by train = 20 km.
![]()
Question 7.
Vinay bought a pizza and cut it into three pieces. When the weighed the first piece he found that it was 7g lighter than the second piece and 4g.heavier than the third piece. If the whole pizza weighed 300g. How much did each of the three pieces weigh?

(Hint: weight of normal piece be ‘x’ then weight of largest piece is ‘x+ 7’, weight of the smallest piece is ‘x-4’)
Solution:
If pizza is cut into three pieces.
Let the weight of first piece he ‘x’ gm say.
Weight of the second piece = (x + 7) gm
Weight of the third piece = (x – 4) gm
According to the sum
∴ x + (x + 7) + (x – 4) = 300
⇒ 3x + 3 = 300
⇒ 3x = 300 – 3 = 297
⇒ x = \(\frac { 297 }{ 3 }\) = 99
∴ x= 99
x + 7= 99 + 7 =106
x – 4 = 99 – 4 = 95
∴ The required 3 pieces of pizza weighs 95 gm. 99 gm, 106 gm.
![]()
Question 8.
The distance around a rectangular field is 400 meters.The length of the field is 26 meters more than the breadth. Calculate the length and breadth of the field’?
Solution:
Let the breadth of a rectangular field = x m
Length = (x + 26) m.
Perimeter of a rectangular field
= 2(l + b) = 400
l + b = 200
x + 26 + x = 200
2x = 200 – 26 = 174
x = \(\frac { 174 }{ 2 }\)
∴ x = 87
∴ The length = x +26
= 87 + 26
= 113 m
Breadth = x = 87 m.
![]()
Question 9.
The length of a rectangular field is 8 meters less than twice its breadth. If the perimeter of the rectangular field is 56 meters, find its length and breadth’?
Solution:
Let the breadth of a rectangular field = xm.
Length = 2 × x – 8 = (2x – 8) m.
Perimeter of a field = 56 m.
∴ 2(l + b) = 56
l + b = 28
2x – 8 + x = 28
3x = 28 + 8 = 36
x = \(\frac { 36 }{ 3 }\)
∴ x= 12
∴ Breadth = 12 m
Length = 2x – 8
= 2 × 12 – 8
= 24 – 8 = 16m.
Question 10.
Two equal sides of a triangle are each 5 meters less than twice the third side. if the perimeter of the triangle is 55 meters, find the length of its sides’?
Solution:
A triangle in which the length of the third side = x m. say.
The length of remaining two equal sides = 2 × x – 5 = (2x – 5) m.
Perimeter of a triangle = 55 m.
∴ (2x – 5) + (2x -5) + x = 55
⇒ 5x – 10 = 55
⇒ 5x = 65
⇒ x = \(\frac { 65 }{ 5 }\)
∴ x = 13m
2x – 5 = 2 × 13 – 5 = 26 – 5 = 21m.
∴ The lengths of three sides of a triangle are 13, 21, 21. (in m.)
![]()
Question 11.
Two complementary angles differ by 12°, find the angles’?
Solution:
Let one angle in two complementary angles be x.
Sum of the two complementary angles = 90°
∴ Second angle = 90° – x
Here two complementary angles differ by 12°.
∴ x – (90°- x) = 12°
x – 90° + x = 12°
2x = 12° + 90° = 102°
∴ \(\frac{102^{\circ}}{2}\) = 51°
one angle = 51°
Second angle 90° – 51° = 39°
![]()
Question 12.
The ages of Rahul and Laxmi arc in the ratio 5:7. Four years later, the sum of their ages will
be 56 years. What are their present ages’?
Solution:
The ratio of ages of Rahul and Lakshmi = 5:7
Let their ages be 5x, 7x say.
After 4 years Rahuls agt. = 5x + 4
After 4 years Lakshmis age = 7x + 4
According to the sum,
After 4 years the sum of their ages = 56
⇒ (5x + 4) + (7x + 4) = 56
⇒ 12x + 8 = 56
⇒ 12x = 56 – 8 = 48
⇒ x= \(\frac { 48 }{ 12 }\) = 4
∴ x = 4
∴ Rahuls present age
= 5x = 5 × 4 = 20 years
∴ Lakshmi’s present age
= 7x = 7 × 4 = 28 years
![]()
Question 13.
There are 180 multiple choice questions in a test. A candidate gets 4 marks for every correct answer, and for every un-attempted or wrongly answered questions one mark is deducted from the total score of correct answers. If a candidate scored 450 marks in the
test how many questions did he answer correctly ?
Solution:
Number of questions attempted for correct answers = x say
umber of questions attempted for wrong answers = 180 – x
4 marks are awarded for every correct answer.
Then numl)er of marks ohtained for correct answers 4 × x = 4x
1 mark is deducted for every wrong answer.
∴ Number of marks deducted for wrong answers
=(180 – x) × 1 = 180 – x
According to the sum.
4x – (180 – x) = 450
⇒ 4x – 180 + x = 450
⇒ 5x = 450 + 180
⇒ 5x = 630
x = \(\frac { 630 }{ 5 }\)
∴ x = 126
∴ Number of questions attempted for correct answers = 126
Question 14.
A sum of ₹ 500 is in the form of denominations of ₹ 5 and ₹ 10. If the total number of notes is 90 find the number of notes of each denomination.
(Hint: let the number of 5 rupee notes be ‘x’, then number of 10 rupee notes = 90 – x)
Solution:
Number of ₹ 5 notes = x say.
Number of ₹ 10 notes = 90 – x
5x + 10(90 – x) = 500
5x + 900 – 10x = 500
– 5x = 500 – 900 = – 400
x = \(\frac { -400 }{ -5 }\)
∴ x = 80
∴ Number of ₹ 5 notes = 80
Number of ₹ 10 notes
= 90 – x = 90 – 80 = 10
![]()
Question 15.
A person spent ₹ 564 in buying geese and ducks,if each goose cost ₹ 7 and each duck ₹ 3 and if the total number of birds bought was 108, how many of each type did he buy?

Solution:
Let the number of pens be x.
The total number of things = 108
∴ The number of pencils = 108 – x
Thecostofpens of x = ₹7 × x = ₹ 7x
The cost of pencils of (108- x)
= ₹3(108 – x) = ₹ (324 – 3x)
Total amount to t)uy eflS and Pencils = ₹564
∴ 7x + (324 – 3x) 5M
7x + 324 – 3x = 564
4x = 564 – 324 = 240
∴ x = \(\frac { 240 }{ 4 }\) = 60
The number of pens = 60
The number of pencils = 108 – 60 = 48
![]()
Question 16.
The perimeter ofa school volleyball court is 177 ft and the length is twice the width. What are the dimensions of the volleyball court’?

Solution:
Breadth of a volleyball court = x feet say.
∴ Its length = 2 × x = 2 x feet.
The perimeter of a court = 177 feet.
⇒ 2(l + b) = 177
⇒ 2(2x + x) = 177
⇒ 2 x 3x = 177
⇒ 6x = 177
⇒ x =\(\frac { 177 }{ 6 }\)
∴ x = 29.5
∴ The breadth of a volleyball court = 29.5 ft
The length of a volleyball court = 2x = 2 × 29.5 = 59ft
Question 17.
The sum of the page numbers on the facing pages of a book is 373. What are the page numbers?
(Hint :Let the page numbers of open pages are x and (x + 1)

Solution:
Number of first page of a opened book x
Number ol second page = x + 1
∴ The surï of the numbers of two pages = 373
⇒ x + (x + 1) = 373
⇒ 2x + 1 = 373
2x = 372
⇒ x = 186
∴x + 1 = 186 + 1 = 187
∴ Numbers of two c(nlsecutive pages = 186, 187