Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Functions Solutions Exercise 1(a) will help students to clear their doubts quickly.
Intermediate 1st Year Maths 1A Functions Solutions Exercise 1(a)
I.
Question 1.
If the function f is defined by
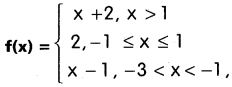
then find the values of
(i) f(3)
(ii) f(0)
(iii) f(-1.5)
(iv) f(2) + f(-2)
(v) f(-5)
Solution:
(i) f(3)
For x > 1, f(x) = x + 2
∴ f(3) = 3 + 2 = 5
(ii) f(0)
For -1 ≤ x ≤ 1, f(x) = 2
∴ f(0) = 2
(iii) f(-1.5)
For -3 < x < -1, f(x) = x – 1
∴ f(-1.5) = -1.5 – 1 = -2.5
(iv) f(2) + f(-2) For x > 1, f(x) = x + 2
∴ f(2) = 2 + 2 = 4
For -3 < x < -1, f(x) = x – 1
∴ f(-2)= -2 – 1 = -3
f(2) + f(-2) = 4 + (-3) = 1
(v) f(-5) is not defined, since domain of x is {X/X ∈ (-3, ∞)}
![]()
Question 2.
If f: R{0}R is defined by f(x) = \(x^{3}-\frac{1}{x^{3}}\); then show that f(x) + \(f\left(\frac{1}{x}\right)\) = 0.
Solution:
Given f(x) = \(x^{3}-\frac{1}{x^{3}}\) ……(i)
Now \(f\left(\frac{1}{x}\right)=\left(\frac{1}{x}\right)^{3}-\frac{1}{\left(\frac{1}{x}\right)^{3}}=\frac{1}{x^{3}}-x^{3}\) ……(2)
Add (1) and (2)
\(f(x)+f\left(\frac{1}{x}\right)=\left(x^{3}-\frac{1}{x^{3}}\right)+\left(\frac{1}{x^{3}}-x^{3}\right)\) = 0
∴ f(x) + \(f\left(\frac{1}{x}\right)\) = 0
Question 3.
If f : R → R is defined by f(x) = \(\frac{1-x^{2}}{1+x^{2}}\), then show that f(tan θ) = cos 2θ.
Solution:
Given f(x) = \(\frac{1-x^{2}}{1+x^{2}}\)
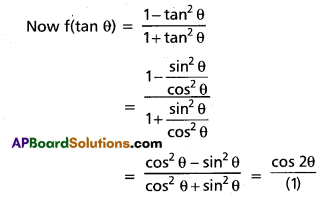
∴ f(tan θ) = cos 2θ
Question 4.
If f : R\{±1} → R is defined by f(x) = \(\log \left|\frac{1+x}{1-x}\right|\), then show that \(f\left(\frac{2 x}{1+x^{2}}\right)\) = 2f(x)
Solution:
f : R\{±1} → R and f(x) = \(\log \left|\frac{1+x}{1-x}\right|\)

∴ \(f\left(\frac{2 x}{1+x^{2}}\right)\) = 2f(x)
![]()
Question 5.
If A = {-2, -1, 0, 1, 2} and f : A → B is a surjection defined by f(x) = x2 + x + 1, then find B.
Solution:
A = {-2, -1, 0, 1, 2} and f : A → B, f(x) = x2 + x + 1
f : A → B is a surjection
f(-2) = (-2)2 + (-2) + 1
= 4 – 2 + 1
= 3
f(-1) = (-1)2 + (-1) + 1
= 1 – 1 + 1
= 1
f(0) = 02 + 0 + 1
= 0 + 0 + 1
= 1
f(1) = 12 + 1 + 1
= 1 + 1 + 1
= 3
f(2) = 22 + 2 + 1
= 4 + 2 + 1
= 7
∴ B = f(A) = {3, 1, 7}
Question 6.
If A = {1, 2, 3, 4} and f : A → R is a function defined by f(x) = \(\frac{x^{2}-x+1}{x+1}\), then find the range of f.
Solution:
A= {1, 2, 3, 4}

∴ Range of f = f(A) = \(\left\{\frac{1}{2}, 1, \frac{7}{4}, \frac{13}{5}\right\}\)
Question 7.
If f(x + y) = f(xy) ∀ x, y ∈ R then prove that f is a constant function.
Solution:
Given f(x + y) = f(x y), x, y ∈ R
take x = y = 0
⇒ f(0) = f(0) ………(1)
Let x = 1, y = 0
⇒ f(1) = f(0) ……..(2)
Let x = 1, y = 1
⇒ f(2) = f(1) ………(3)
from (1), (2), (3)
f(0) = f(1) = f(2)
⇒ f(0) = f(2)
Similarly f(3) = f(0)
f(4) = f(0)
and so on
f(n) = f(0)
∴ f is a constant function
![]()
II.
Question 1.
If A = {x | -1 ≤ x ≤ 1}, f(x) = x2, g(x) = x3, which of the following are surjections?
(i) f : A → A
(ii) g : A → A
Solution:
(i) ∵ A = {x | -1 ≤ x ≤ 1} and f(x) = x2
This implies f(x) is a function from A to A
(i.e.,) f : A → A
Now let y ∈ A
If f(x) = y then x2 = y
x = √y
So, if y = -1 then x = √-1 ∉ A
∴ f : A → A is not a surjection.
(ii) ∵ A = {x | -1 ≤ x ≤ 1} and g(x) = x3
⇒ g : A → A
Let y ∈ A. Then g(x) = y
⇒ x3 = y
⇒ x = \((y)^{1 / 3}\) ∈ A
So if y = -1 then x = -1 ∈ A
y = 0, then x = 0 ∈ A
y = 1, then x = 1 ∈ A
∴ g : A → A is a surjections.
Question 2.
Which of the following are injections or surjections or bijections? Justify your answers.
(i) f : R → R defined by f(x) = \(\frac{2 x+1}{3}\)
Solution:
f(x) = \(\frac{2 x+1}{3}\)
Let x1, x2 ∈ R
∵ f(x1) = f(x2)
⇒ \(\frac{2 x_{1}+1}{3}=\frac{2 x_{2}+1}{3}\)
⇒ 2x1 + 1 = 2x2 + 1
⇒ 2x1 = 2x2
⇒ x1 = x2
∵ f(x1) = f(x2) ⇒ x1 = x2, ∀ x1, x2 ∈ R
So f(x) = \(\frac{2 x+1}{3}\), f : R → R is an injection
If y ∈ R (co-domain) then y = \(\frac{2 x+1}{3}\)
⇒ x = \(\frac{3 y-1}{2}\)
Then f(x) = \(\frac{2 x+1}{3}=\frac{2\left(\frac{3 y-1}{2}\right)+1}{3}=y\)
∴ f is a surjection
∴ f : R → R defined by f(x) = \(\frac{2 x+1}{3}\) is a bijection
(ii) f : R → (0, ∞) defined by f(x) = 2x
Solution:
Let x1, x2 ∈ R
∵ f(x1) = f(x2)
⇒ \(2^{x_{1}}=2^{x_{2}}\)
⇒ x1 = x2
∴ f(x1) = f(x2) ⇒ x1 = x2 ∀ x1, x2 ∈ R
∴ f(x) = 2x, f : R → (0, ∞) is injection
If y ∈ (0, ∞) and y = 2x ⇒ x = log2 (y)
Then f(x) = 2x
= \(2^{\log _{2}(y)}\)
= y
∴ f is a surjection
Hence f is a bijection.
![]()
(iii) f : (0, ∞) → R defined by f(x) = logex
Solution:
Let x1, x2 e (0, ∞)
f(x1) = f(x2)
⇒ \(\log _{e}\left(x_{1}\right)=\log _{e}\left(x_{2}\right)\)
⇒ x1 = x2
∵ f(x1) = f(x2)
⇒ x1 = x2 ∀ x1, x2 ∈ (0, ∞)
∴ f(x) is injection.
Let y ∈ R.
y = logex ⇒ x = ey
Then f(x) = logex
= loge(ey)
= y . logee
= y(1)
= y
∴ f is a surjection.
∴ f is a bijection.
(iv) f : [0, ∞) → [0, ∞) defined by f(x) = x2.
Solution:
Let x1, x2 ∈ [0, ∞) (i.e.,) domain of f.
Now f(x1) = f(x2)
⇒ \(x_{1}^{2}=x_{2}^{2}\)
⇒ x1 = x2
∵ x1, x2 ≥ 0
∴ f(x) = x2, f : {0, ∞) → {0, ∞) is injection
Let y ∈ (0, ∞), co-domain of f
Let y = x2 ⇒ x = √y, ∵ y ≥ 0
Then f(x) = x2
= \((\sqrt{y})^{2}\)
= y
∴ f is surjection.
Hence f is a bijection.
(v) f : R → [0, ∞) defined by f(x) = x2.
Solution:
Let x1, x2 ∈ R.
f(x1) = f(x2)
⇒ \(x_{1}^{2}=x_{2}^{2}\)
⇒ x1 = ±x2, ∵ x1, x2 ∈ R
Hence f is not injection
Let y ∈ [0, ∞)
y = x2
⇒ x = ±√y, where y ∈ [0, ∞)
Then f(x) = x2
= \((\sqrt{y})^{2}\)
= y
∴ f is surjection
Hence f is not a bijection
(vi) f : R → R defined by f(x) = x2.
Solution:
Let x1, x2 ∈ R, (domain of f)
∴ f(x1) = f(x2)
⇒ \(x_{1}^{2}=x_{2}^{2}\)
⇒ x1 = ±x2, ∵ x1, x2 ∈ R
∴ f(x) is not injection
For elements that belong to (-∞, 0) codomain of f has no pre-image in f.
∴ f is not a surjection
Hence f is neither injection nor surjection.
![]()
Question 3.
Is g = {(1, 1) (2, 3) (3, 5) (4, 7)} is a function from A = {1, 2, 3, 4} to B = {1, 3, 5, 7}. If this is given by the formula g(x) = ax + b, then find a and b.
Solution:
A = {1, 2, 3, 4}; B = {1, 3, 5, 7}
g : {(1, 1), (2, 3), (3, 5), (4, 7)}
∵ g(1) = 1, g(2) = 3, g(3) = 5, g(4) = 7
So for each element a ∈ A, there exists a unique b ∈ B such (a, b) ∈ g
∴ g : A → B is a function
Given g(x) = ax + b, ∀ x ∈ A
g(1) = (a) + b = 1
⇒ a + b = 1 ……..(1)
g(2) = 2a + b = 3
⇒ 2a + b = 3 …….(2)
Solve (1) and (2)
a = 2, b = -1
Question 4.
If the function f : R → R defined by f(x) = \(\frac{3^{x}+3^{-x}}{2}\), then show that f(x + y) + f(x – y) = 2f(x) f(y).
Solution:
f : R → R and f(x) = \(\frac{3^{x}+3^{-x}}{2}\)

∴ f(x + y) + f(x – y) = 2 f(x).f(y)
Question 5.
If the function f : R → R defined by f(x) = \(\frac{4^{x}}{4^{x}+2}\), then show that f(1 – x) = 1 – f(x) and hence reduce the value of \(f\left(\frac{1}{4}\right)+2 f\left(\frac{1}{2}\right)+f\left(\frac{3}{4}\right)\)
Solution:


∴ f(1 – x) = 1 – f(x)
Question 6.
If the function f : {-1, 1} → {0, 2), defined by f(x) = ax + b is a surjection, then find a and b.
Solution:
f : {-1, 1} → {0, 2} and f(x) = ax + b is a surjection
Given f(-1) = 0 and f(1) = 2 (or) f(-1) = 2, f(1) = 0
Case (i):
f(-1) = 0 and f(1) = 2
a(-1) + b = 0 ⇒ -a + b = 0 ……..(1)
a(1) + b = 2 ⇒ a + b = 2 ……(2)
Solve eq’s (1) and (2), we get a = 1, b = 1
Case (ii):
f(-1) = 2 and f(1) = 0
a(-1) + b = 2 ⇒ -a + b = 2 ……(3)
a(1) + b = 0 ⇒ a + b = 0 ……….(4)
Solve eq’s (3) and (4), we get a = -1, b = 1
Hence a = ±1 and b = 1
![]()
Question 7.
If f(x) = cos (log x), then show that \(f\left(\frac{1}{x}\right) \cdot f\left(\frac{1}{y}\right)-\frac{1}{2}\left[f\left(\frac{x}{y}\right)+f(x y)\right]=0\)
Solution:
Given f(x) = cos(log x)
\(f\left(\frac{1}{x}\right)=\cos \left(\log \left(\frac{1}{x}\right)\right)\)
= cos(log 1 – log x)
= cos(-log x)
= cos (log x) (∵ log 1 = 0)
Similarly
\(f\left(\frac{1}{y}\right)\) = cos (log y)
\(f\left(\frac{x}{y}\right)=\cos \log \left(\frac{x}{y}\right)\)
= cos (log x – log y)
and f(x y) = cos log (x y) = cos (log x + log y)
\(f\left(\frac{x}{y}\right)\) + f(x y) = cos (log x – log y) + cos (log x + log y)
= 2 cos (log x) cos (log y)
[∵ cos (A – B) + cos (A + B) = 2 cos A . cos B]
LHS = \(f\left(\frac{1}{x}\right) \cdot f\left(\frac{1}{y}\right)-\frac{1}{2}\left[f\left(\frac{x}{y}\right)+f(x y)\right]\)
= cos (log x) cos (log y) – \(\frac{1}{2}\) [2 cos (log x) cos (log y)]
= 0