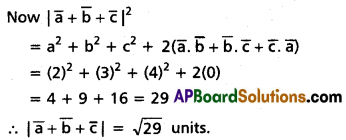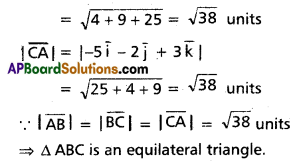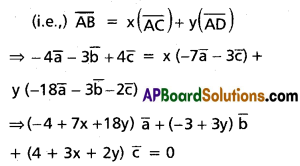Mahesh

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Products of Vectors Solutions Exercise 5(b) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Products of Vectors Solutions Exercise 5(b)

I.

Question 1.
If \(|\overline{\mathbf{p}}|=2,|\overline{\mathbf{q}}|=3\) and \((\bar{p}, \bar{q})=\frac{\pi}{6}\), then find \(|\bar{p} \times \bar{q}|^{2}\).
Solution:

Question 2.
If \(\overline{\mathbf{a}}=2 \overline{\mathbf{i}}-\overline{\mathbf{j}}+\overline{\mathbf{k}}\) and \(\overline{\mathbf{b}}=\overline{\mathbf{i}}-3 \overline{\mathbf{j}}-5 \overline{\mathbf{k}}\), then find \(|\overline{\mathbf{a}} \times \overline{\mathbf{b}}|\).
Solution:

Question 3.
If \(\bar{a}=2 \bar{i}-3 \bar{j}+\overline{\mathbf{k}}\) and \(\bar{b}=\bar{i}+4 \bar{j}-2 \bar{k}\), then find \((\overline{\mathbf{a}}+\overline{\mathbf{b}}) \times(\overline{\mathbf{a}}-\overline{\mathbf{b}})\).
Solution:

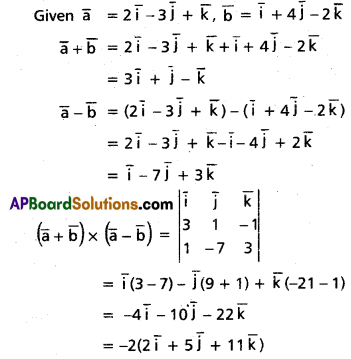
Question 4.
If \(4 \bar{i}+\frac{2 p}{3} \bar{j}+p \bar{k}\) is parallel to the vector \(\overline{\mathbf{i}}+2 \overline{\mathbf{j}}+3 \overline{\mathbf{k}}\), find p.
Solution:

Question 5.
Compute \(\overline{\mathbf{a}} \times(\overline{\mathbf{b}}+\overline{\mathbf{c}})+\overline{\mathbf{b}} \times(\overline{\mathbf{c}}+\overline{\mathbf{a}})+\overline{\mathbf{c}} \times(\overline{\mathbf{a}}+\overline{\mathbf{b}})\)
Solution:

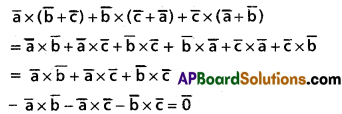
Question 6.
If \(\overline{\mathbf{p}}=\mathbf{x} \overline{\mathbf{i}}+\mathbf{y} \overline{\mathbf{j}}+\mathbf{z} \overline{\mathbf{k}}\), find the value of \(|\overline{\boldsymbol{p}} \times \overline{\mathbf{k}}|^{2}\)
Solution:

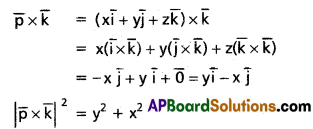
Question 7.
Compute \(2 \bar{j} \times(3 \bar{i}-4 \bar{k})+(\bar{i}+2 \hat{j}) \times \bar{k}\).
Solution:

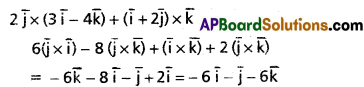
Question 8.
Find a unit vector perpendicular to both \(\overline{\mathbf{i}}+\overline{\mathbf{j}}+\overline{\mathbf{k}}\) and \(2 \bar{i}+\bar{j}+3 \bar{k}\).
Solution:

Question 9.
If θ is the angle between the vectors \(\overline{\mathbf{i}}+\overline{\mathbf{j}}\) and \(\overline{\mathbf{j}}+\overline{\mathbf{k}}\), then find sin ?.
Solution:

Question 10.
Find the area of the parallelogram having \(\bar{a}=2 \bar{j}-\bar{k}\) and \(\overline{\mathbf{b}}=-\overline{\mathbf{i}}+\overline{\mathbf{k}}\) as adjacent sides.
Solution:
Vector area of the parallelogram having \(\bar{a}=2 \bar{j}-\bar{k}\) and \(\overline{\mathbf{b}}=-\overline{\mathbf{i}}+\overline{\mathbf{k}}\) as adjacent sides.

Question 11.
Find the area of the parallelogram, whose diagonals are \(3 \overline{\mathbf{i}}+\overline{\mathbf{j}}-2 \overline{\mathbf{k}}\) and \(\bar{i}-3 \bar{j}+4 \bar{k}\).
Solution:

Question 12.
Find the area of the triangle having \(3 \bar{i}+4 \bar{j}\) and \(-5 \bar{i}+7 \bar{j}\) as two of its sides.
Solution:

Question 13.
Find unit vector perpendicular to the plane determined by the vectors \(\bar{a}=4 \bar{i}+3 \bar{j}-\bar{k}\) and \(\overline{\mathbf{b}}=2 \tilde{i}-6 \overline{\mathbf{j}}-3 \overline{\mathbf{k}}\).
Solution:

Question 14.
Find the area of the triangle whose vertices are A(1, 2, 3), B(2, 3, 1) and C(3, 1, 2).
Solution:
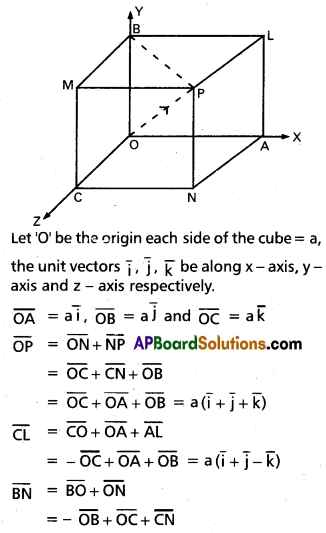
Suppose \(\bar{i}, \bar{j}, \bar{k}\) are unit vectors along the co-ordinate axes.
Position vectors of A, B, C are

II.

Question 1.
If \(\overline{\mathbf{a}}+\overline{\mathbf{b}}+\overline{\mathbf{c}}=\overline{\mathbf{0}}\), then prove that \(\overline{\mathbf{a}} \times \overline{\mathbf{b}}=\overline{\mathbf{b}} \times \overline{\mathbf{c}}=\overline{\mathbf{c}} \times \overline{\mathbf{a}}\).
Solution:

Question 2.
If \(\overline{\mathbf{a}}=2 \bar{i}+\bar{j}-\bar{k}, \quad \bar{b}=-\bar{i}+2 \bar{j}-4 \bar{k}\) and \(\overline{\mathbf{c}}=\overline{\mathbf{i}}+\mathbf{j}+\overline{\mathbf{k}}\), then find \((\bar{a} \times \bar{b}) \cdot(\bar{b} \times \bar{c})\).
Solution:

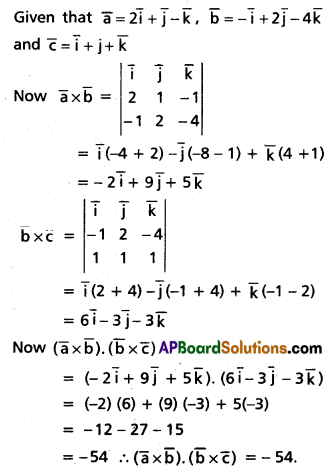
Question 3.
Find the vector area and the area of the parallelogram having \(\overline{\mathbf{a}}=\overline{\mathbf{i}}+2 \overline{\mathbf{j}}-\overline{\mathbf{k}}\) and \(\overline{\mathbf{b}}=2 \overline{\mathbf{i}}-\overline{\mathbf{j}}+\mathbf{2} \overline{\mathbf{k}}\) as adjacent sides.
Solution:

Question 4.
If \(\overline{\mathbf{a}} \times \overline{\mathbf{b}}=\overline{\mathbf{b}} \times \overline{\mathbf{c}} \neq \overline{\mathbf{0}}\), show that, \(\overline{\mathbf{a}}+\overline{\mathbf{c}}=\mathbf{p} \overline{\mathbf{b}}\), where p is some scalar.
Solution:

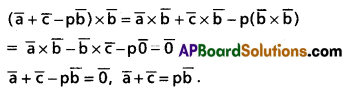
Question 5.
Let \(\overline{\mathbf{a}}\) and \(\overline{\mathbf{b}}\) be vectors, satisfying \(|\overline{\mathbf{a}}|=|\overline{\mathbf{b}}|=5\) and \((\bar{a}, \bar{b})=45^{\circ}\). Find the area of the triangle having \(\overline{\mathbf{a}}-\mathbf{2} \overline{\mathbf{b}}\) and \(3 \bar{a}+2 \bar{b}\) as two of its sides.
Solution:

Question 6.
Find the vector having magnitude ?6 units and perpendicular to both \(\mathbf{2} \overline{\mathbf{i}}-\overline{\mathbf{k}}\) and \(\mathbf{3} \overline{\mathbf{i}}-\overline{\mathbf{j}}-\overline{\mathbf{k}}\).
Solution:

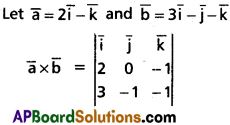
Question 7.
Find a unit vector perpendicular to the plane determined by the points P(1, -1, 2), Q(2, 0, -1) and R(0, 2, 1).
Solution:

Question 8.
If \(\overline{\mathbf{a}} \cdot \overline{\mathbf{b}}=\overline{\mathbf{a}} \cdot \overline{\mathbf{c}}\) and \(\overline{\mathbf{a}} \times \overline{\mathrm{b}}=\overline{\mathrm{a}} \times \overline{\mathrm{c}}, \overline{\mathbf{a}} \neq 0\), then show that \(\overline{\mathbf{b}}=\overline{\mathbf{c}}\).
Solution:

Question 9.
Find a vector of magnitude 3 and perpendicular to both the vector \(\overline{\mathbf{b}}=2 \bar{i}-2 \bar{j}+\bar{k}\) and \(\bar{c}=2 \bar{i}+2 \bar{j}+3 \bar{k}\).
Solution:

Question 10.
If \(|\overline{\mathbf{a}}|\) = 13, \(|\overline{\mathbf{b}}|\) = 5 and \(\overline{\mathbf{a}} \cdot \overline{\mathbf{b}}=\mathbf{6 0}\), then find \(|\overline{\mathbf{a}} \times \overline{\mathbf{b}}|\).
Solution:

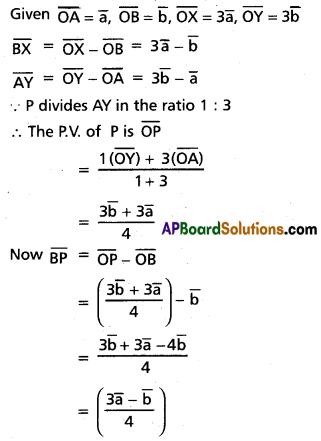
Question 11.
Find a unit vector perpendicular to the plane passing through the points (1, 2, 3), (2, -1, 1) and (1, 2, -4).
Solution:
Let ‘O’ be the origin and let A, B, C be the given points.

III.

Question 1.
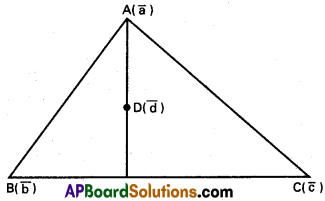
If \(\overline{\mathbf{a}}\), \(\overline{\mathbf{b}}\) and \(\overline{\mathbf{c}}\) represent the vertices A, B and C respectively of ∆ABC, then prove that \(|(\overline{\mathbf{a}} \times \overline{\mathbf{b}})+(\overline{\mathbf{b}} \times \overline{\mathbf{c}})+(\overline{\mathbf{c}} \times \overline{\mathbf{a}})|\) is twice the area of ∆ABC.
Solution:

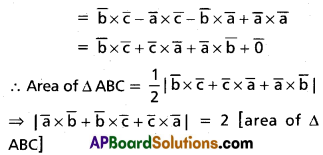
Question 2.
If \(\overline{\mathbf{a}}=2 \overline{\mathbf{i}}+3 \overline{\mathbf{j}}+4 \overline{\mathbf{k}}, \overline{\mathbf{b}}=\overline{\mathbf{i}}+\overline{\mathbf{j}}-\overline{\mathbf{k}}\) and \(\overline{\mathbf{c}}=\overline{\mathbf{i}}-\overline{\mathbf{j}}+\overline{\mathbf{k}}\), then compute \(\overline{\mathbf{a}} \times(\overline{\mathbf{b}} \times \overline{\mathbf{c}})\) and verify that it is perpendicular to \(\bar{a}\).
Solution:

Question 3.
If \(\overline{\mathbf{a}}=7 \overline{\mathbf{i}}-2 \overline{\mathbf{j}}+3 \overline{\mathbf{k}}, \overline{\mathbf{b}}=2 \overline{\mathbf{i}}+8 \overline{\mathbf{k}}\) and \(\overline{\mathbf{c}}=\overline{\mathbf{i}}+\overline{\mathbf{j}}+\overline{\mathbf{k}}\) then compute \(\overline{\mathbf{a}} \times \mathbf{b}, \overline{\mathbf{a}} \times \overline{\mathbf{c}}\) and \(\bar{a} \times(\bar{b}+\bar{c})\). Verify whether cross product is distributive over vector addition.
Solution:

Question 4.
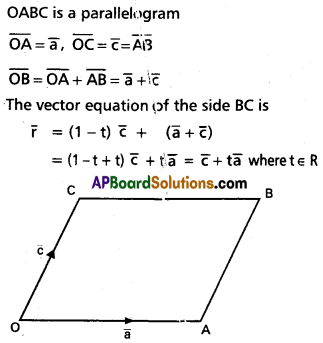
If \(\overline{\mathbf{a}}=\overline{\mathbf{i}}+\overline{\mathbf{j}}+\overline{\mathbf{k}}, \overline{\mathbf{c}}=\overline{\mathbf{j}}-\overline{\mathbf{k}}\), then find vector \(\overline{\mathbf{b}}\) such that \(\overline{\mathbf{a}} \times \overline{\mathbf{b}}=\overline{\mathbf{c}}\) and \(\bar{a} \cdot \bar{b}=3\).
Solution:

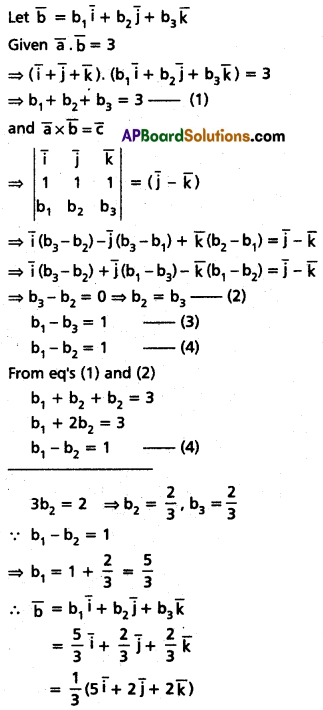
Question 5.
\(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) are three vectors of equal magnitudes and each of them is inclined at an angle of 60° to the others. If \(|\bar{a}+\bar{b}+\bar{c}|=\sqrt{6}\), then find \(|\overline{\mathbf{a}}|\).
Solution:

Question 6.
For any two vectors \(\bar{a}\) and \(\bar{b}\), show that \(\left(1+|\bar{a}|^{2}\right)\left(1+|\bar{b}|^{2}\right)\) = \(|\mathbf{1}-\overline{\mathbf{a}} \cdot \overline{\mathbf{b}}|^{2}+|\overline{\mathbf{a}}+\overline{\mathbf{b}}+\overline{\mathbf{a}} \times \overline{\mathbf{b}}|^{2}\)
Solution:

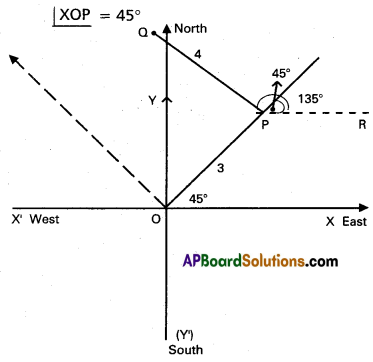
Question 7.
If \(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) are unit vectors such that \(\overline{\mathbf{a}}\) is perpendicular to the plane of \(\overline{\mathbf{b}}, \overline{\mathbf{c}}\) and the angle between \(\overline{\mathbf{b}}\) and \(\overline{\mathbf{c}}\) is \(\frac{\pi}{3}\), then find \(|\bar{a}+\bar{b}+\bar{c}|\).
Solution:
Given that \(|\bar{a}|=|\bar{b}|=|\bar{c}|=1\)

Question 8.
\(\overline{\mathbf{a}}=3 \overline{\mathbf{i}}-\overline{\mathbf{j}}+2 \overline{\mathbf{k}}, \overline{\mathbf{b}}=-\overline{\mathbf{i}}+3 \overline{\mathbf{j}}+2 \overline{\mathbf{k}}\), \(\bar{c}=4 \bar{i}+5 \bar{j}-2 \bar{k}\) and \(\bar{d}=\bar{i}+3 \bar{j}+5 \bar{k}\) then compute the following.
(i) \((\overline{\mathbf{a}} \times \overline{\mathbf{b}}) \times(\bar{c} \times \bar{d})\) and
(ii) \((\overline{\mathbf{a}} \times \overline{\mathbf{b}}) \cdot \overline{\mathbf{c}}-(\overline{\mathbf{a}} \times \overline{\mathbf{d}}) \cdot \overline{\mathbf{b}}\)
Solution:

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Products of Vectors Solutions Exercise 5(a) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Products of Vectors Solutions Exercise 5(a)

I.

Question 1.
Find the angle between the vectors \(\bar{i}+2 \bar{j}+3 \bar{k}\) and \(3 \bar{i}-\bar{j}+2 \bar{k}\).
Solution:
Let \(\overline{\mathrm{a}}=\overline{\mathrm{i}}+2 \overline{\mathrm{j}}+3 \overline{\mathrm{k}}\) and \(\overline{\mathrm{b}}=3 \overline{\mathrm{i}}-\overline{\mathrm{j}}+2 \overline{\mathrm{k}}\) and ‘θ’ be the angle between them (i.e.,) \((\bar{a}, \bar{b})\) = θ

Question 2.
If the vectors \(\mathbf{2} \overline{\mathbf{i}}+\lambda \overline{\mathbf{j}}-\overline{\mathbf{k}}\) and \(4 \bar{i}-2 \bar{j}+2 \bar{k}\) are perpendicular to each other, then find λ.
Solution:

Question 3.
For what values of λ, the vectors \(\overline{\mathbf{i}}-\lambda \overline{\mathbf{j}}+2 \overline{\mathbf{k}}\) and \(8 \overline{\mathbf{i}}+6 \overline{\mathbf{j}}-\overline{\mathbf{k}}\) are at right angles?
Solution:

Question 4.
\(\overline{\mathbf{a}}=2 \overline{\mathbf{i}}-\overline{\mathbf{j}}+\overline{\mathbf{k}}, \overline{\mathbf{b}}=\overline{\mathbf{i}}-3 \overline{\mathbf{j}}-5 \overline{\mathbf{k}}\). Find the vector C such that \(\overline{\mathbf{a}}\), \(\overline{\mathbf{b}}\) and \(\overline{\mathbf{c}}\) form the sides of a triangle.
Solution:

Question 5.
Find the angle between the planes \(\bar{r} \cdot(2 \bar{i}-\bar{j}+2 \bar{k})=3\) and \(\overline{\mathrm{r}} \cdot(3 \overline{\mathrm{i}}+6 \bar{j}+\bar{k})=4\).
Solution:

Question 6.
Let \(\overline{\mathbf{e}}_{1}\) and \(\overline{\mathbf{e}}_{2}\) be unit vectors makingangle θ. If \(\frac{1}{2}\left|\bar{e}_{1}-\bar{e}_{2}\right|=\sin \lambda \theta\), then find λ.
Solution:

Question 7.
Let \(\overline{\mathbf{a}}=\overline{\mathbf{i}}+\overline{\mathbf{j}}+\overline{\mathbf{k}}\) and \(\overline{\mathbf{b}}=\mathbf{2} \overline{\mathbf{i}}+3 \overline{\mathbf{j}}+\overline{\mathbf{k}}\). Find
(i) The projection vector of \(\overline{\mathbf{b}}\) on \(\overline{\mathbf{a}}\) and its magnitude.
(ii) The vector components of \(\overline{\mathbf{b}}\) in the direction of a and perpendicular to \(\overline{\mathbf{a}}\).
Solution:

Question 8.
Find the equation of the plane through the point (3, -2, 1) and perpendicular to the vector (4, 7, -4).
Solution:

Question 9.
If \(\overline{\mathbf{a}}=2 \bar{i}+2 \bar{j}-3 \bar{k}\); \(\overline{\mathbf{b}}=3 \overline{\mathbf{i}}-\overline{\mathbf{j}}+2 \overline{\mathbf{k}}\), then find the angle between \(2 \overline{\mathbf{a}}+\overline{\mathbf{b}}\) and \(\bar{a}+2 \bar{b}\).
Solution:

II.

Question 1.
Find unit vector parallel to the XOY- plane and perpendicular to the vector \(4 \bar{i}-3 \bar{j}+\bar{k}\).
Solution:
Any vector parallel to XOY-plane will be of the form \(p \bar{i}+q \bar{j}\)
∴ The vector parallel to the XOY-plane and perpendicular to the vector \(4 \bar{i}-3 \bar{j}+\bar{k}\) is \(3 \bar{i}+4 \bar{j}\)
Its magnitude = \(|3 \bar{i}+\overline{4 j}|=\sqrt{9+16}=5\)
∴ Unit vector parallel to the XOY-plane and perpendicular to the vector \(4 \bar{i}-3 \bar{j}+\bar{k}\) is \(\pm \frac{(3 \overline{\mathrm{i}}+4 \overline{\mathrm{j}})}{5}\)

Question 2.
If \(\overline{\mathbf{a}}+\overline{\mathbf{b}}+\overline{\mathrm{c}}=0,|\overline{\mathbf{a}}|=3,|\overline{\mathbf{b}}|=5\) and \(|\bar{c}|=7\), then find the angle between \(\overline{\mathbf{a}}\) and \(\overline{\mathbf{b}}\).
Solution:

Question 3.
If \(|\overline{\mathbf{a}}|\) = 2, \(|\overline{\mathbf{b}}|\) = 3 and \(|\overline{\mathbf{c}}|\) = 4 and each of \(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) is perpendicular to the sum of the other two vectors, then find the magnitude of \(\overline{\mathbf{a}}+\overline{\mathbf{b}}+\overline{\mathbf{c}}\).
Solution:

Question 4.
Find the equation of the plane passing through the point \(\overline{\mathbf{a}}=\mathbf{2} \overline{\mathbf{i}}+3 \bar{j}-\overline{\mathbf{k}}\) and perpendicular to the vector \(3 \bar{i}-2 \bar{j}-2 \bar{k}\) and the distance of this plane from the origin.
Solution:
Equation of the plane passing through the point \(\overline{\mathbf{a}}=\mathbf{2} \overline{\mathbf{i}}+3 \bar{j}-\overline{\mathbf{k}}\) and perpendicular to the vector \(\bar{n}=3 \bar{i}-2 \bar{j}-2 \bar{k}\) is

Question 5.
\(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) and \(\overline{\mathbf{d}}\) are the position vectors of four coplanar points such that \((\mathbf{a}-\overline{\mathbf{d}}) \cdot(\bar{b}-\bar{c})=(\bar{b}-\bar{d}) \cdot(\bar{c}-\bar{a})=0\). Show that the point \(\bar{d}\) represents the orthocentre of the triangle with \(\bar{a}\), \(\bar{b}\) and \(\bar{c}\) as its vertices.
Solution:
Position vectors of A, B, C, D are \(\bar{a}\), \(\bar{b}\), \(\bar{c}\) and \(\bar{d}\) respectively.


⇒ BD is perpendicular to AC
∴ BD is another altitude of ∆ABC.
Altitudes AD and BD intersect at D.
∴ D is the orthocentre of ∆ABC.

III.

Question 1.
Show that the points (5, -1, 1), (7, -4, 7), (1, -6, 10) and (-1, -3, 4) are the vertices of a rhombus.
Solution:
Let A(5, -1, 1), B(7, -4, 7), C(1, -6, 10) and D(-1, -3, 4) are the given points.

∵ AB = BC = CD = DA = 7 units
AC ≠ BD
∴ A, B, C, D points are the vertices of a rhombus.

Question 2.
Let \(\bar{a}=4 \bar{i}+5 \bar{j}-\bar{k}, \quad \bar{b}=\bar{i}-4 \bar{j}+5 \bar{k}\) and \(\overline{\mathbf{c}}=\mathbf{3} \overline{\mathbf{i}}+\overline{\mathbf{j}}-\overline{\mathbf{k}}\). Find the vector which is perpendicular to both \(\overline{\mathbf{a}}\) and \(\overline{\mathbf{b}}\) and whose magnitude is twenty one times the magnitude of \(\overline{\mathbf{c}}\).
Solution:

Question 3.
G is the centroid of ΔABC and a, b, c are the lengths of the sides BC, CA and AB respectively prove that a² + b² + c² = 3 (OA² + OB² + OC²) – 9(OG)² where O is any point.
Solution:
Given that \(\overline{\mathrm{BC}}=\overline{\mathrm{a}}, \overline{\mathrm{CA}}=\overline{\mathrm{b}}, \overline{\mathrm{AB}}=\overline{\mathrm{c}}\)
Let ‘O’ be the origin and let \(\overline{\mathrm{OA}}=\overline{\mathrm{p}}, \overline{\mathrm{OB}}=\overline{\mathrm{q}} \text { and } \overline{\mathrm{OC}}=\overline{\mathrm{r}}\)
Then P.V. of the centroid of ΔABC is

From (1) and (2)
∴ a² + b² + c² = 3(OA² + OB² + OC²) – 9(OG)².

Question 4.
A line makes angles θ₁, θ₂, θ₃, and θ₄ with the diagonals of a cube. Show that cos²θ₁ + cos²θ₂ + cos²θ₃ + cos²θ₄ = \(\frac{4}{3}\).
Solution:

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Addition of Vectors Solutions Exercise 4(b) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Addition of Vectors Solutions Exercise 4(b)

I.

Question 1.
Find the vector equation of the line passing through the point \(2 \bar{i}+3 \bar{j}+\bar{k}\) and parallel to the vector \(4 \bar{i}-2 \bar{j}+3 \bar{k}\).
Solution:

Question 2.
OABC is a parallelogram. If \(\overline{O A}=\bar{a}\) and \(\overline{O C}=\bar{c}\), find the vector equation of the side BC.
Solution:

Question 3.
If \(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) are the position vectors of the vertices A, B and C respectively of ∆ABC, theind the vector equation of the median through the vertex A.
Solution:

Question 4.
Find the vertor equation of the line joining the points \(2 \bar{i}+\bar{j}+3 \bar{k}\) and \(-4 \bar{i}+3 \bar{j}-\bar{k}\).
Solution:

Question 5.
Find the vector equation of the plane passing through the points \(\overline{\mathbf{i}}-2 \overline{\mathbf{j}}+5 \overline{\mathbf{k}},-5 \overline{\mathbf{j}}-\overline{\mathbf{k}} \text { and }-3 \overline{\mathbf{i}}+5 \overline{\mathbf{j}}\).
Solution:

Question 6.
Find the vector equation of the plane through the points (0, 0, 0), (0, 5, 0) and (2, 0, 1).
Solution:

II.

Question 1.
If \(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) are noncoplanar find the point of intersection of the line passing through the points \(2 \bar{a}+3 \bar{b}-\bar{c}\), \(3 \bar{a}+4 \bar{b}-2 \bar{c}\) with the line joining the points \(\bar{a}-2 \bar{b}+3 \bar{c}, \bar{a}-6 \bar{b}+6 \bar{c}\).
Solution:

Question 2.
ABCD is a trapezium in which AB and CD are parallel. Prove by vector methods, that the mid points of the sides AB, CD and the intersection of the diagonals are collinear.
Solution:




⇒ M, P, N are collinear
Hence the midpoints of parallel sides of a trapezium and the point of intersection of the diagonals are collinear.

Question 3.
In a quadrilateral ABCD, if the midpoints of one pair of opposite sides and the point of intersection of the diagonals are collinear, using vector methods, prove that the quadrilateral ABCD is a trapezium.
Solution:

III.

Question 1.
Find the vector equation of the plane which passes through the points \(2 \bar{i}+4 \bar{j}+2 \bar{k}, 2 \bar{i}+3 \bar{j}+5 \bar{k}\) and parallel to the vector \(3 \overline{\mathbf{i}}-2 \overline{\mathbf{j}}+\overline{\mathbf{k}}\). Also find the point where this plane meets the line joining the points \(2 \overline{\mathbf{i}}+\overline{\mathbf{j}}+3 \overline{\mathbf{k}}\) and \(4 \bar{i}-2 \bar{j}+3 \bar{k}\).
Solution:

Question 2.
Find the vector equation of the plane passing through points \(4 \overline{\mathbf{i}}-3 \overline{\mathbf{j}}-\overline{\mathbf{k}}\), \(3 \overline{\mathbf{i}}+7 \overline{\mathbf{j}}-10 \overline{\mathbf{k}}\) and \(2 \bar{i}+5 \bar{j}-7 \bar{k}\), and show that the point \(\overline{\mathbf{i}}+2 \bar{j}-3 \overline{\mathbf{k}}\) lies in the plane.
Solution:

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Addition of Vectors Solutions Exercise 4(a) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Addition of Vectors Solutions Exercise 4(a)

I.

Question 1.
ABCD is a Parallelogram. If L and M are the middle points of BC and CD, respectively, then find (i) AL and AM in terms of AB and AD (ii) λ, if AM = λ AD – LM.
Solution:

Question 2.
In ∆ABC, P, Q, and R are the midpoints of the sides AB, BC, and CA respectively. If D is any point.
(i) then express \(\overline{\mathrm{DA}}+\overline{\mathrm{DB}}+\overline{\mathrm{DC}}\) interms of \(\overline{D P}\), \(\overline{D Q}\) and \(\overline{D R}\).
(ii) If \(\overline{\mathbf{P A}}+\overline{\mathbf{Q B}}+\overline{\mathbf{R C}}=\bar{\alpha}\) then find \(\bar{\alpha}\)
Solution:

Question 3.
Let \(\overline{\mathbf{a}}=\overline{\mathbf{i}}+2 \overline{\mathbf{j}}+3 \overline{\mathbf{k}}\) and \(\overline{\mathbf{b}}=\mathbf{3} \overline{\mathbf{i}}+\overline{\mathbf{j}}\). Find the unit vector in the direction of \(\overline{\mathbf{a}}+\overline{\mathbf{b}}\).
Solution:

Question 4.
If the vectors \(-3 \overline{\mathbf{i}}+4 \bar{j}+\lambda \overline{\mathbf{k}}\) and \(\mu \bar{i}+8 \bar{i}+6 \bar{k}\) are coilinear vectors , then find λ and µ.
Solution:

Question 5.
ABCDE is a pentagon. If the sum of the vectors \(\overline{\mathrm{AB}}, \overline{\mathrm{AE}}, \overline{\mathrm{BC}}, \overline{\mathrm{DC}}, \overline{\mathrm{ED}}\) and \(\overline{\mathbf{A C}}\) is λ \(\overline{\mathbf{A C}}\), then find the value of λ.
Solution:

Question 6.
If the position vectors of the points A, B and C are \(-2 \overline{\mathbf{i}}+\overline{\mathbf{j}}-\overline{\mathbf{k}},-4 \overline{\mathbf{i}}+2 \overline{\mathbf{j}}+2 \overline{\mathbf{k}}\) and \(6 \bar{i}-3 \bar{j}-13 \bar{k}\) respectively and \(\overline{\mathbf{A B}}=\lambda \overline{\mathrm{AC}}\), then find the value of λ.
Solution:

Question 7.
If \(\overline{\mathrm{OA}}=\overline{\mathbf{i}}+\overline{\mathbf{j}}+\overline{\mathbf{k}}, \overline{\mathrm{AB}}=3 \bar{i}-2 \overline{\mathbf{j}}+\overline{\mathbf{k}}\), \(\overline{B C}=\bar{i}+2 \bar{j}-2 \bar{k}\) and \(\overline{C D}=2 \bar{i}+\bar{j}+3 \bar{k}\), then find the vector \(\overline{O D}\).
Solution:

Question 8.
\(\overline{\mathbf{a}}=2 \overline{\mathbf{i}}+5 \overline{\mathbf{j}}+\overline{\mathbf{k}}\) and \(\bar{b}=4 \bar{i}+m \bar{j}+n \bar{k}\) are collinear vectors, then find m and n.
Solution:

Question 9.
Let \(\bar{a}=2 \bar{i}+4 \overline{\mathbf{j}}-5 \overline{\mathbf{k}}, \bar{b}=\hat{i}+\bar{j}+\bar{k}\) and \(\bar{c}=\bar{j}+2 \bar{k}\). Find the unit vector in the opposite direction of \(\overline{\mathbf{a}}+\overline{\mathbf{b}}+\overline{\mathbf{c}}\).
Solution:

Question 10.
Is the triangle formed by the vectors \(3 \bar{i}+5 \bar{j}+2 \bar{k}, 2 \bar{i}-3 \bar{j}-5 \bar{k}\) and \(-5 \bar{i}-2 \bar{j}+3 \bar{k}\) equilateral?
Solution:

Question 11.
If α, β and γ be the angles made by the vector \(3 \bar{i}-6 \bar{i}+2 \bar{k}\) with the positive directions of the co-ordinate axes, then find cos α, cos β, cos γ.
Solution:
Unit vectors along the co-ordinate axes are respectively \(\bar{i}, \bar{j}, \bar{k}\).

Question 12.
Find the angles made by the straight line passing through the points (1, -3, 2) and (3, -5, 1) with the co-ordinate axes.
Solution:
Unit vectors along the co-ordinate axes are respectively \(\bar{i}, \bar{j}, \bar{k}\).
Let A(1, -3, 2) and B(3, -5, 1) be two given points.
Let ‘O’ be the origin. Then

II.

Question 1.
If \(\overline{\mathbf{a}}+\overline{\mathbf{b}}+\overline{\mathbf{c}}=\alpha \overline{\mathbf{d}}, \overline{\mathbf{b}}+\overline{\mathbf{c}}+\overline{\mathbf{d}}=\beta \overline{\mathbf{a}}\) and \(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathrm{c}}\) are non-coplanar vectors, then show that \(\overline{\mathbf{a}}+\overline{\mathbf{b}}+\overline{\mathbf{c}}+\overline{\mathbf{d}}=\mathbf{0}\).
Solution:

Question 2.
\(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) are non-coplanar vectors. Prove that the following four points are coplanar.
(i) \(-\overline{\mathbf{a}}+4 \overline{\mathbf{b}}-3 \bar{c}, \quad 3 \bar{a}+2 \bar{b}-5 \bar{c}\), \(-3 \overline{\mathbf{a}}+8 \overline{\mathbf{b}}-5 \overline{\mathbf{c}},-3 \overline{\mathbf{a}}+2 \overline{\mathbf{b}}+\overline{\mathbf{c}}\)
Solution:
Let ‘O’ be the origin and A, B, C, D be the four points.


4 + 2x + 2y = 0 ……..(1)
-2 – 4x + 2y = 0 ……..(2)
-2 + 2x – 4y = 0 …….(3)
Solve (1) and (3)
6y + 6 = 0 ⇒ y = -1
Substitute in (1)
2x + 2 (-1) + 4 = 0
⇒ 2x + 2 = 0
⇒ x = -1
Substitute x = -1, y = -1 in (2)
-2 – 4(-1) + 2(-1) = -4 + 4 = 0
∴ The vectors \(\overline{\mathrm{AB}}, \overline{\mathrm{AC}}, \overline{\mathrm{AD}}\) are coplanar
⇒ A, B, C, D are coplanar
Hence the given points are coplanar.

(ii) \(6 \bar{a}+2 \bar{b}-\bar{c}, 2 \bar{a}-\bar{b}+3 \bar{c},-\bar{a}+2 \bar{b}-4 \bar{c},\)\(-12 \bar{a}-\bar{b}-3 \bar{c}\)
Solution:
Let O be the origin. Let A, B, C, D be the given points.

Let us suppose that one vector can be expressed as a linear combination of the other two.

∵ \(\bar{a}, \bar{b}, \bar{c}\) are non-coplanar vectors.
7x + 18y – 4 = 0 ………(1)
-3 + 3y = 0 ⇒ y = 1 …….(2)
3x + 2y + 4 = 0 ………(3)
Substitute y =1 in (3)
3x + 2 + 4 = 0 ⇒ x = -2
Substitute x = -2 and y = 1 in (1)
7(-2) + 18(1) – 4 = 0 ⇒ 0 = 0
Hence \(\overline{\mathrm{AB}}, \overline{\mathrm{AC}}\) and \(\overline{\mathrm{AD}}\) are coplanar.
⇒ The points A, B, C, D are coplanar.

Question 3.
If \(\overline{\mathbf{i}}, \overline{\mathbf{j}}, \overline{\mathbf{k}}\) are unit vectors along the positive directions of the coordinate axes, then show that the four points \(4 \overline{\mathbf{i}}+5 \overline{\mathbf{j}}+\overline{\mathbf{k}},-\overline{\mathbf{j}}-\overline{\mathbf{k}}, 3 \overline{\mathbf{i}}+9 \overline{\mathbf{j}}+4 \overline{\mathbf{k}}\) and \(-4 \bar{i}+4 \bar{j}+4 \bar{k}\) are coplanar.
Solution:
Let ‘O’ be the origin and let A, B, C, D be the given points.


⇒ The given points A, B, C, D are coplanar.
Second Method:
\(\left[\begin{array}{lll}
\overline{\mathrm{AB}} & \overline{\mathrm{AC}} & \overline{\mathrm{AD}}
\end{array}\right]\) = \(\left|\begin{array}{ccc}
-4 & -6 & -2 \\
-1 & 4 & 3 \\
-8 & -1 & 3
\end{array}\right|\)
= -4(12 + 3) + 6(-3 + 24) – 2(1 + 32)
= -60 + 126 – 66
= 0
Hence the vectors \(\overline{\mathrm{AB}}, \overline{\mathrm{AC}}\) and \(\overline{\mathrm{AD}}\) are coplanar.
⇒ The given points A, B, C, D are coplanar.

Question 4.
If a, b, c are non-coplanar vectors, then test for the collinearity of the following points whose position vectors are given by
(i) \(\bar{a}-2 \bar{b}+3 \bar{c}, 2 \bar{a}+3 \bar{b}-4 \bar{c},-7 \bar{b}+10 \bar{c}\)
Solution:
Let ‘O’ be the origin. A, B, C be the given points.
Then \(\overline{\mathrm{OA}}=\overline{\mathrm{a}}-2 \overline{\mathrm{b}}+3 \overline{\mathrm{c}}\)

(ii) \(3 \bar{a}-4 \bar{b}+3 \bar{c}\), \(-4 \bar{a}+5 \bar{b}-6 \bar{c}\), \(4 \overline{\mathbf{a}}-7 \overline{\mathbf{b}}+6 \overline{\mathbf{c}}\)
Solution:

(iii) \(\begin{aligned}
&2 \bar{a}+5 \bar{b}-4 \bar{c}, \bar{a}+4 \bar{b}-3 \bar{c}, \\
&4 \bar{a}+7 \bar{b}-6 \bar{c}
\end{aligned}\)
Solution:
Let ‘O’ be the origin and A, B, C be the given points.
Then \(\overline{\mathrm{OA}}=2 \overline{\mathrm{a}}+5 \overline{\mathrm{b}}-4 \overline{\mathrm{c}}\), \(\overline{\mathrm{OB}}=\overline{\mathrm{a}}+4 \overline{\mathrm{b}}-3 \overline{\mathrm{c}}\)

∴ The points A, B, C are collinear.

III.

Question 1.
In the Cartesian plane, O is the origin of the coordinate axes. A person starts at O and walks a distance of 3 units in the NORTH-EAST direction and reaches point P. From P he walks 4 units of distance parallel to NORTH-WEST direction and reaches the point Q. Express the vector \(\overline{\mathbf{O Q}}\) in terms of \(\overline{\mathbf{i}}\) and \(\overline{\mathbf{j}}\) (observe that ∠XOP = 45°)
Solution:
‘O’ the origin of co-ordinate axes.

Question 2.
The points O, A, B, X and Y are such that \(\overline{\mathbf{O A}}=\overline{\mathbf{a}}, \overline{\mathbf{O B}}=\overline{\mathbf{b}}, \overline{\mathbf{O X}}=\mathbf{3} \overline{\mathbf{a}}\) and \(\overline{\mathbf{O Y}}=\mathbf{3} \overline{\mathbf{b}}\). Find \(\overline{\mathbf{B X}}\) and \(\overline{\mathbf{A Y}}\) interms of \(\bar{a}\) and \(\bar{b}\). Futher, if the point P divides AY in the ratio 1 : 3, then express \(\overline{\mathrm{BP}}\) interms of \(\bar{a}\) and \(\bar{a}\).
Solution:

Question 3.
If ∆OAB, E is the midpoint of AB and F is a point on OA such that OF = 2(FA). If C is the point of intersection of \(\overline{\mathrm{OE}}\) and \(\overline{\mathrm{BF}}\), then find the ratios OC : CE and BC : CF.
Solution:

Question 4.
Point E divides the segment PQ internally in the ratio 1 : 2 and R is any point not on the line PQ. If F is a point on QR such that QF : FR = 2 : 1, then show that EF is parallel to PR.
Solution:

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Matrices Solutions Exercise 3(i) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Matrices Solutions Exercise 3(i)

Solve the following systems of homogeneous equations.

Question 1.
2x + 3y – z = 0, x – y – 2z = 0, 3x + y + 3z = 0
Solution:
The Coefficient matrix is \(\left[\begin{array}{ccc}
2 & 3 & -1 \\
1 & -1 & -2 \\
3 & 1 & 3
\end{array}\right]\)
det of \(\left[\begin{array}{ccc}
2 & 3 & -1 \\
1 & -1 & -2 \\
3 & 1 & 3
\end{array}\right]=\left[\begin{array}{ccc}
2 & 3 & -1 \\
1 & -1 & -2 \\
3 & 1 & 3
\end{array}\right]\)
= 2(-3 + 2) – 3(3 + 6) – 1(1 + 3)
= -2 – 27 – 4
= -33 ≠ 0, ρ(A) = 3
Hence the system has the trivial solution x = y = z = 0 only.

Question 2.
3x + y – 2z = 0, x + y + z = 0, x – 2y + z = 0
Hint: If the determinant of the coefficient matrix ≠ 0 then the system has a trivial solution (i.e.) ρ(A) = 3.
Solution:
The coefficient matrix is \(\left[\begin{array}{ccc}
3 & 1 & -2 \\
1 & 1 & 1 \\
1 & -2 & 1
\end{array}\right]\)
\(\left|\begin{array}{ccc}
3 & 1 & -2 \\
1 & 1 & 1 \\
1 & -2 & 1
\end{array}\right|\)
= 3(1 + 2) – 1(1 – 1) – 2(-2 – 1)
= 9 + 6
= 15 ≠ 0, ρ(A) = 3
Hence the system has the trivial solutions x = y = z = 0 only.

Question 3.
x + y – 2z = 0, 2x + y – 3z = 0, 5x + 4y – 9z = 0
Solution:
The coefficient matrix is \(\left[\begin{array}{rrr}
1 & 1 & -2 \\
2 & 1 & -3 \\
5 & 4 & -9
\end{array}\right]\) = A (say)
|A| = \(\left|\begin{array}{rrr}
1 & 1 & -2 \\
2 & 1 & -3 \\
5 & 4 & -9
\end{array}\right|\)
= 1(-9 + 12) – 1(-18 + 15) – 2(8 – 5)
= 3 + 3 – 6
= 0
∴ Rank of A = 2 as the submatrix \(\left[\begin{array}{ll}
1 & 1 \\
2 & 1
\end{array}\right]\) is non-singular, ρ(A) < 3
Hence the system has a non-trivial solution.
A = \(\left[\begin{array}{lll}
1 & 1 & -2 \\
2 & 1 & -3 \\
5 & 4 & -9
\end{array}\right]\)
R₂ → R₂ – 2R₁, R₃ → R₃ – 3R₁
A ~ \(\left[\begin{array}{ccc}
1 & 1 & -2 \\
0 & -1 & 1 \\
0 & -1 & -1
\end{array}\right]\)
The system of equation is equivalent to the given system of equations are x + y – 2z = 0, -y + z = 0
Let z = k
⇒ y = k, x = k
∴ x = y = z = k for real number k.

Question 4.
x + y – z = 0, x – 2y + z = 0, 3x + 6y – 5z = 0
Solution:
Coefficient matrix A = \(\left[\begin{array}{ccc}
1 & 1 & -1 \\
1 & -2 & 1 \\
3 & 6 & -5
\end{array}\right]\)
R₂ → R₂ – R₁, R₃ → R₃ – 3R₁
A ~ \(\left[\begin{array}{ccc}
1 & 1 & -1 \\
0 & -3 & 2 \\
0 & 3 & -2
\end{array}\right]\)
⇒ det A = 0 as R₂, R₃ are identical.
and rank (A) = 2 as the submatrix \(\left[\begin{array}{cc}
1 & 1 \\
0 & -3
\end{array}\right]\) is non-singular.
Hence the system has a non-trivial solution, ∵ ρ(A) < 3
The system of equations equivalent to the given system of equations are
x + y – z = 0
3y – 2z = 0
Let z = k
⇒ y = \(\frac{2 k}{3}\)
x = \(\frac{k}{3}\)
∴ x = \(\frac{k}{3}\), y = \(\frac{2 k}{3}\), z = k for any real number of k.

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Matrices Solutions Exercise 3(h) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Matrices Solutions Exercise 3(h)

Solve the following systems of equations.
(i) by using Cramer’s rule and matrix inversion method, when the coefficient matrix is non-singular.
(ii) by using the Gauss-Jordan method. Also, determine whether the system has a unique solution or an infinite number of solutions, or no solution, and find the solutions if exist.

Question 1.
5x – 6y + 4z = 15
7x + 4y – 3z = 19
2x + y + 6z = 46
Solution:
(i) Cramer’s rule:
Δ = \(\left|\begin{array}{ccc}
5 & -6 & 4 \\
7 & 4 & -3 \\
2 & 1 & 6
\end{array}\right|\)
= 5(24 + 3) + 6(42 + 6) + 4(7 – 8)
= 135 + 288 – 4
= 419
Δ₁ = \(\left|\begin{array}{ccc}
15 & -6 & 4 \\
19 & 4 & -3 \\
46 & 1 & 6
\end{array}\right|\)
= 15(24 + 3) + 6(114 + 138) + 4(19 – 184)
= 405 + 1512 – 660
= 1917 – 660
= 1257
Δ₂ = \(\left|\begin{array}{ccc}
5 & 15 & 4 \\
7 & 19 & -3 \\
2 & 46 & 6
\end{array}\right|\)
= 5(114 + 138) – 15(42 + 6) + 4(322 – 38)
= 1260 – 720 + 1136
= 1676
Δ₃ = \(\left|\begin{array}{ccc}
5 & -6 & 15 \\
7 & 4 & 19 \\
2 & 1 & 46
\end{array}\right|\)
= 5(184 – 19) + 6(322 – 38) + 15(7 – 8)
= 825 + 1704 – 15
= 2529 – 15
= 2514

Solution is x = 3, y = 4, z = 6.

(ii) Matrix inversion method:



Solution is x = 3, y = 4, z = 6

(iii) Gauss-Jordan method:

∴ Unique solution exists.
Solution is x = 3, y = 4, z = 6.

Question 2.
x + y + z = 1
2x + 2y + 3z = 6
x + 4y + 9z = 3
Solution:
(i) Cramer’s rule:
Δ = \(\left|\begin{array}{lll}
1 & 1 & 1 \\
2 & 2 & 3 \\
1 & 4 & 9
\end{array}\right|\)
= 1(18 – 12) – 1(18 – 3) + 1(8 – 2)
= 6 – 15 + 6
= -3
Δ₁ = \(\left|\begin{array}{lll}
1 & 1 & 1 \\
6 & 2 & 3 \\
3 & 4 & 9
\end{array}\right|\)
= 1(18 – 12) – 1(54 – 9) + 1(24 – 6)
= 6 – 45 + 18
= -21
Δ₂ = \(\left|\begin{array}{lll}
1 & 1 & 1 \\
2 & 6 & 3 \\
1 & 3 & 9
\end{array}\right|\)
= 1(54 – 9) – 1(18 – 3) + 1(6 – 6)
= 45 – 15
= 30
Δ₃ = \(\left|\begin{array}{lll}
1 & 1 & 1 \\
2 & 2 & 6 \\
1 & 4 & 3
\end{array}\right|\)
= 1(6 – 24) – 1(6 – 6) + 1(8 – 2)
= -18 – 0 + 6
= -12

Solution is x = 7, y = -10, z = 4

(ii) Matrix inversion method:



∴ Solution is x = 7, y = -10, z = 4

(iii) Gauss-Jordan method:
Augmented matrix is A = \(\left[\begin{array}{llll}
1 & 1 & 1 & 1 \\
2 & 2 & 3 & 6 \\
1 & 4 & 9 & 3
\end{array}\right]\)
R₂ → R₂ – 2R₁, R₃ → R₃ – R₁

Unique solution exists.
∴ Solution is x = 7, y = -10, z = 4

Question 3.
x – y + 3z = 5
4x + 2y – z = 0
-x + 3y + z = 5
Solution:
(i) Cramer’s rule:
Δ = \(\left|\begin{array}{ccc}
1 & -1 & 3 \\
4 & 2 & -1 \\
-1 & 3 & 1
\end{array}\right|\)
= 1(2 + 3) + 1(4 – 1) + 3(12 + 2)
= 5 + 3 + 42
= 50
Δ₁ = \(\left|\begin{array}{ccc}
5 & -1 & 3 \\
0 & 2 & -1 \\
5 & 3 & 1
\end{array}\right|\)
= 5(2 + 3) + 1(0 + 5) + 3(0 – 10)
= 25 + 5 – 30
= 0
Δ₂ = \(\left|\begin{array}{ccc}
1 & 5 & 3 \\
4 & 0 & -1 \\
-1 & 5 & 1
\end{array}\right|\)
= 1(0 + 5) – 5(4 – 1) + 3(20 – 0)
= 5 – 15 + 60
= 50
Δ₃ = \(\left|\begin{array}{ccc}
1 & -1 & 5 \\
4 & 2 & 0 \\
-1 & 3 & 5
\end{array}\right|\)
= 1(10 – 0) + 1(20 – 0) + 5(12 + 2)
= 10 + 20 + 70
= 100

∴ Solution is x = 0, y = 1, z = 2.

(ii) Matrix inversion method:



Solution is x = 0, y = 1, z = 2

(iii) Gauss Jordan method:

Unique solution exists.
∴ Solution is x = 0, y = 1, z = 2

Question 4.
2x + 6y + 11 = 0
6x + 20y – 6z + 3 = 0
6y – 18z + 1 = 0
Solution:
(i) Cramer’s rule:
Δ = \(\left|\begin{array}{ccc}
2 & 6 & 0 \\
6 & 20 & -6 \\
0 & 6 & -18
\end{array}\right|\)
= 2(-360 + 36) – 6(-108 – 0)
= -648 + 648
= 0
∴ Cramer’s rule and matrix inversion method cannot be used.
∵ Δ = 0

(ii) Gauss Jordan method:

ρ(A) = 2, ρ(AB) = 3
ρ(A) ≠ ρ(AB)
∴ The given system of equations does not have a solution.

Question 5.
2x – y + 3z = 9
x + y + z = 6
x – y + z = 2
Solution:
(i) Cramer’s rule:
Δ = \(\left|\begin{array}{ccc}
2 & -1 & 3 \\
1 & 1 & 1 \\
1 & -1 & 1
\end{array}\right|\)
= 2(1 + 1) + 1(1 – 1) + 3(-1 – 1)
= 4 + 0 – 6
= -2
Δ₁ = \(\left|\begin{array}{ccc}
9 & -1 & 3 \\
6 & 1 & 1 \\
2 & -1 & 1
\end{array}\right|\)
= 9(1 + 1) + 1(6 – 2) + 3(-6 – 2)
= 18 + 4 – 24
= -2
Δ₂ = \(\left|\begin{array}{lll}
2 & 9 & 3 \\
1 & 6 & 1 \\
1 & 2 & 1
\end{array}\right|\)
= 2(6 – 2) – 9(1 – 1) + 3(2 – 6)
= 8 – 0 – 12
= -4
Δ₃ = \(\left|\begin{array}{ccc}
2 & -1 & 9 \\
1 & 1 & 6 \\
1 & -1 & 2
\end{array}\right|\)
= 2(2 + 6) + 1(2 – 6) + 9(-1 – 1)
= 16 – 4 – 18
= -6

Solution is x = 1, y = 2, z = 3.

(ii) Matrix inversion method:


Solution is x = 1, y = 2, z = 3.

(iii) Gauss-Jordan method:

∴ The given equations have a unique solution.
Solution is x = 1, y = 2, z = 3

Question 6.
2x – y + 8z = 13
3x + 4y + 5z = 18
5x – 2y + 7z = 20
Solution:
(i) Cramer’s rule:
Δ = \(\left|\begin{array}{ccc}
2 & -1 & 8 \\
3 & 4 & 5 \\
5 & -2 & 7
\end{array}\right|\)
= 2(28 + 10) + 1(21 – 25) + 8(-6 – 20)
= 76 – 4 – 208
= -136
Δ₁ = \(\left|\begin{array}{ccc}
13 & -1 & 8 \\
18 & 4 & 5 \\
20 & -2 & 7
\end{array}\right|\)
= 13(28 + 10) + 1(126 – 100) + 8(-36 – 80)
= 494 + 26 – 928
= -408
Δ₂ = \(\left|\begin{array}{lll}
2 & 13 & 8 \\
3 & 18 & 5 \\
5 & 20 & 7
\end{array}\right|\)
= 2(126 – 100) – 13(21 – 25) + 8(60 – 90)
= 52 + 52 – 240
= -136
Δ₃ = \(\left|\begin{array}{ccc}
2 & -1 & 13 \\
3 & 4 & 18 \\
5 & -2 & 20
\end{array}\right|\)
= 2(80 + 36) + 1(60 – 90) + 13(-6 – 20)
= 232 – 30 – 338
= -136

∴ Solution is x = 3, y = 1, z = 1

(ii) Matrix inversion method:



∴ Solution is x = 3, y = 1, z = 1

(iii) Gauss Jordan method:

∴ The given equations have a unique solution and Solution is x = 3, y = 1, z = 1.

Question 7.
2x – y + 3z = 8
-x + 2y + z = 4
3x + y – 4z = 0
Solution:
(i) Cramer’s rule:
Δ = \(\left|\begin{array}{ccc}
2 & -1 & 3 \\
-1 & 2 & 1 \\
3 & 1 & -4
\end{array}\right|\)
= 2(-8 – 1) + 1(4 – 3) + 3(-1 – 6)
= -18 + 1 – 21
= -38
Δ₁ = \(\left|\begin{array}{ccc}
8 & -1 & 3 \\
4 & 2 & 1 \\
0 & 1 & -4
\end{array}\right|\)
= 8(-8 – 1) + 1(-16 – 0) + 3(4 – 0)
= -72 – 16 + 12
= -76
Δ₂ = \(\left|\begin{array}{ccc}
2 & 8 & 3 \\
-1 & 4 & 1 \\
3 & 0 & -4
\end{array}\right|\)
= 2(-16 – 0) – 8(4 – 3) + 3(-0 – 12)
= -32 – 8 – 36
= -76
Δ₃ = \(\left|\begin{array}{ccc}
2 & -1 & 8 \\
-1 & 2 & 4 \\
3 & 1 & 0
\end{array}\right|\)
= 2(0 – 4) + 1(0 – 12) + 8(-1 – 6)
= -8 – 12 – 56
= -76

∴ Solution is x = 2, y = 2, z = 2.

(ii) Matrix inversion method:


Solution is x = 2, y = 2, z = 2

(iii) Gauss Jordan method:


∴ The given equations have a unique solution and solution is x = 2, y = 2, z = 2.

Question 8.
x + y + z = 9
2x + 5y + 7z = 52
2x + y – z = 0
Solution:
(i) Cramer’s rule:
Δ = \(\left|\begin{array}{ccc}
1 & 1 & 1 \\
2 & 5 & 7 \\
2 & 1 & -1
\end{array}\right|\)
= 1(-5 – 7) – 1(-2 – 14) + 1(2 – 10)
= -12 + 16 – 8
= -4
Δ₁ = \(\left|\begin{array}{ccc}
9 & 1 & 1 \\
52 & 5 & 7 \\
0 & 1 & -1
\end{array}\right|\)
= 9(-5 – 7) – 1(-52 – 0) + 1(52 – 0)
= -108 + 52 + 52
= -4
Δ₂ = \(\left|\begin{array}{ccc}
1 & 9 & 1 \\
2 & 52 & 7 \\
2 & 0 & -1
\end{array}\right|\)
= 1(-52 – 0) – 9(-2 – 14) + 1(0 – 104)
= -52 + 144 – 104
= -12
Δ₃ = \(\left|\begin{array}{ccc}
1 & 1 & 9 \\
2 & 5 & 52 \\
2 & 1 & 0
\end{array}\right|\)
= 1(0 – 52) – 1(0 – 104) + 9(2 – 10)
= -52 + 104 – 72
= -20

(ii) Matrix inversion method:


Solution is x = 1, y = 3, z = 5

(iii) Gauss Jordan method:

∴ The given equations have a unique solution and solution is x = 1, y = 3, z = 5.

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Matrices Solutions Exercise 3(g) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Matrices Solutions Exercise 3(g)

Examine whether the following systems of equations are consistent or inconsistent and if consistent find the complete solutions.

Question 1.
x + y + z = 4
2x + 5y – 2z = 3
x + 7y – 7z = 5
Solution:

ρ(A) = 2, ρ(AB) = 3
ρ(A) ≠ ρ(AB)
∴ The given system of equations are in consistent.

Question 2.
x + y + z = 6
x – y + z = 2
2x – y + 3z = 9
Solution:

Question 3.
x + y + z = 1
2x + y + z = 2
x + 2y + 2z = 1
Solution:

ρ(A) = 2 = ρ(AB) < 3
The given system of equations are consistent and have infinitely many solutions.
The solutions are given by [(x, y, z) 1x = 1, y + z = 0].

Question 4.
x + y + z = 9
2x + 5y + 7z = 52
2x + y – z = 0
Solution:

∴ ρ(A) = ρ(AB) = 3
The given system of equations are consistent have a unique solution.
∴ Solution is given by x = 1, y = 3, z = 5.

Question 5.
x + y + z = 6
x + 2y + 3z = 10
x + 2y + 4z = 1
Solution:
Augmented matrix A = \(\left[\begin{array}{cccc}
1 & 1 & 1 & 6 \\
1 & 2 & 3 & 10 \\
1 & 2 & 4 & 1
\end{array}\right]\)
By R₂ → R₂ – R₁, R₃ → R₃ – R₂, we obtain

∴ ρ(A) = ρ(AB) = 3
The given system of equations are consistent.
They have a unique solution.
∴ Solution is given by x = -7, y = 22, z = -9.

Question 6.
x – 3y – 8z = -10
3x + y – 4z = 0
2x + 5y + 6z = 13
Solution:
The Augmented matrix

ρ(A) = ρ(AB) = 2 < 3
∴ The given system of equations are consistent have infinitely many solutions.
x + y = 2 and y + 2z = 3
Taking z = k, y = 3 – 2z = 3-2k
x = 2 – y
= 2 – (3 – 2k)
= 2 – 3 + 2k
= 2k – 1
∴ The solutions are given by x = -1 + 2k, y = 3 – 2k, z = k where ‘k’ is any scalar.

Question 7.
2x + 3y + z = 9
x + 2y + 3z = 6
3x + y + 2z = 8
Solution:

∴ ρ(A) = ρ(AB) = 3
The given system of equations are consistent have a unique solution.
∴ Solution is given by x = \(\frac{35}{18}\), y = \(\frac{29}{18}\), z = \(\frac{5}{18}\)

Question 8.
x + y + 4z = 6
3x + 2y – 2z = 9
5x + y + 2z = 13
Solution:

∴ ρ(A) = ρ(AB) = 3
∴ The given system of equations are consistent have a unique solution.
∴ Solution is given by x = 2, y = 2, z = \(\frac{1}{2}\)

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Matrices Solutions Exercise 3(f) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Matrices Solutions Exercise 3(f)

I. Find the rank of each of the following matrices.

Question 1.
\(\left[\begin{array}{ll}
1 & 0 \\
0 & 0
\end{array}\right]\)
Solution:
Det A = \(\left|\begin{array}{ll}
1 & 0 \\
0 & 0
\end{array}\right|\) = 0 – 0 = 0
and |1| = 1 ≠ 0
∴ ρ(A) = 1

Question 2.
\(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)
Solution:
Det A = \(\left|\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right|\) = 1 – 0 = 1 ≠ 0
∴ ρ(A) = 2

Question 3.
\(\left[\begin{array}{ll}
1 & 1 \\
0 & 0
\end{array}\right]\)
Solution:
Det A = \(\left|\begin{array}{ll}
1 & 1 \\
0 & 0
\end{array}\right|\) = 0 – 0 = 0
|1| = 1 ≠ 0
∴ ρ(A) = 1

Question 4.
\(\left[\begin{array}{ll}
1 & 1 \\
1 & 0
\end{array}\right]\)
Solution:
Det A = \(\left|\begin{array}{ll}
1 & 1 \\
1 & 0
\end{array}\right|\) = 0 – 1 = -1 ≠ 0
∴ ρ(A) = 2

Question 5.
\(\left[\begin{array}{ccc}
1 & 0 & -4 \\
2 & -1 & 3
\end{array}\right]\)
Solution:
\(\left|\begin{array}{cc}
1 & -4 \\
2 & 3
\end{array}\right|\) = 3 + 8 = -11 ≠ 0
∴ ρ(A) = 2

Question 6.
\(\left[\begin{array}{lll}
1 & 2 & 6 \\
2 & 4 & 3
\end{array}\right]\)
Solution:
\(\left|\begin{array}{ll}
2 & 6 \\
4 & 3
\end{array}\right|\) = 6 – 24 = -18 ≠ 0
∴ ρ(A) = 2

II.

Question 1.
\(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 0 & 1 \\
0 & 1 & 0
\end{array}\right]\)
Solution:
Det A = \(\left|\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right|\)
= 1(1 – 0) – 0(0 – 0) + 0(0 – 0)
= 1 – 0 + 0
= 1 ≠ 0
∴ ρ(A) = 3

Question 2.
\(\left[\begin{array}{ccc}
1 & 4 & -1 \\
2 & 3 & 0 \\
0 & 1 & 2
\end{array}\right]\)
Solution:
Det A = \(\left|\begin{array}{ccc}
1 & 4 & -1 \\
2 & 3 & 0 \\
0 & 1 & 2
\end{array}\right|\)
= 1(6 – 0) – 2(8 + 1) + 0(0 + 3)
= 6 – 18
= -12 ≠ 0
∴ ρ(A) = 3

Question 3.
\(\left[\begin{array}{lll}
1 & 2 & 3 \\
2 & 3 & 4 \\
0 & 1 & 2
\end{array}\right]\)
Solution:
Det A = \(\left|\begin{array}{lll}
1 & 2 & 3 \\
2 & 3 & 4 \\
0 & 1 & 2
\end{array}\right|\)
= 1(6 – 4) – 2(4 – 3) + 0(8 – 9)
= 2 – 2 + 0
= 0
∴ ρ(A) ≠ 3, ρ(A) < 3
Take \(\left|\begin{array}{ll}
1 & 2 \\
2 & 3
\end{array}\right|\) = 3 – 4 = -1 ≠ 0
∴ ρ(A) = 2

Question 4.
\(\left[\begin{array}{lll}
1 & 1 & 1 \\
1 & 1 & 1 \\
1 & 1 & 1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{lll}
1 & 1 & 1 \\
1 & 1 & 1 \\
1 & 1 & 1
\end{array}\right]\), det A = 0, ρ(A) ≠ 3
All 2 × 2 sub-matrix det. is zero
∴ ρ(A) ≠ 2
|1| = 1 ≠ 0
∴ ρ(A) = 1

Question 5.
\(\left[\begin{array}{cccc}
1 & 2 & 0 & -1 \\
3 & 4 & 1 & 2 \\
-2 & 3 & 2 & 5
\end{array}\right]\)
Solution:
Take sub-matrix B = \(\left|\begin{array}{ccc}
1 & 2 & 0 \\
3 & 4 & 1 \\
-2 & 3 & 2
\end{array}\right|\)
= 1(8 – 3) – 2(6 + 2)
= 5 – 16
= -11 ≠ 0
Rank of the given matrix is 3.

Question 6.
\(\left[\begin{array}{cccc}
0 & 1 & 1 & -2 \\
4 & 0 & 2 & 5 \\
2 & 1 & 3 & 1
\end{array}\right]\)
Solution:
Take sub matrix A = \(\left[\begin{array}{lll}
0 & 1 & 1 \\
4 & 0 & 2 \\
2 & 1 & 3
\end{array}\right]\)
= -1(12 – 4) + 1(4 – 0)
= -8 + 4
= -4 ≠ 0
∴ ρ(A) = 3

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Matrices Solutions Exercise 3(e) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Matrices Solutions Exercise 3(e)

I.

Question 1.
Find the adjoint and inverse of the following matrices.
(i) \(\left[\begin{array}{cc}
2 & -3 \\
4 & 6
\end{array}\right]\)
Solution:

(ii) \(\left[\begin{array}{cc}
\cos \alpha & -\sin \alpha \\
\sin \alpha & \cos \alpha
\end{array}\right]\)
Solution:

(iii) \(\left[\begin{array}{lll}
1 & 0 & 2 \\
2 & 1 & 0 \\
3 & 2 & 1
\end{array}\right]\)
Solution:

(iv) \(\left[\begin{array}{lll}
2 & 1 & 2 \\
1 & 0 & 1 \\
2 & 2 & 1
\end{array}\right]\)
Solution:

Question 2.
If A = \(\left[\begin{array}{cc}
a+i b & c+i d \\
-c+i d & a-i b
\end{array}\right]\), a² + b² + c² + d² = 1, then find the inverse of A.
Solution:

Question 3.
If A = \(\left[\begin{array}{ccc}
1 & -2 & 3 \\
0 & -1 & 4 \\
-2 & 2 & 1
\end{array}\right]\), then find A^-1
Solution:

Question 4.
If A = \(\left|\begin{array}{ccc}
-1 & -2 & -2 \\
2 & 1 & -2 \\
2 & -2 & 1
\end{array}\right|\), then show that the adjoint of A = 3A’ find A^-1.
Solution:

Question 5.
If abc ≠ 0, find the inverse of \(\left[\begin{array}{lll}
a & 0 & 0 \\
0 & b & 0 \\
0 & 0 & c
\end{array}\right]\)
Solution:

II.

Question 1.
If A = \(\left[\begin{array}{lll}
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 0
\end{array}\right]\) and B = \(\frac{1}{2}\left[\begin{array}{lll}
b+c & c-a & b-a \\
c-b & c+a & a-b \\
b-c & a-c & a+b
\end{array}\right]\) then show that ABA^-1 is a diagonal matrix.
Solution:

Question 2.
If 3A = \(\left[\begin{array}{ccc}
1 & 2 & 2 \\
2 & 1 & -2 \\
-2 & 2 & -1
\end{array}\right]\) then show that A^-1 = A’
Solution:

Question 3.
If A = \(\left[\begin{array}{rrr}
3 & -3 & 4 \\
2 & -3 & 4 \\
0 & -1 & 1
\end{array}\right]\), then show that A^-1 = A³
Solution:

∴ A⁴ = I
det A = 3(1) – 3(-2) + 4(-2) = 1
∵ A ≠ 0 ⇒ A^-1 exists
∵ A⁴ = I
Multiply with A^-1
A⁴ (A^-1) = I (A^-1)
⇒ A³ (AA^-1) = A^-1
⇒ A³ (I) = A^-1
∴ A^-1 = A³

Question 4.
If AB = I or BA = I, then prove that A is invertible and B = A^-1
Solution:
Given AB = I
⇒ AB| = |1|
⇒ |A| |B| = 1
⇒ |A| ≠ 0
∴ A is a non-singular matrix and BA = I
⇒ |BA| = |I|
⇒ |B| |A| = 1
⇒ |A| ≠ 0
∴ A is a non-singular matrix.
AB = I or BA = I, A is invertible.
∴ A^-1 exists.
AB = I
⇒ A^-1AB = A^-1I
⇒ IB = A^-1
⇒ B = A^-1
∴ B = A^-1

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Matrices Solutions Exercise 3(d) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Matrices Solutions Exercise 3(d)

I.

Question 1.
Find the determinants of the following matrices.
(i) \(\left[\begin{array}{cc}
2 & 1 \\
1 & -5
\end{array}\right]\)
Solution:
det A = ad – bc
= 2(-5) – 1(1)
= -10 – 1
= -11

(ii) \(\left[\begin{array}{cc}
4 & 5 \\
-6 & 2
\end{array}\right]\)
Solution:
det A = 4(2) – (-6)(5)
= 8 + 30
= 38

(iii) \(\left[\begin{array}{cc}
\mathbf{i} & 0 \\
0 & -\mathbf{i}
\end{array}\right]\)
Solution:
det A = -i² – 0
= 1 – 0
= 1

(iv) \(\left[\begin{array}{lll}
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 0
\end{array}\right]\)
Solution:
det A = 0(0 – 1) – 1(0 – 1) + 1(1 – 0)
= 1 + 1
= 2

(v) \(\left[\begin{array}{ccc}
1 & 4 & 2 \\
2 & -1 & 4 \\
-3 & 7 & 6
\end{array}\right]\)
Solution:
det A = 1(-6 – 28) – 4(12 + 12) + 2(14 – 3)
= -34 – 96 + 22
= -108

(vi) \(\left[\begin{array}{ccc}
2 & -1 & 4 \\
4 & -3 & 1 \\
1 & 2 & 1
\end{array}\right]\)
Solution:
det A = 2(-3 – 2) + 1(4 – 1) + 4(8 + 3)
= -10 + 3 + 44
= 37

(vii) \(\left[\begin{array}{ccc}
1 & 2 & -3 \\
4 & -1 & 7 \\
2 & 4 & -6
\end{array}\right]\)
Solution:
det A = 0 since R₁ and R₃ are proportional.

(viii) \(\left[\begin{array}{lll}
a & h & g \\
\text { h } & b & f \\
g & f & c
\end{array}\right]\)
Solution:
det A = a(bc – f²) – h(ch – fg) + g(hf – bg)
= abc – af² – ch² + fgh + fgh – bg²
= abc + 2fgh – af² – bg² – ch²

(ix) \(\left[\begin{array}{lll}
\mathbf{a} & \mathbf{b} & \mathbf{c} \\
\mathbf{b} & \mathbf{c} & \mathbf{a} \\
\mathbf{c} & \mathbf{a} & \mathbf{b}
\end{array}\right]\)
Solution:
det A = a(bc – a²) – b(b² – ac) + c(ab – c²)
= abc – a³ – b³ + abc + abc – c³
= 3abc – a³ – b³ – c³

(x) \(\left[\begin{array}{ccc}
1^{2} & 2^{2} & 3^{2} \\
2^{2} & 3^{2} & 4^{2} \\
3^{2} & 4^{2} & 5^{2}
\end{array}\right]\)
Solution:
det A = \(\left|\begin{array}{ccc}
1 & 4 & 9 \\
4 & 9 & 16 \\
9 & 16 & 25
\end{array}\right|\)
= 1(225 – 256) – 4(100 – 144) – 9(64 – 81)
= -31 + 176 – 153
= -184 + 176
= -8

Question 2.
If A = \(\left[\begin{array}{ccc}
1 & 0 & 0 \\
2 & 3 & 4 \\
5 & -6 & x
\end{array}\right]\) and det A = 45 then find x.
Solution:
det A = 45
\(\left|\begin{array}{ccc}
1 & 0 & 0 \\
2 & 3 & 4 \\
5 & -6 & x
\end{array}\right|\) = 45
⇒ 3x + 24 = 45
⇒ 3x – 45 + 24 = 0
⇒ 3x – 21 = 0
⇒ x = 7

II.

Question 1.
Show that \(\left|\begin{array}{lll}
b c & b+c & 1 \\
c a & c+a & 1 \\
a b & a+b & 1
\end{array}\right|\) = (a – b)(b – c)(c – a)
Solution:

Question 2.
Show that \(\left|\begin{array}{ccc}
\mathbf{b}+\mathbf{c} & \mathbf{c}+\mathbf{a} & \mathbf{a}+\mathbf{b} \\
\mathbf{a}+\mathbf{b} & \mathbf{b}+\mathbf{c} & \mathbf{c}+\mathbf{a} \\
\mathbf{a} & \mathbf{b} & \mathbf{c}
\end{array}\right|\) = a³ + b³ + c³ – 3abc
Solution:

= (a + b + c) [(-ac + b²) – (-c² + ab) + (-bc + a²)]
= (a + b + c) (-ac + b² + c² – ab – bc + a²)
= (a + b + c) (a² + b² + c² – ab – bc – ca)
= a³ + b³ + c³ – 3abc

Question 3.
Show that \(\left|\begin{array}{ccc}
\mathbf{y}+\mathbf{z} & \mathbf{x} & \mathbf{x} \\
\mathbf{y} & \mathbf{z}+\mathbf{x} & \mathbf{y} \\
\mathbf{z} & \mathbf{z} & \mathbf{x}+\mathbf{y}
\end{array}\right|\) = 4xyz
Solution:
L.H.S = \(\left|\begin{array}{ccc}
\mathbf{y}+\mathbf{z} & \mathbf{x} & \mathbf{x} \\
\mathbf{y} & \mathbf{z}+\mathbf{x} & \mathbf{y} \\
\mathbf{z} & \mathbf{z} & \mathbf{x}+\mathbf{y}
\end{array}\right|\)
= (y + z) [(z + x) (x + y) – yz] – x[y(x + y) – yz] + x[yz – z(z + x)]
= (y + z) (zx + yz + x² + xy – yz) – x(xy + y² – yz) + x(yz – z² – zx)
= (y + z) (zx + x² + xy) – x(xy + y² – yz) + x(yz – z² – zx)
= xyz + x²y + xy² + xz² + x²z + xyz – x²y – xy² + xyz + xyz – xz² – x²z
= 4xyz
= R.H.S

Question 4.
If \(\left|\begin{array}{ccc}
a & a^{2} & 1+a^{3} \\
b & b^{2} & 1+b^{3} \\
c & c^{2} & 1+c^{3}
\end{array}\right|\) = 0 and \(\left|\begin{array}{ccc}
a & a^{2} & 1 \\
b & b^{2} & 1 \\
c & c^{2} & 1
\end{array}\right|\) ≠ 0 then show that abc = -1
Hint: If each element in a row (column) of a square matrix is the sum of two numbers, then its discriminant can be expressed as the sum of discriminants of two square matrices.
Solution:

Question 5.
Without expanding the determinant, prove that
(i) \(\left|\begin{array}{ccc}
a & a^{2} & b c \\
b & b^{2} & c a \\
c & c^{2} & a b
\end{array}\right|=\left|\begin{array}{ccc}
1 & a^{2} & a^{3} \\
1 & b^{2} & b^{3} \\
1 & c^{2} & c^{3}
\end{array}\right|\)
Solution:

(ii) \(\left|\begin{array}{ccc}
a x & b y & c z \\
x^{2} & y^{2} & z^{2} \\
1 & 1 & 1
\end{array}\right|=\left|\begin{array}{ccc}
a & b & c \\
x & y & z \\
y z & z x & x y
\end{array}\right|\)
Solution:

(iii) \(\left|\begin{array}{lll}
1 & b c & b+c \\
1 & c a & c+a \\
1 & a b & a+b
\end{array}\right|=\left|\begin{array}{ccc}
1 & a & a^{2} \\
1 & b & b^{2} \\
1 & c & c^{2}
\end{array}\right|\)
Solution:
L.H.S = \(\left|\begin{array}{ccc}
1 & b c & b+c \\
1 & c a & c+a \\
1 & a b & a+b
\end{array}\right|\)

= (b – a) (c – a) (c + a – b – a)
= (a – b) (b – c) (c – a)
∴ LHS = RHS

Question 6.
If ∆₁ = \(\left|\begin{array}{ccc}
a_{1}^{2}+b_{1}+c_{1} & a_{1} a_{2}+b_{2}+c_{2} & a_{1} a_{3}+b_{3}+c_{3} \\
b_{1} b_{2}+c_{1} & b_{2}^{2}+c_{2} & b_{2} b_{3}+c_{3} \\
c_{3} c_{1} & c_{3} c_{2} & c_{3}^{2}
\end{array}\right|\) and ∆₂ = \(\left|\begin{array}{lll}
a_{1} & b_{2} & c_{2} \\
a_{2} & b_{2} & c_{2} \\
a_{3} & b_{3} & c_{3}
\end{array}\right|\), then find the value of \(\frac{\Delta_{1}}{\Delta_{2}}\)
Solution:

Question 7.
If ∆₁ = \(\left|\begin{array}{ccc}
1 & \cos \alpha & \cos \beta \\
\cos \alpha & 1 & \cos \gamma \\
\cos \beta & \cos \alpha & 1
\end{array}\right|\), ∆₂ = \(\left|\begin{array}{ccc}
0 & \cos \alpha & \cos \beta \\
\cos \alpha & 0 & \cos \gamma \\
\cos \beta & \cos \gamma & 0
\end{array}\right|\) and ∆₁ = ∆₂, then show that cos²α + cos²β + cos²γ = 1
Solution:
∆₁ = \(\left|\begin{array}{ccc}
1 & \cos \alpha & \cos \beta \\
\cos \alpha & 1 & \cos \gamma \\
\cos \beta & \cos \alpha & 1
\end{array}\right|\)
= 1(1 – cos²γ) – cos α (cos α – cos β cos γ) + cos β (cos α cos γ – cos β)
= 1 – cos²γ – cos²α + cos α cos β cos γ + cos α cos β cos γ – cos²β
= 1 – cos²γ – cos²α – cos²β + 2 cos α cos β cos γ
∆₂ = \(\left|\begin{array}{ccc}
0 & \cos \alpha & \cos \beta \\
\cos \alpha & 0 & \cos \gamma \\
\cos \beta & \cos \gamma & 0
\end{array}\right|\)
= 0(0 – cos²γ) – cos α (0 – cos γ cos β) + cos β (cos α cos γ – 0)
= cos α cos β cos γ + cos α cos β cos γ
= 2 cos α cos β cos γ
Given ∆₁ = ∆₂
1 – cos²α – cos²β – cos²γ + 2 cos α cos β cos γ = 2 cos α cos β cos γ
1 – cos²α – cos²β – cos²γ = 0
1 = cos²α + cos²β + cos²γ

III.

Question 1.
Show that \(\left|\begin{array}{ccc}
\mathbf{a}+\mathbf{b}+2 \mathbf{c} & \mathbf{a} & \mathbf{b} \\
\mathbf{c} & \mathbf{b}+\mathbf{c}+\mathbf{2} \mathbf{a} & \mathbf{b} \\
\mathbf{c} & \mathbf{a} & \mathbf{c}+\mathbf{a}+\mathbf{2} \mathbf{b}
\end{array}\right|\) = 2(a + b + c)³
Solution:

Question 2.
Show that \(\left|\begin{array}{lll}
a & b & c \\
b & c & a \\
c & a & b
\end{array}\right|^{2}\) = \(\left|\begin{array}{ccc}
2 b c-a^{2} & c^{2} & b^{2} \\
c^{2} & 2 a c-b^{2} & a^{2} \\
b^{2} & a^{2} & 2 a b-c^{2}
\end{array}\right|\) = (a³ + b³ + c³ – 3abc)²
Solution:

Question 3.
Show that \(\left|\begin{array}{ccc}
a^{2}+2 a & 2 a+1 & 1 \\
2 a+1 & a+2 & 1 \\
3 & 3 & 1
\end{array}\right|\) = (a – 1)³
Solution:

Question 4.
Show that \(\left|\begin{array}{ccc}
a & b & c \\
a^{2} & b^{2} & c^{2} \\
a^{3} & b^{3} & c^{3}
\end{array}\right|\) = abc(a – b)(b – c)(c – a)
Solution:

Question 5.
Show that \(\left|\begin{array}{ccc}
-2 \mathbf{a} & \mathbf{a}+\mathbf{b} & \mathbf{c}+\mathbf{a} \\
\mathbf{a}+\mathbf{b} & -\mathbf{2} \mathbf{b} & \mathbf{b}+\mathbf{c} \\
\mathbf{c}+\mathbf{a} & \mathbf{c}+\mathbf{b} & -2 \mathbf{c}
\end{array}\right|\) = 4(a + b) (b + c) (c + a)
Solution:

∴ (c + a) is a factor for ∆
Similarly a + b, b + c are also factors ∆.
∵ ∆ is a third-degree expression in a, b, c.
∆ = k(a + b) (b + c) (c + a),
where k is a non-zero scalar.
Put a = 1, b = 1, c = 1, then
\(\left|\begin{array}{ccc}
-2 & 2 & 2 \\
2 & -2 & 2 \\
2 & 2 & -2
\end{array}\right|\) = k(1 + 1) (1 + 1) (1 + 1)
⇒ -2(4 – 4) – 2(-4 – 4) + 2(4 + 4) = 8k
⇒ 16 + 16 = 8k
⇒ k = 4
∴ ∆ = 4(a + b) (b + c) (c + a)
Hence \(\left|\begin{array}{ccc}
-2 \mathbf{a} & \mathbf{a}+\mathbf{b} & \mathbf{c}+\mathbf{a} \\
\mathbf{a}+\mathbf{b} & -\mathbf{2} \mathbf{b} & \mathbf{b}+\mathbf{c} \\
\mathbf{c}+\mathbf{a} & \mathbf{c}+\mathbf{b} & -2 \mathbf{c}
\end{array}\right|\) = 4(a + b) (b + c) (c + a)

Question 6.
Show that \(\left|\begin{array}{lll}
\mathbf{a}-\mathbf{b} & \mathbf{b}-\mathbf{c} & \mathbf{c}-\mathbf{a} \\
\mathbf{b}-\mathbf{c} & \mathbf{c}-\mathbf{a} & \mathbf{a}-\mathbf{b} \\
\mathbf{c}-\mathbf{a} & \mathbf{a}-\mathbf{b} & \mathbf{b}-\mathbf{c}
\end{array}\right|\)
Solution:
L.H.S = \(\left|\begin{array}{ccc}
0 & 0 & 0 \\
b-c & c-a & a-b \\
c-a & a-b & b-c
\end{array}\right|\) = 0
By R₁ → R₁ + (R₂ + R₃)

Question 7.
Show that \(\left|\begin{array}{ccc}
1 & a & a^{2}-b c \\
1 & b & b^{2}-c a \\
1 & c & c^{2}-a b
\end{array}\right|\) = 0
Solution:

Question 8.
Show that \(\left|\begin{array}{lll}
\mathbf{x} & \mathbf{a} & \mathbf{a} \\
\mathbf{a} & \mathbf{x} & \mathbf{a} \\
\mathbf{a} & \mathbf{a} & \mathbf{x}
\end{array}\right|\) = (x + 2a) (x – a)²
Solution:

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Matrices Solutions Exercise 3(c) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Matrices Solutions Exercise 3(c)

I.

Question 1.
If A = \(\left[\begin{array}{ccc}
2 & 0 & 1 \\
-1 & 1 & 5
\end{array}\right]\) and B = \(\left[\begin{array}{ccc}
-1 & 1 & 0 \\
0 & 1 & -2
\end{array}\right]\), then find (AB’)’.
Solution:

Question 2.
If A = \(\left[\begin{array}{cc}
-2 & 1 \\
5 & 0 \\
-1 & 4
\end{array}\right]\) and B = \(\left[\begin{array}{ccc}
-2 & 3 & 1 \\
4 & 0 & 2
\end{array}\right]\) then find 2A + B’ and 3B’ – A.
Solution:

Question 3.
If A = \(\left[\begin{array}{cc}
2 & -4 \\
-5 & 3
\end{array}\right]\), then find A + A’ and A.A’
Solution:

Question 4.
If A = \(\left[\begin{array}{ccc}
-1 & 2 & 3 \\
2 & 5 & 6 \\
3 & x & 7
\end{array}\right]\) is a symmetric matrix, then find x.
Hint: ‘A’ is a symmetric matrix ⇒ A^T = A
Solution:
A is a symmetric matrix
⇒ A’ = A

Equating 2nd row, 3rd column elements we get x = 6.

Question 5.
If A = \(\left[\begin{array}{ccc}
0 & 2 & 1 \\
-2 & 0 & -2 \\
-1 & x & 0
\end{array}\right]\) is a skew-symmetric matrix, find x.
Solution:
∵ A is a skew-symmetric matrix
⇒ A^T = -A

Equating second-row third column elements we get x = 2.

Question 6.
Is \(\left[\begin{array}{ccc}
0 & 1 & 4 \\
-1 & 0 & 7 \\
-4 & -7 & 0
\end{array}\right]\) symmetric or skewsymmetric?
Solution:

∴ A is a skew-symmetric matrix.

II.

Question 1.
If A = \(\left[\begin{array}{cc}
\cos \alpha & \sin \alpha \\
-\sin \alpha & \cos \alpha
\end{array}\right]\), show that A.A’ = A’. A = I₂
Solution:

From (1), (2) we get A.A’ = A’. A = I₂

Question 2.
If A = \(\left[\begin{array}{ccc}
1 & 5 & 3 \\
2 & 4 & 0 \\
3 & -1 & -5
\end{array}\right]\) and B = \(\left[\begin{array}{ccc}
2 & -1 & 0 \\
0 & -2 & 5 \\
1 & 2 & 0
\end{array}\right]\) then find 3A – 4B’.
Solution:

Question 3.
If A = \(\left[\begin{array}{cc}
7 & -2 \\
-1 & 2 \\
5 & 3
\end{array}\right]\) and B = \(\left[\begin{array}{cc}
-2 & -1 \\
4 & 2 \\
-1 & 0
\end{array}\right]\) then find AB’ and BA’.
Solution:

Question 4.
For any square matrix A, Show that AA’ is symmetric.
Solution:
A is a square matrix
(AA’)’ = (A’)’A’ = A.A’
∵ (AA’)’ = AA’
⇒ AA’ is a symmetric matrix.

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Matrices Solutions Exercise 3(b) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Matrices Solutions Exercise 3(b)

I.

Question 1.
Find the following products wherever possible.
Hint: (1 × 3) by (3 × 1) = 1 × 1
(i) \(\left[\begin{array}{lll}
-1 & 4 & 2
\end{array}\right]\left[\begin{array}{l}
5 \\
1 \\
3
\end{array}\right]\)
(ii) \(\left[\begin{array}{ccc}
2 & 1 & 4 \\
6 & -2 & 3
\end{array}\right]\left[\begin{array}{l}
1 \\
2 \\
1
\end{array}\right]\)
(iii) \(\left[\begin{array}{cc}
3 & -2 \\
1 & 6
\end{array}\right]\left[\begin{array}{cc}
4 & -1 \\
2 & 5
\end{array}\right]\)
(iv) \(\left[\begin{array}{lll}
2 & 2 & 1 \\
1 & 0 & 2 \\
2 & 1 & 2
\end{array}\right]\left[\begin{array}{ccc}
-2 & -3 & 4 \\
2 & 2 & -3 \\
1 & 2 & -2
\end{array}\right]\)
(v) \(\left[\begin{array}{ccc}
3 & 4 & 9 \\
0 & -1 & 5 \\
2 & 6 & 12
\end{array}\right]\left[\begin{array}{ccc}
13 & -2 & 0 \\
0 & 4 & 1
\end{array}\right]\)
(vi) \(\left[\begin{array}{c}
1 \\
-2 \\
1
\end{array}\right]\left[\begin{array}{ccc}
2 & 1 & 4 \\
6 & -2 & 3
\end{array}\right]\)
(vii) \(\left[\begin{array}{cc}
1 & -1 \\
-1 & 1
\end{array}\right]\left[\begin{array}{ll}
1 & 1 \\
1 & 1
\end{array}\right]\)
(viii) \(\left[\begin{array}{ccc}
0 & c & -b \\
-c & 0 & a \\
b & -a & 0
\end{array}\right]\left[\begin{array}{ccc}
a^{2} & a b & a c \\
a b & b^{2} & b c \\
a c & b c & c^{2}
\end{array}\right]\)
Solution:

(v) \(\left[\begin{array}{ccc}
3 & 4 & 9 \\
0 & -1 & 5 \\
2 & 6 & 12
\end{array}\right]\left[\begin{array}{ccc}
13 & -2 & 0 \\
0 & 4 & 1
\end{array}\right]\)
First matrix is a 3 × 3 matrix and second matrix is 2 × 3 matrix.
No. of columns in the first matrix ≠ No. of rows in the second matrix.
∴ Matrix product is not possible.

(vi) \(\left[\begin{array}{c}
1 \\
-2 \\
1
\end{array}\right]\left[\begin{array}{ccc}
2 & 1 & 4 \\
6 & -2 & 3
\end{array}\right]\)
No. of columns in first matrix = 1
No. of rows in second matrix = 2
No. of columns in the first matrix ≠ No. of rows in the second matrix
Multiplication of matrices is not possible.

Question 2.
If A = \(\left[\begin{array}{ccc}
1 & -2 & 3 \\
-4 & 2 & 5
\end{array}\right]\) and B = \(\left[\begin{array}{ll}
2 & 3 \\
4 & 5 \\
2 & 1
\end{array}\right]\), do AB and BA exist? If they exist, find them. Do A and B commute with respect to multiplication?
Solution:

AB ≠ BA
∴ A and B are not commutative with respect to the multiplication of matrices.

Question 3.
Find A² where A = \(\left[\begin{array}{cc}
4 & 2 \\
-1 & 1
\end{array}\right]\)
Solution:

Question 4.
If A = \(\left[\begin{array}{ll}
i & 0 \\
0 & i
\end{array}\right]\), find A².
Solution:

Question 5.
If A = \(\left[\begin{array}{cc}
i & 0 \\
0 & -i
\end{array}\right]\), B = \(\left[\begin{array}{cc}
0 & -1 \\
1 & 0
\end{array}\right]\) and C = \(\left[\begin{array}{ll}
0 & \mathbf{i} \\
\mathbf{i} & \mathbf{0}
\end{array}\right]\), and I is the unit matrix of order 2, then show that
(i) A² = B² = C² = -I
(ii) AB = -BA = -C
Solution:

Question 6.
If A = \(\left[\begin{array}{ll}
2 & 1 \\
1 & 3
\end{array}\right]\) and B = \(\left[\begin{array}{lll}
3 & 2 & 0 \\
1 & 0 & 4
\end{array}\right]\), find AB. Find BA if it exists.
Solution:
Given A = \(\left[\begin{array}{ll}
2 & 1 \\
1 & 3
\end{array}\right]\) and B = \(\left[\begin{array}{lll}
3 & 2 & 0 \\
1 & 0 & 4
\end{array}\right]\)

The order of AB is 2 × 3
BA does not exist since no. of columns in B ≠ No. of rows in A.

Question 7.
If A = \(\left[\begin{array}{cc}
2 & 4 \\
-1 & k
\end{array}\right]\) and A² = 0, then find the value of k.
Solution:

II.

Question 1.
If A = \(\left[\begin{array}{lll}
3 & 0 & 0 \\
0 & 3 & 0 \\
0 & 0 & 3
\end{array}\right]\) then find A⁴.
Solution:

Question 2.
If A = \(\left[\begin{array}{ccc}
1 & 1 & 3 \\
5 & 2 & 6 \\
-2 & -1 & -3
\end{array}\right]\) then find A³.
Solution:

Question 3.
If A = \(\left[\begin{array}{ccc}
1 & -2 & 1 \\
0 & 1 & -1 \\
3 & -1 & 1
\end{array}\right]\), then find A³ – 3A² – A – 3I, where I is unit matrix of order 3 × 3.
Solution:

Question 4.
If I = \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\) and E = \(\left[\begin{array}{ll}
0 & 1 \\
0 & 0
\end{array}\right]\), show that (aI + bE)³ = a³I + 3a²bE, Where I is unit matrix of order 2.
Solution:

III.

Question 1.
If A = [a₁, a₂, a₃,], then for any integer n ≥ 1 show that Aⁿ = \(\left[\begin{array}{lll}
a_{1}, & a_{2}^{n}, & a_{3}^{n}
\end{array}\right]\)
Solution:
Given A = diag [a₁, a₂, a₃,] = \(\left[\begin{array}{ccc}
a_{1} & 0 & 0 \\
0 & a_{2} & 0 \\
0 & 0 & a_{3}
\end{array}\right]\)
Aⁿ = diag \(\left[\begin{array}{lll}
a_{1}^{n} & a_{2}^{n} & a_{3}^{n}
\end{array}\right]=\left[\begin{array}{ccc}
a_{1}^{n} & 0 & 0 \\
0 & a_{2}^{n} & 0 \\
0 & 0 & a_{3}^{n}
\end{array}\right]\)
This problem can be should by using Mathematical Induction
put n = 1
A¹ = \(\left[\begin{array}{ccc}
a_{1} & 0 & 0 \\
0 & a_{2} & 0 \\
0 & 0 & a_{3}
\end{array}\right]\)
∴ The result is true for n = 1
Assume the result is true for n = k
A^k = \(\left[\begin{array}{ccc}
a_{1}^{k} & 0 & 0 \\
0 & a_{2}^{k} & 0 \\
0 & 0 & a_{3}^{k}
\end{array}\right]\)
Consider

∴ The result is true for n = k + 1
Hence by the Principle of Mathematical Induction, the statement is true ∀ n ∈ N

Question 2.
If θ – φ = \(\frac{\pi}{2}\), then show that \(\left[\begin{array}{cc}
\cos ^{2} \theta & \cos \theta \sin \theta \\
\cos \theta \sin \theta & \sin ^{2} \dot{\theta}
\end{array}\right]\) \(\left[\begin{array}{cc}
\cos ^{2} \phi & \cos \phi \sin \phi \\
\cos \phi \sin \phi & \sin ^{2} \phi
\end{array}\right]\) = 0
Solution:

Question 3.
If A = \(\left[\begin{array}{rr}
3 & -4 \\
1 & -1
\end{array}\right]\) then show that Aⁿ = \(\left[\begin{array}{cc}
1+2 n & -4 n \\
n & 1-2 n
\end{array}\right]\), for any integer n ≥ 1 by using Mathematical Induction.
Solution:
We shall prove the result by Mathematical Induction.

∴ The given result is true for n = k + 1
By Mathematical Induction, the given result is true for all positive integral values of n.

Question 4.
Give examples of two square matrices A and B of the same order for which AB = 0 but BA ≠ 0.
Solution:

Question 5.
A Trust fund has to invest ₹ 30,000 in two different types of bonds. The first bond pays 5% interest per year, and the second bond pays 7% interest per year. Using matrix multiplication, determine how to divide ₹ 30,000 among the two types of bonds if the trust fund must obtain an annual total interest of (a) ₹ 1800 (b) ₹ 2000
Solution:
Let the first bond be ‘x’ and the second bond be 30,000 – x respectively
The rate of interest is 0.05 and 0.07 respectively.
(a) \([x, 30,000-x]\left[\begin{array}{l}
0.05 \\
0.07
\end{array}\right] \quad=[1800]\)
[0.05x + 0.07(30,000 – x)] = 1800
\(\frac{5}{100} x+\frac{7}{100}(30,000-x)=1800\)
5x + 21,0000 – 7x = 1,80,000
-2x = 1,80,000 – 2,10,000 = -30,000
x = 15,000
∴ First bond = 15,000
Second bond = 30,000 – 15,000 = 15,000

(b) \(\left[\begin{array}{ll}
x & 30,000-x
\end{array}\right]\left[\begin{array}{l}
0.05 \\
0.07
\end{array}\right]=[2000]\)
[0.05x + 0.07(30,000 – x)] = [2000]
\(\frac{5 x}{100} \times \frac{7}{100}(30,000-x)=2000\)
5x + 2,10,000 – 7x = 2,00,000
-2x = 2,00,000 – 2,10,000
-2x = -10,000
x = 5,000
∴ First bond = 5000
Second bond = 30,000 – 5000 = 25,000