Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Matrices Solutions Exercise 3(c) will help students to clear their doubts quickly.
Intermediate 1st Year Maths 1A Matrices Solutions Exercise 3(c)
I.
Question 1.
If A = \(\left[\begin{array}{ccc}
2 & 0 & 1 \\
-1 & 1 & 5
\end{array}\right]\) and B = \(\left[\begin{array}{ccc}
-1 & 1 & 0 \\
0 & 1 & -2
\end{array}\right]\), then find (AB’)’.
Solution:

![]()
Question 2.
If A = \(\left[\begin{array}{cc}
-2 & 1 \\
5 & 0 \\
-1 & 4
\end{array}\right]\) and B = \(\left[\begin{array}{ccc}
-2 & 3 & 1 \\
4 & 0 & 2
\end{array}\right]\) then find 2A + B’ and 3B’ – A.
Solution:


Question 3.
If A = \(\left[\begin{array}{cc}
2 & -4 \\
-5 & 3
\end{array}\right]\), then find A + A’ and A.A’
Solution:

Question 4.
If A = \(\left[\begin{array}{ccc}
-1 & 2 & 3 \\
2 & 5 & 6 \\
3 & x & 7
\end{array}\right]\) is a symmetric matrix, then find x.
Hint: ‘A’ is a symmetric matrix ⇒ AT = A
Solution:
A is a symmetric matrix
⇒ A’ = A
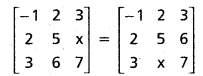
Equating 2nd row, 3rd column elements we get x = 6.
![]()
Question 5.
If A = \(\left[\begin{array}{ccc}
0 & 2 & 1 \\
-2 & 0 & -2 \\
-1 & x & 0
\end{array}\right]\) is a skew-symmetric matrix, find x.
Solution:
∵ A is a skew-symmetric matrix
⇒ AT = -A

Equating second-row third column elements we get x = 2.
Question 6.
Is \(\left[\begin{array}{ccc}
0 & 1 & 4 \\
-1 & 0 & 7 \\
-4 & -7 & 0
\end{array}\right]\) symmetric or skewsymmetric?
Solution:

∴ A is a skew-symmetric matrix.
II.
Question 1.
If A = \(\left[\begin{array}{cc}
\cos \alpha & \sin \alpha \\
-\sin \alpha & \cos \alpha
\end{array}\right]\), show that A.A’ = A’. A = I2
Solution:

From (1), (2) we get A.A’ = A’. A = I2
![]()
Question 2.
If A = \(\left[\begin{array}{ccc}
1 & 5 & 3 \\
2 & 4 & 0 \\
3 & -1 & -5
\end{array}\right]\) and B = \(\left[\begin{array}{ccc}
2 & -1 & 0 \\
0 & -2 & 5 \\
1 & 2 & 0
\end{array}\right]\) then find 3A – 4B’.
Solution:

Question 3.
If A = \(\left[\begin{array}{cc}
7 & -2 \\
-1 & 2 \\
5 & 3
\end{array}\right]\) and B = \(\left[\begin{array}{cc}
-2 & -1 \\
4 & 2 \\
-1 & 0
\end{array}\right]\) then find AB’ and BA’.
Solution:


![]()
Question 4.
For any square matrix A, Show that AA’ is symmetric.
Solution:
A is a square matrix
(AA’)’ = (A’)’A’ = A.A’
∵ (AA’)’ = AA’
⇒ AA’ is a symmetric matrix.