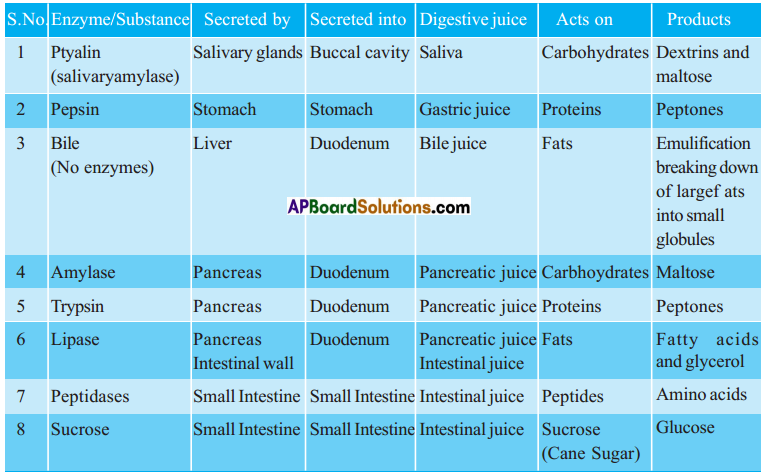
AP State Board Syllabus AP SSC 10th Class Biology Solutions Chapter 3 Transportation – The Circulatory System Textbook Questions and Answers.
AP State Syllabus SSC 10th Class Biology Solutions 3rd Lesson Transportation – The Circulatory System
10th Class Biology 3rd Lesson Transportation – The Circulatory System Textbook Questions and Answers
Improve your learning
Question 1.
What is transport system? How does this help to the organism?
(OR)
What is the importance of transport system in the organisms?
Answer:
Transport system: The system which transports the material that is needed to organism is called transport system or circulatory system.
Importance :
- The system supplies O2 to parts of the body and also recollects the CO2 which is excretory product in life process.
- It supplies food materials to all parts of the body.
- Hormones can travel through circulatory system.
- It also helps in regulation of body temperature.
- It collects the waste materials from parts of the body.
- It has antibodies to protect our body from pathogens.
- It helps in maintaining osmatic pressure in the cells.
- In plant it transports the water through xylem and food materials through phloem.
![]()
Question 2.
What is the relationship between blood and plasma?
(OR)
What are the differences between blood and plasma.
Answer:
| Blood | Plasma | |
| 1. Definition | Blood is the main body fluid that is responsible for transporting materials. | Plasma is the yellow liquid component of blood and constitutes 55% of the total blood volume. |
| 2. Composition | It has liquid portion called plasma and soiled substances called blood cells. | It contains water (90%), proteins, nutrients, waste products, clotting factors, minerals and hormones. |
| 3. Cells | It has R.B.C, W.B.C and thrombocytes | It does not have any cells. |
| 4. Colour | Red in colour | It has straw – yellow colour. |
| 5. Clotting factors | It has clotting factors known as fibrinogen, prothrombin. | After the clotting plasma turns into serum. |
Question 3.
Which type of blood vessels carry blood away from the heart?
(OR)
Which blood vessels carry blood from heart to body parts?
Answer:
- The rigid vessels are called arteries which originate from the heart and supply blood to various organs in the body.
- The largest artery is the aorta which arises from the left ventricle supplies oxygenated blood to all parts of the body except lungs.
- The relatively smaller one is pulmonary artery supplies deoxygenated blood to lungs.
- A pair of coronary arteries carry oxygenated blood to the muscles of heart.
Question 4.
What are the three main types of blood vessels in the body?
Answer:
The three main types of blood vessels in the human body are:
- Arteries
- Veins and
- Capillaries.
Question 5.
Which is the largest artery in the body? Why is it big in size?
Answer:
- The Aorta is the largest artery in the body.
- It is big in size because it has to supply oxygenated blood from heart to various organs in the body from head to fingers and toes.
![]()
Question 6.
Which blood vessel carries blood for oxygenation?
Answer:
- The PULMONARY ARTERY originates in the right ventricle. Outside the heart, it divides into two branches – RIGHT and LEFT PULMONARY ARTERIES.
- They carry deoxygenated blood to right and left lungs for oxygenation.
Question 7.
Name the structures which are present in veins and lymph ducts and absent in arteries.
Answer:
- The structures that are present in the veins and lymph ducts are VALVES.
- These are absent in arteries.
- They are one-way valves. If the blood moves in the opposite direction, the valves closed and avoid the backward flow of blood in veins and lymph ducts.
Question 8.
Answer:
What is the use of platelets?
- Platelets help in clotting of blood at the site of injury thus it controls the loss of blood from the wound.
- When blood flows out, the platelets release an enzyme called THROMBOK1NASE.
- This acts on another substance called PROTHROMBIN converting it into THROMBIN.
- Thrombin acts on FIBRINOGEN, converting it into FIBRIN.
- The blood cells entangle in the fibrin fibres forming the CLOT.

Question 9.
Write differences between
a) Systole – Diastole
b) Veins – Arteries
c) Xylem – Phloem
Answer:
a) Systole – Diastole:
| Systole | Diastole |
| 1. Definition: It measures the amount of pressure that blood exerts on arteries when the heart is contracted. | 1. It is the pressure that is exerted when the heart is relaxed. |
| 2. Range: Its normal range is 60-80 mm Hg. | 2. Its normal range is 90 – 120 mm Hg |
| 3. Blood pressure: It represents the maximum pressure exerted on the arteries. | 3. It represents minimum pressure in the arteries. |
| 4. Blood vessels: They are contracted in this phase. | 4. Blood vessels are relaxed in this phase. |
| 5. Ventricles: Ventricles are contracted and they push the blood in this phase. | 5. Ventricles are relaxed and filled with blood in this phase. |
b) Veins – Arteries:
| Viens | Arteries |
| 1. Moves towards the heart. | 1. Moves away from the heart. |
| 2. Collects blood from body organs. | 2. Distributes blood to the body organs. |
| 3. Blood pressure in veins is low. | 3. Blood pressure is high in arteries. |
| 4. Valves are present. | 4. Valves are absent. |
| 5. Carry deoxygenated blood, except pulmonary vein. | 5. Carry oxygenated blood except pulmonary artery. |
| 6. Veins start in blood capillaries. | 6. Arteries end in capillaries. |
| 7. They can be seen subcutaneously. | 7. They are deep seated. |
| 8. They collapse when there is no blood in it or cut across. | 8. They do not collapse when there is no blood in it. |
| 9. Veins are further divided into venules. | 9. Arteries are further divided into arterioles. |
| 10. Veins are usually flattened or collapsed with thin walls. | 10. They are round and relatively thick walled. |
| 11. Veins have large lumen. | 11. Arteries have small lumen. |
| 12. Veins are bluish in colour. | 12. Arteries are reddish in colour. |
| 13. Veins show sluggish movement of blood. | 13. Arteries show spurty movement of blood giving pulse. |
| 14. If venous wall is injured, blood comes out, collects in a pool in a small area around vein. | 14. If arterial wall is injured, the blood comes out like a fountain in a large area all around the artery. |
c) Xylem – Phloem:
| Xylem | Phloem |
| 1. In plants water and mineral salts are transported by xylem tissue. | 1. In plants food material is transported by phloem tissue. |
| 2. Xylem consists of trachieds, vessels, xylem fibres and xylem parenchyma. | 2. Phloem consists of sieve tubes, sieve cells, companion cells, phloem fibres and phloem parenchyma. |
| 3. Only xylem parenchyma is living tissue. | 3. Sieve tubes, sieve cells, companion cells and phloem parenchyma are living. |
| 4. Trachieds, vessels, xylem fibres are dead tissues. | 4. Phloem fibres are dead tissues. |
| 5. Xylem gives mechanical strength to the plant. | 5. Phloem does not give mechanical strength. |
| 6. Conduction of water by xylem is unidirectional i.e., from roots to apical parts of the plant. | 6. Food material conduction is bidirectional i.e., from leaves to storage organs or growing points and from storage organs to all growing parts of plants. |
| 7. Xylem is star shaped. | 7. Phloem is not star shaped. |
| 8. Xylem occupies the center of the vascular bundle. | 8. Phloem occurs on outer side of the vascular bundle. |
| 9. Tubular with hard walled cells. | 9. Tubular with soft walled cells. |
![]()
Question 10.
Explain the way how plants get water by osmosis through root hairs.
(OR)
Explain the mechanism of entry of water into root hair by osmosis with the help of a diagram.
(OR)
Explain the process of water entry into the root hair in plants with the help of diagram.
(OR)
In plants, what is the role of root hair in the absorbtion of water and minerals from the soil?
Answer:
- Root hair plays an important role in absorption of water by osmosis.
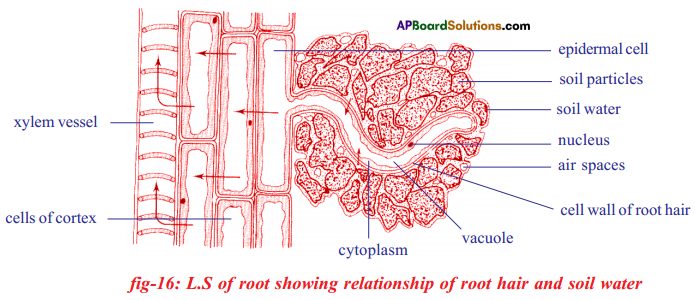
- Root hairs grow out into the spaces between the soil particles and that the hairs are surrounded by moisture.
- The Cytoplasm of the cells in root hairs is called cell sap. It has dissolved salts.
- The cell sap of the root hair is more concentrated than that of the concentration of salt solution present in the soil.
- The cell membrane of root hair acts as semi-permeable membrane.
- It separates the cell sap from the salt solution of the soil.
- Therefore water passes into the vacuole of the root hair by osmosis.
- The entry of water dilutes the contents of the root hairs vacuole. So it becomes more diluted than the neighboring cells.
- Water passes into the neighboring cell which becomes diluted, finally water enters the xylem vessels.
- As there are vast number of root hairs and root cells involved, pressure in the xylem vessels develops which forces the water upwards.
- This total pressure is known as root pressure.
- Root pressure is not the main cause of movement of water in xylem but it is certainly one factor.
![]()
Question 11.
What is root pressure? How is it useful to the plant?
Answer:
The pressure exerted by the root hair while absorbing water from the soil is called root pressure.
- Soil water concentration is more dilute than that of the cell sap in the root hair, therefore water passes into vacuole of the root hair by osmosis.
- The entry of water dilutes the cell sap so it become more dilute than it’s neighbouring cells.
- So, water passed into the neighbouring cell which in turn becomes diluted, finally water enters the xylem vessels.
- As there are vast number of roots hairs and root cells involved, pressure in the xylem vessels develops which forces the water upwards.
Question 12.
Phloem is a food source for some animals. How can you justify the statement ?
Answer:
- Certain mammals scratching the bark of trees to get the food stored in the phloem, especially during hard winters when food is scarce.
- Voles do this to young saplings at ground level and rabbits can do much damage to older ones.
- Aphids absorb so much sugar from the phloem that they cannot assimilate all of it and it passes out of the anus as a sticky syrup called honeydew.
- Grey squirrels too do great damage particularly to beech and sycamore, and for this reason, in some parts it is impossible to grow these trees as a crop.
![]()
Question 13.
Read the given para and name the parts of heart.
We have observed that the heart is divided into four chambers by muscular structure. Any structure that divides two chambers is known as septum. Now let us try to name the septa present in the heart.
A) The septum that divides the two atria can be named as ———-.
Answer: Interatrial septum.
B) The septum that divides the two ventricles can be named as ———-.
Answer: Interventricular septum.
C) The septum that divides the atrium and ventricle can be named as ———-.
Answer: Interatrioventricular septum.
The holes that connect two chambers are called apertures. Let us try to name the apertures which connect the atria and ventricles.
D) The aperture that is connecting the right atrium and right ventricle can be named as ———-.
Answer: Right atrioventricular aperture.
E) The aperture that is connecting the left atrium and left ventricle can be named as ———-.
Answer: Left atrioventricular aperture.
Any structure that closes an aperture, and allows one way movement of materials is called valve. Now let us name the valves that are present in the chambers of the heart.
F) The valve that is present between left atrium and left ventricle can be named as ———-.
Answer: Left atrioventricular valve (Bicuspid or Mitral valve).
G) The valve that is present between right atrium and right ventricle can be named as ———-.
Answer: Right atrioventricular valve (Tricuspid valve).
![]()
Question 14.
If the valves in veins of the legs fail to stop the flow of blood, what could be the consequences of this failure?
Answer:
- If the valves in veins of the legs fail to stop flow of blood, the blood accumulates in the veins and causes swelling or inflammation and more clotting.
- Clotting can block or slow blood flow through the veins raising the blood pressure and possibly causing more damage.
- The swelling of the veins also results in varicose veins and spider veins.
- If varicose veins are untreated for long time, it leads to venous ulceration.
Question 15.
What will happen if cell sap of root hair cells contain high concentration of ions?
Answer:
- The cell membrane of root hair is a semipermeable membrane. It allows the movement of molecules from low concentration to high concentration.
- Cell sap of root hair cells contain high concentration of ions and salts than the water present around it in the soil.
- As a result, water flows from the soil into cell sap of root hairs.
- From the root hairs water pass from cell to cell by osmosis through the epidermis, root cortex, endodermis and reach the root xylem.
![]()
Question 16.
John prepared stethoscope with paper cup and plastic tube. Write down the procedure of preparation.
Answer:
Aim : To prepare a paper cup stethoscope
Apparatus: Three paper cups, plastic tube, scissors, T – bend and thread.
Procedure:
- Take three paper cups and put a small hole in the bottom of the cups.

- Take a T – bend and arrange it in the back side of one cup as hanging.
- T – bend is connected to plastic pipe, by the two sides and arrange the paper cups.
- Put the two upper cups at your ears and bottom one is on the friend’s chest.
- Now you can hear the sound of heart beat.
Question 17.
How can you prove that the water is transport through the xylem?
Answer:
Aim: To observe the path of water through a plant.
Apparatus: Balsam plant, beaker, Eosine solution, stand.
Procedure:
- A leafy green shoot of Balsam plant with a transparent stem is placed in Eosine solution (It is red dye resulting from the action of bromine).
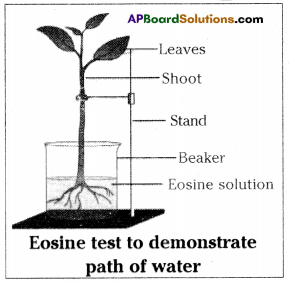
- After sometime red streaks appear in the stem and veins of leaves become red.
- If a transverse section is cut through the root stem and leaf, the tissue that has been stained is xylem tissue.
- This shows that water moves up the root into the stem and leaves in the xylem tracheids and vessels.
- The other tissues remain in the same colour.
Conclusion: The xylem tissue is responsible for the upward movement of water through the plant.
![]()
Question 18.
What is your inference about experiments with aphids?
Answer:
- Biologists studied about food transportation in plants with the help of aphids.
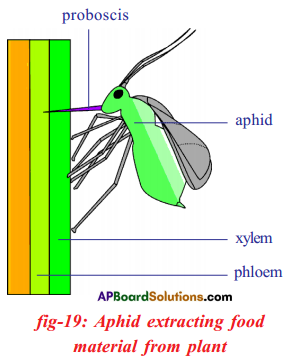
- Aphids feed on the plant juices of young stems.
- Aphid uses its long needle like organ proboscis to extract plant juices from phloem tissue.
- The proboscis of the Aphid only penetrates up to a phloem sieve tube.
- It is found experimentally that the contents of the phloem sieve tubes are under slight pressure the fluid slowly comes out from the cut end of the proboscis in the form of drops.
- These drops were collected and analysed and it contain sugars and amino acids.
- Aphids absorb so much sugar from the phloem that they cannot assimilate all of it and it excretes out of the body as sticky syrup called honey dew.
Question 19.
Collect information about blood pressure of your school teachers or your neighbours and prepare a report on their health problems.
Answer:
| Name of the person | Blood pressure | Health condition |
| 1. Mr. Vijay | 120/80 | Normal |
| 2. Mrs. Kamala | 125/85 | Irritation, worried |
| 3. Mr. Raju | 140/90 | Fear, easily getting anger, high irritation, tiredness. |
| 4. Mrs. Chandu | 110/70 | Weakness, dizziness, fainting |
| 5. Mr. Rama Rao | 140/100 | Dizziness, fainting |
![]()
Question 20.
Draw a block diagram to explain single and double circulation. Write differences between them.
(OR)
What is single circulation and double circulation? Write differences between them with the help of diagrams.
Answer:
- Single circulation: In a blood circulation the blood passes through the heart only once. This type of circulation is called single circulation and the heart is called single circuit. Ex: Fish
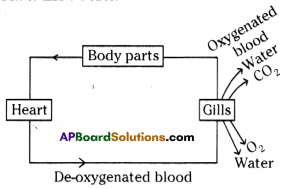
- Double circulation: Blood passes twice through the heart. Once between heart and lungs and second time from heart to body parts. Such circulation is called double circulation and the heart is called double circuit heart.
Ex: Frog and other higher animals.
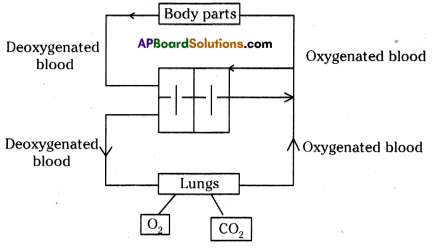
-
Single Circulation Double Circulation 1. Found only in fishes. 1. Found in amphibians, reptiles, birds and mammals. 2. Blood passes only once through the heart to supply once to the body. 2. Blood passes twice through the heart to supply once to the body. 3. Only deoxygenated blood passes through the heart. 3. Mixed blood (Oxygenated and deoxygenated) pass through the heart. 4. It is less efficient in function as the oxygenated blood flows at a low pressure which decreases the rate of oxygen supply. 4. It is most efficient in function as the blood flows at a higher pressure which increases the rate of oxygen supply.
![]()
Question 21.
Prepare a block diagram showing from water absorption by roots to transpiration by leaf.
Answer:
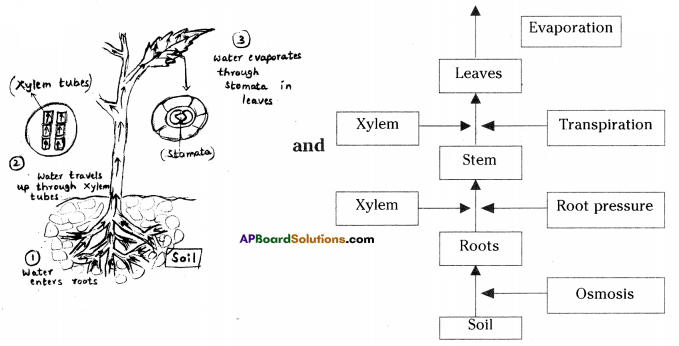
Question 22.
What do you want to compare with the transportation in blood vessels in man?
(OR)
What can circulatory system in man be compared with?
Answer:
I compare the circulatory system in man with motor water system in our houses, as below.
Heart – motor Blood vessels – pipes
Blood – water Tank – body parts
![]()
Question 23.
How do you feel about transportation of water in huge trees?
(OR)
How do you appreciate the movement of water through xylem in tall trees?
Answer:
- It is a wonder to see the transportation of water in huge trees.
- It is surprising how the root pressure and the transportation pull are responsible for the water to reach such heights against the gravitation force.
- It is a great mechanism evolved in the beautiful plants which give us pleasure.
- We can really appreciate the creation done by God towards plants and their functions for mankind.
Question 24.
Prepare a cartoon on heart beating.
Answer:
![]()
Question 25.
After reading this lesson what precautions you would suggest to your elders about edema?
(OR)
What is edema? How it occurs? What are the precautions required not to be affected with edema?
Answer:
Precautions I would suggest to my elders about edema:
- Edema is abnormal accumulation of fluid in the interstitium which is located beneath the skin or one or more cavities of the body.
- Avoid sitting and standing for too long. It promotes fluid flow into the legs and feet.
- Hence I suggest elders getting up and stretching the legs once in a while travelling long in bus and trains.
- Leg exercise and feet moving and using leg muscles help pump excess fluids back to the heart.
- People suffer with edema can keep the legs elevated above the level of heart for 30 minutes a day or 3 or 4 times a day.
- Massage the edema effected area with firm pressure towards the heart which helps to move the excess fluid away from swelling.
- Reducing the amount of salt in the diet may prevent swelling problems from reoccuring.
- Avoid hot baths, hot showers when swelling occurs.
Choose the correct answer.
- The term cardiac refers to which organ in the body? [ ]
A) Heart
B) Vein
C) Lymph
D) Capillary
Answer: A - On which side of the human heart is low in oxygen? [ ]
A) Left ventricle
B) Right ventricle
C) Left atrium
D) Right atrium
Answer: B & D - Which structures of the heart control the flow of the blood? [ ]
A) Arteries
B) Veins
C) Valves
D) Capillaries
Answer: C - Which of the following opinions is correct? [ ]
A) Ravi said xylem and phloem cells arranged one upon the other to form a tube like structure.
B) John said xylem and phloem are not separate tube like structures.
C) Salma said, xylem and phloem cells connect together to form tube like structure.
D) Hari said because of its shape they said to be tube like structure.
Answer: C - An aphid pierces its proboscis into the ———- to get plant juices. [ ]
A) Xylem
B) Phloem
C) Cambium
D) Vascular bundle
Answer: B
10th Class Biology 3rd Lesson Transportation – The Circulatory System InText Questions and Answers
10th Class Biology Textbook Page No. 57
![]()
Question 1.
Answer the following after reading the experiment conducted by William Harvey.
- In which blood vessels valves are found? What do you think is the function of the valves in them?
Answer:
Valves are present in the veins. If the blood moves in one direction, the valves fold towards the walls of the vessel, so that the blood can pass without trouble. If the blood moves in the opposite direction, the valves close. - Why do subcutaneous blood vessels bulge on the side away from the heart when the hand is tied?
Answer:
When the hand is tied the blood which is passing away from heart is stopped. So the subcutaneous blood vessels bulge. - The deep seated blood vessels (the arteries) bulge on the side towards the heart when tied. What do you understand from it?
Answer:
The blood which is passing towards the heart is stopped so the blood accumulates in the blood vessels and they bulge. - There are valves in the heart between atria and ventricles. Is the purpose of valves in the veins and arteries same ?
Answer:
The valves between each atrium and its ventricles are one way valves. They allow the blood to flow from the atrium to the ventricle without any hindrance.
The purpose is same, back flow of blood is stopped. - Arteries are deeply seated in the body? Whereas veins are superficial why?
Answer:- Arteries are deep seated to prevent them from any damage. As arteries carry oxygenated blood, a damage to them results in loss of the oxygenated blood.
- Arteries lie deeper in the body because it helps them to contain high pressure so that they can carry blood from the heart to all the body parts.
- Because the deeper the arteries are in the body, the warmer the blood is. The warmer the blood, the more oxygen the haemoglobin is able to carry.
- Veins are located superficially as the pressure inside them is very low and contain deoxygenated blood.
Also their superficial location helps in efficient flow of blood in them by muscular contraction and relaxation in our body.
![]()
Question 2.
After reading the experiments by Harvey fill in the following table. Use the clues/ options given in the first column.
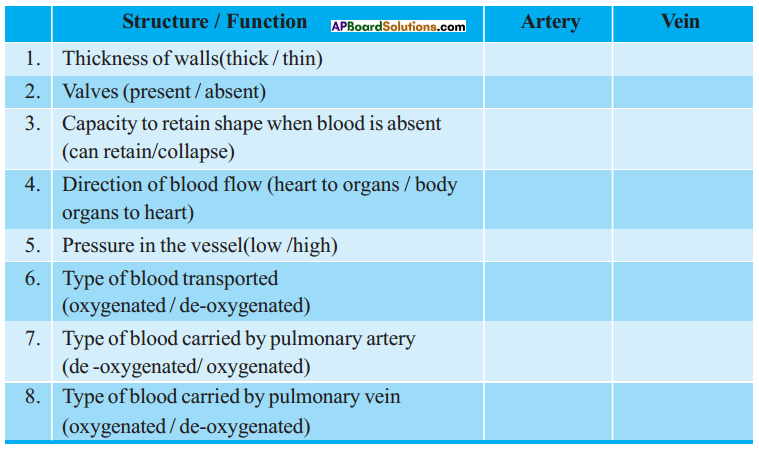 Answer:
Answer:
| Structure / Function | Artery | Vein |
| 1. Thickness of walls (thick / thin) | Thick | Thin |
| 2. Valves (present / absent) | Absent | Present |
| 3. Capacity to retain shape when blood is absent (can retain / collapse) | Can retain | Can not retain |
| 4. Direction of blood flow (heart to organs / body organs to heart) |
Heart to organs | Body organs to heart |
| 5. Pressure in the vessel (low / high) | High | Low |
| 6. Type of blood transported (oxygenated / de-oxygenated) | Oxygenated (except pulmonary artery) | De-oxygenated (except pulmonary veins) |
| 7. Type of blood carried by pulmonary artery (de-oxygenated / oxygenated) | Deoxygenated | – |
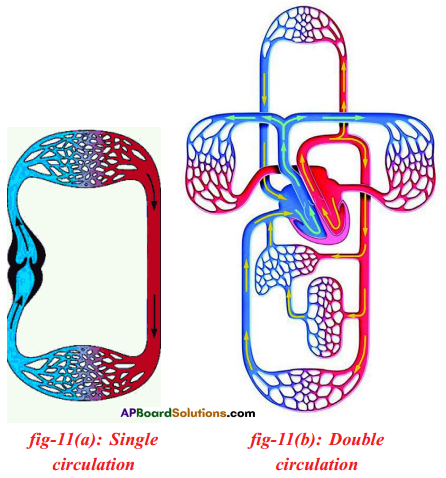
Question 3.
How many times did your pointer touch body parts in fig – 11(a) and (b)?
Answer:
One time.
![]()
Question 4.
How many times did your pointer touch the heart in fig – 11(a) and (b)?
Answer:
a) One time
b) Two times
Question 5.
How many times did the pointer touch respiratory organs in fig – 11(a) and (b)?
Answer:
One time.
![]()
Question 6.
Why do our legs swell?
Answer:
After overnight journey, in sitting position without moving, we feel that our feet (the lower part of the legs) swollen. This is called edema.
Because the blood circulation becomes slow in the lower portion and causes swelling.
10th Class Biology Textbook Page No. 64
Question 7.
Is there anything like that in plants which corresponds to circulatory system?
Answer:
Yes.
Vascular bundles are present in the plant parts which have xylem and phloem. These are responsible for the transportation of materials in plats.
Xylem transports water from roots to the leaves. Phloem transports food prepared by leaves to all the parts of the plant.
Question 8.
What is the mechanism behind this?
Answer:
Root absorb water due to Root Pressure and transpiration.
Question 9.
Are roots directly in contact with water?
Answer:
Yes. The root hairs are directly contact with water.
![]()
Question 10.
How is water absorbed?
Answer:
Water is absorbed due to Osmosis.
10th Class Biology Textbook Page No. 66
Question 11.
Is there any increase in the water level?
Answer:
Yes. There is an increase in the water level.
Question 12.
What is the role of xylem?
Answer:
Water absorbed by roots is transported to all the parts of the plant by Xylem
Think and Discuss
10th Class Biology Textbook Page No. 58
Question 1.
Artery walls are very strong and elastic. Why?
Answer:
- When the blood enters with a pressure into arteries the walls will stretch.
- This enables the arteries to withstand the increase in the pressure, without bursting. So the walls of the arteries are very strong and elastic.
![]()
Question 2.
Why do we compare arteries like tree which divides into smaller and smaller branches?
Answer:
- Arteries carry oxygenated blood to the tissues.
- The largest aorta after comes outside of the heart, it divides into small branches called arteries.
- These arteries still divide into small arterioles and supply oxygenated blood to the tissues which are present throughout the body.
- It looks like a tree with smaller and smaller branches. So we compare arteries like tree.
Question 3.
The lumen size is bigger in vein when compared with artery. Why?
Answer:
- Veins are generally large in diameter, carry more blood volume.
- Arteries are general small in diameter when compared with veins.
- The walls of veins are more thick when compared with the walls of arteries.
- So the lumen’s bigger in vein when compared with artery.
10th Class Biology 3rd Lesson Transportation – The Circulatory System Activities
![]()
Activity – 1
How can you find your pulse rate?
Answer:
1) Keep your index and middle fingers on your wrist below the thumb as shown in the figure.
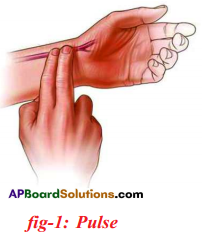 2) You feel something pushing your fingers rhythmically up and down.
2) You feel something pushing your fingers rhythmically up and down.
3) Count the rhythm also called pulse rate per minute.
4) Now stand up and jog for one minute standing at the same place. Note the pulse for a minute.
| Name of the person | Pulse rate per minute | |
| at rest | after jogging | |
| Naganeeraj | 72 | 80 |
| Nagamani | 70 | 81 |
| Chandra Sekhar | 71 | 79 |
| Shabnum | 74 | 84 |
| Mani | 72 | 83 |
a) What did you observe? Is the pulse rate same in both conditions?
Answer:
No the pulse rate is not same in both condition. There is increase in pulse rate after jogging for one minute.
![]()
Activity – 2
Now observe the pulse rate of students of your class.
Try to observe your pulse rhythm in other ways such as climbing stairs, running etc. Take your shirt button and insert a matchstick and place it on your wrist.
- What did you find?
Answer:
We find the button placed on the wrist moves up and down rhythmically - When do you think that our pulse rate goes up?
Answer:
The pulse rate goes up, when we climb up stairs or run, etc. - What does the pulse rate show?
Answer:
There is a relationship between the pulse rate and the heart beat. The pulse rate shows the heart beat.
Activity – 3
How do you measure the Heart beat and pulse rate at rest?
Answer:
- I will make a paper tube 10 inch long and one inch in diameter.
- Keep one end of it on the chest of a friend on a point in the centre around 6 inches below from his or her neck.
- I keep my ear at the other end.
- Listen carefully and count the beats for a minute.
- Also find my friend’s pulse rate. Then 1 will note down my observations at least 10 students of my class in the following.
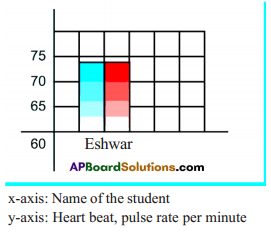
Name of the student Heart beat at rest/minute Pulse rate at rest/minute Eswar 72 72 Venkateswar Rao 70 70 Gopinath 69 69 Yashwanth 71 71 Srinivas 72 72 Manasa 68 68 Kamala 70 70 Lakshmi 71 71 Kavitha 69 69 Latha 70 70 - Observation: It is found that the heart beat and the pulse rate are same in every movement.
Prepare histogram between persons and heart beat and pulse rate at rest as shown in the sample graph. Here (a) bar indicates heart beat,
(b) bar indicates pulse rate.
X-axis: Name of the student Y-axis: Heart beat, pulse rate per minute.
Activity – 4
![]()
Aim: Observation of the internal structure of the mammalian heart.
Material required: Since the structure of all the mammalian hearts is similar, we take the sheep’s or goat’s heart for our observation. For this, we need the following materials.
Material required: Freshly collected specimen of heart of sheep/goat from the butcher, soda straw, sharp and long blade/ scalpel, tray and a jug of water, dissection scissors and forceps.
Procedure: Before coming to the class wash the heart thoroughly so that, blood is completely drained from the chambers of heart.
Take the soda straws and insert them into the stumps of the blood vessels.
Note your observations as you proceed.
- How many layers are covering the heart?
Answer:
Two thin, transparent layers are covering the heart. - What is the shape of the heart?
Answer:
Heart is a pear shaped structure, triangle in outline, wider at the anterior end and narrower at the posterior end. - How many large blood vessel stumps are attached to the heart?
Answer:
There are five large blood vessels attached to the heart. - Which end of the heart is broader and which end is narrow?
Answer:
The anterior end of the heart is broader and the posterior end is narrow.
Observe the internal structure – observe the wall of the heart. - Is the thickness of the wall of the heart uniform throughout?
Answer:
No, the thickness of the wall of the heart is not uniform throughout. Atria are thin and ventricles are thick. - How many chambers are there in the heart?
Answer:
There are four chambers in the heart. They are right atrium, left atrium, left ventricle and right ventricle. - Are all the chambers of the same size?
Answer:
All the chambers of the heart are not of the same size. Left atrium and ventricle are smaller when compared to that of right atrium and ventricle. - What other differences could you observe between the chambers?
Answer:
Left auricle and ventricle are smaller than right auricle and right ventricle. - Do you find any specific observation in between two chambers?
Answer:
Yes, I can find some specific observation in between two chambers. - Are all the chambers connected to each other?
Answer:
No, only atria and ventricles are connected to each other. - How are they connected to each other ? How are they separated?
Answer:
Auricles are connected to ventricles by valves and are separated by septae (septum). - How many blood vessels are attached to the heart?
Answer:
Five blood vessels are attached to the heart.
They are- Aorta,
- Pulmonary artery,
- Pulmonary vein,
- Superior venacava,
- Inferior venacava.
- Are all the blood vessels rigid? How many of them are rigid?
Answer:
The rigid blood vessels are called arteries. They are- The largest artery Aorta
- Pulmonary artery – which carries deoxygenated blood from heart to lungs.
- Do you think that the stiffness / rigidity of blood vessel is something to do with circulation?
Answer:
The walls of the arteries are stiff/rigid. They are made up of muscle fibre and are elastic. When heart pumps blood into the arteries, the blood enters with a pressure into the arteries. Their walls will stretch and this enables the arteries to withstand the increase in the pressure without bursting.
Activity – 5
![]()
Write your observation of blood flow in arteries and veins.
Answer:
a) Aim: Observation of blood flow in arteries and veins.
Procedure:
- Sit on a table with one leg dangling and the other resting on it so that the back of one knee rests on the knee of the other.
- After some time we feel the leg which is on top give a series of small movements with each heart beat.
- Repeat it for a long time.
Observation: The blood flow reduces to the leg and so develop “pins and needles”.
Conclusion: The blood flow from arteries to legs slowed down results pins and needles.
b) Swing the arm round several times to fill the veins with blood, hold the arm vertically downwards and gently press your finger along a prominent vein – stroking it in the reverse direction to the blood flow.
Observation: We can see the swellings.
Conclusion: Veins have to carry blood from body parts to the heart. When the arm is hold tightly blood is stopped in the veins there forms swelling.
Activity – 6
How is water absorbed? Explain with an experiment.
Answer:
Aim: To show that water is absorbed by the root hairs.
Required material : Mustard seedlings, filter paper slide and cover slip, a drop of water, microscope, hand lens.
Procedure: We need to germinate some mustard seeds. Examine some mustard seeds which have been grown on wet filter paper. Observe the mass of fine threads coming from the root by using hand lens. These are root hairs through which water enters the plant.
Gently squash a portion of the root hair between the slide and cover slip in a drop of water and examine under a microscope.
Note the thinness of the walls of the root hairs. The water enters the root hairs and passes inwards from cell to cell until it gets into the xylem vessels. Osmosis plays an important role in this.
Observation: It is observed that water is present in the xylem vessels.
Conclusion: The root hairs absorbs water with mineral salts into the transport tissue called xylem vessels by the process of osmosis.
![]()
Activity – 7
What is root pressure? Explain with an experiment.
Answer:
Aim: To demonstrate root pressure in plants.
Apparatus : Potted plant with stem cut, rubber tube, glass tube, clamp.
Procedure:
- Take a regularly watered potted plant and cut the stem portion 1 cm above the ground level.
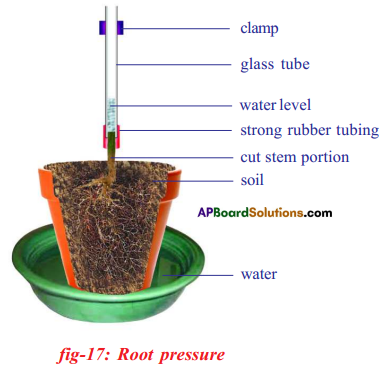
- Then connect a glass tube by means of a strong rubber tubing as shown in the figure.
- The size of glass tube should be equal to the size of the stem.
- Take care while joining tube and stem being bound tightly, water cannot escape from the tube.
- Now pour some water in the glass tube until water level can be seen above the rubber tube.
- Mark the level of water (M1) in tube.
- Keep your arrangement aside for 2 to 3 hours.
- Then observe and mark the water level (M2) in the tube.
Observation: There is increase in the level.
Result: The raise in the water level is due to the root pressure created in the plant.
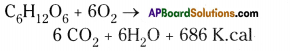
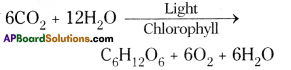





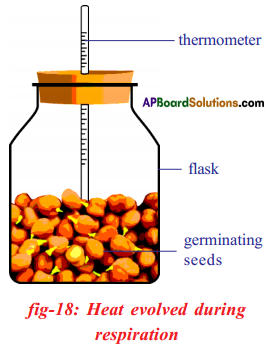


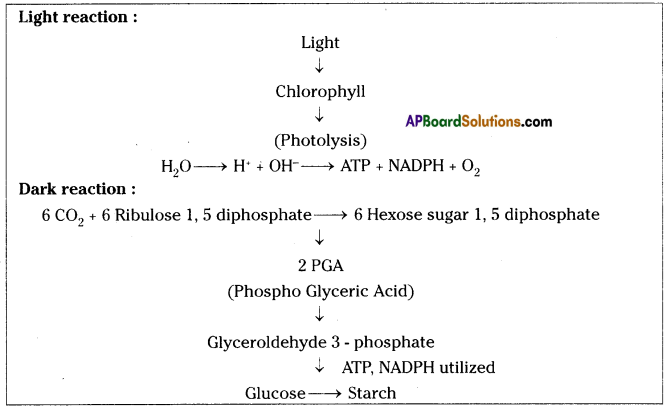
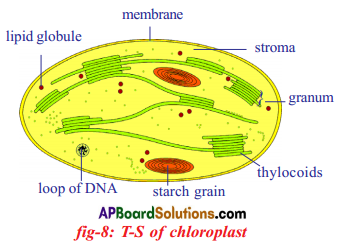

 Answer:
Answer:
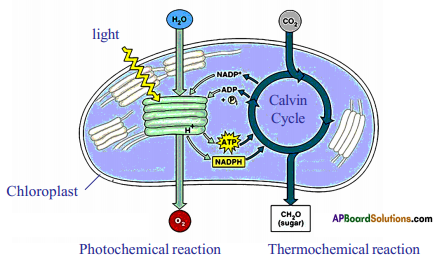
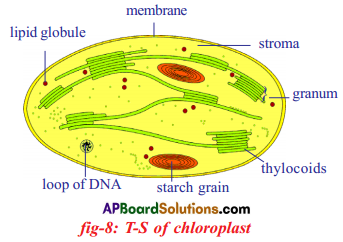 Role of Chloroplast in photosynthesis:
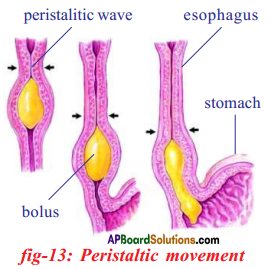
Role of Chloroplast in photosynthesis: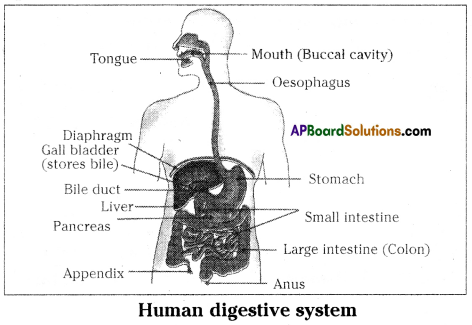 Parts where peristalsis takes place: Oesophagus, stomach, small intestine and large intestine.
Parts where peristalsis takes place: Oesophagus, stomach, small intestine and large intestine.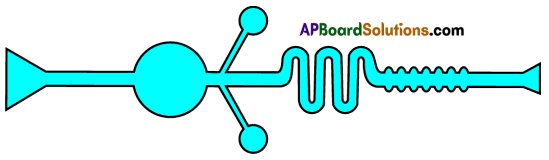 Answer:
Answer: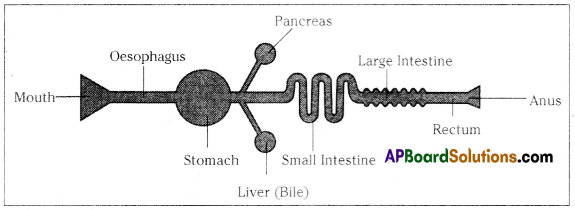
 Answer:
Answer: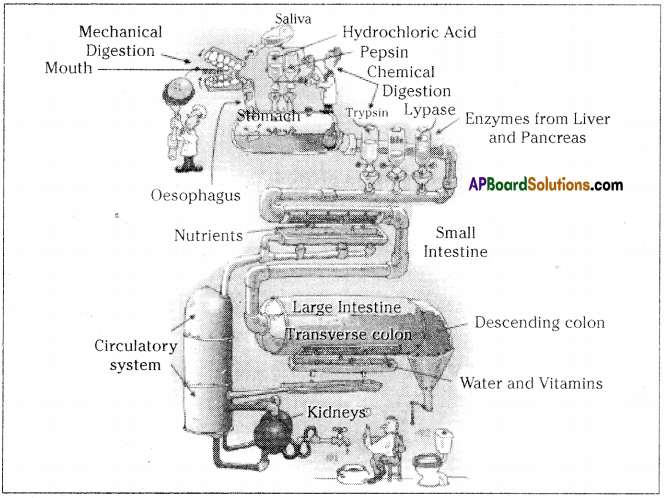
 Apparatus:
Apparatus:
 Priestly should have tilted the bell jar to one side and introduced the mint plant without disturbing the experimental set up.
Priestly should have tilted the bell jar to one side and introduced the mint plant without disturbing the experimental set up.