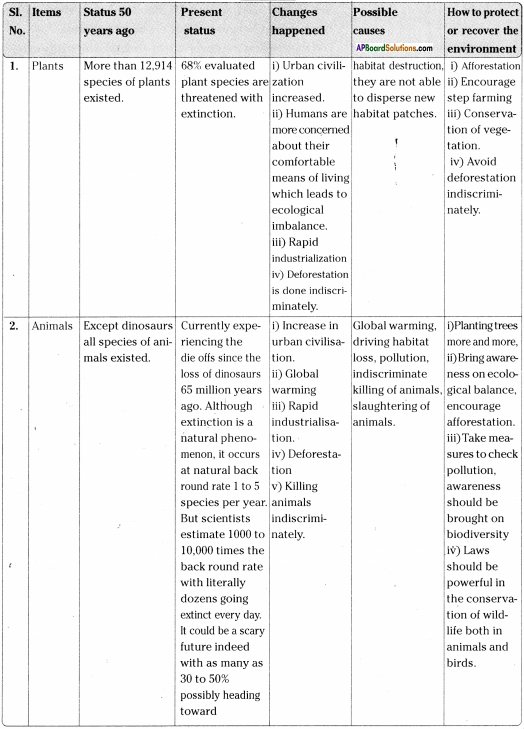
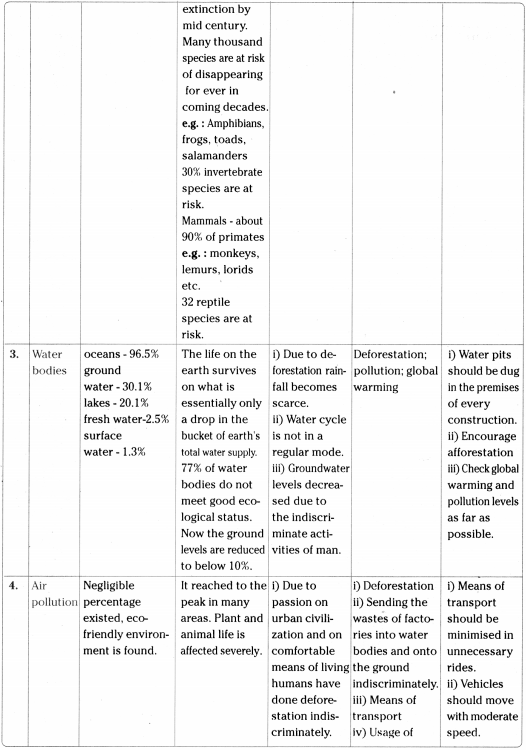
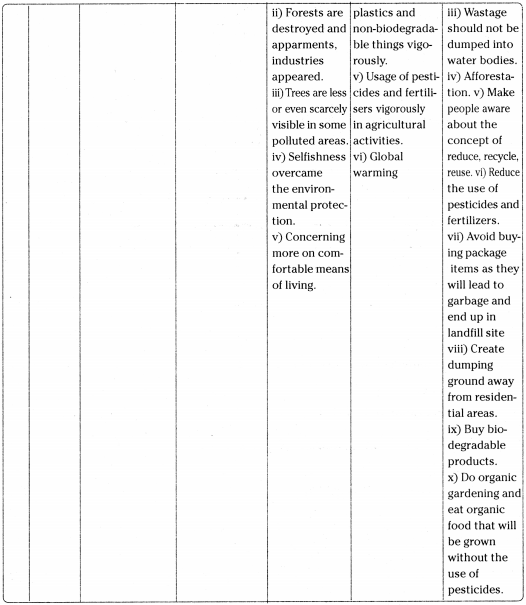
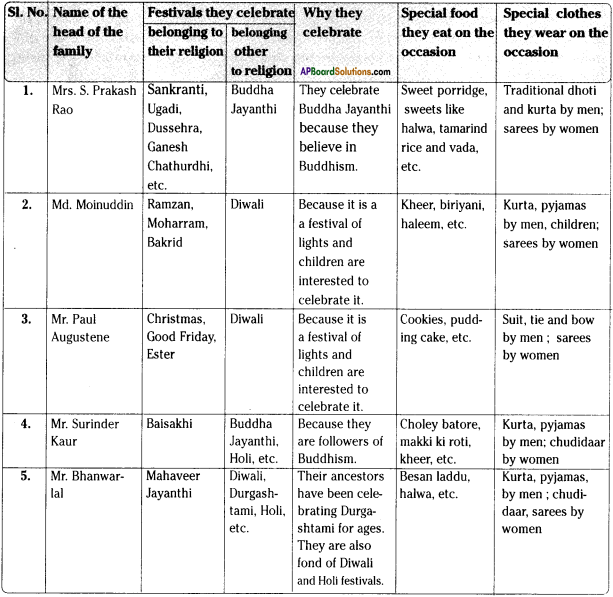
AP State Board Syllabus AP SSC 10th Class English Textbook Solutions Chapter 4A Rendezvous with Ray Textbook Questions and Answers.
AP State Syllabus SSC 10th Class English Solutions Chapter 4A Rendezvous with Ray
10th Class English Chapter 4A Rendezvous with Ray Textbook Questions and Answers
Look at the picture and answer the questions that follow.

Question 1.
Is this picture (a) a poster, (b) an advertisement, or (c) a painting? Justify your option.
Answer:
It is a poster. The word/expression “RAJKAPOORS” tells us that it is directed by Raj Kapoor, a well-known Hindi actor. “SHREE 420” is the title of the movie. The persons in the picture are the actors of this film. Hence, it is evident that it is the poster of a movie.
Question 2.
Who do you think are the persons shown in this picture? Name them.
Answer:
The persons in this picture are cine actors. They are Raj Kapoor and Nargis.
![]()
Question 3.
What do you think is ‘SHREE 420?
Answer:
I think ’SHREE 420’ is a North Indian movie. It was directed and produced by Raj Kapoor. Raj Kapoor, Nargis, and Nadira were the main characters in this movie. It hit the screen on 6th September 1955.
Comprehension
Answer the following questions.
Question 1.
What did Ray’s detractors accuse him of? Did Roberge agree to their accusation? If not, why?
Answer:
Ray’s detractors accused him that he made his reputation selling India’s poverty to the West. Roberge didn’t agree to their accusation. He was not attracted by the material poverty depicted in Ray’s films. The thing struck him most was that the enormous spiritual poverty of some rich people is much more deplorable than material poverty.
Question 2.
‘I didn’t come here to convert. In fact, I am the one who got converted.’ Who said these words? What different shades of meanings do you find in the words of the speaker?
Answer:
Roberge, the French-Canadian priest said these words. Although he came from the West, he didn’t speak with the arrogance of the West. He told that he came to India on a quest to know the world and in the process know himself. He also told that he didn’t come to India to convert and in fact he was the one who got converted.
The word ‘convert’ means ‘change’. Usually, the West come to India to convert the Indian people. They are known for their arrogance and look down upon Indians. They think that they are superiors in terms of knowledge, culture, civilization, etc. In one sense they want to convert the Indians and make them refined. In the other sense, the Westerners want to convert the Indians to Christianity. As far as Roberge is concerned, he was the one who got converted with the newly acquired knowledge about the world and got a chance to know about himself.
![]()
Question 3.
Roberge took nine years to meet Ray in person after joining St. Xavier’s college. Why did he take so long time? What would you do if you were in his place?
Answer:
Roberge wanted to meet Ray in person but it took him nine years after reaching Kolkata and joining St. Xavier’s college, to meet him. Although he wanted to meet Ray right way, he didn’t want to just go and see him as he was a living museum piece. Roberge wanted to prepare himself, get to know his works more, so that when they met, there could be a worthwhile dialogue between them. If I were in Roberge’s place, I would do the same as he did.
Question 4.
How was Ray perceived by the outsiders? Was this perception true of Ray’s real character?
Answer:
The outsiders perceived Ray that Ray’s massive physical and intellectual stature might have made him come across as cold, aloof and even intimidating. This perception was not true of Ray’s real character. In reality Ray was a very simple and unassuming man with a subtle sense of humour.
Question 5.
What is meant by the line, ‘Ray took off where Tagore signed out.’ What was Ray searching for?
Answer:
Roberge feels that there is a striking comparison between Tagore and Ray. He also feels that philosophically too, Ray took off where Tagore signed out. This means that Ray began his work where Tagore ended. In a way Ray continued to walk on the path shown by Tagore. We find the analogy in Ray’s last three films ‘Ganashatru’, ‘Shakha Prashakha’ and ‘Agantuk’ with Tagore’s ‘Shabhyatar Sankat’. Both their works contain the message that it would be a sin to lose faith in man. Ray was an agnostic throughout his life. Even in the face of death, Ray was searching for answer about the existence of God. This was suggested by some of the music that he used in Shakha Prashaka.
Question 6.
How did Roberge try to take ‘Chitrabani’ forward? How did ‘Chitrabani’ help filmmaking in Bengali?
Answer:
Roberge founded ‘Chitrabani’, a communication and film institute in 1970. It is the first of its kind in West Bengal. He lent Ray’s name as cofounder as a token of their friendship. Ray was made the member of the first governing body and later, he became its adviser. Roberge arranged most of the initial funding from Canadian agencies. Thus, Roberge tried to take ‘Chitrabani’ forward. He acted as the director of Chitrabani for a period of 26 years. Chitrabani not only produced important documentary features, but also became breeding ground for local talent for film-making. Thus, the institute helped film-making in Bengali.
![]()
Question 7.
The theme of ‘Rendezvous with Ray’ is… (Tick any two options.)
a) To explain the efforts of Chitrabani.
b) To picturize the illustrious life of Ray.
c) To explain the experiences of Roberge with Ray.
Answer:
(b)To picturize the illustrious life of Ray. (✓)
(c) To explain the experiences of Roberge with Ray. (✓)
Vocabulary
1. Read the following passage and notice the underlined words.
It was a Sunday evening. It was already dark. We wanted to watch the film ‘Gajani’.We had a square meal and came out. There were no lights. There was a power cut. It was pitch dark. It was bitterly cold. We looked here and there …….
The word pairs ‘square meal’, ‘pitch dark’ and ‘bitterly cold’ are found together. That means they co-occur. Such co-occurring words or word combinations are called collocations(co + locate = collocate). These expressions are natural.
Let us look at another example.
| We say | We don’t say |
| Ride a motor cycle | Drive a motor cycle |
Read the following report and fill in the blanks with the word from the box below that collocates with the underlined words or phrases.

The venue of the celebration was ‘Ravindra Bharathi’, Hyderabad. It was the 100 days’ celebration of the film ‘Animals Forever’. Avinash, the hero, was full of life with his ……..(1)……… performance in the film. He was admired by everyone. In fact, he was considered to be the main reason for the success of the film. The hall resonated with ……..(2)……… clapping when he came onto the dais. The auditorium with packed audience honoured him with a ……..(3)……… ovation. The producer felicitated every one in the unit in a ……..(4)……… manner. The event was momentous and unforgettable.
Answer:
- outstanding (outstanding performance)
- thunderous (thunderous clapping)
- standing (standing ovation)
- fitting (fitting manner)
II. One-word substitutes
‘Rendezvous’ is a one-word substitute for ‘a meeting place’.
You can work in groups and pick out similar one-word substitutes from the text equivalent to the meanings given below:
- A short stay between two places in one’s journey → stopover
- A person who brings out new books → compiler
- A group of three films that has the same characters or subject → trilogy
- An impressive entrance to a building → portal
- A person who tries to make something less good by criticising it → detractor
- A person who is extremely important or large in size → colossus
- A person who is responsible for a problem or a crime → culprit
- A handwritten document → manuscript
- A statement that expresses something people believe is true and is to be followed → dictum
- Using more words than needed → verbose
- Something designed to teach people some moral → didactic
- A person who is not sure about the existence of God → agnostic
- A branch of philosophy that studies the principles of beauty in art → aesthetics
- A result of a situation or of an action → fallout
- A film that gives facts about something → documentary
III. In the lesson ‘Rendezvous with Ray’ we come across certain words /expressions that are not from English, e.g.: en route. This means ‘on the way’. These expressions are taken from languages like Latin, Greek, and Portuguese and so on. There are certain instances where these expressions are used in English perhaps because of their precision in meaning. Some of them along with their meanings are given below…
- en masse = all together, in large numbers.
- viva voce = a spoken exam
- in toto = totally
- alma mater = mother of the soul (school or university) included
- ex officio = because of the rank or job/by virtue of office
- in absentia = in the absence
- detour = a longer route we take to avoid a danger
- verbatim = word for word, exactly as spoken or written
- status quo = situation as it is now
- ad hoc = not planned in advance
- bona fide = genuine, real or legal
- lingua franca = link language
- magnum opus = the greatest work
- sine die = indefinitely
![]()
Read the following paragraph and All in the blanks with appropriate expressions given in the list above.
Children for Films
On the 14th november, on the occasion of Children’s Day, the children across the state requested the officials to conduct Children’s Film Festivals more often. They submitted a memorandum to the Secretary to the Government in Hyderabad in this regard.
The Government conceded to the request and came out with a proposal to set up an ___(1)___ committee to serve the purpose before a permanent body is in place. It was proposed by the Government that the committee would be led by a de-partment official as an ___(2)___ president. The committee should conduct a written exam along with a ___(3)___ to identify student representatives at mandal, district and state level to strengthen the culture of film festivals among the children. The ___(4)___ of the students should be verified for such identification. The proposal made the screening of at least a ___(5)___ of a director mandatory every year. The children were thrilled to bits on this.
Answer:
- ad hoc
- ex officio
- viva voce
- en masse
- magnum opus
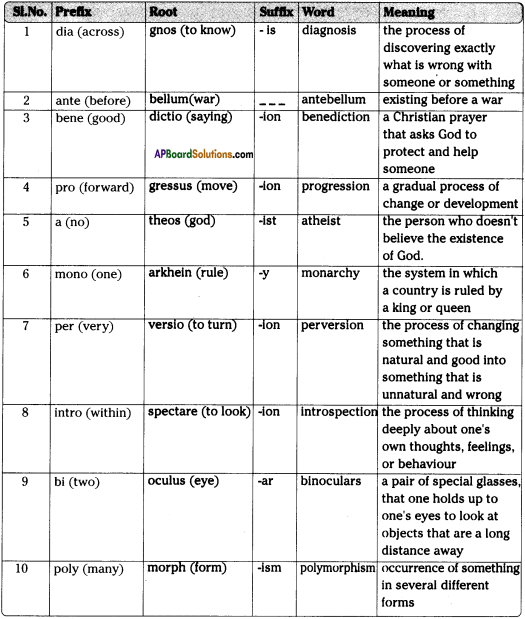
IV. In the previous classes we learnt how the words form with the help of prefixes and suffixes. Now, we will learn another aspect of word formation i.e. through roots. In the lesson we have a word ‘agnostic’ which is formed out of the root ‘gnos’ that means ‘to know’. When the prefix ‘a-‘ is added to the root ‘gnos’, we have the word ‘agnostic’.
A. Given below are some prefixes, roots and suffixes. Form words using them and write their meanings.
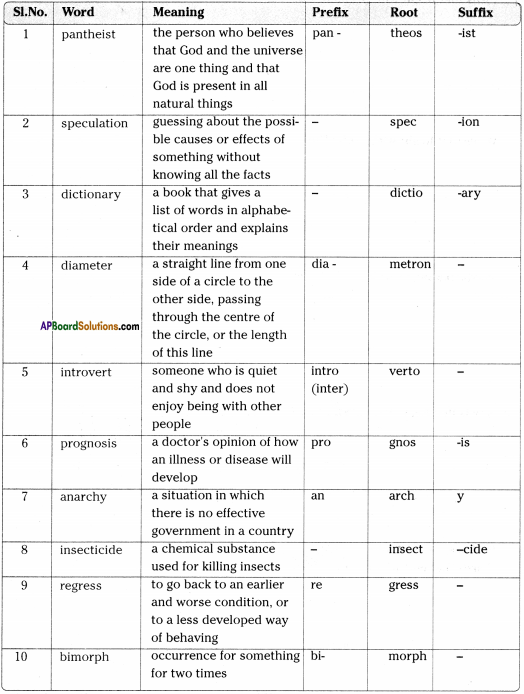
B. Analyse the following words in terms of the prefixes, roots and suffixes and their meanings.
C. Think of some words that begin and end with the following prefixes and suffixes.
Prefixes: dis-, bi-, pro-, pre-
i) Words that begin with prefix a “dis-” :

ii) Words that begin with prefix “bi-“:

iii) Words that begin with prefix “pro-“:

iv) Words that begin with prefix “pre-” :

Suffixes:
i) Words that end with suffix “-cide” :

ii) Words that end with suffix “-tion” :

iii) Words that end with suffix “-ist” :

iv) Words that end with suffix “-logy”:

Grammar
I. Arrange the following sentences in proper order and write a paragraph.You may insert appropriate linkers wherever necessary.
Stream of Comedy
In every Indian language, a comedian is an essential character of films. In Telugu,Relangi and Ramanareddy provided comedy which made the audiences laugh heartily. Their appearance appealed to the film lovers.
Relangi was fat and short.
Ramana Reddy was lean and tall.
Their accent amused the film lovers.
Padmanabham and Allu Ramalingaiah followed their footsteps.
Rao Gopal Rao’s stint as villain-cum-comedian has been admired by all.
Mr. 101 Districts, Nutan Prasad left an indelible mark in the hearts of the audience.
Ali and Sunil are comedians.
They are also considered heroes.
Rajababu came later.
Brahmanandam has had a long career.
He has a world record.
His name found place in the Guinness Book of World Records.
He amused the people for long.
People have been laughing.
Sorrows of people are taking a back seat.
Answer:
Stream of Comedy :
In every Indian language, a comedian is an essential character of films. In Telugu, Relangi and Ramanareddy provided comedy which made the audiences laugh heartily. Their appearance appealed to the film lovers. Relangi was fat and short whereas Ramana Reddy was lean and tall. Their accent amused the film lovers. Then Padmanabham and Allu Ramalingaiah followed their foot steps. Raja Babu came later and amused the people for long. Rao Gopal Rao’s stint as villain-cum-comedian has been admired by all. Mr. 101 Districts, Nutan Prasad left an indelible mark in the hearts of the audience. Another familiar comedian, Brahmanandam has had a long career. He has a world record and his name found place in the Guinness Book of World Records. Ali and Sunil are comedians and they are also considered heroes. People have been laughing with the efforts of comedians and sorrows of people are taking a back seat.
![]()
II. Prepositions following ‘adjectives’ and ‘verbs’:
In ‘Rendezvous with Ray’ we come across certain verbs and adjectives followed by prepositions. For example, acquainted with, brought out, prevented from, explained to
Read the following sentences and observe the underlined words.
1. I am amazed at you, Victoria.
2. Victoria, a precocious girl of ten, was dressed in colours.
3. He is trying to adapt himself to the regrettable occasion.
4. He was very fond of Jimmy.
5. I am sure I am sorry for it.
6. You’ve been waiting for me to begin tea.
7. I see the little trifles that belonged to father lying around.
8. This always appealed to me.
In the above sentences, the underlined adjectives and verbs are usually followed by certain prepositions.
A. Here is a list of adjectives and verbs. Tick( ✓ ) the prepositions that follow the adjectives and the verbs. Later, use them in sentences of your own.
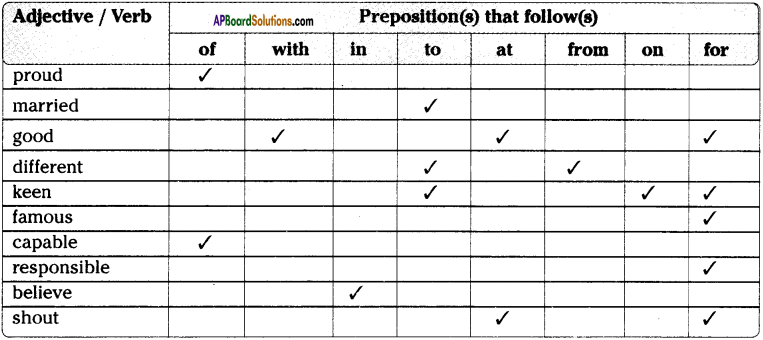

1. a) Mr. Bhargav is proud of his son’s achieving the title.
b) Miss Lalitha is the proud owner of her new flat.
2. a) Raju is married to Brahmam’s sister.
b) She got married to Sujan.
3. a) Mr. Williams is good at English.
b) She is very good with her neighbours.
c) It is good weather for going on a picnic.
4. a) Both the brothers are different from each other
b) His car is different to mine.
5. a) The district collector is keen to help them.
b) He is not keen on playing with them.
c) Our boss is keen for the work to resume.
6. a) Guntur is famous for tobacco and mirchi.
b) France is famous for its wine.
7. a) She is capable of looking after my child.
b) He is not capable of doing this job.
8. a) My brother is responsible for all this mess.
b) The police caught the man who was responsible for the theft.
9. a) An atheist is a person who doesn’t believe in God.
b) Believe in yourself; or you can’t achieve the success.
10. a) The HM is shouting at Gopal for his misdeed.
b) The boy is shouting for somebody’s help.
11. a) Mr. Teja is thinking of his new college.
b) Why don’t you think of your job seriously ?
12. a) I don’t agree with him in any case.
b) They don’t agree on everything.
c) She agreed to meet him at the airport.
13. a) She has to depend on her grandparents as she lost her parents.
b) They depend entirely on the funds given by the government.
14. a) He is recovering from his severe illness.
b) The gold has been recovered from the culprit.
15. a) This site belongs to Rama Rao.
b) These assets belong to Raju.
16. a) I have applied for a job of typist.
b) She applied to two foreign universities and was accepted by them.
B. Fill in the blanks with suitable prepositions.
1. All last winter Sharath suffered ________ conghs and colds.
2. Anand is unaccustomed _________ the heat.
3. Kumar was afraid _________ his enemies.
4. Sriram was always arguing ________ his brother.
5. Sindhu was dedicated _______ her job.
6. Priyanka was shocked _______ the hatred they had shown.
7. I said _______ you, “I am thinking going ___________ to America. I have actually dreamt ________ it.”
8. I want to talk ________ the group about their exams.
9. I was terrified ________ her.
10. I’ve always been terribly fond _______ you.
11. If you continue to support someone who is in trouble you are loyal _______ them.
12. If you don’t understand any of these words, you could refer ________ a dictionary.
13. It wasn’t his car, in fact I don’t know who it belongs ________ .
14. My problems are very similar _______ yours.
15. People started to shout ________ the driver.
16. She had always been bad ________ languages.
17. She listened me and then told me _______ her problems.
18. The accident sadly resulted ________ the death of a man.
19. The buses are often late, so you can’t depend _______ them.
20. They may feel jealous ________ your success.
Answer:
- from
- to
- of
- with
- to
- at
- to; about/of; of
- to
- of
- of
- to
- to
- to
- to
- at
- at
- to ; about
- in
- on/upon
- of
III. Read the following paragraph and notice the use of the past perfect and simple past.
A. As all the actors had taken their positions, the curtain rose. They started acting as thedirector had asked them to. The audience enjoyed the play very much. The hero kicked the comedian since the comedian had done mischievous things. The musician fell off his chair after the comedian had fallen on him. The power went off after the musician had landed on the cables. There was darkness and silence everywhere. After a while two persons in the audience started a conversation.
B. Read the following conversation and fill in the blanks with appropriate verb forms,
i. e. past perfect/simple past.
1. Sarath : Oh ! What ________ (happen)? Everything ________ (be) disturbed before the play ________ (come) to an end.
2. Bharath : Damn it! The play ________ (be) very interesting. Someone on the stage ________ (do) something when the hero ________ (throw) him off.
3. Sarath : I too ________ (see) it. It was the comedian. The hero ________ (hurl) him since he ________ (do) a mischievous thing.
4. Bharath : How disgusting! I (pay) one hundred rupees before I ________ (enter) this theatre. Everything has become a chaos.
5. Sarath : Where ________ (be) the director? Had he ________ (try) to set things right before the audience ________ (start) leaving, it would have been nice.
6. Bharath : The electrician ________ (restore) the power before the audience ________ (leave). Thank God! At last the play resumed.
Answer:
- happened, had been, came
- was, had done, threw
- saw, hurled, had done
- had paid, entered
- was, tried, started
- had restrored, left
IV. Given below is a paragraph with ten errors in the areas of ‘concord,tense, prepositions, punctuation and articles’. Edit the paragraph.
The Indian film industry has witnessed sweeping changes in the past hundred years. It started of with mute (mooki) films. Even then, people liked this new form of entertainment.There was several intervals in a film show because of a single projector. Later, the technology changes made a talkie films possible. A theatre of those days is like a rice mill. This type of theatre were called Touring Talkies’. But these didn’t tour. There were bamboo screens to served the purpose of walls of the modern theatre. ‘Cut Shows’ were a luxury of those days. Have you ever watch them Now, the modern theatres is completely different. Multiplexes with dts, 3D and 4D are a present reality.
Answer:
The Indian film industry has witnessed sweeping changes for the past hundered years. It started off with mute (mooki) films. Even then, people liked this new form of entertainment. There were several intervals in a film show because of a single projector. Later, the technological changes made the talkie films possible. A theatre of those days was like a rice mill. This type of theatres were called ‘Touring Talkies”. But these didn’t tour. There were bamboo screens to serve the purpose of walls of the modern theatre. ‘Cut Shows’ were a luxury of those days. Have you ever watched them? Now, the modern theatres are completely different. Multiplexes with dts, 3D, and 4D are a present reality.
Study Skills
Read the following passage and rewrite it replacing all idioms, without changing the meaning of the passage.
Tragedy in Comedy
“Cut!…. Shot OK”, shouted the director. The funny face of the comedian suddenly wore a worried look. He said to the director, “sir,….” The director did not allow him to
say anything. He said, “Yes, you can go ” Where should he go? The comedian really did not understand what the director had meant. He could not make out what he said. As per the original plans, the comedian had to attend the schedule for 15 more days continuously. This put the comedian in soup as his wife was seriously ill. He was referring to the break he needed to visit his wife and maybe the director was referring to the sets. Perhaps both of them were talking to cross purposes. He had always been loyal to the firm that brought him into the limelight. But he could not help his wife. He was in a tight corner then. Yes! He had to face difficulties, yet he had to make people laugh. This was the paradox of his life. Wasn’t it a ‘tragedy in comedy’?
Answer:
“Cut! Shot OK”, shouted the director. The funny face of the comedian suddenly wore a worried look. He said to the director, “Sir. ” The director did not allow him to say anything. He said, “Yes, you can go ” Where should he go ? The comedian really did not understand what the director had meant. He could not understand what he said. As per the original plans, the comedian had to attend the schedule for 15 more days continuously.
This put him in a difficult situation as his wife was seriously ill. He was referring to the break he needed to visit his wife and maybe the director was referring to the sets. Perhaps both of them understood the other’s words incorrectly- He had always been loyal to the firm that made him catch the public attention. But he could not help his wife. He was in a trouble then. Yes ! He had to face difficulties, yet he had to make people laugh. This was the peculiar situation of his life. Wasn’t it a ‘tragedy in comedy’?
Listening
Listen to the radio programme and tick (✓) the right answer to the following questions.
Jewels of India
This is All India Radio, Hyderabad.
Welcome to ‘Jewels of India Programme’ presented by Meenakshi.
In our programme today, we will know about the most famous Indian filmmaker.
We know that Bengal is a beehive of cultural activities. It has witnessed cultural reforms. It is the birthplace of many writers and intellectuals.
To continue this tradition, another great son of India took birth in Calcutta on 2nd May 1921. Who ioiiicl that be? It is none other than Satyajit Ray, the son of a writer… a grandson ol an amateur astronomer. His home provided him with an ambiance to think and feel
Graduating from Presidency College, Calcutta, Ray moved to the open air university, ’Shantiniketan1. A keen observer that he was, Ray imbibed the spirit of Shantiniketan. There he read extensively and developed interest in painting.
Back in Calcutta, Ray started working for a London-based advertising firm. Wasn’t it a right place for a creative man like Ray? He worked there for some time and moved to London to work there.
There he watched films. Film after film. He liked the film ‘Bicycle Thieves’.That kindled interest in Young Ray in film-making. Slowly his interest led him to a world of creativity. That was the birth of a great film maker. And Ray became a film maker.
His films ‘Pather Panchali’, ’Aparajito’, ’Agantuk’ were some of his master pieces. His vision for Bengali films was matchless.
Along with the Oscar Award, he received the Bharata Ratna. The legendary film maker passed away in 1992. But the film world cherishes his memories forever.
Next week we will know about another great personality.
Till then, good bye.
1. What was the programme about?
a) Ray
b) Jewels of India
c) Film-making
Answer:
b) Jewels of India
![]()
2. Which film inspired Ray?
a) Agantuk
b) Bicycle Thieves
c) Shantiniketan
Answer:
b) Bicycle Thieves
3. The highest civilian award Ray received was
a) Oscar Award
b) Bharath Ratna
c) Padma Vibhushan
Answer:
b) Bharath Ratna
Oral Activity
Make a short speech of 2-3 minutes about the film you have seen recently. You
should include the following points in your speech.
– What the film was.
– Why you liked it so much (You can talk about the direction, actors, costumes, music, songs, etc.)
Answer:
Dear Sir and my dear friends,
I am very glad to take this chance of speaking on the film (movie) ‘Satamanam Bhavathi”, which I have seen recently along with my family members. I like it so much as it is a family sentiment movie. All the family members can sit and watch it pleasantly.
The director of this film, Satish Vegesna presented it in a nice manner. We don’t find the scenes of violence, more fights, horror, sex, etc. in this movie. The famous music director Mickey J Meyer composed beautiful songs for this movie. Audience can easily be mesmerised by the melodious songs written by lyricists Sri Mani and Ramajogaiah Sastry. In the characters of Raju and Nitya, Sarvanand and Anupama Parameswaran acted su-perbly. Prakash Raj and Jayasudha’s action is wonderful. Sameer Reddy’s cinematography is one of the attractions of this film. I conclude that it is a super hit movie which attracts the attention of the spectators.
Thank you one and all for giving me this opportunity.
Rendezvous with Ray Summary in English
Rendezvous with Ray’ is the news report published by Frontline on July 29 and on August 11, 2006. This is all about Satyajit Ray, the distinguished cine director from Calcutta (Kolkata). Gaston Roberge, a French-Candian priest presents his experiences with Ray in this lesson.
In 1961, when Fr. Gaston Roberge was 26 years old, he was acquainted with the works of Satyajit Ray through the Apu Trilogy. He saw all the three films in one sitting -the incident which made him love the people of India and Bengali cinema and culture. Roberge gives a scholarly, original analysis of Ray’s works in his latest book, “Satyajit Ray, Essays : 1970-2005”. In his youth, Roberge knew of Bengal through Mircea Eliade’s La Nuit Bengalie, some of Tagore’s poems and a Reader’s Digest article on Mother Teresa. He was haunted by the harsh image of poverty shown in “Saint of the Slums” and Apu’s world came as a reassurance. Ray’s critics accused him that he made his reputation selling India’s poverty to the West. But Roberge was struck by the enormous spiritual poverty of some rich people which is worse than material poverty.
He wanted to meet Ray and make friends with him but it took him nine years after reaching Kolkata. He wanted to get to know Ray’s works more so that there could be a worthwhile dialogue between them when they met. Their friendship lasted about 22 years until Ray’s death in 1992. Their quiet friendship developed over the years. Ray’s friends called him Manikda. He was shy and discreet about showing his emotions. He was very simple and modest with a subtle sense of humour. Both the friends used to meet on Sundays at 9 a.m. at Ray’s residence on Bishop Lefroy Road, Kolkata. Ray used to show Roberge the private screenings and welcome his comments. Ray often addressed Roberge as the French- speaking priest in Bengali and Roberge felt it was Ray’s appreciation for him. Ray wrote his manuscripts in Bengali, with notes in English for his set-designer, with sketches and staff notation of music. Once, he missed the Charulatha screenplay. Though he knew who the culprit was, he didn’t want to take any action with humane concern.
We find striking comparison between Tagore and Ray in their works. There is a philosophical analogy too between them. We find all the characters – the rich, the poor, the powerful, the humble, the peasants, the city persons, children, teenagers, adults, old people, men, women, etc. in Ray’s movies.
Rendezvous with Ray Glossary
rendezvous : a meeting place
unique (adj) : usually good and special
en route (adv) : on the way
stopover (n) : a halt in a long journey
acquainted (v) : deliberately found out about something
trilogy (n) : a set of three films with the same artists or characters [The Apu Trilogy comprises three Begali fims directed by Satyajit Ray: Pather Panchali (1955), Aparajito (1956), and Apur Sansar (1959)]
fascinating (v) : being attracted
path-breaking (adj) : totally new
compilation (n) : book, list, record, etc., which consists of different pieces of information, songs, etc.
insight (n) : a sudden clear understanding of something especially a complicated situation or idea
portal (n) : an entrance
haunted (v) : obsessed
reassurance (n) : something that is said or done which makes someone feel calmer and less worried or frightened about a problem
accusation (n) : the act of charging somebody
detractors (n) : people who criticise
deplorable (adj) : very bad, unpleasant and shocking
arrogance (n) : showing pride
quest (n) : a long search for something that is difficult to find
muster up confidence (idiom) : gain confidence
right away (idiom) : immediately
worthwhile (adj) : important or useful
discreet (adj) : careful about what you say or do, so that you do not offend, upset, embarrass people or tell secrets
stature (n) : the degree to which someone is admired or regarded as important
aloof (adj) : unfriendly and deliberately not talking to other people
intimidating (adj) : making you feel worried and not confident
unassuming (adj) : showing no desire to be noticed or given special treatment, modest
subtle (adj) : not easy to notice or understand
screening (n) : the showing of a film or television programme
cemented (v) : made a relationship between people, countries or organizations firm and strong
elegance (n) : the state of being beautiful, attractive or graceful
manuscript (n) : a book or piece of writing before it is printed
notation (n) : a system of written marks or signs used to represent something such as music, mathematics or scientific ideas
culprit (n) : the person who is guilty of a crime or doing something wrong
reputation (n) : the opinion that people have about someone or something because of what has happened in the past
humane (adj) : treating people or animals in a way that is not cruel and causes them as little suffering as possible
colossus (n) : someone or something that is extremely big or extremely important
sign out (phr.v.) : to write one’s name in a book when one leaves a place such as a hotel, an office or a club
dictum (n) : a statement that is believed to be true and followed
analogy (n) : a feature that is similar
didactic (adj) : intended to teach people a moral lesson
verbose (adj) : using or containing too many words
impulse (n) : a sudden strong desire to do something without thinking about whether it is a sensible thing to do
aesthetics (n) : the art of judging beauty
denying (v) : saying that something is not true
agnostic (n) : a person who does not know whether God exists
frail (adj) : weak and thin
fallout (n) : result