Category: Class 10

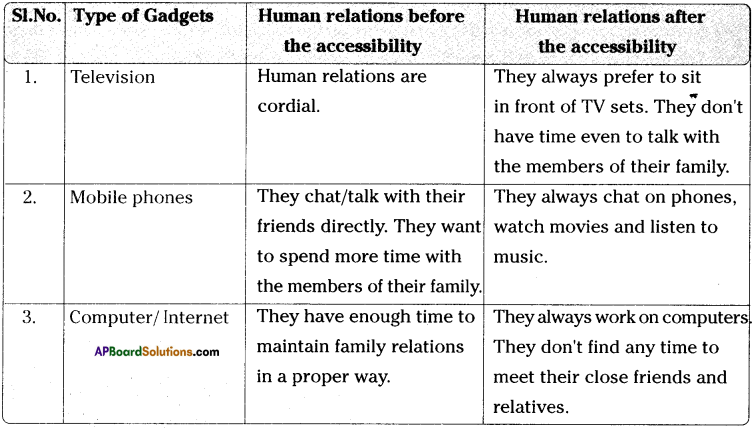
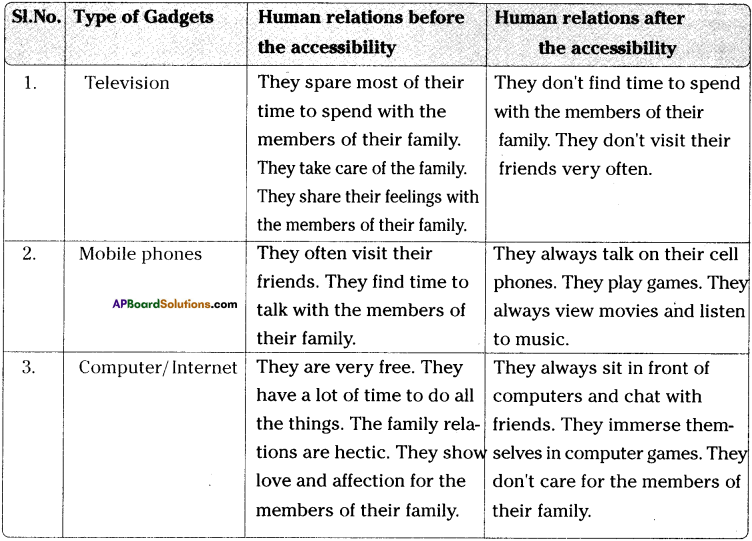
AP State Board Syllabus AP SSC 10th Class English Textbook Solutions Chapter 1A Attitude is Altitude Textbook Questions and Answers.

AP State Syllabus SSC 10th Class English Solutions Chapter 1A Attitude is Altitude

10th Class English Chapter 1A Attitude is Altitude Textbook Questions and Answers

Look at the pictures and answer the questions.

Question 1.
What qualities have made these persons great?
Answer:
The persons in the above pictures are Sudha Chandran, Stephen Hawking and Helen Keller.
Sudha Chandran is an accomplished Bharatanatyam dancer, Indian film and television actress, who showed great courage even though she had lost her leg in an accident.

Stephen Hawking is one of the famous scientists. Despite his debilitating illness, he has done ground-breaking work in physics.

Helen Keller overcame the adversity of being blind and deaf to become one of the 20th century’s leading humanitarians.
These three great persons showed that anything can be done, if one tries hard enough. From their lives, it is understood that one need not lose hope. Their lives show us that disability need not prevent one from reaching great heights. The qualities such as grit, determination, confidence, will power, dedication, discipline, etc. have made these persons great.

Question 2.
What qualities do you think a person requires to become successful ?
Answer:
The qualities a person requires to become successful are determination, dedication, discipline, grit, courage, faith, positive thinking, responsibility, hard work, commitment, desire, persistence, good character, etc. These qualities make a person highly successful.

Comprehension

I. Answer the following questions.

Question 1.
‘I call it my chicken drumstick,’ joked Nick. What does ‘it’ refer to? How does it help him ?
Answer:
‘It’ refers to the small foot that Nick has on his left hip. It helps him balance and enables him to kick. Nick uses his one foot to type, write with a pen and pick things up between his toes.

Question 2.
‘His parents decided not to send him to a special school.’ Was Nick happy about his parents’ decision? Why or why not? What do you think about this decision?
Answer:
Nick’s was not happy with his parents’ decision because there might be the risk of bullying. His companions at mainstream school might tease him.
But later, he realised that his parents’ decision was the best one. I think that this decision was the best one his parents could have made for him as he was able to achieve a degree in Financial Planning and Real Estate. The decision made him independent.

Question 3.
How did Nick’s parents help him to become independent?
Answer:
Right from the start Nick’s parents did their best to make him independent. His father put Nick in the water at 18 months and gave him the courage to learn how to swim. He encouraged Nick to get into football and skating. He taught Nick how to type with his toe at just six years old. Nick’s mother invented a special plastic device that meant Nick could hold a pen and pencil. Despite the risk of bullying, Nick’s parents insisted on his attending mainstream school.

Question 4.
Pick out the symptoms of Nick’s depression. Do you think his depression was normal or something unique about him? Give reasons for your opinion.
Answer:
Nick was deeply depressed when he was eight years old. When he was in depression, he went to his mother crying and told her that he wanted to kill himself. He felt cold and bitter. He hated God for doing this to him. He was terrified about his future without his parents. At age ten Nick tried to drown himself in the bath. These were the symptoms of Nick’s depression. I think his depression was normal. Any human being born like Nick might have the same depression.

Question 5.
Which incident in this text is funny? What makes it funny?
Answer:
Once Nick was in a car and a girl at traffic lights was looking at him interestingly. She could only see Nick’s head so he decided to do a 360 in the car seat to freak her out. When she saw the torso, she sped off really quickly. This is the funny incident in the text. The idea of Nick showing the girl his torso makes the scene funny.

Question 6.
What made Nick choose Bethany Hamilton as his teacher to learn surfing?
Answer:
Nick went to Hawaii in 2008 and met surfing master Bethany Hamilton. She had her arm bitten off by a shark when she was 12. Nick chose Bethany Hamilton as she too was a disabled person and still she performed surfing very well. Though she had no arm she did well. As a disabled person, she could know how a disabled person could learn how to surf. She could know the psychological condition of a disabled person.

Question 7.
Which aspect of Nick’s physical condition helps him to do a 360 degree spin?
Answer:
Nick has a very low centre of gravity so he has got pretty good balance. This condition helps Nick to do 360 degree spin.

Question 8.
What are the distinct features of this text? List them.
Answer:

1. It is an autobiography.
2. Varied sentences are used.
3. Ideas are arranged in a logical sequence.
4. Emotive and persuasive language is used.
5. Ideas are exemplified very well.
6. Cohesion is found in the text. The sentences are connected with proper linkers.
7. Unity of ideas is maintained for coherence. The sentences are connected in a clear and reasonable way.
8. Certain quotations and examples are given.
9. Proper introduction, development and conclusion are ensured.
10. The ideas are given formally and precisely.
11. As far as the content is concerned, it touches the emotions of a reader.
12. The content is message-oriented.
13. Physical description of the main character is given properly.
14. The main character’s attitudes, likes, dislikes, strengths and weaknesses are given effectively.

Question 9.
What do you learn from the life of Nick Vujicic?
Answer:
Nick Vujicic uses his life story to inspire people of all around the world. From the life of Nick, we learn that if we fail, we should try again and again until we succeed. Nick shows us that anything can be done, if we try hard enough. Undoubtedly, I feel that his life is a source of inspiration to everyone of us. He has been able to do all these because of his faith, hope, perseverance and strong will power. Nick proves that disability need not prevent one from reaching great heights. Hence I learn that we shouldn’t lose our faith and hope under any circumstances.

II. Given below are some of the statements made by Nick Vujicic. Which of these are substantiated by Nick’s life ?

• I realised why God had made us like this – to give hope to others.
• I wanted to concentrate on something good that / had.
• I tell people to keep on getting up when they fall and to always love themselves.
• If I can encourage just one person, then my job in this life is done.

Answer:
I think all the above statements are substantiated by Nick’s life.
i) I realised why God had made us like this – to give hope to others:
When Nick was 13, he read a newspaper article about a disabled man who had managed to achieve great things and help others. Nick was inspired very much by the disabled man mentioned in the article. He got a hope from him. Then he decided to use his life to encourage others and give them hope.

ii) I wanted to concentrate on something good that I had:
Nick was not discouraged with his disability. He knew that he had no arms and legs but he thought that they would never take away the beauty of his eyes. With his positive approach, he thought that his eyes were very good ones for him. He wanted to love his positive qualities such as faith, will power and perseverance. Further, he was quite satisfied with what he had, i.e. a small foot on his left hip. He said he would be lost with it.

iii) I tell people to keep on getting up when they fall and to always love themselves: If Nick fails, he tries again and again until he succeeds. When Nick was learning how to surf, he was terrified at first but later he did very well. Though he has no limbs, he always loves himself. I know this by his statement, “I decided to be thankful for what I do have, not get angry about what I don’t.”

iv) If I can encourage just one person, then my job in this life is done:
This statement was substantiated by Nick aptly. He encouraged many people in the world. He used his life story to inspire others. He made many people realise their inner beauty and personality. He was able to rise many people from the state of despair to the state of great hope.

Vocabulary

I. Look at the list of adjectives in the box. Which of them describe Nick Vujicic. Tick (✓) them.

Answer:

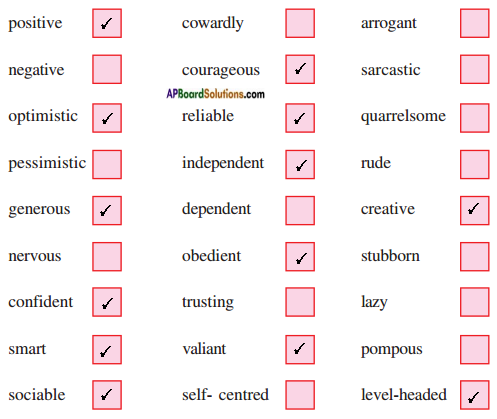
Explanation:

1. positive: hopeful and confident
2. negative: harmful, unpleasant or not wanted
3. optimistic: believing that good things will happen In the future
4. pessimistic: expecting that bad things will happen in the future
5. generous: willing to give money, spend time, etc. in order to help people or give them pleasure
6. nervous: worried or frightened about something
7. confident: sure that something will happen in the way that you want or expect
8. smart: fashionable, clever
9. sociable: friendly and enjoys being with other people
10. cowardly: not at all brave
11. courageous: brave
12. reliable: dependable
13. Independent: confident and able to do things by oneself in ones own way
14. dependent: needing someone or something in order to exist, be successful, be healthy, etc.
15. obedient: always doing what one is told to do
16.  trusting: willing to believe that other people are good and honest
17. valiant: very brave in difficult situation
18. self-centred: paying so much attention to oneself that one doesn’t notice what is happening
19. arrogant: behaving in an unpleasant or rude way
20. sarcastic: saying things that are the opposite of what one means, in order to make an unkind joke
21. quarrelsome: one who quarrels a lot with people
22. rude: not polite and annoys others
23. creative: good at using imagination to make things
24. stubborn: determined not to change one’s mind when people think one is being unreasonable
25. lazy: not making any effort to do anything
26. pompous: trying to seem magnificent or very important; fond of display, acting too proudly, self-important.
27. level-headed: sensible in making judgements

Pick out from the text the examples that support these attributes.

Attribute	Example from the text
1. Positive	In spite of his disability he has become great.
2. Optimistic	He always thinks, “If I fail, I try again, and again, and again. If I can encourage just one person, then my job is done.”
3. Generous	He spends most of his time delivering motivational speeches all over the world.
4. Confident	Though he has no limbs, he gains faith and hope and tries to give them to others.
5. Smart	He appears to be smart and shows his cleverness in learning things.
6. Sociable	He enjoys being with others by delivering speeches, playing football, golf, surfing, etc.
7. Courageous	Despite the absence of his limbs, he didn’t get discouraged. With great courage, he tries again and again and becomes a football player, a swimmer and a surfer.
8. Reliable	He is the most reliable person. As an Evangelical Christian he has faith and gives the same to others with his motivational speeches. The people believe his reliability and are attracted towards him.
9. Independent	He independently has done the things what he has wanted to do. e.g.: Playing football and golf, swimming, surfing, delivering speeches, etc.
10. Obedient	He seems to be obedient in accepting the unlucky birth.
11. Valiant	With great determination, he has reached a great position in his life. He becomes an international symbol of triumph over adversity.
12. Creative	He also plays golf with a club tucked under his chin.
13. Level-headed	He judges well when he says, “The challenges in our lives are there to strengthen our convictions. They are not there to run us over.”

II. Given below are words that describe the positive or negative attitude of a person. Discuss them with your partner and put a tick (✓) against the positive qualities and a cross (✕) against the negative qualities.

Answer:

Explanation:

1. sullen: angry and silent (negative quality)
2. sneaky: doing things in a secret and dishonest way (negative quality)
3. exuberant: happy and full of energy and excitement (positive quality)
4. bossy: always telling other people what to do in a way that is annoying (negative quality)
5. cautious: careful to avoid danger or risk (positive quality)
6. aggressive: behaving in an angry threatening way (negative quality)
7. competitive: determined or trying very hard to he more successful than other people (positive quality)
8. finicky: too concerned with unimportant details and small things that you like or dislike (negative quality)
9. imaginative: good at thinking of new and interesting ideas (positive quality)
10. observant: good or quick at noticing things (positive quality)
11. enthusiastic: showing a lot of interest and excitement about something (positive quality)
12. outgoing: someone who Is outgoing likes to meet and talk to new people (positive quality)
13. haughty: behaving in a proud. unfriendly way (negative quality)
14. intrepid: willing to do dangerous things; fearless, brave (positive quality)
15. malicious: very unkind and cruel and is trying to do harm to others (negative quality)
16. meticulous: very careful about small details and always makes sure that everything is done correctly (positive quality)
17. slovenly: lazy untidy and careless (negative quality)
18. obnoxious: very offensive, unpleasant or rude (negative quality)
19. stingy: not generous. especially with money (negative quality)
20. Idealistic: believing that one should live according to high standards and principles, even when they are very difficult to achieve (positive quality)
21. affable: friendly and easy to talk to (positive quality)
22. logical: reasonable and sensible (positive quality)
23. mean: cruel (negative quality)
24. cultured: intelligent, polite and interested in art, literature, music etc. (positive quality)

III. Tick (✓) the word/expression which is nearest in meaning to the word underlined in each sentence given below.

1. Water sports aren’t Nick’s only thing – he also plays golf with a dub tucked under his chin.
a) kept
b) pulled
c) covered
d) tied
Answer: a

2. His distraught mother couldn’t bring herself to hold him until he was four months old.
a) angry
b) careless
c) shy
d) anxious
Answer: d

3. Despite the risk of bullying, his parents insisted on Nick’s attending mainstream school.
a) discrimination
b) humiliation
c) negligence
d) failure
Answer: b

4. Nick, who was teased and bullied, had an electric wheelchair for mobility, and a team of carers to help him.
a) socialising
b) movement
c) travel
d) safety
Answer: b

5. Nick managed to pull through to become an international symbol of triumph over adversity.
a) disability
b) poverty
c) difficulties
d) opposition
Answer: c

6. The challenges in our lives are there to strengthen our convictions.
a) feelings
b) practices
c) beliefs
d) characters
Answer: c

IV. Read the following descriptions about persons and fill in the blanks with the words that match with these descriptions.

1. Ashok is a very unpleasant and rude fellow. I don’t talk to him. He is ———–.
2. Srinu is very confident, elegant and polite. But sometimes he does not appear to be sincere. He is ———–.
3. Sujatha is quiet and calm. She doesn’t like to spend time with others. She is interested in her thoughts and feelings. So she is an ———–.
4. Ramesh is very sensitive. He always shows sympathy for people who are suffering. He is ———–.
5. My neighbour is such a person that he has a feeling of hatred for others. He desires to hurt others’ feelings. He is ———–.
6. My father pays careful attention to every detail. He makes thorough planning for everything in our home. He is ———–.
7. Prem is an extremely unpleasant person. He always tries to offend people. He is ———–.
8. My mother is very calm and peaceful. She doesn’t get excited or irritated easily. She is ———–.
9. Rahul is a very lively and confident person. He enjoys being with his friends. He is an ———–.
10. Sridhar is always afraid of speaking in the class. He is ———–.
Answers:
1. boorish
2. suave
3. introvert
4. compassionate
5. malicious
6. meticulous
7. obnoxious
8. placid
9. extrovert
10. timid

GRAMMAR

I. Read the text again and identify some more Defining and Non-defining Relative Clauses.

1. —————————————————————
2. —————————————————————
3. —————————————————————
4. —————————————————————
5. —————————————————————
Answer:
1. Nick has a small foot, which helps him balance. (Non-defining Relative Clause)
2. Nick, who was born in Melbourne, now lives in Los Angeles. (Non-defining Relative Clause)
3. I read about a disabled man who had managed to achieve great things and help others. (Defining Relative Clause)
4. I decided to give people the courage that the article had given me. (Defining Relative Clause)
5. Nick, who later achieved a degree, says this. (Non-defining Relative Clause)

II. Read the following sentences and circle the Non-defining Relative Clauses and put a comma/a hyphen wherever necessary.

1. The meeting which was held in the town hall was a great success.
2. The people who live in glass houses must not throw stones.
3. The teachers who have taught Abhiram say that he is an exceptionally creative student.
4. Napoleon who won the French honour died at St. Helena.
5. The silk sarees which are made in Banares are popular all over the world.
Answer:
1. The meeting which was held in the town hall was a great success. (Defining Relative Clause)
2. The people who live in glass houses must not throw stones. (Defining Relative Clause)
3. The teachers who have taught Abhiram say that he is an exceptionally creative student. (Defining Relative Clause)
4. Napoleon, who won the French honour, died at St. Helena. (Non-defining Relative Clause)
5. The silk sarees which are made in Benares are popular all over the world. (Defining Relative Clause)

III. Complete the sentences with Defining or Non-defining Relative Clauses.

1. This is the peaceful place __________________________ .
2. The Mahaprasthanam’ is a popular book __________________________ .
3. Suresh ____________________________ has left the school just now.
4. Is this the street _______________________________________________ ?
5. The express __________________________________ has just arrived.
6. The place ___________________________ has been closed to traffic.
7. This is a famous engineering college _____________________________ .
8. My sister_______________ has secured ajob as an engineer in BHEL.
9. The theatre _____________________________ was designed by Mr Rao.
10. Viswanath is one of the outstanding directors in Telugu film industry______________________ .
Answer:
1. This is the peaceful place that is liked by every naturalist.
2. The Mahaprasthanam’ is a popular book which I have bought in Hyderabad.
3. Suresh, who is mv cousin, has left the school just now.
4. Is this the street where meat is sold?
5. The express which runs between Delhi and Chennai has just arrived.
6. The place which is behind our house has been closed to traffic.
7. This is a famous engineering college that is founded by Mr. Yashwanth.
8. My sister, who has completed her education in Bengaluru, has secured a job as an engineer in BHEL.
9. The theatre which was built in 2012 was designed by Mr. Rao.
10. Viswanath is one of the outstanding directors in Telugu film industry which produces a number of creative directors.

WRITING

I. Writing a biographical sketch

A biographical sketch is an account of the life and activities of an individual. It includes information about the person’s name, place of residence, education, occupation, life and activities and other important details. It is written by another person. If a person writes an account of his/her own life, it is called an autobiography.

Given below in the table is the biographical information about Stephen Hawking. Based on this information write a biographical sketch.

Points to be covered	Details of the person
Date and place of birth	January 8,1942, Oxford, England
Information about the family	Eldest one of four sons Mother: Isobel Hawking Father: Frank Hawking, a medical researcher with a speciality in tropical diseases
Important events in life	Early academic life: recognized as a bright student High school years: third from the bottom of his class Pursuits outside of school: loved board games, constructed a computer out of recycled parts at the age of 16, solved rudimentary mathematical equations Marriage: married Jane Wilde Health: Suffered from Amyotrophic Lateral Sclerosis Research: on black holes Discovery: Hawking Radiation
Awards, prizes, honours	Fellow of the Royal Society at the age of 32 Albert Einstein Award. The Pius XI- Gold Medal for Science from Pope Paul VI in 1975
Contribution to his field and society	Contributed to the advancement of science and research

Answer:

Biographical Sketch of Stephen Hawking

Stephen William Hawking is one of the greatest scientists of the world. He was born at Oxford in England on 8 January, 1942 to Isobel Hawking and Frank Hawking. He was the eldest of four sons. His father, Frank Hawking, was a medical researcher with a speciality in tropical diseases.

Hawking was recognised as a bright student. But he was not initially successful academically. During his high school years, Stephen stood the third from the bottom of his class.

Hawking used to remain with a close group of friends with whom he enjoyed board games, the manufacture of fireworks, model aeroplanes and boats. With the help of the mathematics teacher, Dickran Tahta, Hawking and his companions built a computer from clock parts, an old telephone switchboard and other recycled components when he was 16. Hawking solved rudimentary mathematical equations.

He married Jane Wilde on 14 July, 1965. The first years after their marriage were hectic. Hawking has achieved many things in the field of science in spite of his prolonged illness. He has been suffering from an incurable disease, Amyotrophic Lateral Sclerosis (ALS) which has weakened his muscles since he was 17 years old.

Stephen Hawking is known for his work regarding black holes and for authoring several popular science books. In 1974, Hawking’s research turned him into a celebrity within the scientific world when he showed that black holes are not the information vacuums that scientists had thought they were. In simple terms, Hawking demonstrated that matter, in the form of radiation, can escape the gravitational force of a collapsed star. Thus Hawking Radiation was invented.

As a mark of his eminence, Professor Hawking obtained twelve honorary degrees which he deserved. He was named a Fellow of the Royal Society at the age of 32, and later earned the prestigious Albert Einstein Award. In 1975, Hawking journeyed to Rome, where he was honoured with the Pius XI – Gold Medal for science from Pope Paul VI in 1975.

Attitude is Altitude Summary in English

This is the story of a great person, Nicholas James Nick Vujicic, who stands as an inspiration to other people with his great qualities-faith, will power and perseverance- even though he is a disabled person. His disability has not stopped him from doing what he has wanted to do. Nick Vujicic was born on 4 December 1982 in Melbourne, Australia with a rare disability called Phocomelia characterised by the absence of all four limbs. Despite the absence of his limbs, he plays football and golf, swims and surfs. He is an Australian Christian evangelist and motivational speaker. As a child, he struggled mentally and emotionally as well as physically. It was a shock to Nick’s parents that he was born without limbs. His mother was a nurse and his father was a computer programmer and accountant. His parents did their very best when they decided to send him to mainstream school despite the risk of humiliation.

Nick has a small foot on his left hip. It gives him balance and enables him to kick. With his foot, he writes with a pen and picks things up between his toes. He also plays golf with a heavy stick tucked under his chin. He is a huge fan of the English Premier League. His parents did their best to make him independent from the start. His father gave him the courage to learn how to swim by putting him in water at 18 months. His mother invented a special plastic device to enable him to hold a pen and pencil.

At age eight, Nick was deeply depressed and went to his mother crying. He told her that he wanted to kill himself. When he was ten years old, he decided to end his life by drowning himself in a bathtub but luckily he was unsuccessful in his attempt. When Nick was 13, he was inspired when he read about a disabled man who had managed to achieve great things and helped others. He understood that God had given him the life to give hope to others and so he decided to use his life to encourage other people and give them the courage. He believes that challenges strengthen our opinions. With the help of his religion, friends and family, Nick becomes an international symbol of triumph over adversity. Nick won the Australian Young Citizen of the Year award in 1990 for his bravery and perseverance. His persistence made him achieve a degree in Financial Planning and Real Estate. He went to Hawaii in 2008 and was trained in surfing by Bethany Hamilton. Nick was on the cover of Surfer magazine with his feat of doing the 360 degree spins. He is able to do this feat because of his low centre of gravity.
Nick and Kanae Miyahara, whose mother was a Mexican and father was a Japanese, got married on February 12, 2012 and on February 13, 2013 they were blessed with the birth of a healthy baby boy with full body.

Nick has travelled to over 24 countries speaking to groups of up to 110,000 people. He keeps telling the people to keep on getting up when they fall and to always love themselves. He spreads his messages of faith and hope around the world.

Nick uses his story to inspire and inform people all around the world. Nick presents values, principles, attitudes and perspectives that challenge and equip people from all walks of life to overcome their adversities.

Attitude is Altitude Glossary

stretch (v): to straighten one’s arms, legs or body

wrap (v): put ones arms around something

skateboard (n): a short narrow board with small wheels at each end, which you stand on and ride as a sport

torso (n): the main part of the body, not including the head, arms or legs

surf: to take part in the sport of riding on waves on a surfboard

despite (pre): In spite of

limb (n): an arm or leg

hip (n): one of the two parts on each side of one’s body between the top of one’s leg and one’s waist

chicken drumstick (n): the lower part of the leg of a chicken or other bird that is cooked and eaten as food

faith (n): belief or trust in God

virgin (n): someone who has never had sex

modest (adj): shy about attracting sexual interest

publicist (n): someone whose job is to make sure that people know about a new product, film, book, etc.

club (n): a heavy stick with one end thicker than the other

tuck (v): to put something into a space

distraught (adj): so upset and worried

bully (v): to threaten to hurt someone or frighten them

bullying (n): humiliation

carer (n): someone who looks alter an old or ill person at home

wall-mounted (adj): attached to a wall

pump-action (adj): a pump-action piece of equipment is operated by pulling or pressing a part in or out. so that the contents come out in short bursts

drown (v): to die from being under water for too long time

lack: to not have something that one needs

triumph (n): an important success or victory

adversity (n): a difficulty or unpleasant situation

Inspirational (adj): providing encouragement or new ideas for what one should do

conviction (n): a very strong belief or opinion

run over (phr.v.): to hit someone or something with something (a vehicle, challenge, etc.) and drive over them

perseverance (n): the quality of continuing to try to achieve a particular aim despite difficulties

give somebody the eye (n.phrase): to look at someone in a way that shows one thinks they are sexually attractive

freak out (phr.v.): make someone very anxious. upset or afraid

amazing (adj): (here) very good

spin (n): an act of turning around quickly

centre of gravity (n.phrase): the point in any object on which it can balance

AP State Board Syllabus AP SSC 10th Class English Textbook Solutions Chapter 3C What is My Name? Textbook Questions and Answers.

AP State Syllabus SSC 10th Class English Solutions Chapter 3C What is My Name?

10th Class English Chapter 3C What is My Name? Textbook Questions and Answers

Comprehension

Answer the following questions.

Question 1.
What made Mrs. Murthy so restless to know her name?
Answer:
In her scrubbing zeal, Mrs. Murthy had forgotten her name. At once she felt that she had lost her own identity. She had lost her self-respect. That made her so restless to know her name.

Question 2.
How did Mrs. Murthy’s husband look upon her desire to know her name?
Answer:
Mrs. Murthy’s husband laughed at her when she asked him about her name. He did not take it seriously. He wanted her to be called by his name ‘Mrs. Murthy’. He did not give any importance to her feelings.

Question 3.
Do you notice any change in Mrs.Murthy in the first picture and Sarada in the second picture?
Answer:
Yes. I have found a lot of difference in her being Mrs. Murthy and her being Sarada. After she got her name back she got her confidence back. After she recollected her name she felt like a real person because she got her identity and self-respect back. When she was a housewife she was different, and after she has remembered her name she has become flamboyant.

Question 4.
Do you find any similarities between Mrs.Murthy and the women in your family? If yes, list them.
Answer:
Yes. There are so many similarities between Sarada and the members of our family. Not only in our family but almost in all families we can find a woman like Sarada because she is a representative of women of any class of Indian society who are always confined to domestic work like cleaning floors, washing clothes, cooking, and looking after her children, her husband, and other family members.

Question 5.
Why do you think the writer decided to focus on the question of married women’s identity?
Answer:
The writer decided to focus on the question of married women’s identity because she wanted them to live with their own identity and self-respect. She did not want them to confine to their homes. She wanted them to be given equal rights, equal respect. She wanted that they should also assume some responsibility in nation building activity.

Question 6.
Do you really think a woman can forget her name? What do you think is the intention of the author here?
Answer:
No. I don’t think any woman can forget her own name. The intention of the author is that the women should be respected and should not be confined to the domestic work. She feels that women should not lose their own identity.

Question 7.
Which part of the story shows that Mrs. Murthy feels her identity restored?
Answer:
In the last part of the story, when she returned to her husband’s house Mrs. Murthy feels her identity restored. It is clear from her words “…. from now onwards don’t call me yemoi, geemoi. My name is Sarada – call me Sarada, understood ?”

Writing

I. Translation

Read the following news item in Telugu and compare it with its translation in English given after that.

The following is the translated version of the above Telugu news item.
Centre’s Nod to Kasturi Rangan Committee Recommendations on Western Ghats

NEW DELHI :
The Ministry of Environment has accepted the report made by the Kasturi Rangan Committee on the conservation of Western Ghats. The committee, in its recommendations, made it clear that no further development activities be undertaken in the Western Ghats spread across the 60 thousand square kilometers in six states. The committee was appointed by the Union Government and headed by Kasturi Rangan to suggest measures to conserve the rarest ecosystem of the Western Ghat forests. The committee submitted its Report on 15th of April. The Ministry of Environ¬ment , after taking opinions of the six state governments and the people of the states, accepted the recommendations. The Western Ghats extend in Gujarat, Maharashtra, Goa, Karnataka, Kerala and Tamil Nadu states.

Let’s think of the following :

Question 1.
Do you think that translation is just translation of language ? Or does it also include translation of ideas?
Answer:
No. I don’t think that translation is just a translation of language. It includes linguistic, pragmatic and cultural elements. A literary translation must reflect the imaginative intellectual and intuitive writing of the author. Literary translation must reflect all the literary features of the source text such as sound effects, selection of words, figures of speech, etc.

Question 2.
Which translation is better, true translation or free translation?
Answer:
True translation is a dynamic equivalent translation which focuses on creating an equivalent effect in the target languagae.

Free translation is a formal equivalent translation in which the form and content of the originaUmessage is to be preserved. Of these two types of translations, true translation is better. Since true translation yields in the equivalent effect and it conveys the message of the original to the receptor audience and are equivalent to the original text in a dynamic way, true translation is better.

Question 3.
Do you find any change in the order of the sentence? For e.g : We have Subject, Verb,Object in English but the order is Subject, Object, Verb in Telugu.
Answer:
Not only the structure of the sentence but the diction and style and the order of arrangement of phrases also changes from Telugu to English.
Languages have different pragmatic linguistic structures and norms transferring the norms of one language may well lead to pragmatic failure.

Question 4.
Do you think sometimes it creates problems in the choice of vocabulary while attempting to translate a text?
Answer:
Translation should implicate accurate meaning. It may be problematic for translators. Wrong choice of words may cause ambiguity. While choosing the apt words for translating a text the translator should consider the situationality, intentionality and acceptability.

Question 5.
Is it possible to translate a poem from one language to the other?
Answer:
No. Poetry is not possible to translate because no poem means just one thing. It is very difficult to translate a poem into another language because we may not be aware of many of the possible meanings of the poem.

Question 6.
Is it necessary to take cultural aspects into consideration?
Answer:
Yes. It is necessary to take cultural aspects into consideration while translating. Because translation is a kind of activity which inevitably involves at least two languages and two cultural traditions. There may be cultural difference between the source text and the target text.

The lesson, “What Is My Name?” is a translated version in English from Telugu.The following is a part of the Telugu version of the lesson. Read the Telugu version and observe how it was translated into English.

Activities :

Question 1.
Is this a good translation? Yes or no? Give reasons.
Answer:
Yes. This is a good translation because this translation is a formal equivalent to the original text in the form and the content. It is a good translation because it reflected the imaginative intellectual and intuitive writing to the author. But we have found some difficulties in the structure of the sentences, in diction and style.

Question 2.
Now translate the Telugu version on this page into English and list the difficulties you face.
Answer:
A young woman, before she became a housewife had been an educated, cultured, intelligent, capable, and quick-witted with a sense of humour and elegance.

A young man, who liked her beauty and intelligence and was attracted by the dowry offered by her father, tied the three sacred knots around her neck and made her a housewife. After making her his housewife he told her, “Look Ammadu. This house is yours”. On hearing his words the housewife at once pulled the edge of her sari and tucked it in at the waist and swabbed the entire house and decorated the floor with rangoli designs. On seeing this that young man praised her promptly by saying “Ammadu ! You are dexterous in swabbing floors and even more adept in drawing the muggulu. Sabash Keep it up.” He said it in English, giving her a pat on the shoulder in appreciation.

Overjoyed with this, the housewife continued to live with swabbing as the chief mission of her life. Always she used to scrub the floor spotlessly and decorate it with beautiful multi-coloured rangoli designs. Thus her life went on with a sumptuous and ceaseless supply of swabbing cloths and muggu baskets.

But one day while scrubbing the floor, the housewife suddenly asked herself, “What is my name?”. The query shook her up. Leaving the mopping cloth and the muggu basket there itself, she stood near the window scratching her head, lost in thoughts.

“What is my name ? What is my name ?”. The house across the street carried a name-board, Mrs. M. Suhasini, M.A., Ph.D., Principal, ‘X’ College. Yes, she too had a name as her neighbour did. “How could I forget like that? In my scrubbing zeal I have forgotten my name — what shall I do now?” The housewife was perturbed. Her mind became totally restless. Somehow she finished her daubing for the day.

Meanwhile, the maidservant came there. Hoping that at least she would remember her name, the housewife asked her, “Look ammayi, do you know my name ?”

Question 3.
Translate the following extract from the story into Telugu and compare it with the original story in Telugu. (Refer to teacher’s handbook for Telugu version.)
‘Sarada! My dear Sarada!’ she shouted and embraced her. The housewife felt like a person — totally parched and dried up, about to die of thirst — getting a drink of cool water from the new earthen kooja poured into her mouth with a spoon and given thus a new life.The friend did indeed give her a new life — ‘You are Sarada. You came first in our school in the tenth class. You came first in the music competition conducted by the college. You used to paint good pictures too. We were ten friends altogether — I meet all of them some time or other. We write letters to each other. Only you have gone out of our reach! Tell me why you are living incognito?’ her friend confronted her.
Answer:

Project Work

I. Influence of technical gadgets on human relations.
Visit five houses in your neighbourhood and collect the information in the given format related to human relations, i.e. spending quality time with the members of the family and friends, sharing and caring. Analyse the information and write a report by adding your opinion on how the modern gadgets are influencing human relations and present it before the class.

Family-1 (House-1) (Raja Rao’s Family)

Family-2 (House-2) (Rama Rao’s Family)

Family-3 (House-3) (Venkat’s Family)

Family-4 (House-4) (Nageswara Rao’s Family)

Family-5 (House-5) (Bhaskar’s Family)

We all know very well that electronic gadgets such as TVs, Mobile phones, Computers occupy a major place in our day-to-day lives. Though these gadgets have their own advantages, they also have a negative influence on the human relationships. They play a vital role in our lives today. Most of us are addicted to them. There are hundreds of channels which are viewed on TV by us. We start watching TV programmes from a very early time in the morning till midnight. Thus we don’t have any time to talk to our near and dear. In the same way, mobile phones too have advantages as well as disadvantages. Most of the children and youth are spending all their time in using their mobile phones. They talk, watch movies, listen to music, play games on their mobile phones. When they engage in using their mobile phones, how can they find time to spend with their family members? Today, computers have become indispensable to each one of us.

In most of the families, we find a complete different situation in managing human relationships before and after the accessibility of the electronic gadgets. Before the accessibility of these modern gadgets, people share most of their time to spend with their family members. They take care of all the family members. They try to share their feelings with their famiy members. They often visit their friends. Their relationships with their family members and friends are very cordial. They find a lot of time to do all the things leisurely. Thus family relations are hectic. They show love and affection for their family members. They find time to play with their friends. They help their family members in all the matters.

After the accessibility of the modern gadgets, they try to spend all their time in using them only. They spend with them hours together. They don’t find time to spend with their family members. They don’t visit their friends very often. They don’t care for their family members. They give importance to the gadgets only. They become mechanical. They don’t have any affection for their family members. They don’t understand the warmth of relationship. They don’t know how much they are missing the joyous family interaction. They should understand that no artificial media can substitute their family’s warmth and interaction. They should give importance to human relationships.

II. Nowadays, we can easily find children even as young as two years old playing with electronic devices and gadgets anywhere. It is not only the video games that make children stay, it also includes television, mobile phones, computers, tablet computers, PSP (Play Station Portable) games, etc. Parents may find it easier to make their children stay in one place by giving them a gadget to play with.

Work in groups and discuss the following:

Ways of managing children’s electronic devices consumption and preventing
Answer:
Group 1 :
The parents should make their children know the bad effects of spending more time with electronic devices.

Group 2:
The parents should monitor their children’s media consumption – television, mobile phones, computers, tablet computers, PSP games, etc.

Group 3 :
The parents should make their children aware about the advantages of playing games, doing exercises and yoga instead of their spending more time with electronic devices.

Group 4 :
The parents should stop themselves from using the electronic gadgets for longer times. Thus they can set an example for their children.

Group 5 :
The parents should make their children aware about the health problems that would arise with spending longer times with electronic gadgets.

Group 6 :
The parents should share thier feelings with their children. They should discuss with them the ill effects of the games they play. They should try to move closer to their children.

Sum up:
Today most of the children are addicted to the modern gadgets such as television, mobile phones, computers, tablet computers, PSP games, etc. These all become an integral part of children’s lives. Today children are heavily exposed to media. Parents may find it easier to make their children stay in one place by giving them a gadget to play with. The parents should watch carefully what their children are doing with the gadgets and how they are using it. They should prevent their children’s addiction to games. They should find ways to manage their children’s electronic device consumption.

They should make their children know the bad effects of spending more time with electronic devices. They should monitor their children’s media consumption. They should make them play games and do exercise and yoga. The parents should stop themselves from using the electronic gadgets and stand as an example to their children. They should share their feelings with their children. They should try to move closer to their children.

Thus, parents can manage their children’s electronic device consumption and prevent their addiction to games.

What is My Name? Summary in English

Sarada, before she got married, was a well-educated and cultured young woman. She was intelligent, capable, quick-witted and she had a sense of humour and elegance. She used to stand first in her class. She was good at music and dance. She used to paint good pictures.

Falling to her beauty, and intelligence and attracted by the dowry her father offered, a young man married her. Later he showed his house and told her that it was her house. Immediately she began to swab the floors and decorated the floor with rangoli designs. On seeing this, her husband praised that she was dexterous at swabbing the floor. Overjoyed by his applause, Sarada began living with swabbing as a mission of her life. Thus, her life went on scrubbing the house spotlessly and decorating the house with multi-coloured designs. In her scrubbing zeal she had forgotten her name. One day she tried to recollect what her name was. But she could not. She became restless. She asked her maid servant, her neighbours, her husband, and her children about her name. But they all told the name by which they used to call her by using their relation. Her husband laughed and did not take it seriously.

Finally the housewife decided to go to her parents’ house and look for her name in her certificates. But her certificates were kept on the attic. Meanwhile she met her classmate. She called the housewife by her name ‘Sarada’. At once Sarada felt like a person. Because our name gives us our personal identity and self-respect. Our name is our own- unique to us.

Here the author wants to tell that every woman has her own responsibility in nation-building. Women should be given equal rights with men. Women should not be confined to the four walls of the house. She should be let free. She can reach to the heights of sky. She can ascend to the pinnacles of any success and thus she can make any nation greater and stronger.

What is My Name? Glossary

quick-witted (adj) : intelligent; able to think quickly

elegance (n) : a satisfying or admirable neatness; ingenious simplicity or precision in something

dowry (n) : money and property paid by a bride’s family to the bridegroom at the time of marriage

swab (v) : clean

dexterous (adj) : skilful

appreciation (n) : recognizing and enjoying the good qualities of somebody or something

sumptuous (adj) : luxurious, splendid

cease (v) : stop

ceaseless (adj) : continuous

zeal (n) : great energy and enthusiasm

mopping (v) : cleaning/washing

perturb (v) : bother/disturb/trouble

daubing (n) : the act of spreading a substance such as mud thickly

take somebody aback : to shock or surprise somebody very much

immerse (v) : absorb oneself in something

urge (v) : to try hard to persuade

giggling (v) : laughing nervously

anguish (n) : severe pain, unhappiness

frantically (adv) : worriedly/anxiously

chore (n) : a task that you do regularly

attic (n) : a room or space just below the roof of a house often used for storing things ; loft

wail (v) : to make a long loud cry

maternity home (n) : hospital for deliveries

parch (v) : dehydrate

incognito (adv) : having a concealed identity

fish (v) : search

AP State Board Syllabus AP SSC 10th Class English Textbook Solutions Chapter 2A The Dear Departed Part 1 Textbook Questions and Answers.

AP State Syllabus SSC 10th Class English Solutions Chapter 2A The Dear Departed Part 1

10th Class English Chapter 2A The Dear Departed Part 1 Textbook Questions and Answers

Look at the pictures and answer the questions.

Question 1.
What do you understand from the picture?
Answer:
The rat is pointing a pistol at the cat and intimidating him. I understand that it is a funny picture. One can easily open one’s lips without knowing to smile on seeing this unusual picture.

Question 2.
Can you recall anything comic associated with these animals?
Answer:
The most popular comic Tom and Jerry’ is associated with them.
‘Tom and Jerry’ is a series of animated cartoon films. We find humour with the rivalry between a cat (Tom) and a mouse (Jerry), Tom’s chasing Jerry and slapstick scenes. “Tom’s making numerous attempts to capture Jerry which leads to destruction” – it creates fun. The scenes such as slicing Tom in half, shutting his head in a window or a door, stuffing Tom’s tail in a mangle, kicking him into a refrigerator, plugging his tail into an electric socket, sticking matches into his feet and lighting them, etc. amuse all the viewers.

(Or)
Yes. I can recall an incident which happened a long time ago in my old house. We used to see many mice in our old house because we stored paddy bags in the house. One day our pet cat jumped on a little mouse which was eating the paddy grains. The little mouse began running. Our cat ran after it. The funny thing was that the mouse did not run away from the place. It began running around the paddy bags. After some time both the cat and the mouse stopped running as they were tired much. At that stage 1 interfered and drove the cat away to save the life of the rat.

Question 3.
Can you imagine, what may be the conversation between the rat and the cat?
Answer:
Conversation between the rat and the cat:
Rat : Hands up!
Cat : Don’t shoot me. I will not eat you.
Rat : No, I don’t believe you. You are cruel.
Cat : Believe me. I decided not to eat rats.
Rat : I don’t believe you. You ran after me yesterday, didn’t you?
Cat : Yes. But not to kill you.
Rat : Then, why?
Cat : I just wanted to tell that I would not kill you thereafter.
Well, how did you get the pistol?
Rat : I stole it from the owner of the house last night.
Cat : Ok. Do you know how to shoot with it?
Rat : I will not tell you.
Cat : Ok. Bye.
Rat : Bye.

Comprehension

Answer the following questions.

Question 1.
What qualities of Mrs. Slater have you noticed?
Answer:
Mrs. Slater is unscrupulous, greedy, deceitful, dishonest, selfish, impolite and insensitive. She unfairly claims her father s things. This shows her unscrupulous and dishonest manner. She has shifted her father’s bureau and clock from his room before her sister’s arrival. Hence 1 can say Mrs. Slater is greedy. She wants to deceive her sister by pinching their father’s things. 1 can say that she is impolite and insensitive as she doesn’t even wait for her father s funeral and has started dividing things between them (the two sisters).

Question 2.
Why does Mrs. Slater decide to shift the bureau from her father’s room before the arrival of the Jordans? How does Henry react to the suggestion?
Answer:
Mrs. Slater wants to own her father’s bureau as he likes it very much. After her father’s death, she decides to shift the bureau to sitting room before the arrival of the Jordans. She thinks that her sister will lay a claim to it. At first, Henry is shocked at her decision. He feels that the two sisters should amicably divide their father’s things. Henry suggests her that it is not a good thing pinching her father’s things in an unfair way. Moreover, Henry is worried about the arrival of the Jordans while they are shifting the bureau.

Question 3.
Why do the Jordans take a long time to get to the house of the Slaters? What does it show about the two sisters’ attitude towards each other?
Answer:
I think the Jordans are late as they have bought mourning dresses to wear before they come to Slater’s house. They are not sorrowful at their father’s death but they are worried about their appearances and how they can come out to each other. In their relationship, we don’t find any kind of emotions and sisterly love.

Question 4.
Ben appreciates his father-in-law saying, ‘It’s a good thing he did’. Later, he calls him a ‘drunken old beggar’. Why does he change his opinion about his father-in-law?
Answer:
Ben appreciates his father-in-law saying it’s a good thing he did’ when he comes to know from Mrs. Slater that the old man has gone out to pay his insurance premium on the day of his death. Later, he comes to know that he has not paid the premium and therefore calls him a drunken old beggar’. Ben has changed his opinion about his father-in-law when be realises that he hasn’t paid premium because, now after his death, they can t claim the insurance company.

Question 5.
What made Mr.Henry feel shocked to hear Victoria say ‘Are you planning to pinch it ?’?
Answer:
When Victoria asked Slaters “Are you planning to pinch it ?”, Mr. Henry felt shocked. He thought that Victoria was innocent. But when she asked him the above question, Mr. Henry came to know that Victoria had wisdom beyond her age. He actually didn’t expect that question from his little daughter.He came to know that she was a precocious girl and had the ability to distinguish between good and bad.

The Dear Departed Part 1 Summary in English

The one-act play “The Dear Departed” by William Stanley Houghton is a satirical play that explores family relationships and the falsehood and hypocrisy and greed that often lie beneath it. The story exposes the sad fact that human beings often become dehumanized in the face of greed and minor material gains. This play satirizes the degradation of moral values in respect and care within the members of the family itself. This story clearly reveals how elderly people are mistreated. Stanley Houghton uses various literary devices to criticize basic human characteristics in his play. He uses irony, sarcasm, humour and a twist in the plot to criticize human traits. He tries to bring out the qualities of the two daughters called Mrs. Slater and Mrs. Jordan towards their father. He tries to show how the sisters are interested in the property of their father rather than to show true care and affection towards their father.

The story begins with Mrs. Slater telling her daughter, Victoria to change her dress before the arrival of her sister (Slater’s sister) Elizabeth and Elizabeth’s husband, Ben. Mrs. Slater’s husband, Henry has sent them a telegram with the message of the death of his father-in-law and Elizabeth and Ben are coming to talk over the old man’s affairs. Henry wonders if they would come at all because Elizabeth has said that she would never set foot in their house again. But Mrs. Slater says that her sister will come fast enough after her share of what their father has left. Mrs. Slater asks her husband to wear the new slippers of her father. She also suggests that they should replace their shabby old chest of drawers with the valuable bureau of her father which is in his bedroom. He agrees to do it after some hesitation. Mrs. Slater wants to do it before their arrival.

Mrs. Slater fastens the door and she and her husband carry the old chest of drawers upstairs. Henry is shocked when Victoria asks him if they are pinching grandpa’s bureau. He replies that grandpa has given it to her mother before his death. Mrs. Slater carries a handsome clock and puts it on the mantelpiece. Mrs. Slater and her husband carry the pretty old-fashioned bureau downstairs and put it in the place of the chest of drawers. At the same time Victoria ushers in Mrs. Jordan and Ben. Mrs. Jordan goes straight to Mrs. Slater and kisses her and the men shake hands. Mrs. Jordan remarks that their father has gone at last. Mrs. Slater replies that he is seventy-two a fortnight the previous Sunday. She tells them that the old man has been merry that morning and has gone out to pay his insurance. Ben and Mrs. Jordan remark that it is a good thing on his part.

According to Mrs. Slater, their father is found dead when she takes up a bit of something for him on tray.
Ben and Mrs. Jordan don’t want to look at the old man ; they prefer to have tea and so Mrs. Slater gets tea ready. They think of publishing the announcement of the death of the old man in the papers. Then they decide to look through the old man’s things and make a list of them. Mrs. Jordan tells that the old man has promised his gold watch to their Jimmy. Then Victoria tells them that grandpa hasn’t paid his insurance. Ben calls him “the drunken old beggar”. Both the sisters complain that they have to put up with their father for all those years. Then Mrs. Slater asks Victoria to go and bring the bunch of keys from grandpa’s room. Victoria is afraid to go but she does. After some time, she gets back very scared and tells them that grandpa is getting up. They are transfixed with amazement. The vigorous and well coloured old man Abel Merry weather comes in.

The Dear Departed Part 1 Glossary

lay (v): (here) to put the cloth, plates, knives, forks etc. on a table, ready for a meal

vigorous (adj): using a lot of energy and strength or determination

plump (adj): slightly fat in a fairly pleasant way

vulgar adj): rude and offensive

get her own way (idiom): persuade other people to allow you to do what you want

D’ye: Do you (used in awkward situations)

amazed (adj): very surprised

ages (n): long time

stooping (adj): bent towards and down

drooping (adj): hanging or bending down

come after (phr.v.): to look for someone to get something from them

worn out (adj): too old or damaged to be used

break down (phr.v.): stop working in a successful way

trifle (n): something unimportant or not valuable

precocious (adj): Intelligent/gifted/talented

bureau (n): a writing desk with drawers

drive a liard bargain (idiom): work hard to negotiate agreements in on&s own favour

startled (v): made someone suddenly surprised or slightly shocked

stupefied (adj): so surprised, tired or bored thai one cant think clearly

daft (adj): stupid/silly

shabby (adj): untidy and bad

fasten (v): to firmly close a window, door etc. so that it will not open

pinch (w): steal

mantelpiece (n): a shelf projecting from the wail over the fireplace

usher (v): lead/show the way/welcome

appeal: be attractive

stagger (v): to walk or move unsteadily, almost falling over

complacent (adj): sell-satisfied/unconcerned

mourning (n): feeling of sadness to miss someone after they have died

fortnight (n): two weeks

chirpily (adv): cheerfully and actively

snug (adj): warm and comfortable

wipe (v): to rub a surface with something in order to remove liquid, dirt, etc.

look through (phr.v.): look for something

overdue (adj): not paid by the expected time

annoy (v): to make someone feel slightly angry and unhappy about something

put up with (phr.v.): to accept an unpleasant situation or person without complaining

swindling (v): cheating somebody for property or money

reluctantly (adv): unwillingly

AP State Board Syllabus AP SSC 10th Class English Textbook Solutions Chapter 3A The Journey Textbook Questions and Answers.

AP State Syllabus SSC 10th Class English Solutions Chapter 3A The Journey

10th Class English Chapter 3A The Journey Textbook Questions and Answers

Look at the picture and read the following excerpt from the diary of a 72-year-old man. Answer the questions that follow.

As I sit here alone and waiting
I gaze at people passing me by.
I try to smile and reach out to them
But no one notices; no one waits.
They look to me like I am nothing
Are they afraid to be seen saying “Hi”
to an old man like me?

Question 1.
What is the excerpt about?
Answer:
The excerpt is about an old man’s inner feelings. He feels sorry for himself. Through this excerpt, he tries to tell the readers about his pathetic condition. He feels that he is totally neglected.

Question 2.
How do people respond to the old man’s smile?
Answer:
When the old man tries to smile and reach out to others, no one notices and no one waits. They look to him like he is nothing. The old man feels that they are afraid to be seen saying “Hi” to an old man like him.

Question 3.
How should old people be treated so that they do not feel neglected?
Answer:
The old people should be treated equally. They should be respected and treated with honour. They should not be bullied or laughed at. We should share our feelings with them. We should give value to their feelings. We should obey them and try to follow their pieces of advice. If we treat the old people as mentioned above, they don’t feel neglected.

I. Answer the following questions.

Question 1.
‘After spending a leisurely Sunday at home, the very thought of returning to work on Monday is tiring.’ Do you agree? Have you ever felt so?
Answer:
Yes, 1 agree to the above statement. After spending a leisurely holiday at home, the very thought of returning to work on the next day is tiring to anyone. I have felt so many a time. I felt so after Dussehra holidays, Pongal holidays and summer vacation previously. It would be a difficult day for me going to school on the very first day after the holidays are over.

Question 2.
The last sentence of the first paragraph and the first sentence of the second paragraph appear to contradict each other. What could be the reason for the change in the decision?
Answer:
The last sentence of the first paragraph says that the author didn’t want to go but the first sentence of the second paragraph says that the author decided to go finally. Both the sentences contradict each other. At first he didn’t want to go as he had got married. He didn’t want to leave behind his newly-wed wife. But, when he remembered his increased responsibilities because of his marriage and his debts, he decided to return to work.

Question 3.
‘Why did the author get into debt? Think of some possible reasons.
Answer:
The author felt that he had got into debt after his marriage.
The possible reasons are :
i) The author might have met his marriage expenses.
ii) He spent leisurely at home for about six months without going to work.
iii) The increased expenses for the new couple.
iv) The author might have bought new furniture.
v) He might have bought a new flat.
vi) He might have bought a number of sarees for his newly-wed wife.
vii) He might have spent money carelessly.
viii) He might have given money to his old parents.

Question 4.
Why was the author reluctant to carry his own luggage? What would you do if you were in the author’s place?
Answer:
The author was reluctant to carry his own luggage as he had the feeling that if he carried the luggage, the whole world would laugh at him. He thought that his education had made him shun physical labour. In fact, the author looked for someone’s help. He felt that his guilt, shame, self-consciousness and pride might have stopped him from carrying the luggage. If I were in the author’s place, I would not do like he did. I would myself carry the luggage without looking for others’ help.

Question 5.
The author feared that the whole world would laugh at him if he carried the trunk. Was the fear imaginary or real? Give reasons for your answer.
Answer:
The author feared that the whole world would laugh at him if he carried the trunk. I think his fear was imaginary. No one laughs at us when we do our work. In fact, carrying the trunk should not have been such a worry for him. For a young man like the author it should not have been an issue to carry his luggage on his back. Actually the others will praise his modesty, if he carries his luggage himself.

Question 6.
Choose one sentence from the story that best expresses the author’s false prestige. Support your answer with details from the story.
Answer:
“Somehow, I had the feeling that if 1 carried the luggage, my father and my people, in fact the whole world would laugh at me and I would be belittled,” – this sentence expresses the author’s false prestige. He thought that his education had made him avoid physical labour. As a government officer, he didn’t accept the idea of people seeing him carry his own luggage. He was of the opinion that it was through him that his parents had earned a greater degree of admiration and respect from the villagers. He felt that his father would not like to see him carrying a trunk on his back and would be very hurt if he did so. These are all the facts which show the author’s false prestige.

Question 7.
What does the phrase ‘opposite directions’ in the last sentence suggest?
Answer:
When the bus started moving, the author saw his father gradually receding into the distance. The author felt that their journeys started in two opposite directions, with him seated in the luxurious seat of a bus and father walking back with tired legs on the pebble-strewn road. The phrase ‘opposite directions’ suggests that both their directions were different. Actually, the son and the father had to travel in opposite directions to reach their destinations. In the other sense, the writer’s way was a luxurious one as he was an educated one and a government officer. He didn’t need to lead such a hard and laborious life like his father used to lead. When compared with his life, his father’s life was much harder one.

Question 8.
How was the story told? Were the events narrated in the order in which they had happened? Spot the sentences where the course of narration changed its direc¬tions. How effective was it?
Answer:
‘The Journey’ is a beautiful narrative by Yeshe Dorjee Thongchi. Most of the events were narrated in the order in which they had happened. Here and there we find that the narration changed its directions.
The sentences where the course of narration changed its directions:
a) “I did not have much to carry byway of luggage – just a trunk. Ours is a hilly terrain
Here the author tried to give the reason. Then he explained the purpose of his coming to his place. Thus, the course of narration was changed.
b) “Nobody had time to spare for me. In fact, carrying the trunk should not have been such a worry”
The course of narration was changed after the first sentence when the author tried to tell us about his inner feelings.
c) “We were walking up a narrow hilly road and neither of us uttered a word as if we were strangers who spoke different languages. I did not know what was going on in his mind.”
When we observe the two sentences given above, the first one changed its direc¬tion when the author tried to present his thoughts.
d) “Father wanted to say something but the bus started moving.” Later the narrative was changed its course when the author tried to think about his way in comparison with his father’s.
A reader could understand very well about the author’s inner thoughts by this way of narration. He too would try to think in his own way imagining that if he were in the author’s place. Thus it was effective in provoking the thoughts.

II. Write the number of the paragraph that gives the stated information in each of the following sentences.

1. The author enjoyed his married life.
Answer:
Paragraph 1 (The first paragraph)

2. The author tried to convince himself that he had not done anything wrong.
Answer:
Paragraph 11.

3. The author was ashamed of making his father carry his trunk.
Answer:
Paragraph 10.

4. The author looks at himself and his father as two travellers taking two different roads.
Answer:
Paragraph 16 (The last paragraph).

III. The following statements are false. Correct them.

1. The author offered to carry the trunk for some time.
2. The author could decide on whether to allow his father to carry the trunk or not.
3. The author took unpaid leave.
4. The father was not happy with the old shoes his son gave him.
Answer:
Corrections:

1. The author didn’t carry the trunk at all throughout the story. His father carried it all the way.
2. The author decided that it would be better to let his father carry the trunk.
3. The author initially thought of taking unpaid leave but later he decided against it.
4. The father was happy with the old shoes his son gave him. His face lit up with content-ment when he noticed the author taking out his pair of shoes from the trunk.

Vocabulary

I. Look at these words from the story :

1. newly-wed wife
2. bus stop
3. forehead

They are all compound words. A compound word is a union of two or more words to convey a unit idea or special meaning that is not as clearly or quickly conveyed by separated words. As shown above, compound words may be hyphenated, written open (as separate words), or written solid (closed). The use of compounding in English is an evolving process. As expressions become more popular or adopt special meanings, they follow a gradual evolution from two or more separate or hyphenated words to single words.

audio visual	audio-visual	audiovisual
copy editor	copy-editor	copyeditor
wild life	wild-life	wildlife

The words in the first, second and third columns are called ‘open compounds’, ‘hyphenated compounds’ and ‘closed compounds’ respectively. In this unit we focus on hyphenated compounds.

A hyphenated compound is a combination of words joined by a hyphen or hyphens. Here, the hyphen aids understanding and readability and ensures correct pronunciation. Words are hyphenated mainly to express the idea of a unit and to avoid ambiguity.

A. Pick out all the compound words from the story and group them under the head-ings as explained above.

Open compounds	Hyphenated compounds	Closed compounds
1. bus stop	1. newly-wed	1. anyone
2. government officer	2. far-off	2. someone
3. tea shop	3. 20-kilo	3. forehead
4. each other	4. home-made	4. moreover
5. bare feet	5. matter-of-fact	5. myself
	6. self-consciousness	6. anyway
	7. white-collar	7. childhood
	8. pebble-strewn	8. useless
		9. anything
		10. somehow

B. Fill in the blanks to make hyphenated compound words. Refer to a dictionary and get the meaning. Write a few sentences using them appropriately.

1.	20	kilo	chest
		rupee	note
		inch cake	tin
2.	newly	wedded	wife
		formed	association
		constructed	building
		discovered	particle
3.	flood	hit	area
	home	made	wine
	flood	hit	villages
	pebble	strewn	road
	kind	hearted	people
	well	mannered	man
4.	white	collar	job
	pink	card	holder
	new	tradp	union

Own Sentences:
1. a) He can easily lift a 20-kilo chest.
b) My father gave me a 20-rupee note.
c) We ordered a 20-inch cake tin and it has just been delivered.

2. a) Mr. Prakash came to his native place along with his newly-wedded wife.
b) The newly-formed association held an important meeting yesterday.
c) Theirs is a newly-constructed building.
d) The scientists declared that it was a newly-discovered particle-
e) The CM has visited the flood-hit area.

3. a) They served the home-made wine in the party.
b) The officials listed out the flood-hit villages.
c) I have to walk over pebble-strewn road to reach the temple.
d) They are kind-hearted people; they have made their contribution in building this hospital.
e) Mr. Rajan is a well-mannered man; he always tries to be friendly with others.

4. a) Mr. Ravi Teja was offered a white-collar job.
b) Mr. Bharat is a pink-card holder, who is eligible to take all the fair-price goods.
c) Yesterday, they formed a new-trade union.

C. Fill in the blanks with the missing parts of compound words.

Kedarnath lived in Uttarakhand. Due to heavy rains, his village was hit by floods. His newly ____(1) ____ house fell down and he became ______(2)_____ less. The Chief Minister visited all the _____ (3) ____ hit villages and announced immediate help. However, Kedarnath lost his self ____(4) ____ and tried to commit suicide by jumping into the flooded river. Some brave and ____(5) ____ hearted people rescued him risking their lives. They told their stories too. Someone had lost his ____(6) ____ wedded wife, and someone else had lost all his family members. One of them offered him a ____(7) ____ collar job. It required him to carry rice bags. But he could not carry even a 20 ____(8) ____ bag, so he asked for a ____(9) ____ job. But no such jobs were available. One of them suggested ____(10) ____ employment scheme. But Kedarnath had no money. One day as he was walking on the pebble ____(11) ____ road, he found some ____(12) ____ plated idols and jewellery in a box.
Answer:

1. built (newly-built)
2. home (homeless)
3. flood (flood-hit)
4. confidence (self-confidence)
5. kind (kind-hearted)
6. newly (newly-wedded)
7. blue (blue-collar)
8. kilo (20-kilo)
9. white-collar
10. self (self-employment)
11. strewn (pebble-strewn)
12. gold (gold-plated)

II. Look at the word ‘dilly-dally from the text. This is a reduplicative word. The words super-duper and bye bye are also reduplicative words. But they belong to different categories shown below:
1. Duplicative type :
Here, the first part of the word is repeated without any change.
e.g.: bye bye

2. Alliterative type :
Here, the two parts have the same consonants but different vowels.
e.g. : dilly-dally, chit-chat

3. Rhyming type :
Here, the second word starts with a different consonant but rhymes with the first part.
e.g. : super-duper

A. Look at the following reduplicatives carefully and put them under proper headings in the table given below.

Answer:

Duplicative	Alliterative	Rhyming
aye-aye	ding-dong	bow-wow
chuk-chuk	ping-pong	easy-peasy
bang-bang	zig-zag	okey-dokey
chop-chop	see-saw	hodge-podge
tata	hip-hop	helter-skelter
papa	chit-chat	itsy-bitsy
ha ha	pitter-patter	nitty-gritty
boo-boo	tip-top	hanky-panky
hush-hush	tick-tock	teeny-weeny
night-night	mish-mash	hurly-burly

Reduplicatives are used in a variety of ways. Some simply imitate sounds: ding- dong, bow-wow. Some suggest alternative movements: flip-flop, ping-pong. And some intensify meaning: teeny-weeny(very small), tip-top(very good).

Find the meanings of the words you like and use them in your own sentences. You will find similar words in your language too. For example, in Telugu, we have words like chi-chi, pho-pho, kaadu-kaadu, tara-tama, taado-pedo, pilla-jella, auto-ito. Give some examples from your language. Don’t they sound musical?

Reduplicative Words in Telugu

B. Answer each of the following questions using a reduplicative word.

1. What does the clock say? ____________________
2. What does the school bell say? ____________________
3. How does the rain drop? ____________________
4. What does the dog say? ____________________
5. How do you laugh? ____________________
Answer:

1. tick-tock
2. ding-dong
3. pitter-patter
4. bow-wow
5. ha ha

Grammar

I. In this story the author used past perfect tense (had + past participle) in many sentences. If you observe the following sentences from the story and the rules given under them, you will understand why and how the past perfect tense is used.’

1. It was 10.20 My father had already left, (para 6)
Answer:
When an action takes place before a point of time in the past, the action is expressed in the past perfect tense. (Sometimes the point of time can be understood from the earlier sentences and other contextual clues.)

2. Finally we reached Dirang. The bus from Tawang had not yet reached Dirang. (para 11)
Answer:
When two actions in the past are clearly separated by time, the earlier action is expressed in the past perfect tense.

3. I quickly sat down on a rock. My father laughed at my plight, (para 7)
Answer:
When two actions in the past happen simultaneously, both of them are expressed in the past tense.

4. a) Sunitha never saw a bear before she was transferred to Maredumilli. (not from the story)
b) Shindh closed the doors because she heard loud noises from outside.
c) I never met him after I left India.
Answer:
Normally, when the time relation is unambiguous, (by the use of before, after, because, etc.), the simple past (past perfect is optional) is used to refer to both past actions.

Comment on the use of the simple past tense/past perfect tense (as illustrated above) in the following sentences. Identify the tense and give reasons for the use of the tense used.

1. I had come home this time round for a special purpose: to get married. My parents had arranged my marriage according to the customs of our tribal society.
Answer:
In both the sentences, the part perfect tense is used as those two actions had already completed before his narration, (had come, had arranged)

2. Time flew, and five months into my marriage I realized it.
Answer:
In the above sentence both the verbs are in the simple past tense as the time relation is unambiguous and those two occur in the past simultaneously.

3. But after some dilly-dallying I finally decided against it because marriage had increased my responsibilities and I had got into debt.
Answer:
“Marriage had increased my responsibilities and 1 had got into debt.” – These two actions occurred before “I finally decided against it.” Hence, in the earlier two actions the past perfect tense is used while the simple past tense is used in the latter.

4. On my way home from the bus stop my trunk had been carried by a porter, (para 3)
Answer:
The above action occurred before his narrating the story. Hence, the past perfect tense (had been carried) is used.

5. A large crowd gathered at our place the day I was to leave. People had come to wish me luck, (para 6)
Answer:
A large crowd gathered at our place the day I was to leave. → In this sentence the simple past tense is used as it occurred later.

People had come to wish me luck. → In this sentence the past perfect tense is used as it occurred earlier.

People had come and then the large crowd gathered. Hence, the two tenses are used.

6. Father was quiet for some time. He thoughtfully looked at the sun for a moment, and then his eyes fell on the can of home-made wine that I was carrying, (para 9)
Answer:
The actions in the above sentences occurred in the past simultaneously. Hence, the simple past tense is used in all the actions except the last part of the second sentence. ” ……….. that I was carrying.” Here the past continuous tense is used as it was going on at the time of narrating.

7. I gave him the can of wine. He poured himself a mug and handed me the can. He drank all of it at one go. He then arranged the belt that was attached to the trunk carefully on his forehead. (para 10)
Answer:
All the actions are in the simple past tense as they all occurred in the past simultaneously and also the time relation is unambiguous.

8. I had never got used to physical labour having stayed in hostels right from my childhood. (para 11)
Answer:
“I had never get used to …………”
Here the past perfect tense is used as the author while narrating, went intq the past and told. Hence, the past perfect tense is used.

9. His feet had developed cracks and somehow resembled those of an elephant. (para 14)
Answer:
When two actions in the past are clearly separated by time, the earlier action is expressed in the past perfect tense. “His feet had developed cracks” …. This action took place before “his feet resembled those of an elephant.” Hence, the earlier action is expressed in the past perfect tense and the latter is expressed in the simple past, (had developed, resembled)

10. I noticed this for the first time. 1 hadn’t noticed that the road was uneven, (para 14)
Answer:
“I noticed this for the first time.”
Here the simple past tense is used as it is the author’s narration.
“I hadn’t noticed that …….. ”
This action might have occurred if the author did it but this action didn’t take place. Hence, the past perfect tense (+ not) is used.
” the road was uneven.” The condition of the road was mentioned here. It was
the condition of the road when he narrated. Hence, the simple past tense is used.

11. I checked my wallet and saw I still had around Rs.40 with me. (para 14)
Answer:
Both the actions in the above sentences occurred in the past simultaneously. Hence, the simple past tense is used in both the contexts.

12. I then took out my pair of leather shoes from the trunk, and noticed my father’s face lighting up with contentment, (para 15)
Answer:
The above two actions occurred in the past simultaneously and the time relation is unambiguous. Hence, the simple past tense is used, (took, noticed)

13. I saw that the road we had come by looked like a giant motionless rope, (para 16)
Answer:
“I saw that ” — Here the past tense is used to refer to the past action as it is the writer’s narration.
” ………… we had come by looked …………”
— Here the past perfect tense is used as this action had completed before his narration.
” …………… looked like a giant motion rope.” — Here the simple past tense is used to refer to the action as it is the writer’s narration.

14. He stopped his business after he became old.
Answer:
In this sentence both the verbs ‘stopped’ and ‘became’ are in the past tense as the time is unambiguous.

15. I never ate ‘haleem’ before I visited Hyderabad.
Answer:
In this sentence the verbs ’ate’ and ‘visited’ are in the past tense as the time is unambiguous.

II. Adverbial Clauses

Study the following examples from the story.
1. As I had to do a bit of catching up, I walked fast.
2. As I was going to take my first sip. 1 heard father’s voice.
3. He decided to go to his work place because he got into debts.

In all the above sentences there are two clauses. The underlined part is the adverbial clause.
There are several types of adverbial clauses.

Combine the pairs of sentences by using the words given in brackets.
1. There was nobody in the village to carry the author’s luggage. Everbody was engaged in some important work, (because)
2. The roads were not good. He preferred less luggage, (as)
3. He wanted to stay at home for some more days. He wanted to apply for leave, (since)
4. You may not attend the class. You don’t want to come again, (if)
5. The boy was about to come down the stairs. Then it crumbled down, (when)
Answer:

1. There was nobody in the village to carry the author’s luggage because everybody was engaged in some important work.
2. As the roads were not good, he preferred less luggage.
3. Since he wanted to stay at home for some more days, he wanted to apply for leave.
4. If you want to come again, you have to attend the class.
5. Whan the boy was about to come down the stairs, it crumbled down.

More about Adverbial Clauses :

1. Adverbial Clauses of Time :
Adverbial Clauses of Time are introduced by the subordinating conjunctions when-ever, since, after, before, while, as, etc.
e.d.:
1) As Bayaji came home, his children returned.
2) As soon as the bell rang, the children came out crying.
3) While Sachin was batting, there was a heavy noise all over the stadium.

2. Adverbial Clauses of Place :
Adverbial Clauses of Place are introduced by the subordinating conjunctions where and whereas.
e.g.:
1) You can go wherever you like.
2) I want to live where you live.

3. Adverbial Clauses of Reason :
Adverbial Clauses of Reason are introduced by the subordinating conjunctions because, that, as, since.
e.g.:
1) Because he was ill, he didn’t come.
2) He was very happy that his son had passed.
3) As she was absent from school, the teacher punished her.

4. Adverbial Clauses of Manner :
Adverbial Clauses of Manner are introduced by the subordinating conjunctions like, as, as if.
e.g.:
1) He finished the work as she requested.
2) He is acting like he doesn’t like her.
3) They talked as if they had read.

5. Adverbial Clauses of Purpose :
Adverbial Clauses of Purpose are introduced by the subordinating conjunctions so that, in order that and lest
e.g.:
1) Work hard lest you should fail.
2) We eat so that we may live.
3) Sunlight is needed in order that the process of photosynthesis takes place.

6. Adverbial Clauses of Condition :
Adverbial Clauses of Condition are introduced by the subordinating conjunctions if, whether, unless.
e.g.:
1) Unless you work harder, you will fail.
2) If I go to Hyderabad, I will meet your brother.
3) She was uncertain whether to stay or leave.

7. Adverbial Clauses of Consequence :
Adverbial Clauses of Consequence are introduced by the subordinating conjunction that.
e.g.:
1) She is such a kind man that all love him.
2) She speaks in such a low voice that nobody can hear her.

8. Adverbial Clauses of Comparison :
Adverbial Clauses of Comparison of Degree are introduced by the subordinating conjunction than, or by the Relative Adverb as …. as.
e.g.:
1) She is younger than he.
2) He is as stupid as he is lazy.

9. Adverbial Clauses of Concession :
Adverbial Clauses of Concession are introduced by the subordinating conjunctions though, although, even if.
e.g.:
1) Though he is poor he is honest.
2) Even if it rains 1 shall come.
3) He passed in first division although he didn’t work hard.

Writing

I. In the story ‘The Journey’ the author says “…. my education had made me shun physical labour”. This is an adverse effect of education. Now write an essay on ‘The Adverse Effects of Education’. Here are some points:
Effect on
• doing some work that involves physical labour
• dress/fashion
• family relationships
• giving respect to elders
• the treatment of illiterate people
Answer:

The Adverse Effects of Education

It is a well-known fact that education plays a vital role in bringing up both economically and socially. It is thought that education helps people in so many ways. Highly educated people are enjoying the status in the present day society. People with high education attain a good job, more money and many other benefits. A literate person can show the right path to others. We usually think of the benefits of education only but we should not ignore the adverse effects of education.

When the pupils spend all their time in reading and writing, there is no scope for them to do any other work. They don’t find time even to play games. Their education makes them physically weak. They are unable to do any work that involves physical labour. “A sound mind in a sound body” is a proverb. Both the sound mind and the sound body are needed if one desires to be successful. When we are helathy, we can perform our functions regularly and properly. Today, most of the pupils stay in hostels right from their childhood. Hence, they never get the chance to do physical labour. One’s physical labour will make oneself both physically and mentally strong. But today’s education system doesn’t allow the pupils to do physical labour. And the other thing is that the educated people think that others will laugh at them if they do any kind of physical labour. They think that theirs is an important position in the society. Doing their own things is the point of prestige for them. Their false prestige makes them think in a wrong way.

The second point is their dress sense. The persons with high education try to wear fashionable dresses which are different from other ones. As far as the educated Indians are concerned, they give more value to the western culture. They try to adapt the foreigners’ culture. They never think of our culture and traditions. They think that only illiterate people wear such kind of dresses which reflect our culture. In their view, they will be degraded if they don’t wear modern dresses. This thought only leads to other social problems. The young women’s dress sense will cause them a threat. They think that they are superior to the uneducated ones and behave arrogantly.

Another important point is how education affects the family relations. When a person completes his education, he starts thinking that he is greater than the other uneducated members of his family. He wants to show his dominance. If he gets employment, he doesn’t find time to spend with them. He always thinks about earning money. He gives importance to money only. He doesn’t show any love and affection even for his parents. Thus, one’s education leads to the absence of human relationships.

Most of the literates don’t give any respect to elders. As Indians, we generally have faith in our values, traditions and culture. What we have learnt from our ancestors is that we should give utmost respect to our elders. At present, we witness a different scenario. Some educated persons think that there is no use of elders. They forget the sacrifices made by them. They ill-treat their family members who are illiterates. This will lead to the destruction of family relationships.

No doubt, there are so many advantages with the education one gets. But one’s education makes one senseless. The educated persons must not move away from physical labour. They must do some work that involves physical labour. They should take care about their dress. They should not deviate from our traditional way of dressing. They should maintain good family relationships. They should respect elders. They should treat the illiterate people with courtesy. Then only their education is meaningful.

II. Summarising

A few guidelines and tips to summarize a text are given below. Read them carefully. Then read the essay ‘On Umbrella Morals’ and summarize it.

Guidelines and tips to summarize a text

To summarize is to condense a text to its main points and to do so in your own words. To include every detail is neither necessary nor desirable. In order to write a good summary, you may have to gather minor points or components of an argument from different places in the text in order to summarize the text in an organized way. A point made in the beginning of an essay and then one made toward the end may need to be grouped together in your summary to concisely convey the argument that the author is making.

Here are a few key points:

1. Read the article carefully – as many times as you require!
2. Begin your summary by mentioning the author and title. The publication and date may also be mentioned.
3. Summarize in your own words in third person using simple present tense.
4. Use transition words (however, moreover, then, also, etc.).
5. Avoid unnecessary details and direct quotes.
6. Do not give your own opinion.
7. Keep it within the word limit given or one third of the original text.
8. Prefer short and simple sentences.
9. Be consistent with the tense.
10. Check for grammar and punctuation errors.

Read the following essay.

On Umbrella Morals

-Alfred George Gardiner

A sharp shower came on as I walked along the street, but 1 did not put up my umbrella. The truth is I couldn’t put up my umbrella. The frame would not work for one thing, and even if it had worked, I would not have put the thing up, because it was falling to pieces and I would be the laughing stock. The fact is, the umbrella is not my umbrella at all. It is the umbrella of some person who I hope will read these lines: He has got my silk umbrella. I have got the cotton one he left in exchange. I imagine him walking along the street under my umbrella, and throwing a scornful glance at the fellow who was carrying his ugly thing. I dare say the rascal laughed silently as he eyed the fool with his cotton umbrella. He is one of those people who have what I may call an umbrella conscience.

I hope you know the sort of person I mean. He would never put his hand in another’s pocket, or forge a cheque or rob a cashbox —not even if he had the chance. But he will swap umbrellas, or forget to return a book, or take a rise out of the railway company. In fact he is a thoroughly honest man who allows his honesty the benefit of the doubt. Perhaps he takes your umbrella at random from the barber’s stand. He knows he can’t get a worse one than his own. He may get a better one. He doesn’t look at it very closely until he is well on his way. Then, “Dear me! I’ve taken the wrong umbrella,” he says, with an air of surprise, for he likes really to feel that he has made a mistake. “Ah, well, it’s no use going back now. He’d be gone. And I’ve left him mine! “It is thus that we play hide-and-seek with our own conscience. It is not enough not to be found out by others; we refuse to be found out by ourselves. Quite impeccable people, people who ordinarily seem unspotted from the world, are afflicted with umbrella morals.

It was a well-known preacher who was found dead in a first-class railway carriage with a third-class ticket in his pocket. And as for books, who has any morals where they are concerned? I remember some years ago the library of a famous divine and literary critic, who had died, being old. It was a splendid library of rare books, chiefly concerned with seventeenth-century writers, about whom he was a distinguished authority. Multitudes of the books had the marks of libraries all over the country. He had borrowed them and never found a convenient opportunity of returning them. They clung to him like pre-cedents to law. Yet he was a holy man and preached admirable sermons, as I can bear witness. And, if you press me on the point, I shall have to own that it is hard to part with a book you have come to love.

It is possible, of course, that the gentleman who took my silk umbrella did really make a mistake. Perhaps if he knew the owner, he would return it with his compliments. After my experience to-day, I think I will engrave my name on my umbrella. But not on that baggy thing standing in the corner. I do not care who relieves me of that. It is anybody’s for the taking.

Study Skills

Use the following graphic organizers to represent your understanding of the story ‘The Journey’. Modify the layout to suit your needs.

i) 1. How could I allow my old father to carry my trunk?
2. What would people think?
3. What would they say?
4. It was improper for me to let father carry the luggage.
5. It was through me that they (my parents) had earned a greater degree of admiration and respect from the villagers.
6. He was stronger and more skilled than I in these matters.

ii) 1. His education had made him shun physical labour.
2. His father, his people, and the whole world would laugh at him and he would be belittled.
3. His father would not like him to see him carrying a trunk on his back.

iii) I would myself carry my luggage. I wouldn’t make my father carry it.
iv) The author’s action is inhuman. He is thankless and selfish.
v) The author is ungrateful. He doesn’t show any respect, love, and affection for his father.

Listening

Listen to the story and answer the questions that follow.

Once there was a very rich man. His name was Dhanaraju. He had two sons, Ganiraju and Pothuraju. Ganiraju was hard working and obedient. He always helped his father in the fields. But Pothuraju was lazy. He never went to fields. He was disobedient to his father. He always wanted to lead a free, lavish life, so one day he said to his father, “Father, give me my share of property.” The father was heart-broken. He divided the property between his two sons. Pothuraju left home with his share. He went to a distant land, made a lot of friends and soon spent all his property lavishly on friends, food and drinks. All his friends left him.

At that time, there was a famine and Pothuraju had no work and food. None of his friends gave him food or money. He took up the job of feeding pigs. Sometimes, he had to eat the food kept for the pigs. He was very sad about his condition. He soon began to think of his father and his brother. He said to himself, “In my father’s house, even the servants have enough food. They get good shelter too. But here, I am struggling for food and shelter. I will go back to my father. 1 will beg him to take me as his servant.”
So decided, the dishonest son set out for his father’s house. In the meantime, his father was always thinking of his second son. He would sit near the windows. He would look out at the road, expecting his son to return home.

One day Dhanaraju saw his son coming at a distance. He rah out of the house in great joy and hugged his son. His son knelt down. He said, “Father, 1 am not fit to be your son. Take me as your servant.”

I. Read the statements given below and mark True or False against each of them.

1. Pothuraju went to far-off lands to enjoy free life.
2. Ganiraju asked his father to give his share of property.
3. Pothuraju had a lavish life from the beginning.
4. Dhanaraju did not care about Pothuraju.
Answer:
1. True
2. False
3. False
4. False

II. Which of the following is the most appropriate title for the story you have just listened to?
a) A Rich Son
b) Repentance
c) Two Sons
Answer:
(b) Repentance

The Journey Summary in English

The Journey’ is an excellent piece of work written by Yeshe Dorjee Thongchi, a prominent Assamese writer and it is translated into English by D.P. Nath. The author was a government officer. He came to his village to get married. His parents had arranged his marriage, according to the customs of their tribal society. After spending six months at home, he was preparing to return to his place of work. But he didn’t want to leave behind his newly-wed wife. He thought of extending his leave too. But his responsibilities made him decide to go.

As theirs is a hilly terrain, without any motorable roads, the author always prefers to carry less luggage. Now, his problem was that he needed someone to carry his luggage as his education had made him avoid physical labour. Since most of the villagers were busy in the fields, he couldn’t find even one who could help him carry the trunk to the bus stop. Finally, the writer’s father told him that he would see him off at Dirang. He didn’t want to allow his old father to carry his trunk and so he protested. But his father decided to carry the chest to the bus stop. On the day of his departure, a large crowd gathered to wish him luck and the author left for Dirang at 10 : 20. His father had already left and he had to walk fast to catch up his father. He was very tired when he caught up with his father. He sat on a rock to rest for a while. His father drank all the wine given by him and resumed carrying the luggage on his back. The author followed his father. Neither of them spoke a word as if they were strangers. The author thought that it was improper for him to let his father carry the luggage. Although he wanted to tell his father that he would like to carry the trunk himself, he couldn’t do so because of his guilt, shame and pride. He felt that the whole world would laugh at him if he did so.

The author knew that his father had provided for his education. He thought that it was through him that his parents had earned admiration and respect from the villagers. He knew that he was physically useless in spite of his youth and strength. He concluded that it would be better to let his father carry the luggage and followed him silently After resting at two places for tiffin, they reached Dirang finally. They entered a tea shop and started sipping tea. His father asked him if he had a pair of old shoes. Then the author looked at his father’s bare feet and noticed that they were full of cracks. He noticed this for the first time. He offered his father money but he refused to take. Instead, he wanted the author’s old pair. So, the author gave him the hunting boots he was wearing. His father filled with satisfaction when he saw the author taking out his pair of leather shoes from the trunk. His father wanted to say something to him but the bus started moving. Finally the author realized that both their ways were different – his way was a luxurious one while his father’s was a difficult one.

The Journey Glossary

lethargy (n) : the state of not having any energy or enthusiasm for doing things
creeps (v) : develops very slowly
terrain (n) : a particular type of land
extend (v) : to continue for a longer period of time
dilly-dallying (v) : taking a long time to do something, go somewhere or make a decision
debt (n) : a sum of money that a person or organization owes
shun (v) : to avoid something or somebody
chest (n) : a large strong box
see off (phr.v.) : to go to an airport, station, etc. to say goodbye to someone
protest (v) : to say that one strongly disagrees with
dissuade (v) : to convince somebody not to do something
catch up (phr.v.) : to come from behind and reach someone in front of you by going faster
plight (n) : a difficult and sad situation
utter (v) : to say something
guilt (n) : the unhappy feelings caused by knowing that you have done something wrong
self-consciousness (n) : feelings of nervousness about what other people think of you
belittle (v) : to make someone or something seem small or unimportant
hardly (adv) : almost not
sip (n) : a very small amount of a drink
pebbles (n) : small smooth stones
bare feet (n.phrase) : the feet without chappals or shoes
contentment (n) : a feeling of happiness or satisfaction
recede (v) : move back from a previous position further and further until it disappears
weary (adj) : very tired
pebble-strewn road (n.phrase) : the road over which pebbles are scattered

AP State Board Syllabus AP SSC 10th Class English Textbook Solutions Chapter 1C I Will Do It Textbook Questions and Answers.

AP State Syllabus SSC 10th Class English Solutions Chapter 1C I Will Do It

10th Class English Chapter 1C I Will Do It Textbook Questions and Answers

Comprehension

I. Answer the following questions briefly.

Question 1.
What is the ultimate aim of a bright student? And why?
Answer:
The ultimate aim of a bright student is to continue his/her studies at a world-class educational institute. He/She wants to join it as there are high standards. One will do great things when one studies at a top-class institute. So, a bright student wants to join a top-ranked institute.
(Or)
The ultimate aim of a bright student is to study at IIT. It is because, these institutions maintain high standards. One can do big things if one studies at IIT. Hence, a bright student’s ultimate aim is to study at IIT.

Question 2.
‘His heart sank in sorrow.’ Whose heart sank in sorrow? Why?
Answer:
Narayana Murthy’s heart sank in sorrow. Because of the poor financial position, Murthy’s father refused to send him to IIT. Though he had passed with a high rank, there was no chance for him to study at IIT which was his dream. So, he was very sorrowful.

Question 3.
How did Murthy react when his father expressed his helplessness to send him to IIT?
Answer:
When his father expressed his helplessness to send him to IIT, Murthy was disappointed. It seemed his dreams had burnt to ashes. His heart sank in sorrow. He didn’t share his feelings with anybody. His heart was bleeding but he didn’t get angry with anybody.

Question 4.
The author calls Murthy an introvert. Which action of Murthy substantiates this claim of the author about Murthy?
Answer:
‘Introvert’ means someone who is quiet and shy, and does not enjoy being with other people. When Murthy’s father refused to send him to IIT, he became sorrowful. Though he was sorrowful, he never shared his unhappiness or helplessness with anybody. He did not reply. He remained silent. So, we can say that Murthy was an introvert by nature.

Question 5.
What, according to Narayana Murthy, can change the life of a person?
Answer:
According to Narayana Murthy, a person himself can change his life by hard work. It is not the institution or any other thing that can change the life of a person.

Question 6.
How does the motto ‘Powered by intellect and driven by values’ describe Murthy’s life?
Answer:
Murthy really believes in the motto, ‘Powered by intellect and driven by values’. He worked very hard. He didn’t bother about his personal life or comforts. He was a genius right from the beginning. He shared his wealth with others. He never used the help of any caste, community or political connections to go up in life. He proved that it was possible to earn wealth legally and ethically. He built a team of people who were equally good. The above words reveal that he was powered by intellect and driven by values.

II. Given below are some sentences from the lesson. What do they tell us about Narayana Murthy’s qualities? Use the adjectives given in the box to describe Murthy’s character. You may also use some more adjectives you like.


Answer:

Sentences from the lesson	Aspects of Murthy’s character
1. His seniors used to ask him to solve their difficulties in science.	bright
2. He was a guide for the others.	intelligent
3. While others struggle to solve the problems in the question papers, he would smile shyly and solve them in no time.	brilliant
4. His principle was never to hurt anyone.	gentle
5. He did not reply. He never shared his unhappiness or helplessness with anybody.	introverted
6. He went to station to say goodbye and good luck to them for their future life.	encouraging
7. He never used the help of any caste, community or political connections to go up in life.	uncompromising
8. He built a team of people who were equally good.	hard-working

Vocabulary

Let’s look at some more one-word substitutes.

Word	Meaning
fatalist	a person who believes in fate
centenarian	a person who is above hundred years
omnipresent	one who is present everywhere
mercenary	a person who can do anything for money
misogynist	one who hates women
monogamy	a practice of having one wife or husband
autobiography	a life history written by oneself
biography	a life history written by somebody else
honorary	a position for which no salary is paid
ambiguous	a sentence whose meaning is unclear
inimitable	that which cannot be imitated
theist	one who believes in God
spendthrift	one who spends too much
teetotaler	one who abstains from taking alcohol

Tick (✓) the most appropriate one-word substitutes for the following.
1. A person or thing that cannot be corrected
a) unintelligible
b) Indelible
c) illegible
d) incorrigible
Answer: d

2. A persoiì of good understanding. knowledge and reasoning power
a) expert
b) intellectual
c) snob
d) literate
Answer: b

3. A person who knows many languages
a) linguist
b) grammarian
c) polyglot
d) bilingual
Answer: c

4. One who possesses many talents
a) versatile
b) prodigy
c) exceptional
d) gifted
Answer: a

5. Words inscribed on a tomb
a) epitome
b) epistle
c) epilogue
d) epitaph
Answer: d

Project Work

You have read about Nick Vujicic, who has accomplished every seemingly impossible thing in life despite having the most difficult form of disability. You have read about Narayana Murthy, who is one of the most remarkable examples to win over the unbeatable difficulties. You may also have heard or read about some remarkable Indian women such as Sudha Murthy, Sudha Chandran, Kiran Bedi and many other women who have crossed all the hurdles to become successful.

Now, work in pairs and collect information about the women who you think have excelled in their lives though they may not have come into limelight.

You may read articles in newspapers, magazines, books (autobiographies, biogra¬phies etc.), browse internet and watch TV reports on women.

Answer:

Name of the woman	Details eg. birth, childhood, education, etc.	Challenges they faced/disabilities they have / had	Remarkable achievements	The qualities that inspired you
Mary Griffith	A 13 year old girl. She is studying at Mundelein Middle School	She has cerebral palsy	Set records at the National Junior Disabi­lity Champion­ship.	Hard work and will power
Karin Korb	A 38-year-old woman. She spent her childhood with her grandparents. She had studied well till she broke her back. Later she joined a law school.	She broke her back at age 17 while competing in gymnastics.	Wheelchair tennis competitor	Courage and determination
Emily Anne Schaefer	A 44 year old woman. A French town resident. She spent her childhood in a foster s care.	When she was a child, she suffe­red from trauma­tic brain injuries. She is develop­mentally disabled.	The facilitator for the project’s network in Hunterdon County. Despite the trauma, she earned a college degree in fine arts. She is a printmaker and painter, and has self- published two books on art and poetry,	Grit and perseverance
Rama Lakshmi	She is the resident of T. Nagar, Tamil Nadu. She was born on 20th May, 1995. Spent her childhood very joyously till she lost her sight in a ghastly incident. Now she is a stu­dent of engineering.	She became blind when she was 12 years old in an accident.	She is a play­wright and poet. She has written more than twenty poems and eight plays,	Courage and determination
Srivalli	She is the resident of Kothapet, Kurnool. She was born in a poor family on 15th August, 1992. She took her degree in arts with distinc­tion marks.	She lost both her legs in an accident.	She is a wonder­ful singer. She composes songs.	Will power, determination perseverance

I. Based on the information you gather about the persons, prepare a short biographical account of the person you like the most, emphasizing the exemplary work done by him/her and present it to the group/ whole class.
Answer:
Ms. Srivalli was born on 15th August, 1992. She came from a poor family. Her father was a musician and her mother was a teacher. She was a bright student. Unfortunately, she met with an accident when she was eleven and the doctors amputated both her legs. After two years of relentless struggle, she could go back to her school. She could walk with the help of artificial limbs and slowly run. Now, she can do anything like a normal woman. She learnt music from guru Rama Sastry and now she is a good singer and composer of songs. In spite of her disability, she has worked hard with great determination, discipline and dedication and achieved her target.

After she had met with the accident, her heart sank in sorrow. Sometimes she wanted to die. She hated God for doing this to her. She was terrified of her losing both the limbs. Her doctor Mr. Rao always encouraged her by telling her that she could walk and run normally. She tried and tried until she could walk. She didn’t give up at any stage. Srivalli always says, “The challenges in our lives are there to strengthen our convictions. They are not there to run us over.” With the help of her parents, friends . and guru, Srivalli has managed to reach such a position in her life. She has proved that anything can be done, if one tries hard. From her life, we can understand that one need not lose hope. Her life shows us that one s disability can’t prevent one from reaching one’s target. I feel that her life is a source of inspiration to every woman. She is able to do all these only because of her strong will power. Hence, I believe in will power with which one can achieve wonders in one’s life. I would like to wish all the best for her in the future.

II. You may also present this write up on the occasion of “Women’s Day” in your school.
Answer:
Our beloved headmaster, dear teachers and my fellow students!
I wish you a very good morning and welcome you all to the programme. At the outset, I would like to greet all the women a very happy ‘Women’s Day.’

As we all know that 8th March is celebrated as International Women’s Day to commemorate women’s achievements and the contributions made by them to the society This day is also known as the United Nations Day for women’s rights and international peace.

I have a great pleasure to say a few words about a great girl Mary Griffith on this occasion. Mary Griffith, a thirteen year old girl, has set national records in track and swimming. She has been studying at the Mundelein Middle School and has cerebral palsy. In spite of her disability she set her records in 2004 and 2005 at the National Junior Disability Championships. She always say that sports have given her a lot more confidence and taught her to balance her life. Though she has been suffering from cerebral palsy, she hasn’t lost her hope. With great faith and determination she has done so well and set her own records. Her efforts are inspirational to all the women.

We all wish her a great future and with this I will end my speech. I thank one and all for giving me this chance to share my views with you.

I Will Do It Summary in English

Nagavara Ramarao Narayana Murthy is the founder of Infosys, a leading IT company in the world. He is an icon of simplicity, uncompromising quality and fairness, apart from being a philanthropist. He believes in the motto, ‘Powered by intellect and driven by values.’

As a school going lad, Narayana Murthy was the brightest boy in his class. He could solve the most difficult problems which were very hard for his seniors. He came from a poor but educated family. His father was a high-school teacher. As all other students, Narayana Murthy wanted to get admission in the IIT. He appeared for the entrance test and did well. He always dreamt of studying at IIT. He was thrilled to know that he had passed the test with a high rank.

When Narayana Murthy told his father that he wanted to join IIT, his father reminded him of their poverty. Murthy’s father advised him to stay in Mysore and study as much as he wanted. His father was very sad to say this. Murthy was disappointed and his heart sank in sorrow. He was an introvert so he never shared his sorrowfulness or helplessness with anybody. When his classmates were leaving for Madras, Murthy went to the station to say goodbye to them. Though they were all excited and talking loudly, Murthy remained silent. He wished them and they waved at him as the train slowly left the platform. Even after the train had left, he stood there motionless. He believed that he only could change his life by hard work. He unknowingly followed “Your best friend is yourself and your worst enemy is yourself, the philosophy of the Bhagavath Gita. With great determination, Narayana Murthy reached great heights in his life. He proved that it was possible to earn wealth legally and ethically.

I Will Do It about the Author

Sudha Murthy, wife of N.R. Narayana Murthy, is an Indian social worker and author. Murthy began her professional career as a computer scientist and engineer. She is the chairperson of the Infosys Foundation. She has founded several orphanages, participated in rural development efforts, supported the movement to provide all Karnataka government schools with computer and library facilities, and established the ‘The Murthy Classical Library of India’ at Harvard University.

Murthy also teaches Computer Science. She composed a fiction, Dollar Sose. The present story is an extract from one of her most successful stories ‘How I Taught my Grandmother to Read & Other Stories.’

I Will Do It Glossary

sharp (adj): quick to notice something/able to grasp quickly

bright (adj): clever / intelligent / sharp / brilliant

unnoticed (adj): ignored / overlooked

spark (n): a small amount of particular quality or feeling

grasp (v): understand something completely

avid (adj): doing something as much as possible

literature (n): written works like novels, plays, poems, technical works, newspapers and magazines

admission (n): the right to join an institution

aspirant (n): someone who hopes to get a position of importance or honour

sleepy (adj): quiet and peaceful

guide (n): a person who can advise others

mandap (n): a raised platform

uitlmate (adj): main and most important / vital / final

D-Day (n): a date on which something important is expected to happen.(From the name given to June 6, 1944. the day on which the US., British, and other armies landed on the beaches of northern France in the Second World War.)

Implied (v): gave the meaning / meant

Anna (n): a word used to address a respectable elder 1 older male

afford (v): pay for / have funds for

expenses (n): expenditure / money that one spends on something

bitter (adj): making somebody feel unhappy

burnt to ashes: lost hopes

fondest (adj): most liking

introvert(n): a quite person who is interested in his / her own thoughts and feelings.

chirping (v): making short high sounds

monsoon (n): rainy season

set in (phr.v.): begin / start

drizzle (v): light rain / sprinkle

motionless (adj): without movement

jealously (adv): being unhappy over something

philosophy (n): attitude / way of life

ethically (adv): morally

pioneer (n): a person who is the first to do something

wave (n): raise or increase

icon (n): a famous person or thing that people admire and see as a symbol of a particular idea, way of life, etc.

uncompromising (adj): unwilling to change opinions or behaviour

philanthropist (n): one who devotes his service or wealth for the love of mankind

powered by intellect and driven by values: According to Narayana Murthy Intellect (mind power) should be the power of every man. He should be driven (influenced) by values.

AP State Board Syllabus AP SSC 10th Class English Textbook Solutions Chapter 3B Once Upon a Time Textbook Questions and Answers.

AP State Syllabus SSC 10th Class English Solutions Chapter 3B Once Upon a Time

10th Class English Chapter 3B Once Upon a Time Textbook Questions and Answers

Comprehension

I. Tick (✓) the option that will complete each of the following statements. In some cases more than one option may be possible.

1. In the first five stanzas the poet is talking about
a) the honest and innocent world of children.
b) the insincere world of adults.
c) the difference between the past and the present.
d) the old and the young.
Answer:
(b) ✓
(c) ✓

2. The last four lines of the poem suggest
a) hope.
b) regret.
c) a sense of loss.
d) eagerness to learn.
Answer:
(a) ✓
(b) ✓

3. The expression ice-cold-block eyes’ means
a) The eyes are wet with tears.
b) expressionless eyes,
c) a state of lack of feelings.
d) a dead man’s eyes.
Answer:
(b) ✓
(c) ✓

4. ‘They’ in line 4 of stanza 1 refers to
a) people in the past.
b) present day people.
c) all adults.
d) young children.
Answer:
(c) ✓

5. ‘Their …………. eyes search behind my shadow’ means
a) they avoid meeting his eyes.
b) they try to look at the darker side of the person.
c) they convey no emotions.
d) they try to see what is not there.
Answer:
(b) ✓

6. The poet has learnt
a) to shake hands.
b) the ways of the world.
c) to laugh.
d) to put on masks.
Answer:
(d) ✓

7. The poet wants to learn from his son because his son
a) is not corrupted by the ways of the world.
b) is more informed.
c) knows about good manners more than his father.
d) is more caring.
Answer:
(a) ✓

II. Answer the following questions in a sentence or two each.

Question 1.
When did people shake hands with their hearts?
Answer:
The people, in their childhood, when they didn’t know the falsehood and hypocrisies of the world, when they were not corrupted by the ways of the world, shook hands with their hearts.

Question 2.
What is the poet crying over? What help does he want from his son?
Answer:
The poet regrets for losing the traits of his own character such as honesty, modesty, and sincerity. He laments over getting corrupted by the ways of the world. He regrets for his character being influenced by hypocrisy and fallacies of the world. The poet requests his son to help him regain his sincere and heartful, innocent and child-like smile.

Question 3.
“Most of all, I want to relearn
how to laugh, for my laugh in the mirror
shows only my teeth like a snake’s bare fangs !”
What does the poet mean by these lines?
Answer:
The poet feels his smile as fictitious, insincere, and hypocritic. He feels such a smile is dangerous. The comparison of his teeth to snake’s fangs makes false, mask-like smile seem dangerous.

Question 4.
What is the tone of the poem?
Answer:
The tone of the poem is roughly equivalent to the mood it creates in the reader. In Once Upon a Time’ the tone of the poem in the earlier stanzas is abashed, regretful but in the last stanza the poet ends the poem in an optimistic and hopeful tone. Thus the poet begins the poem in a negative tone i.e. somber but ends positively i.e. opti¬mism.

Question 5.
“Now they shake hands without hearts :
while their left hands search
my empty pockets.”
Why do the left hands search empty pockets now? What does this indicate?
Answer:
The poet expresses his concern for the influence of the western world on age-old African custom. He feels that the once enthusiastic and friendly society of Africa now treated its own people like strangers and looked at each other with suspicion and hostility. The white imperialists always exploited and plundered the wealth of their colonies. So their left hands search the empty pockets of their subjects in an endeavour to rob them further.

Question 6.
The poet uses certain words to express frustration and sorrow. Identify these words.
Answer:
The phrases “ice-block-cold eyes”, “shake hands without hearts”, “doors shut on me”, “learned to wear many faces”, “teeth like a snake’s bare fangs” are used to express the poet’s regret. The phrases or lines such as “…believe me, son. I want to be what 1 used to be”, “unlearn these muting things”, “want to relearn how to laugh” are the lines used to express his frustration.

Once Upon a Time Summary in English

Once upon a time, the people used to laugh with their hearts. There used to be sincerity in their laugh. Their laugh came from their hearts. There was genuinety in their actions and feelings. But people laugh superficially, in present. Their laugh is ficticious, feelingless. The eyes are dead like feelingless, and unsympathetic/apathetical. Even people shake hands mechanically and wish the people artificially but not heartfully.

In the third stanza the poet explains more about the changes the man possesses as he grows in age. He has noticed falsehood, superfluous feelings and deteriorating human relations in present day society. The poet also says that the people lie when they say the positive phrases like “Feel at home” and “Come again.” When the poet visits their house for the third time thinking that their words are genuine, the doors are shut on his face. In this material and artificial world the poet has learnt many things especially wearing many faces, like putting on many dresses. That means he changes his expressions and feelings to suit the situations and needs of the people with whom he is to deal with.

In behaving like that he loses his own character and traits of his self. As this is the way of the world the poet has also learnt to laugh with teeth but not with heart. He also has learnt to shake the hands of others but not with heart. He has learnt to say ‘Goodnight’ when he means Good riddance’. He has learnt to say Glad to meet you,’ when he is not glad and he says, ‘It’s nice talking to you’ when he is bored of talking.

But the writer is fed up with the forcible hypocrisy and pretension of falsehood. He wants to regain his real spirit and character. He wants to abandon all this falsehood. He wants to laugh sincerely as the children do. His laugh reveals all the fallacies of the world. When he looks at himself in the mirror his teeth are exposed and they appear like the fangs of a snake.

In the last stanza the poet appeals to his son to show him how to smile whole-heartedly. The poet’s desire to regain his original traits of his character, sincerity and to give up his falsehood and hypocrisy reveals his yearning for the innocence, faithfulness and sincerity.

Once Upon a Time Glossary

cock-tail (n) : a drink usually made from a mixture of one or more alcoholic drinks

conform (v) : to be and thinking the same way as most other people in a group or society; normally acceptable

portrait (n) : a painting, drawing or photograph of a person especially of the head and shoulders

good-riddance (n) : a feeling of relief when an unwanted person leaves

muting (adj) : changing all the time; expressionless/not expressed in speech

fangs (n) : long, sharp teeth of some animals like snakes and dogs

AP State Board Syllabus AP SSC 10th Class Physical Science Important Questions Chapter 11 Electric Current.

AP State Syllabus SSC 10th Class Physics Important Questions 11th Lesson Electric Current

10th Class Physics 11th Lesson Electric Current 1 Mark Important Questions and Answers

Question 1.

Find the quantity of current in the above circuit. (AP March 2017)
Answer:
R = 3 + 5 + 2 = 10 Ω
I = \(\frac{1.5}{10}\) = 0.15 A.

Question 2.

Three resistors A, B and C are connected as shown in the figure. Each of them dissipates energy to a maximum of 18 W. Find the maximum current that can flow through the three resistors. (TS March 2015)
Answer:

Question 3.
What happens if we use a fuse made up of same wire which is used to make the electric circuit? (TS March 2017)
Answer:
It doesn’t work as a fuse. If high voltage occurs fuse do not melt and circuit will not be opened / breaked. So home appliances will be damaged.

Question 4.
Write any two differences between ohmic and non- ohmic conductors. (TS June 2018)
Answer:

Ohmic conductors	Non-ohmic conductors
Ohmic conductors follow the Ohms law.	Non-ohmic conductors do not follow the Ohms law.
Ohmic conductors are electric conductors.	Non-ohmic conductors are semicon­ductors.
V-I graph of ohmic conductors is a straight line.	V-I graph of non-ohmic conductors is a curve.

Question 5.
Draw the electric circuit with the help of a Battery, Voltmeter, Ammeter, Resistance and connecting wires. (TS March 2018)
Answer:

Question 6.
What happens, if the household electric appliances are connected in series? (TS March 2019)
Answer:
If all household appliances are connected in series, then if one appliances stop working due to failure then all the appliances stops working due incomplete circuit.

Question 7.
Define lightning.
Answer:
Lightning is an electric discharge between two clouds or between cloud and earth.

Question 8.
Define drift speed or drift velocity.
Answer:
The electrons in the conductor move with a constant average speed called drift speed or drift velocity.

Question 9.
Define conductors.
Answer:
The materials which can conduct electricity are called conductors.
Eg : Copper, Silver, Aluminium.

Question 10.
Define insulators.
Answer:
The materials which can’t conduct electricity are called insulators or non – conductors.
Eg: Wood, Rubber.

Question 11.
Define semi-conductors.
Answer:
The materials whose resistivity is 10⁵ to 10¹⁰ times more than that of metals and 10¹⁵ to 10¹⁶ times less than that of insulators.
Eg: Silicon, Germanium,

Question 12.
How does a battery work?
Answer:
In a circuit, the battery stores chemical energy and this energy converts into electric energy. Thus a battery works.

Question 13.
Define lattice.
Answer:
Conductors like metals contain a large number of free electrons while the positive ions are fixed in their locations. The arrangement of the positive ions is called lattice.

Question 14.
Define potential difference.
Answer:
Work done by the electric force on unit positive charge to move it through a distance is called potential difference.

Question 15.
Define electromotive force.
Answer:
Electromotive force (emf) is defined as the work done by the chemical force to move unit positive charge from negative terminal to positive terminal of the battery.

Question 16.
Define resistance of a conductor.
Answer:
The obstruction to the motion of the electrons in a conductor is called resistance of a conductor.

Question 17.
Define resistivity (ρ).
Answer:
Resistivity is a constant.

Question 18.
Write Ohm’s formula.
Answer:
V = IR, where V is the potential difference (voltage), I is the electric current and R is the resistance.

Question 19.
Define resistor.
Answer:
The material which offers resistance to the motion of electrons is called a resistor.

Question 20.
What is a multimeter?
Answer:
It is an electronic measuring instrument that combines several measurement functions in one unit.

Question 21.
Define electric power.
Answer:
The product of voltage and electric current is called electric power.

Question 22.
Define electric energy.
Answer:
The product of electric power and time is called electric energy.

Question 23.
What is lattice?
Answer:
The arrangement of positive ions in a conductor is known as lattice.

Question 24.
Name two special characteristics of fuse wire.
Answer:
High resistivity and low melting point.

Question 25.
Name two special characteristics of heating coil.
Answer:
High resistivity and high melting point.

Question 26.
How does resistivity vary with material of conductor?
Answer:
The resistivity is less for a good conductor and is large for a bad conductor.

Question 27.
If length of a particular conductor increased by two times and its area of crosssection decreased by four times, then what happens to its resistivity?
Answer:
The resistivity of the conductor does not change because resistivity does not depend on dimensions of conductor.

Question 28.
What does the slope of V -1 graph for an Ohmic conductor represent?
Answer:
For an Ohmic conductor the slope of V -1 graph represents the resistance.

Question 29.
Express the units of ohm in terms of volt and ampere.
Answer:
1) The SI unit of resistance is ‘Ohm’.
2) Ohm = \(\frac{\text { Volt }}{\text { Ampere }}\)

Question 30.
What is the resultant resistance of this combination?

Answer:
R, R, R Ω resistances are in parallel.
⇒ Resultant resistance = \(\frac{R}{3}\)

Question 31.
What are the quantities are conserved in Kirchhoff’s and Is’ laws?
Answer:
According to Ist law, charge, and 2^nd law, energy are conserved.

Question 32.
If the length and radius of a conductor are both halved. What happend resistance of wire?
Answer:
Length and radius are halved.

Resistance is doubled.

Question 33.
If work done is W and the charge that flows through is Q, then what is the equation 1 of potential difference?
Answer:

Question 34.
How many electrons constitutes a current of one ampere?
Answer:
6.25 × 10¹⁸ electrons in one second.

Question 35.
What are the maximum and minimum resistances are prepared by 30Ω, 30Ω, 30Ω?
Answer:
Maximum resistance = 30 + 30 + 30 = 90Ω
Minimum resistance = \(\frac{30}{3}\) = 10 Ω

Question 36.
Electric current I = nqA,v_d. Write the representation of letters.
Answer:
n = Electron density
A = Area of cross – section
v_d = drift velocity
q = charge of electron .

Question 37.
What is the resistance of bulb marked 60W and 120V?
Answer:

Question 38.
From figure, if V_A = 10V, then V_B = ?

Answer:
V_A – IR – E = V_B
10 – 1 × 5 – 3 = V_B
10 – 5 – 3 = V_B
2 = V_B
∴ V_B = 2 volts

Question 39.
Write the examples of non-ohmic conductors.
Answer:
Non-ohmic conductors are electrolytes, semi conductors, vacuum tubes.

Question 40.
What is meant by electric shock?
Answer:
When the current flows through the body the functioning of organs inside the body gets disturbed. This disturbance inside the body is felt as electric shock.

Question 41.
There is no electric shock on bird, when stand on the Electric wires. Why?
Answer:
When the bird stands on a high voltage wire, there is no potential differences between the legs of the bird, so no current passes through the bird.

Question 42.
Which factors are influence the resistivity of wire?
Answer:
a) Temperature,
b) Nature of material.

Question 43.
The length of wire is doubled and area of cross-section also doubled. What is the change in resistivity.
Answer:
Resistivity is independent of length and Area of cross-section.
Resistivity is not change.

Question 44.
A battery of 6V is applied across a resistance of 15Ω. Find the current flowing through the circuit.
Answer:

Question 45.
The formula V = I R is applicable for what substances?
Answer:
V = IR is applicable for
a) Ohmic conductors,
b) Non-ohmic conductor.

Question 46.
Resistance of a conductor of length 75 cm is 3.250. Calculate the length of a similar conductor, whose resistance is 16.25Ω.
Answer:

Question 47.
If four wires of each resistance R are joined to form a square, then what is the resistance between its opposite vertices?
Answer:

Resistance of ABC = 2R
Resistance of ADC = 2R
2R & 2R are parallel ⇒ Resultant = ‘R’

Question 48.
How much power consumption in a day of 100W television utilised 10 hours?
Answer:
Power consumption = \(\frac{100 \mathrm{~W} \times 10 \mathrm{~h}}{1000}\)
1 KWH or 1 unit.

Question 49.
How should we connect a voltmeter to measure voltage?
Answer:
The voltmeter must be connected in parallel to the electric device to measure the potential difference across the ends of the electric device.

Question 50.
How are ammeter and voltmeter connected in a circuit?
Answer:
Ammeter is always connected in series and voltmeter is always connected in parallel in a circuit.

Question 51.
Is the voltmeter connected in series or parallel in circuit? Why?
Answer:
Voltmeter should be connected parallel in the circuit to measure the potential difference between two points of conductor.

Question 52.
State whether the home appliances like Fridge, TV, Computer are connected in series or parallel Why?
Answer:
They are connected in parallel because if any one device is damaged, the rest will work as usual because the circuit does not break.

Question 53.
Why are copper wires used as connecting wires?
Answer:
Copper is a good conductor of electricity so copper wires are used as connecting wires.

Question 54.
Why is the fuse wire fitted in a porcelain casing?
Answer:
Porcelain is an insulator of electricity. So fuse wire is fitted in a porcelain casing.

Question 55.
Draw the diagram of potential – current of a copper conductor.
Answer:

Temperature T = 27°C
It is a straight line passing through origin.

Question 56.
Draw the shape of V – I graph for a silicon.
Answer:

Silicon is a semi conductor.
It is not obey the Ohm’s law.

Question 57.
Is there any application of Ohm’s Law in daily life?
Answer:

• Electrical device like electric bulb, iron box and regulators are some applications of Ohm’s Law.
• Fuse in household circuits is also another application of Ohm’s Law.

Question 58.
Two wires of the same material and same length have radii r₁ and r₂ respectively. Compare (i) their resistance, (ii) their resistivities.
Answer:

Resistivity for a same material is same. So their ratio =1:1.

Question 59.
A wire of resistance is doubled on itself, then what is its new resistance?
Answer:
Suppose length is l, area of cross-section is A and resistance is R.

Question 60.
Calculate effective resistance between points A and B.

Answer:
R₁ = 1 Ω, R₂ = 2 Ω are in series. So R’ = 1 + 2 = 3 Ω.
Now R₃ and R’ are in parallel.

Question 61.
A fuse is rated 8A. Can it be used with an electrical appliance of rating 5 KW and 200 V?
Answer:
Given P = 5 KW = 5 × 1000 = 5000 W; V = 200 V.

So a fuse of rate 8 A is not suitable because it uses current of 25 A.

Question 62.
A current of 2A is passed through a coil of resistance 75 Ω for 2 minutes. How much heat energy is produced?
Answer:
Given i = 2A, R = 75 Ω and t = 2 min. = 2 × 60 sec. = 120 sec.
Heat energy produced H = i² Rt = 2² × 75 × 120 = 36000 J = 36 KJ.

Question 63.
What is ,the resistance under normal working conditions of a 240 V electric lamp rated at 60 W?
Answer:
P = 60 W; V = 240V.

Question 64.
State the use of Ammeter. How should the Ammeter be connected in electric circuit?
Answer:
Ammeter should be connected in series in a circuit.

Question 65.
What is current value of x?

Answer:
2 + 3 = 5 of ‘A’
5 – 1 = 4 of ‘B’
2x = 4
x = 2 A at ‘C’

Question 66.
What is the value of V_A, when V_B = 8V?

Answer:
V_A – 6 × 1 – 3 = V_B
V_A – 6 – 3 = 8
V_A = 8 + 9
V_A = 17 volts

Question 67.
In the figure, how much current passing through 6Ω resistor?

Answer:
Answer:
R₁ : R₂ = 6 : 4
R₁ : R₂ = 3 : 2
i₁ : i₂ = R₂ : R₁ = 2 : 3
∴ i₁= 2A
i₂ = 3A

10th Class Physics 11th Lesson Electric Current 2 Marks Important Questions and Answers

Question 1.
Observe the graph of potential difference (V) drawn between two ends of a conductor and current (I) passing through it. Answer the following questions :

a) Which law is used to explain the graph? State it.
b) What is the resistance of the conductor? (AP June 2017)
Answer:
a) Ohm’s law is used to explain the given graph.
Ohm’s Law :
The potential difference between the ends of a conductor is directly proportional to the electric current passing through it at constant temperature.

Question 2.
Draw the experimental set-up to verify that V/I is constant for a conductor. (TS March 2016)
Answer:

Question 3.
A house has 3 tube-lights of 20 watts each. On the average, all the tube-lights are kept on for five hours. Find the energy consumed in 30 days. (AP SCERT : 2019-20)
Answer:
Number of tube lights = 3
Wattage = 20 watts each
Consumed hours = 5 hrs

Consumed energy for 30 days = 0.3 × 30 = 9 KWH (or) 9 units.

Question 4.
How do the resistors 6 Ω, 10 Ω to be connected in a circuit to get minimum resistance? Find the resultant resistant of the circuit. (TS June 2019)
Answer:

1. Resistors 6Ω, 10Ω should be connected in parallel connection in a circuit to get minimum resistance.
2. Resultant resistance
   

Question 5.
Write two examples for ohmiq and non-ohmic materials each. (TS June 2019)
Answer:
Ohmic materials : Copper, Aluminium
Non – ohmic materials : Germanium, Silicon

Question 6.
Give reasons for using lead in making fuses.
Answer:

• Lead is used in making fuses because it has low melting point EK resistivity.
• If the current in the lead wire exceeds certain value, the wire will heat up and melt, so the circuit in the households is opened and all the electric devices are saved.

Question 7.
How can we decide the direction of electric current in a conductor?
Answer:
We know I = nqAv_d. In this n and A are positive. Hence the direction of current is determined by the signs of the charge ‘q’ and drift speed v_d.

1. For electrons, q is negative and v_d is positive. Then the product of q and v_d is negative. So the direction of electric current is opposite to the flow of negative charge.
2. For positive charge, the product of q and v_d is positive. Hence, the direction of electric current can be taken as the direction of flow of positive charges.

Question 8.
What are the devices used in a circuit?
Answer:
1) Ammeter :
It is used to measure current.

2) Volt meter:
It is used to measure potential difference across the ends of conductor.

3) Rheostat:
It varies current in a circuit.

4) Switch :
It is useful to make a circuit or break a circuit.

5) Cell:
It is source of electric energy in the circuit.

6) Multimeter :
It is useful to measure current, voltage and resistance in the circuit.

Question 9.
A student says “Potential difference and Emf are same.” Justify your answer.
Answer:
Both are different because potential difference is the work done by the electric force on unit positive charge to move it through a distance between two points whereas emf is the chemical force to move unit positive charge from negative terminal to positive terminal of the battery.

Question 10.
Define Ohmic and non-ohmic conductors and give two examples each of them.
Answer:
Ohmic conductors :
The conductors which obey Ohm’s law are called ohmic conductors, e.g, : Copper, Iron.

Non-ohmic conductors :
The conductors which do not obey Ohm’s law are called non-ohmic conductors, e.g. : Semiconductors, Electrolytes.

Question 11.
Explain the Junction law of Kirchhoff.
Answer:

1. At any junction point the sum of the currents into the junction must be equal to the sum of currents leaving the junction.
2. There is no accumulation of electric charges at any junction in a circuit.
   I₁ + I₄ + I₆ = I₅ + I₂ + I₃

Question 12.
Write differences between overloading and short circuiting.
Answer:
Current chooses a path which has least resistance. So sometimes electrical appliances get damaged by passage of excess of current due to short circuit.

When so many electrical appliances are connected to the same electrical main point, maximum current can be drawn from the mains which causes overheating and may cause a fire which is called overloading.

Question 13.
The V-I graph for a series combination and for parallel combination of two resistors is shown in figure. Which of the two A or B, represent parallel combination? Give reason for your answer.

Answer:
i) For same change in I, change in V is less for the straight line A than for the straight line B (i.e., straight line A is less steeper than B).
ii) So the straight line A represents small resistance, while straight line B represents more resistance.
iii) In parallel combination, the resistance decreases, while in series combination, the resistance increases, so A represents a parallel combination.

Question 14.
Two resistors are joined with a battery such that
a) same current flows in each resistor.
b) potential difference is small across each resistor.
c) equivalent resistance is less than either of the two resistors.
d) equivalent resistance is more than either of the resistors.
State how are the resistors connected in each of the above case.
Answer:
a) Since same current is flowing in each resistor, they are connected in series.

b) Potential difference is same across same resistor that shows they are connected in parallel.

c) Equivalent resistance is less than the either of the two resistances which shows they are connected in parallel because in parallel connection resistance decreases.

d) Equivalent resistance is more than the individual resistances which indicate that they are connected in series. Since in series connection resistance increases.

Question 15.
Which of the cables, one rated 5A and other 15 A will be thicker wire? Give reason for your answer.
Answer:
i) To carry larger current, the resistance of wire should be low, so its area of cross-section should be large.

ii) Because the second cable carrying 15 A ampere current which indicates it has low resistance that is more surface area which implies it is thicker wire.

Question 16.
When a potential difference 30V is applied across a resistor, it draws a current of 3A. If 20V is applied across the same resistor, what will be the current?
Answer:
Situation : 1

Situation : 2

Question 17.
Is Ohm’s Law universally applicable for all conducting elements? If not, give example of elements which do not obey the Ohm’s Law.
Answer:

• Ohm’s Law is not applicable for all conducting elements.
• For example, some semi-conductors like silicon, germanium do not obey the Ohm’s Law.
• Those which do not obey Ohm’s Law are called non-ohmic materials.
• LED’s are non-ohmic materials.

Question 18.
Alloys are used in electrical heating devices rather than the pure metal. Why?
Answer:
Alloys are homogeneous mixtures of two or more metals. Generally alloys have more resistivity than the metals from which they have been prepared. As the resistivity increases heating effect of conductor also increases. So alloys are preferred in heating devices.

Question 19.
A switch should not be touched with wet hands. Why?
Answer:

• A switch should not be touched with wet hands.
• If water reaches the live wire, it forms a conducting layer between the hand and the live wire of the switch through which the current passes to the hand, and the person may get a total shock.

Question 20.
Which material is used for power transmission? Why?
Answer:

• The wires which are used for connections and for power transmission are made of material such as copper or aluminium.
• The reason is their resistivity is very small and they are made thick so that their resistance can be considered to be negligible.
• Further, the loss of electrical energy due to heating is also negligible in them.

Question 21.
Which material is preferred for heating element? Why?
Answer:

• The heating elements or resistance wires (or standard resistors) are made of material such as nichrome, manganin, constantan, etc. for which the resistivity is quite large and the effect of change in temperature on their resistance is negligible.
• So electrical energy is converted into heat energy when current passes through the wire.

Question 22.
Draw the symbols of the following.
i) Battery
ii) Resistance
iii) Ammeter
iv) Voltmeter
v) Key
vi) Rheostat
Answer:

Question 23.
Draw V-I graphs of Ohmic and non-ohmic conductors.
Answer:

Question 24.
Draw a circuit diagram with a cell, an electric bulb, an ammeter and plug key.
Answer:

Question 25.
Draw a circuit diagram to verify the Ohm’s Law.
Answer:

Question 26.
If 60 C of charge passes through a conductor for 1 minute, find the current through the conductor.
Answer:

Question 27.
The work done in moving 6 C of charge through a circuit is 12 J. Find the potential difference in the circuit.
Answer:

Question 28.
Resistance of two resistors are 6 Ω, 12 Ω respectively. Find the resultant resistance if the resistors are connected (1) in series (2) in parallel.
Answer:

Question 29.
10 equal resistors of resistance 20 are connected in a circuit. Find the resultant resistance if they are connected in series or in parallel ?
n = 10; R = 20 Ω
In series connection resultant resistance R’ = nR = 10 × 20 = 200 Ω

Question 30.
From the figure find the current through 6 Ω, 12 Ω resistors and find the resultant resistance in the circuit and also find current in the circuit.

Answer:
R₁ =6 Ω; R₂ = 12 Ω; V = 6 V

Question 31.
Find which has greater resistance. 1 KW heater or a 100 W tungsten bulb, both marked for 230 V.
Answer:

Question 32.
Two wires (one is copper and other is aluminium) have equal area of cross-section and have the same resistance. Find which one is longer.
Answer:
Suppose the resistance of copper and aluminium wires are R₁ and R₂. Suppose their area of cross-section is A.
The resistivity of copper (ρ₁) = 1.68 × 10^-8
The resistivity of aluminium (ρ₂) = 2.82 × 10^-8

Question 33.
Three equal resistances are connected In series, then in parallel. What will be the ratio of their resultant resistances?
Answer:
Suppose the resistance of equal resistors is ‘R’. Suppose they are connected in series. Then their equivalent resistance R’ = R + R + R = 3R
If they are connected in parallel their equivalent resistance R” = \(\frac{R}{3}\)
∴ Ratio of resultant resistances = R’: R” = 3R : \(\frac{R}{3}\) = 9 : 1

Question 34.
How is Ideal earthing helpful during short circuiting?
Answer:

• During short circuiting an excessive current flows through the live wires.
• It will pass to earth through the earth wire if there is local earthing otherwise it may cause a fire due to overheating of the live wires.

Question 35.
You have three resistor values 2Ω, 3Ω and 5Ω. How will you join them Sd that the total resistance Is less than 2Ω? Find resultant resistance.
Answer:
Given R₁ = 2Ω, R₂ = 3Ω, R₃ = 5Ω.
The resistors should be joined in parallel.

Question 36.
An electric kettle Is rated 3 KW, 250 V. Give reason whether this kettle can be used in a circuit which contains a 13 A fuse?
Answer:
V = 250 V, P = 3KW = 3000 W

The fuse is suitable because safe limit of current for kettle is 12 A.

Question 37.
Two resistors of 4 Ω and 6 Ω are connected parallel. The combination is connected across 6 V battery of negligible resistance. Find, i) the power supplied by the battery and ii) the power dissipated in each resistance.
Answer:
i) R₁ = 4 Ω, R₂ = 6 Ω, V = 6V.

ii) In parallel connection the resultant resistance

Question 38.
In the circuit shown below calculate the value of x if the equivalent resistance between A and B is 4 Ω.

Answer:
Given R₁ = 4 Ω, R₂ = 8Ω, R₃ = x Ω and R₄ = 5 Ω.
And resultant resistance R = 4 Ω.
R₁ and R₂ are in series.
Resultant resistance R’ = R₁ + R₂ = 4Ω + 8Ω = 12 Ω.
R₃ and R₄ are also in series.
Resultant resistance R” = R₃ + R₄ = x + 5
R’ and R” are in parallel.

Question 39.
A wire of 9 Ω resistance having 30 cm length is tripled on itself. What is its new resistance?
Answer:
Given R = 9 Ω, l = 30 cm and suppose area of cross-section A.

10th Class Physics 11th Lesson Electric Current 4 Marks Important Questions and Answers

Question 1.
A house has four tube-lights, three fans and a television. Each tube-light draws 40 W. The fan draws 80 W and the television draws 100 W. On an average, all the tube-lights are kept on for 5 hours, all fans for 12 hours and the television for 6 hours everyday. Find the cost of electric energy used in 30 days at the rate of Rs. 3.00 per KWH. (AP March 2015)
Answer:
The power used by
1) Four tube-lights of 40 W for 5 hours in 30 days
= 4 × 40 × 5 × 30 = 2400 WH

2) Three fans of 80 W for 12 hours in 30 days
= 3 × 80 × 12 × 30 = 86400 WH

3) One television of 100 W for 6 hours in 30 days
= 1 × 100 × 6 × 30 = 18000 WH

4) Total electric energy used
= 24000 + 86400 + 18000 = 128400 WH

W.H. converted into K.W.H. = 128.4 K.W.H. \(\left[\because \frac{128400}{1000}\right]\)
Cost of 1 unit = Rs. 3.00
Amount to be paid for 128.4 units = 128.4 × 3 = Rs. 385.20

Question 2.
Observe the given circuit. (AP June 2017)
R₁ and R₂ are two resistors and R₁ = R₂ = 4Ω. Emf of the battery E is 10 V.

Answer the following questions.
a) How are the resistors R₁ and R₂ connected in the circuit ?
b) What is the potential difference across R₁?
c) What is the effective resistance of the circuit?
d) What is the total current drawn from the battery?
Answer:
a) Resistors R₁ and R₂ are connected in parallel in the given circuit.
b) The potential difference across R₁ is ‘E’ volts = 10 V.

Question 3.
State Kirchhoff’s Loop law and explain. (AP June 2018)
Answer:
Loop law :
The algebraic sum of the increases and decreases in potential difference across various components of the circuit in a closed circuit loop must be zero.

Explanation :
Let us imagine in a circuit loop the potential difference between the two points at the beginning of the loop has a certain value. As we move around the circuit loop and measures the potential difference across each component in the loop, the potential difference may decrease or increase depending upon the nature of the element like a resistor or battery. But when we have completely traversed the circuit loop and arrive back at starting point. The net change in the potential difference must be zero. Thus the algebraic sum of changes in potential difference is to be zero.
(OR)
Let us apply loop law to a circuit as below.

for the loop ACDBA
– V₂ + I₂R2₂ – I₁R₁ + V₁ = 0

for the loop EFDCE
-(I₁ + I₂)R₃ – I₂R₂ + V₂ = 0

for the loop EFBAE
-(I₁ + I₂)R₃ – I₁R₁ + V₁ = 0

Question 4.

Observe the above diagram and answer the following. (AP March 2018)
a) Are all the resistors connected in parallel or series?
b) What is the equivalent resistance of the combination of three resistors?
c) In this system, which physical quantity is constant?
d) If R₁ = 2Ω, R₂ = 3Ω, R₃ = 4Ω. find equivalent resistance.
Answer:
a) Connected in series.
b) R_eq = R₁ + R₂ + R₃
c) Current (I)
d) R_eq = R₁ + R₂ + R₃
=2 + 3 + 4
= 9Ω

Question 5.
How do you verify that resistance of a conductor of uniform cross-section area is proportional to the length of the conductor at constant temperature? (TS March 2015)
Answer:
Aim :
To verify the relation between re.M+iance and lenath of the conductor.

1) Required material :
Wires or spokes of different lengths with same cross-section area of the same metal.
2) Battery
3) Ammeter
4) Key
5) Connecting wires.

Procedure :
1) Construct a circuit with Battery, Ammeter, Switch (key) and connecting wires, keeping some space at the both ends.
2) Connect the selected wires or spokes at the ends to complete the circuit.

3) Connect the wires or spokes individually and record the current using ammeter.

Conclusion :
If the current flowing in the circuit decreases with an increase in the length of the wire or spokes (Resistance increases), we can say that the resistance of the conductor is proportional to the length of the conductor.

Question 6.
What are the factors affecting the resistance of an electric conductor? Explain any two factors. (TS June 2015)
Answer:
The factors affecting the resistance of an electrical conductor are

1. Nature of material
2. Temperature
3. Length of the conductor
4. Area of cross-section of conductor

Explanation :

1. As the temperature increases the resistance increases and vice versa.
2. As the material changes resistance changes.
3. Resistance is directly proportional to length of the conductor (if T and A are kept constant). R ∝ l
4. Resistance is inversely proportional to area of cross-section (if 1 and T are kept constant). R ∝ \(\frac{1}{A}\)

Question 7.
What is the relationship between length of a conductor and its resistance? Write the experimental procedure to verify that relationship. (TS Junc 2017)
Answer:

• The resistance of a conductor is directly proportional to its lenght for a constant potential difference.
• Take iron spokes of different lengths with same cross-sectional arreas.
• Make a circuit by connecting an iron spoke with battery, ammeter and switch in series.
• Put the switch on and allow the current to pass in the circuit. Measure the ammeter reading.
• Repeat this for other lengths of the iron spokes. Note the corresponding values of currents.
• The resistance of each spoke increases with increase in the length of the spoke.

Question 8.
Find the resultant resistance for the following given arrangement. Find the current when this arrangement is connected with 9 V battery. (TS March 2017)

Answer:
The diagram is not clear so award 4 marks in the public examinations.

Question 9.
12 V battery is conncected in a circuit and to this 4Ω, 12Ω resistors are connected in parallel, 3Ω resistor is connected in series to this arrangement. Draw the electric circuit from this information and find the current in the circuit. (TS June 2018)
Answer:

Question 10.
In a circuit,60V battery, three resistances R₁ = 10 Ω, R₂ = 20 Ω and R₃ = x Ω are connected in series. If 1 ampere current flows in the circuit, find the resistance in R₃ by using Kirchhoffs loop law. (TS March 2018)
Answer:

Given
I = 1 amp
R₁ = 10Ω
R₂ = 20Ω
R₃ = xΩ
V = 60V
In ADCBA loop
– IR₃ – IR₂ – IR₁ + V = 0
– lx – 1 × 20- 1 × 10 + 60 = 0
– x – 30 + 60 = 0
– x + 30 = 0
x = 30Ω

Question 11.
List out the material required for the experiment “The effect of increasing of cross-section of a conductor upon its resistance” and write the experimental procedure. (TS June 2019)
Answer:
Aim :
To show that the effect of increasing of cross-section of a conductor upon its resistance.

Required Material :
Battery eliminator, Key, Ammeter, Manganin wires of equal lengths but different cross sectional areas, Copper connecting wires.

Procedure :

• Collect manganin wires of equal lengths but different cross sectional areas.
• Make a circuit as shown in the figure.

• Connect one of the wires between points ‘P’ and ‘Q’.
• Note the value of the current using the ammeter connected to the circuit and note it.
• Repeat this with other wires.
• Note the corresponding values of currents in each case and note them.

Conclusion :
We can notice that the current flowing through the wire increases with increasing their cross sectional area.

Question 12.
Derive an expression to find drift velocity of electrons.
Answer:

• Consider a conductor with cross sectional area A. Assume that the two ends of the conductor are connected to a battery to make the current flow through it.
• Let ‘v_d‘ be the drift speed of the charges and ‘n’ be the number of charges present in the conductor in a unit volume.
• The distance covered by each charge in one second is ‘v_d‘

• Then the volume of the conductor for this distance = Av_d
• ∴ The number of charges contained in that volume = n.Av_d
• Let q be the charge of each carrier.
• Then the total charge crossing the cross sectional area at position D in one second is ‘n q A_d‘.
  This is equal to electric current.
  ∴ Electric current I = n q Av_d.
  ∴ v_d = \(\frac{I}{nqA}\)

Question 13.
Derive an expression to measure emf of a battery.
Answer:
Electromotive force (emf) is defined as the work done by the chemical force to move unit positive charge from negative terminal to positive terminal of the battery.

1. Let this chemical force be F_c.

2. This chemical force does some work to move a negative charge ‘q’ from positive terminal to negative terminal against the electric force Fe. Let this work be ‘W’.

3. ∴ The work done by the chemical force to move 1 coloumb of charge from the

This S.I unit of emf is ‘volt’ and is measured using voltmeter.

Question 14.
What are the factors on which the resistance of conductor depends? Give the corresponding relation.
Answer:

• The value of resistance of a conductor depends on temperature for constant potential difference.
• Resistance of a conductor depends on the material of the conductor.
• Resistance of a conductor is directly proportional to its length, i.e., R ∝ l.
• Resistance of a conductor is inversely proportional to the area of cross-section of the material, i.e., R ∝ \(\frac{1}{A}\)

Question 15.
What do you mean by (i) short circuit (ii) overloading? What are the safety precautions taken to avoid these problems in domestic electric circuits?
Answer:
Short circuit:
Sometimes current chooses a path which has least resistance which is called short circuit.

Overloading :
The over heating due to drawing excess of current from a single main is called overloading.
Precautions to avoid damage due to short circuit and overloading.

1. Using fuse
2. Connecting electrical appliances in various mains.
3. Earthing

Question 16.
A circuit is set up as shown in the figure. Calculate the current and potential difference across R₁, R₂ and R₃, when
a) keys K₁ and K₂ are both closed,
b) key K₁ is closed and K₂ is open,
c) key K₁ is open and K₂ is closed.

Answer:
a) When both the keys K₁ and K₂ are closed :
The resistors R₁ and R₃ are parallel.
So resultant resistance R_p = \(\frac{R_{1} R_{3}}{R_{1}+R_{3}}=\frac{6 \times 4}{6+4}\) = 2.4 Ω.
The resistor R₁ and R_p are in series as shown in figure.

Total resistance of circuit R_s= R₁ + R_p = 6 + 2.4 = 8.4 Ω
Current I = \(\frac{V}{R_{S}}=\frac{4.2}{8.4}\) = 0.5 =A.
Potential difference across R₁ is V₁ = IR₁ = 0.5 × 6 = 3V.
Potential difference across the combination of R₂ and R₃ is
V’ = V – V₁ = 4.2 – 3 = 1.2 V.
Now since R₂ and R₃ are in parallel,
Potential difference across R₂ = Potential difference atross R₃ = V’ = 1.2 V

b) When the key K₁ is closed and key K₂ is open : The resistor R₃ will not be in circuit.
The resistors R₁ and R₂ are in series.
Total, resistance R_s = R₁ + R₂ = 6 + 6=12 Ω.
Current I = \(\frac{V}{R_{s}}=\frac{4.2}{12}\) = 0.35 A
The same current will flow through each resistor R₁ and R₂.
Potential difference across R₁ is V₁ = IR₁ = 0.35 × 6 = 2.1 V.
Potential difference across R₂ is V₂ = IR₂ = 0.35 × 6 = 2.1 V.
The current and potential difference across R₃ will be zero.

c) When key K₁ is open and key K₂ is closed :
No current flows through R₁ R₂ and R₃ since the circuit is incomplete. Hence potential difference across R₁, R₂ and R₃ is zero.

Question 17.
For the combination of resistance shown in figure, find the equivalent resistance between (a) C and D, (b) A and B.

Answer:
a) Between C and D :
The resistors R₂, R₃ and R₄ are in series. They can be replaced by an equivalent resistance R_s where
R_s = R₂ + R₃ + R₄ = 3 + 3 + 3 = 9 Ω
The resistance R₅ and R_s are in parallel between the points C and D.
The equivalent resistance between C and D then

Thus the equivalent resistance between C and D is 2.25 Ω.

b) Between A and B :
Now the resistors R₁, R_p and R₆ are in series between the points a and B.

The equivalent resistance between A and B is
R_AB = R₁ + R_p + R₆ = 3 +2.25 + 3 = 8.25 Ω.

Question 18.
How does resistance and resistivity vary with temperature?
Answer:

• For a metallic conductor, the resistance increases w ith the increase in temperature. The resistance of filament of bulb is more w hen it is glowing than when it is not glowing. The specific resistance or resistivity also increases with increase in temperature.
• For alloys (such as constantan and manganin), the resistance and the resistivity remains practically unchanged with the increase in temperature.
• For semi conductors (such as silicon, germanium, etc.), the resistance decreases with the increase in temperature.
  eg.: the resistance of carbon also decreases with the increase in its temperature.

Question 19.
Why is a copper wire unsuitable for making fuse wire?
Answer:

• A fuse is a short piece of wire made up of a material of high resistivity and of low melting point so that it may easily melt due to overheating when current in excess to the prescribed limit passes through it.
• The thickness of wire is different in different fuses depending on the amount of current which is permitted to flow through them.
• Generally an alloy of lead and tin is used as the material of the fuse wire because it has a high resistivity and low’ melting point.
• A copper wire is unsuitable for using as fuse wire because copper has low resistivity and high melting point.
• Therefore the use of an ordinary’ wire as a fuse must be avoided.

Question 20.
Why is current rating of a fuse required?
Answer:
1) The electric wiring for light and fan circuit uses a thin fuse wire of low current carrying capacity because the line wire has a current carrying capacity of 5A.

2) Thicker fuse wires of higher current carry ing capacity (15 A) are used for large current consuming appliances such as air conditioner, geyser, washing machine, etc. because the line wire for such dev ices have current carrying capacity of 15A.
The current rating of a fuse in a circuit can be obtained by the following relation.

Question 21.
Describe the activity with the help of diagram to establish the relationship between Current (I) flowing in a conductor and potential difference (V) maintained across its ends.
Answer:
Aim :
To establish the relationship between Current (I) flowing in a conductor and potential difference (V) maintained across its ends.

Material required :
5 dry cells of 1.5 V each, conducting wires, an ammeter, a volt meter, thin iron spoke of length 10 cm, LED and key.
Diagram :

Procedure :

• Connect a circuit as shown in the figure.
• Solder the conducting wires to the ends of the iron spoke.
• Close the key.
• Note the readings- of current from ammeter and potential difference from volt meter in the given table,

• Now connect two cells (in series) instead of one cell in the circuit.
• Note the respective readings of the ammeter and voltmeter and record the values in the table.
• Repeat the same for three cells, four cells and five cells respectively.
• Record the values of V and I corresponding to each case in the table.
•  Find \(\frac{V}{I}\) for each set of values.
  Conclusion : The ratio of \(\frac{V}{I}\) is constant.
• From this activity we can conclude that the potential difference between the ends of the iron spoke (conductor) is directly proportional to the current passing through it. This means V ∝ I.

Question 22.
In an experiment to verify Ohm’s Law the following values are given below. Draw a graph of ‘I’ versus ‘V’. Show that the graph conforms Ohm’s Law and find the resistance of the resistor.

Answer:
1) Graph between ‘V’ and ‘I’.

2) From the above graph,
Straight line §hows that the relation between potential difference (V) and current (I) as \(\frac{V}{I}\) is constant.

3) V ∝ I.

4) The potential difference between the ends of a conductor is directly prbportional to the electric current passing through it at constant temperature.

5) This is the Ohm’s Law and the graph conforms it.
Resistance of the resistor

Question 23.
Identify the defects 1ft the circuit. Redraw it.

Answer:
Defects in the circuit:

1. Ammeter was connected in parallel in the circuit.
2. Volt meter was connected in series in the circuit.
3. Positions of resistor and battery were reversed.

Correct diagram :

Question 24.
What is the advantage of MCB over fuse?
Answer:

• These days instead of fuses, Miniature Circuit Breakers (MCB) are used for each lighting circuit.
• They switch off the circuit in a very short time duration in case of short-circuiting or some fault in the line.
• After repairing the fault in the circuit, the MCB is again switched on.
• Thus, the use of MCB is better than a fuse. It avoids the inconvenience of connecting a new fuse wire and it is much safer due to its quick response.

Question 25.
A circuit is shown in the picture.

The current passing through A is I.
a) What is the potential difference between A and B?
b) What is the equivalent resistance between A and B?
c) What amount of current is flowed through C and D?
Answer:
a) According to KirchhofPs loop law the algebraic sum of increase and decrease in potential difference across various components of the circuit in a closed circuit loop must be zero.
So the potential difference across CD is zero because it is a closed loop.

b) Here 20 Ω, 5 Ω are parallel to each other and resultants are in series to each other. Resultant resistance of 20 Ω and 5 Ω.

Question 26.

Observe the picture. The potential values at A, B, C are 70 V, 0 V, 10 V
a) What is the potential at D?
b) Find the ratio of the flow of current in AD, DB, DC.
Answer:

a) By following Ohm’s law potential difference is (V) = IR
In the given circuit we are applying junction laws.
‘D’ works as junction so, I = I₁ + I₂
Let p.d at D is V₀.

b)

Question 27.
Observe the circuit R₁ = R₂ = R₃ = 200 Ω. If reading of voltmeter is 100 V, resistance of voltmeter is 1000 Ω.
Find the Emf of the battery.

Answer:
Given values are R₁ = R₂ = R₃ = 200 Ω.
and Voltmeter reading = V = 100 V.
Resistance of Voltmeter = R_v = 1000 Ω.
In the given circuit R₁ and R₂ are in series R = R₁ + R₂ = 200 + 200 = 400 Ω
Resultant resistance (400 Ω) and voltmeter (1000 Ω) are always in parallel.

Question 28.
A circuit is made with a copper wire as shown in the diagram. We know that conductor’s resistance is directly proportional to its length. Calculate the equivalent resistance between points 1 and 2.

Answer:

Let the resistance of the wire be ‘R’ and length of the wire be ‘l’.
The shape of the circuit be square length of the side (l) = R
In a square, diagonal is \(\sqrt{2}\) times its length = \(\sqrt{2}\)l
Resistance towards diagonal is \(\sqrt{2}\)R
The circuit diagrams for the given arrangement are along PTR and QTS is ineffective as no current flows through it.
PQ and PS are in series so effective resistance is R₁ + R₂ = R + R = 2R.
QR and SR are in series so effective resistance is R₁ + R₂ = R + R = 2R.
Redrawn of the circuit again as resultant resistance between the points 1 and 2 is

Question 29.
From the adjacent figure,

i) Find the potential at D.
ii) Find the current that passes through AD, DB and DC.
Answer:
Suppose from A and C current is flowing through the circuit and at B current is flowing away from the circuit. Suppose potential at D is V.
∴ I₁ + I₂ = I₃ (where I₁ I₂ are current into the junction. I₃ is the current away from the junction)

Question 30.
Find the electric current drawn from the battery of emf 8V from the given circuit.
Answer:

According Kirchhoffs loop law
6I₁ + 3I₁ – 8 = 0
9I₁ = 8
I₁ \(\frac{8}{9}\) = 0.89 A
∴ Cuttent in 8 V is 0.89 A

Question 31.
A household uses the following electric appliances.
i) Refrigerator of rating 400 W each for ten hours each day.
ii) Two electric fans of rating 80 W each for 12 hours each day.
iii) Six electric tubes of rating 18 W each for 6 hours each day. Calculate the electric bill of the household in a month if the cost per unit electric energy is Rs. 3.00.
Answer:
i) Electrical energy consumed by Refrigerator in a month (in KWH)

ii) Electrical energy consumed by two electrical fans in a month (in KWH)

iii) Electrical energy consumed by electric tubes in a month (in KWH)

Total electrical energy consumed by all the electrical appliances
= 120 + 57.6 + 19.44 = 197.04 units
Cost of 1 unit = ₹ 3
Cost of 197.04 units = 197.04 × 3 = ₹ 591.12

Question 32.
What is the reason for connecting the fuse in the live wire?
Answer:

• The fuse is always connected in the live wire of the circuit.
• If the fuse is put in the neutral wire, due to excessive flow of current the fuse burns, current stops flowing in the circuit.
• But the appliance remains connected to the high potential point of the supply through the live wire.
• Now if a person touches the appliance, he may get a shock as the person will come in contact with the live wire through the appliance.

Question 33.
In the diagram given below, two resistors R₁ and R₂ of 3Ω and 6Ω respectively are connected in parallel across a battery of potential difference 12 V. Calculate the electrical energy consumed in 1 minute in each resistance.

Answer:
Given R₁ = 3 Ω, R₂ = 6 Ω, V= 12 V, t = 1 min 60 sec.
The resistors R₁ and R₂ are connected in parallel, so the voltage V across each resistor is equal to 12 V.

Question 34.
Calculate the electrical energy consumed in a month, in a house using 2 bulbs of 100 W each and 2 fans of 60 W each, if the bulbs and fans are used for an average of 10 hours each day.
If the cost per unit is ₹ 3, calculate the amount of electrical bill to be paid per month.
Answer:
Given power of each bulb = 100 W
Power of each fan = 60 W
Time t =10 hours each day
Power of 2 bulbs = 2 × 100 = 200 W
Power of 2 fans = 2 × 60 = 120 W
Total power = 200 + 120 = 320 W = \(\frac{320}{1000}\) = 0.32 KW
Time duration of consumption 10 hours per day per month
= 10 hours × 30 = 300 hours
∴ Total energy consumed = Total power x Time duration
= 0.32 KW × 300 h = 96 KWh
∴ Total cost = 96 x 3 = ₹ 288.

Question 35.
What resistance must be connected to a 15 Ω resistance to provide an effective resistance of 6 Ω?
Answer:
Given R₁ = 15 Ω, R₂ = ?, Effective resistance R_p = 6 Ω.
Since the effective resistance has decreased, R2 must be connected in parallel with R₁

AP State Board Syllabus AP SSC 10th Class Chemistry Solutions Chapter 4 Acids, Bases and Salts Textbook Questions and Answers.

AP State Syllabus SSC 10th Class Chemistry Solutions 4th Lesson Acids, Bases and Salts

10th Class Chemistry 4th Lesson Acids, Bases and Salts Textbook Questions and Answers

Review of Your Previous Knowledge

Question 1.
Which property do you think of while suggesting the remedy from a problem of acidity?
Answer:
Neutralization Property. Antacid tablets neutralise acidity.

Improve your learning

Question 1.
Five solutions A, B, C, D and E when tested with universal indicator showed pH as 4, 1, 11,7 and 9 respectively, which solution is : (AS1)
a) neutral
b) strongly alkaline
c) strongly acidic
d) weakly acidic
e) weakly alkaline
Arrange the pH in increasing order of hydrogen ion concentration.
Answer:
Solution – pH Value
A → 4
B → 1
C → 11
D → 7
E → 9
a) Solution ‘D’ is neutral
b) Solution ‘C’ is strongly alkaline
c) Solution ‘B’ is strongly acidic
d) Solution ‘A’ is weakly acidic
e) Solution ‘E1 is weakly alkaline
∴ Increasing order of Hydrogen ion concentration : C < E < D < A < B.

Question 2.
What is a neutralization reaction? Give two examples. (AS1)
Answer:
Neutralization reaction : When acid reacts with base, forms its salt and water. This reaction is called a neutralization reaction.
Examples :

Equation: HCl + NaOH → NaCl + H₂O
ii) Acetic Acid + Sodium Hydroxide → Sodium Acetate + Water
Equation : CH₃COOH + NaOH → CH₃COONa + H₂O
Formula : Acid + Base > Salt + Water

Question 3.
What happens when an acid or base is mixed with water? (AS1)
Answer:
When an acid or base is mixed with water it changes into dilute acid or dilute base.
(OR)
Dilute acid or dilute base will be formed when an acid or base is mixed with water. Mixing an acid or base with water results in decrease in the concentration of ions (H30+/ OH-) per unit volume. Such a process is called dilution and the acid or base is said to be diluted.

Question 4.
Why does tooth decay start when the pH of mouth is lower than 5.5? (AS1)
(OR)
Does the pH change tooth decay? Explain.
Answer:

1. Tooth enamel is the hardest substance in the body.
2.  It doesn’t dissolve in water but corroded when the pH in the mouth is below 5.5.
3. It happens due to the bacteria which produce acids by degradation of sugar and food particles remaining in the mouth.

Question 5.
Why does not distilled water conduct electricit? (AS2)
Answer:

1. Distilled water does not contain impurities.
2. It is also extremely weak electrolyte.
3. So it does not dissociate into ions.
4. It does not have charge carriers.
5. Because of that it does not conduct electricity.

Question 6.
Dry hydrogen chloride gas does not turn blue litmus to red whereas hydrochloric acid does. Why? (AS1)
Answer:
1. Dry hydrogen chloride gas is not an acid. Because it does not produce H⁺_(aq) ions. Hence it can’t turn blue litmus into red.
2. Hydrochloric acid is an aqueous solution. So it can produce H⁺_(aq) ions. Hence it can turn blue litmus into red.

Question 7.
Why pure acetic acid does not conduct electricity? (AS1)
Answer:
The reasons for pure acetic acid does not conduct electricity are :
i) Acetic acid is a weak acid.
ii) It gives fewer H₃O⁺ ions.

Question 8.
A milkman adds a very small amount of baking soda to fresh milk. (AS2)
a) Why does he shift the pH of the fresh milk from 6 to slightly alkaline?
Answer:
1. By adding a very small amount of baking soda to fresh milk, the milkman keeps the milk unspoiled for little more time than usual time.
2. As the pH value increases the milk turns to slightly alkaline.

b) Why does this milk take a long time to set as curd?
Answer:

1. Curd form from the milk by the action of Lactic acid produced by bacteria in the milk.
2. If milk man add Baking soda (NaHCO₃) to the milk it neutralise acid, which is produced by the bacteria.
3. Excess acid is required to change the milk as curd.
4.  It takes long time.

Question 9.
Plaster of Paris should be stored in a moisture-proof container. Explain why? (AS2)
Answer:
Storing of Plaster of Paris :

1. Plaster of Paris is a white powder.
2. It easily absorbs water in air and forms hard gypsum.
3. So, it should be stored in a moisture-proof container.

Question 10.
Fresh milk has a pH of 6. Explain why the pH changes as it turns into curd.
Answer:
1. Fresh milk has a pH of 6. Hence it is a weak acid.
2. To turn the milk as curd, we have to add yeast in the form of some curd. The fermentation takes place during this process and lactose changes in lactic acid and the pH decreases as milk sets as curd.

Question 11.
Compounds such as alcohols and glucose contain hydrogen but are not categorized as acids. Describe an activity to prove it. (AS3)
(OR) (Activity – 7)
Write an activity to show that the solutions of compounds like alcohol and glucose do not show acidic character even though they are having Hydrogen.
(OR)
Write an activity which proves acids are good conductors of electricity.
(OR)
The acidity of acids is attributed to the H+ ions produced by them in solution explain the above statement with an activity.
List out the material for the experiment to investigate whether all compounds containing Hydrogen are acids or not and write the experimental procedure.
Answer:
List of the material required :

1. Glucose
2. Alcohol
3. Dil. HCl
4. Dil-H₂SO₄
5. Beaker
6. Connecting wires
7. 230 voltage AC supply
8. Bulb
9. Graphite rods.

Procedure :

1. Prepare glucose, alcohol, hydrochloric acid and sulphuric acid solutions.
2. Connect two different coloured electrical wires to graphite rods separately as shown in figure.
3. Connect free ends of the wire to 230 volts AC plug.
4. Complete the circuit as shown in the figure by connecting a bulb to one of the wires.
5. Now pour some dilute HCl in the beaker and switch on the current.

Observation :
The bulb starts glowing.

Repetition:
Repeat activity with dilute sulphuric acid, glucose and alcohol solutions separately.

Observation :

1. We will notice that the bulb glows only in acid solutions.
2. But the bulb does not glow in glucose and alcohol solutions.

Result:

1. Glowing of bulb indicates that there is flow of electric current through the solution.
2. Acid solutions have ions and the movement of these ions in solution helps for flow of electric current through the solution.

Conclusion :

1. The positive ion (cation) present in HCl solution is H⁺.
2. This suggests that acids produce hydrogen ions H⁺ in solution, which are, responsible for their acidic properties.
3. In glucose and alcohol solution the bulb did not glow indicating the absence of H⁺ ions in these solutions.
4. The acidity of acids is attributed to the H⁺ ions produced by them in solutions.

Question 12.
What is meant by “water of crystallization” of a substance? Describe an activity to show the water of crystallisation. (Activity – 16) (AS3)
Answer:
Water of Crystallization : Water of crystallization is the fixed number of water molecules present in one formula unit of a salt in its crystaline form.
Ex : CuSO₄ • 5H₂O.
It means that five water molecules are present in one formula unit of copper sulphate.

Activity to show the water of crystallization :

1. Take a few crystals of copper sulphate in a dry test tube and heat the test tube.
2. We observe water droplets on the walls of the test tube and salt turns white.
3. Add 2 – 3 drops of water on the sample of copper sulphate obtained after heating.
4. We observe, the blue colour of copper sulphate crystals is restored.

Reason :
1. In the above activity copper sulphate crystals which seem to be dry contain the water of crystallization, when these crystals are heated, water present in crystals is evaporated and the salt turns white.

2. When the crystals are moistened with water, the blue colour reappears.
Removing water of crystallization

Question 13.
Equal lengths of magnesium ribbons are taken in test tubes A and B. Hydrochloric acid is added to test tube A, while acetic acid is added to test tube B. Amount and concentration of both the acids are same. In which test tube will the fizzing occur more vigorously and why? (AS4)
Answer:
1. The volatility of acetic acid (CH₃COOH) is more than that of hydrochloric acid.
2. But HCl solution has more strength than acetic acid.
3. Hence magnesium ribbon in test tube A will react more vigorously than in B.
4. So fizzing occurs more vigorously in test tube ‘A’.

Question 14.
Draw a neat diagram showing acid solution in water conducts electricity. (AS5)
(OR)
Draw a neat diagram which shows acids contains H⁺ ions.
(OR)
Draw a neat diagram showing how does dilute HCl solution conduct electricity.
Answer:

Question 15.
How do you prepare your own indicator using beetroot ? Explain. (AS5)
Aim : To prepare own indicator.
Materials required :
1) Beetroots-2 or 3
2) Knife
3) Bowls
4) Water
5) Spoon
6) Mixy
7) Orange juice

Procedure:
1) Take the beetroots and peel them with the help of a knife. (Firstly wash them).
2) Chop them into pieces.
3) Put those pieces into a mixy jar and make a paste.
4) Add some water to the paste. Now filter this and collect only juice from this.

Observation and Result:
1) Now add 5 to 6 drops of this juice, (beetroot juice (indicator)) to orange juice (5 to 6 drops) and mix it.
2) We can see the colour changes. This indicates the presence of acidic nature in orange juice.

Question 16.
How does the flow of acid rain into a river make the survival of aquatic life in a river difficult? (AS7)
(OR)
What are the harmful effects of acid rain?
Answer:
1) Acid rains are combination of carbonic acid, sulphuric acid and nitric acid with rain water.
2) The pH of acid rain is less than 5.6.
3) Living organisms can survive only in a narrow range of pH change.
4) When acid rain with pH value less than 5.6, flows into rivers, it lowers the pH of river water.
5) Due to less pH, the river water becomes acidic and hence the aquatic life in such rivers becomes difficult.

Question 17.
What is baking powder? How does it make the cake soft and spongy? (AS7)
Answer:
1) Baking Powder:
Baking powder is a mixture of baking soda (NaHCO₃) and a mild edible acid such as tartaric acid. COOH (CHOH)₂ COOH

2) Chemical reaction :
When baking powder is heated or mixed in water, the following reaction takes place.
NaHCO₃ + H⁺ → CO₂ + H₂O + Sodium salt of acid.

3) Carbondioxide produced during the reaction causes bread or cake to rise making them soft and spongy.

Question 18.
Give two important uses of washing soda and baking soda. (AS7)
(OR)
Write the chemical formulae for washing soda and Baking soda and give their uses.
(OR)
Write any four uses of washing soda.
Answer:
Uses of washing soda (Na₂CO₃.10H₂O) :
1) Washing soda (sodium carbonate) is used in glass, soap and paper industries.
2) It is used in the manufacture of sodium compounds such as borax.
3) Sodium carbonate can be used as a cleaning agent for domestic purposes.
4) It is used for removing permanent hardness of water.

Uses of baking soda (NaHCO₃ 10H₂O) :
1) Baking soda (Sodium hydrogen carbonate) is used for faster cooking.
2) Baking powder (a mixture of baking soda and a mild acid) is used in preparation of cakes.
3) Sodium hydrogen carbonate is also an ingredient in antacids.
4) It is also used in soda – acid, fire extinguishers.
5) It acts as a mild antiseptic.

Fill in the Blanks

1. i) ………………….. taste is a characteristic property of all acids in aqueous solution.
ii) Acids react with some metals to produce ………………….. gas.
iii) Because aqueous acid solutions conduct electricity, they are identified as …………………..
iv) Acids react with bases to produce a ………………….. and water.
v) Acids turn methyle orange into ………………….. colour.
Answer:
1. i) Sour
ii) hydrogen
iii) electrolytes or conductors
iv) salt
v) red

2. i) Bases tend to taste ………………….. and feel ………………….. .
ii) Like acids, aqueous basic solutions conduct ………………….., and are identified as ………………….. .
iii) Bases react with ………………….. to produce a salt and
iv) Bases turn phenophthalein into ………………….. colour.
Answer:
2. i) bitter, soapy (slippery) to touch
ii) electricity, electrolytes
iii) acids, water
iv) pink

Match the following :

a) Plaster of Paris	1) CaOCl2
b) Gypsum	2) NaHCO3
c) Bleaching powder	3) Na2CO3
d) Baking soda	4) CaSO4.½H2O
e) Washing soda	5) CaSO4.2H2O

Answer:
3. a – 4,
b – 5,
c – 1,
d – 2,
e – 3.

Multiple Choice Questions

1. The colour of methyl orange indicator in acidic medium is
A) yellow
B) green
C) orange
D) red
Answer:
D) red

2. The colour of phenolphthalein indicator in basic solution is
A) yellow
B) green
C) pink
D) orange
Answer:
C) pink

3. Colour of methyl orange in alkali conditions
A) orange
B) yellow
C) red
D) blue
Answer:
B) yellow

4. A solution turns red litmus blue, its pH is likely to be
A) 1
B) 4
C) 5
D) 10
(OR)
If a solution converts red litmus into blue colour, then its pH value is …………….. .
A) 1
B) 4
C) 5
D) 10
Answer:
D) 10

5. A solution reacts with crushed egg-shells to give a gas that turns lime-water milky, the solution contains …………….. .
A) NaCl
B) HCl
C) LiCl
D) KCl
Answer:
B) HCl

6. If a base dissolves in water, by what name is it better known?
A) neutralization
B) basic
C) acid
D) alkali
Answer:
D) alkali

7. Which of the following substances when mixed together will produce table salt?
A) Sodium thiosulphate and sulphur dioxide
B) Hydrochloric acid and sodium hydroxide
C) Chlorine and oxygen
D) Nitric acid and sodium hydrogen carbonate
Answer:
B) Hydrochloric acid and sodium hydroxide

8. What colour would hydrochloric acid (pH = 1) turn universal indicator?
A) Orange
B) Purple
C) Yellow
D) Red
Answer:
D) Red

9. Which one of the following types of medicines is used for treating indigestion?
A) antibiotic
B) analgesic
C) antacid
D) antiseptic
Answer:
C) antacid

10. What gas is produced when magnesium is made to react with hydrochloric acid?
A) hydrogen
B) oxygen
C) carbon dioxide
D) no gas is produced
Answer:
A) hydrogen

11. Which of the following is the most accurate way of showing neutralization?
A) Acid + base → acid-base solution
B) Acid + base → salt + water
C) Acid + base → sodium chloride + hydrogen
D) Acid + base → neutral solution
Answer:
B) Acid + base → salt + water

10th Class Chemistry 1st Lesson Acids, Bases and Salts InText Questions and Answers

10th Class Chemistry Textbook Page No. 25

Question 1.
Is the substance present in antacid tablet acidic or basic?
A. The substance present in antacid tablet is basic.

Question 2.
What type of reaction takes place in stomach when an antacid tablet is consumed?
mrearx
A. Neutralization reaction takes place in stomach when an antacid tablet is consumed.

10th Class Chemistry Textbook Page No. 26

Question 3.
You are provided with three test tubes containing distilled water, an acid and a base solution respectively. If you are given only blue litmus paper, how do you identify the contents of each test tube?
Answer:
I know that acid turns blue litmus to red. With the help of this test I can find the acid. Distilled water and base don’t do so. Thus I identify each.

Question 4.
Which gas is usually liberated when an acid reacts with a metal? How will you test for the presence of this gas?
Answer:
Usually acids generate hydrogen gas on reacting with metals.

Test: When a burning splinder is brought near to the collected gas (H₂), it puts off with a pop sound.
This test proves that the gas is H₂.

Question 5.
A compound of a calcium reacts with dilute hydrochloric acid to produce effervescence. The gas evolved extinguishes a burning candle ; turns lime water milky. Write a balanced chemical equation for the reaction if one of the compounds formed is calcium chloride.
Answer:
Equation is : CaCO₃ + 2 HCl → CaCl₂ + CO₂ + H₂O

10th Class Chemistry Textbook Page No. 30

Question 6.
Why do HCl, HNO₂ etc. show acidic characters in aqueous solutions while solutions of compounds like alcohol and glucose do not show acidic character?
Answer:
HCl, HNO₃, etc. show acidic characters in aqueous solutions as they liberate H⁺ ions. But alcohol and glucose don’t liberate H⁺ ions. So, they do not show acidic character.

Question 7.
While diluting an acid, why is it recommended that the acid should be added to water and not water to the acid?
Answer:
1) If water is added to a concentrated acid, the heat generated may cause the mixture to splash out and cause burns.
2) The glass container may also break due to excessive local heating.

10th Class Chemistry Textbook Page No. 33

Question 8.
What will happen if the pH value of chemicals in our body increases?
Answer:
When pH value of chemicals in our body increases then the body will effect by some problems. They are
1) Digestion problems raise in the stomach.
2) pH changes as the cause of tooth decay.

Question 9.
Why do living organism have narrow pH range?
Answer:
Because increasing acidity is thought to have a range of possibly harmful consequences such as depressing metabolic rate and immune response in some organisms and causing coral bleaching

10th Class Chemistry 4th Lesson Acids, Bases and Salts Activities

Activity – 1

Question 1.
Observe the change in colour in each case and tabulate the results in the table.
Answer:
Procedure:
1) Collect the following samples from the science laboratory ;
i) Hydrochloric acid (HCl)
ii)Sulphuric acid (H₂SO₄)
iii) Nitric acid (HNO₃)
iv) Acetic acid (CH₃COOH)
v) Sodium hydroxide (NaOH)
vi) Calcium hydroxide[Ca(OH)₂]
vii) Magnesium hydroxide [Mg(OH)₂]
viii) Ammonium hydroxide(NH₄OH)
ix) Potassium hydroxide (KOH)
2) Prepare dilute solutions of the respective substances.
3) Take four watch glasses.
4) Put one drop of the first solution in each one of them and test the solution as follows.
i) Dip the blue litmus paper in the first watch glass.
ii) Dip the red litmus paper in the second watch glass.
iii) Add a drop of methyl orange to the third watch glass.
iv) Add a drop of phenolphthalein to the fourth watch glass.

Observation :
Observe the respective colour changes and note down in the chart below.

1. What do you conclude from the observations noted in the above table? (AS1)
Answer:
Conclusion : Acids turn blue litmus to red and bases turn red litmus to blue. Acids turn phenolphthalein to colourless and bases turn pink. Acids turn methyl orange to red and bases turn methyl orange to yellow.

2. Identify the above sample as acidic or basic solution. (AS4)
Answer:
Acids : HCl, H₂SO₄, HNO₃, CH₃COOH.
Bases : NaOH, KOH, Mg(OH)₂, NH₄OH, Ca(OH)₂.

Activity -2

Question 2.
What are Olfactory indicators? Write an activity to prove them.
(OR)
What is the name given to a substance which identifies an acid or base by virtue of smell? Write an activity to prove the fact with an example.
Answer:
Olfactory Indicators : There are some substances whose odour changes in acidic or basic media. These are called olfactory indicators.
Activity :
Aim : To check the olfactory indicator.
Required materials :
1) Onions
2) Knife
3) Plastic bag
4) Clean clothes.

Procedure :
1) Take some onions and finely chop them.
2) Put the chopped onions in a plastic bag along with some clean cloth.
3) Tie up the bag tightly and keep it overnight in the fridge.
4) Then remove onions from fridge and add some base. We observe it loses its smell. Observation : Check the odour of the cloth strips.

Result: It is used as the basic indicator.

LAB ACTIVITY Reaction of Acids with metals

Question 3.
Write an experiment showing the reaction of acids with metals. (AS3)
(OR)
Ramu added acid to active metal then what is the gas which has been liberated. What are the apparatus required to prove the experiment. Write the experimental acitivity.
(OR)
Write the required material and experimental procedure for the experiment, “Hydrochloric acid reacts with ‘Zn’ pieces and liberates H₂“.
Answer:
Aim : To show the reaction of acids with metals.

Required Materials :

1. Test tube
2. Delivery tube
3. Glass trough
4. Candle,
5. Soap water
6. Dil. HCl
7. Zinc granules
8. One holed rubber stopper
9. Retard stand

Experimental procedure :

1. Take some zinc granules in a test tube and arrange the test tube to the retart stand.
2. Fix a delivery tube to the rubber stopper and immerse the second end of the delivery tube into the soap water.
3. Add about 10 m/ of dilute hydrochloric acid to Zn granules and fix rubber stopper to the test tube.
4. Evolved gas forms bubbles in soap water.
5. Bring a lightened candle near to the gas bubbles. We can observe the burning of gas bubble with pop sound.

Result: We can conform that the evolved gas is hydrogen.
Chemical reaction:
Acid + Metal → Salt + Hydrogen
2Hcl_(aq) + Zn_(s) → Zncl_2(aq) + H_2(g)

Additional Experiment :

• Repeat the above experiment with H₂SO₄ and HNO₃.
• We observe the same observation of the HCL experiment.

Conclusion : From the above activities we can conclude that when acid reacts with metal, H₂ gas is evolved.

Activity – 3 Reaction of Bases with metals

Question 4.
Write an activity to show the reaction of bases with metals.
(OR)
Write an activity which proves certain bases produce hydrogen gas when they react with metals.
Answer:
Aim : To show the reaction of bases with metals.

Required Materials :

1. Test tube,
2. Delivery tube
3. Glass trough
4. Candle
5. Soap water
6. Sodium hydroxide (NaOH) Solution
7. Zinc granules
8. One holed rubber stopper

Procedure :

1. Set the apparatus as shown in figure.
2. Take about 10 ml of dilute Sodium hydroxide (NaOH) solution in a test tube.
3. Add a few granules of zinc metal to it.
4. We will observe formation of gas bubbles on the surface of granules.
5. The gas will pass through delivery tube evolved from soap solution as bubbles.
6. Bring burning candle near the gas filled bubble.
7. The gas in the bubble puts off the candle with pop sound.

Result: The evolved gas is hydrogen.

Chemical reaction :
Base + Metal → Salt + Hydrogen

Note : It is better to use cone. NaOH solution for this reaction.

Activity – 4 Reaction of carbonates and metal hydrogen carbonates with Acids

Question 5.
Write an activity to show that all metal carbonates and hydrogen carbonates react with acids to give a corresponding salt. (AS3)
Answer:
Aim : To show that all metal carbonates and hydrogen carbonates react with acids to give a corresponding salt.

Required Materials :

1. Two test tubes
2. Sodium Carbonate (Na₂CO₃)
3. Sodium Hydrogen Carbonate (NaHCO₃)
4. Two holed rubber stopper
5. Thistle funnel
6. Stand
7. Dilute hydrochloric acid
8. Delivery tube
9. Calcium Carbonate (in a test tube)

Procedure :

1. Take a test tube A with 0.5 gm of sodium carbonate.
2. Close the test tube A with two holed rubber cork.
3. Insert a thistle funnel through one hole and insert a delivery tube through the other hole.
4. Pour 2 ml of dilute HC/ to the test tube A.
5. Do the same as above with test tube B with sodium hydrogen carbonate.

Observation :
Carbon dioxide is released from test tube A and B. Passing CO₂ gas through Ca(OH)₂ solution

Chemical Reaction :
Na₂CO_3(s) + 2 HCl_(aq) → 2 NaCl_(aq) + CO_2(g) + H₂O_(l)
Metal Carbonate + Acid → Salt + Carbon dioxide + Water

NaHCO_3(s) + HCl_(aq) → NaCl_(aq) + CO_2(g) + H₂O_(l)
Metal Hydrogen Carbonate + Acid → Salt + Carbon dioxide + Water

Result : All metal carbonates and hydrogen carbonates react with acids to give a corresponding salt.

Activity – 5 Neutralization reaction

Question 6.
Write an activity to find the change of colour in the reaction of an acid with a base (Neutralization) reaction. (AS3)
(OR)
Explain neutralization reaction with an activity.
Answer:
Aim : To test the change of colour in the reaction of an acid with a base.

Required Materials :

1. 2 ml of dilute NaOH (Sodium Hydroxide) solution.
2. Phenolphthalein indicator solution.
3. dilute HCl (Hydrochloric) solution.

Procedure :

1. Take about 2 ml of dilute NaOH solution in a test tube.
2. Add two drops of phenolphthalein indicator solution.

Observation (i) :

1. It turns to red or pink colour.
2. It shows that NaOH is a base.

Experiment (1) : Add dilute HCl solution to the above solution drop by drop.
Observation (ii) : Pink colour disappears due to the reaction of NaOH (base) with HCl (acid).

Experiment (2) : Now add one or two drops of NaOH to the above mixture.
Observation (iii) : Pink colour reappears on adding NaOH.
NaOH + HCl → NaCl + H₂O
base + acid → salt + water
Result: This reaction is called a neutralization reaction.

Activity – 6 Reaction of metallic oxides with acids

Question 7.
Write an activity to show that metal oxide reacts with acid is a neutralization. (AS3)
(OR)
How can you prove metallic acids are basic in nature?
Answer:
1) Take a small amount of copper oxide (CuO) in a beaker.
2) Add dilute HCl slowly while stirring.
3) Copper oxide dissolves in dilute HCl and the solution becomes blueish green colour due to the formation of copper (II) chloride.

Equation : Metal oxide + Acid → Salt + Water
Result: This reaction is same as the reaction of base with acid, (neutralization)

Question 8.
Write an activity to show that non-metallic oxide reacts with base is a neutralization.
Answer:
1) Take a small amount of calcium hydroxide (base).
2) Add CO₂ into it.
3) Salt and water are produced.
Equation : Non-metallic oxide + Base → Salt + Water
Result: It is a neutralization reaction.

Question 9.
Repeat the activity – 7 using alkalis such as sodium hydroxide, calcium hydroxide solutions, etc. instead of acid solutions.
i) Does the bulb glow?
Answer:
Yes, the bulb will glow.

ii) What do you conclude from the results of this activity?
Answer:
Basic solutions are also good conductors of electricity due to released OH^– ions.

iii) What happens to an acid or a base in aqueous solution?
Answer:
Acids produce H⁺ ions and bases produce OH^– ions in aqueous solutions.

iv) Do acids produce ions only in aqueous solution?
Answer:
Yes.

Activity – 8

Question 10.
Do acids produce ions only in aqueous solution? Prove it. (AS3)
(OR)
Acids produce ions only in aqueous solution. Justify your answer with an activity.
Answer:
Procedure :

1. Take about 1.0 g of solid NaCl in a clean and dry test tube.
2. Add some concentrated sulphuric acid to the test tube. .

Observation :

1. A gas comes out of the delivery tube.
2. If we test the gas with dry and wet blue litmus paper, there is no change in colour.

Chemical equation : 2 NaCl_(s) + H₂SO_4(l) > 2 HCl + Na₂SO_4(s)

Conclusion :

1. We can conclude that dry HCl gas (hydrogen chloride) is not an acid.
2. Because we have noticed that there is no change in colour of dry litmus paper.
3. But HCl aqueous solution is an acid because wet blue litmus paper turned into red.

Activity – 9 Reaction of water with acids or bases

Question 11.
Write an activity to show that dissolving of an acid in water is an exothermic process (or) endothermic process. (AS3)
(OR)
What do you observe when water is mixed with acid or base?
Answer:
Experiment :

1. Take 10 ml water in a beaker.
2. Add a few drops of concentrated H₂SO₄ to it and swirl the beaker slowly.
3. Touch the base of the beaker.
4. The base is hot.
5. Do this experiment with other concentrated acids like HCl, HNO₃ Result: This is an exothermic process called dilution.

Activity -10 Strength of acid or base

Question 12.
Write an activity to know whether the acid is strong or weak. (AS3)
Answer:

1. Take dilute HCl in a beaker.
2. Close it with a cardboard and introduce two different colour electrical wires through the holes made on it.
3. Connect a bulb and make the connection as shown in the figure.
4. Do the same replacing dilute HCl with dilute CH₃COOH (acetic acid).

Observation :
The bulb glows brightly in HCl solution, while the bulb’s intensity is low in acetic acid solution.

Result:
More ions are present in HCl solution which is a strong acid than in CH₃COOH solution which is a weak acid.

Activity – 11

Question 13.
Test the pH value of solution given in table. Record your observations. What is the nature of each substance on the basis of your observations?
Answer:

Activity – 12

Question 14.
Write an activity to check the colour change in dilute HCl and antacid solution in addition of methyl orange. (AS3)
Answer:
Procedure :

1. Take dilute HCl in a beaker.
2. Add two to three drops of methyl orange indicator to it.
3. The solution colour turns to red.
4. Now take the same solution and mix antacid tablet powder.

Observation :
Check the colour change.

Result:
The colour of the solution turns to light yellow.

Chemical equation:
2 HCl + Mg(OH)₂ → MgCl₂ + 2H₂O

Activity – 13

Question 15.
How can we test the pH value of the soil? (AS3)
Answer:

1. Take about 2g of soil in a test tube.
2. Add 5 ml water to it.
3. Shake it well.
4. Filter the content.
5. Collect the filtrate in a test tube.
6. Add 2 drops of universal solution to it.
7. Observe the colour.
8. Compare the colour with strip colour on the bottle and find the pH value.
9. In this way we can test the pH of the soil.

Activity – 14

Question 16.
Write the formulae of the following salts and classify them as families based on radicals.
Potassium Sulphate, Sodium Sulphate, Calcium Sulphate, Magnesium Sulphate, Copper Sulphate, Sodium Chloride, Sodium Nitrate, Sodium Carbonate and Ammonium Chloride. (AS4)
Answer:

Name of the Salt	Formula
1. Potassium Sulphate	K2SO4
2. Sodium Sulphate	Na2SO4
3. Calcium Sulphate	CaSO4
4. Magnesium Sulphate	MgSO4
5. Copper Sulphate	CuSO4
6. Sodium Chloride	NaCl
7. Sodium Nitrate	NaNO3
8. Sodium Carbonate	Na2CO3
9. Ammonium Chloride	NH4Cl

Sodium family : Na₂SO₄, NaCl, NaNO₃, Na₂CO₃, etc.
Family of chloride salts : NaCl, NH₄Cl, etc.
Family of sulphate salts : K₂SO₄, Na₂SO₄, CaSO₄, MgSO₄, CuSO₄, etc.
Family of carbonate salts : Na₂CO₃ MgCO₃ CaCO₃, etc.

Question 17.
Identify the acids and bases from which they are obtained. (AS4)
Answer:

Name of the Salt	Parent Acid	Parent Base
1. Potassium Sulphate	Sulphuric Acid	Potassium Hydroxide
2. Sodium Sulphate	Sulphuric Acid	Sodium Hydroxide
3. Calcium Sulphate	Sulphuric Acid	Calcium Carbonate
4. Magnesium Sulphate	Sulphuric Acid	Magnesium Hydroxide
5. Copper Sulphate	Sulphuric Acid	Copper Hydroxide
6. Sodium Chloride	Hydrochloric Acid	Sodium Hydroxide
7. Sodium Nitrate	Nitric Acid	Sodium Hydroxide
8. Sodium Carbonate	Carbonic Acid	Sodium Hydroxide
9. Ammonium Chloride	Hydrochloric Acid	Ammonium Hydroxide

Activity – 15 pH of Salts

Question 18.
Collect the salt samples like sodium chloride, aluminium chloride, copper sulphate, sodium acetate, ammonium chloride, sodium hydrogen carbonate and sodium carbonate. Dissolve them in distilled water. Check the action of these solutions with litmus papers. Find the pH using pH paper (universal indicator. Classify them into acidic, basic or neutral salts. Identify the acid and base used to form the above salts. Record your observations in table. (AS4)
Answer:

Salt	pH	Acid	Base	Neutral
Sodium Chloride	7	–	–	✓
Aluminium Chloride	7	–	–	✓
Copper Sulphate	< 7	✓	–	–
Sodium Acetate	> 7	–	✓	–
Ammonium Chloride	< 7	✓	–	–
Ammonium Chloride	> 7	–	✓	–
Sodium Carbonate	> 7	–	✓	–

 

AP State Board Syllabus AP SSC 10th Class Physical Science Important Questions Chapter 7 Human Eye and Colourful World.

AP State Syllabus SSC 10th Class Physics Important Questions 7th Lesson Human Eye and Colourful World

10th Class Physics 7th Lesson Human Eye and Colourful World 1 Mark Important Questions and Answers

Question 1.
Define the power of lens. (AP June 2016)
Answer:
The reciprocal of focal length is called “power of lens”.

Question 2.
What physical quantity can be found in an experiment done with prism? (AP June 2017)
Answer:

1. Angle of deviation.
2. Refractive index of a prism.

Question 3.
What is the relation between Power and Focal length of the lens? (AP June 2018)
Answer:
\(P=\frac{1}{f(\text { in metres })}\) (OR) \(P=\frac{100}{f(\text { in cms })}\)

Question 4.
Draw the diagram of a lens which will be recommended by an eye doctor to a long sighted patient. (TS June 2015)
Answer:

The lens is convex lens.

Question 5.
What is the cause of Presbyopia? (TS March 2015)
Answer:
Presbyopia is vision defect when the ability of accommodation of the eye decreases with ageing.

Question 6.
Draw a ray diagram to show the angle of deviation when a ray of light passes through a glass prism. (TS March 2015)
Answer:

d = angle of deviation

Question 7.
Suggest reasons for the phenomenon associated with the following. The sky appearing blue. (TS March 2015)
Answer:
The reason for blue sky is due to the scattering of light by the molecules of N₂ and O₂ whose size is comparable to the wavelength of blue light.

Question 8.
+50 cm focal length bi-convex lens is recommended to correct the defect of vision of a mart. Find the power of the lens. (TS June 2016)
Answer:
f = +50 cm
Power (P) = \(\frac{100}{\mathrm{f}}\) D (in cm); P = \(\frac{100}{50}\) = 2 D
Power of the bi-convex lens is 2D.

Question 9.
What happens if the eye lens of a person cannot accommodate its focal length more than 2.4 cm? (TS March 2017)
Answer:
The person can able to see certain distance only he cannot see distance objects. For correction, he should use concave lens.

Question 10.
Write the reason for Sun appears red during the Sun-rise and Sun-set. (TS June 2018)
Answer:
Due to the high velocity (wave length) of red right, it reaches our eye without under go scattering. So, sun appears red during sunrise and sunset.

Question 11.
A person is unable to see distant objects. Show the defect of vision of the person with the help of ray diagram. (TS March 2018)
Answer:
1) His vision defect is myopia.
2) Ray diagram

Question 12.
Which molecules of atmosphere act as scattering centres are responsible for the blue sky? (TS June 2019)
Answer:
Oxygen and Nitrogen molecules.

Question 13.
Write any one application of a prism. (AP SA-I; 2019-20)
Answer:

1. Prism is used in scopes like binoculars, telescopes and light houses.
2. Prism is used to create artificial rainbow.

Question 14.
Mention the function of retina in a human eye.
Answer:
It acts as a screen, (which the image is formed) for image formed.

Question 15.
State the role of ciliary muscles in accommodation.
Answer:
It can adjust the focal length of the eye lens.

Question 16.
Why is normal eye not able to see clearly the objects kept closer than 25 cm?
Answer:
The maximum accommodation of a normal human eye is reached when the object is at a distance of 25 cm from the eyes. The focal length of the eye lens cannot be decreased this minimum limit.

Question 17.
What is “Power of accommodation of the eye” (or) “Least distance of clear vision”?
Answer:
The ability of the eye lens to adjust its focal length to see nearby and distant objects clearly.

Question 18.
What is “Iris” and “Pupil”?
Iris :
The muscular diaphragm between the aqueous humour and the lens is called ‘iris’. Iris is the coloured part that we see in an eye.

Pupil:
The small hole in iris is called ‘pupil’.

Question 19.
What are three common defects of vision?
Answer:
The common defects of vision are i) Myopia ii) Hypermetropia iii) Presbyopia.

Question 20.
What is “Far point”?
Answer:
The point of maximum distance at which the eye lens can form an image on retina is called ‘far point’.

Question 21.
What is power of lens?
Answer:
The reciprocal of focal length is called power of lens. Power of lens focal length = \(\frac{1}{\text { focal length }}\)

Question 22.
What is the function of pupil in human eye?
Answer:
It allows the light falling on iris.

Question 23.
What is the purpose of human eye?
Answer:
The purpose of eye is to see and perceive the objects around us.

Question 24.
What is the principle of the working of human eye?
Answer:
It acts as camera having a lens system forming an invented real image on the light sensitive screen, retina.

Question 25.
What is the nature of the image formed on the retina?
Answer:
Real, inverted and same sized.

Question 26.
What is meant by dispersion of light?
The splitting of white light into its component colours when it passes through the prism is called dispersion of light.

Question 27.
On which factors does the colour of the scattered white light depend?
Answer:

1. Angle of scattering
2. Distance travelled by light
3. Size of the molecules.

Question 28.
Why is normal eye not able to see clearly the objects placed closer than 25 cm?
Answer:
The focal length of eye lens cannot decrease below 25 cm.

Question 29.
A person is advised to wear spectacles with concave lenses. What type of defect of vision is he suffering from?
Answer:
Myopia (or) short sightedness.

Question 30.
A person suffering from an eye-defect uses lenses of power – 1D. Name the defect he is suffering from and the nature of lens is used.
Answer:
Defect:
Myopia, Nature of lens, Concave/divergence.

Question 31.
Name the two phenomena involved in the formation of rainbow.
Answer:
Dispersion of light and internal reflection.

Question 32.
Identify the following part of the human eye.
1. Where is image of an object formed?
2. Which controls size of pupil?
Answer:

1. Image of an object is formed on retina.
2. Iris controls the size of pupil.

Question 33.
What is the relation between power of lens and focal length (f)?
Answer:
Power of lens (concave/convex)
\(P=\frac{1}{f(\text { in metres })}\) (OR) \(P=\frac{100}{f(\text { in cms })}\)

Question 34.
Explain about “Bending of light”.
Answer:

1. When a light travels from rarer to denser medium, it bends towards the normal.
2. And from denser to rarer medium, it moves away from the normal.

Question 35.
What is sclerotic?
Answer:
It is the outermost covering of the eye. It protects the vital internal parts of the eye.

Question 36.
What is “Retina”?
Answer:
Retina is the internal part and the light sensitive surface of the eye. It is equivalent to the photographic film in a camera.

Question 37.
What is “Atmospheric refraction”?
Answer:
When the light rays pass through the atmosphere having layers of different densities and refractive indices, refraction of light takes place. This refraction of light by the earth’s atmosphere is called atmospheric refraction.

Question 38.
What is a “Telescope”?
Answer:
The instrument which is used to see the distant objects such as a star, planet (moon, sun) or distant tree is called telescope.

Question 39.
Have you seen a rainbow in the sky after rain? How is it formed?
Answer:

1. A rainbow is a natural spectrum of sunlight in the form of bows appearing in the sky when the sun shines on raindrops after the rain.
2. It is formed due to reflection, refraction and dispersion of sunlight by tiny water droplets present in the atmosphere.

Question 40.
“To look at the twinkling of stars is a wonderful experience.” How does it happen?
Answer:
The continuous changing atmosphere (due to varying atmospheric temperature and density) refracts the light from the stars by varying amounts and in different directions from one moment to the next.

Question 41.
Some things appear blue on a misty day. Give two examples.
Answer:

1. The long distance hills covered with thick growth of trees appear blue.
2. The smoke coming from a cigarette or an incense stick (agarbatti) appears blue on a misty day.

Question 42.
Which coloured suits do rescue workers wear?
Answer:
Rescue workers wear orange coloured suits during any rescue operations.

Question 43.
Which colour is best for school buses?
Answer:
Orange or yellow colour is best for school busses.

Question 44.
What is persistence of vision?
Answer:
The time for which the sensation of vision (of an object) continues in the eye is called persistence of vision. It is about 1/16^th part of a second.

Question 45.
Why can’t some people identify some colours?
Answer:
Rods identify the colours in the retina. If some rods are absent, the distinction of colours is not possible. In such cases, persons can’t identify some colours.

Question 46.
Write the reasons for colour blindness.
Answer:

1. Absence of colour responding rod cells in the retina.
2. Due to genetic disorder.

Question 47.
Why does it take some time to see objects in a dim room when we enter the room from bright sunlight outside?
Answer:
In bright light, the size of the pupil is small to control the amount of light entering the eye. When we enter a dim room, it takes some time so that the pupil expands and allows more light to enter and helps to see things clearly.

Question 48.
What is tyndall effect?
Answer:
The phenomenon of scattering of white light by colloidal particles is known as ‘Tyndall effect”.

Question 49.
Give two examples illustrating “Tyndall effect”.
Answer:

• A fine beam of sunlight entering a smoke filled room through a hole. Smoke particles scatter the white light and hence the path of light beam becomes visible.
• Sunlight passing through the trees in forest.
• Tiny water droplets through the trees in forest.

Question 50.
An eye camp was organised by the doctors in a village. What were the benefits to organise such camps in rural areas?
Answer:

1. To make people aware of eye diseases
2. To take proper and balanced diet.

Question 51.
What happens to the image distance in the eye when we increase the distance of an object from the eye?
Answer:
In the eye, the image distance (distance between eye lens and retina) is fixed and it cannot be changed. So when we increase the distance of an object, there is no change in the image distance.

Question 52.
Why is a normal eye not able to see clearly the objects placed closer than 25 cm?
Answer:
The maximum accommodation of a normal eye is at a distance of 25 cm from the eye.
The focal length of the eye lens cannot be decreased below this. Thus an object placed closer than 25 cm cannot be seen clearly by a normal eye.

Question 53.
Write the relation between intensity of scattered light (I) and wavelength (λ).
Answer:
Light of short wavelength is scattered more than the light of long wavelength.
i.e., Intensity of scattered light (I) ∝ \(\frac{1}{\text { wavelength }(\lambda)}\)

Question 54.
Why would the sky look dark if the earth had no atmosphere?
Answer:
If the earth has no atmosphere, no particles present either. Thus no scattering of light. Then, the sky appears dark.

Question 55.
Why do different coloured rays deviate differently in the prism?
Answer:
Because the angle of refraction of different colours is different while passing through the glass prism.

Question 56.
What prevents rainbow from being seen as complete circles?
Answer:
The earth comes in the way of the rainbow and prevents it to form a complete circle.

Question 57.
When a monochromatic light passes through a prism will it show dispersion?
Answer:
No, it will not show any dispersion but show deviation.

Question 58.
Will a star appear to twinkle if seen from free space (say moon)?
Answer:
No, because there is no atmosphere in free space for refraction to take place.

Question 59.
A short-sighted person may read a book without spectacles. Comment.
Answer:
The statement is true, because a short-sighted person has difficulty in observing far off objects.

Question 60.
What is angle of vision?
Answer:
The maximum angle, at which we can see the whole object is called angle of vision.

Question 61.
What is cornea?
Answer:
The front curved portion of eye, which is covered by a transparent protective membrane is called the cornea.

Question 62.
Which lens do you use to correct the eye defect, Myopia?
Answer:
Bi-concave lens are used to correct the eye defect, Myopia.

Question 63.
What happens to power of lens if (i) focal length is increased, (ii) focal length is decreased?
Answer:

1. If focal length is increased, then power of lens decreases.
2. If focal length is decreased, then power of lens increases.

Question 64.
What type of image is formed by magnifying glass?
Answer:
It forms virtual, erect and magnified image.

Question 65.
How is power of lens related to its focal length?
Answer:
Power of lens is inversely proportional to its focal length.

Question 66.
What is “Scattering of light”?
Answer:
The process of re-emission of light in all directions with different intensity is called scattering of light. The re-emitted light is called scattered light.

Question 67.
Ramu is unable to see letters on the blackboard sitting at the last bench in the class¬room. What is the defect from which Ramu is suffering?
Answer:
Ramu is suffering from Myopia.

Question 68.
Vinay is able to read letters in a book beyond certain distance from least distance of distinct vision. What is the eye defect of Vinay?
Answer:
Vinay is suffering from Hypermetropia.

Question 69.
How can an eye lens accommodate its focal length?
Answer:
To see an object comfortably and distinctly, one must hold at a distance about 25 cm from his/her eyes. This distance is called least distance of distinct vision.

Question 70.
Write the uses of “rods” and “cones”.
Answer:
Retina contains about 125 million receptors called rods and cones. Rods identify the colour and cones identify the intensity of light.

Question 71.
Frame some questions, that you are going to ask your friend who is suffering from eye sight.
Answer:

1. Are you not able to see near objects or far objects?
2. Are you not able to see both near and far objects?

Question 72.
Write some more examples to find dispersion of light as VIBGYOR.
Answer:

1. Formation of rainbow.
2. When white light passes through water drop.

Question 73.
Why do stars twinkle?
Answer:
Due to change in atmospheric conditions, density changes so position keeps on changing.

Question 74.
“Sky appears dark to passengers flying at very high altitudes.” Why?
Answer:
At very high altitude, there is no atmosphere. So there is no scattering of light at such heights. So sky appears dark to passengers.

Question 75.
Why are danger signals red? (OR) Why are danger signals shown in red colour?
Answer:
Among the colours of visible light, red has more wavelength and least scattered. Thus, red colour can easily go through fog or mist or smoke without getting scattered. It can be seen from long distance. So red colour is used in universal danger signal.

Question 76.
How can you identify regarding the type of defect a person is suffering from by physically touching his spectacles?
Answer:
By touching the spectacles we can find out whether the lens is concave or convex lens and hence the defect from which he suffers.

Question 77.
A person cannot see objects beyond 1-2 m distinctly. What should be the nature of the defect and what type of lens should be used to correct the defect?
Answer:
The person is suffering from Myopia. It can be corrected by using concave lens.

Question 78.
How do you appreciate the working of “Retina”?
Answer:

1. It is the innermost delicate membrane having a large number of receptors called ‘rods’ and ‘cones’.
2. The rods identify the colour and the cones identify the intensity of light.
3. The retina is a part on which the image of an object is formed.

Question 79.
How do you appreciate the working of “Optic nerve”?
Answer:

1. Optic nerve consists of a large number of fibres.
2. These optic nerve fibres are connected to the rods and cones.
3. Optic nerve fibers transmit the light signals to the brain.

Question 80.
We see advertisements for eye donation on television or in newspaper. Write the importance of such advertisements.
Answer:
Eye donation advertisements are important as :

1. The people aw;are about donation of organs after their death.
2. Sympathetic nature towards others.

Question 81.
An eye donation camp is being organised by social workers in your locality. How and why would you help in this cause?
Answer:

1. We can intimate other people to participate in the camp.
2. As a human being, we should also register our eyes for donation after death.

Question 82.
A short sighted person cannot see clearly beyond 2m. Calculate the power of lens required to correct his vision.
Answer:

Question 83.
How does the power of a lens change if its focal length is doubled?
Answer:
The power get halved.

Question 84.
A person cannot see distinctly objects kept beyond 2m. Which among these lens is useful to correct the defect
a) – 0.2D
b) – 0.5 D
c) + 0.2D
d) +0.5D?
Answer:
The person is suffering from Myopia.
The lens is concave and its focal length f = – 2m.
\(P=\frac{1}{5}=\frac{1}{-2}=-0.5 D\)
So to correct the defect concave lens of – 0.5 D power should be used (b).

Question 85.
Express the power of concave lens of focal length 20 cm with its sign.
Answer:

10th Class Physics 7th Lesson Human Eye and Colourful World 2 Marks Important Questions and Answers

Question 1.
How do you appreciate the working of iris in the eye? (AP June 2018)
Answer:
Iris helps in controlling the amount of light entering the eye through pupil.

Question 2.
What is the reason for the blue colour of the sky? (AP March 2018)
How do you appreciate the role of molecules in the atmosphere in this regard?
Answer:
Blue colour of sky :

1. Atmosphere contains more O₂ and N₂ molacules and they are caused to blue colour of the sky.
2. The size of molecules of O₂ and N₂ are comparable with the blue colour and scatter blue colour only.

Role of molecules in the atomosphere in scattering :

1. Light of certain frequency falls on that atom or molecule.
2. This molecule responds to the light whenever the size of the molecule is comparable to the wavelength of light and vibrates.
3. Due to these vibration, molecule reemits a certain fraction of absorbed energy in all directions. The emitted light is called scattered light.
4. The atoms or molecules are called scattering centres.
5. I appreciate the role of the molecules in scattering.

Question 3.
In which conditions does a rainbow form? Why? (TS June 2015)
Answer:
1) Rainbow forms and appears when,
i) tiny water droplets present in the atmosphere (after rain shower),
ii) sunlight falls on the droplets,
iii) observer watches the rainbow in a specific direction.
2) Rainbow forms due to dispersion of sunlight by tiny droplets, present in the atmosphere, which acts as small prisms.

Question 4.
Draw the ray diagram, showing the correction of defect of vision hyper metropia by using a convex lens. (TS June 2016)
Answer:

Question 5.
Least distance of distinct vision of a person is observed as 35 cm. What lens is useful for him to see his surroundings clearly? Why? (TS March 2016)
Answer:
The least distance of distinct vision is 35 cm. This is more than the least distance of distinct vision of an ordinary person. Hence the person is suffering from Hypermetropia. He has to use double convex lens to see his surroundings clearly.

Question 6.
What happens, if Ciliary muscles do not perform contraction and expansion? Guess and write. (TS June 2018)
Answer:

1. If Ciliary muscles do not perform contraction and expansion, foal length of eye lens do not change.
2. Human eye can see the objects at specific distance only, eye cannot see the object either nearer or far distance.

Question 7.
Write any two situations to observe dispersion of light in your daily life. (TS June 2018)
Answer:
We can observe the dispersion of light in the following situations in our daily life.

1. In the formation of rainbow.
2. When observing sun light through the triangular transparent material like prism, scale edge.
3. At the time of curing of walls of new houses with water.
4. Dispersion of light by inclained plane mirror which is in water.

Question 8.
Write the material that you use to find out the value of refractive index of a prism. What is the necessity of the graph in this experiment? (AP March 2019)
Answer:
The material used to find out the value of refractive index of a prism:
Prism, Piece of white chart, Pencil, Pins, Scale and Protractor.

Necessity of the graph :
To find the angle of minimum deviation graph is required.

Question 9.
Draw a ray diagram showing the correction of myopia eye defect. (TS March 2019)
Answer:
Diagram of Myopia correction :
Note : Draw the diagram using Bi Concave Lens and show the far point (M). Image should form on Retina.

Question 10.
What happen if dispersion and scattering of light do not occur? (TS March 2019)
Answer:
If dispersion does not occur in nature, then there is no rainbow formation and splitting of light into seven different colors. If there is no scattering then the oceans and sky appears to be black. The sun appears white all the time (Including Sunrise and Sunset).

Question 11.
When Mohan viewed white light through a transparent scale, he observed some colours. Predict and write the phenomenon involved in his observation. (AP SCERT: 2019-20)
Answer:

1. The phenomenon involved in his observation is dispersion of light.
2. Splitting of white light into different colours (VIBGYOR) is called dispersion.

Question 12.
A boy who is suffering from eye defect has been given a prescription as -2D. Based on the information given, answer the following questions.
a) Identify the eye defect he is suffering.
b) Write the nature and focal length of the lens. (AP SCERT: 2019-20)
Answer:
a) The boy is suffering from myopia.
b) Nature of the lens :
The lens is biconcave lens.
It is thin at the middle and thicker at the edges.
Focal length of the lens :
Given that power is – 2D

Question 13.
How does eye lens change its focal length? (AP SA-I:2019-20)
Answer:

• Eye lens changes its focal length by the ciliary muscle attached to it.
• By relaxing ciliary muslces, the focal length of the eye lens is reached its maximum value.
• By straining ciliary muscles, the focal length of the eye lens is reached its minimum value.

Question 14.
Kishore wore spectacles. When you saw through his spects the size of his eyes seemed bigger than their original size.
a) Which lens did he use?
b) Explain that defect of vision.
Answer:
a) When we saw through Kishore’s spects the size of his eyes seemed bigger than their original size. This is possible with convex lens only because magnification of the lens is greater than T.

b) The defect he suffers is hypermetropia. This is also called farsightedness.

A person who suffers with this type of defect, he can’t see the objects clearly which are placed near distance because the image is formed beyond the retina. So by using convex lens the rays can be converged on retina.

Question 15.
“God has given the gift for us to see the sunrise and sunset.” Explain the feeling of it.
Answer:

• The sun is visible two minutes before the actual sunrise and remains visible two minutes after the actual sunset.
• The actual sunrise takes place when the sun is just above the horizon.
• The actual sunset takes place when the sun is just below the horizon.

Question 16.
“Smoke coming out of coal fired chimney appears blue on a misty day.” Why?
Answer:

• On a misty day, the air has large amount of tiny particles of water droplets, dust and smoke.
• These tiny particles present in the air scatter blue colour of the white light passing through it.
• When this scattered blue light reaches our eyes the smoke appears blue.

Question 17.
“Motorists use orange light on a foggy day rather than normal white light.” Why?
Answer:

• On a foggy day, the air has large amount of water droplets.
• If a motorist uses white light, the water droplets present in the air scatter large amount of the blue light.
• This on reaching our eyes decreases visibility and hence driving becomes extremely difficult.
• Whereas orange light has longer wavelength and hence it is least scattered.

Question 18.
A rainbow viewed from an airplane may form a complete circle. Where will the shadow of the airplane appear? Explain.
Answer:

• A rainbow viewed from an airplane form a complete circle because the earth does not come along the way of the airplane and rainbow.
• A rainbow is a three dimensional cone of dispersed light it appear as a complete circle.
• The shadow of the airplane appears within the circle of the rainbow.

Question 19.
How do we see colours?
Answer:

• The retina of human eye has a large number of receptors.
• These receptors are of two types i.e., rods and cones.
• The rod cells recognise the colour of light rays, while the cones identify the intensity of light.
• It is these cone cells, which make it possible for a men to see different colours and distinguish between them.

Question 20.
Why do we use lenses in spectacles to correct defects of vision?
Answer:
The process of adjusting focal length is called “accommodation”. This process has to be done by eye itself. Sometimes the eye may gradually lose its power of accommodation. In such condition, the person cannot see the object clearly and comfortably. In this situation, we have to use lenses in spectacles to correct defects of vision.

Question 21.
What is a) far point of the eye and b) near point of the eye?
Answer:
a) The farthest point up to which the eye can see objects clearly without strain (in the eye) is called the far point of the eye. For a normal eye, the far point is at infinity.

b) The minimum distance at which objects can be seen most clearly without strain (in the eye) is called the least distance of distinct vision or the near point of the eye.

Question22.
Write the difference between “Myopia” and “Hypermetropia”.
(OR)
Distinguish between Myopia and Hypermetopia.
Answer:
The eye defect in which people cannot see at long distances but can see nearby objects clearly is called Myopia. The eye defect in which people cannot see near distant objects but can see distant objects is called hypermetropia.

Question 23.
Define the following words.
a) Prism
b) Dispersion of light
c) Scattering of light
Answer:
a) Prism :
A prism is a transparent medium separated from the surrounding medium by at least two plane surfaces which are inclined at a certain angle.

b) Dispersion of light :
The splitting of white light into different colours is called dispersion of light.

c) Scattering of light:
The process of reemission of absorbed light in all directions with different intensities by atoms or molecules is called scattering of light.

Question 24.
Define the words associated with prism with the help of figure.

1) Angle of incidence :
The angle between incident ray and normal is called angle of incidence.

2) Angle of emergence :
The angle between normal and emergent ray is called angle of emergence.

3) Normal:
Perpendicular drawn to the surface of prism.

4) Angle of deviation:
The angle between extended incident ray and emergent ray is called angle of deviation.

Question 25.
State the cause of dispersion, when white light enters a glass prism. Explain with a diagram.
Answer:

• Light is made up of different colours. Each colour travels at its own speed inside a prism.
• Due to this different colours of light bends through different angles with respect to the incident ray, as it passes through a prism.
• The red light bends the least while the violet most.
• Thus, the rays of each colour emerge along different paths and become distinct.
• It is the bond of distinct colours that we see in a spectrum.

Question 26.
What happens to the lens and the ciliary muscles when you are looking at distant objects and near objects?
Answer:
a) The ciliary muscles become relaxed and the lens becomes thin, i.e. its radius of curvature increases. So focal length of eye lens increases for distant object.

b) The ciliary muscles contract and the lens becomes thick, i.e. its radius of curvature decreases. So focal length of eye lens decreases for near objects.

Question 27.
Why does it take some time to see objects in cinema hall when we just enter the hall from bright sunlight? Explain in brief.
Answer:

• The pupil regulates and controls the amount of light entering eye.
• In bright sunlight, the size of pupil is small and when we enter the cinema hall it takes some time for the pupil to expand in size due to dim light.

Question 28.
What are the factors which influence the total angle of deviation?
Answer:

• The angle of incidence at the first surface (i).
• The angle of prism (A).
• Refractive index of the material.

Question 29.
How does eye change its focal length take place in the eyeball?
Answer:

• Eye lens changes its focal length by the ciliary muscle attached to it.
• By relaxing ciliary muslces, the focal length of the eye lens is reached its maximum value.
• By straining ciliary muscles, the focal length of the eye lens is reached its minimum value.

Question 30.
Stars twinkle while planets do not. Why?
Answer:
1) Continuously changing atmosphere refracts light from the stars by different amounts from one moment to the other, when atmosphere refracts more starlight towards us and the stars appear to be bright and when the atmosphere refracts less star-light then the stars appear to be dim.

2) However the planets are nearer to us than the stars, they appear to be comparatively bigger to us so they cannot be considered as a point source, hence no twinkling is seen.

Question 31.
How do earth and stars appear for a person who is on the moon?
Answer:

• For the person who is on the moon, the earth appears blue due to blue colour of sunlight scattered by the earth’s atmosphere reaching him.
• Stars and other heavenly bodies are seen as usual, but without twinkling.

Question 32.
Why does the sky appear dark and black to an astronaut instead of blue?
(OR)
Why does the sky appear dark to the passenger flying at high altitudes?
Answer:

• This is because there is no atmosphere containing air in the outer space to scatter light.
• Since there is no scattered light which can reach our eyes in outer space, the sky looks dark and black there.
• This is why the astronauts who go to outer space find the sky to be dark and black instead of blue.

Question 33.
A person is able to see objects clearly only when these are lying at distance between 60 cm and 250 cm from his eye. What kind of defect of vision is he suffering from?
Answer:
For a normal eye, the near point is at 25 cm and the far point is at infinity. The given person cannot see object clearly either close to the eye or far away from the eye. So he is suffering from presbyopia.

Question 34.
Write the material required in finding the refractive index of a prism.
Answer:
Materials required:
Prism, piece of white chart of size 20 x 20 cm, pencil, pins, scale and protractor.

Question 35.
Draw the graph between angle of incidence and angle of deviation.
Answer:

Question 35.
Draw the diagram of scattering of sunlight.
Answer:

Question 35.
How do you appreciate the “Eye Donor”?
Answer:
The human eye is one of the most important sense organs. Without eye we are unable to see the beautiful world. So we have to appreciate “eye donor” for his kindness to give sight to blind people.

Question 36.
How can we appreciate the working of “Iris”?
Answer:

• Iris consists of muscles which help in controlling the amount of light entering the eye through pupil.
• In case of low light the iris makes the pupil to expand and allow more light to enter the eye.
• In case of bright or excess light the iris makes the pupil to contract in order to decrease the amount of light entering the eye. The iris consists of muscles that expand and contract the pupil.

Question 37.
The power of lens is 2.0 D. Find its focal length and state what kind of lens it is.
Answer:
P = \(\frac{1}{f}\) (f in metres)
Given P = 2D
∴ f= \(\frac{1}{P}\) = \(\frac{1}{2}\) = 0. 5 m = 50 cm.
The focal length positive indicates it is a convex lens.

Question 38.
Two convex lenses of powers 1D and 2D are combined together to form a new lens. Then what is the resultant power and focal length of lens?
Answer:
P₁ = 1 D ; P₂ = 2D
Resultant power P = P₁ + P₂ = 1 + 2 = 3D
P = \(\frac{1}{f}\) (f in metres)
∴ f= \(\frac{1}{P}\) = \(\frac{1}{3}\) = 0.3333 m = 33.33 cm.

Question 40.
Figure shows the refraction of light through an equilateral prism. Incident at an angle of 30°. The ray suffers a deviation of 37°. What are the angles marked at A, e and f respectively?
Answer:

Since the prism is an equilateral prism,
A = 60°, also D = 37° and i = 30° (i.e., i₁), e = i₂ = ?
We know that i₁ + i₂ = A + D
30° + e = 60 + 37
e = 97 – 30 = 67°
Also A + f = 180°
f = 180°-60° = 120°

10th Class Physics 7th Lesson Human Eye and Colourful World 4 Marks Important Questions and Answers

Question 1.
Kavya can see distant objects clearly but cannot see objects at near distance. With what eye defect is she suffering? Draw the diagrams showing the defected eye and its correction. (AP June 2016)
Answer:
Kavya is suffering from hypermetropia.
The following diagram shows the defective eye and its correction.

Question 2.
Revathi is a front bench student. She is unable to draw the picture drawn on the blackboard. She got permission from the teacher and sat in the back row. What could be the defect that Revathi is suffering from? Draw the diagram, which shows the correction of the above defect? (AP Mareh 2017)
Answer:
Hypermetropia

Question 3.
An eye specialist suggested a + 2D lens to the person with defect in vision. Which kind of defect in vision does he have? Draw the diagrams to show the defect of vision and its correction with a suitable lens. (TS June 2017)
Answer:
Eye specialist suggested +2D lens, that is convex lens is used to correct Hypermetropia. So the person has Hypermetropia.
Deffect of Vision:

Correction :

Question 4.
How will you calculate the focal length of a biconvex lens that is used to correct the defect of Hypermetropia? Explain it mathematically. (TS March 2017)
Answer:
The person who has hypermetropia cannot see near objects. He can see the objects those are beyond near point (H). For correction of this eye defect the image of the object placed at “least distance of distinct vision (L)” should be at near point (H).
u = -25 cm; v = -d cm

here d > 25, so ‘f gets positive value.
Hence, convex lens should be used.

Question 5.
Mention the required material and chemicals for the experiment of “scattering of light.” Write the experiment procedure. (TS March 2018)
(OR)
Write the required apparatus and chemicals to show the scttering of light experimentally and write the experimental process.
(OR)
How can you demonstrate scatteing of light by an experiment?
Answer:
Aim :
To show the scattering of light.

Material required :
Beaker, sodium thiosulphate, sulphuric acid.

Procedure:

1. Take a solution of sodium-thio-sulphate (hypo) and sulphuric acid in a glass beaker.
2. Place the beaker in an open place where abundant sun light is available.
3. Watch the formation of grains of sulphur and observe the changes in the beaker.
4. We will notice that sulphur participates as the reaction is in progress. At the beginning, the grains of sulphur are smaller in size and as the reaction progress, their size increases due to precipitation.
5. Sulphur grains appear blue in colour at the beginning and slowly their colour becomes white as their size increases.
6. The reason for this is scattering of light.
7. At the beginning, the size of grains is small and almost comparable to the wavelength of blue light. Hence they appear blue in colour.
8. As the size of grains increases, their size becomes comparable to wavelength of other colours.
9. As a result, they acts as scattering centres of all colours.

Question 6.
A boy has been playing games in mobile phone and is suffering from eye defect. The doctor prescribed him to use spectacles of power – 5D. What eye defect is he suffering from? (AP SA-I:2018-19)
Draw a neat diagram which shows the correction of above eye defect.
Answer:
Doctor suggested the boy – 5D lens, that is concave lens. Concave lens is used to correct myopia. So the boy has myopia.
Defect of Vision :

Correction:

Question 7.

Answer the following questions from the above information. (TS June 2019)
i) What is the defect of vision in ‘D’ suffering from? Why does it happen?
ii) Whose defect of vision can be corrected by using Biconcave lens?
iii) Who is suffering with similar defect of vision as of ‘B’?
iv) Who among the above do not have any defect of vision?
Answer:
i) 1) The vision defect of person ‘D’ is presbyopia.
2) Presbyopia happens due to gradual weakening of ciliary muscles and diminishing flexibility of the eye lens. This effect can be seen in aged people.
ii) Person A’ defect of vision can be corrected by using Biconcave lens.
iii) Person ’C’ is suffering with similar defect of vision as of ’B’.
iv) Person ‘E’ has no defect of vision.

Question 8.
A prism causes dispersion of white light while a rectangular glass block does not. Explain.
Answer:

• In a prism the refraction of light occurs at two plane surfaces.
• The dispersion of white light occurs at the first surface of prism where its constituent colours are deviated through different angles.
• At the second surface, these split colours suffer only refraction and they get further separated.
• But in a rectangular glass block, the refraction of light takes place at the two parallel surfaces.
• At the first surface, although the white light splits into its constituent colours on refractions, but they split colours on suffering refraction at the second surface emerge out in the form of a parallel beam, which gives an impression of white light.

Question 9.
A convex lens of power 4D is placed at a distance of 40 cm from a wall. At what distance from the lens should a candle be placed so that its image is formed on the wall?
Answer:

So candle should be placed 66.66 cm from the lens.

Question 10.
Explain briefly the reason for the blue of the sky.
Answer:

• Our atmosphere contains different types of molecules and atoms.
• The reason for blue sky is the molecules N₂ and O₂.
• The sizes of these molecules are comparable to the wavelength of blue light.
• These molecules act as scattering centres for scattering of blue light.

Question 11.
What happens to the image distance in the eye when we increase the distance of an object from the eye?
Answer:

• For a normal eye, image distance in the eye is fixed.
• This is equal to the distance of retina from the eye lens.
• When we increase the distance of the object from the eye, focal length of eye lens is changed on account of power of accommodation of the eye so as to keep the image distance constant.

Question 12.
A person is able to see objects clearly only when they are lying at distance between 60 cm and 250 cm from his eye. What kind of lenses will be required to increase his range of vision from 25 cm to infinity? Explain.
Answer:
A bi-focal lens consists of concave and convex lens of suitable focal lengths will be required to correct the defect and to increase his range of vision from 25 cm to infinity. In bi-focal lens, the upper half of the lens is concave lens which corrects distant vision and the lower half is convex which corrects near vision.

Question 13.
Discuss why sun is visible before actual sunrise and after actual sunset?
Answer:

• The sun is visible to us about 2 minutes before the actual sunrise and 2 minutes after the actual sunset because of atmospheric refraction.
• By actual sunrise we mean the actual crossing of the horizon by the sun.

• Figure shows the actual and apparent positions of the sun with respect to the horizon.
• The time difference between actual sunset and the apparent sunset is about 2 minutes.
• The apparent flattering of the sun’s disc at sunrise and sunset is also due to the same phenomenon.

Question 14.
When does the colour of sky appear black for an observer?
Answer:

• In the absence of atmosphere, there will not be any scattering of light and so light will reach our eye, i.e. the sky will appear black instead of blue at night in the absence of light.
• On the moon, since there is no atmosphere, there is no scattering of sunlight reaching the moon surface. Hence to an observer on the surface of moon, no light reaches except the light directly from sun. Thus sky will have no colour and will appear black to an observer on the moon surface. This is applicable for any planet which does not have atmosphere.
• When an astronaut goes above the atmosphere of the earth in rocket he sees the sky black.

Question 15.
Why does the colour of clouds appear black?
Answer:

• The clouds are nearer the earth surface and they contain dust particles and aggregates of water molecules of size bigger than the wavelength of visible light.
• Therefore, the dust particles and water molecules present in clouds scatter all colours of incident white light from sun to the same extent and hence when the scattered light does not reach our eye, the clouds seem black.

Question 16.
Give daily life examples of scattering of light by earth’s atmosphere.
Answer:
Some daily life effects of scattering of sunlight by earth’s atmosphere are

1. Red colour of sun at sunrise and sunset.
2. White colour of sky at noon.
3. Blue colour of sky is due to molecules N₂ and O₂.
4. Black colour of sky is due to the absence of atmosphere.
5. Use of red light for the danger signal because it is least scattered by particles due to its greater wavelength.
6. White colour of clouds is due to rise in temperature.

Question 17.
What is the relation between scattering and wavelength of light? Explain.
Answer:

• Scattering is the process of absorption and then re-emission of light energy.
• The air molecules of size smaller than the wavelength of incident light absorb the energy of incident light and then re-emit it without change in its wavelength.
• The intensity of scattered light is found to be inversely proportional to fourth power of wavelength of light.
• The wavelength of violet is least and red light is most, therefore from the incident white light, violet light is scattered the most and red light is scattered the least.

Question 18.
How can we get this (in human eye) same image distance for various positions of objects?
Answer:

• The ciliary muscle attached with eye lens helps to change the focal length of eye lens.
• When the eye is focussed on a distant object, these are relaxed. So the focal length of eye lens increases to its maximum value.
• F_(max) – 2.5 cm,u = oo, v = 2.5 cm. The parallel rays coming from a distant object are focussed on the retina with 2.5 cm image distance.
• When the eye is focussed on a nearer object the muscles are strained. So the focal length of the eye lens decreases its minimum value.
• F_(min)= 2.27 cm, u = 25 cm, v = 2.5 cm. The rays from an object (u = 25 cm) at L (point of least distance of distinct vision) are focussed on the retina with 2.5 cm image distance.

Question 19.
Does eye lens form a real image or virtual image? Explain it.
Answer:

• Eye lens forms a real image.
• The light that enters the eye forms an image on the retina.

• The image is obtained on a screen (retina) and it is an inverted image.
• So, we can say eye lens forms a real image.

Question 20.
How does the image formed on retina help us to perceive the object without change its shape, size and colour?
Answer:

• The eye-lens forms a real and inverted image of an object on the retina.
• The retina is a delicate membrane which contains about 125 million receptors called ‘rods’ and ‘cones’ which receive the light signals.
• Rods identify the colour.
• Cones identify the intensity of light.
• These signals are transmitted to the brain through about 1 million optic nerve fibres.
• The brain interprets these signals and finally processes the information so that we perceive the object in terms of its shape, size and colour.

Question 21.
How do you prove that a prism does not produce colours itself?
Answer:

• A white light from a slit ‘S’ is made to pass through prism P which forms spectrum on a white screen AB.
• A narrow slit H is made on the screen AB, parallel to slit S to allow the light of particular colour to pass through it.
• The light of a particular colour is made to fall on the second prism Q placed with its base in opposite direction to that of the prism P.
• The light after passing through the second prism Q is received on another white screen M.
• It is observed that the colour of light obtained on the screen M is same as that of the light incident on the second prism Q through the slit H.

Question 22.
Draw the structure of human eye and explain its parts.
Answer:

Question 23.
What is the part indicated by an arrow mark? What is its working function?
Answer:

• The part indicated by the arrow mark is ciliary muscle.
• Ciliary muscles help to change the focal length of the eye lens.
• When it relaxes the focal length of the eye lens is maximum.
• When it strains, the focal length of the eye lens is minimum.
• In this way the ciliary muscles to which eye lens is attached help to give us clear vision.

Question 24.
Two observers standing apart from each other do not see the “same” rainbow. Explain.
Answer:

• All the rain drops that disburse the light to form rainbow lie within a cone of semi vertical angle 40° to 42°.
• If two observers are standing at a distance apart, they will observe rainbow at different parts on the surface of the cone.
• So the portion of the rainbow observed by an observer depends on the position of the observer.
• Two different observers will form two different cones with the observer standing at the vertex of the cone, therefore rainbow seen by them will be different.

Question 25.
A prism with an angle A = 60° produces an angle of minimum deviation of 30°. Find the refractive index of material of the prism.
Answer:
Given, A = 60° and D = 30°

Question 26.
A person cannot see the objects distinctly, when placed at a distance less than 50 cm. Calculate the power and nature of the lens he should be using to see clearly the object placed at a distance of 25 cm from his eyes.
Answer:

Question 27.
A person cannot see the objects distinctly, when placed beyond 2 m.
Calculate the power and nature of the lens he should be using to see the distant objects clearly.
Answer:
For myopia the focal length = – far point distance = – 2m
Power = \(\frac{1}{\mathrm{f}}=\frac{1}{-2}\) = 0.5 D.

AP State Board Syllabus AP SSC 10th Class Physical Science Important Questions Chapter 6 Refraction of Light at Curved Surfaces.

AP State Syllabus SSC 10th Class Physics Important Questions 6th Lesson Refraction of Light at Curved Surfaces

10th Class Physics 6th Lesson Refraction of Light at Curved Surfaces 1 Mark Important Questions and Answers

Question 1.
Suppose you are inside the water in a swimming pool. Your friend is standing on the edge. Do you find your friend taller or shorter than his actual height? Why? (AP June 2018)
Answer:
Friend is seemed to be taller. Because of refraction of light.

Question 2.
What happens to the image, if a convex lens is made up of two different transparent materials as shown in figure? (TS March 2016)

Answer:
The convex lens is made up of two different materials. So the refractive i these two materials will be different. Hence two images will be formed.

Question 3.
Write the list of materials required for the experiment to find the focal length of a convex lens. (TS June 2017)
Answer:
Convex Lens, Scale, Piece of paper, Sunrays.
(OR)
Convex Lens, V-Stand, Candle, Match box, Screen, Scale.

Question 4.
Complete the following ray diagram. (TS March 2019)

Answer:

The parallel rays coming with some angle to principal axis meet on focal plane.

Question 5.
If the object is placed between the focal point and the optical centre of a convex lens, what will be the characteristics of the image formed? (AP SA-1:2019-20)
Answer:
Object is placed between F₂ and optic centre P :

Nature :
Virtual, erect and magnified.

Position :
Same side of the lens where object is placed.

Question 6.
For a concave lens, what type of image will be formed if the object is placed at the centre of curvature? (AP SA-1:2019-20)
Answer:
Same size of object, inverted and real image will be formed.

Question 7.
Write lens formula. (AP SA-I:2019-20)
Answer:
\(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\)

Question 8.
What is a lens? (or) Define lens.
Answer:
A lens is formed when a transparent material is bounded by two spherical surfaces.

Question 9.
What is a double convex lens?
The lens having two spherical surfaces bulging outwards is called double convex lens.

Question 10.
What about the thickness of double convex lens?
Answer:
It is thick at the middle as compared to edges.

Question 11.
What is a double concave lens?
Answer:
The lens having two spherical surfaces curved inward is called a double concave lens.

Question 12.
Write about the thickness of concave lens.
Answer:
It is thin at the middle and thicker at the edges.

Question 13.
What is centre of curvature?
Answer:
The centre of sphere which contains the part of curved surface is called centre of curvature.

Question 14.
What is radius of curvature?
Answer:
The distance between the centre of curvature and curved surface is called radius of curvature.

Question 15.
What is the mid point of lens called?
Answer:
The mid point of lens is called pole (or) optical centre.

Question 16.
What is a focus?
Answer:
The point where rays converge or the point from which rays seem emanate is called focal point (or) focus.

Question 17.
What is the distance between pole and focal point called?
Answer:
Focal length.

Question 18.
What happens if the ray passes through principal axis?
Answer:
It will be undeviated.

Question 19.
Where do light rays travelling to principal axis converge?
Answer:
They converge at focus.

Question 20.
What happens to light rays passing through focus?
Answer:
The path of the rays is parallel to principal axis after refraction.

Question 21.
What is a focal plane?
Answer:
A plane which is perpendicular to principal axis at the focus is called focal plane.

Question 22.
What is lens formula?
Answer:
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)

Question 23.
On what factor does focal length of a lens depend?
Answer:
It depends on refractive index of the medium, object distance and image distance.

Question 24.
What is lens maker formula?
Answer:
\(\frac{1}{\mathrm{f}}=(\mathrm{n}-1)\left(\frac{1}{\mathrm{R}_{1}}-\frac{1}{\mathrm{R}_{2}}\right)\)

Question 25.
What happens to be image formed by a convex lens if its lower part is blackened?
Answer:
Every part of a lens forms a complete image. If the lower part of the lens is blackened the complete image will be formed but its intensity will be decreased.

Question 26.
From which point of lens are all the distances are measured?
Answer:
The optical centre of lens.

Question 27.
Is it possible for a lens to Act as a convergent lens in are medium and a divergent lens in another?
Answer:
Yes. A convergent lens is placed in a higher refractive index of medium the nature of the lens changes i.e., it acts as divergent lens.

Question 28.
What are paraxial rays?
Answer:
The rays which move very close to the principal axis which can be treated as parallel are called paraxial rays.

Question 29.
What is absolute refractive index?
Answer:
It is the ratio of speed of light in air to speed of light in any medium.

Question 30.
Give mathematic expression for power lens and explain the terms in the formula.
Answer:
Power (P) = \(\frac{1}{f}\)
where f is focal length of lens.

Question 31.
If the size of image is same as object through a convex lens, then where is the object placed?
Answer:
The object is placed at centre of curvature.

Question 32.
How will you identify a concave lens by touching it?
Answer:
A concave lens is thinner at centre and thicker at edges.

Question 33.
How will you identify a convex lens by touching it?
Answer:
A convex lens is thicker at centre and thinner at edges.

Question 34.
Give the sign conventions for lenses with regard to the object and image distance.
Answer:
The distance measured in the direction of incident ray is taken as positive.
The distance measured against the direction of incident ray is taken as negative.

Question 35.
Give the sign conventions for lenses with regard to the height of objects and images.
Answer:
All the heights of objects and images above principal axis are positive and below the axis are negative.

Question 36.
When light of two colours A and B passes through a plane boundary, A is bent more than B. Which colour travels more slowly in the second medium?
Answer:
Colour A travels slowly.

Question 37.
What type of lens behaviour will an air bubble inside water show?
Answer:
It will act as a concave lens.

Question 38.
Is it possible for a lens to act as a convergent lens in one medium and a divergent lens in another?
Answer:
Yes. A lens is placed in a medium of a high refractive index than that of the lens then nature of lens changes (M_L > M_g).

Question 39.
The image formed by a lens is always erect and diminished. What is the nature of lens?
Answer:
Given that the lens is forming an image which is always erect and diminished. So it is virtual also. Such type of image is formed by concave lens.

Question 40.
If a student observed an image of same size with a convex lens of focal length 20 cm, then where should he keep the object in front of lens?
Answer:
Because the student got image of same size the object should be placed at a distance of twice the focal length, i.e. 40 cm.

Question 41.
For an object placed at a distance of 20 cm in front of convex lens, the image formed is at a distance of 20 cm behind the lens. Find the focal length of lens.
Answer:
The object distance and image distance are same. So the object is kept at twice the focal length. So the focal length of the convex lens is 10 cm.

Question 42.
A doctor suggested spectacles for a student which has negative focal length. Which type of lens is that?
Answer:
Focal length negative indicates that it is a concave lens.

Question 43.
What happens to a light ray which passes through optical centre?
Answer:
The light ray which passes through optical centre does not deviate.

Question 44.
When do you get image at infinity with a convex lens?
Answer:
When the object is at the focal point.

Question 45.
When do you get a virtual image with a convex lens?
Answer:
When the object is placed between focus and pole.

Question 46.
Is focal length of a lens zero? If not, why?
Answer:
No, focal length of lens never equals to zero because it is the distance between focal point and optical centre.

Question 47.
A thin lens has a focal length of 12 cm. Is it a convex leps or a concave lens?
Answer:
It is a convex lens, because f is positive.

Question 48.
Name the different apparatus where we are using the convex and concave lenses.
Answer:
The magnifying lense, telescope, microscope.

Question 49.
Draw the given diagram in your answer book and complete it for the path of ray of light beyond the lens.

Answer:

Question 50.
The diagram below shows two incident rays P and Q which emerge as parallel rays R and S respectively. The appropriate device used in the box is ……..

Answer:
The rays are diverging and they produced the parallel from the device after refraction. So the device is concave lens.

Question 51.
The following figure shows the incident and refracted rays pass through a lens kept in the box. Draw the lens and complete the path of rays.

Answer:
The incident rays 1 and 2 have converged after refraction. So the lens is convex.

10th Class Physics 6th Lesson Refraction of Light at Curved Surfaces 2 Marks Important Questions and Answers

Question 1.
A convex lens is made of five different materials as shown in the figure. How many images does it form? Why? (AP March 2017)

Answer:
The given convex lens is made up of five different materials.
So they have different refractive indices / different focal lengths.
Hence they form five different images.

Question 2.
The focal length of a converging lens is 20cm. An object is 60cm from the lens. Where will be image be formed and write characteristics of the image. (AP March 2018)
Answer:
Focal length = f = 20 cm (+ 20cm)
Object distance = u = 60 cm (- 60cm)
Image distance = v = ?

Here, (-) indicates inverted images.
m = \(\frac{1}{2}\) < 1 indicates diminished image.
Image forms between F₁ and 2F₁.
Characteristics of the image :

1. real
2. inverted
3. diminished.

Question 3.
When a light rays enters a medium with refractive index n2 from a medium with refractive index n, at curved interface with radius of curvature R is given by
\(\frac{\mathbf{n}_{2}}{\mathbf{v}}-\frac{\mathbf{n}_{1}}{\mathbf{u}}=\frac{\mathbf{n}_{2}-\mathbf{n}_{1}}{\mathbf{R}}\)
Now assume that the surface is plane and rewrite the formula with suitable changes.
Answer:
Assume that the interface is plane surface
Then R becomes infinity
R = ∞ (or) R = 1/0
Substitute the above value in the given equation

Question 4.
Two convex lenses of same focal length are fixed in a PVC pipe at a distance double to their focal length. What happens if a boy sees the moon with that arrangement? (TS March 2017)
Answer:

• The rays coming from moon are parallel. The first lens converges the rays at focus.
• The converging point is the focus of second lens. So the second lens convert the diverging rays into parallel.
• Hence, in the rays of moon, there will be no change when we see moon with this arrangement or without this arrangement.

(OR)

This arrangement does not make any difference in the rays coming from moon.
The moon appears same if we see directly or with this arrangement.

Question 5.
Focal length of the lens depends on its surrounding medium. What happens, if we use a liquid as surrounding media of refractive index, equal to the refractive index of lens? (TS June 2018)
Answer:

• When the refractive index of surrounding media is equal to the refractive index of lens, the lens looses its characteristics.
• Lens do not diverge or converge the light.
• Light do not get refracted when it passes through that lens.

Question 6.
Complete the ray diagram given below (TS March 2018)

Answer:

Question 7.
The refractive index of convex lens material is 1.46. The refractive index of Benzene and water is 1.5 and 1.0 respectively. How does the lens behaves when it is kept in Benzene and water? Given and write. (TS March 2018)
Answer:

• When the convex lens with refractive index 1.46 is kept in Benzene with refractive index 1.5, then the lens acts as a diverging lens.
• If the same lens is kept in water whose refractive index is 1, then it acts as a converging lens.

Question 8.
Write the applications of lenses in day to day life. (AP SCERT: 2019-20)
Answer:
Uses of lenses in day to day life :

• Lenses are used for correcting eye defects.
• They are used as magnifying lenses.
• They are used in microscopes, telescopes, binoculars.
• They are used in cinema projectors and cameras.

Question 9.
Water lens is made of double convex lens of radius of curvature “R”. Write lens makers formula for water lens. (AP SA-I: 2019-20)
Answer:
1) Radius of curvatures of water lens are R₁ = R₂ = R and n = 1.5.
2) Sign conversion R₁ = + R₁, R₂ = -R₂.
3) Lens makers formula

Question 10.
Find the focal length of plane convex dens if its radius of curvature is R and its refractive index is n.
Answer:
Given lens is plano-convex lens; radius of curvature = R
Refractive index = n

Question 11.
In a classroom, four friends found out the focal length of a lens by conducting an experiment. The value came out to be 12.1cm, 12.2cm, 12.05 cm, 12.3 cm. The friends discussed the reasons for the differences or defects. Mention those reasons.
Answer:
Students got different focal lengths.

1. By observing the values they got all positive values. This indicates they are given by convex lens.
2. All the students got exact interger but different decimal value.

Reasons :
The difference in values is due to least count errors, parallax errors, random errors and systematic errors, etc.

Question 12.
How will you decide whether a given piece of glass is a convex lens, concave lens or a plane plate?
Answer:
Hold the given piece of glass over some printed matter.

1. If the letters appear magnified, then the given piece of glass is convex lens.
2. If the letters appear diminished, then the given piece of glass is concave lens.
3. If the letters appear to be same size, then it is a plane glass piece.

Question 13.
State the type of lens used as a magnifying glass. Draw a labelled ray diagram to show that the image of the object is magnified.
Answer:

A single convex lens is used as a magnifying glass, i.e. for seeing small object magnified. When the object to be seen in between the focus and optical centre of the lens, a vertical, erect magnified image of the object is formed as shown and convex lens is and to act as magnifying glass AB’ is the magnified image of AB.

Question 14.
Give conventions used in lenses.
(OR)
Write the signs of convex and concave lens using in drawing ray diagrams.
Answer:

• All distances are measured from optical centre of the lens.
• Distances measured along the direction of the incident light are taken as positive.
• The distances against the incident light are taken as negative.
• The heights measured vertically above the axis, are taken as positive.
• The heights measured vertically down the axis, are taken as negative.

Question 15.
A convex lens of focal length 20 cm can produce a magnified virtual as well as real image. Is this a correct statement? If yes, where shall the object be placed in each case for obtaining these images?
Answer:
Yes, the statement is correct.
For magnified virtual image :
The object should be placed between optic centre (C) and focus (F) (< 20)

For magnified real image:
Placed between focus (F) and centre of curvature (2F) (20 – 40)

Question 16.
Sudha finds out that the sharp image of the window pane of her science laboratory is formed at a distance of 15 cm from the lens. She now tries to focus the building visible to her outside the window instead of the window pane without disturbing the lens. In which direction will she move the screen to obtain a sharp image of the building ? What is the approximate focal length of this lens?
Answer:
As the image is real, therefore the lens use is convex lens. The distance of the real image formed by a convex lens from the lens decreases as the object distance from the lens increases. Hence, the screen has to be moved towards the lens to obtain the sharp image of the building. Approximate focal length of the lens =15 cm as the rays of light coming the window pane are considered to come from infinity. These rays of light are focussed by the convex lens at its focus, (i.e. on the screen).

Question 17.
What do you see when your friend brings a sheet of paper on which arrow was drawn behind the empty cylindrical shaped transparent vessel? Why do you see a diminished image?
Answer:
We will see a diminished image of the arrow.

When the vessel is empty, light from the arrow refracts at the curved interface, moves through the glass and enters air, then it again undergoes refraction curved surface of the vessel and comes out into the air. In this way, light travels in two media, comes out of the vessel and forms a diminished image.

Question 18.
Using the formula of refraction at curved surfaces, write the formula for plane surfaces.
Answer:
For curved surfaces the formula for refraction is \(\frac{\mathrm{n}_{2}}{\mathrm{v}}-\frac{\mathrm{n}_{1}}{\mathrm{u}}=\frac{\left(\mathrm{n}_{2}-\mathrm{n}_{1}\right)}{\mathrm{R}}\)

For plane surface, the radius of curvature (R) approaches infinity. Hence 1/R becomes zero.
\(\frac{\mathrm{n}_{2}}{\mathrm{v}}-\frac{\mathrm{n}_{1}}{\mathrm{u}}=0 \Rightarrow \frac{\mathrm{n}_{2}}{\mathrm{v}}=\frac{\mathrm{n}_{1}}{\mathrm{u}}\)

Question 19.
Explain how a convex lens behaves on converging lens and diverging lens.
Answer:
The convex lens behaves as a converging lens, if it is kept in a medium with refractive index less than the refractive index of the lens. It behaves like a diverging lens when it is kept in transparent medium with greater refractive index than that of lens.
e.g. : Air bubble in water behaves like a diverging lens.

Question 20.
When does Snell’s law fail?
Answer:

• Snell’s law fails when light is incident normally on the surface of refracting medium.
• Both media have same refractive index.

Question 21.
If on applying sign convention for lens the image distance obtained is negative, state the significance of negative sign.
Answer:

• Negative sign of image distance means the image is virtual and erect.
• It is formed on the same side of the object with respect to lens.

Question 22.
Magnification of lens is found to be +2. What type of lens is that?
Answer:
Magnification +ve indicates the image is erect and virtual.
Magnification 2 indicates it is magnified.
Magnified virtual image is formed by only convex lens.

Question 23.
For same angle of incidence in media A, B and C the angle of refractions are 30°, 25° and 20° respectively. In which medium will the velocity of light be minimum?
Answer:
In medium R the velocity of light is minimum because it has greater refractive index. Refractive index and velocity of light in a medium are inversely proportional. So in medium R the velocity is minimum.

Question 24.
The radius of curvature (twice the focal length) of a convex lens is 40 cm. A student wants to get various images of following types (a) enlarged virtual image, (b) enlarged real image, (c) image of same size, (d) diminished image.
In order to get these images where should the object should be kept in front of convex lens?
Answer:
a) The object should be kept in less than 20 cm (i.e. less than focal length).
b) In order to get enlarged real image, object should be kept between 20 cm to 40 cm in front of lens.
c) In order to get image of same size object should be kept at a distance of 40 cm from the lens.
d) In order to get diminished image the object should be kept beyond 40 cm from the lens.

Question 25.
A convex lens of focal length 20 cm can produce a magnified virtual as well as real image. Is this a correct statement? If yes, where shall the object be placed in each case for obtaining these images.
Answer:

• Yes, the statement is correct.
• A convex lens of focal length 20 cm will produce a magnified virtual image if object is placed at a distance less than 20 cm from the lens.
• A convex lens of focal length 20 cm will produce magnified real image if the object is placed at a distance more than 20 cm and less than 40 cm.

Question 26.
A concave mirror and a convex lensare held in water. What changes, if any, do you expect in their focal length?
Answer:
The focal length of a concave mirror independent of the medium and A convex lens depends on medium when they are placed in water.
The focal length of the mirror – Does not change.
The focal length of the convex lens – Changes (means increases 4 times).

Question 27.
When does a convex lens behave like a diverging lens? Given example.
Answer:
A Convex lens behaves like a diverging lens when it is kept in a tranparent medium with greater refractive index than that of the lens.
Eg : An air bubble in water behaves like a diverging lens.

Question 28.
A pond appears to be shallower than it really is when viewed obliquely. Why?
Answer:

• Suppose two rays are originated from the bottom of the pond.
• As these rays get refracted into air, they bend away from the normal.
• When these two refracted rays produced backwards they seem to meet at a point higher than the bottom of the pond.
• This point gives the apparent position of the bottom of the pond.
• Thus the pond appears to be shallower.

Question 29.
What happens to the image formed by a convex lens if its lower part is blackened?
Answer:

1. Every part of lens forms complete image.
2. If lower part of the lens is blackened, the complete image will be formed.
3. But its intensity will decrease.

Question 30.
Is it possible for a lens to act as a convergent lens in one medium and a divergent lens in another?
Answer:

• Yes, the type of lens changes, if it is placed in medium having higher refractive index that of lens.
• For example, convex lens acts as converging lens when it is placed in a medium of lower refractive index otherwise it behaves like a diverging lens.

Question 31.
Draw the different types of convex and concave lens.
Answer:

Question 32.
Complete the ray diagram and give reason.

Answer:

The light ray which passes through optical centre does not undergo refraction. So it goes straight.

Question 33.
How do you appreciate the refraction at plane surfaces and at curved surfaces?
Answer:
The refraction of curved surfaces are used in various aspects such as

1. In microscope to enlarge microscopic objects.
2. In telescopes to see celestial objects.
3. To correct eye defects like myopia, hypermetropia and presbyopia.

So refraction at curved surfaces is thoroughly appreciated.

Question 34.
An object is placed at a distance of 50 cm from a concave lens of focal length 20 cm. Find the nature and position of the image.
Answer:

Image distance is negative that indicates it is a virtual and erect image.

Question 35.
A bird is flying at the height 3m above the river surface while a fish is 4 m below the surface. At what depth would the fish appear to the bird ? At what height the bird would appear to the fish? (given a/w = 4/3)
Answer:
Given that refractive index of air / water = \(\frac{4}{3}\)
The height the bird would appear to fish = 4 + \(\frac{4}{3}\) × 3 = 4 + 4 = 8m

10th Class Physics 6th Lesson Refraction of Light at Curved Surfaces 4 Marks Important Questions and Answers

Question 1.
Complete the ray diagram when an object is placed between F₂ and 2F₂. (AP June 2017)

Answer:

Question 2.
An object is placed at the following distances from a convex lens of focal length 10 cm.
(a) 8 cm.
(b) 15 cm.
(c) 20 cm.
(d) 25 cm.
Which position of the object will produce……. (TS March 2015)
(i) a diminished, real and inverted image?
(ii) a magnified, real and inverted image?
(iii) a magnified, virtual and erect image?
(iv) an image of same size as the object?
Justify your answer in each case.
Answer:
i) d (or) 25 cm
Reason : Object placed between centre of curvature and focal point.

ii) b (or) 15 cm
Reason : Object placed beyond centre of curvature.

iii) a (or) 8cm
Reason : Object placed between focal point and optic centre.

iv) c (or) 20 cm
Reason :Object placed at centre of curvature.

Question 3.
The ray diagrams showing the image formed by a convex lens are given in the following table. From these diagrams complete the table. (TS June 2016)

Answer:

Question 4.
Explain the behaviour of light rays in any four situations of their incidence on a convex lens. (TS March 2016)
Answer:
1) A ray passing along the principal axis is undeviated.

2) Any ray passing through optic centre is also undeviated.

3) The rays passing parallel to principal axis converge at focus.

4) The rays passing through the focus will take a path parallel to principal axis.

Question 5.
Draw the ray diagrams to find the images when an object is placed in front of the lens (i) at a distance of 8 cm, and (ii) at a distance of 10 cm on the principal axis of a convex lens whose focal length is 4 cm. Write the characteristics of images in both the cases. (TS June 2017)
Answer:
(i) Ray diagram :

Characteristics of Image :
i) Size of the image equal to the size of the object,
ii) Inverted image,
iii) Real image,
iv) Image formed at C.

(ii) Ray diagram

Characteristics of Image :
i) Image size is less than that of object size,
ii) Inverted image,
iii) Real image,
iv) Image is formed between F & C.

Question 6.
A double concave lens with the refractive index (n) = 1.5 is kept in the air. Its two spherical surfaces have radii R₁ = 20 cm and R₂ = 60 cm. Find the focal length of the lens. Write the characteristics of the lens. (TS March 2017)
Answer:

Hence f = – 30 cm (Here minus indicates that the lense is divergent)
Characteristics of the biconcave lens :

1. It is a diverging lens.
2. It is thin at the middle and thicker at the edges.

Question 7.
Draw ray diagrams for a double concave lens of focal length 4 cm, when objects are placed at 3 cm and 5 cm on principal axis. Write characteristics of images. (TS June 2018)
Answer:
i)

ii)

Characteristics of images :

1. Image formed between P and F
2. Diminished image
3. Errected image
4. Virtual image

Question 8.
Write the characteristics of the images which are formed when objects are placed at 50cm and 75cm on the principle axis of a convex lens with focal length of 25 cm. (TS March 2018)
Answer:
i) Object is placed at 50cm.

Characteristics of the image :

1. Image forms at 2Fp
2. Image is real,
3. Image is inverted,
4. Image is same size

ii) Object is placed at 75cm
f = +25cm; u = -75cm; v = ?

Characteristics of the image :

1. Image forms between F₁ and 2F₁
2. Image is real
3. Image is inverted
4. Image is diminished.

Question 9.
Write the role of lenses in our daily life. (AP March 2019)
Answer:
The role of lenses in our daily life :

1. Used for correcting eye defects.
2. Used as magnifying lens.
3. Used in Microscopes.
4. Used in Telescopes.
5. Used in Binoculars.
6. Used in Cinema Projectors.
7. Used in Cameras.

Question 10.
Draw the ray diagrams for the following positions of objects in front of a convex lens mention the characteristics of the image. (AP SCERT: 2019-20)
a) Object is placed beyond 2F₂.
b) Object is placed between focal point and opint center.
Answer:
a)

b)

a) Characteristics of the Image :

1. real
2. inverted
3. diminished.

b) Characteristics of the Image :
If we place an object between focus and optic centre, we will get an image which is virtual, erect and magnified.

Question 11.
The focal length of a convex lens is 2 cm. Draw the ray diagram of an object placed on principal axis at the ‘C’ of lens and at a distance of 3 cm from its optic centre.
Answer:
1) Object is placed on principal axis of a convex lens at ‘C’.

2) Object is placedon principal axis at a distance of 3 cm from its optic center.

Question 12.
Using biconvex lens, a point image is made on its principal axis S. Let us assume that we know optical centre P and its focus F. We also know PF > PS. Draw the ray diagram to identify the point source and give reasons.
Answer:

Given lens is biconvex lens and given condition is PF > PS’ means image is formed between optic centre (P) and Focus (F).

According to Snell’s law this condition is possible when the object is also placed between P and F. Because reflected rays are divergent.

Question 13.
Write about the behaviour of light rays when they incident on a lens.
Answer:
1) Situation I:
Ray passing through the principal axis.
⇒ It is not deviated.

2) Situation II:
Ray passing through the pole.
⇒ It is also undeviated.

3) Situation III:
Rays travelling parallel to the principal axis.
⇒ They converge at focus or diverge from the focus.

4) Situation IV :
Ray passing through focus.
⇒ It will take a path parallel to principal axis after refraction.

5) Situation V :
Parallel rays fall on a lens making some angle with principal axis.
⇒ They converge at a point or diverge from a point lying on a focal plane.

Question 14.
Write characteristics of image formed due to convex lens at various distances.
Answer:

Question 15.
Write characteristics of image formed by a concave lens at various distances.
Answer:

Question 16.
You are given a convex lens of focal length 10 cm. Where would you place an object to get a real inverted and highly enlarged image of the object? Draw a ray diagram.
Answer:
If an object is placed at the focus of the lens it forms real, inverted and highly enlarged image. Thus, the distance of the object from the optical centre of the lens is equal to the focal length of the lens =10 cm.
The ray diagram is as shown

Question 17.
Derive the formula of image formation in refraction at curved surfaces.
Answer:
1) Object at infinity :
The rays coming from the object at infinity are parallel to principal axis and converge to the focal point after refraction. So, a point-sized image is formed at the focal point.

2) Object placed beyond the centre of curvature on the principal axis :
When an object is placed beyond the centre of curvature 2F₂, a real, inverted and diminished image is formed on the principal axis between F₁ and 2F₁

3) Object placed at the centre of curvature :
When an object is placed at the centre of curvature (2F₂) on the principal axis, a real, inverted image is formed at 2F₁ which is same size as that of the object.

4) Object placed between the centre of curvature and focal point:
When an object is placed between centre of curvature (2F₂) and focus (F2), we will get an image which is real, inverted and magnified. This image will form beyond 2F₁.

5) Object located at focal point:
When an object is placed at focus (F₂), the image will be at infinity.

6) Object placed between focal point and optic centre :
If we place an object between focus and optic centre, we will get an image which in virtual, erect and magnified.

Question 18.
Distinguish between convex lens and concave lens.
Answer:

Convex lens	Concave lens
1. Objects appear to be big in the lens.	1. Objects appear to be shrink in the lens.
2. It generally forms real image, (except object is placed between optical centre and focal point)	2. It always forms virtual image.
3. Light rays tend to converge after refraction from lens.	3. Light rays tend to diverge from lens after refraction.
4. The image due to lens may be enlarged or same size or diminished.	4. The image is always diminished.
5. The image due to lens may be inverted or erect.	5. The image is always erect.
6. It is used to correct hypermetropia.	6. It is used to correct myopia.

Question 19.
The ray diagram given below illustrates the experimental set up for the determination of the focal length of a converging lens using a plane mirror.

1) State the magnification of the image formed.
2) Write the characteristics of the ipiage formed.
3) What is the name given to the distance between the object and optical centre of the lens in the following diagram?
Answer:

1. The magnification of the image formed is unity (or 1).
2. The image is a) real and b) inverted is at the same position of the object.
3. The distance between the object and the optical centre of the lens is called object distance.

Question 20.
A concave lens made of a material of refractive index n₁ is kept in medium of refractive index n₂. A parallel beam of light incident on the lens. Complete the path of rays of light emerging from the concave lens if
i) n₁ > n₂
ii) n₁ = n₂
iii) n₁ < n₂.
Answer:
i) When n₁ > n₂, light goes from rarer to denser medium. Therefore, in passing through a concave lens it diverges.

ii) When n₁ = n₂, there is no change in medium. Therefore no bending or refraction occurs.

iii) When n₁ < n2, light goes from a denser to rarer medium. Therefore, in passing through a concave lens it converges.

Question 21.
One half of a convex lens is covered with a black paper. Will this lens produce a complete image of the object? Verify your answer experimentally. Explain your observations.
Answer:

• Every part of a lens forms an image.
• For formation of image we require only two light rays to converge.
• Therefore, if the lower half of the lens is covered, it will still form a complete image.
• However the intensity of the image will be reduced.
• This can be verified experimentally by observing the image of distant object like tree on a screen, when lower half of the lens covered with a black paper.

Question 22.
Complete the following table if the object is placed at various positions in front of a convex lens.

Position of object	Position of image	Nature of image
1. At infinity
2.	Between F1 and 2F1
3.		Same size, real and inverted
4.	Seen in the lens

Answer:

Position of object	Position of image	Nature of image
1. At infinity	On Fj (focal point)	Highly diminished, real and inverted
2. Beyond 2F2	Between F1 and 2F1	Diminished, real and inverted
3. On 2F1	On 2F2	Same size, real and inverted
4. Between focus and optical centre	Seen in the lens	Enlarged, virtual and erect

Question 23.
A student focused the image of a candle flame on a white screen by placing the flame at various distances from a convex lens. He noted his observations.

Distance of flame from the lens (cm)	Distance of the screen from the lens (cm)
1. 60	20
2. 40	24
3. 30	30
4. 24	40
5. 15	70

a) From the above table, find the focal length of lens without using lens formula.
b) Which set of observations is incorrect and why?
c) In which case the size of the object and image will be same? Give reason for your answer.
Answer:
a) From the observations, it is clear that for u = 30, v = 30 cm. This means this value must be equal to twice the focal length of the convex lens.
∴ Focal length of convex lens = 30/2 = 15 cm

b) The observation (5) is not correct because if u = 15 cm i.e., the object is kept at focus so the image should be at infinity and not at 70 cm.

c) For twice the focal length we know size of object = size of image. So when object is kept at 30 cm the size of object and image are same.

Question 24.
Draw the ray diagrams when incident ray striking a convex surface or a concave surface moving from one medium to another medium.
Answer:

Question 25.
Draw ray diagrams of image formed by a convex lens at various distances.
Answer:
1) Object at infinity.

2) Object placed beyond the centre of curvature (2F₂).

3) Object placed at the centre of curvature.

4) Object placed between 2F₂ and F₂.

5) Object at the focal point.

6) Object placed between F and P

Question 26.
Write about the focal length of the lens with diagram.
Answer:

• A parallel beam of light incident on a lens converges to a point as shown in figure (a) or seems to emanate from a point on the principal axis as shown in figure (b).
• The point of convergence (or) the point from which rays seem to emanate is called focal point or focus (F).
• Every lens has two focal points.
• The distance between the focal point and optic centre is called the focal length of lens denoted by ‘f’
• To draw ray diagram for lenses, we need two more points in addition to focal points F₁ and F₂.
• These points are equidistant from centre of the lens and also equal to double the focal length. So we call them 2F₁ and 2F₂.
• For drawing ray diagrams related to lenses, we represent convex lens with a symbol £ and concave lens with J as shown in the figure c and d.

Question 27.
The diagram shows an object OA and its image IB formed by a lens. The image is same size as the object.
a) Complete the ray diagram and locate the focus of lens by labelling it as F.
b) State whether the lens is convex or concave.
Show it in the diagram.

Answer:

a)

1. Optical centre goes undeviated, therefore to find the optical centre, join A to B to meet the line 01 at the point P which gives the position of optical centre of the lens.
2. Draw a line CP through P perpendicular to the line 01 to represent lens.
3. Draw another ray AC from the point A parallel to the principal axis 01 to meet the lens line CP at a point C.
4. This ray AC will reach the image point B while passing through the focus, therefore join C to B to meet line 01 at a point F which is the focus of the lens. The completed ray diagram is shown above.

b) Since the image is real and inverted, the lens is convex.

c) Since the size of object and image of equal, the object must be at a distance of twice the focal length, i.e., at 2F₂.

Question 28.
The diagram shows an object AB placed on the principal axis of the lens L. The two foci of lens are F₁ and F₂. The image formed by the lens is erect, virtual, and diminished.

i) Draw the outline of the lens L used and name it.
ii) Draw a ray of light starting from B and passing through ‘O’. Show the same ray after refraction by the lens.
iii) Draw another ray from B which is incident and parallel to the principal axis. Show how it emerges after refraction from the lens.
iv) Locate the final image formed.
Answer:
i) Since the image formed by the lens is erect, virtual, and diminished, the lens is concave.
ii) The light ray BO incident at the optical centre ‘O’ of the lens, passes undeviated as OC after refraction by the lens.
iii) The light ray BP is incident and parallel to the principal axis. It emerges as PQ after refraction which appears to diverge from the second focus F₂ of the lens.
iv) The refracted rays OC and PQ do not actually meet, but they appear to diverge from a point B’ (i.e. they meet at a point B’ when they are produced backwards).
v) Thus, B’ is the complete image A’B’ is obtained by drawing perpendicular from B’ on the line F₂OF₁. The image is formed between the optical centre O and focus F₂ of the lens.

Question 29.
Figure below shows the refracted ray BC through a concave lens and its foci marked as F₁ and F₂. Complete the diagram by drawing the corresponding incident ray and also give reason.

Answer:

1. Figure shows the refracted ray parallel to the principal axis. Therefore, the incident ray must be travelling towards the focus F₂.
2. Thus, to find incident ray, F₂ is joined to the starting point B of the refracted ray and produced backward as BA.
3. Then AB is the required incident ray.
4. The completed diagram is shown below.

Question 30.
State the type of lens used as a simple magnifying glass. Draw a labelled diagram to show that the image of the object is magnified.
Answer:

• A single convex lens is used as a magnifying glass, i.e. for seeing small object magnified.
• When the object to be seen between the focus and optical centre of the lens, a virtual, erect and enlarged image is formed.
• So a convex lens acts as magnifying glass for object AB as shown in the figure.

Question 31.
Radii of biconvex lens are equal. Let us keep an object at one of the centres of curvature. Refractive index of lens is ‘n’. Assume lens is in the air. Let us take R as the radius of the curvature.
a) How much is the focal length of the lens?
b) What is the image distance ?
c) Discuss the nature of the image.
Answer:
Radii of curvatures (R) of biconvex lens are equal, so R₁ = R₂ = R


c) The nature of the image is inverted and v < u.

Question 32.
Refractive index of a lens is 1.5. When an object is placed at 30 cm, image is formed at 20 cm. Find its focal length. Which lens is it? If the radii of curvature are equal, then what is its value?
Answer:
Object distance = u = – 30 cm (Infornt of the lens)
Image distance = v = 20 cm

Question 33.
A convex lens of focal length 10 cm is placed at a distance of 12 cm from a wall. How far from the lens should an object be placed so as to form its real image on the wall?
Answer:

Question 34.
A 5 cm tall object is placed perpendicular to the principal axis of a convex lens of focal length 20 cm. If image distance is thrice the focal length, find object distance, image distance and nature of image.
Answer:
Given that
Focal length of lens = + 20 cm
Object distance = -u
Image distance (v) = + 3u

So the object is between F₂ and 2F₂. So the image beyond 2F₁ it is real, inverted, and magnified.

Question 35.
What are the various applications of lens?
Answer:

• The objective lens of a telescope, camera, slide projector, etc. is a convex lens which forms real and inverted image of object.
• Our eye lens is also a convex lens. The eye lens forms the inverted image of the object on the retina.
• The eye defects are corrected by lenses.
• A magnifying glass is nothing but a convex lens of short focal length fitted in a steel (or plastic) flame provided with a handle.
• In spectroscope, convex lenses are used for obtaining a pure spectrum.
• A concave lens is used as eye lens in a Galilean telescope to obtain an erect final image of the object.

AP State Board Syllabus AP SSC 10th Class Physical Science Important Questions Chapter 4 Acids, Bases and Salts.

AP State Syllabus SSC 10th Class Chemistry Important Questions 4th Acids, Bases and Salts

10th Class Chemistry 4th Lesson Acids, Bases and Salts 1 Mark Important Questions and Answers

Question 1.
Take some water in a test tube and add concentrated H₂SO₄ to it. Shake the test tube well. If you touch the bottom of the test tube, you feel it as hot. Now, instead of H₂SO₄, if you add NaOH pellets to water in another test tube and touch the bottom, what do you observe? (TS June 2015)
Answer:
The bottom of test tube is also hot because reactions of acids, bases with water are exothermic reactions.

Question 2.
What happens if the copper sulphate crystals taken into dry test tube are heated? (TS June 2016)
Answer:

• When copper sulphate crystals are heated, water present in crystals is evaporated and the salt turns white.
• Evaporated water appears as droplets on the walls of the test tube.
• Blue coloured copper sulphate (CuSO₄ 5H₂O) is turned into white colour because 5H20 molecules are evaporated from crystals.

Question 3.
Why does the soil of agricultural lands get tested for pH?
Answer:
Plants require a specific pH range for their healthy growth. So, finding pH of a soil suggested the farmers to treat the fields with acidic or basic substances to maintain the required pH range.

Question 4.
Write the molecular formulae of common salt and baking soda which are widely used at home. (TS June 2017)
Answer:
Common Salt: NaCl; Backing soda : NaHCO₃

Question 5.
Mention the precautions to take while conducting an experiment to prove acids produce ions only in aqueous solutions. (TS June 2018)
Answer:

• Testing of the evolved gas by using dry litmus paper first. Then with wet litmus paper.
• Use gaurd tube containing calcium chloride.

Question 6.
What are antacids?
Antacids are mild alkalies. These are used for getting relief from acidity and indigestion and sometimes even headache. When taken orally, it reacts with hydrochloric acid present in the stomach and reduces its strength by consuming some of it.
Ex: Milk of magnesia.

Question 7.
Tap water conducts electricity whereas distilled water does not. Why?
Answer:
Tap water contains some impurities in the form of salts. Due to presence of salts, it conducts electricity. Distilled water is free from all kinds of salts and hence does not conduct electricity.

Question 8.
What do you mean by dilution of an acid or base? Why is it done?
Answer:
Dilution of an acid or base means mixing an acid or base with water. This is done to decrease the concentration of ions per unit volume. In this way the acid or the base is said to be diluted.

Question 9.
What is a universal indicator?
Answer:
An indicator which passes through a series of colour changes over a wide range of H₃O⁺ ions concentration is called universal indicator.

Question 10
What is tooth decay?
Answer:
Tooth enamel is chemically calcium phosphate Ca₃(PO₄)₂. It starts corroding when pH falls below 5.5. Food particles left in the mouth degrade to produce acid which lower the pH of the mouth. This is called tooth decay.

Question 11.
Define Alkalis and give some examples.
Answer:
Alkalis : An alkali is a base that dissolves in water.

Examples :
i) Sodium Hydroxide (NaOH),
ii) Potassium Hydroxide (KOH),
iii) Magnesium Hydroxide (Mg(OH)₂)

Question 12.
Why should we not taste or touch alkalis?
Answer:
We should not taste or touch alkali. Because they are corrosive.

Question 13.
Salts conduct electricity. Why?
Answer:
Salts contains ions. So they conduct electricity.

Question 14.
Why are calcium sulphate hemihydrates called Plaster of Paris?
Answer:
Calcium sulphate hemihydrates are used as plaster for supporting fractured bones in the right position. So, it is called Plaster of Paris.

Question 15.
Why does an aqueous solution of acid conduct electricity?
Answer:
An aqueous solution of acid liberates H⁺ ions. This makes the aqueous solution of acid to conduct electricity.

Question 16.
How is the concentration of hydronium ions (H₃O⁺) affected when a solution of an acid is diluted?
Answer:
When a solution of an acid is diluted, concentration of H₃O⁺ ions decreases.

Question 17.
What is pH?
A. pH is a scale for measuring hydrogen ion concentration in a solution. It is the negative logarithm of H⁺ concentration.
pH = – log [H⁺].

Question 18.
How is pH of a solution related to the [H₃O⁺] of that solution?
Answer:
The presence of H₃O⁺ ions indicate us whether it is a strong acid or weak acid.

Question 19.
There are two solutions of pH values 6 and 8. Which solution has more hydrogen ion concentration? Which of this is acidic and which one is basic?
Answer:

• The solution whose pH value 6 is acid and has more hydrogen ion concentration.
• The solution of pH value 8 is basic and has less hydrogen ion concentration.

Question 20.
Can you give example for use of olfactory indicators in daily life?
Answer:
Examples of olfactory indicators : Onion, vanilla extract.

Question 21.
How do acids neutralize bases?
(OR)
How do acids and bases react with each other?
Answer:
According to Arrhenius theory acids produce H⁺ ions and bases produce OH^– ions in aqueous media.
The combination of H⁺ and OH^– ions is called ‘neutralization’.
Thus acids neutralize bases.

Question 22.
How strong are acids and base solutions?
Answer:
The acids of pH value as much less as possible have more concentration [pH < 7], Basic nature increases as pH value increases.

Question 23.
What do you say about salts of both weak acid and weak base?
Answer:
The pH of aqueous solutions of salt obtained from both weak acid and weak base is nearly 7.

Question 24.
Which base is used for removing permanent hardness of water?
Answer:
Sodium carbonate is used for removing permanent hardness of water.

Question 25.
Name two antacids used to get rid of our indigestion problem.
Answer:
Magnesium hydroxide and a mild base (baking soda).

Question 26.
Under what soil conditions would a farmer would treat the soil of his fields with quicklime (calcium hydroxide) or calcium carbonate?
Answer:
When the field has acidic nature, the farmer uses quicklime or calcium carbonate to neutralize it.

Question 27.
Write the formulas of Gypsum and Plaster of Paris.
Answer:
The formulae of Gypsum is CaSO₄ . 2H₂O and Plaster of Paris is CaSO₄ . ½H₂O.

Question 28.
Write any two Acid Base indicators.
Answer:

1. Methyl orange
2. Phenolphthalein.

Question 29.
Which salt is used in the manufacture of borax?
Answer:
Washing soda (Na₂CO₃.10H₂O)

Question 30.
What is family of salts? Give examples.
Answer:
Salt having the same positive or negative radical is called family of salts.
Eg : Family of sodium salts : NaCl, Na₂SO₄
Family of chloride salts : NaCl, KCl.

Question 31.
‘A’ is a substance which is acidic and it is added in solution to preserve pickles. What is A and what is the name given to its dilute solution?
Answer:
‘A’ is acetic acid and its dilute solution is called vinegar.

Question 32.
What are the chemical names of the following?
1) Baking soda
2) Gypsum
Answer:

• The chemical name of baking soda is sodium hydrogen carbonate (NaHCO₃).
• The chemical name of gypsum is calcium sulphate dihydrate (CaSO₄ • 2 H₂O).

Question 33.
Write the water of crystallisation of following compound.
a) Hydrous copper sulphate
b) Washing soda
c) Gypsum
d) Plaster of Paris
Answer:

Compound	Formula	Water of crystallisation
1) Hydrous copper sulphate	CuSO4 . 5H2O	5
2) Washing soda	Na2CO3 . 10 H2O	10
3) Gypsum	CaSO4 . 2 H2O	2
4) Plaster of Paris	CaSO4 . ½H2O	½

Question 34.
Why don’t we use a strong base like NaOH as antacid?
Answer:
Strong bases like potassium hydroxide (KOH), sodium hydroxide (NaOH) are corrosive in nature. So they can harm the internal organs. Therefore we should not use them as antacid.

Question 35.
What do you mean by HsO⁺ ion?
Answer:
Hydrogen ions cannot exist as base ions. They associate with water molecules and exist as hydrated ions with each H⁺ attached by 4 to 6 water molecules. For this we represent H⁺ as hydronium ion, H³O⁺.
H⁺ + H₂O → H₃O⁺

Question 36.
Which indicator is useful at all pH? Why?
Answer:
Universal indicator is useful to test solutions of all pH because it gives different colours at different pH range.

Question 37.
Which substance is useful in removing permanent hardness of water?
Answer:
The permanent hardness of water is due to chloride and sulphate salts of magnesium and calcium, which can be removed by adding washing soda.

Question 38.
Given two examples for strongest bases.
Answer:
Sodium hydroxide – NaOH
Potassium hydroxide – KOH

Question 39.
What is the confirmation test for hydrous and anhydrous salt?
Answer:

• On heating hydrous salt in a test tube it will form water droplets on the sides of test tube.
• On heating anhydrous salt in a test tube it will not form water droplets on the sides of test tube.

Question 40.
P.O.P, cement, calcium chloride should be stored in moisture proof containers. Why?
Answer:

• P.O.P, cement and calcium chloride react with moisture (H₂O) in the atmosphere and set into hard solid masses.
• To avoid availability of moisture they should be stored in moisture proof containers.

Question 41.
Give some examples for hydrous and anhydrous salts.
Eg : For hydrous salts :

1. CuSO₄ . 5H₂O
2. Na₂CO₃ . 10H₂O
3. CaSO₄ . 2H₂O

Eg : for anhydrous salts :

1. NaCl
2. MgCl₂
3. Na₂CO₃

Question 42.
How are bitter and sour taste substances tested without testing?
Answer:

• Sour taste substances turn blue litmus to red.
• Bitter taste substances turn red litmus to blue. By these tests we can test them as acids and bases.

Question 43.
Do the metallic oxides react with acids?
Answer:
Yes, metallic oxides are basic in nature. They react with acids and form salt and water.

Question 44.
Does non-metallic oxide react with base?
Answer:
Yes, non-metallic oxide is acidic in nature. It reacts with base and forms salt and water.

Question 45.
Why does dry HCl gas not change the colour of the dry litmus paper?
(OR)
Prove that dry HCl gas is not an acid but HCl aqueous solution is an acid using an activity.
Answer:

• Dry hydrogen chloride gas is not an acid. Hence it can’t turn blue litmus into red.
• Hydrochloric acid is an aqueous solution. Hence it can turn blue litmus into red.

Question 46.
Do you know that the atmosphere of Venus is made up of thick white and yellowish clouds of sulphuric acid? Do you think life can exist on this planet?
Answer:

1. No, it is not possible.
2. When pH value decreases, the survival of living organisms becomes difficult.
3. Hence there is not any possibility of life on Venus.

Question 47.
Why do acids not show acidic behaviour in the absence of water?
Answer:
Acids don’t show acidic behaviour in the absence of water as H⁺ ions are absent in them.

Question 48.
How is the concentration of hydroxide ions (OH^–) affected when excess base is dissolved in a solution of sodium hydroxide?
Answer:
When a base like NaOH (Sodium hydroxide) is dissolved in water, it liberates (OH^–) ions.
Equation :

OH^– ion concentration increases.

Question 49.
How does the nature of the solution change with change in concentration of H⁺_(aq) ions?
Answer:
The concentration of H⁺ ions is responsible for the acidic nature of a substance.
If [H⁺] > 1 × 10^-7 mol/lit the solution is acidic.
If [H⁺] < 1.0 × 10^-7 mol/lit the solution is basic.

Question 50.
Do basic solutions also have H⁺_(aq) ions? If yes, then why are these basic?
Answer:
Yes. Basic solutions have OH^–_(aq) ions and bases have less number of H₃O⁺ ions. H⁺_(aq) ions are less in base. In basic solution [OH^–] > [H⁺].

Question 51.
What do acids have in common?
Answer:
(Acids have sour taste and conduct electricity. They release H₂ (Hydrogen) gas on reacting with metals). All acids have H⁺_(aq) ions.

Question 52.
What do bases have in common?
Answer:
Bases are slippery to touch and bitter to taste. All bases have OH^–_(aq) ions.

Question 53.
Why does pure acetic acid not turn blue litmus to red?
Answer:
Pure acetic acid is a weak acid so it does not have sufficient H⁺_(aq) ion to change the colour of blue litmus to red.

Question 54.
What will happen if the pH value in your body increases?
Answer:
It affects our digestion system.

Question 55.
A student checked pH of a salt solution and found that its pH is more than 7. How is that type of salt formed?
Answer:

• When a strong base reacts with weak acid then the solution is basic in nature. So its pH is more than 7.
• For example when acetic acid reacts with sodium hydroxide the salt formed has basic nature.

Question 56.
Explain the procedure that you follow to reduce water from a given salt.
Answer:
Procedure to reduce water from a given salt :

1. Take a boiling test tube.
2. Drop given salt in the test tube.
3. Heat the test tube gently.
4. Water from salt evaporates.
5. In this way we can reduce the water from salt.

Question 57.
Write the observations, when the hydrated salt or unhydrated salt is heated.
Answer:

• When hydrated salt is heated water droplets form inside the walls of test tube and sometimes blue or green colour salt turns into white colour.
• When unhydrated salt is heated it does not form water droplets inside the test tube walls and colour also does not change.

Question 58.
On heating the hydrated salt it loses water molecules present in it. To show this what are the equipment required?
Answer:
1) On heating the hydrated salt it loses water molecules present in it.
2) To show this the given equipment are required

1. Boiling tube
2. Test tube holder
3. Burner

Question 59.
Try to collect the information to reasons for calling calcium sulphate hemihydrates as Plaster of Paris (POP).
Answer:

• Gypsum plaster (or) Plaster of Paris (POP) is produced by heating gypsum to about 300°F.
• A large gypsum deposit is found at Montmartre in Paris (France).
• This gave the name Plaster of Paris to calcium sulphate hemihydrates.
• The term plaster can refer to gypsum.

Question 60.
Is the substance present in antacid tablet acidic or basis?
Answer:
The substance present antacid is weakly basic.

Question 61.
Give pH of neutral, acid and base.
Answer:

Nature of substance	pH range
Neutral	7
Acid	0 – 7
Base	7 – 14

Question 62.
Which nature of Plaster of Paris makes its importance? Appreciate it.
Answer:
Plaster of Paris is a white powder. It is very soft and can be used to make toys, materials for decoration and to make surfaces smooth.

But on mixing with water, it changes to a hard solid mass (Gypsum). This is the important character of Plaster of Paris (POP).

Question 63.
What is acid rain? How does it affect our aquatic life?
Answer:
When the pH of rain water is less than 5.6 it is called acid rain. When acid rain flows into the rivers, it lowers the pH of the river water. Since our body works within a narrow pH range close to 7 the survival of aquatic life in river water mixed with rain water becomes difficult.

Question 64.
Why are pickles and sour substances not kept in brass and copper vessels?
Answer:
Pickles and sour substances contain acidic nature which may react with brass and copper vessels to produce toxic substances.
So, we don’t keep them in brass arid copper vessels.

Question 65.
Can you suggest some examples of use of pH in everyday life?
Answer:
Uses of pH in everyday life :

1. pH value helps us to identify acids, bases and neutrals.
2. If pH value is less in our mouth, it leads to tooth decay. We can find it as the reason for our tooth decay.
3. pH value helps us to know about acid rain.

Question 66.
Write any two uses of Bleaching powder.
Answer:

• It is used for disinfecting drinking water to make it free of germs.
• It is used as a reagent in the preparation of chloroform.

10th Class Chemistry 4th Lesson Acids, Bases and Salts 2 Marks Important Questions and Answers

Question 1.
What value of pH in the mouth leads to tooth decay? Why? (TS June 2015)
Answer:

• Tooth decay starts when the pH of the mouth is lower than 5.5.
• Tooth enamel, made of calcium phosphate is the hardest substance in the body.
• It does not dissolve in water, but is corroded when the pH in the mouth is below 5.5.
• Bacteria present in the mouth produce acids by degradation of sugar and food particles remaining in the mouth.

Preventions :

1. Clean the mouth after eating food.
2. Using tooth pastes, which are generally basic neutralize the excess acid and pre¬vent tooth decay.

Question 2.
Equal lengths of Magnesium ribbons are taken in two test-tubes X and Y. Hydro¬chloric acid is added to test-tube X and Acetic acid is added to test-tube Y. In which test-tube, the reaction will be more vigorous? Why? (TS March 2015)
Answer:
The speed of the reactions is higher in X test tube than Y test tube.

Reason :
Due to strong acidic nature, Hydrochloric acid reacts very fast with magnesium ribbon.

Question 3.
Name the four chemicals that are obtained from common salt and write their molecular formulae. (TS March 2015)
Answer:
Chemicals that can be obtained from common salt are

1. Sodium Hydroxide – NaOH
2. Baking soda / Cooking soda / Caustic soda / Sodium bicarbonate / Sodium Hydrogen carbonate. – NaHCOv
3. Washing soda / Sodium carbonate – Na₂CO₃ 10H₂O
4. Bleaching powder / Calcium Oxy Chloride – CaOCl₂

Question 4.
Observe the information given in the table and answer the questions given below the table. (TS March 2017)

Substance (in aqueous solution)	Colour change with Blue Litmus	Colour change with Red Litmus
A	Red	No change
B	No change	Blue
C	No change	No change

i) Which one of them may be the neutral salt among A, B, C?
ii) What may happen when some drops of phenolphthalein is added to the substance B?
Answer:
i) C
ii) Pink Colour

Question 5.
Why do we use antacids? Write it’s nature. (TS March 2018)
Answer:
Pain and irritation will be caused in stomach during the acidity problem/indigestion problem. Antacids used to neutralize the excess acid in the stomach and gives relief from acidity Antacids are basic in nature.

Question 6.
Which product will form when CaO is dissolved in water? How do you find the nature of product? (TS March 2018)
Answer:
CaO reacts with water and gives calcium hydroxide [Ca(OH₂)]. The nature of the calcium hydroxide will be tested with red litmus paper or pH paper.

Calcium Hydroxide turns red litmus into blue. Thus we can say that ca(OH)₂ is basic in nature.

Ca(OH)₂ shows pH value more than 7. Thus we can say that Ca(OH)₂ is basic in nature.

Question 7.
How do you test the nature of the solution formed by dissolving CaO in water? What is the nature of the solution? (TS June 2019)
Answer:

• The solution formed by dissolving CaO in water is tested with red litmus paper, it turns into blue colour, (or) It is tested with methyl orange, it turns into yellow in colour.
• The solution of CaO and water is basic in nature.

Question 8.
Write the experimental procedure to test carbon dioxide gas. (AP SCERT: 2019-20)
Answer:

1. Pass the CO₂ gas through lime water [Ca(OH)₂].
2. The lime water appears as milky white.
3. The reaction is Ca(OH)₂ + CO₂ → CaCO₃ ↓ + H₂O.
4. The milky white is caused by CaCO₃.

Question 9.
Write two reactions of acids with carbonates and metal hydrogen carbonates. (AP SA-I : 2019-20)
Answer:
Reactions :

Question 10.
What do acids have in common?
Answer:
Common characteristics of acids :

1. Similar chemical properties.
2. Acids generate hydrogen gas on reacting with metals.
3. Hydrogen is common to acids.
4. Acids are sour in taste and turn blue to red when react with bases form salt and water.

Question 11.
What do bases have in common?
Answer:
Common characteristics of bases :

1. Bitter in taste.
2. Soapy in nature.
3. Turn red to blue colour.
4. On heating decompose into metal oxides and water.
5. React with acids to form salt and water.
6. Produce OH^– ions in aqueous solution.

Question 12.
How is bleaching powder produced?
Production of bleaching powder :
Bleaching powder is produced by the action of chlorine on dry slaked lime (Ca(OH)₂).
Equation :

Question 13.
What can you conclude about the ideal soil pH for the growth of plants in your region?
Answer:
1) Soil is considered the ‘skin of the earth’. The soil pH plays a vital role in the growth of a plant and it influences plant nutrition.
2) Soil pH strongly affects the nutrients required for the plant growth.
3) The nutrients may be stored on soil colloids, and live or dead organic matter, but may not be accessible to plants due to extremes of pH.

Conclusion :
For optimum plant growth, the generalized content of soil components by volume should be roughly 50% solids (45% mineral & 5% organic matter), and 50% voids of which half is occupied by water and half by gas.

Question 14.
How can you prepare turmeric indicator? What is the use of it?
Answer:
i) Turmeric indicator is prepared from turmeric.
ii) It has red colour in basic solution.

Question 15.
Name two salts and write their formulae which possess water of crystallization.
Answer:

1. Hydrous copper sulphate. Its formula is CuSO₄ . 5H₂O
2. Gypsum. Its formula is CaSO₄ . 2H₂O

Question 16.
What is neutralization reaction? Give two examples.
Answer:
When an acid reacts with base it forms salt and water. This reaction is called neutralisation reaction.
e.g.: NaOH_(aq) + HCl_(aq) → NaCl_(aq) + H₂O_(l)
H₂SO_4(aq) + 2Na0H_(aq) → Na₂SO_4(aq) + 2H₂O_(l)

Question 17.
All alkalis are bases but all bases are not alkalis. Do you agree with the statement? If yes, why?
Answer:
Yes, I agree with the statement. Because alkalis are those bases which are soluble in water. So all alkalis are bases but all bases are not alkalis.

Question 18.
Why are solutions of acids, bases and salts good conductors of electricity?
Answer:
For passage of electricity through a material or substance charged particles are required. In metals charged particles are electrons whereas in solutions ions are charged particles which carry electrical energy. Solutions of acids, bases and salts undergo ionisation and produce ions. So they are good conductors of electricity.

Question 19.
What is strength of acid ? What are the factors that influence strength of acid?
Answer:
The extent which an acid undergoes ionisation is called strength of acid.
Factors influence strength of acid :

1. Degree of ionisation.
2. Concentration of hydronium ions produced by acid.

Question 20.
Why are organic acids weak acids when compared with mineral acids?
Answer:

• Strength of acid depends on extent of ionisation.
• Organic acids do not undergo 100% ionisation. Their ionisation is less than 30%. There is equilibrium between ionised and unionised molecules whereas mineral acids undergo complete ionisation.
• So mineral acids behave like strong acids when compared with organic acids.

Question 21.
“Acids do not contain OH^– ions”. Do you agree with this statement? If not, why?
Answer:
No. I do not agree with the statement because all acids also contain OH^– ions but in acid solutions, H⁺ ions are more than OH^– whereas in bases OH^– ions are more than H⁺.

Question 22.

If B is calcium chloride, what are A, C, D and E?
Answer:
A is calcium carbonate or calcium hydrogen carbonate.
C is water and D is carbon dioxide.
E is calcium carbonate and F is water.

Question 23.
Some salts are given below. Classify them into hydrous and anhydrous salts. Sodium carbonate, Sodium chloride, Sodium hydrogen carbonate, Copper sulphate, Hypo, Magnesium Sulphate (epsum salt)
Answer:
Hydrous salts :

1. Hypo (Na₂S₂O₃ • 2H₂O)
2. Epsum (MgSO₄ • 7H₂O)
3. Copper sulphate (CuSO₄ • 5H₂O)

Anhydrous salts :

1. Sodium chloride (NaCl)
2. Sodium carbonate (Na₂CO₃)
3. Sodium hydrogen Carbonate (NaHCO₃)

Question 24.
If someone in the family is suffering from a problem of acidity, which of the following would you suggest as a remedy : lemon juice, vinegar or baking soda solution? Which property do you think of while suggesting the remedy?
Answer:

• I suggest baking soda solution. As acidity can be neutralized by baking soda solution, we can use it.
• Neutralizing property of baking soda solution.

Question 25.
Why are curd and sour substances not kept in copper vessels?
Answer:
Curd and sour substances contain acids which react with copper vessels and form poisonous substances. So curd and sour substances should not be kept in copper vessels.

Question 26.
Which gas is liberated when acids react with metals? Give one example.
Answer:
When acids react with active metals they release hydrogen gas.
Zn_(s) + 2HCl_(aq) → Zncl_2(aq) + H₂ ↑_(g)

Question 27.
Why should pickles not be stored in metallic containers?
Answer:
Pickles contain acids which react with metallic containers and form poisonous substance. So they are kept in plastic containers.

Question 28.
Solution x turned blue litmus red and Solution y turned red litmus blue.
a) What products could be formed when x and y are mixed?
b) Which gas is released when we put magnesium pieces in solution x?
c) Will any chemical reaction take place when zinc pieces are put in solution y?
d) Which of the above solutions contain more hydrogen ions?
Answer:
Given solution Y turned blue litmus into red so, Y is an acid.
Given solution ‘y’ turned red litmus into blue so, ‘y’ is a base.
a) The reaction of an acid (x) with a base to give a salt and water.
b) When we put magnesium pieces in solution releases hydrogen gas.
c) When zinc pieces are put in solution y, a chemical reaction will take place there.
d) Acids contain more H+ ions in the given solutions, Y has more H+ ions because it is an acid.

Question 29.
Acid should be added to water but not water to the acid. Why?
Answer:

• The dissolving of an acid or base in water is an highly exothermic process. Care must be taken while mixing concentrated HNO₃ or concentrated H₂SO₄ with water.
• The acid must always be added slowly to water with constant stirring.
• If water is added to a concentrated acid, the heat generated may cause the mixture to splash out and cause bums.
• The glass container may also break due to excessive local heating.

Question 30.
Explain the procedure to confirm the given salt is a hydrous or anhydrous.
Answer:

1. Take given salt in a test tube
2. Observe the colour of salt
3. Heat the test tube gently
4. Observe the colour of salt and also moisture (droplets) inside of the test tube walls.
5. If its colour changes or forms water droplets, it is hydrous salt.
6. Otherwise, it is anhydrous salt.

Question 31.
Categorize the following as acids, bases, and salts :
Lemon juice, salt water, soap water, tamarind juice, surf water, lime water.
Answer:
Acids :

1. Lemon juice
2. Tamarind juice

Bases :

1. Soap water
2. Surf water
3. Lime water

Salts :

1. Salt water

Question 32.
Classify the following salts as family of salts having same cation or anion and prepare a table.
Potassium sulphate, Sodium sulphate, Calcium sulphate, Magnesium sulphate, Copper sulphate, Sodium chloride, Sodium nitrate, Sodium carbonate and Ammonium chloride.
Answer:

Question 33.
Observe the table and answer the following questions.

Solutions	pH value
Blood	7.3
Pure water	7.0
Gastric fluid	1.2
Sodium hydroxide	13

1) Which of the solutions among these is a strongest base?
2) Which body fluid has slightly basic nature?
3) What is the nature of pure water?
4) Which body fluid is strongest acid?
Answer:

1. Sodium hydroxide because its pH is 13.
2. Blood because its pH is 7.3.
3. Pure water is neutral in nature because its pH is 7.
4. Gastric juice because its pH is 1.2.

Question 34.
The diagram given below shows the removal of water crystallisation. Find error in the diagram.

Answer:
Error in the diagram

1. Test tube is placed towards observer. It causes bums on his hands.
2. So, test tube should be placed away from the observer.

Question 35.
What are the uses of Plaster of Paris?
Answer:

• The substance which doctors use as plaster for supporting fractured bones in the right position.
• Plaster of Paris is used for making toys, materials for decoration and for making surfaces smooth.

Question 36.
What are the applications of pH in daily life?
Answer:
1) In medical science :
The pH values of urine and blood are taken for diagnosis of various diseases.

2) In dairies :
Milk has pH of 6.6. A change in the pH of milk indicates that milk has turned sour.

3) In agriculture :
For better growth of crops the pH of the soil is regularly tested.
For examples :

1. Citrus fruits require slightly alkaline soil.
2. Rice requires acidic medium.
3. Sugarcane requires neutral soil.

4) In technology:
Organic and biochemical reactions are carried out under control pH.

10th Class Chemistry 4th Lesson Acids, Bases and Salts 4 Marks Important Questions and Answers

Question 1.
Draw a neat diagram showing a base solution in water conducts electricity. Why the solution of sugar/glucose in water do not conduct electricity? (AP March 2017)
Answer:

The solution of sugar/glucose in water do not conduct electricity because there is no H⁺ ions in the solution.

Question 2.
Explain an activity to show the water of crystallisation in CuSO₄ • 5H₂O. (AP June 2018)
Answer:

• Take a few crystals of copper sulphate in a dry test tube and heat the test tube.
• We observe water droplets on the walls of the test tube and salt turns white.
• Add 2 – 3 drops of water on the sample of copper sulphate obtained after heating.
• We observe the blue colour of copper sulphate crystals is restored.

Question 3.
Read the information given in the table and answer the following questions. (TS March 2016)

a) List out the acids in the above table.
Answer:
The acids are HCl and lemon juice.

b) What is the nature of the solution which gives pink colour with Phenolphthalene solution?
Answer:
The nature of the solution which turns pink colour with phenolphthalene solution is basic.

c) List out the neutral solutions in the above table.
Answer:
The neutral solutions are distilled water and NaCl.

d) Name the strongest acid and the strongest base among the given solutions.
Answer:
The strongest acid is HCl and the strongest base is NaOH.

Question 4.
Observe the following table and answer the questions given below. (TS June 2o17)
The table contains the aqueous solutions of different substances with the same concentrations and their respective pH values.

i) Which one of the above acid solutions is the weakest acid? Give a reason.
Answer:
Weakest acid is ‘C’. Because its pH value is less than 7 and it is nearer to 7.

ii) Which one of the above solutions is the strongest base? Give a reason.
Answer:
Strongest base is ‘D’. Because it’s pH value is near to 14.

iii) Which of the above two produce maximum heat when they react ? What does that heat energy called?
Answer:
B, D produce maximum heat when they react. This heat energy is known as neutralization energy.

iv) Which one of the above solutions has the pH equal to that of the distilled water? What is the name given to solutions of that pH value?
Answer:
‘G’ has the pH equal to that of the distilled water. These type of solutions are known as neutral solution.

Question 5.
List out the materials required to test whether the solutions of given acids and bases contain ions or not. Explain the procedure of the experiment. (TS March 2017)
Answer:
Required Materials :
Beaker, Bulb, Graphite rods, connecting wires, 230 V AC current, water, different acids, bases.

Experimental Procedure :

1. Connect the two connecting wires to the graphite rods.
2. Keep the graphite rods into the beaker, take care that two graphite rods do not touch each other.
3. Arrange a bulb in the circuit.
4. Pour dilute acid into the beaker.
5. Connect the ends of the connectors to 230 V AC.
6. In this way, change the acid / base and do the experiment.

The bulb glows in the experiment when the beaker contains acid or base. Hence, when the bulb glows we can say that acid or base contain ions.

Question 6.
List out the material for the experiment “when Hydrochloric acid reacts with NaHCO₃ and evolves CO₂“. Write the experimental procedure. (TS March 2018)
Answer:
Required material : Stand, test tubes, delivery tube, thistle funnel, two hole rubber corks, Ca(OH)₂, NaHCO₃, HCl.

Experimental procedure :

1. Take NaHCO₃ in a test tube and fix two hole cork to the test tube.
2. Fix thistle funnel in one hole of cork and insert delivery tube in the second hole of the cork. Insert the second end of the delivery tube in the other test tube which is containing Ca(OH)₂/lime water.
3. Pour dil. HCl into the test tube using thistle funnel.
4. Due to chemical reaction, gas is evolved and pass into the Ca(OH)₂ through delivery tube. It turns in to milky. We can conclude that it is CO₂ gas.

Question 7.
Prepare a table based on the colour responses of acid, base and salt with indicators such as indicators. (AP SA-I:2018-19)
Answer:

Question 8.
Draw universal pH value indicator and identify different substances. (AP SA-I : 2019-20)
(OR)
Draw a neat diagram showing variation of pH with the chage in concentration of H⁺_(aq) ion and OH^–_(aq) ions.
Answer:

Variation of pH with the change in concentration of H⁺_(aq) ions and OH^–_(aq) ions.

Question 9.

Answer the following questions by using above information. (TS June 2019)
1) Which of the above is neutral solution?
2) Which of the above is used to neutralize the acidity in stomach?
3) Which is the strong acid among the above solutions?
4) What is the colour of Phenolphthalein indicator in NaOH solution?
Answer:

1. Distilled water
2. Milk of Magnesia
3. Gastric juice
4. Pink

Question 10.
If the pH values of solutions X, Y and Z are 13, 6 and 2 respectively, then
a) Which solution is a strong acid? Why?
b) Which solution contains ions along with molecules of solution?
c) Which solution is a strong base? Why?
d) Does the pH value of a solution increase or decrease when a base is added to it? Why?
Answer:
The strength of an acid (or) an alkali can be tested by using pH value of a solution. If the value of a pH of a solution is less, then that solution exhibits acidic nature.

If the value of a pH of a solution is more, then that solution exhibits basic nature.
pH value of a solution “X” is 13
pH value of a solution “Y” is 6
pH value of a solution “Z” is 2

a) Solution ‘Z’ is strong acid because its pH is 2.
b) Among given solutions, solution X is weakest acid. Weak solution contains ions along with molecules of solution. So X exhibits like this character.
c) Solution X is strong base. Because its pH is 13.
d) If base is added to solution ‘Z’, then its pH will increase.

Question 11.
Distinguish between acids and bases.
Answer:

Acids	Bases
1) They are sour to taste.	1) They are better to taste and soapy to touch.
2) When non-metallic oxides dissolved in water they form acids.	2) When metallic oxides dissolved in water they form bases.
3) They react with bases to form salt and water.	3) They react with acids to form salt and water.
4) They produce aqueous H+ ions.	4) They produce aqueous OH- ions.
5) They turn blue litmus into red.	5) They turn red litmus into blue.
6) They turn methyl orange indicator to red.	6) They turn methyl orange indicator to yellow.
7) The turn phenolphthalein indicator to colourless.	7) They turn phenolphthalien indicator to pink.

Question 12.
Explain chlor-alkali process.
Answer:
When electricity is passed through an aqueous solution of sodium chloride, it decomposes to form sodium hydroxide. The process is called chloralkali process because of the products formed chlor for chlorine and alkali for sodium hydroxide.
2 NaCl (aq) + 2H₂O(l) → 2NaOH(aq) + Cl₂(g) + H₂(g)

Chlorine gas is given off at the anode and hydrogen gas at the cathode and sodium hydroxide is formed near the cathode.

Question 13.
Define the following. Give one example for each.
a) Strong acid
b) Strong base
c) Weak acid
d) Weak base.
Answer:
a) Strong acid :
The acid which undergoes 100% ionisation is called strong acid.
e.g.: HCl, H₂SO₄

b) Strong base :
The base which undergoes 100% ionisation is called strong base.
e.g.: NaOH, KOH

c) Weak acid:
The acid which undergoes less than 100% ionisation is called weak acid.
e.g.: CH₃COOH, H₂CO₃

d) Weak base:
The base which undergoes less than 100% ionisation is called weak base.
e.g.: NH₄OH, Mg(OH)₂

Question 14.
Write any four chemical properties of acids.
Answer:
Chemical properties of acids :
1) Active metals react with acids and liberate hydrogen gas.
Zn + HCl → ZnCl₂ + H₂ ↑

2) Acids react with bases to form salt and water.
HCl_(aq) + NaOH_(aq) → NaCl_(aq) + H₂O_(l)

3) Acids react with metallic oxides to form salt and water.
MgO_(s)+ 2HCl_(aq) → MgCl_2(aq) + H₂O_(l)

4) Acids react with carbonates and hydrogen carbonates and release carbon dioxide gas.
CaCO_3(s) + 2HCl_(aq) → CaCl_2(aq)+ H₂O_(l) + CO_2(g) ↑
Ca(HCO₃)_2(l) + 2HCl_(aq) → CaCl_2(aq) + 2H20((| + 2CO_2(g) ↑

Question 15.
Write the formulae of the following salts.
a) Sodium sulphate
b) Ammonium chloride
Identify the acids and bases for which the above salts are obtained. Also write chemical equations for the reactions between such acids and bases. Which type of chemical reactions are they?
Answer:
a) Formula of sodium sulphate is Na2S04. When sulphuric acid reacts with sodium hydroxide it forms sodium sulphate.
H₂SO_4(aq)+ 2NaOH_(aq) → Na₂SO_4(aq) + 2H₂O_(l)

b) Formula of Ammonium chloride is NH4C/. When Ammonium hydroxide reacts with hydrochloric acid it forms Ammonium chloride.
NH₄OH_(aq) + HCl_(aq) → NH₄Cl_(aq) + H₂O_(l)

Question 16.
Write balanced equations to satisfy each statement,
a) Acid + Active metal → Salt + Hydrogen
Answer:
Zn_(s) + 2HCl_(aq) → ZnCl_2(aq) + H_2(g)

b) Acid + Base → Salt + Water
Answer:
NaOH_(aq) + HCl_(aq) → NaCl_(aq) + H₂O_(l)

c) Acid + Carbonate / Hydrogen carbonate → Salt + Water + Carbon dioxide
Answer:
CaCO_3(s) + 2 HCl_(aq) → CaCl_2(aq) + H₂O_(l) + CO_2(g) ↑
NaHCO_3(s) + HCl_(aq) → NaCl_(aq) + H₂O_(l) + CO_2(g) ↑

d) Metal oxide + Acid → Salt + Water
Answer:
CaO_(s) + 2 HCl_(aq) → CaCl_2(aq) + H₍₂₎O_(l)

e) Non metal oxide + base → Salt + Water
Answer:
CO_2(g) + 2 NaOH_(aq) → Na₂CO_3(aq) + H₂O_(l)

Question 17.
Give important products obtained from chloralkali process.

Answer:
Result:
Five water molecules are present in one formula unit of copper sulphate. Water of crystallization proves that the crystals contain a fixed quantity of water in them.

Question 18.
Give the equations for the preparation of each of the following.
i) Copper sulphate from copper (II) oxide.
Answer:
CuO + H₂SO₄ → CuSO₄ + H₂O

ii) Potassium sulphate from potassium hydroxide solution.
Answer:
2 KOH + H₂SO₄ → K₂SO₄ + 2 H₂O

iii) Lead chloride from lead carbonate.
Answer:
PbCO₃ + 2 HCl → PbCl₂ + H₂O + CO₂

Question 19.
How are the following salts prepared?
1) Calcium sulphate from calcium carbonate
Answer:
When calcium carbonate is treated with sulphuric acid it forms calcium sulphate.
CaCO₃ + H₂SO₄ → CaSO₄ + H₂O + CO₂

2) Lead carbonate from lead nitrate
Answer:
When lead nitrate is treated with carbonic acid we will get lead carbonate.
Pb(NO₃)₂ + H2CO₃ → PbCO₃ + 2 HNO₃

3) Sodium nitrate from sodium hydroxide
Answer:
When sodium hydroxide is reacted with nitric acid it will form sodium nitrate.
NaOH + HNO₃ → NaNO₃ + H₂O

4) Magnesium carbonate from magnesium chloride
Answer:
When magnesium carbonate is reacted with hydrochloric acid it forms magnesium chloride.
MgCO₃ + 2 HCl → MgCl₂ + H₂O + CO₂

Question 20.
Which of the following reactions are considered as neutralization reactions? Why?
1) NaOH + HCl → NaCl + H₂O
2) CaO + 2 HCl → CaCl₂ + H₂O
3) CO₂ + 2 NaOH → Na₂CO₃ + H₂O
4) SiO₂ + CaO → CaSiO₃
Answer:
All of them are considered as neutralization reactions.

1. An acid (HCl) reacts with base (NaOH) and forms salt and water. So it is a neutralization reaction.
2. Here metallic oxide which is basic in nature reacts with acid and forms salt and water. So it is also a neutralization reaction.
3. In third case non-metallic oxide (acidic oxide) reacts with base (NaOH) and forms salt and water. So it is also a neutralization reaction.
4. In fourth case a metallic oxide (CaO) reacts with non-metallic oxide (SiO₂) and forms salt. So it is also a neutralization reaction in the absence 6f water.

Question 21.
Which metals produce hydrogen gas when they are reacted with bases like NaOH and KOH? Write the chemical equations for the reactions.
Answer:
Zinc, aluminium and lead react with bases like NaOH and KOH and produce hydrogen gas.

Question 22.
i) A solution has a pH of 7. How would you increase its pH and decrease its pH? Explain.
Answer;
We can increase the pH of a solution by adding base because we know that bases have pH > 7. We can decrease the pH of a solution by adding an acid because acidic solution have pH < 7.

ii) If a solution changes the colour of litmus from red to blue, then what can you say about its pH?
Answer:
Bases can change red litmus into blue. So the pH of the solution is greater than 7.

iii) What can you say about pH of a solution that liberates carbon dioxide from sodium carbonate?
Answer:
Acids react with carbonates and liberate hydrogen gas. So the pH of the solution is less than 7.

Question 23.
Write the pH values of some solutions.
Answer:

pH value	Solutions
0	Battery Acid
1	Con. H2S04
2	Lemon juice
3	Orange juice
4	Tomato juice
5	Black coffee, Bananas
6	Milk, urine
7	Pure water
8	Sea water, eggs
9	Baking soda
10	Milk of magnesia
11	Ammonia solution
12	Soapy water
13	Bleach oven cleaner
14	Liquid drain cleaner

Question 24.
Fill the following table of results of reactions between some substances (acids, bases, neutral substances) and indicators.

Answer:

Question 25.
The pH values of six solutions A, B, C, D, E, F are given as 5,2,1,3,7 and 9 respectively. Which solution is
a) Neutral
b) Strongly alkaline
c) Strongly acidic
d) Weakly acidic?
Arrange the pH in increasing order of Hydrogen ion concentration.
Answer:
a) Solution E is neutral.
b) Solution F is Alkaline.
c) Solution C is strongly acidic.
d) Solution A is weakly acidic.
e) Solution B is strongly acidic.
f) Solution D is strongly acidic.
g) Ascending order of increase of Hydrogen ion concentration is F, E, A, D, B, C.

Question 26.
Collect information about various organic acids different occurring naturally and prepare a table.
Answer:

1. Acetic acid	Vinegar (obtained from fruits after fermentation).
2. Citric acid	Citrus fruits like orange and lemons.
3. Butyric acid	Butter gone bad or rancid
4. Lactic acid	Curd
5. Malic acid	Apples
6. Oleic acid	Olive oil
7. Tartaric acid	Fruits such as grapes, apples and tamarind
8. Stearic acid	From fats
9. Succinic acid	From vegetables like lettuce and unripe fruits
10. Uric acid	From urine

Question 27.
Complete the table.

Answer:

Question 28.
Fill the table.

Answer:

Question 29.
Draw a diagram to show the reaction of acids with metals.
Answer:

Reaction of Zinc granules with dil. HCl and testing hydrogen gas by a burning candle

Question 30.
Draw a diagram to show that all metal carbonates and react hydrogen carbonates
Answer:

Question 31.
What are the uses of Bleaching powder?
Answer:

• It is used for bleaching cotton and linen in the textile industry for bleaching wood pulp in paper industry and for bleaching washed clothes in laundry.
• Used as an oxidizing agent in many chemical industries.
• Used for disinfecting drinking water to make it free of germs.
• Used as a reagent in the preparation of chloroform.

Question 32.
What are the uses of Baking soda?
Answer:
1) Baking powder is a mixture of baking soda and a mild edible acid such as tartaric acid. When baking powder is heated or mixed in water, the following reaction takes place.

Carbon dioxide produced during the reaction causes bread or cake to rise making them soft and spongy.

2) Sodium hydrogen carbonate is also an ingredient in antacids. Being alkaline, it neutralizes excess acid in the stomach and provides relief.

3) It is also used in soda-acid, fire extinguishers.

4) It acts as mild antiseptic.

Question 33.
What are the uses of Washing soda?
Answer:

• Sodium carbonate (washing soda) is used in glass, soaps and paper industries.
• It is used in the manufacture of sodium compounds such as borax.
• Sodium carbonate can be used” as a cleaning agent for domestic purposes.
• It is used for removing permanent hardness of water.

Question 34.
Write the chemical formulae of the following :
i) Bleaching powder
ii) Sodium Chloride
iii) Slaked lime
iv) Baking Soda
v) Washing Soda
vi) Gypsum
vii) Plaster of Paris
viii) Acetic acid
ix) Sodium Hydroxide
x) Limestone
Answer:
i) Bleaching powder = CaOCl₂
ii) Sodium Chloride = NaCl (Common Salt)
iii) Slaked lime (or) lime water = Ca(OH)₂
iv) Baking Soda = NaHCO₃
v) Washing Soda = Na₂CO₃, 10H₂O
vi) Gypsum = CaSO₄ . 2H₂O
vii) Plaster of Paris = CaSO₄ . ½H₂O
viii) Acetic acid = CH₃COOH
ix) Sodium Hydroxide = NaOH
x) Limestone = CaCO₃

Question 35.
What are the various applications of neutralization?
Answer:

• The acidity of soil is reduced by adding slaked lime.
• The sting of yellow wasps contains alkalis. If acetic acid is rubbed on affected area, they are neutralized.
• Ants and bees have formic acid in their stings which can be neutralised by applying soap and some other alkali.
• Antacids tablets contain magnesium hydroxide, persons suffering from acidity are administered these tablets.
• The affect of nettle plant leaves is neutralized by leaves of dock plant.

Question 36.
Mention two situations where you use hydrated and unhydrated salts in your daily life.
Answer:

• NaCl is unhydrated salt. It flows freely when filled in a container.
• NaHCl (Baking soda) is unhydrated salt. It flows freely when filled in a container.
• NaCO₃ . 10H₂O (washing soda) is hydrated salt. It leaves wetness inside the container.
• CaSO₄ . 2H₂O (Gypsum) is also hydrated salt. On careful heating of gypsum it loses water molecules partially to become (CaSO₄ . ½H₂O) P.O.P. It is used in hospitals as plaster for supporting fractured bones in right position.