AP SSC 10th Class Maths Solutions Chapter 6 Progressions Ex 6.1

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 6 Progressions Ex 6.1 Textbook Questions and Answers.

AP State Syllabus SSC 10th Class Maths Solutions 6th Lesson Progressions Exercise 6.1

10th Class Maths 6th Lesson Progressions Ex 6.1 Textbook Questions and Answers

Question 1.
In which of the following situations, does the list of numbers involved make an arithmetic progression, and why?
i) The taxi fare after each km when the fare is Rs. 20 for the first km and rises by Rs. 8 for each additional km.
Answer:
Fare for the first km = Rs. 20 = a
Fare for each km after the first = Rs. 8 = d
∴ The fares would be 20, 28, 36, 44, …….
The above list forms an A.P.
Since each term in the list, starting from the second can be obtained by adding ‘8’ to its preceding term.

ii) The amount of air present in a cylinder when a vacuum pump removes \(\frac{1}{4}\)th of the air remaining in the cylinder at a time.
Answer:
Let the amount of air initially present in the cylinder be 1024 lit.
First it removes \(\frac{1}{4}\)th of the volume
i.e., \(\frac{1}{4}\) × 1024 = 256
∴ Remaining air present in the cylinder = 768
At second time it removes \(\frac{1}{4}\)th of 768
i.e., \(\frac{1}{4}\) × 768 = 192
∴ Remaining air in the cylinder = 768 – 192 = 576
Again at third time it removes \(\frac{1}{4}\)th of 576
i.e., \(\frac{1}{4}\) × 576 = 144
Remaining air in the cylinder = 576 – 144 = 432
i.e., the volume of the air present in the cylinder after 1st, 2nd, 3rd,… times is 1024, 768, 576, 432, …..
Here, a₂ – a₁ = 768 – 1024 = – 256
a₃ – a₂ = 576 – 768 = – 192
a₄ – a₃ = 432 – 576 = – 144 .
Thus the difference between any two successive terms is not equal to a fixed number.
∴ The given situation doesn’t show an A.P.

iii) The cost of digging a well, after, every metre of digging, when it costs ? 150 for the first metre and rises by ? 50 for each subsequent metre.
Answer:
Cost for digging the first metre = Rs. 150
Cost for digging subsequent metres = Rs. 50 each.
i.e.,

The list is 150, 200, 250, 300, 350, ……..
Here d = a₂ – a₁ = a₃ – a₂ = a₄ – a₃ = ……. = 50
∴ The given situation represents an A.P.

iv) The amount of money in the account every year, when Rs. 10000 is deposited at compound interest at 8 % per annum.
Answer:
Amount deposited initially = P = Rs. 10,000
Rate of interest = R = 8% p.a [at C.I.]
∴ \(A=P\left(1+\frac{R}{100}\right)^{n}\)

The terms 10800, 11664, 12597.12, ……. a₂ – a₁ = 800
Here, a = 10,000                                     a₃ – a₂ = 864
But, a₂ – a₁ ≠ a₃ – a₂ ≠ a₄ – a₃                a₄ – a₃ = 953.12
∴ The given situation doesn’t represent an A.P.

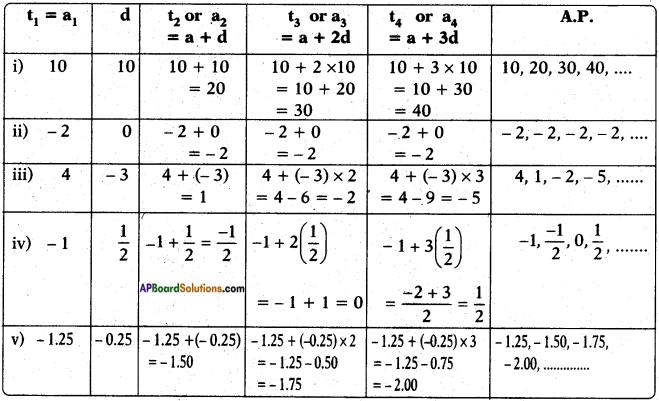
Question 2.
Write first four terms of the AP, when the first term a and the common difference d are given as follows:
i) a = 10, d = 10
ii) a = -2, d = 0
iii) a = 4, d = – 3
iv) a = – 1, d = 1/2
v) a = – 1.25, d = – 0.25
Answer:

Question 3.
For the following A.Ps, write the first term and the common difference:
i) 3, 1, – 1, – 3,….
ii) – 5, – 1, 3, 7,….
iii) \(\frac{1}{3}\), \(\frac{5}{3}\), \(\frac{9}{3}\), \(\frac{13}{3}\), ……..
iv) 0.6, 1.7, 2.8, 3.9,…
Answer:

Question 4.
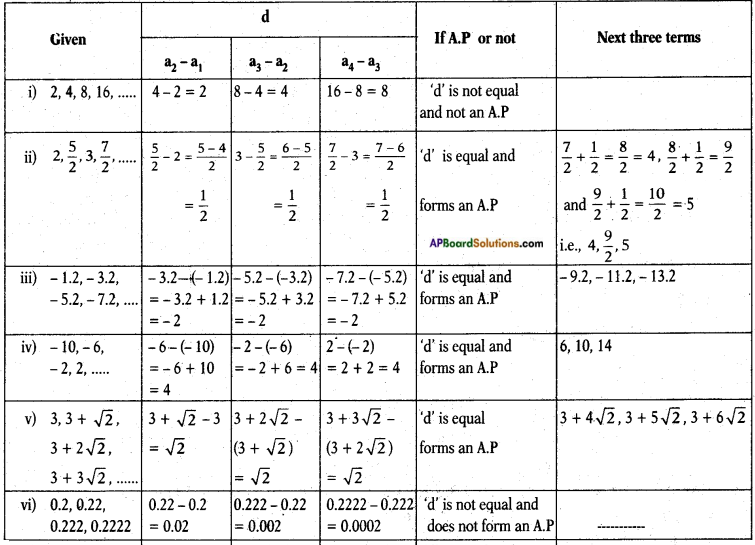
Which of the following are APs ? If they form an AP, find the common difference d and write three more terms.
i) 2, 4, 8, 16, …….
ii) 2, \(\frac{5}{2}\), 3, \(\frac{7}{2}\), …….
iii) – 1.2, – 3.2, – 5.2, – 7.2,……
iv) -10,-6, -2, 2, …….
v) 3, 3 + √2, 3 + 2√2, 3 + 3√2, …….
vi) 0.2, 0.22, 0.222, 0.2222, ……
vii) 0, -4, -8, -12, …….
viii) –\(\frac{1}{2}\), –\(\frac{1}{2}\), –\(\frac{1}{2}\), –\(\frac{1}{2}\)
ix) 1, 3, 9, 27,…..
x) a, 2a, 3a, 4a,….
xi) a, a², a³, a⁴, …..
xii) √2, √8, √18, √32, …….
xiii) √3, √6, √9, √12, …….
Answer: