Students get through Maths 1A Important Questions Inter 1st Year Maths 1A Functions Important Questions which are most likely to be asked in the exam.
Intermediate 1st Year Maths 1A Functions Important Questions
I.
Question 1.
If f: R – {0} → R is defined by f(x) = x + \(\frac{1}{x}\), then prove that (f(x))2 = f(x2) + f(1).
Solution:
f : R – {0} → R and
f(x) = x + \(\frac{1}{x}\)
Now f(x2) + f(1) = (x2 + \(\frac{1}{x^{2}}\)) + (1 + \(\frac{1}{1}\))
= x2 + 2 + \(\frac{1}{x^{2}}\) = (x + \(\frac{1}{x}\))2 = (f(x))2
∴ (f(x))2 = f(x2) + f(1)
![]()
Question 2.
If the function f is defined by
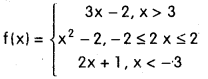
then find the values, if exist, of f(4), f(2.5), f(-2), f(-4), f(0), f(-7). (Mar. ’14)
Solution:
Domain of f is(-∞, -3) ∪ [-2, 2] ∪ (3, ∞)
i) Since f(x) = 3x – 2 for x > 3
f(4) = 3(4) – 2 = 10
ii) 2.5 does not belong to domain off, hence
f(2.5) is not desired.
iii) ∵ f(x) = x2 – 2 for -2 ≤ x ≤ 2
f(-2) = (-2)2 – 2 = 4 – 2 = 2
iv) ∵ f(x) = 2x + 1 for x < -3
f(-4) = 2(-4) + 1 = – 8 + 1 = -7
v) ∵ f(x) = x2 – 2, for -2 ≤ x ≤ 2
f(0)= (0)2 – 2 = 0 – 2 = -2
vi) ∵ f(x) = 2x + 1 for x < -3
f(-7) = 2(-7) + 1 = -14 + 1 = -13
Question 3.
If A = {0, \(\frac{\pi}{6}\), \(\frac{\pi}{4}\), \(\frac{\pi}{3}\), \(\frac{\pi}{2}\)} and f : A → B is a surjection defined by f(x) = cos x, then find B. (A.P. Mar. ’16, ’11; May ’11)
Solution:
∵ f : A → B is a sujection defined by
f(x) = cos x
B = Range of f = f(A)
= {f(0), f(\(\frac{\pi}{6}\)), f(\(\frac{\pi}{4}\)), f(\(\frac{\pi}{3}\)), f(\(\frac{\pi}{2}\))}
= {cos 0, cos \(\frac{\pi}{6}\), cos \(\frac{\pi}{4}\), cos \(\frac{\pi}{3}\), cos \(\frac{\pi}{2}\)}
= {1, \(\frac{\sqrt{3}}{2}\), \(\frac{1}{\sqrt{2}}\), \(\frac{1}{2}\), 0}
Question 4.
Determine whether the function f: R → R defined by f(x) = \(\frac{e^{|x|}-e^{-x}}{e^{x}+e^{-x}}\) is an injection or a surjection or a bijection.
Solution:
f(x) = \(\frac{e^{|x|}-e^{-x}}{e^{x}+e^{-x}}\)
f(0) = \(\frac{e^{0}-e^{-0}}{e^{0}+e^{-0}}\) = \(\frac{1-1}{1+1}\) = 0
f(-1) = \(\frac{e^{1}-e^{1}}{e^{-1}+e^{1}}\) = 0
∵ f(0) = f(-1)
⇒ f is not an injection.
Let y = f(x) = \(\frac{e^{|x|}-e^{-x}}{e^{x}+e^{-x}}\)
When y = 1, there is no x ∈ R such that f(x) = 1
⇒ f is not a surjection
if there is such x ∈ R then
\(\frac{e^{|x|}-e^{-x}}{e^{x}+e^{-x}}\) = 1
⇒ e|x| – e-x = ex + e-x, clearly x ≠ 0
for x > 0, this equation gives
ex – e-x = ex + e-x ⇒ -e-x = e-x which is not possible
for x < 0, this equation gives
e-x – e-x = ex + e-x
⇒ e-x = ex which is also not possible.
![]()
Question 5.
Determine whether the function f: R → R defined by
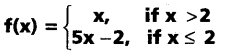
is an injection or a surjection or a bijection
Solution:
∵ f(x’) = x for x > 2
⇒ f(3) = 3
∵ f(x) = 5x – 2, for x ≤ 2
⇒ f(1) = 5(1) – 2 = 3
∵ 1 and 3 have same f-image.
Hence f is not an injection.
Let y ∈ R then y > 2 (or) y ≤ 2.
If y > 2 take x = y ∈ R so that
f(x) = x = y
If y ≤ 2 take x = \(\frac{y+2}{5}\) ∈ R and
x = \(\frac{y+2}{5}\) < 1
∴ f(x) = 5x – 2 = 5\(\left[\frac{y+2}{5}\right]\) – 2 = y
∴ f is a surjection
∵ f is not an injection ⇒ It is not a bijection.
Question 6.
Find the domain of definition of the function y(x), given by the equation 2x + 2y = 2.
Solution:
2x = 2 – 2y < 2 (∵ 2y > 0)
⇒ log2 2x < log22
⇒ x < 1
∴ Domain = (-∞, 1)
Question 7.
It f: R → R is defined as f(x + y) = f(x)+ f(y) ∀ x, y ∈R and f(1) = 7, then find \(\sum_{r=1}^{n} f(r)\).
Solution:
Consider f(2) = f(1 + 1) = f (1) + f (1) = 2f(1)
f(3) =f(2 + 1) = f(2) + f(1) = 3f(1)
Similarly f(r) = rf(1)
∴ \(\sum_{r=1}^{n} f(r)\) = f(1) + f(2) + ….. + f(n)
= f(1) + 2f(1)+ ….. + nf(1)
= f(1) (1 + 2 + ….. + n)
= \(\frac{7 n(n+1)}{2}\)
Question 8.
If f(x) = \(\frac{\cos ^{2} x+\sin ^{4} x}{\sin ^{2} x+\cos ^{4} x}\) ∀ x ∈ R then show that f(2012) = 1.)
Solution:
f(x) = \(\frac{\cos ^{2} x+\sin ^{4} x}{\sin ^{2} x+\cos ^{4} x}\)
= \(\frac{1-\sin ^{2} x+\sin ^{4} x}{1-\cos ^{2} x+\sin ^{4} x}\)
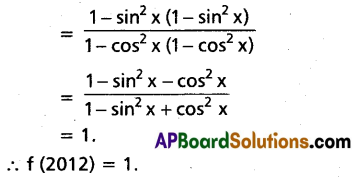
Question 9.
If f : R → R, g : R → R are defined by f(x) = 4x – 1 and g(x) = x2 + 2 then find
i) (gof)(x)
ii) (gof)\(\left(\frac{a+1}{4}\right)\)
iii) (fof)(x)
iv) go(fof)(0) (Mar. ’05)
Solution:
Given f : R → R and g : R → R and
f(x) = 4x – 1 and g(x) = x2 + 2
(i) (gof) (x) = g (f(x))
= g (4x – 1), ∵ f(x) = 4x – 1
= (4x – 1)2 + 2, ∵ g(x) = x2 + 2
= 16x2 – 8x + 1 + 2
= 16x2 – 8x + 3
(ii) (gof)\(\left(\frac{a+1}{4}\right)\) = \(g\left(f\left(\frac{a+1}{4}\right)\right)\)
= \(g\left(4\left(\frac{a+1}{4}\right)-1\right)\)
= g(a)
= a2 + 2
(iii) (fof)(x) = f(f(x))
= f(4x – 1), ∵ f(x) = 4x – 1
= 4(4x – 1) – 1
= 16x – 4 – 1 = 16x – 5
![]()
(iv) (fof)(0) = f(f(0))
= f(4 × 0 – 1)
= f(-1)
= 4(-1) – 1 = -5
Now go(fof)(0)
= g(-5) = (-5)2 + 2 = 27
Question 10.
If f: [0, 3] → [0, 3] is defined by
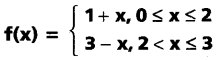
then show that f[0,3] ⊆ [0, 3] and find fof.
Solution:
0 ≤ x ≤ 2 ⇒ 1 ≤ 1 + x ≤ 3 ——— (1)
2 < x ≤ 3 ⇒ -3 ≤ -x ≤ -2
⇒ 3 – 3 ≤ 3 – x ≤ 3 – 2
⇒ 0 ≤ 3 – x < 1 ——- (2)
from (1) and (2).
f[0, 3] ⊆ [0, 3]
When 0 ≤ x ≤ 1, we have
(fof) (x) = f(f(x))
= f(1 + x) = 1 + (1 + x) = 2 + x
[∵ 1 ≤ 1 + x ≤ 2]
When 1 < x ≤ 2, we have
(fof) (x) = f(f(x))
= f(1 + x)
= 3 – (1 + x)
= 2 – x, [∵ 2 < 1 + x ≤ 3]
When 2 < x ≤ 3, we have
(fof) (x) = f(f(x))
= f(3 – x)
= 1 + (3 – x)
= 4 – x, [∵ 0 ≤ 3 – x < 1]
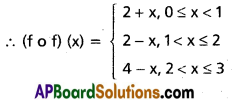
Question 11.
If f, g : R → R are defined
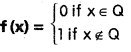
and 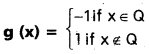
then find (fog)(π) + (gof)(e).
Solution:
(fog)(π) = f(g(π)) = f(0) = 0
(gof)(e) = g(f(e)) = g (1) = -1
∴ (fog)(π) + (gof) (e) = -1.
Question 12.
Let A = {1, 2, 3), B = {a, b, c}, C = (p, q, r}
If f: A → B, g: B → C are defined by
f = {(1, a), (2, c), (3, b)},
g = {(a, q), (b, r), (c, p)} then
show that f-1og-1 = (gof)-1
Solution:
Given that
f = {(1, a), (2, c), (3, b)} and
g = {(a, q), (b, r), (c, p)}
then g f = {(1, q), (2, p), (3, r)}
⇒ (gof)-1 = {(q, 1), (p, 2), (r, 3)}
⇒ g-1 = {(q, a), (r, b), (p, c)} and
f-1 = {(a, 1), (c, 2), (b, 3)}
f-1 g-1 = {(q, 1), (r, 3), (p, 2)}
⇒ (gof)-1 = f-1og-1
![]()
Question 13.
If f: Q → Q, is defined by f(x) = 5x + 4 for all x ∈ Q, show that f is a bijection and find f-1.(A.P Mar. ’16, May ’12, ’05)
Solution:
Let x1, x2 ∈ Q
Now f(x1) = f(x2)
⇒ 5x1 + 4 = 5x2 + 4
⇒ 5x1 = 5x2
⇒ x1 = x2
∴ f is an injection.
Let y ∈ Q then x = \(\frac{y-4}{5}\) ∈ Q and
f(x) = f\(\left(\frac{y-4}{5}\right)\) = 5\(\left(\frac{y-4}{5}\right)\) + 4 = y
∴ f is a surjection.
Hence f is a bijection
∴ f-1 : Q → Q is also bijection
We have (fof-1)(x) = I(x)
⇒ f(f-1(x)) = x, ∵ f(x) = 5x + 4
⇒ 5f-1(x) + 4 = x
⇒ f-1(x) =\(\frac{x-4}{5}\) for ∀ x ∈ Q
Question 14.
Find the domains of the following real valued functions.
i) f(x) = \(\frac{1}{6 x-x^{2}-5}\)
Solution:
f(x) = \(\frac{1}{6 x-x^{2}-5}\) = \(\frac{1}{(x-1)(5-x)}\) ∈ R
⇔ (x – 1) (5 – x) ≠ 0
⇔ x ≠ 1, 5
∴ Domain of f is R – {1, 5}
ii) f(x) = \(\frac{1}{\sqrt{x^{2}-a^{2}}}\), (a > 0) (A.P.) (Mar. ’15)
Solution:
f(x) = \(\frac{1}{\sqrt{x^{2}-a^{2}}}\) ∈ R
⇔ x2 – a2 > 0
⇔ (x + a)(x – a) > 0
⇔ x ∈ (-∞, -a) ∪ (a, ∞)
∴ Domain of f is (-∞, -a) ∪ (a, ∞) = R – [-a, a]
![]()
iii) f(x) = \(\sqrt{(x+2)(x-3)}\)
Solution:
f(x) = \(\sqrt{(x+2)(x-3)}\) ∈ R
⇔ (x + 2)(x – 3) ≥ 0
⇔ x ∈ (-∞, -2) ∪ [3, ∞)
∴ Domain of f is
(-∞, -2] ∪ [3, ∞) = R – (-2, 3)
iv) f(x) = \(\sqrt{(x-\alpha)(\beta-x)}\) (0 < α < β)
Solution:
f(x) = \(\sqrt{(x-\alpha)(\beta-x)}\) ∈R
⇔ (x – α) (β – α) ≥ 0
⇔ α ≤ x ≤ β ; (∵ α < β)
⇔ x ∈ [α, β]
∴ Domain of f is [α, β]
v) f(x) = \(\sqrt{2-x}\) + \(\sqrt{1+x}\)
Solution:
f(x) = \(\sqrt{2-x}\) + \(\sqrt{1+x}\) + x ∈ R
⇔ 2 – x ≥ 0 and 1 + x ≥ 0
⇔ 2 ≥ x and x ≥ -1
⇔ -1 ≤ x ≤ 2
⇔ x ∈ [-1, 2]
∴ Domain of f is [-1, 2].
vi) f(x) = \(\sqrt{x^{2}-1}\) + \(\frac{1}{\sqrt{x^{2}-3 x+2}}\)
Solution:
f(x) = \(\sqrt{x^{2}-1}\) + \(\frac{1}{\sqrt{x^{2}-3 x+2}}\) ∈ R
⇔ x2 – 1 ≥ 0 and x2 – 3x + 2 > 0
⇔ (x + 1)(x – 1) ≥ 0 and (x – 1)(x – 2) > 0
⇔ x ∈ (-∞, -1] ∪ [1, ∞) and x ∈ (-∞, 1)u(2, ∞)
⇔ x ∈ (R – (-1, 1)) ∩ (R – [1, 2])
⇔ x ∈ R – {(-1, 1) ∪ [1,2]}
⇔ x ∈ R – (-1, 2]
⇔ x ∈ (-∞, -1] ∪ (2, ∞)
∴ Domain of f is (-∞, -1) ∪ (2, ∞) = R – (-1, 2]
vii) f(x) = \(\frac{1}{\sqrt{|x|-x}}\)
Solution:
f(x) = \(\frac{1}{\sqrt{|x|-x}}\) ∈ R
⇔ |x| – x > 0
⇔ |x| > x
⇔ x ∈ (-∞, 0)
∴ Domain of f is (-∞, 0)
viii) f(x) = \(\sqrt{|x|-x}\)
Solution:
\(\sqrt{|x|-x}\) ∈ R
⇔ |x| – x ≥ 0
⇔ |x| ≥ x
⇔ x ∈ R
∴ Domain of f is R
Question 15.
If f = ((4, 5), (5, 6), (6, -4)} and g = ((4, -4), (6, 5), (8, 5)} then find
(i) f + g
(ii) f – g
(iii) 2f + 4g
(iv) f + 4
(v) fg
(vi) \(\frac{\mathbf{f}}{\mathbf{g}}\)
(vii) |f|
(viii) \(\sqrt{f}\)
(ix) f2
(x) f3
Solution:
Given that f = ((4, 5), (5, 6), (6, -4)}
g {(4, —4), (6, 5), (8, 5)}
Domain of f = {4, 5, 6} = A
Domain of g = (4, 6, 8} = B
Domain of f ± g = A ∩ B = {4, 6}
i) f + g = {4, 5 + (-4), (6, -4 + 5)}
= {(4, 1), (6, 1)}
ii) f – g = {(4, 5 – (-4)), (6, -4, -5)}
= {(4, 9), (6, -9)}
iii) Domain of 2f = A = {4, 5, 6}
Domain of 4g = B = {4, 6, 8}
Domain of 2f + 4g = A ∩ B = {4, 6}
∴ 2f = {(4, 10), (5, 12), (6, -8)}
4g = {(4, —16), (6, 20), (8, 20)}
∴ 2f + 4g = {(4, 10 + (-16), 6, -8 + 20)}
= {(4, -6), (6, 12)}
iv) Domain of f + 4 = A= {4, 5, 6}
f + 4 ={4, 5 + 4), (5, 6 +4), (6, -4 + 4)}
= ((4, 9), (5, 10), (6, 0)}
![]()
v) Domain of fg = A ∩ B = {4, 6}
fg = {(4, (5) (-4), (6, (-4) (5))}
= {(4, -20), (6, -20)}
vi) Domain of \(\frac{f}{g}\) = {4, 6}
∴ \(\frac{f}{g}\) = {(4, \(\frac{-5}{4}\)), (6, \(\frac{-4}{5}\))}
vii) Domain of |f| = {4, 5, 6}
∴ |f| = {(4, |5|), (5, |6|), (6, |-4|)}
= {(4, 5), (5, 6), (6, 4))
viii) Domain of \(\sqrt{f}\) = {4, 5}
∴ \(\sqrt{f}\) = {(4, \(\sqrt{5}\)), (5, \(\sqrt{6}\))}
ix) Domain of f2 = {4, 5, 6} = A
∴ f2 = ((4, (5)2) (5, (6)2, (6, (-4)2)}
f2 = {(4, 25), (5, 36), (6, 16)}
x) Domain of f3 = A = {4, 5, 6}
∴ f3 = {(4, 53), (5, 63), (6, (-4)3}
= {(4, 125) (5, 216) (6, -64)}
Question 16.
Find the domains and ranges of the following real valued functions.
i) f(x) = \(\frac{2+x}{2-x}\)
ii) f(x) = \(\frac{x}{1+x^{2}}\)
iii) f(x) = \(\sqrt{9-x^{2}}\) (A.P.)(Mar. ’15)
Solution:
i) f(x) = \(\frac{2+x}{2-x}\) ∈ R
⇔ 2 – x ≠ 0 x ⇔ x ∈ R -{2}
∴ Domain of f is R – {2}
Let f(x) = \(\frac{y}{1}\) = \(\frac{2+x}{2-x}\).
Apply componendo and dividendo rule
⇒ \(\frac{y+1}{y-1}\) = \(\frac{(2+x)+(2-x)}{(2+x)-(2-x)}\)
⇒ \(\frac{y+1}{y-1}\) = \(\frac{4}{2 x}\)
⇒ x = \(\frac{2(y-1)}{y+1}\)
Clearly x is not defined for y + 1 = 0
(i.e.,) y = -1
∴ Range of f is R – {-1}.
ii) f(x) = \(\frac{x}{1+x^{2}}\)
Solution:
f(x) = \(\frac{x}{1+x^{2}}\) ∈ R
∵ ∀ x ∈ R, x2 + 1 ≠ 0
Domain of f is R
Let f(x) = y = \(\frac{x}{1+x^{2}}\)
⇒ x2y – x + y = 0
⇒ x = \(\frac{-(-1) \pm \sqrt{1-4 y^{2}}}{y}\) is a real number.
iff 1 – 4y2 ≥ 0; y ≠ 0
⇔ (1 – 2y)(1 + 2y) ≥ 0 and y ≠ 0
⇔ y ∈ \(\left[-\frac{1}{2} ; \frac{1}{2}\right]\) – {0}
Also x = 0 ⇒ y = 0
∴ Range of f = \(\left[-\frac{1}{2}, \frac{1}{2}\right]\)
iii) f(x) = \(\sqrt{9-x^{2}}\)
Solution:
f(x) = \(\sqrt{9-x^{2}}\) ∈ R
⇔ 9 – y2 ≥ 0
⇔ x ∈ [-3, 3]
∴ Domain of f is [-3, 3]
Let f(x) = y = \(\sqrt{9-x^{2}}\)
⇒ x = \(\sqrt{9-y^{2}}\) ∈ R
⇔ 9 – y2 ≥ 0 ⇔ (3 + y)(3 – y) ≥ 0
∴ -3 ≤ y ≤ 3
But f(x) attains only non negative values
∴ Range of f = [0, 3].
![]()
Question 17.
If f(x) = x2 and g(x) = |x|, find the following functions.
i) f + g
ii) f – g
iii) fg
iv) 2f
v) f2
vi) f + 3
Solution:
Given f(x) = x2
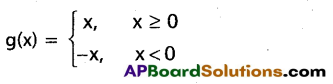
Domain of f = Domain of g = R
Hence domain of all the functions (i) to (vi) is R

iv) 2f(x) = 2 f(x) = 2x2
v) f2(x) = (f(x))2 = (x2)2 = x4
vi) (f + 3)(x) = f(x) + 3 = x2 + 3.
Question 18.
Determine whether the following functions are even or odd.
i) f(x) = ax – a-x + sin x
Solution:
Given f(x) = ax – a-x + sin x
∴ f(- x) = a-x – ax + sin (-x)
= a-x – ax – sin x
= – (ax – ax – sin x) = – f(x)
∴ f(x) is an odd function.
ii) f(x) = x\(\left(\frac{e^{x}-1}{e^{x}+1}\right)\)
Solution:
f(x) = x\(\left(\frac{e^{x}-1}{e^{x}+1}\right)\)

∴ f is an even function.
![]()
iii) f(x) = log (x + \(\sqrt{x^{2}+1}\))
Solution:
Given f(x) = log (x + \(\sqrt{x^{2}+1}\))
Then f(-x) = log (-x + \(\sqrt{(-x)^{2}+1}\))
= log (\(\sqrt{x^{2}+1}\) – x)
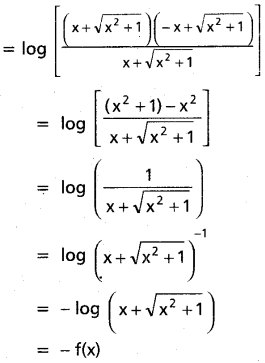
∴ f is an odd function.
Question 19.
Find the domains of the following real valued functions.
i) f(x) = \(\frac{1}{\sqrt{[x]^{2}-[x]-2}}\)
Solution:
f(x) = \(\frac{1}{\sqrt{[x]^{2}-[x]-2}}\) ∈ R
⇔ [x]2 – [x] – 2 > 0
⇔ ([x] + 1) ([x] – 2) > 0
⇔ [x] < -1, (or) [x] > 2
But [x] < -1 ⇒ [x] = -2, -3, -4, ……..
⇒ x < -1 [x] > 2 ⇒ [x] = 3, 4, 5, ……
⇒ x ≥ 3
∴ Domain of f = (-∞, -1) ∪ [3, ∞]
= R – [-1, 3)
ii) f(x) = log (x – [x])
f(x) = log (x – [x]) ∈ R
⇔ x – [x] > 0
⇔ x > [x]
⇔ x is a non integer
∴ Domain of f is R – Z
iii) f(x) = \(\sqrt{\log _{10}\left(\frac{3-x}{x}\right)}\)
Solution:
f(x) = \(\sqrt{\log _{10}\left(\frac{3-x}{x}\right)}\) ∈ R
⇔ log10\(\left(\frac{3-x}{x}\right)\) ≥ 0 and \(\frac{3-x}{x}\) > 0
⇔ \(\frac{3-x}{x}\) ≥ 10° = 1 and 3 – x > 0, x > 0
⇔ 3 – x ≥ x and 0 < x < 3
⇔ x ≤ \(\frac{3}{2}\) and 0 < x < 3
⇔ x ∈ (-∞, \(\frac{3}{2}\)] ∩ (0, 3) = (0, \(\frac{3}{2}\)]
∴ Domain of f is (0, \(\frac{3}{2}\)]
iv) f(x) = \(\frac{\sqrt{3+x}+\sqrt{3-x}}{x}\)
Solution:
f(x) = \(\frac{\sqrt{3+x}+\sqrt{3-x}}{x}\) ∈ R
⇔ 3 + x ≥ 0, 3 – x ≥ 0 and x ≠ 0
⇔ x ≥ -3, x ≤ 3 and x ≠ 0
⇔ -3 ≤ x ≤ 3, and x ≠ 0
⇔ x ∈ [-3, 3] and x ≠ 0
⇔ x ∈ [-3, 3] – {0}
∴ Domain of f is [-3, 3] – {0}
Question 20.
If f : A → B and g : B → C are two injective functions then the mapping gof : A → C is an injection.
Solution:
f : A → B and g: B → C are one—one.
∴ gof : A → C
To prove that g o f is one — one function
Let a1, a2 ∈ A ∴ f(a1), f(a2) ∈ B and g(f(a1)), g(f(a2)) ∈ C i.e., (gof) (a1), gof(a2) ∈ C
Now (gof) (a1) = gof (a2)
⇒ g(f(a1)) = g(f(a2))
⇒ f(a1) = f(a2) (∵ g is one -one)
⇒ a1 = a2 (∵ f is one-one)
Hence gof: A → C is a one-one function.
Note : The converse of the above theorem is not true.
If f : A → B, g: B → C and go f is one-one then both f and g need not be one-one.
For, consider
A = {1, 2}, B = {p, q, r), C = {s, t}
Let f = {(1, p), (2, q)} and
g = {(p, s), (q, t), (r, t)}
Now gof = {(1, s), (2, t)} ⇒ gof is one—one
from A to C
Observe that g: B → C is not one—one.
![]()
Question 21.
If f : A → B and g : B → C are two onto (surjective) functions then the mapping gof : A → C is a surjection. (May. ’08)
Solution:
f : A → B and g : B → C are onto.
∴ gof : A → C
To prove that gof is onto. Let c be any element of C.
Since g : B → C is an onto function there exists an element b ∈ B such that g(b) = c
Since f : A → B is an onto function, there exists an element a ∈ A such that f(a) = b
Now g(b) = c ⇒ g [f(a)] c = (gof) (a) = c
Thus for any element c ∈ C there is an element a ∈ A such that (gof) (a) = c
∴ gof : A → C is a surjection
Question 22.
If f : A → B and g : B → C are two bijective functions then the mapping gof : A → C is a bijection. (Mar. ’16, May ’12)
Solution:
f and g are injections gof: A → C is an injection.
f and g are surjections= gof : A → C is a surjection.
Hence it follows that if f and g are bijections,
gof is also a bijection.
Note : The converse of the above theorem is not true.
Question 23.
If f : A → B and g : B → C are such that gof is a surjection, then g is necessarily a surjection.
Solution:
Let c ∈ C. Since gof is a surjection, from A to
C there exists an element a ∈ A such that (gof) (a) = c, i.e., g(f(a)) = c
Since g: B → C and f(a) ∈ B, ∀ c ∈ C there exists an element belonging to B.
Hence g is a surjection.
Question 24.
If f : A → B and g : B → C and h : C → D are functions then ho(gof) = (hog)of (Mar. ’12, ’08)
Solution:
f : A → B and g : B → C gof : A → C
Now gof : A → C and h : C → D
⇒ ho(gof) : A → D
Similarly (hog) of : A → D
Thus ho (gof) and (hog) of both exist and have the same domain A and co-domain D.
Let a be an element of A.
Now [ho(gof)](a) = h[(gof)(a)] = h[g(f(a))]
= (hog) [f(a)] = [(hog)of] (a)
∴ ho(gof) = (hog)of
Note : Thus composition of mappings is associative.
Question 25.
Let f : A → B, IA and IB are identity functions on A and B respectively. Then for IA = f = IB of Mar.’12, ’08
Solution:
∵ IA : A → A and f : A → B are functions foIA is a function from A to B. Hence foIA and f are definded on same domain A.
i) Let a ∈ A then (foIA)(a) = f(IA(a))
= f(a)
[∵ IA(a) = a, ∀ a ∈ A]
∴ foIA = f ————- (1)
ii) ∵ f : A → B, IB : B → B are functions, IB of is a function from A to B
∴ The functions IB of and f are defined on the same domain A.
Let a ∈ A, then (IB of)(a)
= IB(f (a)) = f(a)
∵ f : A → B, we have f(a) ∈ B
∴ IB of = f ———– (2)
From(1) & (2) foIA = IBof = f
![]()
Question 26.
Let A and B be two non-empty sets. If f : A → B is a bijection, then f-1 : B → A is also a bijection.
Solution:
f : A → B is a bijection.
∴ f-1 : B → A is a unique function.
(i) To prove that f-1 is one—one:
Let b1 and b2 be any two different elements of B. i.e., b1 ≠ b2.
Then, we have to prove that
f-1(b1) ≠ F-1(b2)
Let f-1(b1) = a1 and f-1(b2) = a2
such that a1, a2 ∈ A
Then b1 = f(a1) and b2 = f(a2)
Now b1 ≠ b2 ⇒ f(a1) ≠ f(a2)
⇒ a1 ≠ a2 (∵ f is a bijection)
⇒ f-1(b1) ≠ f-1(b2)
∴ f-1 is one—one.
(ii) To prove that f-1 is onto:
Let ‘a’ be an element of A.
Then there exists an element b ∈ B such that f(a) = b (or) f-1(b) = a
(or) a = f-1(b)
Thus ‘a’ is the f-1 – image of the element b ∈ B
Hence f-1 is onto.
∴ f : B → A is a bijection.
Question 27.
If f : A → B is a bijection, then f-1of = IA and fof-1 = IB
(A.P) (Mar. 15,12, ’07; May ’07, ‘06)
Solution:
f : A → B is a bijection ⇒ f-1 : B → A is also a bijection.
By definition, fof-1 : B → B and f-1of : A → A are bijection
Also IA : A → A and IB : B → B
To prove that f-1of = IA
Let a ∈ A
Since f : A → B there exists a unique element
b ∈ B such that f(a) = b
a = f-1 (b) (∵ f is a bijection)
∴ (f-1of) (a) = f-1[f(a)]
= f-1(b) = a = IA (a)
f-1 of = IA
Similarly it can be shown that fof-1 = IB
Question 28.
If f : A → B and g : B → A are two functions such that gof = IA and fog = IB then g = f-1.
Solution:
(i) To prove that f is one—one:
Let a1, a2 ∈ A.
Since f: A → B, f(a1), f(a2) ∈ B
Now f(a1) = f(a2)
⇒ g[f(a1)] = g[f(a2)]
⇒ (gof)(a1) = gof(a2)
⇒ IA (a1) = IA (a2)
∴ a1 = a2 = ∴ f is one — one
(ii) To prove that f is onto :
Let b be an element of B
∴ b = IB fog(b)
⇒ b = f{(g(b)} ⇒ f{g(b)} = b
i.e., there exists a pre-image g(b) ∈ A for b, under the mapping f. ∴ f is onto
Thus f is one-one, onto and hence
f-1 : B → A exists and is also one — one and onto.
(iii) To prove g = f-1:
Now g : B → A and f-1 : B → A
Let a ∈ A and b be the f – image of a, where b ∈ B
∴ f(a) = b ⇒ a =f-1(b)
Now g(b) = g[f(a)] (gof) (a)
= IA(a) = a = f-1(b)
∴ g = f-1
![]()
Question 29.
If f : A → B and g : B → C are bijective functions, then (gof)-1 = f-1og-1(AP) (Mar. ‘16’14, ‘11; May ‘11)
Solution:
f : A → B, g : B → C are bijections
⇒ gof : A → C is a bijection
Also g-1 : C → B and f-1 : B → A are bijections
⇒ f-1og-1 : C → A is a bijection.
Let c be any element of C.
Then ∃ an element b ∈ B such that g(b) = c
⇒ b = g-1(c)
Also ∃ an element a A such that f(a) = b
⇒ a = f-1(b)
Now (gof) (a) = g(f(a) = g(b) = c
⇒ a = f-1(b)
Now (gof) (a) = g(f(a) = g(b) = c
⇒ a = (gof)-1 (c) ⇒ (gof) (c) = a
Also (f-1og-1) (c) ⇒ f-1 (g-1 (c)) = f-1 (b) = a
∴ From (1) and (2);
(gof)-1 (c) = (f-1og-1(c))
⇒ (gof)-1 = f-1og-1