Inter 1st Year Maths 1A Properties of Triangles Important Questions

Students get through Maths 1A Important Questions Inter 1st Year Maths 1A Properties of Triangles Important Questions which are most likely to be asked in the exam.

Intermediate 1st Year Maths 1A Properties of Triangles Important Questions

Question 1.
In ∆ABC, if a = 3, b = 4 and sinA = \(\frac{3}{4}\), find angle B.
Solution:
By sine Rule \(\frac{a}{\sin A}\) = \(\frac{b}{\sin B}\)
⇒ sin B = \(\frac{\text { b. } \sin A}{a}\) = \(\frac{4}{3}\) (\(\frac{3}{4}\)) = 1
⇒ sin B = 1 ⇒ B = 90°

Question 2.
If the lengths of the sides of a triangle are 3, 4, 5 find the circumradius of the triangle.
Solution:
∴ 3² + 4² = 5²
∴ The triangle is right angled and its hypotenuse = 5 = circum diameter.
∴ Circum radius = \(\frac{1}{2}\) (hypotenu) = \(\frac{5}{2}\) cms.

Question 3.
If a = 6, b = 5, c = 9, then find angle A.
Solution:
∵ cos A = \(\frac{\mathrm{b}^{2}+c^{2}-a^{2}}{2 b c}\)
= \(\frac{5^{2}+9^{2}-6^{2}}{2(5)(9)}\) = \(\frac{25+81-36}{2(5)(9)}\)
= \(\frac{70}{90}\) = \(\frac{7}{9}\)
∴ A = cos^-1(\(\frac{7}{9}\))

Question 4.
If ∆ABC, show that ∆ (b + c) cos A = 2s.
Solution:
L.H.S. = (b + c) cos A + (c + a) cos B + (a + b) cos C
= (b cos A + a cos B) + (c cos B + b cos C) + (a cos C + c cos A)
= c + a + b = 2S = R.H.S.

Question 5.
If the sides of a triangle are 13, 14, 15, then find the circum diameter.
Solution:
Let a = 13, b = 14, c = 15
Then 2s = a + b + c = \(\frac{13+14+15}{2}\) = \(\frac{42}{2}\)
∴ s = 21
s – a = 21 – 13 = 8
s – b = 21 – 14 = 7
s – c = 21 – 15 = 6
Now ∆ = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{21 \times 8 \times 7 \times 6}\)
= \(\sqrt{21 \times 21 \times 16}\) = 21 × 4 = 84
∵ ∆ = \(\frac{a b c}{4 R}\) ⇒ 4R = \(\frac{a b c}{\Delta}\)
= \(\frac{13 \times 14 \times 15}{84}\) = \(\frac{65}{2}\)
∴ R = \(\frac{65}{8}\)
∴ Circum diameter(2R) = 2 × \(\frac{65}{8}\) = \(\frac{65}{4}\)cms.

Question 6.
In a ∆A B C, if (a + b + c) (b + c – a) = 3 be, find A.
Solution:
(2s – sa) = 3bc ⇒ \(\frac{s(s-a)}{b c}\) = \(\frac{3}{4}\)
⇒ cos² \(\frac{A}{2}\) = \(\frac{3}{4}\) ⇒ cos \(\frac{A}{2}\) = \(\frac{1}{2}\) = cos 30°
∴ \(\frac{A}{2}\) = 30° = A = 60°

Question 7.
If a = 4, b = 5, c = 7, find cos \(\frac{B}{2}\).
Solution:
2s = a + b + c = 4 + 5 + 7 = 16
⇒ s = 8 and s – b = 8 – 5 = 3
Now cos \(\frac{B}{2}\) = \(\sqrt{\frac{s(s-b)}{a c}}\) = \(\sqrt{\frac{8 \times 3}{4 \times 7}}\) = \(\sqrt{\frac{6}{7}}\)

Question 8.
In ∆ ABC, find b cos² \(\frac{C}{2}\) + c cos² \(\frac{B}{2}\).
Solution:
b cos² \(\frac{C}{2}\) + c cos ² \(\frac{B}{2}\) = b[latex]\frac{s(s-c)}{a b}[/latex] + c[latex]\frac{s(s-b)}{c a}[/latex]
= \(\frac{s(s-c)}{a}\) + \(\frac{s(s-b)}{a}\) = \(\frac{\mathrm{s}}{\mathrm{a}}\)[s – c + s – b]
= \(\frac{\mathrm{s}}{\mathrm{a}}\) • a = s

Question 9.
If tan \(\frac{A}{2}\) = \(\frac{5}{6}\) and tan \(\frac{C}{2}\) = \(\frac{2}{5}\), determine the relation between a, b, c.    [Mar 05]
Solution:
tan \(\frac{A}{2}\) • tan \(\frac{C}{2}\) = \(\frac{5}{6}\) • \(\frac{2}{5}\)
\(\sqrt{\frac{(s-b)(s-c)}{s(s-a)}} \sqrt{\frac{(s-a)(s-b)}{s(s-c)}}\) = \(\frac{2}{6}\)
⇒ \(\frac{s-b}{s}\) = \(\frac{1}{3}\) ⇒ 3s – 3b = s ⇒ 2s = 3b
⇒ a + b + c = 3b ⇒ a + c = 2b Hence a, b, c are in A.P.

Question 10.
If cot \(\frac{A}{2}\) = \(\frac{b+c}{a}\), find angle B.
Solution:
cot \(\frac{A}{2}\) = \(\frac{b+c}{a}\) ⇒ \(\frac{\cos \frac{A}{2}}{\sin \frac{A}{2}}\) = \(\frac{\cos \left(\frac{B-C}{2}\right)}{\sin \frac{A}{2}}\) (by Mollweide rule)
⇒ \(\frac{A}{2}\) = \(\frac{B-C}{2}\)
⇒ A = B – C ⇒ A + C = B ⇒ A + B + C = 2B
∴ 2B = 180° ⇒ B = 90°

Question 11.
If tan (\(\frac{C-A}{2}\)) = k cot \(\frac{B}{2}\), find k.
Solution:
Comparing with tan (\(\frac{C-A}{2}\)) = \(\frac{c-a}{c+a}\) cot \(\frac{B}{2}\), (by tangent law)
we get that k = \(\frac{c-a}{c+a}\)

Question 12.
In ∆ABC, show that \(\frac{b^{2}-c^{2}}{a^{2}}\) = \(\frac{\sin (B-C)}{\sin (B+C)}\).
Solution:

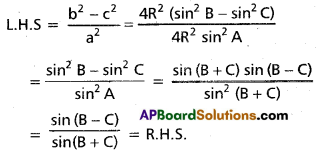
Question 13.
Show that a² cot A + b² cot B + c² cot C = \(\frac{a b c}{R}\).    [Mar 14]
Solution:
L.H.S. = a² cot A + b² cot B + c² cot C
= 4R² sin² A. \(\frac{\cos A}{\sin A}\) + 4R² sin²B. \(\frac{\cos B}{\sin B}\) + 4R² sin²C. \(\frac{\cos C}{\sin C}\) (by sine rule)
= 2R² (2 sin A cos A + 2 sin B cos B + 2 sin C cos C)
= 2R² (sin 2A + sin 2B + sin 2C) .
= 2R² (4 sin A sin B sin C) (from transformations)
= \(\frac{1}{R}\) (2R sin A) (2R sin B) (2R sin C)
= \(\frac{abc}{R}\) = R.H.S

Question 14.
Show that (b – c)² cos² \(\frac{A}{2}\) + (b + c)² sin² \(\frac{A}{2}\) = a².
Solution:
L.H.S. = (b² + c² – 2bc) cos² \(\frac{A}{2}\) + (b² + c² + 2bc) sin² \(\frac{A}{2}\)
= (b² + c²) [cos² \(\frac{A}{2}\) + sin² \(\frac{A}{2}\)] – 2bc (cos² \(\frac{A}{2}\) – sin² \(\frac{A}{2}\))
= b² + c² – 2bc cos A = a²

Question 15.
Prove that a (b cos C – c cos B) = b² – c²     [Mar 07]
Solution:
L.H.S. = ab cos C – ca cos B
= (\(\frac{a^{2}+b^{2}-c^{2}}{2}\)) – (\(\frac{c^{2}+a^{2}-b^{2}}{2}\)) (by cosine rule)
= \(\frac{1}{2}\)[a² + b² – c² – c² – a² + b²]
= b² – c² = R.H.S.

Question 16.
Show that \(\frac{c-b \cos A}{b-c \cos A}\) = \(\frac{\cos B}{\cos C}\).
Solution:
From projection rule c = a cos B – b cos A and b = c cos A + a cos C

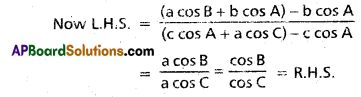
Question 17.
In ∆ABC, if \(\frac{1}{a+c}\) + \(\frac{1}{b+c}\) = \(\frac{3}{a+b+c}\) show that C = 60°.
Solution:
\(\frac{1}{a+c}\) + \(\frac{1}{b+c}\) = \(\frac{3}{a+b+c}\)
⇒ \(\frac{b+c+a+c}{(a+c)(b+c)}\) = \(\frac{3}{a+b+c}\)
⇒ 3(a + c) (b + c) = (a + b + 2c) (a + b + c)
⇒ 3(ab + ac + bc + c²) = (a² + b² + 2ab) + 3c(a + b) + 2c²
⇒ ab = a² + b² – c²
⇒ 2ab cos C (from cosine rule)
⇒ cos C = \(\frac{1}{2}\) ⇒ C = 60°

Question 18.
If a = (b – c) sec θ, prove that tan θ = \(\frac{2 \sqrt{b c}}{b-c}\) sin \(\frac{A}{2}\).    [Mar 16]
Solution:
a = (b – c) sec θ ⇒ sec θ = \(\frac{a}{b-c}\)
tan² θ = sec² θ – 1

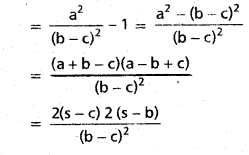
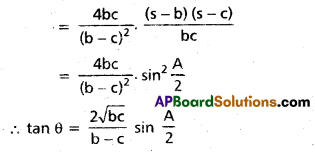
Question 19.
In ∆ABC, show that (a + b + c) (tan \(\frac{A}{2}\) + tan \(\frac{B}{2}\)) = 2c cot \(\frac{C}{2}\).
Solution:

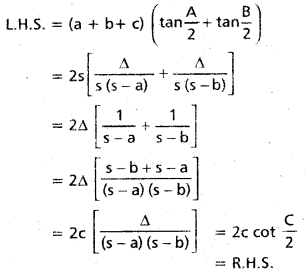
Question 20.
Show that b² sin 2C + c² sin 2B = 2bc sin A.
Solution:
L.H.S. = b² sin 2C + c² sin 2B
= 4R² sin² B (2 sin C cos C) + 4R² sin² C (2 sin B cos B)
= 8R² sin B sin C (sin B cos C + cos B sin C)
= 8R² sin B sin C sin (B + C)
= 2(2R sin B) (2R sin C) sin A
= 2bc sin A = R.H.S.

Question 21.
Prove that cot A + cot B + cot C = \(\frac{a^{2}+b^{2}+c^{2}}{4 \Delta}\)    [Mar 15]
Solution:

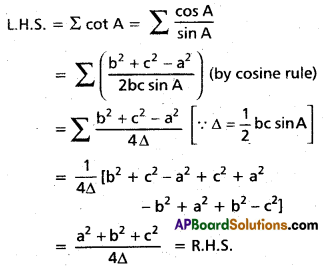
Question 22.
Show that a cos² \(\frac{A}{2}\) + b cos² \(\frac{B}{2}\) + c cos ² \(\frac{C}{2}\) = s + \(\frac{\Delta}{R}\).
Solution:
L.H.S. = Σ a cos² \(\frac{A}{2}\) = \(\frac{1}{2}\) Σ a (1 + cos A)
= \(\frac{1}{2}\) Σ (a + a cos A) = \(\frac{1}{2}\) (a + b + c) + \(\frac{1}{2}\) Σ (2R sin A cos A)
= \(\frac{1}{2}\) (2s) + \(\frac{R}{2}\) Σ sin 2A
= s + \(\frac{R}{2}\) (sin 2A + sin 2B + sin 2C)
= s + \(\frac{R}{2}\) (4 sin A sin B sin C)
= s + \(\frac{1}{R}\) (2R² sin A sin B sin C)
= s + \(\frac{\Delta}{R}\) (∵ ∆ = 2R² sin A sin B sin C)
= R.H.S.

Question 23.
In ∆ ABC, if a cos A = b cos B, prove that the triangle is either isosceles or right angled.
Solution:
a cos A = b cos B
⇒ 2R sin A cos A = 2R sin B cos B
⇒ sin 2A = sin 2B (or) = sin (180° – 2B)
Hence 2A = 2B or 2A = 180° – 2B
⇒ A = B or A = 90° – B ⇒ A = B or A + B = 90°
⇒ C = 90°
∴ The triangle is isosceles or right angled.

Question 24.
If cot \(\frac{A}{2}\) : cot \(\frac{B}{2}\) : cot \(\frac{C}{2}\) = 3 : 5 : 7, show that a : b : c = 6 : 5 : 4.
Solution:

Then s – a = 3k, s – b = 5k, s – c = 7k
Adding 3s – (a + b + c) = 3k + 5k+ 7k
⇒ 3s – 2s = 15k ⇒ s = 15k
Now a = 12k, b = 10k, c = 8k
∴ a : b : c = 12k : 10k : 8k = 6 : 5 : 4

Question 25.
Prove that a³ cos (B – C) + b³ cos (C – A) + c³ cos(A – B) = 3abc.
Solution:
L.H.S. = Σ a³ cos (B – C)
= Σ a² (2R sin A) cos (B – C)
= R Σ a² [2 sin (B + C) cos (B- C)]
= R Σ a² (sin 2B + sin 2C)
= R Σ a² (2 sin B cos B + 2 sin C cos C)
= Σ [a²(2R sin B) cos B + a²(2R sin C) cos C] Σ (a² b cos B + a²c cos C)
= (a²b cos B + a²c cos C) + (b²c cos C + b² a cos A) + (c² a cos A + c²b cos B)
= ab (a cos B + b cos A) + bc (b cos C + c cos B) + ca (c cos A + a cos C)
= ab(c) + bc(a) + ca(b) = 3 abc = R.H.S

Question 26.
If p₁, p₂, p₃ are the altitudes of the ∆ A, B, C show that \(\frac{1}{p_{1}^{2}}+\frac{1}{p_{2}^{2}}+\frac{1}{p_{3}^{2}}\) = \(\frac{\cot A+\cot B+\cot C}{\Delta}\)
Solution:
Since p₁, p₂, p₃ are the altitudes of ∆ ABC,

Question 27.
The angle of elevation of the top point P of the vertical tower PQ of height h from a point A is 45° and from a point B is 60°, where B is a point at a distance 30 meters from the point A measured along the line AB which makes an angle 30° with AQ. Find the height of the tower.
Solution:

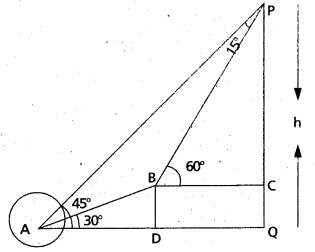
PQ = h, ∠PAQ = 45°
∠BAQ = 30° and ∠PBC = 60°
Also AB = 30 mts.
∴ ∠BAP = ∠APB = 15°.
This gives BP = AB = 30 and h = PC + CQ = BP sin 60° + AB sin 30°
= 15 \(\sqrt{3}\) + 15 = 15(\(\sqrt{3}\) +1) metres.

Question 28.
Two trees A and B are on the same side of a river. From a point C in the river the distances of the trees A and B are 250m and 300m respectively. If the angle C is 45°, find the distance between the trees (use \(\sqrt{2}\) = 1.414).
Solution:

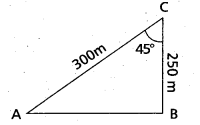
From the triangle ABC, using the cosine rule
AB² = 250² + 300² – 2(250) (300) cos 45°
= 100 (625 + 900 – 750\(\sqrt{2}\)) = 46450.
∴ AB = 215.5m. (approximately).

Question 29.
In A ABC, prove that \(\frac{1}{r_{1}}\) + \(\frac{1}{r_{2}}\) + \(\frac{1}{r_{3}}\) = \(\frac{1}{r}\).
Solution:
L.H.S. = \(\frac{1}{r_{1}}\) + \(\frac{1}{r_{2}}\) + \(\frac{1}{r_{3}}\) = \(\frac{s-a}{\Delta}\) + \(\frac{s-b}{\Delta}\) + \(\frac{s-c}{\Delta}\)
= \(\frac{3 s-(a+b+c)}{\Delta}\) = \(\frac{3 s-2 s}{\Delta}\) = \(\frac{s}{\Delta}\) = \(\frac{1}{r}\)
= R.H.S

Question 30.
Show that rr₁r ₂r₃ = ∆²
Solution:
L.H.S. = rr₁r ₂r₃ = \(\frac{\Delta}{s} \cdot \frac{\Delta}{s-a} \cdot \frac{\Delta}{s-b} \cdot \frac{\Delta}{s-c}\)
= \(\frac{\Delta^{4}}{\Delta^{2}}\) = ∆² = R.H.S

Question 31.
In an equilateral triangle, find the value of \(\frac{r}{R}\).
Solution:
\(\frac{r}{R}\) = \(\frac{4 R \sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2}}{R}\)
= 4 sin³ 30° (∵ A = B = C = 60°)
= 4 . (\(\frac{1}{2}\))³ = \(\frac{1}{2}\)

Question 32.
The perimeter of ∆ ABC is 12 cm. and its in radius is 1 cm. Then find the area of the triangle.
Solution:
Given that 2s = 12 ⇒ s = 6 cm.
and r = 1 cm
Area of ∆ ABC = ∆ = rs = (1) (6) = 6 sq.cms.

Question 33.
Show that rr₁ = (s – b) (s – c).
Solution:
L.H.S. = rr₁
= [(s – b) tan \(\frac{B}{2}\)] [(s – c) cot \(\frac{B}{2}\)]
= (s – b) (s – c) = R.H.S.
ans:

Question 34.
Express \(\frac{a \cos \mathbf{A}+\mathbf{b} \cos \mathbf{B}+\cos \mathbf{C}}{\mathbf{a}+\mathbf{b}+\mathbf{c}}\) in terms of R and r.
Solution:

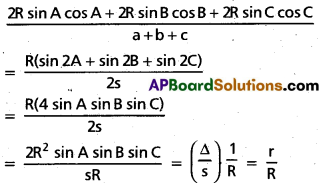
Question 35.
In ∆ABC, ∆ = 6sq.cm and s = 1.5 cm, find r.
Solution:
r = \(\frac{\Delta}{s}\) = \(\frac{6}{1.5}\) = 4 cm.

Question 36.
Show that rr₁ cot\(\frac{A}{2}\) = ∆.
Solution:
rr₁ cot\(\frac{A}{2}\) = \(\frac{\Delta}{s}\) (s tan \(\frac{A}{2}\)) cot \(\frac{A}{2}\) = ∆

Question 37.
If a = 13, b = 14, c = 15, find r₁.
Solution:
2s = a + b +c = 42
⇒ s = 21
s – a = 8, s – b = 7, s – c = 6
∆² = 21 × 8 × 7 × 6
⇒ ∆ = 7 × 12 = 84 sq. units
∴ r₁ = \(\frac{\Delta}{s-b}\) = \(\frac{84}{8}\) = 10.5 units

Question 38.
If rr₂ = r₁r₃, then find B.
Solution:

Question 39.
In a ∆ABC, show that the sides a, b, c are in A.P if and only if r₁, r₂, r₃ are in H.P.
Solution:
r₁, r₂, r₃ are in A.P.
⇔ \(\frac{1}{r_{1}}\), \(\frac{1}{r_{2}}\), \(\frac{1}{r_{3}}\) are in A.P.
⇔ \(\frac{s-a}{\Delta}\), \(\frac{s-b}{\Delta}\), \(\frac{s-c}{\Delta}\) are in A.P.
⇔ s – a, s – b, s – c are in A.P.
⇔ -a, -b, -c are in A.P.
⇔ a, b. c, are in A.R

Question 40.
If A = 90°, show that 2(r + R) = b + c.
Solution:
L.H.S = 2r + 2R
= 2(s – a) tan \(\frac{A}{2}\) + 2R.1
= 2(s – a) tan 45°+ 2RsinA
(∵A = 90°)
= (2s – 2a). 1 + a
= b + c = R.H.S.

Question 41.
If (r₂ – r₁) (r₃ – r₁) = 2r₂r₃, show that A = 90°.
Solution:
(r₂ – r₁) (r₃ – r₁) = 2r₂r₃

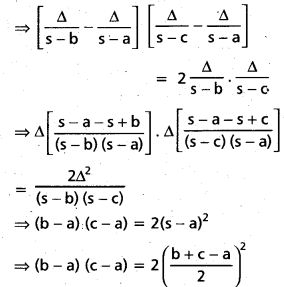
⇒ 2(bc – ca – ab + a²) = b² + c² + a² + 2bc – 2ca – 2ab
⇒ 2a² = b² + c² + a²
⇒ b² + c² = a²
Hence △ABC is right angled and A = 90°.

Question 42.
Prove that \(\frac{r_{1}\left(r_{2}+r_{3}\right)}{\sqrt{r_{1} r_{2}+r_{2} r_{3}+r_{3} r_{1}}}\) = a
Solution:

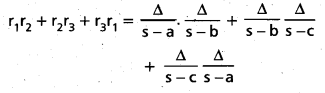
Question 43.
Show that \(\frac{1}{r^{2}}+\frac{1}{r_{1}^{2}}+\frac{1}{r_{2}^{2}}+\frac{1}{r_{3}^{2}}\) = \(\frac{a^{2}+b^{2}+c^{2}}{\Delta^{2}}\)
Solution:

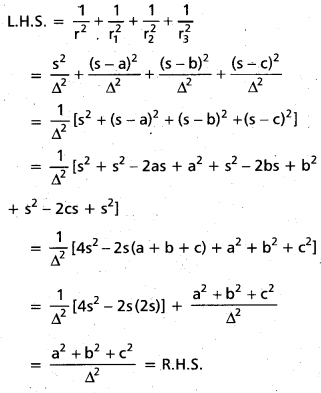
Question 44.
Prove that Σ(r + r₁) tan \(\left(\frac{B-C}{2}\right)\) = 0
Solution:
r + r₁ = 4R sin \(\frac{A}{2}\) sin \(\frac{B}{2}\) sin \(\frac{C}{2}\) + 4R sin \(\frac{A}{2}\) cos \(\frac{B}{2}\) cos \(\frac{C}{2}\)
= 4R sin\(\frac{A}{2}\)[sin \(\frac{B}{2}\) sin \(\frac{C}{2}\) + cos \(\frac{B}{2}\) cos \(\frac{C}{2}\)]

Question 45.
Show that \(\frac{r_{1}}{b c}+\frac{r_{2}}{c a}+\frac{r_{3}}{a b}=\frac{1}{r}-\frac{1}{2 R}\) .    [May 07]
Solution:

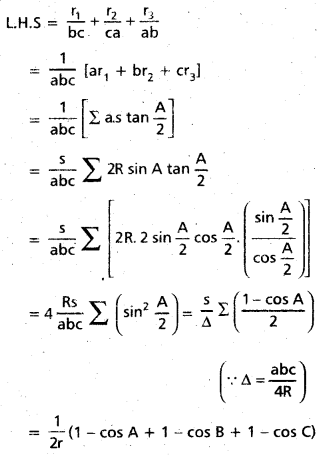
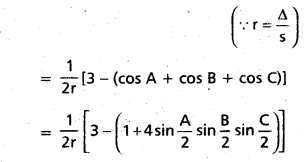
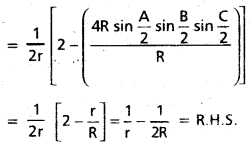
Question 46.
If r: R: r₁ = 2 : 5 : 12. then prove that the triangle ¡s right angled at A.
Solution:
r : R : r₁ = 2 : 5 : 12 then r = 2k. R = 5k and r₁ = 12K
r₁ – r = 12k – 2k = 10k = 2(5k) = 2R
⇒ 4R sin \(\frac{A}{2}\)[cos \(\frac{B}{2}\) cos \(\frac{C}{2}\) – sin \(\frac{B}{2}\) sin \(\frac{C}{2}\)] = 2R
⇒ 2 sin\(\frac{A}{2}\) cos\(\left(\frac{B+C}{2}\right)\) = 1
⇒ 2 sin \(\frac{A}{2}\) = \(\frac{1}{2}\) [cos \(\left(\frac{B+C}{2}\right)\) = sin \(\frac{A}{2}\)]
⇒ sin \(\frac{A}{2}\) = \(\frac{1}{\sqrt{2}}\) = sin 45°
⇒ \(\frac{A}{2}\) = 45° ⇒ A = 90°
Hence the triangle is right angled at A.

Question 47.
Show that r + r₃ + r₁ – r₂ = 4R cos B.
Solution:
r + r₃

Question 48.
If A, A₁, A₂, A₃ are the areas of incircle and excircles of a triangle respectively, then prove that \(\frac{1}{\sqrt{A_{1}}}+\frac{1}{\sqrt{A_{2}}}+\frac{1}{\sqrt{A_{3}}}=\frac{1}{\sqrt{A}}\) .
Solution:
r, r₁, r₂, r₃ are the in radius and ex-radii of the circles whose areas are A, A₁, A₂, A₃ respectively, then
A = itr², A₁ = πr₁², A₂ = πr₂², A₃ = πr₃²

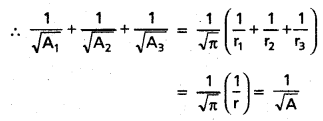
Question 49.
Show that (r₁ + r₂) sec² \(\frac{C}{2}\) = (r₂ + r₃) sec² \(\frac{A}{2}\) = (r₃ + r₁) sec² \(\frac{B}{2}\).
Solution:
r₁ + r₂ = 4R cos \(\frac{C}{2}\) [sin\(\frac{A}{2}\) cos\(\frac{B}{2}\) + cos \(\frac{A}{2}\) sin \(\frac{B}{2}\)]
= 4R cos\(\frac{C}{2}\) sin\(\left(\frac{A+B}{2}\right)\)
= 4R cos²\(\frac{C}{2}\) ___________ (1)
⇒ (r₁ + r₂) sec²\(\frac{C}{2}\) = 4R
Similarly, we can show that
(r₂ + r₃) sec²\(\frac{A}{2}\) = (r₃ + r₁) sec²\(\frac{B}{2}\) = 4R
∴ (r₁ + r₂)sec²\(\frac{C}{2}\) = (r₂ + r₃)
sec²\(\frac{A}{2}\) = (r₃ + r₁) sec²\(\frac{B}{2}\) = 4R

Question 50.
In ∆ABC, if AD, BE, CF are the perpendiculars drawn from the vertices A, B, C to the opposite sides, show that
i) \(\frac{1}{A D}+\frac{1}{B E}+\frac{1}{C F}=\frac{1}{r}\) and
ii) AD. BE. CF = \(\frac{(a b c)^{2}}{8 R^{3}}\)
Solution:
Since AD ⊥r to BC,

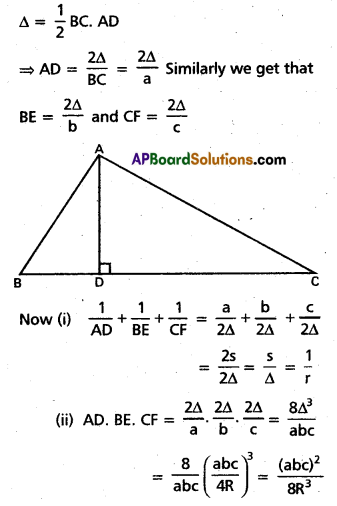
Question 51.
In ∆ ABC, if r₁ = 8, r₂ = 12, r₃ = 24, find a, b, c.
Solution:
∵ \(\frac{1}{r}\) = \(\frac{1}{r_{1}}\) + \(\frac{1}{r_{2}}\) + \(\frac{1}{r_{3}}\)
⇒ \(\frac{1}{r}\) = \(\frac{1}{8}\) + \(\frac{1}{12}\) + \(\frac{1}{24}\)
⇒ \(\frac{1}{r}\) = \(\frac{3+2+1}{24}\) ⇒ r = 4
But ∆² = rr₁r₂r₃ = 4 × 8 × 12 × 24
= (8 × 12)²
⇒ ∆ = 96 sq. cm
∵ r = \(\frac{\Delta}{\mathrm{s}}\) ⇒ 4 = \(\frac{96}{s}\) ⇒ s = 24
∵ r₁ = \(\frac{\Delta}{s-a}\)
⇒ δ = \(\frac{96}{s-a}\) ⇒ s – a = \(\frac{96}{8}\) ⇒ 24 – a
= 12 ⇒ a = 12
Similarly s – b = \(\frac{96}{12}\) ⇒ 24 – b = 8 ⇒ b = 16
s – c = \(\frac{96}{24}\) ⇒ 24 – c = 4 ⇒ c = 20

Question 52.
Show that \(\frac{a b-r_{1} r_{2}}{r_{3}}\) = \(\frac{b c-r_{2} r_{3}}{r_{1}}\) = \(\frac{c a-r_{3} r_{1}}{r_{2}}\)   [May 08; Mar 08]
Solution: