Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A De Moivre’s Theorem Solutions Exercise 2(a) will help students to clear their doubts quickly.
Intermediate 2nd Year Maths 2A De Moivre’s Theorem Solutions Exercise 2(a)
I.
Question 1.
If n is an integer then show that (1 + i)2n + (1 – i)2n = 2n+1 cos \(\frac{n \pi}{2}\)
Solution:



![]()
Question 2.
Find the values of the following:
(i) (1 + i√3)3
Solution:
Let 1 + i√3 = r (cos θ + i sin θ)
Equating real and imaginary parts
r cos θ = 1 and r sin θ = √3
⇒ r2 (1) = 1 + 3 = 4
⇒ r = 2
cos θ = \(\frac{1}{2}\) and sin θ = \(\frac{\sqrt{3}}{2}\)
⇒ θ = \(\frac{\pi}{3}\)
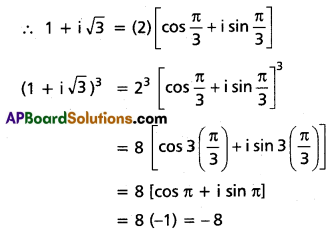
(ii) (1 – i)8
Solution:

(iii) (1 + i)16
Solution:

(iv) \(\left(\frac{\sqrt{3}}{2}+\frac{i}{2}\right)^{5}-\left(\frac{\sqrt{3}}{2}-\frac{i}{2}\right)^{5}\)
Solution:

![]()
II.
Question 1.
If α, β are the roots of the equation x2 – 2x + 4 = 0 then for any n ∈ N show that αn + βn = 2n+1 cos(\(\frac{n \pi}{3}\))
Solution:
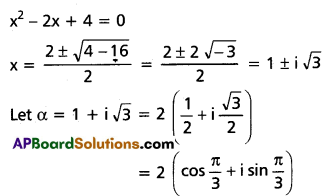

Question 2.
If cos α + cos β + cos γ = 0 = sin α + sin β + sin γ then show that
(i) cos 3α + cos 3β + cos 3γ = 3 cos(α + β + γ)
(ii) sin 3α + sin 3β + sin 3γ = 3 sin(α + β + γ)
(iii) cos(α + β) + cos(β + γ) + cos(γ + α) = 0
Solution:
Given that cos α + cos β + cos γ = 0 and sin α + sin β + sin γ = 0
From the hypothesis, we have
(cos α + cos β + cos γ) + i (sin α + sin β + sin γ) = 0
i.e., (cos α + i sin α) + (cos β + i sin β) + (cos γ + i sin γ) = 0
We know that if a + b + c = 0, then a3 + b3 + c3 = 3abc
Hence (cos α + i sin α)3 + (cos β + i sin β)3 + (cos γ + i sin γ)3 = 3 (cos α + i sin α) (cos β + i sin β) + (cos γ + i sin γ)
i.e., cos 3α + i sin 3α + cos 3β + i sin 3β + cos 3γ + i sin 3γ = 3[cos(α + β + γ) + i sin(α + β + γ)] …….(1)
On equating the real parts on both sides of equation (1) we get
(i) cos 3α + cos 3β + cos 3γ = 3 cos(α + β + γ)
On equation thenmaginary parts on both sides of equation (1) we get,
(ii) sin 3α + sin 3β + sin 3γ = 3 sin(α + β + γ)
(iii) Let a = cos α + i sin α then \(\frac{1}{a}\) = cos α – i sin α
b = cos β + i sin β and \(\frac{1}{b}\) = cos β – i sin β
c = cos γ + i sin γ and \(\frac{1}{c}\) = cos γ – i sin γ
Now \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\) = (cos α + cos β + cos γ) – i (sin α + sin β + sin γ)
⇒ \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\) = 0 – i(0)
⇒ \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\) = 0
⇒ bc + ca + ab = 0
⇒ [cos(β + γ) + i sin(β + γ)] + [cos(γ + α) + i sin(γ + α)] + [cos(α + β) + i sin(α + β)] = 0
⇒ [cos(α + β) + cos(β + γ) + cos(γ + α)] + i [sin(α + β) + sin(β + γ) + sin(γ + α)] = 0
By equation real parts on both sides
cos (α + β) + cos (β + γ) + cos (γ + α) = 0
![]()
Question 3.
If n is an integer and z = cis θ, (θ ≠ (2n + 1) π/2), then show that \(\frac{z^{2 n}-1}{z^{2 n}+1}\) = i tan nθ.
Solution:
z = cis θ = cos θ + i sin θ, θ ≠ (2n + 1) π/2
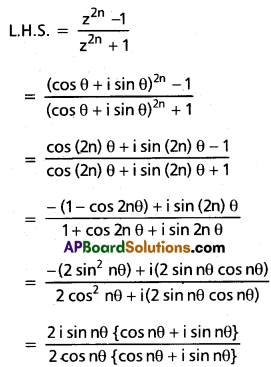
(∵ i2 = -1)
= i tan(nθ)
= R.H.S
Question 4.
If (1 + x)n = a0 + a1x + a2x2 + ……… + anxn, then show that
(i) a0 – a2 + a4 – a6 + …….. = \(2^{n / 2} \cos \frac{n \pi}{4}\)
(ii) a1 – a3 + a5 – a7 + ……… = \(2^{n / 2} \sin \frac{n \pi}{4}\)
Solution:

