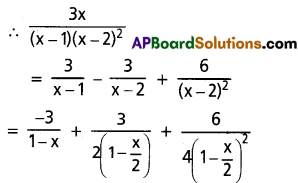Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Partial Fractions Solutions Exercise 7(d) will help students to clear their doubts quickly.
Intermediate 2nd Year Maths 2A Partial Fractions Solutions Exercise 7(d)
Question 1.
Find the coefficient of x3 in the power series expansion of \(\frac{5 x+6}{(x+2)(1-x)}\) specifying the region in which the expansion is valid.
Solution:

![]()
Question 2.
Find is the coefficient of x4 in the power series expansion of \(\frac{3 x^2+2 x}{\left(x^2+2\right)(x-3)}\) specifying the interval in which the expansion is valid.
Solution:
Let \(\frac{3 x^2+2 x}{\left(x^2+2\right)(x-3)}=\frac{A}{x-3}+\frac{B x+C}{x^2+2}\)
Multiplying with (x2 + 2) (x – 3)
3x2 + 2x = A(x2 + 2) + (Bx + C) (x – 3)
x = 3
⇒ 27 + 6 = A(9 + 2)
⇒ 33 = 11A
⇒ A = 3
Equating the coefficients of x2
3 = A + B
⇒ B = 3 – A = 3 – 3 = 0
Equating the constants,
2A – 3C = 0
⇒ 3C = 2A = 6
⇒ C = 2

Question 3.
Find the coefficient of xn in the power series expansion of \(\frac{x-4}{x^2-5 x+6}\) specifying the region in which the expansion is valid.
Solution:
Let \(\frac{x-4}{x^2-5 x+6}=\frac{A}{x-2}+\frac{B}{x-3}\)
Multiplying with (x – 2) (x – 3)
x – 4 = A(x – 3) + B(x – 2)
x = 2
⇒ -2 = A(2 – 3) = -A
⇒ A = 2
x = 3
⇒ -1 = B(3 – 2) = B
⇒ B = -1

![]()
Question 4.
Find the coefficient of xn in the power series expansion of \(\frac{3 x}{(x-1)(x-2)^2}\)
Solution:
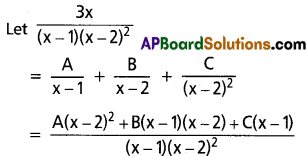
∴ 3x = A(x – 2)2 + B(x – 1) (x – 2) + C(x – 1) ……..(1)
putting x = 1,
3 = A(1 – 2)2
⇒ A = 3
putting x = 2,
6 = C(2 – 1)
⇒ C = 6
Now equating the co-efficient of x2 terms in (1)
0 = A + B
⇒ B = -A
⇒ B = -3