Students get through Maths 2B Important Questions Inter 2nd Year Maths 2B Definite Integrals Important Questions which are most likely to be asked in the exam.
Intermediate 2nd Year Maths 2B Definite Integrals Important Questions
Question 1.
\(\int_{2}^{3} \frac{2 x}{1+x^{2}} d x\) [T.S. Mar. 16; May 06]
Solution:
I = \(\left[\ln \left|1+x^{2}\right|\right]_{2}^{3}\)
= ln 10 – ln 5
= ln (10/5)
= ln 2
![]()
Question 2.
\( \int_{0}^{\pi} \sqrt{2} \cdot \sqrt{2} \sqrt{\cos ^{2} \frac{\theta}{2} d \theta}\) [A.P. Mar. 16; Mar. 05]
Solution:
I = \( \int_{0}^{\pi} \sqrt{2} \cdot \sqrt{2} \sqrt{\cos ^{2} \frac{\theta}{2} d \theta}\)
= \(\int_{0}^{\pi} 2 \cdot \cos \theta / 2 d \theta\)
= \([4 \sin \theta / 2]_{0}^{\pi}\)
= 4 (sin \(\frac{\pi}{2}\) – sin 0)
= 4
Question 3.
\(\int_{0}^{2}|1-x| d x\) [A.P. Mar. 15; May 11]
Solution:

Question 4.
I = \(\int_{1}^{5} \frac{d x}{\sqrt{2 x-1}}\) [T.S. Mar. 15]
Solution:
Let 2x – 1 = t2
2 dx = 2t dt
dx = t dt
UL : t = 3
LL : t = 1
I = \(\int_{1}^{3} \frac{t d t}{t}\)
= \(\int_{1}^{3} d t\)
= \([\mathrm{t}]_{1}^{3}\) = 3 – 1
= 2
![]()
Question 5.
I = \(\int_{0}^{1} \frac{x^{2}}{x^{2}+1} d x\) [Mar. 11]
Solution:
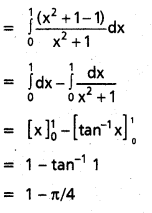
Question 6.
\(\int_{0}^{2 \pi}\) sin2x cos4; x dx [T.S. Mar. 15; Mar 14]
Solution:
sin2x cos4x is even function.
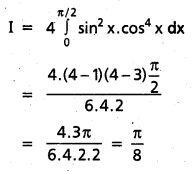
Question 7.
Evaluate \(\int_{0}^{a} \sqrt{a^{2}-x^{2}} d x\) [T.S. Mar. 16]
Solution:
Put x = a sin θ ⇒ dx = a cos θ . dθ
θ = 0 ⇒ x = 0, x = a ⇒ θ = \(\frac{\pi}{2}\)

Question 8.
Find \(\int_{-\pi / 2}^{\pi / 2}\) sin2 x cos4 x dx [A.P. Mar. 16]
Solution:
f(x) is even
∴ \(\int_{-\pi / 2}^{\pi / 2}\) sin2 x cos4 x dx = 2 \(\int_{0}^{\pi / 2} \sin ^{2} x \cdot \cos ^{4} x d x\)
= 2 . \(\frac{3}{6}\) . \(\frac{1}{4}\) . \(\frac{1}{4}\) . \(\frac{\pi}{4}\) = \(\frac{\pi}{16}\)
![]()
Question 9.
\(\int_{0}^{\pi / 2} \cdot \frac{\sin ^{5} x}{\sin ^{5} x+\cos ^{5} x} d x\) [Mar. 14, 08]
Solution:
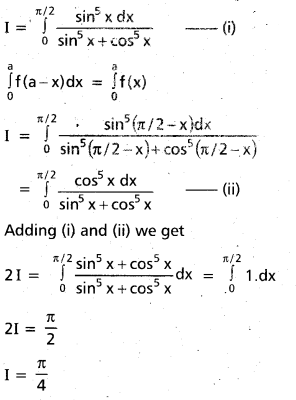
Question 10.
I = \(\int_{0}^{\pi / 4} \frac{\sin x+\cos x}{9+16 \sin 2 x} d x\) [Mar. 08]
Solution:

= –\(\frac{1}{40} \ln \left[\frac{1 / 4}{9 / 4}\right]\) = \(\frac{1}{40}\) . 2ln . 3 = \(\frac{1}{20}\) ln 3
Question 11.
y = x3 + 3, y = 0, x = -1, x = 2 [Mar. 05]
Solution:
Required area PABQ
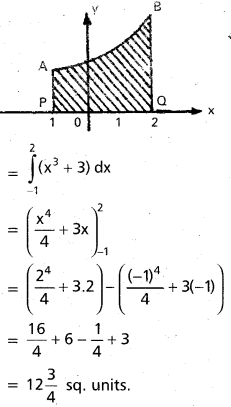
![]()
Question 12.
x = 4 – y2, x = 0. [Mar. 11]
Solution:
The given parabola x = 4 – y2 meets, the x – axis at A (4, 0) and Y – axis at P(0, 2) and Q(6, -2).
The parabola is symmetrical about X – axis
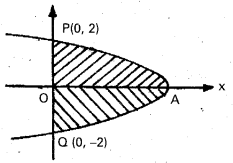
Required area = 2 Area of OAP
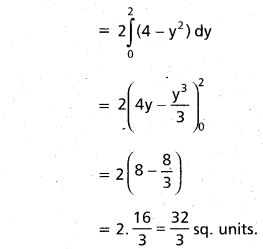
Question 13.
Evaluate the following definite integrals.
(i) \(\int_{0}^{\pi / 2} \sin ^{4} x \cos ^{5} x d x\)
(ii) \(\int_{0}^{\pi / 2} \sin ^{5} x \cos ^{4} x d x\)
(iii) \(\int_{0}^{\pi / 2} \sin ^{6} x \cos ^{4} x d x\)
Solution:
(i) \(\int_{0}^{\pi / 2} \sin ^{4} x \cos ^{5} x d x\)
= \(\frac{4}{9}\) . \(\frac{2}{7}\) . \(\frac{1}{5}\) = \(\frac{8}{315}\)
(ii) \(\int_{0}^{\pi / 2} \sin ^{5} x \cos ^{4} x d x\)
= \(\frac{3}{9}\) . \(\frac{1}{7}\) . \(\frac{4}{5}\) . \(\frac{2}{3}\) = \(\frac{8}{315}\)
(iii) \(\int_{0}^{\pi / 2} \sin ^{6} x \cos ^{4} x d x\)
= \(\frac{3}{10}\) . \(\frac{1}{8}\) . \(\frac{5}{6}\) . \(\frac{3}{4}\) . \(\frac{1}{2}\) . \(\frac{\pi}{2}\)
= \(\frac{3}{512}\) π
Question 14.
\(\int_{0}^{\pi / 2} \frac{d x}{4+5 \cos x}\) [A.P. Mar. 16, 15]
Solution:

= \(\frac{1}{3}\left[\ln \frac{4}{2}\right]=\frac{1}{3} \ln 2\)
![]()
Question 15.
\(\int_{0}^{\pi} \frac{x}{1+\sin x} d x\) [May 11]
Solution:
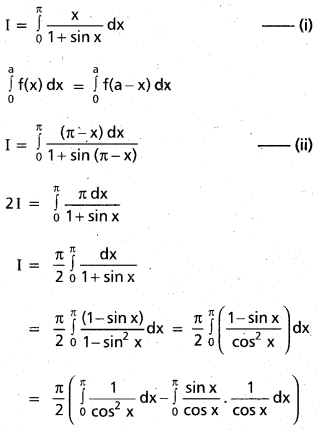
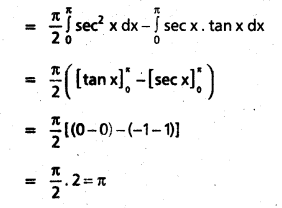
Question 16.
\(\int_{0}^{\pi} \frac{x \sin ^{3} x}{1+\cos ^{2} x} d x\) [T.S. Mar. 15; Mar. 11]
Solution:

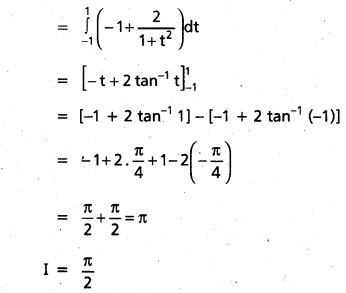
![]()
Question 17.
\(\int_{0}^{1} \frac{\log (1+x)}{1+x^{2}} d x\) [Mar. 07, 05]
Solution:
Put x = tan θ
dx = sec2 θ dθ
x = 0 ⇒ θ = 0
x = 1 ⇒ θ = \(\frac{\pi}{4}\)
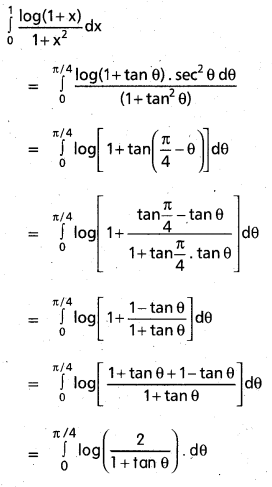
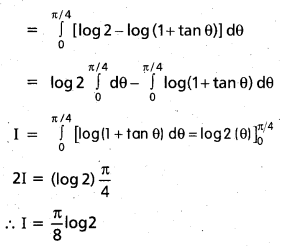
![]()
Question 18.
\(\int_{0}^{\pi / 4} \log (1+\tan x) d x\) [A.P. Mar. 16]
Solution:
I = \(\int_{0}^{\pi / 4} \log \left[1+\tan \left(\frac{\pi}{4}-x\right)\right] d x\)
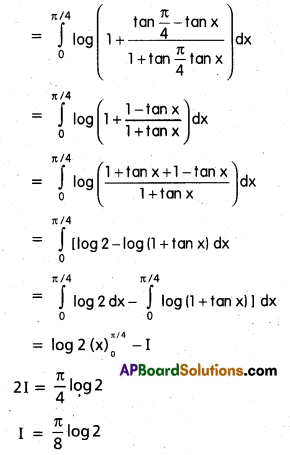
Question 19.
y = 4x – x2, y = 5 – 2x. [T.S. Mar. 16]
Solution:
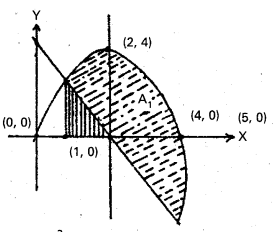
y = 4x – x2 …………….. (i)
y = 5 – 2x ……………….. (ii)
y = -([x – 2]2) + 4
y – 4 = (x – 2)2
Solving equations (i) and (ii) we get
4x – x2 = 5 – 2x
x2 – 6x + 5 = 0
(x – 5) (x – 1) = 0
x = 1, 5
Required area = \(=\int_{1}^{5}\left(4 x-x^{2}-5+2 x\right) d x\)
= \(\int_{-1}^{5}\left(6 x-x^{2}-5\right) d x\)
= \(\left(3 x^{2}-\frac{x^{3}}{3}-5 x\right)_{1}^{5}\)
= (75 – \(\frac{125}{3}\) – 25) – (3 – \(\frac{1}{3}\) – 5)
= 50 – \(\frac{125}{3}\) + 2 + \(\frac{1}{3}\)
= \(\frac{150-125+6+1}{3}\) = \(\frac{32}{3}\) sq. units.
Question 20.
y2 = 4x, y2 = 4(4 – x) [May 11]
Solution:
Equations of the curves are y2 = 4x ………………… (1)
y2 = 4(4 – x) …………………. (2)
Eliminating y, we get
4x = 4 (4 – x)
2x = 4 ⇒ x = 2
Substituting in equation (1), y2 = 8
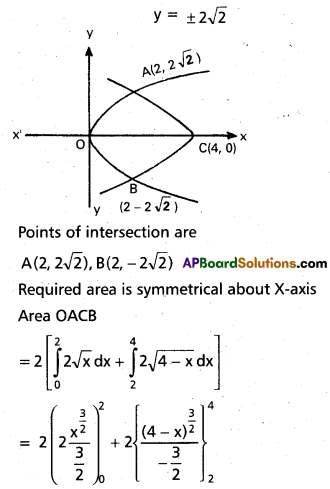
= 2[\(\frac{4}{3}\)(2\(\sqrt{2}\)) – \(\frac{4}{3}\)(-2\(\sqrt{2}\))]
= 2(\(\frac{8 \sqrt{2}}{3}\) + \(\frac{8 \sqrt{2}}{3}\))
= 2(\(\frac{16 \sqrt{2}}{3}\)) = \(\frac{32 \sqrt{2}}{3}\) sq. units
![]()
Question 21.
Show that the area of the region bounded by \(\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}}\) = 1 (ellipse) is it ab. also deduce the area of the circle x2 + y2 = a2. [Mar. 14, May 05]
Solution:
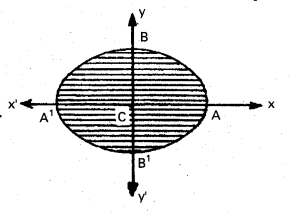
The ellipse is symmetrical about X and Y axis
Area of the ellipse = 4 Area of CAB
= 4 . \(\frac{\pi}{4}\) ab

(from Prob. 8 in ex 10(a))
= πab
Substituting b = a, we get the circle
x2 + y2 = a2
Area of the circle = πa(a) = πa2 sq. units.
Question 22.
Evaluate \(\int_{\pi / 6}^{\pi / 3} \frac{\sqrt{\sin x}}{\sqrt{\sin x}+\sqrt{\cos x}} d x\) [Mar. 14]
Solution:
Let A = \(\int_{\pi / 6}^{\pi / 3} \frac{\sqrt{\sin x}}{\sqrt{\sin x}+\sqrt{\cos x}} d x\)
Put x = \(\frac{\pi}{2}\) – t, dx = – dt
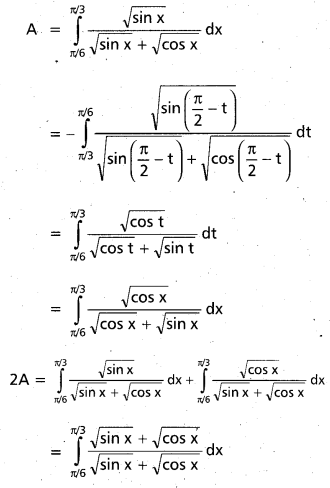
= \(\int_{\pi / 6}^{\pi / 3} d x=(x)_{\pi / 6}^{\pi / 3}\)
= \(\frac{\pi}{3}-\frac{\pi}{6}=\frac{\pi}{6}\)
A = \(\frac{\pi}{12}\)
![]()
Question 23.
Find \(\int_{0}^{\pi} \frac{x \cdot \sin x}{1+\sin x} d x\) [T.S. Mar. 16] [A.P. Mar. 15]
Solution:
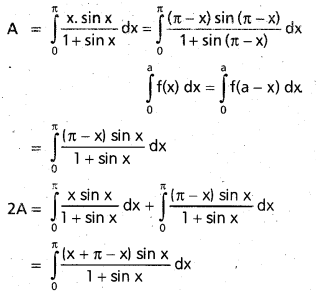

= \(\left(2 \tan \frac{x}{2}\right)_{0}^{\pi / 2}\)
= 2 . tan \(\frac{\pi}{2}\) – 2 . 0
= 2 – 1 = 2
2A = \(\pi(x)_{0}^{\pi}\) – 2π = π(π) – 2 = π2 – 2π
A = \(\frac{\pi^{2}}{2}\) – π
Question 24.
Find \(\int^{\pi} x \sin ^{7} x \cos ^{6} x d x .\) [May 05] [T.S. Mar. 19]
Solution:
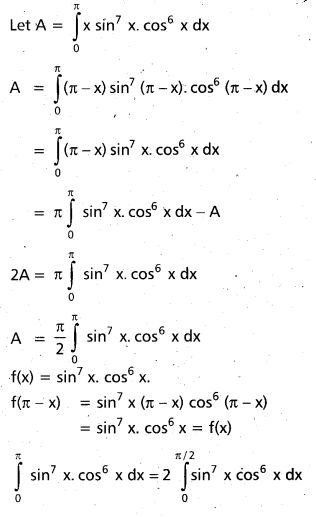
A = \(\pi \int_{0}^{\pi / 2} \sin ^{7} x \cos ^{6} x d x\)
= π . \(\frac{6}{17}\) . \(\frac{3}{11}\) . \(\frac{1}{9}\) . \(\frac{6}{7}\) . \(\frac{4}{5}\) . \(\frac{2}{3}\)
= π \(\frac{16}{3003}\)
Question 25.
Evaluate \(\int_{1}^{2} x^{5} d x\) dx
Solution:
\(\int_{1}^{2} x^{5} \cdot d x=\left[\frac{x^{6}}{6}\right]_{1}^{2}\)
= \(\frac{2^{6}}{6}-\frac{1}{6}=\frac{63}{6}=\frac{21}{2}\)
![]()
Question 26.
Evaluate \(\int_{0}^{\pi} \sin x d x\)
Solution:
\(\int_{0}^{\pi} \sin x d x=[-\cos x]_{0}^{\pi}\)
= – cos π – (- cos 0)
= + 1 + 1= 2
Question 27.
Evaluate \(\int_{0}^{a} \frac{d x}{x^{2}+a^{2}}\)
Solution:
\(\int_{0}^{a} \frac{d x}{x^{2}+a^{2}}=\left[\frac{1}{a} \tan ^{-1}\left(\frac{x}{a}\right)\right]_{0}^{a}\)
= \(\frac{1}{a}\) [tan-1 (1) – tan-1 (0)]
= \(\frac{1}{a}\) (\(\frac{\pi}{4}\) – 0) = \(\frac{\pi}{4 a}\)
Question 28.
Evaluate \(\int_{1}^{4} x \sqrt{x^{2}-1} d x\)
Solution:
g(x) = x2 – 1
f(t) = \(\sqrt{t}\)
g'(x) = 2x

Question 29.
Evaluate \(\int_{0}^{2} \sqrt{4-x^{2}} d x\)
Solution:
Let g(θ) = 2 sin θ ⇒ g'(θ) = 2 cos θ
f(x) = \(\sqrt{4-x^{2}}\)
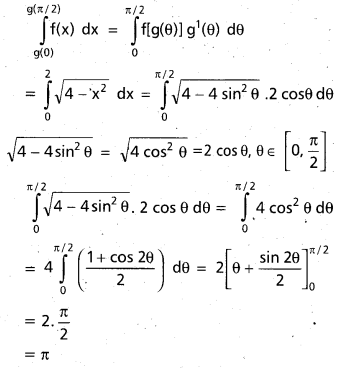
![]()
Question 30.
Evaluate \(\int_{0}^{16} \frac{x^{1 / 4}}{1+x^{1 / 2}} d x\)
Solution:
Put t4 = x ⇒ dx = 4t3 . dt
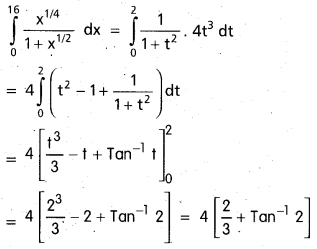
Question 31.
Evaluate \(\int_{-\pi / 2}^{\pi / 2} \sin |x| d x\)
Solution:
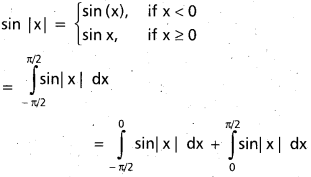
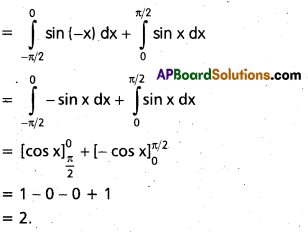
Question 32.
Show that \(\int_{0}^{\pi / 2} \sin ^{n} x d x=\int_{0}^{\pi / 2} \cos ^{n} x d x\)
Solution:
f(x) = sinnx.
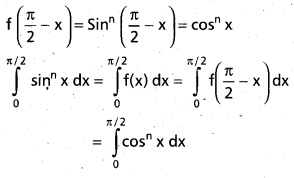
![]()
Question 33.
Evaluate \(\int_{0}^{\pi / 2} \frac{\cos ^{5 / 2} x}{\sin ^{5 / 2} x+\cos ^{5 / 2} x} d x\)
Solution:
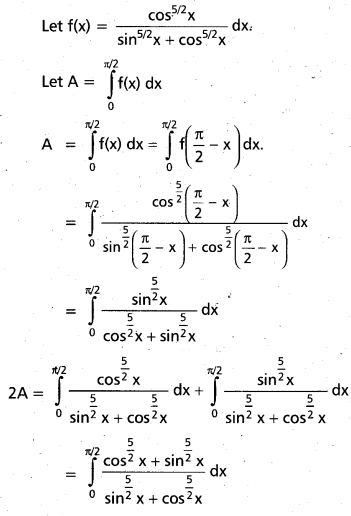
= \(\int_{0}^{\pi / 2} d x=(x)_{0}^{\pi / 2}=\frac{\pi}{2}\)
A = \(\int_{0}^{\pi / 2} \frac{\cos ^{\frac{5}{2}} x}{\sin ^{\frac{5}{2}} x+\cos ^{\frac{5}{2}} x} d x=\frac{\pi}{4}\)
Question 34.
Show that \(\int_{0}^{\pi / 2} \frac{x}{\sin x+\cos x} d x=\frac{\pi}{2 \sqrt{2}} \log (\sqrt{2}+1)\)
Solution:
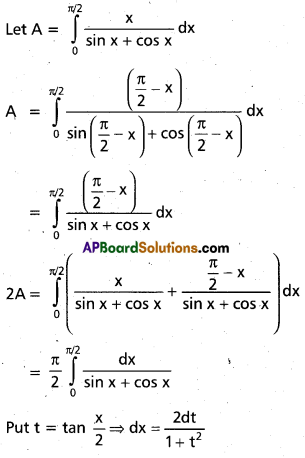
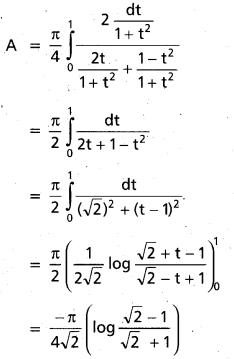
= \(\frac{\pi}{4 \sqrt{2}}\) log (\(\sqrt{2}\) + 1)2
= \(\frac{\pi}{4 \sqrt{2}}\) 2 log (\(\sqrt{2}\) + 1)
= \(\frac{\pi}{4 \sqrt{2}}\) log (\(\sqrt{2}\) + 1)
![]()
Question 35.
Evaluate \(\int_{\pi / 6}^{\pi / 3} \frac{\sqrt{\sin x}}{\sqrt{\sin x}+\sqrt{\cos x}} d x\) [Mar 14]
Solution:
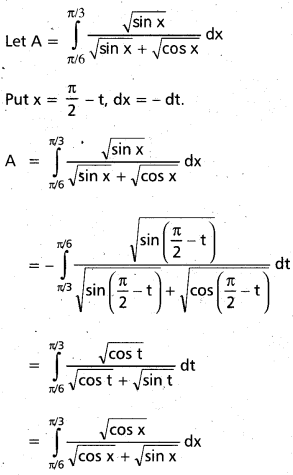
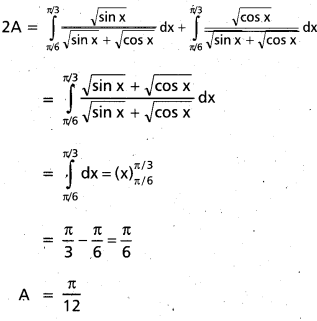
Question 36.
Find \(\int_{-a}^{a}\left(x^{2}+\sqrt{a^{2}-x^{2}}\right) d x\)
Solution:

= 2(\(\frac{a^{3}}{3}\) – 0) + 2(0 + \(\frac{a^{2}}{3}\) sin-1 (1) – 0 – 0)
= \(\frac{2a^{3}}{3}\) + a2 . \(\frac{\pi}{2}\)
Question 37.
Find \(\int_{0}^{\pi} \frac{x \cdot \sin x}{1+\sin x} d x\) [T.S. Mar. 16] [A.P. Mar. 15]
Solution:
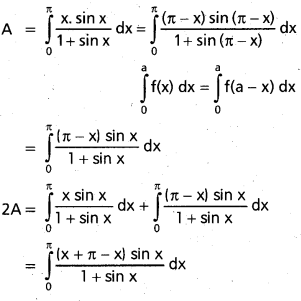
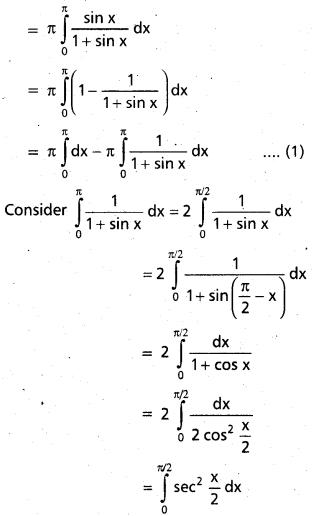
= \(\left(2 \tan \frac{x}{2}\right)_{0}^{\pi / 2}\)
= 2 . tan \(\frac{\pi}{2}\) – 2 . 0
= 2 – 1 = 2
2A = \(\pi(x)_{0}^{\pi}\) – 2π = π(π) – 2 = π2 – 2π
A = \(\frac{\pi^{2}}{2}\) – π
![]()
Question 38.
Evaluate \(\int_{0}^{\pi / 2} x \sin x d x\)
Solution:
\(\int_{0}^{\pi / 2} x \cdot \sin x d x=(-x \cdot \cos x)_{0}^{\pi / 2}+\int_{0}^{\pi / 2} \cos x d x\)
= (0 – 0) + \((\sin x)_{0}^{\pi / 2}\)
= sin \(\frac{\pi}{2}\) – sin 0 = 1 – 0 = 1
Question 39.
Evaluate \(\lim _{n \rightarrow \infty} \sum_{i=1}^{n} \frac{1}{n}\left[\frac{n-i}{n+i}\right]\) by using the method of finding definite integral as the limit of a sum.
Solution:

Question 40.
Evaluate \(\lim _{n \rightarrow \infty} \frac{2^{k}+4^{k}+6^{k}+\ldots .+(2 n)^{k}}{n^{k+1}}\) by using the method of finding definite integral as the limit of a sum.
Solution:
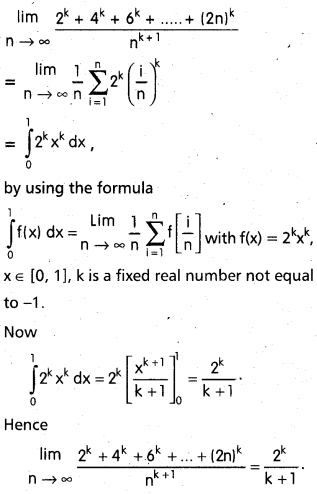
![]()
Question 41.
Evaluate \(\lim _{n \rightarrow \infty}\left[\left(1+\frac{1}{n}\right)\left(1+\frac{2}{n}\right) \cdots\left(1+\frac{n}{n}\right)\right]^{\frac{1}{n}}\)
Solution:

Question 42.
Let f: R → R be a continuous periodic function and T be the period of it. Then prove that for any positive integer n,
\(\int_{0}^{n T} f(x) d x=n \int_{0}^{T} f(x) d x\) ………………. (1)
Solution:
Let k be an integer arid define
g : [kT, (k + 1)T] → [0, T] as g(t) = t – kT.
Then g'(t) = 1 for all t ∈ [kT, (k + 1)T].
Hence by \(\int_{g(c)}^{g(d)} f(t) d t=\int_{c}^{d} f(g(x)) g^{\prime}(x) d x,(f \circ g)\)
g’ is integrable on [kT, (k + 1 )T] and
\(\int_{k T}^{(k+1) T} f(g(t)) g^{\prime}(t) d t=\int_{0}^{T} f(x) d x\) ………… (2)
We have f(g(t)) g'(t) = f(t – kT), 1 = f(t),
since f is periodic with T as the period.
Hence \(\int_{k T}^{(k+1) T} f(g(t)) g^{\prime}(t) d t=\int_{k T}^{(k+1) T} f(t) d t\) ………….. (3)
Thus from (2) and (3),
\(\int_{k T}^{(k+1) T} f(t) d t=\int_{0}^{T} f(t) d t\) ………………. (4)
Let us now prove eq. (1) by using the principle of mathematical induction.
For n = 1, clearly (1) is true.
Assume (1) is true for a positive integer m.
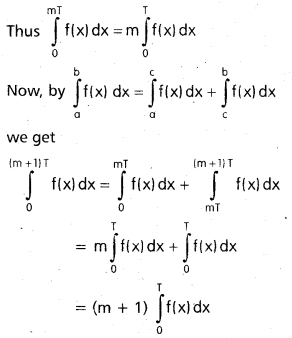
Hence eq. (1) is true for n = m + 1
Thus, eq. (1) ¡s true for any positive integer n, by the principle of mathematical induction.
Question 43.
Find
(i) \(\int_{0}^{\pi / 2} \sin ^{4} x d x\)
(ii) \(\int_{0}^{\pi / 2} \sin ^{7} x d x\)
(iii) \(\int_{0}^{\pi / 2} \cos ^{8} x d x\)
Solution:
(i) \(\int_{0}^{\pi / 2} \sin ^{4} x d x\)
= \(\frac{3}{4}\) . \(\frac{1}{2}\) . \(\frac{\pi}{2}\) = \(\frac{3\pi}{16}\)
(ii) \(\int_{0}^{\pi / 2} \sin ^{7} x d x\)
= \(\frac{6}{7}\) . \(\frac{4}{5}\) . \(\frac{2}{3}\) = \(\frac{16}{35}\)
(iii) \(\int_{0}^{\pi / 2} \cos ^{8} x d x\)
= \(\frac{7}{8}\) . \(\frac{5}{6}\) . \(\frac{3}{4}\) . \(\frac{1}{2}\) . \(\frac{\pi}{2}\) = \(\frac{35\pi}{256}\)
![]()
Question 44.
Evaluate \(\int_{0}^{a} \sqrt{a^{2}-x^{2}} d x\) [T.S. Mar. 16]
Solution:
Put x = a sin θ ⇒ dx = a cos θ . dθ
θ = 0 ⇒ x = 0, x = a ⇒ θ = \(\frac{\pi}{2}\)
\(\int_{0}^{a} \sqrt{a^{2}-x^{2}} d x=\int_{0}^{\pi / 2}(a \cos \theta)(a \cos \theta) d \theta\)
= a2 \(\int_{0}^{\pi / 2}\) cos2 θ dθ
= a2 . \(\frac{1}{2}\) . \(\frac{\pi}{2}\) = \(\frac{\pi a^{2}}{4}\)
Question 45.
Evaluate the following definite integrals.
(i) \(\int_{0}^{\pi / 2}\) sin4 x . cos5 x dx
(ii) \(\int_{0}^{\pi / 2}\) sin5 x . cos4 x dx
(iii) \(\int_{0}^{\pi / 2}\) sin6 x . cos4 x dx
Solution:
(i) \(\int_{0}^{\pi / 2}\) sin4 x . cos5 x dx
= \(\frac{4}{9}\) . \(\frac{2}{7}\) . \(\frac{1}{5}\) = \(\frac{8}{315}\)
(ii) \(\int_{0}^{\pi / 2}\) sin5 x . cos4 x dx
= \(\frac{3}{9}\) . \(\frac{1}{7}\) . \(\frac{4}{5}\) . \(\frac{2}{3}\) = \(\frac{8}{315}\)
(iii) \(\int_{0}^{\pi / 2}\) sin6 x . cos4 x dx
= \(\frac{3}{10}\) . \(\frac{1}{8}\) . \(\frac{5}{6}\) . \(\frac{3}{4}\) . \(\frac{1}{2}\) . \(\frac{\pi}{2}\)
= \(\frac{3}{512}\) π
Question 46.
Find \(\int_{0}^{2 \pi}\) sin4 x . cos6 x dx [T.S. Mar. 19]
Solution:
f(x) = sin4 x . cos6 x dx
f(2π – x) = f(π – x) = f(x)
\(\int_{0}^{2 \pi}\) sin4 x . cos6 x dx = 2 \(\int_{0}^{2 \pi}\) sin4 x . cos6 x dx
= 4 \(\int_{0}^{2 \pi}\) sin4 x . cos6 x dx
= 4 . \(\frac{5}{10}\) . \(\frac{3}{8}\) . \(\frac{1}{6}\) . \(\frac{3}{4}\) . \(\frac{1}{2}\) . \(\frac{\pi}{2}\)
= \(\frac{3}{128}\) π
![]()
Question 47.
Find \(\int_{-\pi / 2}^{\pi / 2}\) sin2 x . cos4 x dx [A.P. Mar. 16, 19]
Solution:
f(x) is even
∴ \(\int_{-\pi / 2}^{\pi / 2}\) sin2 x . cos4 x dx = 2 \(\int_{-\pi / 2}^{\pi / 2}\) sin2 x . cos4 x dx
= 2 . \(\frac{3}{6}\) . \(\frac{1}{4}\) . \(\frac{1}{4}\) . \(\frac{\pi}{4}\)
= \(\frac{\pi}{16}\)
Question 48.
Find \(\int_{0}^{\pi}\) x sin7 x . cos6 x dx [May 05]
Solution:

\(\int_{0}^{\pi}\) x sin7 x . cos6 x dx = 2 \(\int_{0}^{\pi}\) sin7 x . cos6 x dx
A = π \(\int_{0}^{\pi}\) x sin7 x . cos6 x dx
= π . \(\frac{6}{17}\) . \(\frac{3}{11}\) . \(\frac{1}{9}\) . \(\frac{6}{7}\) . \(\frac{4}{5}\) . \(\frac{2}{3}\)
= π . \(\frac{16}{3003}\)
Question 49.
Find \(\int_{-a}^{a}\) a2 (a2 – x2)3/2 dx
Solution:
f(x) = x2 (a2 – x2)
f(x) is even
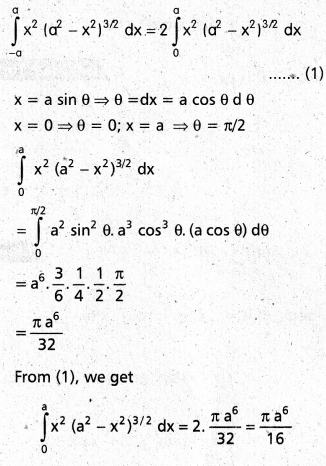
![]()
Question 50.
Find \(\int_{0}^{1} x^{3 / 2} \sqrt{1-x} d x\)
Solution:
Put x = sin2 θ
dx = 2 sin θ . cos θ . dθ
x = 0 ⇒ θ = 0, x = 1 ⇒ θ = \(\frac{\pi}{2}\)
\(\int_{0}^{1} x^{3 / 2} \sqrt{1-x} d x\)
= \(\int_{0}^{\pi / 2} \sin ^{3} \theta \cdot \cos \theta .2 \sin \theta \cos \theta d \theta\)
= \(2 \int_{0}^{\pi / 2} \sin ^{4} \theta \cdot \cos ^{2} \theta d \theta\)
= 2 . \(\frac{3}{6}\) . \(\frac{1}{4}\) . \(\frac{1}{2}\) . \(\frac{\pi}{2}\) = \(\frac{\pi}{16}\)
Question 51.
Find the area under the curve f(x) = sin x in [0, 2π].
Solution:
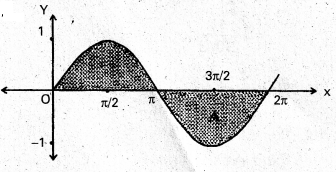
f(x) = sin x,
We know that in [0, π], sin x ≥ 0 and [π, 2π], sin x ≤ 0
Required area = \(\int_{1}^{\pi}\) sinx dx + \(\int_{\pi}^{2 \pi}\) (-sinx) dx
= \((-\cos x)_{0}^{\pi}[\cos x]_{\pi}^{2 \pi}\)
= – cos π + cos 0 + cos 2π – cos π
= -(-1) + 1 + 1-(-1) = 1 + 1 + 1 + 1
= 4.
Question 52.
Find the area under the curve f(x) = cos x in [0, 2π].
Solution:
We know that cos x ≥ 0 in (0, \(\frac{\pi}{2}\)) ∪ (\(\frac{3\pi}{2}\), π) and ≤ 0 in \(\left(\frac{\pi}{2}, \frac{3 \pi}{2}\right)\)
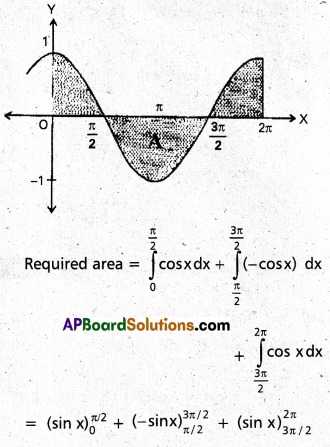
= sin \(\frac{\pi}{2}\) – sin 0 – sin \(\frac{3\pi}{2}\) + sin \(\frac{\pi}{2}\) + sin 2π – sin \(\frac{3\pi}{2}\)
= 1 – 0 – (-1) + 1 + 0 – (-1)
= 1 + 1 + 1 + 1 = 4.
![]()
Question 53.
Find the area bounded by the parabola y = x2, the X-axis and the lines x = -1, x = 2.
Solution:
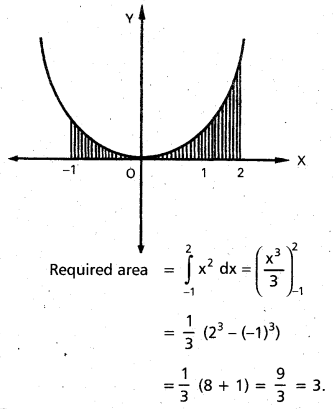
Question 54.
Find the area cut off between the line y = 0 and the parabola y = x2 – 4x + 3.
Solution:
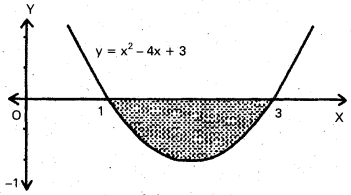
Equation of the parabola is
y = x2 – 4x + 3
Equation of the line is y = 0
x2 – 4x + 3 = 0
(x – 1) (x – 3) = 0
x = 1, 3
The curve takes negative values for the values of x between 1 and 3.
Required area = \(\int_{1}^{3}\) -(x2 – 4x + 3)dx
= \(\int_{1}^{3}\) (-x2 + 4x – 3) dx
= \(\left(-\frac{x^{3}}{3}+2 x^{2}-3 x\right)_{1}^{3}\)
= (-9 + 18 – 9) – (-\(\frac{1}{3}\) + 2 – 3)
= \(\frac{1}{3}\) – 2 + 3 = \(\frac{4}{3}\)
![]()
Question 55.
Find the area bounded by y = sin x and y = cos x between any two consecutive points of intersection.
Solution:
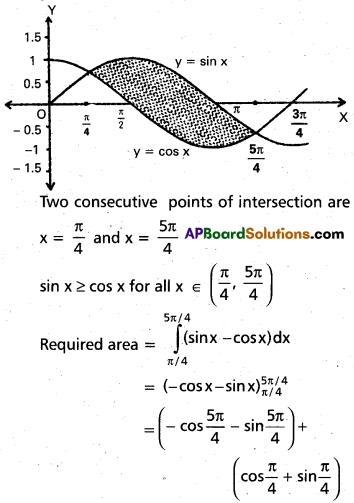
= \(\frac{1}{\sqrt{2}}\) + \(\frac{1}{\sqrt{2}}\) + \(\frac{1}{\sqrt{2}}\) + \(\frac{1}{\sqrt{2}}\) = 4\(\frac{1}{\sqrt{2}}\) = 2\(\sqrt{2}\)
Question 56.
Find the area of one of the curvilinear triangles bounded by y = sin x, y = cos x and X – axis.
Solution:
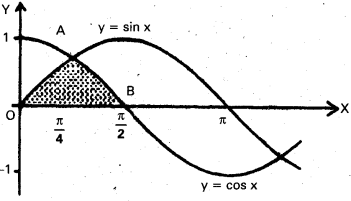
ln (0, \(\frac{\pi}{4}\)) cos x ≥ sin x and (\(\frac{\pi}{4}\), \(\frac{\pi}{2}\)), cos x ≤ sin x.
Required area = \(\int_{0}^{\pi / 4}\) sin x dx + \(\int_{\pi / 4}^{\pi / 2}\) cos x dx
= \((-\cos x)_{0}^{\pi / 4}+(\sin x)_{\pi / 4}^{\pi / 2}\)
= – cos \(\frac{\pi}{4}\) + cos 0 + sin \(\frac{\pi}{2}\) – sin \(\frac{\pi}{4}\)
= – \(\frac{1}{\sqrt{2}}\) + 1 + 1 – \(\frac{1}{\sqrt{2}}\)
= 2(1 – \(\frac{1}{\sqrt{2}}\)) = 2 – \(\sqrt{2}\)
Question 57.
Find the area of the right angled triangle with base b and altitude h, using the fundamental theorem of integral calculus.
Solution:
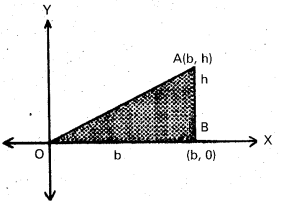
OAB is a right angled triangle and ∠B = 90° take ‘O’ as the origin and OB as positive X-axis
If OB = band AB = h, then Co-ordinates of A are (b, h)
Equation of OA is y = \(\frac{h}{b}\) x
Area of the triangle OAB = \(\int_{0}^{b} \frac{h}{b} x d x\)
= \(\frac{h}{b}\left(\frac{x^{2}}{2}\right)_{0}^{b}=\frac{h}{b} \cdot \frac{b^{2}}{2}=\frac{1}{2} b h .\)
![]()
Question 58.
Find the area bounded between the curves y2 – 1 = 2x and x = 0.
Solution:

= \(\left(-\frac{y^{3}}{3}+y\right)_{0}^{1}\) = 1 – \(\frac{1}{3}\) = \(\frac{2}{3}\)
Question 59.
Find the area enclosed by the curves y = 3x and y = 6x – x2.
Solution:
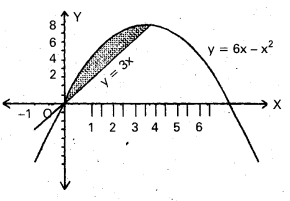
y = 6x – x2
The straight line y = 3x meets the parabola
y = 6x – x2
3x = 6x = x2
x2 – 3x = 0
x(x – 3) = 0
x = 0 or 3
Required area = \(\int_{0}^{3}\left(6 x-x^{2}-3 x\right) d x\)
= \(\int_{0}^{3}\left(3 x-x^{2}\right) d x=\left(\frac{3 x^{2}}{2}-\frac{x^{3}}{3}\right)_{0}^{3}\)
= \(\frac{27}{2}\) – \(\frac{27}{3}\) = \(\frac{27}{6}\) = \(\frac{9}{2}\)
Question 60.
Find the area enclosed between y = x2 – 5x and y = 4 – 2x.
Solution:
Equations of the curves are
y = x2 – 5x ………. (1)
y = 4 – 2x …………….. (2)
x2 – 5x = 4 – 2x
x2 – 3x – 4 = 0
(x + 1)(x – 4) = 0
x = -1, 4

= 44 – \(\frac{64}{3}\) – \(\frac{3}{2}\) – \(\frac{1}{3}\)
= \(\frac{264-128-9-2}{6}\) = \(\frac{125}{6}\)
![]()
Question 61.
Find the area bounded between the curves y = x2, y = \(\sqrt{x}\).
Solution:
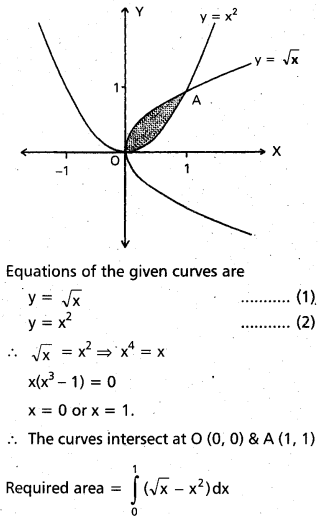
= \(\left(\frac{2}{3} x \sqrt{x}-\frac{x^{3}}{3}\right)_{0}^{1}\)
= \(\frac{2}{3}\) – \(\frac{1}{3}\) = \(\frac{1}{3}\)
Question 62.
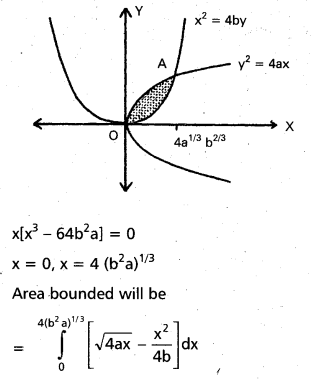
Find the area bounded between the curves y2 = 4ax, x2 = 4by (a > 0, b > 0).
Solution:
Equations of the given curves are
y2 = 4ax …………………… (1)
x2 = 4by ……………………. (2)
From equation (2), y = \(\frac{x^{2}}{4 b}\)
Substituting in (1) \(\left(\frac{x^{2}}{4 b}\right)^{2}\) = 4ax
x4 = (16 b2) |4ax|