Students get through Maths 2B Important Questions Inter 2nd Year Maths 2B Circle Important Questions which are most likely to be asked in the exam.
Intermediate 2nd Year Maths 2B Circle Important Questions
Question 1.
If x2 + y2 + 2gx + 2fy – 12 = 0 represents a circle with centre (2, 3), find g, f and its radius. [Mar. 11]
Solution:
Circle is x2 + y2 + 2gx + 2fy – 12 = 0
C = (-g, -f) C = (2, 3)
∴ g = – 2, f = – 3, c = – 12
Radius = \(\sqrt{g^{2}+f^{2}-c}\)
= \(\sqrt{4+9+12}\) = 5 units
![]()
Question 2.
Obtain the parametric equation of x2 + y2 = 4 [Mar. 14]
Solution:
Equation of the circle is x2 + y2 = 4
C (0, 0), r = 2
Parametric equations are
x = – g + r cos θ = 2 cos θ
y = – b + r sin θ = 2 sin θ, 0 < θ < 2π
Question 3.
Obtain the parametric equation of (x – 3)2 + (y – 4)2 = 82 [A.P. Mar. 16; Mar. 11]
Solution:
Equation of the circle is (x – 3)2 + (y – 4)2 =82
Centre (3, 4), r = 8
Parametric equations are
x = 3 + 8 cos θ, y = 4 + 8 sin θ, 0 < θ < 2π
Question 4.
Find the power of the point P with respect to the circle S = 0 when
ii) P = (-1,1) and S ≡ x2 + y2 – 6x + 4y – 12
Solution:
Power of the point = S11
= 1 + 1 + 6 + 4 – 12 = 0
iii) P = (2, 3) and S ≡ x2 + y2 – 2x + 8y – 23
Power of the point = S11
= 4 + 9 – 4 + 24 – 23 = 10
iv) P = (2, 4) and S ≡ x2 + y2 – 4x – 6y – 12
Power of the point = 4 + 16 – 8 – 24 – 12
= -24.
![]()
Question 5.
If the length of the tangent from (5, 4) to the circle x2 + y2 + 2ky = 0 is 1 then find k. [Mar. 15; Mar. 01]
Solution:
= \(\sqrt{S_{11}}=\sqrt{(5)^{2}+(4)^{2}+8 k}\)
But length of tangent = 1
∴ 1 = \(\sqrt{25+16+8k}\)
Squaring both sides we get 1 = 41 + 8k
k = – 5 units.
Question 6.
Find the polar of (1, -2) with respect to x2 + y2 – 10x – 10y + 25 = 0 [T.S. Mar. 15]
Solution:
Equation of the circle is x2 + y2 – 10x – 10y + 25 = 0
Equation of the polar is S1 = 0
Polar of P(1,-2) is
x . 1 + y(-2) – 5(x + 1) – 5(y – 2) + 25 = 0
⇒ x – 2y – 5x – 5 – 5y + 10 + 25 = 0
⇒ -4x – 7y + 30 = 0
∴ 4x + 7y – 30 = 0
Question 7.
Find the value of k if the points (1, 3) and (2, k) are conjugate with respect to the circle x2 + y2 = 35. [T.S. Mar. 16]
Solution:
Equation of the circle is
x2 + y2 = 35
Polar of P(1, 3) is x. 1 + y. 3 = 35
x + 3y = 35
P(1, 3) and Q(2, k) are conjugate points
The polar of P passes through Q
2 + 3k = 35
3k = 33
k = 11
Question 8.
If the circle x2 + y2 – 4x + 6y + a = 0 has radius 4 then find a. [A.P. Mar. 16]
Solution:
Equation of the circle is
x2 + y2 – 4x + 6y + a = 0
2g = – 4, 2f = 6, c = a
g = -2, f = 3, c = a
radius = 4 ⇒ \(\sqrt{g^{2}+f^{2}-c}\) = 4
\(\sqrt{4+9-a}\) = 4
13 – a = 16
a = 13 – 16 = -3
![]()
Question 9.
Find the value of ‘a’ if 2x2 + ay2 – 3x + 2y – 1 =0 represents a circle and also find its radius.
Solution:
General equation of second degree
ax2 + 2hxy + by2 + 2gx + 2fy + c = 0
Represents a circle, when
a = b, h = 0, g2 + f2 – c ≥ 0
In 2x2 + ay2 – 3x + 2y – 1 = 0
a = 2, above equation represents circle.
x2 + y2 – \(\frac{3}{2}\) x + y – \(\frac{1}{2}\) = 0
2g = – \(\frac{3}{2}\); 2f = 1; c = – \(\frac{1}{2}\)
c = (-g, -f) = (\(\frac{+3}{4}\), \(\frac{-1}{2}\))
Radius = \(\sqrt{g^{2}+f^{2}-c}\) = \(\sqrt{\frac{9}{16}+\frac{1}{4}+\frac{1}{2}}\)
= \(\frac{\sqrt{21}}{4}\) units
Question 10.
If the abscissae of points A, B are the roots of the equation, x2 + 2ax – b2 = 0 and ordinates of A, B are root of y2 + 2py – q2 = 0, then find the equation of a circle for which \(\overline{\mathrm{AB}}\) is a diameter. [Mar. 14]
Solution:
Equation of the circle is
(x – x1) (x – x2) + (y – y1) (y – y2) = 0
x2 – x(x1 + x2) + x1x2 + y2 – y (y1 + y2) + y1y2 = 0
x1, x2 are roots of x2 + 2ax – b2 = 0
y1, y2 are roots of y2 + 2py – q2 = 0
x1 + x2 = – 2a
x1x2 = -b2
y1 + y2 = -2p
y1y2 = -q2
Equation of circle be
x2 – x (- 2a) – b2 + y2– y (- 2p) – q2 = 0
x2 + 2xa + y2 + 2py – b2 – q2 = 0
Question 11.
Find the equation of a circle which passes through (4, 1) (6, 5) and having the centre on 4x + 3y – 24 = 0 [A.P. Mar. 16; Mar. 14]
Solution:
Equation of circle be x2 + y2 + 2gx + 2fy + c = 0 passes through (4, 1) and (6, 5) then
42 + 12 + 2g(4) + 2f(1) + c = 0 ………….. (i)
62 + 52 + 2g(6) + 2f(5) + c = 0 ……………… (ii)
Centre lie on 4x + 3y – 24 = 0
∴ 4(-g) + 3 (-f) – 24 = 0
(ii) – (i) we get
44 + 4g + 8f = 0
Solving (iii) and (iv) we get
f = -4, g = -3, c = 15
∴ Required equation of circle is
x2 + y2 – 6x – 8y + 15 = 0
![]()
Question 12.
Find the equation of a circle which is concentric with x2 + y2 – 6x – 4y – 12 = 0 and passing through (- 2, 14). [Mar. 14]
Solution:
x2 + y2 – 6x – 4y – 12 = 0 …………… (i)
C = (- g, – f)
= (3, 2)
Equation of circle concentric with (i) be
(x – 3)2 + (y – 2)2 = r2
Passes through (-2, 14)
∴ (- 2 – 3)2 + (14 – 2)2 = r2
169 = r2
Required equation of circle be
(x – 3)2 + (y – 2)2 = 169
x2 + y2 – 6x – 4y – 156 = 0
Question 13.
Find the equation of the circle whose centre lies on the X-axis and passing through (- 2, 3) and (4, 5). [A.P. & T.S. Mar. 15]
Solution:
x2 + y2 + 2gx + 2fy + c = 0 ……………… (i)
(- 2, 3) and (4, 5) passes through (i)
4 + 9 – 4g + 6f + c = 0 ………………………. (ii)
16 + 25 + 8g + 10f + c = 0 …………………. (iii)
(iii) – (ii) we get
28 + 12g + 4f = 0
f + 3g = – 7
Centre lies on X – axis then f = 0
g = -, \(\frac{7}{3}\), f = 0, c = \(\frac{67}{3}\) -, we get by substituting g; f in equation (ii)
Required equation will be 3(x2 + y2) – 14x – 67 = 0
Question 14.
Find the equation of circle passing through (1, 2); (3, – 4); (5, – 6) three points.
Solution:
Equation of circle is
x2 + y2 + 2gx + 2fy + c = 0
1 + 4 + 2g + 4f + c = 0 …………………… (i)
9 + 16 + 6g – 8f + c = 0 …………………… (ii)
25 + 36 + 10g – 12f + c = 0 ………………… (iii)
Subtracting (ii) – (i) we get
20 + 4g – 12f = 0
(or) 5 + g – 3f = 0 ……………….. (iv)
Similarly (iii) – (ii) we get
36 + 4g – 4f = 0
(or) 9 + g – f = 0 ………………… (v)
Solving (v) and (iv) we get
f = -2, g = – 11, c = 25
Required equation of circle be x2 + y2 – 22x – 4y + 25 = 0
Question 15.
Find the length of the chord intercepted by the circle x2 + y2 – 8x – 2y – 8 = 0 on the line x + y + 1 = 0 [T.S. Mar. 16]
Solution:
Equation of the circle is x2 + y2 – 8x – 2y – 8 = 0
Centre is C(4, 1), r = \(\sqrt{16+1+8}\) = 5
Equation of the line is x + y + 1 = 0
P = distance from the centre = \(\frac{|4+1+1|}{\sqrt{1+1}}\)
= \(\frac{6}{\sqrt{2}}\) = 3\(\sqrt{2}\)
Length of the chord = 2\(\sqrt{r^{2}-p^{2}}\)
= 2\(\sqrt{25-18}\)
= 2\(\sqrt{7}\) units.
![]()
Question 16.
Find the pair of tangents drawn from (1, 3) to the circle x2 + y2 – 2x + 4y – 11 =0 and also find the angle between them. [T.S. Mar. 16]
Solution:
SS11 = S12
(x2 + y2 – 2x + 4y – 11) (1 + 9 – 2 + 12 – 11) = [x + 3y – 1 (x + 1) + 2 (y + 3) – 11]2
(x2 + y2 – 2x + 4y – 11) 9 = [5y – 6]2
9x2 + 9y2 – 18x + 36y – 99
= 25y2 + 36 – 60y
9x2 – 16y2 – 18x + 96y – 135 = 0
cos θ = \(\frac{|a+b|}{\sqrt{(a-b)^{2}+4 h^{2}}}\) = \(\frac{|9-16|}{\sqrt{(25)^{2}}}\)
= \(\frac{|-7|}{25}\) = \(\frac{7}{25}\) ⇒ θ = cos-1 (\(\frac{7}{25}\))
Question 17.
Find the value of k if the points (4, 2) and (k, -3) are conjugate points with respect to the circle x2 + y2 – 5x + 8y + 6 = 0. [T.S. Mar. 17]
Solution:
Equation of the circle is x2 + y2 – 5x + 8y + 6 = 0
Polar of P(4, 2) is
x . 4 + y . 2 – \(\frac{5}{2}\) (x + 4) + 4 (y + 2) + 6 = 0
8x + 4y – 5x – 20 + 8y + 16 + 12 = 0
3x + 12y + 8 = 0
P(4, 2), Q(k, -3) are conjugate points
Polar of P passes through Q
∴ 3k – 36 + 8 = 0
3k = 28 ⇒ k = \(\frac{28}{3}\)
Question 18.
If (2, 0), (0,1), (4, 5) and (0, c) are concyclic, and then find c. [A.P. & T.S. Mar. 15]
Solution:
x2 + y2 + 2gx + 2fy + c1 = 0
Satisfies (2, 0), (0, 1) (4, 5) we get
4 + 0 + 4g + c1 = 0 …………………. (i)
0 + 1 + 2g. 0 + 2f + c1 = 0 – (ii)
16 + 25 + 8g + 10f + c1 = -0 ……………. (iii)
(ii) – (i) we get
– 3 – 4g + 2f = 0
4g – 2f = – 3 ……………… (iv)
(ii) – (iii) we get
– 40 – 8g – 8f = 0 (or)
g + f = – 5 …………………… (v)
Solving(iv) and (v) we get
g = –\(\frac{13}{6}\), f = –\(\frac{17}{6}\)
Substituting g and f values in equation (i) we get
4 + 4 (-\(\frac{13}{6}\)) + c1 = 0
c1 = \(\frac{14}{3}\)
Now equation x2 + y2 – \(\frac{13}{3}\) x – \(\frac{17}{3}\) y + \(\frac{14}{3}\) = 0
Now circle passes through (0, c) then
c2 – \(\frac{17}{3}\) c + \(\frac{14}{3}\) = 0
3c2 – 17c + 14 = 0
⇒ (3c – 14) (c – 1) = 0
(or)
c = 1 or \(\frac{14}{3}\)
![]()
Question 19.
Find the length of the chord intercepted by the circle x2 + y2 – x + 3y – 22 = 0 on the line y = x – 3. [May 11; Mar. 13]
Solution:
Equation of the circle is
S ≡x2 + y2 – x + 3y – 22 = 0
Centre C(\(\frac{1}{2}\), –\(\frac{3}{2}\))

Question 20.
Find the equation of the circle with centre (-2, 3) cutting a chord length 2 units on 3x + 4y + 4 = 0 [Mar. 11]
Solution:
Equation of the line is 3x + 4y + 4 = 0
P = Length of the perpendicular .
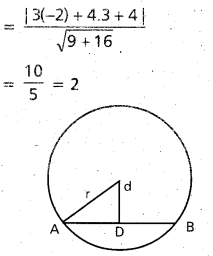
Length of the chord = 2λ = 2 ⇒ λ = 1
If r is the radius of the circle then
r2 = 22 + 12 – 4 + 1 = 5
Centre of the circle is (-2, 3)
Equation of the circle is (x + 2)2 + (y – 3)2 = 5
x2 + 4x + 4 + y2 – 6y + 9 – 5 = 0
i.e., x2 + y2 + 4x – 6y + 8 = 0
Question 21.
Find the pole of 3x + 4y – 45 = 0 with respect to x2 + y2 – 6x – 8y + 5 = 0. [A.P. Mar. 16]
Solution:
Equation of polar is
xx1 + yy1 – 3(x + x1) – 4(y + y1) + 5 = 0
x(x1 – 3) + y(y1 – 4) – 3x1 – 4y1 + 5 = 0 …………………. (i)
Polar equation is same 3x + 4y – 45 = 0 ……………….. (ii)
Comparing (i) and (ii) we get

![]()
Question 22.
i) Show that the circles x2 + y2 – 6x – 2y + 1 = 0 ; x2 + y2 + 2x – 8y + 13 = 0 touch each other. Find the point of contact and the equation of common tangent at their point of contact. [A.P. Mar. 16; Mar. 11]
Solution:
Equations of the circles are
S1 ≡ x2 + y2 – 6x – 2y + 1 = 0
S2 ≡x2 + y2 + 2x – 8y + 13 = 0
Centres are A (3, 1), B(-1, 4)
r1 = \(\sqrt{9+1+1}\) = 3, r1 = \(\sqrt{1+16-13}\) = 2
AB = \(\sqrt{(3+1)^{2}+(1-4)^{2}}\) = \(\sqrt{16+9}\) = \(\sqrt{25}\) = 5
AB = 5 = 3 + 2 = r1 + r1
∴ The circles touch each other externally.
The point of contact P divides AB internally in the ratio r1 : r2 = 3 : 2
Co- ordinates of P are
\(\left(\frac{3(-1)+2.3}{5}, \frac{3.4+2.1}{5}\right)\) i.e., P\(\left(\frac{3}{5}, \frac{14}{5}\right)\)
Equation of the common tangent is S1 – S2 = 0
-8x + 6y – 12 = 0 (or) 4x – 3y + 6 = 0
ii) Show that x2 + y2 – 6x – 9y + 13 = 0, x2 + y2 – 2x – 16y = 0 touch each other. Find the point of contact and the equation of common tangent at their point of contact.
Solution:
Equations of the circles are
S1 ≡ x2 + y2 – 6x – 9y + 13 = 0
S2 ≡ x2 + y2 – 2x – 16y = 0
centres are A(3, \(\frac{9}{2}\)), B(1, 8)
r1 = \(\sqrt{9+\frac{81}{4}-13}\) = \(\frac{\sqrt{65}}{2}\), r2 = \(\sqrt{1+64}\)
= \(\sqrt{65}\)
AB = \(\sqrt{(3-1)^{2}+\left(\frac{9}{2}-8\right)^{2}}\) = \(\sqrt{4+\frac{49}{4}}\)
= \(\frac{\sqrt{65}}{2}\)
AB = |r1 – r2|
∴ The circles touch each other internally. The point of contact ‘P’ divides AB
externally in the ratio r1 : r2 = \(\frac{\sqrt{65}}{2}\) : \(\sqrt{65}\)
= 1 : 2 Co-ordinates of P are
\(\left(\frac{1(1)-2(3)}{1-2}, \frac{1(8)-2\left(\frac{9}{2}\right)}{1-2}=\left(\frac{-5}{-1}, \frac{-1}{-1}\right)\right.\) = (5, 1)
p = (5, 1)
∴ Equation of the common tangent is
S1 – S2 = 0
-4x + 7y + 13 = 0
4x – 7y – 13 = 0
![]()
Question 23.
Find the direct common tangents of the circles. [T.S. Mar. 15]
x2 + y2 + 22x – 4y – 100 = 0 and x2 + y2 – 22x + 4y + 100 = 0.
Solution:
C1 = (-11, 2)
C2 = (11, -2)
r1 = \(\sqrt{121+4+100}\) = 15
r2 = \(\sqrt{121+4-100}\) = 5
Let y = mx + c be tangent
mx – y + c = 0
⊥ from (-11, 2) to tangent = 15
⊥ from (11 ,-2) to tangent = 5

Squaring and cross multiplying
25 (1 + m2) = (11 m + 2 – 22m – 4)2
96m2 + 44m – 21 = 0
⇒ 96m2 + 72m – 28m – 21 = 0
m = \(\frac{7}{24}\), \(\frac{-3}{4}\)
c = \(\frac{25}{2}\)
y = – \(\frac{3}{4}\)x + \(\frac{25}{2}\)
4y + 3x = 50
c = -22m – 4
= -22(\(\frac{7}{24}\)) – 4
= \(\frac{-77-48}{12}\) =\(\frac{-125}{12}\)
y = \(\frac{7}{24}\) x – \(\frac{125}{12}\)
⇒ 24y = 7x – 250
⇒ 7x – 24y – 250 = 0
Question 24.
Find the transverse common tangents of the circles x2 + y2 – 4x – 10y + 28 = 0 and x2 + y2 + 4x-6y + 4 = 0 [A.P. Mar. 15; Mar. 14]
Solution:
C1 =(2, 5), C2 = (-2, 3)
r1 = \(\sqrt{4+25-28}\) = 1,
r2 = \(\sqrt{4+9-4}\) = 3
r1 + r2= 4
C1C2 = \(\sqrt{(2+2)^{2}+(5-3)^{2}}\)
= \(\sqrt{16+4}\) = \(\sqrt{20}\)
‘C’ divides C1C2 in the ratio 5 : 3
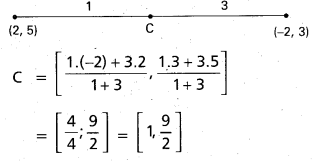
Equation of the pair transverse of the common tangents is
S12 = SS11
(x . 1 + \(\frac{9}{2}\)y – 2(x + 1) – 5(y + \(\frac{9}{2}\)) + 28)2 = [1 + \(\frac{81}{4}\) – 4 – 10 × \(\frac{9}{2}\) + 28]
= – (x2 + y2 – 4x – 10y + 28)
⇒ (-x – \(\frac{1}{2}\)y + \(\frac{7}{2}\))2
= \(\frac{1}{4}\) (x2 + y2 – 4x – 10y + 28)
(-2x – y + 7)2 = (x2 + y2 – 4x – 10y + 28)
4x2 + y2 + 4xy – 28x – 14y + 49 = x2 + y2 – 4x – 10y + 28
3x2 + 4xy – 24x – 4y + 21 = 0
(3x + 4y – 21); (x – 1) = 0
3x + 4y – 21 = 0; x – 1 = 0
![]()
Question 25.
Show that the circles x2 + y2 – 4x – 6y – 12 = 0 and x2 + y2 + 6x + 18y + 26 = 0 touch each other. Also find the point of contact and common tangent at this point of contact. [Mar. 13]
Solution:
Equations of the circles are
x2 + y2 – 4x – 6y – 12 = 0 and x2 + y2 + 6x + 18y + 26 = 0
Centres are C1(2, 3), C2 = (-3, -9)
r1 = \(\sqrt{4+9+12}\) = 5
r2 = \(\sqrt{9+81-26}\) = 8
C1C2 = \(\sqrt{(2+3)^{2}+(3+9)^{2}}\)
= \(\sqrt{25+144}\) = 13 = r1 + r2
∴ Circle touch externally .
Equation of common tangent is S1 – S2 = 0
-10x -,24y – .38 = 0
5x + 12y + 19 = 0

Question 26.
Find the equation of circle with centre (1, 4) and radius ‘5’.
Solution:
Here (h, k) = (1, 4) and r = 5.
∴ By the equation of the circle with centre at C (h, k) and radius r is
(x – h)2 + (y – k)2 = r2
(x – 1)2 + (y – 4)2 = 52
i.e., x2 + y2– 2x – 8y – 8 = 0
Question 27.
Find the centre and radius of the circle x2 + y2 + 2x – 4y – 4 = 0.
Solution:
2g = 2, 2f = -4, c = -4
g = 1, f = -2, c = -4
Centre (-g, -f) = (-1, 2)
radius = \(\sqrt{g^{2}+f^{2}-c}\) = \(\sqrt{1+4-(-4)}\) = 3
Question 28.
Find the centre and radius of the circle 3x2 + 3y2 – 6x + 4y – 4 = 0.
Solution:
Given equation is
3x2 + 3y2 – 6x + 4y – 4 = 0
Dividing with 3, we have
x2 + y2 – 2x + \(\frac{4}{3}\) y – \(\frac{4}{3}\) = 0
2g = -2, 2f = \(\frac{4}{3}\), c = –\(\frac{4}{3}\)
g = -1, f = \(\frac{2}{3}\), c = –\(\frac{4}{3}\)
Centre (-g, -f) = (1, \(\frac{-2}{3}\))
radius = \(\sqrt{g^{2}+f^{2}-c}\) = \(\sqrt{1+\frac{4}{9}+\frac{4}{3}}\)
= \(\sqrt{\frac{9+4+12}{9}}\) = \(\sqrt{\frac{25}{9}}\) = \(\frac{5}{3}\)
![]()
Question 29.
Find the equation of the circle whose centre is (-1, 2) and which passes through (5, 6).
Solution:
Let C(-1, 2) be the centre of the circle
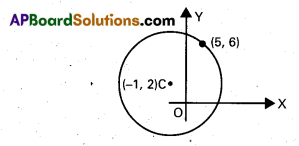
Since P(5,6) is a point on the circle CP = r
CP2 = r2 ⇒ r2 = (-1 – 5)2 + (2 – 6)2
= 36 + 16 = 52
Equation of the circle is (x + 1)2 + (y – 2)2
= 52
x2 + 2x + 1 + y2 – 4y + 4 – 52 = 0
x2 + y2 + 2x – 4y – 47 = 0
Question 30.
Find the equation of the circle passing through (2, 3) and concentric with the circle x2 + y2 + 8x + 12y + 15 = 0.
Solution:
The required circle is concentric with the circle x2 + y2 + 8x + 12y + 15 = 0
∴ The equation of the required circle can be taken as
x2 + y2 + 8x + 12y + c = 0
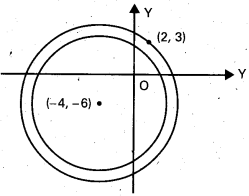
This circle passes through P(2, 3)
∴ 4 + 9 + 16 + 36 + c = 0
c = – 65
Equation of the required circle is x2 + y2 + 8x + 12y – 65 = 0
Question 31.
From the point A(0, 3) on the circle x2 + 4x + (y – 3)2 = 0 a chord AB is drawn and extended to a point M such that AM = 2 AB. Find the equation of the locus of M.
Solution:
Let M = (x’, y’)
Given that AM = 2AB
AB + BM = AB + AB
⇒ BM = AB
B is the mid point of AM
Co- ordinates of B are \(\left(\frac{x^{\prime}}{2}-\frac{y^{\prime}+3}{2}\right)\)
B is a point on the circle
(\(\frac{x^{\prime}}{2}\))2 + 4(\(\frac{x^{\prime}}{2}\)) + (\(\frac{y^{\prime}+3}{2}\) – 3)2 = 0
\(\frac{x^{\prime 2}}{4}\) + 2x’ + \(\frac{y^{\prime 2}-6 y^{\prime}+9}{4}\) = 0
x’2 + 8x’ + y’2 – 6y’ + 9 = 0
Lotus of M(x’, y’) is x2 + y2 + 8x – 6y + 9 = 0, which is a circle.
![]()
Question 32.
If the circle x2 + y2 + ax + by – 12 = 0 has the centre at (2, 3) then find a, b and the radius of the circle.
Solution:
Equation of the circle is
x2 + y2 + ax + by – 12 = 0
Centre = (\(-\frac{a}{2}\), \(-\frac{b}{2}\)) = (2, 3)
\(-\frac{a}{2}\) = 2, \(-\frac{b}{2}\) = 3
a = – 4, b – -6
g = -2, f = -3, c = -12
radius = \(\sqrt{g^{2}+f^{2}-c}\) = \(\sqrt{4+9+12}\) = 5
Question 33.
If the circle x2 + y2 – 4x + 6y + a = 0 has radius 4 then find a. [A.P. Mar. 16]
Solution:
Equation of the circle is x2 + y2 – 4x + 6y + a = 0
2g = – 4, 2f = 6, c = a
g =-2, f = 3, c = a
radius = 4 ⇒ \(\sqrt{g^{2}+f^{2}-c}\) = 4
\(\sqrt{4+9-a}\) = 4
13 – a = 16
a = 13 – 16 = -3
Question 34.
Find the equation of the circle passing through (4, 1), (6, 5) and having the centre on the line 4x + y – 16 = 0.
Solution:
Let the equation of the required circle be x2 + y2 + 2gx + 2fy + c = 0 .
This circle passes through A(4, 1)
16 + 1+ 8g + 2f + c = 0
8g + 2f + c = -17 ………………. (1)
The circle passes through B(6, 5)
36 + 25 + 12g + 10f + c = 0
12g + 10f + c = -61 ……………… (2)
The centre (-g, -f) lies on 4x + y – 16 = 0
– 4g – f – 16 = 0
4g + f + 16 = 0 ……………….. (3)
(2) – (1) gives 4g + 8f = -44 ……………….. (4)
4g + f = -16 …………….. (3)
7f = -28
f = \(\frac{-28}{7}\) = -4
From(3) 4g – 4 = -16
4g = -12 ⇒ g = -3
From(1) 8(-3) + 2(-4) + c = -17
c = -17 + 24 + 8 = 15
Equation of the required circle is
x2 + y2 – 6x – 8y + 15 = 0
Question 35.
Suppose a point (x1, y1) satisfies x2 + y2+ 2gx + 2fy + c = 0 then show that it represents a circle whenever g, f and c are real.
Solution:
Comparing with the general equation of second degree co-efficient of x2 = coefficient of y2 and coefficient of xy = 0
The given equation represents a circle if g2 + f2 – c ≥ 0
(x1, y1) is a point on the given equation
x2 + y2 + 2gx + 2fy + c = 0, we have
x12 + y12 + 2gx1 + 2fy1 + c = 0
g2 + f2 – c = g2 + f2 + x12 + y12 + 2gx1 + 2fy1 = 0
= (x1 + g)2 + (y1 + f)2 ≥ 0
g, f and c are real
∴ The given equation represents a circle.
![]()
Question 36.
Find the equation of the circle whose extremities of a diameter are (1, 2) and (4, 5).
Solution:
Here (x1, y1) = (1, 2) and (x2, y2) = (4, 5)
Equation of the required circle is
(x – 1) (x – 4) + (y – 2) ( y – 5) = 0
x2 – 5x + 4 + y2 – 7y + 10 = 0
x2 + y2 – 5x – 7y + 14 = 0
Question 37.
Find the other end of the diameter of the circle x2 + y2 – 8x – 8y + 27 = 0 if one end of it is (2, 3).
Solution:
A = (2, 3) and AB is the diameter of the circle x2 + y2 – 8x – 8y + 27 = 0
Centre of the circle is C = (4, 4)
Suppose B(x, y) is the other end
C = mid point of AB = \(\left(\frac{2+x}{2}, \frac{3+y}{2}\right)\) = (4, 4)
\(\frac{2+x}{2}\) = 4
2 + x = 8
x = 6
\(\frac{3+y}{2}\) = 4
3 + y = 8
y = 5
The other end of the diameter is B(6, 5)
Question 38.
Find the equation of the circum – circle of the traingle formed by the line ax + by + c = 0 (abc ≠ 0) and the co-ordinate axes.
Solution:
Let the line ax + by + c = 0 cut X, Y axes at A and B respectively co-ordinates of O are (0, 0) A are
Suppose the equation of the required circle is x2 + y2 + 2gx + 2fy + c = 0
This circle passes through 0(0, 0)
∴ c = 0
This circle passes through A(-\(\frac{c}{a}\), 0)
\(\frac{c^{2}}{a^{2}}\) + 0 – 2\(\frac{\mathrm{gc}}{\mathrm{a}}\) = 0
2g . \(\frac{c}{a}\) = \(\frac{c^{2}}{a^{2}}\) ⇒ 2g = \(\frac{c}{a}\) ⇒ g = \(\frac{c}{2a}\)
The circle passes through B (0, –\(\frac{c}{b}\))
0 + \(\frac{c^{2}}{b^{2}}\) + 0 – 2g \(\frac{c}{b}\) = 0
2f\(\frac{c}{b}\) = \(\frac{c^{2}}{b^{2}}\) ⇒ 2g = \(\frac{c}{b}\) ⇒ f = \(\frac{c}{2b}\)
Equation of the circle, through O, A, B is
x2 + y2 + \(\frac{c}{a}\) x + \(\frac{c}{b}\) y = 0
ab(x2 + y2) + (bx + ay) = 0
This is the equation of the circum circle of ∆OAB
![]()
Question 39.
Find the equation of the circle which passes through the vertices of the triangle formed by L1 = x + y + 1 = 0; L2 = 3x + y- 5 = 0 and L3 = 2x + y – 5 = 0.
Solution:
Suppose L1, L2,: L2, L3 and L3, L1 intersect in A, B and C respectively.
Consider a curve whose equation is
k (x + y + 1) (3x + y – 5) + l(3x + y – 5) (2x + y – 5) + m(2x + y – 5) (x + y + 1) = 0 ………………. (1)
This equation represents a circle
i) Co-efficient of x2 = Co – efficient of y2
3k + 6l + 2m = k + l + m
2k + 5l + m = 0 ……………….. (2)
ii) Co-efficient of xy = 0
4k + 5l + 3m = 0 ……………….. (3).
Applying cross multiplication rule for (2) and (3) we get
Substituting in (1), equation of the required circle is
5(x + y + 1) (3x + y – 5) – 1 (3x + y – 5)
(2x + y – 5) – 5(2x + y – 5) (x + y + 1) = 0
i.e., x2 + y2 – 30x – 10y + 25 = 0
Question 40.
Find the centre of the circle passing through the points (0, 0), (2, 0)and (0, 2).
Solution:
Here (x1, y1) = (0, 0); (x2, y1) = (2, 0);
(x3, y3) = (0, 2)
c1 = -(x12 + y12) = 0
c2 = – (x22 + y22) = -(22 + 02) = -4
c3 = -(x32 + y32) = -(02 + 22) – 4
The centre of the circle passing through three non-collinear points P(x1, y1), Q(x2, y2) and R(x3, y3)
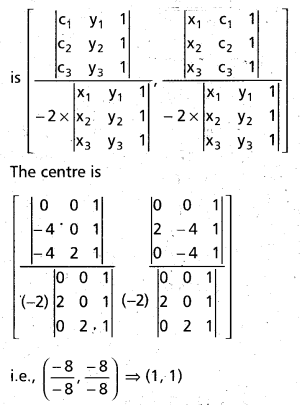
Thus the centre of the required circle is (1, 1)
Question 41.
Obtain the parametric equations of the circle x2 + y2 = 1.
Solution:
Equation of the circle is x2 + y2 = 1
Centre is (0, 0) radius = r = T
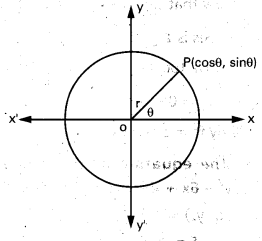
The circle having radius r is x = r cos θ,
y = sin θ where 0 < θ < 2π
The parametric equation of the circle
x2 + y2 = 1 and
x = 1 . cos θ = cos θ
y = 1 . sin θ = sin θ, θ < θ < 2π
Note: Every point on the circle can be expressed as (cos θ, sin θ)
Question 42.
Obtain the parametric equation of the circle represented by
x2 + y2 + 6x + 8y – 96 = 0.
Solution:
Centre (h, k) of the circle is (-3, -4)
radius = r = \(\sqrt{9+16+96}\) = \(\sqrt{121}\) = 11
Parametric equations are
x = h + r cos θ = -3 + 11 cos θ
y = k + r sin θ = -4 + 11 sin θ
where 0 < θ < 2π
![]()
Question 43.
Locate the position of the point (2, 4) with respect to the circle. x2 + y2 – 4x – 6y + 11 = 0.
Solution:
Here (x1, y1) = (2, 4) and
S ≡ x2 + y2 – 4x – 6y + 11
S11 = 4 + 16 – 8 – 24 + 11
= 31 – 32 = – 1 < 0
∴ The point (2, 4) lies inside the circle S = 0
Question 44.
Find the length of the tangent from (1, 3) to the circle x2 + y2 – 2x + 4y – 11 = 0.
Solution:
Here (x1, y1) = (1, 3) and
S = x2 + y2 – 2x + 4y – 11 = 0
P(x1, y1) to S = 0 is \(\sqrt{S_{11}}\)
Length of the tangent = \(\sqrt{S_{11}}\)
= \(\sqrt{1+9-2+12-11}\) = \(\sqrt{9}\) = 3
Question 45.
If a point P is moving such that the length of tangents drawn from P to
x2 + y2 – 2x + 4y – 20 = 0 ……………… (1)
and x2 + y2 – 2x – 8y + 1 = 0 ……………….. (2)
are in the ratio 2 : 1.
Then show that the equation of the locus of P is x2 + y2 – 2x – 12y + 8 = 0.
Solution:
Let P(x1, y1) be any point on the locus and \(\overline{\mathrm{PT}_{1}}\), \(\overline{\mathrm{PT}_{2}}\) be the lengths of tangents from P to the circles (1) and (2) respectively.
x2 + y2 – 2x + 4y – 20 = 0 and
x2 + y2 – 2x – 8y + 1 = 0
\(\frac{\overline{\mathrm{PT}_{1}}}{\overline{\mathrm{PT}_{2}}}=\frac{2}{1}\)
i.e., \(\sqrt{x_{1}^{2}+y_{1}^{2}-2 x_{1}+4 y_{1}-20}\)
= \(2 \sqrt{x_{1}^{2}+y_{1}^{2}-2 x_{1}-8 y_{1}+1}\)
3 (x12 + y12) – 6x1 – 36y1 + 24 = 0
Locus of P (x1, y1) is
x2 + y2 – 2x – 12y + 8 = 0
![]()
Question 46.
If S ≡ x2 + y2 + 2gx + 2fy + c = 0. represents a circle then show that the straight line lx + my + n = 0
i) touches the circle S = 0 if
(g2 + f2 – c) = \(\frac{(g l+m f-n)^{2}}{\left(l^{2}+m^{2}\right)}\)
ii) meets the circle S = 0 in two points if
g2 + f2 – c > \(\frac{(g l+m f-n)^{2}}{\left(l^{2}+m^{2}\right)}\)
iii) will not meet the circle if
g2 + f2 – c < \(\frac{(g l+m f-n)^{2}}{\left(l^{2}+m^{2}\right)}\)
Solution:
Let ‘c’ be the centre and ‘r’ be the radius of the circle S = 0
Then C = (-g, -f) and r = \(\sqrt{g^{2}+f^{2}-c}\)
i) The given straight line touches the circle
if r = \(\frac{|l(-\mathrm{g})+\mathrm{m}(-\mathrm{f})-\mathrm{n}|}{\sqrt{l^{2}+\mathrm{m}^{2}}}\)
\(\sqrt{g^{2}+f^{2}-c}\) = \(\frac{|-(l g+m f-n)|}{\sqrt{l^{2}+m^{2}}}\)
squaring on both sides, we get
g2 + f2 – c = \(\frac{(g l+m f-n)^{2}}{\left(l^{2}+m^{2}\right)}\)
ii) The given line lx + my + n = 0 meets the circle s = 0 in two points if
g2 + f2 – c > \(\frac{(g l+m f-n)^{2}}{\left(l^{2}+m^{2}\right)}\)
iii) The given line lx + my + n = 0 will not meet the circle s = 0 if
g2 + f2 – c < \(\frac{(g l+m f-n)^{2}}{\left(l^{2}+m^{2}\right)}\)
Question 47.
Find the length of the chord intercepted by the circle x2 + y2 + 8x – 4y – 16 = 0 on the line 3x – y + 4 = 0.
Solution:
The centre of the given circle c = (-4, 2) and radius r = \(\sqrt{16+4+16}\) = 6. Let the perpendicular distance from the centre to the line 3x-y + 4 = 0 be ‘d’ then
d = \(\frac{|3(-4)-2+4|}{\sqrt{3^{2}+(-1)^{2}}}\) = \(\frac{10}{\sqrt{10}}\) = \(\sqrt{10}\)
Length of the chord + \(\sqrt{r^{2}-d^{2}}\)
= 2\(\sqrt{6^{2}-(\sqrt{10})^{2}}\) = 2\(\sqrt{26}\)
Question 48.
Find the equation of tangents to x2 + y2 – 4x + 6y – 12 = 0 which are parallel to x + 2y- 8 = 0.
Solution:
Here g = -2, f = 3, r = \(\sqrt{4+9+12}\) = 5
and the slope of the required tangent is \(\frac{-1}{2}\)
The equations of tangents are
y + 3 = \(\frac{-1}{2}\) (x – 2) ± 5 \(\sqrt{1+\frac{1}{4}}\)
2(y + 3) = – x + 2 ± 5\(\sqrt{5}\)
x + 2y + (4 ± 5\(\sqrt{5}\)) = 0
Question 49.
Show that the circle S ≡ x2 + y2 + 2gx + 2fy + c = 0 touches the
i) X – axis if g2 = c
ii) Y – axis if f2 = c.
Solution:
i) We know that the intercept made by S = 0 on X – axis is 2\(\sqrt{g^{2}-c}\)
If the circle touches the X – axis then
22\(\sqrt{g^{2}-c}\) 0 ⇒ g2 = c
![]()
Question 50.
Find the equation of the tangent to x2 + y2 – 6x + 4y – 12 = 0 at (- 1, 1).
Solution:
Here (x1, y1) = (-1, 1) and
S ≡ x2 + y2 – 6x + 4y – 12 = 0
∴ The equation of the tangent is
x(-1) + y (1) – 3(x – 1) + 2(y + 1)- 12 = 0
The equation of the tangent at the point P(1, y1) to the circle
S ≡ x2 + y2 + 2gx + 2fy + c = 0 is S1 = 0
⇒ – x + y – 3x + 3 + 2y + 2 – 12 = 0
⇒ – 4x + 3y – 7 = 0
(or) 4x – 3y + 7 = 0
Question 51.
Find the equation of the tangent to x2 + y2 – 2x + 4y = 0 at (3, -1). Also find the equation of tangent parallel to it.
Solution:
Here (x1, y1) = (3, -1) and
S ≡ x2 + y2 – 2x + 4y = 0
The equation of the tangent at (3, -1) is
x (3) + y (-1) – (x + 3) + 2(y – 1) = 0
3x – y – x – 3 + 2y – 2 = 0
2x + y – 5 = 0
Slope of the tangent is m = -2, for the circle
g = -1, f = 2, c = 0
r = \(\sqrt{1+4-0}\) = \(\sqrt{5}\)
Equations of the tangents are
y = mx ± r \(\sqrt{1+m^{2}}\) is a tangent to the circle x2 + y2 = r2 and the slope of the tangent is m.
y + 2 = -2(x – 1) ± \(\sqrt{5} \sqrt{1+4}\)
y + 2 = -2x + 2 ± 5
2x 4- y = ± 5
The tangents are
2x + y + 5 = 0 and 2x + y – 5 = 0
The tangent parallel to the given tangent is 2x + y ± 5 = 0
Question 52.
If 4x – 3y + 7 = 0 is a tangent to the circle represented by x2 + y2 – 6x + 4y – 12 = 0, then find its point of contact.
Solution:
Let (x1, y1) be the point of contact
Equation of the tangent is
(x1 + g) x + (y1 + f) y + (gx1 + fy1 + c) = 0
We have \(\frac{x_{1}-3}{4}\) = \(\frac{y_{1}+2}{-3}\)
= \(\left(\frac{-3 x_{1}+2 y_{1}-12}{7}\right)\) ……………… (1)
From first and second equalities of (1), we get
3x1 + 4y1 = 1 ………………. (2)
Now by taking first and third equalities of (1), we get
19x1 – 8y1 = -27 ………………. (3)
Solving (2) and (3) we obtain
x1 = -1;, y1 = 1
Hence the point of contact is (-1, 1).
![]()
Question 53.
Find the equations of circles which touch 2x – 3y + 1 = 0 at (1, 1) and having radius \(\sqrt{13}\).
Solution:
The centres of the required circle lies on a line perpendicular to 2x – 3y + 1 =0 and passing through (1, 1)
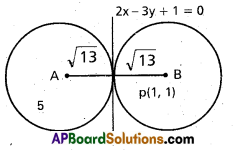
The equation of the line of centre can be taken as
3x + 2y + k = 0
This line passes through (1, 1)
3 + 2 + k = 0 ⇒ k = -5
Equation of AB is 3x + 2y – 5 = 0
The centres A and B are situated on
3x + 2y – 5 = 0 at a distance \(\sqrt{13}\) from (1, 1).
The centres are given by
(x1 ± r cos θ, y1 ± r sin θ)
\(\left(1+\sqrt{13}\left(-\frac{2}{\sqrt{13}}\right) 1+\sqrt{13} \cdot \frac{3}{\sqrt{13}}\right)\) and
\(\left(1-\sqrt{13} \frac{(-2)}{\sqrt{13}}, 1-\sqrt{13} \cdot \frac{3}{\sqrt{13}}\right)\)
i.e., (1 -2, 1 +3) and (1 + 2, 1 – 3)
(-1, 4) and (3, -2)
Centre (3, -2), r = \(\sqrt{13}\)
Equation of the required circles are
(x + 1 )2 + (y – 4)2 = 13 and
(x – 3)2 + (y + 2)2 = 13
i.e., x2 + y2 + 2x – 8y + 4 = 0
and x2 + y2 – 6x + 4y = 0
Question 54.
Show that the line 5x + 12y – 4 = 0 touches the circle x2 + y2 – 6x + 4y + 12 = 0.
Solution:
Equation of the circle is
x2 + y2 – 6x + 4y + 12 = 0
Centre (3, -2), r = \(\sqrt{9+4-12}\) = 1 ……………….. (1)
The given line touches the circle if the perpendicular distance from the centre on the given line is equal to radius of the circle, d = perpendicular distance from (3, -2)
= \(\frac{|5(3)+12(-2)-4|}{\sqrt{25+144}}\)
= \(\frac{13}{13}\) = 1 = radius of the circle ………………… (2)
∴ The given line 5x + 12y – 4 = 0 touches the circle.
Question 55.
If the parametric values of two points A and B lying on the circle x2 + y2 – 6x + 4y – 12 = 0 are 30° and 60° respectively, then find the equation of the chord joining A and B.
Solution:
Here g = -3, f = -2; r = \(\sqrt{9+4-12}\) = 5
∴ The equation of the chord joining the points θ1 = 30°, θ2 = 60°
Equation of chord joining the point; (-g+ r cos θ1(-f + r sin θ1) where r is the radius of the circle; θ2 and (-g + r cos θ2, -f + r sin θ2) is (x + g) cos (\(\frac{\theta_{1}+\theta_{2}}{2}\)) + (y + f)
sin (\(\frac{\theta_{1}+\theta_{2}}{2}\)) = r cos (\(\frac{\theta_{1}+\theta_{2}}{2}\))
(\(\frac{\theta_{1}+\theta_{2}}{2}\)) = r cos \(\frac{\theta_{1}+\theta_{2}}{2}\)
(x – 3) cos [latex]\frac{60^{\circ}+30^{\circ}}{2}[/latex]
(y + 2) sin [latex]\frac{60^{\circ}+30^{\circ}}{2}[/latex]
= 5 cos [latex]\frac{60^{\circ}-30^{\circ}}{2}[/latex]
i.e., (x – 3) cos 45 ° + (y + 2) sin 45°
= 5 cos 15°
= \(\frac{(x-3)+(y+2)}{\sqrt{2}}=5\left[\frac{(\sqrt{3}+1)}{2 \sqrt{2}}\right]\)
i.e., 2x + 2y – (7 + 5\(\sqrt{3}\)) = 0.
![]()
Question 56.
Find the equation of the tangent at the point 30° (parametric value of θ) of the circle is x2 + y2 + 4x + 6y – 39 = 0.
Solution:
Equation of the circle is
x2 + y2 + 4x + 6y – 39 = 0
g = 2,f = 3, r = \(\sqrt{4+9+39}\) = \(\sqrt{52}\) = 2\(\sqrt{3}\)
θ = 30°
Equation of the tangent is
(x + g) cos 30° + (y + f) sin 30° = r
(x + 2) \(\frac{\sqrt{3}}{2}\) +(y + 3) \(\frac{1}{2}\) = 2713
\(\sqrt{3}\)x + 2\(\sqrt{3}\) + y + 3 = 4\(\sqrt{13}\)
\(\sqrt{3}\) x + y + (3 + 2\(\sqrt{3}\) – 4\(\sqrt{13}\)) = 0
Question 57.
Find the area of the triangle formed by the tangent at P(x1, y1) to the circle x2 + y2 = a2 with the co-ordinate axes where x1y1 ≠ 0.
Solution:
Equation of the circle is x2 + y2 = a2
Equation of the tangent at P(x1, y1) is xx1 + yy1 = a2 ……………… (1)
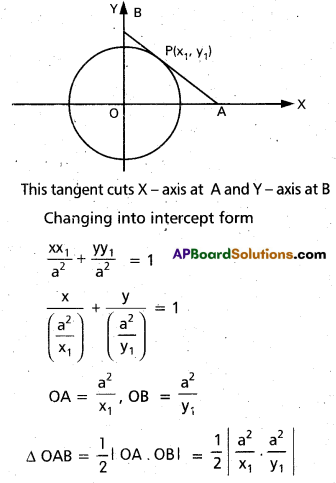
= \(\frac{a^{4}}{2\left|x_{1} y_{1}\right|}\)
Question 58.
Find the equation of the normal to the circle x2 + y2 – 4x – 6y + 11 = 0 at (3, 2). Also find the other point where the normal meets the circle.
Solution:
Let A(3, 2), C be the centre of given circle and the normal at A meet the circle at B(a, b). From the hypothesis, we have
2g = -4 i.e., g = -2
2f = -6 i.e., f = -3
x1 = 3 and y1 = 2
The equation of the normal at P(x1, y1) of the circle
S ≡ x2 + y2 + 2gx + 2fy + c = Q is
(x – x1) (y1 + f) – (y – y1) (x1 + g) = 0
The equation of normal at A(3, 2) is
(x – 3) (2 – 3) – (y – 2) (3 – 2) = 0
i.e., x + y – 5 = 0
The centre of the circle is the mid point of A and B. (Points of intersection of normal and circle).
\(\frac{a+3}{2}\) = 2 ⇒ a = 1
and \(\frac{b+2}{2}\) = 3 ⇒ b = 4
Hence the normal at (3, 2) meets the circle at (1, 4).
Question 59.
Find the area of the triangle formed by the normal at (3, -4) to the circle x2 + y2 – 22x – 4y + 25 = 0 with the co-ordinate axes.
Solution:
Here 2g = -22, 2f = – 4, g = -11, f = -2
x1 = 3, y1 = – 4
Equation of the normal at (3, -4) is
(x – x1) (y1 + f) – (y – y1) (x1 + g) = 0
(x – 3) (-4 – 2) – (y + 4) (3 – 11) = 0
3x + 4y – 25 = 0 ……………….. (1)
This line meets X-axis at A(\(\frac{25}{3}\), 0) and Y – axis at B(0, \(\frac{25}{4}\)) , ∆OAB = \(\frac{1}{2}\) |OA . OB|
= \(\frac{1}{2}\) |\(\frac{25}{3} \times-\left[\frac{25}{4}\right]\)| = \(\frac{625}{24}\)
![]()
Question 60.
Show that the line lx + my + n =0 is a normal to the circle S = 0 if and only if gl + mf = n.
Solution:
The straight line lx + my + n = 0 is normal to the circle
S = x2 + y2 + 2gx + 2fy + c = 0
⇒ If the centre (-g, -f) lies on
lx + my + n = 0
l (- g) + m(- f) + n = 0
gl + fm = n
Question 61.
Find the condition that the tangents drawn from the exterior point (g, f) to S ≡ x2 + y2 + 2gx + 2fy + c = 0 are perpendicular to each other.
Solution:
If the angle between the tangents drawn from P(x1, y1) to S = 0 is θ, then
tan (\(\frac{\theta}{2}\)) = \(\frac{\mathrm{r}}{\sqrt{\mathrm{S}_{11}}}\)
Equation of the circle is
x2 + y2 + 2gx + 2fy + c = 0
r = \(\sqrt{g^{2}+f^{2}-c}\)
S11 = g2 + f2 + 2g2 + 2f2 + c
= 3g2 + 3f2 + c
θ = 90° ⇒ tan \(\frac{\theta}{2}\) = tan 45 = \(\frac{\sqrt{g^{2}+f^{2}-c}}{\sqrt{3 g^{2}+3 f^{2}+c}}\)
1 = \(\frac{g^{2}+f^{2}-c}{3 g^{2}+3 f^{2}+c}\)
⇒ 3g2 + 3f2 + c = g2 + f2 – c
⇒ 2g2 + 2f2 + 2c = 0 ⇒ g2 + f2 + c = 0
This is the condition for the tangent drawn from (g, f) to the circle S = 0 are perpendicular.
Note : Here c < 0
Question 62.
If θ1, θ2 are the angles of inclination of tangents through a point P to the circle x2 + y2 = a2 then find the locus of P when cot θ1 + cot θ2 = k.
Solution:
Equation of the circle is x2 + y2 = a2
If m is the slope of the tangent, then the equation of tangent passing through P(x1, y1) can be taken as
y1 = mx1 ± a\(\sqrt{1+m^{2}}\)
(y1 – mx1)2 = a2 (1 + m2)
m2x12 + y12 – 2mx1y1 – a2 – a2m2 = 0
m2 (x12 – a2) – 2mx1y1 + (y12 – a2) = 0
Suppose m1 and m2 are the roots of this equation
m1 + m2 = tan θ1 + tan θ2 = \(\frac{2 x_{1} y_{1}}{x_{1}^{2}-a^{2}}\)
m1m2 – tan θ1 . tan θ1 = \(\frac{y_{1}^{2}-a^{2}}{x_{1}^{2}-a^{2}}\)
Given that cot θ1 + cot θ2 = k
⇒ \(\frac{1}{\tan \theta_{1}}+\frac{1}{\tan \theta_{2}}\) = k
⇒ \(\frac{\tan \theta_{1}+\tan \theta_{2}}{\tan \theta_{1} \cdot \tan \theta_{2}}\) = k
⇒ \(\frac{2 x_{1} y_{1}}{y_{1}^{2}-a^{2}}\) = k
2x1y1 = k (y12 – a2)
Locus of P(x1, y1) is 2xy = k(y2 – a2)
Also, conversely if P(x1, y1) satisfies the condition 2xy = k(y2 – a2) then it can be show that cot θ1 + cot θ2 = k
Thus the locus of P is 2xy = k(y2 – a2)
![]()
Question 63.
Find the chord of contact of (2, 5) with respect to the circle x2 + y2 – 5x + 4y – 2 = 0.
Solution:
Here (x1, y1) = (2, 5). By
S ≡ x2 + y2 + 2gx + 2fy + c = 0 then the equation of the chord of contact of P with respect to S = 0 is S1 =0, the required chord of contact is
xx1 + yy1 – \(\frac{5}{2}\) (x + x1) + 2(y + y1) – 2 = 0
Substituting x1 and y1 values, we get
x(2) + y(5) – \(\frac{5}{2}\) (x + 2) + 2(y + 5) – 2 = 0
i.e., x – 14y + 6 = 0.
Question 64.
If the chord of contact of a point P with respect to the circle x2 + y2 = a2 cut the circle at A and B such that, AÔB = 90° then show that P lies on the circle x2 + y2 = 2a2.
Solution:
Given circle x2 + y2 = a2 …………… (1)
Let P(x1, y1) be a point and let the chord of contact of it cut the circle in A and B such that AÔB = 90°. The equation of the chord of contact of P(x1, y1) with respect to (1) is
xx1 + yy1 – a2 = 0 ……………………. (2)
The equation of the pair of the lines \(\overleftrightarrow{\mathrm{OA}}\) and \(\overleftrightarrow{\mathrm{OB}}\) is.given by x2 + y2 – a2
\(\left(\frac{x x_{1}+y y_{1}}{a^{2}}\right)^{2}\) = 0
or a2 (x2 + y2)- (xx1 + yy1)2 = 0
or x2 (a2 – x12) – 2x1y1xy + y2 (a2 – y12) = 0 – (3)
Since AÔB = 90°, we have the coefficient of x2 in (3) + coefficient of y2 in (3) = 0
∴ a2 – x12 + a2 – y12 = 0
i.e., x12 + y12 = 2a2
Hence the point P(x1, y1) lies on the circle x2 + y2 = 2a2.
Question 65.
Find the equation of the polar of (2, 3) with respect to the circle x2 + y2 + 6x + 8y – 96 = 0.
Solution:
Here (x1, y1) = (2, 3) ⇒ x1 = 2, y1 = 3
Equation of the circle is
x2 + y2 + 6x + 8y – 96 = 0
Equation of the polar is S1 = 0
Polar of (2, 3) is x . 2 + y . 3 + 3(x + 2) + 4(y + 3) – 96 = 0
2x + 3y + 3x + 6 + 4y + 12 – 96 = 0
5x + 7y – 78 = 0
Question 66.
Find the pole of x + y + 2 = 0 with respect to the circle x2 + y2 – 4x + 6y – 12 = 0.
Solution:
Here lx + my + n = 0 is x + y + 2 = 0
l = 1, m = 1, n = 2
Equation of the circle is
S ≡ x2 + y2 – 4x + 6y – 12 = 0
2g = -4, 2f = 6, c = -12
g = -2, f = 3, c = -12
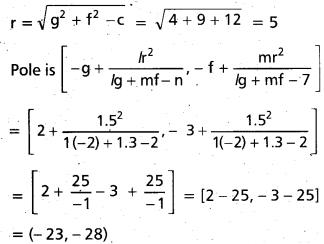
The pole of the given line x + y + 2 = 0 w.r.to the given circle (-23, -28)
![]()
Question 67.
Show that the poles of the tangents to the circle x2 + y2 = a2 with respect to the circle (x + a)2 + y2 = 2a2 lie on y2 + 4ax = 0.
Solution:
Equations of the given circles are
x2 + y2 = a2 …………………. (1)
and (x + a)2 + y2 = 2a2 ………………. (2)
Let P(x1, y1) be the pole of the tangent to the circle (1) with respect to circle (2).
The polar of P w.r.to circle (2) is
xx1 + yy1 + a(x + x1) – a2 = 0
x(x1 + a) + yy1 + (ax1 – a2) = 0
This is a tangent to circle (1)
∴ a = \(\frac{\left|0 .+0+a x_{1}-a^{2}\right|}{\sqrt{\left(\dot{x}_{1}+a\right)^{2}}+y_{1}^{2}}\)
a = \(\frac{a\left|x_{1}-a\right|}{\sqrt{\left(x_{1}+a\right)^{2}}+y_{1}^{2}}\)
Squaring and cross – multiplying
(x1 + a)2 + y12 = (x1 – a)2
(or) y12 + (x1 + a)2 – (x1 – a)2 = 0
i.e., y12 + 4ax1 = 0
The poles of the tangents to circle (1) w.r.to circle (2) lie on the curve y2 + 4ax = 0
Question 68.
Show that (4, -2) and (3, -6) are conjugate with respect to the circle x2 + y2 – 24 = 0.
Solution:
Here (x1, y1) = (4, -2) and (x2, y2) = (3, -6) and
S ≡ x2 + y2 – 24 = 0
Two points (x1, y1) and (x2, y2) are conjugate with respect to the circle S = 0 if S12 = 0;
In this case x1x2 + y1y2 – 24 = 0
S12 = 4.3 + (-2) (-6) – 24 .
= 12 + 12 – 24 = 0
∴ The given points are conjugate with respect to the given circle.
Question 69.
If (4, k) and (2, 3) are conjugate points with respect to the circle x2 + y2 = 17 then find k.
Solution:
Here (x1, y1) = (4, k) and (x2, y2) = (2, 3) and
S ≡ x2 + y2 – 17 = 0
The given points are conjugate ⇒ S12 = 0
x1x2 + y1y2 – 17 = 0
4.2 + k. 3 – 17 = 0
3k = 17 – 8 = 9
k = \(\frac{9}{3}\) = 3
![]()
Question 70.
Show that the lines 2x + 3y + 11 = 0 and 2x – 2y – 1 = 0 are conjugate with respect to the circle x2 + y2 + 4x + 6y – 12 = 0.
Solution:
Here l1 = 2, m1 = 3, n1 = 11
l2 = 2, m2 = -2, n2 = -1
and g = 2, f = 3, c = 12
r = \(\sqrt{9+4-12}\) = 1
We know that l1x + m1y + n1 = 0
l2x + m2y + n2 = 0 are conjugate with respect to S = 0
r2 (l1l2 + m1m2) = (l1g + m1f – n1) (l2g + m2f – n2)
r2 (l1l2 + m1m2) – 1(2.2 + 3(- 2)) = 4 – 6 = -2
(l1g + m1f – n1) (l2g + m2f – n2)
= (2.2 + 3.3-11) (2.2-2.3 + 11)
= 2(- 1) = -2 L.H.S. = R.H.S.
Condition for conjugate lines is satisfied
∴ Given lines are conjugate lines.
Question 71.
Show that the area of the triangle formed by the two tangents through P(xv to the circle S ≡ x2 + y2 + 2gx + 2fy + c = 0 and the chord of contact of P with respect to S = 0 is \(\frac{r\left(S_{11}\right)^{3 / 2}}{S_{11}+r^{2}}\) where r is the radius of the circle.
Solution:
PA and PB are two tangents from P to the circle S = 0
AB is the chord of contact
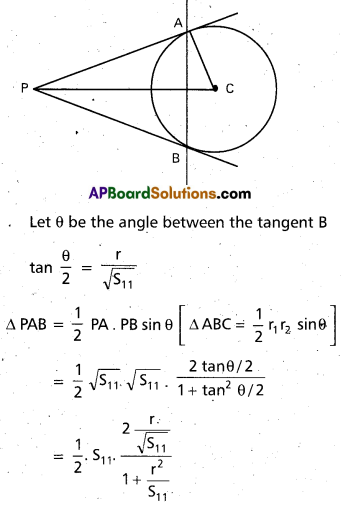
= \(S_{11} \cdot \frac{r}{\sqrt{S_{11}}} \cdot \frac{S_{11}}{S_{11}+r^{2}}\)
= \(\frac{r\left(S_{11}\right)^{3 / 2}}{S_{11}+r^{2}}\)
Question 72.
Find the mid point of the chord intercepted by
x2 + y2 – 2x – 10y + 1 = 0 ………………. (1)
on the line x – 2y + 7 = 0. ……………. (2)
Solution:
Let P(x1, y1) be the mid point of the chord AB
Equation of the chord is S1 = S11
xx1 + yy1 – 1 (x + x1) – 5(y + y1) + 1 = x12 + y12 – 2x1 – 10y1 + 1 .
x(x1 – 1) + y(y1 – 5) – (x12 + y12 – x1 – 5y1) = 0 ………………. (3)
Equation of the given line is x – 2y – 7 = 0
Comparing (1) and (2)
\(\frac{x_{1}-1}{1}=\frac{y_{1}-5}{-2}=\frac{x_{1}^{2}+y_{1}^{2}-x_{1}-5 y_{1}}{-7}\) = k (say)
x1 – 1 = k ⇒ x1 = k + 1
y1 – 5 = -2(k) ⇒ y1 = 5 – 2k
x12 + y12 – x1 – 5y1 = -7k
⇒ (k + 1)2 + (5 – 2k)2 – (k + 1) – 5(5 – 2k) + 7k = 0
⇒ k2 + 2k + 1 + 25 + 4k2 – 20k – k – 1 – 25 + 10k + 7k = 0
⇒ 5k2 – 2k = 0
⇒ k (5k — 2) = 0 ⇒ k = 0, \(\frac{2}{5}\)
k = 0 ⇒ (x1, y1) = (1, 5) and x – 2y + 7
= 1 – 10 + 7 ≠ 0
(1, 5) is not a point on the chord.
k = \(\frac{2}{5}\) (x1, y1) = \(\left(\frac{7}{5}, \frac{21}{5}\right)\)
![]()
Question 73.
Find the locus of mid-points of the chords of contact of x2 + y2 = a2 from the points lying on the line lx + my + n = 0.
Solution:
Let P = (x1, y1) be a point on the locus P is the mid point of the chord of the circle
x2 + y2 = a2
Equation of the chord is lx + my + n = 0 ……………… (1)
Equation of the circle is x2 + y2 = a2
Equation is the chord having (x1, y1) as mid point of S1 = S11
xx1 + yy1 = x12 + y12
xx1 + yy1 – (x12 + y12) = 0 ……………….. (2)
Pole of (2) with respect to the circle in
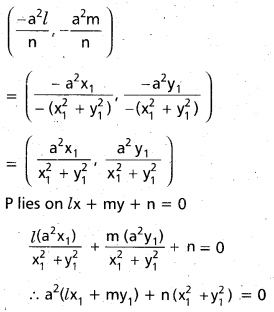
Locus of P(x1, y1) is n(x2 + y2) + a2(lx + my) = 0
Question 74.
Show that the four common tangents can be drawn for the circles given by
x2 + y2 – 14x + 6y + 33 = 0 …………… (1)
and x2 + y2 + 30x – 2y +1 = 0 ……………… (2)
and find the internal and external centres of similitude. [T.S. Mar. 19]
Solution:
Equations of the circles are
x2 + y2 – 14x + 6y + 33 = 0
and x2 + y2 + 30x – 2y + 1 = 0
Centres are A(7, -3), B(-15, 1)
r1 = \(\sqrt{49+9-33}\) = 5
r2 = \(\sqrt{225+1-1}\) = 15
AB = \(\sqrt{(7+15)^{2}+(-3-1)^{2}}\)
= \(\sqrt{484+16}\) = \(\sqrt{500}\) > r1 + r2
∴ Four common tangents can be drawn to the given circle
r1 : r2 = 5 : 15 = 1 : 3

Internal centre of similitude S’ divides AB in the ratio 1 : 3 internally
Co-ordinates of S’ are
\(\left(\frac{1 .(-15)+3.7}{1+3}, \frac{1.1+3(-3)}{1+3}\right)\)
= \(\left(\frac{6}{4}, \frac{1-9}{4}\right)\) = \(\left(\frac{3}{2},-2\right)\)
External centre of similitude S divides AB externally in the ratio 1 : 3
Co-ordinates of S are
\(\left(\frac{1(-15)+3(7)}{1-3}, \frac{1.1-3(-3)}{1-3}\right)\)
= \(\left(\frac{-15-21}{-2}, \frac{1+9}{-2}\right)\) = (18, -5)
![]()
Question 75.
Prove that the circles x2 + y2 – 8x – 6y + 21 = 0 and x2 + y2 – 2y – 15 = 0 have exactly two common tangents. Also find the point of intersection of those tangents.
Solution:
Let C1, C2 be the centres and r1, r2 be their radii.
Equation of the circles are
x2 + y2 – 8x – 6y + 21 = 0
and x2 + y2 – 2y – 15 = 0
C1(4, 3), C2(0, 1)
r1 = \(\sqrt{16+9-21}\) = 2, r2 = \(\sqrt{1+15}\) = 4
\(\overline{\mathrm{C}_{1} \mathrm{C}_{2}^{2}}\) = (4 – 0)2 + (3 – 1)2 = 16 + 4 = 20
C1C2 = 2\(\sqrt{5}\)
|r1 – r2| = |2 – 4| = 2, r1 + r2 = 2 + 4 = 6
|r1 – r2| < C1C2 < r1 + r2
Given circles intersect and have exactly two common tangents.
r1 : r2 = 2 : 4 = 1 : 2
The tangents intersect in external centre of similitude

Co-ordinates of S are
\(\left(\frac{1.0-2.4}{1-2}, \frac{1.0-2.3}{1-2}\right)\) = \(\left(\frac{-8}{-1}, \frac{-5}{-1}\right)\)
= (8, 5)
Question 76.
Show that the circles x2 + y2 – 4x – 6y – 12 = 0 and x2 + y2 + 6x + 18y + 26 = 0 touch each other. Also find the point of contact and common tangent at this point of contact. [Mar. 13]
Solution:
Equations of the circles are
x2 + y2 – 4x – 6y – 12 = 0 and x2 + y2 + 6x + 18y + 26 = 0
Centres are C1(2, 3), C2 = (-3, -9)
r1 = \(\sqrt{4+9+12}\) = 5
r2 = \(\sqrt{9+81-26}\) = 8
C1C2 = \(\sqrt{(2+3)^{2}+(3+9)^{2}}\)
= \(\sqrt{25+144}\) = 13 = r1 + r2
∴ Circle touch externally
Equation of common tangent is S1 – S2 = 0
-10x – 24y – 38 = 0
5x + 12y + 19 = 0

![]()
Question 77.
Show that the circles x2 + y2 – 4x – 6y – 12 = 0 and 5(x2 + y2) – 8x – 14y – 32 = 0 touch each other and find their point of contact.
Solution:
Equations of the circles are
x2 + y2 – 4x – 6y – 12 = 0
and x2 + y2 – \(\frac{8}{5}\) x – \(\frac{14}{5}\) y – \(\frac{32}{4}\) = 0
Centres are A(2, 3), B(\(\frac{4}{5}\), \(\frac{7}{5}\))

The circles touch internally
P divides AB externally the ratio 5 : 3

Question 78.
Find the equation of the pair of tangents from (10, 4) to the circle x2 + y2 = 25.
Solution:
(x1, y1) = (1o, 4)
Equation of the circle is x2 + y2 – 25 = 0
Equation of the pair of tangents is S12 = S . S11
(10x + 4y – 25)2 = (100 + 16 – 25)(x2 + y2 – 25)
100x2 + 16y2 + 625 + 80xy – 500x – 200y = 91x2 + 91y2 – 2275
9x2 + 80xy – 75y2 – 500x – 200y + 2900 = 0
![]()
Question 79.
Find the equation to all possible common tangents of the circles x2 + y2 – 2x – 6y + 6 = 0 and x2 + y2 = 1.
Solution:
Equations of the circles are
x2 + y2 – 2x – 6y + 6 = 0
and x2 + y2 = 1
Centres are A(1, 3), B(0, 0),
r1 = \(\sqrt{1+9-6}\) = 2
r2 = 1
External centre of similitude S divides AB externally in the ratio 2 : 1
Co-ordinates of S are
\(\left(\frac{2.0-1.1}{2-1}, \frac{2.0-1.3}{2-1}\right)\) = (-1, -3)
Equation to the pair of direct common tangents are
(x2 + y2 – 1) (1 + 9 – 1) = (x + 3y + 1)2
This can be expressed as
(y – 1) (4y + 3x – 5) = 0
Equations of direct common tangents are
y – 1 = 0 and 3x + 4y – 5 = 0
Internal centre of S’ divides AB internally in the ratio 2 : 1
Co-ordinates of S’ are
\(\left(\frac{2.0+1.1}{2+1}=\frac{2.0+1.3}{2+1}\right)\left(\frac{1}{3}, 1\right)\)
Equation to the pair of transverse common tangents are
(\(\frac{x}{3}\) +y – 1)2
= (\(\frac{1}{9}\) + 1 – 1) (x2 + y2 – 1)
This can be expressed as
(x + 1)(4x – 3y – 5) = 0
Equation of transverse common tangents are x + 1 = 0 and 4x – 3y – 5 = 0