Inter 1st Year Maths 1A Trigonometric Ratios up to Transformations Formulas

Use these Inter 1st Year Maths 1A Formulas PDF Chapter 6 Trigonometric Ratios up to Transformations to solve questions creatively.

Intermediate 1st Year Maths 1A Trigonometric Ratios up to Transformations Formulas

→ sin θ, cos θ, tan θ, cosec θ, sec θ and cot θ are called circular functions.

→ cosec θ, sec θ and cot θ are reciprocals to sin θ, cos θ and tan θ respectively.

→ sin²θ + cos²θ = 1; 1 + tan²θ = sec²θ; 1 + cot²θ = cosec²θ

→ sec θ + tan θ and sec θ – tan θ are mutual reciprocals.
Similarly cosec θ + cot θ and cosec θ – cot θ are also mutual reciprocals.

→ |sin θ| ≤ 1, |cosec θ| ≥ 1, |cos θ| ≤ 1 and |sec θ| ≥ 1

• sin 0° = o = cos 90°
• sin 15° = \(\frac{\sqrt{3}-1}{2 \sqrt{2}}\) = cos 75°
• sin 18° = \(\frac{\sqrt{5}-1}{4}\) = cos 72°
• sin 30° = \(\frac{1}{2}\) = cos 60°
• sin 36° = \(\frac{\sqrt{10-2 \sqrt{5}}}{4}\) = cos 54°
• sin 45° = \(\frac{1}{\sqrt{2}}\) = cos 45°
• sin 54° = \(\frac{\sqrt{5}+1}{4}\) = cos 36°
• sin 60° = \(\frac{\sqrt{3}}{2}\) = cos 30°
• sin 72° = \(\frac{\sqrt{10+2 \sqrt{5}}}{4}\) = cos 18°
• sin 75° = \(\frac{\sqrt{3}+1}{2 \sqrt{2}}\) = cos 15°
• sin 90° = 1 = cos 0°

Also, tan 15° = 2 – √3, tan 75° = 1 + √3
Sign to the determined by “ALL SILVER CUPS” rules

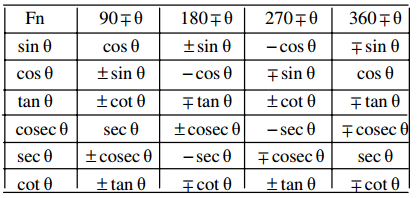
• sin (90° – θ) = cos θ; sin (90° + θ) = cos θ
• cos (90° – θ) – sin θ; cos (90° + θ) = -sin θ
• sin (180° – θ) = sin θ; sin (1800 + θ)= -sin θ
• cos (180° – θ) = -cos θ; cos (180° + θ) = -cos θ
• sin (270° – θ) = -cos θ; sin (270° + θ) = -cos θ
• cos (270° – θ) = -sin θ; cos (270° + θ) = sin θ
  sin (360° – θ) = -sin θ; sin (360° + θ) = sin θ
• cos (360° – θ) = cos θ; cos (360° + θ) = cos θ When ‘n’ is a +ve integer,
• sin (n. 360° – θ) = -sin θ; sin (n. 360° + θ) = +sin θ
• cos (n. 360° – θ) = cos θ; cos (n. 360° + θ) = cos θ
• sin (-θ) = – sin θ, cos (-θ) = cos 0; tan (-θ) = -tan θ.

→ For 0°, 180°, 360° ……………….. (multplies of π), there is no change in the ratios.

→ For 90°, 270°, 450°…………. (odd multiplies of \(\frac{\pi}{2}\) we get change in the ratio.

• For sin we get cos
• For tan we get cot
• For sec we get cosec
• For cos we get sin
• For cot we get tan
• For cot we get sin

→ Any non-constant function f : R → R is said to be “Periodic”, if there exists a real number p(≠ 0) such that f(x + p) = f(x) for each x ∈ R. The least positive value of ‘p’ with this property is called the “Period” of ‘f’.

→ If ‘f’ is a periodic function with period ‘P’ then

• – f is also a periodic function with period ‘P.
• f(x – p) = f(x), f(x + pn) = f(x) ∀ n ∈ Z, x ∈ R.

→ If f(x) is a periodic function with period ‘P, then f(ax + b) is also a periodic function with period \(\frac{P}{|a|}\)

→ If y = f(x), y = g(x) are periodic functions with l, m as the periods respectively, then a, b ∈ R the function h(x) = af(x) + bg(x) is a period function and L.C.M. of {l, m}
(if exist) is a period of h.

→ \(\frac{2 \pi}{k}\) is the period of sin x, cosec x, cos x and sec x.

→ \(\frac{\pi}{k}\) is the period of tan x and cot x.

→ Range of a sin x + b cos x is \(\left[-\sqrt{a^{2}+b^{2}}, \sqrt{a^{2}+b^{2}}\right]\)

→ Range of a sin x + b cos x + c is [c – \(\sqrt{a^{2}+b^{2}}\), c + \(\sqrt{a^{2}+b^{2}}\)]

→ sin x and cos x are continuous on ‘R’

→ tan x is. discontinuous at x = (2n + 1).\(\frac{\pi}{2}\),n ∈ Z.

→ cot x is discontinuous at x = nπ, n ∈ Z.

→ sec x is discontinuous at x = (2n + 1).\(\frac{\pi}{2}\), n ∈ Z.

→ cosecx is discontinuous at x = nπ, n ∈ Z.

→ sin (A ± B) = sin A cos B ± cos A sin B

→ cos (A ± B) = cos A cos B + sin A sin B

→ tan (A ± B) = \(\frac{\tan A \pm \tan B}{1 \mp \tan A \tan B}\)

→ cot (A ± B) = \(\frac{\cot A \cot B \mp 1}{\cot B \pm \cot A}\)

→ sin (A + B). sin (A-B) = sin²A – sin²B = cos²B – cos²A

→ cos (A + B). cos (A – B) = cos²A – sin²B = cos²B – sin²A

→ sin (A + B + C) = sin A cos B cos C + cos A sin B cos C + cos A cos B sin C – sin A sin B sin C

→ cos (A + B + C) = cos A cos B cos C – cos A sin B sin C – sin A cos B sin C – sin A sin B cos C

→ tan (A + B + C) = \(\frac{\sum \tan A-\pi \tan A}{1-\sum \tan A \tan B}\)

→ sin 2A = 2 sin A cos A, sin A = 2 sin \(\frac{A}{2}\) cos \(\frac{A}{2}\)

→ cos 2A = cos²A – sin²A = 1 – 2 sin² A = 2 cos²A – 1

→ cos A = cos²\(\frac{A}{2}\) sin²\(\frac{A}{2}\) = 1 – 2 sin²\(\frac{A}{2}\) = 2 cos² \(\frac{A}{2}\) – 1

→ tan 2A = \(\frac{2 \tan A}{1-\tan ^{2} A}\), tan A = \(\frac{2 \tan \frac{A}{2}}{1-\tan ^{2} \frac{A}{2}}\)(\(\frac{A}{2}\), A are not odd multiples of \(\frac{\pi}{2}\))

→ cot 2A = \(\frac{\cot ^{2} A-1}{2 \cot A}\), cot A = \(\frac{\cot ^{2} \frac{A}{2}-1}{2 \cot \frac{A}{2}}\); (A is not an integral multiple of π)

→ sin 2A = \(\frac{2 \tan A}{1+\tan ^{2} A}\), sin A = \(\frac{2 \tan \frac{A}{2}}{1+\tan ^{2} \frac{A}{2}}\); (\(\frac{A}{2}\), is not an odd multiple of \(\frac{\pi}{2}\))

→ cos 2A = \(\frac{1-\tan ^{2} A}{1+\tan ^{2} A}\), cos A = \(\frac{1-\tan ^{2} \frac{A}{2}}{1+\tan ^{2} \frac{A}{2}}\)

→ sin 3A = 3sin A – 4 sin³A

→ cos 3A = 4cos³A – 3 cos A

→ tan 3A = \(\frac{3 \tan A-\tan ^{3} A}{1-3 \tan ^{2} A}\)

→ cot 3A = \(\frac{3 \cot A-\cot ^{3} A}{1-3 \cot ^{2} A}\)

→ sin(A + B) + sin (A – B) = 2sin A cos B

→ sin(A + B) – sin(A – B) = 2cos A sin B

→ cos (A + B) + cos (A – B) = 2cos A cos B

→ cos(A + B) – cos(A – B) = -2sin A sin B

→ sin C + sin D = 2sin \(\frac{C+D}{2}\) cos \(\frac{C-D}{2}\)

→ sin C – sin D = 2cos \(\frac{C+D}{2}\) sin \(\frac{C-D}{2}\)

→ cos C + cos D = 2 cos \(\frac{C+D}{2}\) cos \(\frac{C-D}{2}\)

→ cos C – cos D = -2 sin \(\frac{C+D}{2}\) sin \(\frac{C-D}{2}\)

→ For any A ∈ R
(a) sin A = ±\(\sqrt{\frac{1-\cos 2 A}{2}}\)
(b) cos A = ±\(\sqrt{\frac{1+\cos 2 A}{2}}\)
(c) IfA ¡s not an odd multiple of \(\frac{\pi}{2}\), then tan A = ±\(\sqrt{\frac{1-\cos 2 A}{1+\cos 2 A}}\)

→ sin \(\frac{A}{2}=\pm \sqrt{\frac{1-\cos A}{2}}\)

→ cos \(\frac{A}{2}=\pm \sqrt{\frac{1+\cos A}{2}}\)

→ If A is not an odd multiple of n, then tan \(\frac{A}{2}=\pm \sqrt{\frac{1-\cos A}{1+\cos A}}\)

→ If a ray \(\overrightarrow{\mathrm{OP}}\) makes an angle θ with the positive direction of X-axis then

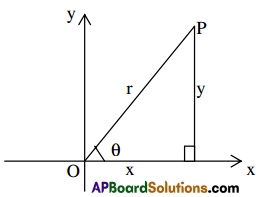
• Sin θ = \(\frac{\mathrm{y}}{\mathrm{r}}\)
• cos θ = \(\frac{\mathrm{x}}{\mathrm{r}}\)
• tan θ = \(\frac{\mathrm{y}}{\mathrm{x}}\) (x ≠ 0)
• cot θ = \(\frac{\mathrm{x}}{\mathrm{y}}\) (y ≠ 0)
• sec θ = \(\frac{\mathrm{r}}{\mathrm{x}}\)(x ≠ 0)
• cosec θ = \(\frac{\mathrm{r}}{\mathrm{y}}\)(y ≠ 0)

Relations :

• sin θ cosec θ = 1
• cos θ sec θ = 1
• tan θ cot θ = 1
• sin² θ + cos² θ = 1
• 1 + tan²θ = sec² θ → (sec θ + tan θ)(sec θ – tan θ) = 1
  → sec θ + tan θ = \(\frac{1}{\sec \theta-\tan \theta}\) = 1
• 1 + cot²θ = cosec²θ → (cosec θ + cot θ) (cosec θ – cot θ) = 1
• sec²θ + cosec²θ = sec²θ. cosec²θ
• tan²θ – sin²θ = tan²θ . sin²θ;
  cot²θ – cos²θ = cot²θ. cos²θ
• sin²θ + cos⁴θ = 1 – sin²θ cos²θ
  = sin⁴θ + cos²θ
• sin⁴θ + cos⁴θ = 1 – 2sin²θ cos²θ
• sin⁶θ + cos⁶ θ = 1 – 3sin²θ cos²θ
• sin²x + cosec²x ≥ 2
• cos²x + sec² x ≥ 2
• tan² x + cot² x ≥ 2.

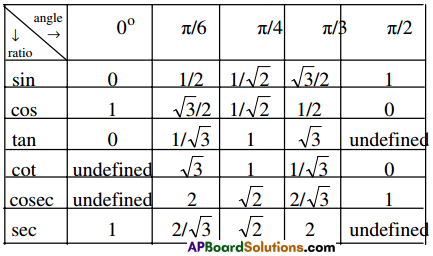
Values of trigonometric ratios of certain angles

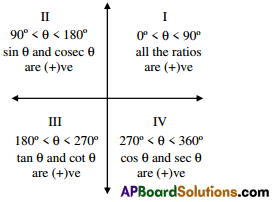
Signs of Trigonometric ratios :
If lies in I, II, III, IV quadrants then the signs of trigonometric ratios are as follows.

Note :

• 0°, 90°, 180°, 270°. 360°, 450°, etc. are called quadrant angles.
• With “ALL SILVER TEA CUPS” symbol we can remember the signs of trigonometric ratios.

Coterminal angles :
If two angles differ by an integral multiples of 360o then two angles are called coterminal angles.
Thus 30°, 390°, 750°, 330° etc., are coterminal angles.

Complementary Angles :
Two Angles A, B are said to complementary ⇒ A + B = 90°

Supplementary angles :
Two angles A, B are said to be supplementary ⇒ A + B = 180°.

→ sin C + sin D = 2sin\(\frac{\mathrm{C}+\mathrm{D}}{2}\). cos \(\frac{\mathrm{C}-\mathrm{D}}{2}\)

→ sin C – sin D = 2cos\( . sin [latex]\frac{\mathrm{C}-\mathrm{D}}{2}\)

→ cos C + cos D = 2cos \(\frac{\mathrm{C}+\mathrm{D}}{2}\). cos \(\frac{\mathrm{C}-\mathrm{D}}{2}\)

→ cos C – cos D = 2sin\(\frac{\mathrm{C}+\mathrm{D}}{2}\). sin \(\frac{\mathrm{D}-\mathrm{C}}{2}\)

→ 2sin A cos B = sin(A + B) + sin(A – B)

→ 2cos A sin B = sin(A + B) – sin(A – B)

→ 2cos A cos B = cos(A + B) + cos(A – B)

→ 2sin A sin B = cos(A – B) – cos(A + B)
(or)
cos(A – B) – cos(A + B) = 2 sin A sin B.

→ \(\frac{\sin A+\sin B}{\sin A-\sin B}\) = tan\(\left(\frac{A+B}{2}\right)\).

→ If sin A + sin B = x, and cos A + cos B = y. Then

• tan\(\left(\frac{\mathrm{A}+\mathrm{B}}{2}\right)=\frac{\mathrm{x}}{\mathrm{y}}\)
• sin(A + B) = \(\frac{2 x y}{y^{2}+x^{2}}\)
• cos (A + B) = \(\frac{y^{2}-x^{2}}{y^{2}+x^{2}}\)
• tan(A + B) = \(\frac{2 x y}{y^{2}-x^{2}}\)