Inter 1st Year Maths 1A Matrices Formulas

Use these Inter 1st Year Maths 1A Formulas PDF Chapter 3 Matrices to solve questions creatively.

Intermediate 1st Year Maths 1A Matrices Formulas

→ An ordered rectangular array of elements is called a matrix.

→ A matrix in which the number of rows is equal to the number of columns, is called a square matrix. Otherwise, it is called a rectangular matrix. In a square matrix, an element a_ij is in principal diagonal, if i = j

→ If each non-diagonal element of a square matrix is equal to zero, then it is called a diagonal matrix.

→ If each non-diagonal element of a square matrix is equal to zero and each diagonal element is equal to a scalar, then it is called a scalar matrix.

→ If each non-diagonal element of a square matrix is equal to zero and each diagonal element is equal to 1, then that matrix is called a unit matrix or Identity matrix.

→ If A is a square matrix then the sum of elements in the principal diagonal of A is called trace of A.

• Matrix addition is commutative.
• Matrix addition is associative.
• Matrix multiplication is associative.
• Matrix multiplication is distributive over matrix addition.

→ A square matrix A is said to be an idempotent matrix if A² = A.

→ A square matrix A is said to be an involuntary matrix if A² = I.

→ A square matrix A is said to be a nilpotent matrix, if there exist a positive integer n such that Aⁿ = 0. If n is the least positive integer such thatAn = 0, then n is called index of the nilpotent matrix A.

→ The matrix obtained by interchanging rows and columns is called transpose of the given matrix. Transpose of A is denoted by A^T (or) A’.

→ For any matrices A and B

• (A^T)^T = A
• (A + B)^T = A^T + B^T (A and B are same order)
• (AB)^T = B^TA^T. (If A and B are of orders m xn and n xp respectively)

→ A square matrix A is said to be symmetric if A^T = A.

→ A square matrix A is said to be skew symmetric if A^T = A.

→ Every square matrix can be uniquely expressed as a sum of symmetric matrix and a skew symmetric matrix.

→ The minor of an element in the square matrix of order ‘3’ is defined as the determinant of 2 × 2 matrix, obtained after deleting the row and the column in which the element is present.

→ The cofactor of an element in the i^th row and j^th column of 3 × 3 matrix is defined as its minor multiplied by (-1)^i+j.

→ The sum of the products of the elements of any row or column with their corresponding cofactors is called the determinant of a matrix.

• A square ‘A’ is said to be a singular matrix if det A = 0.
• A square A’ is said to be a non-singular matrix if det A ≠ 0.

→ The transpose of the matrix obtained by replacing.the elements of a square matrix A by the corresponding cofactors is called the adjoint matrix of A and it is denoted by adj (A).

• A square matrix ‘A is said to be an invertible matrix if there exists a square matrix B such that AB = BA = I the matrix B is called inverse of A and it is denoted by A^-1.
• If A is an invertible then A^-1 = 1.

→ A square matrix A is non-singular if A is invertible.

• If A and B are non-singular matrices of same type then Adj (AB) = (Adj B) (Adj A).
• If A is a square matrix of type n then det (Adj A) = (det A)^n-1.

→ A matrix obtained by deleting some rows or columns (or both) of a matrix is called a submatrix.

→ Let Abe a non-zero matrix, the rank of A is defined as the maximum of the orders of the non-singular square submatrices of A. The rank of a null matrix is zero. The rank of a matrix A is denoted as rank (A) or P (A).

→ A system of linear equations is

• Consistent, if it has a solution
• Inconsistent, if it has no solution

→ Non homogeneous system

• a₁x + b₁y + c₁z = d₁
• a₂x + b₂y + c₂z = d₂
• a₃x + b₃y + c₃z = d₃

→ The above system of equations has

• aunique solution if rank (A) = Rank [AD] = 3
• infinity many solutions, if rank (A) = Rank ([AD]) < 3
• no solution, if rank A ≠ Rank ([AD])

→ Homogeneous system of equations

• a₁x + b₁y + c₁z = d₁
• a₂x + b₂y + c₂z = d₂
• a₃x + b₃y + c₃z = d₃

→ The above system has

• Trival solution x = y = z = 0 only if rank (A) = 3
• infinitely many non-trival solutions if rank (A) < 3.

→ A matrix is an arrangement of real or complex numbers into rows and columns so that all the rows (columns) contain equal no. of elements.

→ If a matrix consists of ‘m’ rows and ‘n’ columns, then it is said to be of order m × n.

→ A matrix of order n × n is said to be a square matrix of order n.

→ A matrix (a_ij)_m×n is said to be a null matrix if a_ij = 0 for all i and j.

→ Two matrices of the same order are said to be equal if the corresponding elements in the matrices are all equal.

→ A matrix (a_ij)_n×n is a diagonal matrix a_ij = 0 for all i ≠ j

→ A matrix (a_ij)_n×n is a scalar matrix if a = 0 for all i ≠ j and a_ij = k (constant) for i = j

→ A matrix (a_ij)_n×n is said to be a unit matrix of order n, denoted by I_n if a_ij = 1, when i = j and a_ij = 0 when i ≠ j
Ex: I₂ = \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)
I₃ = \(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\)

→ If A = (a_ij)_m×n, B = (b_ij)_m×n, then A + B = (a_ij + b_ij)_m×n

→ Matrix addition is commutative and associative

→ Matrix multiplication is not commutative but associative

→ If A is a matrix of order m × n, then AI_n = I_mA = A(AI = IA = A)

→ If AB = CA = I, then B = C

→ If A = (a_ij)_m×n, then A ^T = (a_ij)_n×m

→ (KA)^T = KA^T, (A + B)^T = A^T + B^T, (AB)^T = B^T.A^T

→ A(B + C) = AB + AC, (A + B)C = AC + BC

→ A square matrix is said to be “non-singular” if detA ≠ 0

→ A square matrix is said to be “singular” if detA = 0

→ If AB = 0, where A and B are non-zero square matrices, then both A are singular.

→ A minor of any element in a square matrix is determinant of the matrix obtained by omitting the row and column in which the element is present.

→ In (a_ij)_n×n, the cofactor of a_ij is (-1)^i+j × (minor of a_ij).

→ In a square matrix, the sum of the products of the elements of any row (column) and the corresponding cofactors is equal to the determinant of the matrix.

→ In a square matrix, the sum of the products of the elements of any row (column) and the corresponding cofactors of any other row (column) is alway s zero.

→ If A is any square matrix, then A adjA = adjA. A = detA. I

→ If A is any square matrix and there exists a matrix B such that AB = BA = I, then B is called the inverse of A and denoted by A^-1.

→ AA^-1 = A^-1A = I.

→ If A is non-singular, then A^-1 = \(\frac{{adj} A}{{det} A}\) (or) adj A = |A|AA^-1

→ If A = \(\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right)\), then A^-1 = \(\frac{1}{a d-b c}\left(\begin{array}{cc}
d & -b \\
-c & a
\end{array}\right)\)

→ (A^-1)^-1 = A, (AB)^-1 = B^-1.A^-1, (A^-1)^T =( A^T)^-1; (ABC….)^-1 = C^-1B^-1A^-1.

Theorem:
Matrix multiplication is associative. i.e. if conformability is assured for the matrices A, B and C, then (AB)C = A(BC).
Proof:

Theorem:
Matrix multiplication is distributive over matrix addition i.e. if conformability is assured for the matrices A, B and C, then
(i) A (B + C) = AB + AC
(ii) (B + C) A = BA + CA
Proof:
Let A = (a_ij)_m×n, B = (b_jk)_n×p C = (c_ki)_n×p
B + C = (d_jk)_n×p, where d_jk = b_jk + c_jk

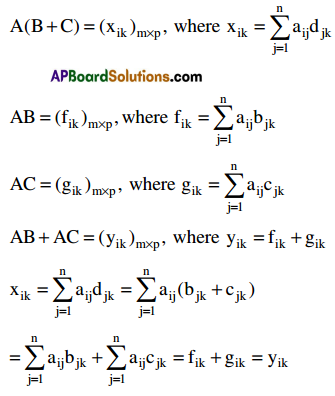
∴ A(B + C) = AB + AC
Similarly we can prove that
(B + C) = BA + CA.

Theorem:
If A is any matrix, then (A^T)^T = A.
Proof:
Let A = (a_ij)_m×n
A^T = (a’_jk)_n×m, where a’_ji = a_ij
(A^T)^T = (a”_ji)_m×n, where a”_ij = a_ji
a”_ij = a’_ji = a_ij
∴ (A^T)^T = A

Theorem:
If A and B are two matrices o same type, then (A + B)^T = A^T + B^T.
Proof:
Let A = (a_ij)_m×n, B = (b_ij)
A + B = (c_ij)_m×n,where c_ij = a_ij + b_ij
(A + B)^T = (c’_ji)_n×m. c’_ji = c_ij
A^T = (a’_ji)_n×m,where a’_ji = a_ij
B^T = (b_ji)_n×m. where. b’_kj = b_jk
A^T + B^T = (d_ji)_n×m, where d_ji = a’_ji + b’_ji
c’_ji = c_ij = a_ij + b_ij = a’_ji + b’_ji = d_ji
∴(A + B)^T = A^T + B^T

Theorem:
If A and B are two matrices for which conformability for multiplication is assured, then (AB)^T = B^TA^T.
Pr0of:
Let A = (a_ij)_m×n, B = (b_ji)_n×p
AB = (c_ik)_m×p, where c_ik = \(\sum_{j=1}^{n}\) a_ijb_jk
(AB)^T = (c_ki)_p×m,where c_ki = c_ik
A^T = (a_ji)_n×m,where a_ji = a_ij
B^T = (b_kj)_p×n, where b_kj = b_jk
B^T . A^T = (d_ki )_p×m, where d_ki= \(\sum_{j=1}^{n}\) b_kja_ji
c’ki = cik = \(\sum_{j=1}^{n}\) a_ijb_jk= \(\sum_{j=1}^{n}\) b_kja_jid_ki
∴ (AB)^T = B^TA^T

Theorem:
If A and B are two invertible matrices of same type then AB is also invertible and (AB)^-1 = B^-1A^-1.
Proof:
A is invertible matrix ⇒ A^-1 exists and AA^-1 = A^-1A = I.
B is an invertible matrix ⇒ B^-1 exists and
BB^-1 = B^-1B = I
Now (AB)(B^-1A^-1) = A(BB^-1)A^-1 = AIA^-1 = AA^-1 = I
(B^-1A^-1)(AB) = B^-1(A^-1A)B ∴ AB is invertible and
= B^-1IB = B^-1B = I
(AB)(B^-1A^-1) = (B^-1A^-1) = (B^-1A^-1)(AB) = 1
(AB)^-1 = B^-1A^-1.

Theorem:
If A is a non-singular matrix then A is invertible and A^-1 = \(\frac{{Adj} A}{{det} A}\).
Proof:
Let A = \(\left[\begin{array}{lll}
\mathrm{a}_{1} & \mathrm{~b}_{1} & \mathrm{c}_{1} \\
\mathrm{a}_{2} & \mathrm{~b}_{2} & \mathrm{c}_{2} \\
\mathrm{a}_{3} & \mathrm{~b}_{3} & \mathrm{c}_{3}
\end{array}\right]\) be a non – singular matrix.
∴ det A ≠ 0