Inter 1st Year Maths 1A Functions Formulas

Use these Inter 1st Year Maths 1A Formulas PDF Chapter 1 Functions to solve questions creatively.

Intermediate 1st Year Maths 1A Functions Formulas

Function:
Let A and B be non-empty sets and f be a relation from A to B. If for each element of A, there exists a unique element b e B such that (a,b) ∈ f, then f is called a function or mapping from A to B (or A into B). It is denoted by f: A → B. The set A is called the domain of f and B is called the co-domain off.

Illustration: Let A = {1, 2, 3, 4} and B = {1, 4, 9, 16, 25}. Consider the relation f(x) = x², then f(1) = 1, f(2) = 4, f(3) = 9, f(4) = 16. Clearly, each element in A has a unique image in B. So, f: A → B.
f = {(1, 1) (2, 4) (3, 9) (4, 16)} is a function from A to. B.
Clearly Domain (f) = {1,2, 3, 4} and Range (f) = {1, 4, 9, 16}
Note : The number of functions that can be defined from, a non-empty finite set A into a non-empty finite set B is [n(B)]^n(A).

If f: A → B a function then f(A) = {f(a) / a ∈ A} is called the range off. It is a subset of B (ie) f(A) ≤ B.

One – one function (Injection):
Let f: A B, then f is said to be one-one function if different elements of A have different f- images in B. Thus f: A → B is one-one. (μ) f: A B is an injection <=> ay a2 e A and f(a7) = f(aj implies that a₁ = a₂

Illustration:
LetA = {1, 2, 3} and B = {2, 4, 6}. Consider f: A → B. f(x) = 2x then f(1) = 2, f(2) = 4 and f(3) = 6. Clearly f is a function from A to B such that different elements in A have different f – images in B.
∴ f: {(1, 2) (2, 4) (3, 6)} is one – one.

Note : The number of one-one functions that can be defined from a non-empty finite set A into a non-empty finite set B is n(B) P_n(A) if n(B) ≥ n(A) and zero if n(B) < n(A).

Onto function (Surjection):
Let f: A → B. If every element of B occurs as the image of at least one element of in A, then fis an onto function. Thus f: A → B is surjection iff for each b e B, 3 a e A such that f(a) = b. Clearly fis onto ⇔ Range (f) = B.

Illustration; Let A = {-1, 7, 2, -2}, B = {1, 4} and Let f: A → B, be a function defined by f(x) = x² then fis onto because f(A) = {f(-1), f(1), f(2), f(-2)} = {1, 4} = B.
Note : The number of onto functions that can be defined from a non – empty finite set A onto a two element set B is 2^n(A) – 2 if n(A) ≥ 2 and zero if n(A) < 2.

Bijective function :
A function f: A → B is a bijection if

• It is one – one i.e., f(a) – f(b) ⇒ a = b ∀ a, b ∈ A.
• It is onto i.e., ∀ b ∈ B ∃ a ∈ A such that f(a) = b.

Note : Number of bijections that can be defined from A to B is [n(A)]!, [n(A) = n(B)].

If f: A → B is a bijection then the relation f^-1 = {(b, a) / (a, b) ∈ f} is a function from B to A and is called the inverse function off.

Constant function :
Let f: A B defined in such a way that all the elements of A have the same f- image in B, then f is said to be a constant function.

Illustration : Let A – {1, 2, 3} and B = {6, 7, 8}. Let f: A → B
f(x) = 6 ∀ x ∈ A i.e., f = {(1, 6) (2, 6) (3, 6)} is a constant function.
The range of a constant function is a singleton set.

Identity function :
Let A be a non-empty set then the function f: A → A defined by, f(x) = x ∀ x ∈ I_A is called the identity function on A and is denoted by I_A. The identity function is bijective.

Let f: A → B, g: B → C be functions. Then gof: A → C is a function and (gof) (a) = g If (a)] ∀ a ∈ A, is called composite of ‘g’ with ‘f.

If f : A → B, g B → C are bijections so is (go f) : A → C and (gof)^-1 = f^-1o g^-1.

• If f: A → B is a bijection, then fof^-1 = I_B and f^-1of = I_A.
• If f: A → B, g: B → C such that go f = I_A fog = I_B then f is a bijection and g = f^-1

Let A be a non-empty subset of R such that – x ∈ A, for all x ∈ A and f: A → R.

• If f(-x) = f(x), ∀ x ∈ A then fis called an EVEN function.
• If f(-x) = – f(x), ∀ x ∈ A then f is called an ODD function.

Functions:
Def 1:
A relation f from a set A into a set B is said to be a function or mapping from A into B if for each x ∈ A there exists a unique y ∈ B such that (x, y) ∈ f. It is denoted
by f : A → B.
Note: Example of a function may be represented diagrammatically. The above example can be written diagrammatically as follows.

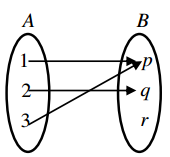
Def 2:
A relation f from a set A into a set B is a said to be a function or mapping from a into B if
i) x ∈ A ⇒ f (x) ∈ B
ii) x₁, x₂ ∈ A, x₂ ⇒ f (x₁) = f (x₂)

Def 3:
If f : A → B is a function, then A is called domain, B is called codomain and f (A) = {f (x): x ∈ A} is called range of f.

Def 4:
A function f : A → B if said to be one one function or injection from A into B if different element in A have different f-images in B.
Note:

• A function f : A → B is one one if f(x₁, y) ∈ f,(x₂, y) ∈ f ⇒ x₁ = x₂.
• A function f : A → B is one one iff x₁, x₂ ∈ A, x₁ ≠ x₂ ⇒ f (x₁) ^ f (x₁)
• A function f : A → B is one one iff x₁, x₂ ∈ A, f (x₁) = f (x₂) ⇒ x₁ = x₂
• A function f : A → B which is not one one is called many one function
• If f : A → B is one one and A, B are finite then n(A) < n(B).

Def 5:
A function f : A → B is said to be onto function or surjection from A onto B if f(A) = B.

Note:

• A function f : A → B is onto if y e B U ⇓ ∃x ∈ A ∋ f (x) = y .
• A function f : A → B which is not onto is called an into function.
• If A, B are two finite sets and f : A → B is onto then n(B) ≤ n(A).
• If A, B are two finite sets and n (B) = 2, then the number of onto functions that can be defined from A onto B is 2^{n( A)} – 2.

Def 6:
A function f : A → B is said to be one one onto function or bijection from A onto B if f : A → B is both one one function and onto function.

Theorem: If f : A → B, g : B → C are two functions then the composite relation gof is a function a into C.
Theorem: If f : A → B, g : B → C are two one one onto functions then gof : A → C is also one one be onto.
i) Let x₁, x₂ ∈ A and f (x₁) = f (x₂).
x₁,x₂ ∈ A, f : A → B ⇒ f (x₁), f (x₂) ∈ B
f (x₁), f (x₂) ∈ B → C, f (x₂) ⇒ g[f (x₁)] = g[f (x₂)] ⇒ (gof)(x₁) = (gof)(x₂)
x₁, x₂ ∈ A,(gof)(x₁) = (gof): A → C is one one ⇒ x₁ = x₂
x₁, x₂ ∈ A, f (x₁) = f (x₂) ⇒ x₁ = x₂.
∴ f: A → B Is one one.

ii) Proof: let z ∈ C,g : B → C is onto B y ∈ B ∃:g (y) = z y ∈ Bf : A → B is onto
∃x ∈ A ∋ f (x) = y
G {f(x)} = t
(g o f) x = t
∀ z ∈ CB x ∈ A ∋ (gof)(x) = z.
∴ g is onto.

Def 7:
Two functions f : A → B, g : C → D are said to be equal if

• A = C, B = D
• f (x) = g (x) ∀ x ∈ A. It is denoted by f = g

Theorem:
If f : A → B, g : B → C , h: C → D are three functions, then ho(gof) = (hof )of

Theorem:
if A is set, then the identify relation I on A is one one onto.

Def 8:
If A is a set, then the function I on A defined by I(x) = x ∀ x ∈ A, is called identify function on A. it is denoted by IA.

Theorem: If f : A → B and IA, IB are identify functions on A, B respectively then
foIA = IBof = f .
Proof:
I_A: A → A , f: A → B ⇒ foI_A: A → B
f : A → B , I_B : B → B ⇒ I_Bof: A → B
(foIA)(x) = f {IA(x)} = f (x), ∀x ∈ A ∴ f0I_A = f
(IBof)(x) = IB{f (x)} = f (x), ∀ x ∈ A ∴ I_Bof = f
∴ foI_A = I_Bof = f

Def 9:
If f : A → B is a function then {(y, x) ∈ B × A:(x, y) ∈ f} is called inverse of f. It is denoted by f^-1.

Def 10:
If f : A → B is a bijection, then the function f^-1: B → A defined by f^-1(y) = x iff f (x) = y ∀ y ∈ B is called inverse function of f.

Theorem:
If f : A → B is a bijection, then f^-1 of = IA, fof^-1 = IB
Proof:
Since f : A → B is a bijection f^-1: B → A is also a bijection and
f^-1 (y) = x ⇔ f (x) = y ∀ y ∈ B
f : A → B, f^-1: B → A ⇒ f^-1 of: A → A
Clearly I_A : A → A such that I_A (x) = x, ∀ x ∈ A.

Let x ∈ A
x ∈ A, f : A → B ⇒ f (x) ∈ B
Let y = f(x)
y = f (x) ⇒ f^-1(y) = x
(f -1 of)(x) = f ^-1[ f (x) = f^-1( y) = x = I_A (x)
(f^-1 of) (x) = IA (x) ∀ x ∈ A f^-1of = I_A
f^-1: B → A, f: A → B ⇒ fof^-1: B → B

Clearly I_B : B → B such that I_B (y) = y ∀ y ∈ B
Let y ∈ B
y ∈ B, f^-1: B → A = f^-1(y) ∈ A
Let f^-1(y) = x
f^-1(y) = x ⇒ f (x) = y
(fof’)(y) = f [ f ^-1( y)] = f (x) = y = I_B (y)
∴ (fof^-1)(y) = I_B (y) ∀ y ∈ B
∴ fof^-1 = I_B

Theorem: If f : A → B, g : B → C are two bijections then (gof )^-1 = f^-1og^-1.
Proof:
f : A → B, g : B →C are bijections gof: A → C is bijection (gof )^-1: C → A is a bijection.
f : A → B is a bijection f^-1: B → A is a bijection
g : B → C Is a bijection ⇒ g^-1: C → B is a bijection
g^-1:C → B , g^-1: B → A are bijections ⇒ f^-1 og^-1: C → A is a bijection

Let z ∈ C
z ∈ C, g : B → C is onto ⇒ ∃ y ∈ B ∋ g (y) = z ⇒ g^-1(z) = y
y e B, f: A → B is onto ⇒ ∃ x ∈ A ∋ f (x) = y ⇒ f^-1(y) = x
(gof) (x) = g[ f (x)] = g (y) = z ⇒ (gof )^-1(z) = x
∴ (gof)^-1 (z) = x = f^-1( y) = f^-1 [ g^-1 (z) ] = (f ^-1og^-1)(z)
∴ (gof )^-1 = f^-1og^-1

Theorem:
If f : A → B, g : B → A are two functions such that gof = I_A and fog = I_B then f : A → B is a bijection and f^-1 = g .
Proof:
Let x₁, x₂ ∈ A, f (x₁) = f (x₂)
x₁, x₂ ∈ A, f : A → B ⇒ f (x₁), f (x₂) ∈ B
f (x₁), f (x₂) ∈ B, f (x₁) = f (x₂), g = B → A
⇒ g [ f (x₁)] = g[ f (x₂)]
⇒ (gof)(x₁) = (gof)(x₁) ⇒ I_A (x₂) ⇒ x₁ = x₂
x₁,x₂ ∈ A, f (x₁) = f (x₂) ⇒ x₁ = x₂.
∴ f : A → B is one one

Let y ∈ B .
y ∈ B, g : B → A ⇒ g(y) ∈ A

Def 11:
A function f : A → B is said tobe a constant function if the range of f contain only one element i.e., f (x) = c ∀ x ∈ A where c is a fixed element of B

Def 12:
A function f : A → B is said to be a real variable function if A ⊆ R.

Def 13:
A function f : A → B is said to be a real valued function iff B ⊆ R.

Def 14:
A function f : A → B is said to be a real function if A ⊆ R, B ⊆ R.

Def 15:
If f : A → R, g : B → R then f + g : A ∩ B → R is defined as (f + g)(x) = f (x) + g (x) ∀ x ∈ A ∩ B

Def 16:
If f : A → R and k e R then kf : A → R is defined as (kf)(x) = kf (x), ∀ x ∈ A

Def 17:
If f : A → B, g : B → R then fg : A n B → R is defined as (fg)(x) = f (x)g(x) ∀ x ∈ A ∩ B .

Def 18:
If f : A → R, g : B → R then : C → R is defined as
C = {x ∈ A n B: g(x) ≠ 0}.

Def 19:
If f : A → R then |f| (x) =| f (x)|, ∀ x ∈ A

Def 20:
If n ∈ Z , n ≥ 0, a₀, a₁, a₂, ………….. a_n ∈ R, a_n ≠ 0, then the function f : R → R defined by
f (x) = a₀ + a₁x + a₂x² + + a_nxⁿ ∀ x ∈ R is called a polynomial function of degree n.

Def 21:
If f : R → R, g : R → R are two polynomial functions, then the quotient f/g is called a rational function.

Def 22:
A function f : A → R is said to be bounded on A if there exists real numbers k1, k2 such that k1 < f (x) < k2 ∀ x ∈ A Def 23: A function f : A → R is said to be an even function if f (-x) = f (x) ∀ x ∈ A Def 24: A function f : A → R is said to be an odd function if f (-x) = – f (x) ∀ x ∈ A .  Def 25: If a ∈ R, a > 0 then the function f : R → R defined as f (x) = ax is called an exponential function.

Def 26:
If a ∈ R, a > 0, a ≠ 1 then the function f : (0, ∞) → R defined as f (x) = log_a x is called a logarithmic function.

Def 27:
The function f : R → R defined as f(x) = n where n ∈ Z such that n ≤ x < n + 1 ∀ x ∈ R is called step function or greatest integer function. It is denoted by f (x) = [x]

Def 28:
The functions f(x) = sin x, cos x, tan x, cot x, sec x or cosec x are called trigonometric functions.

Def 29:
The functions f (x) = sin^-1 x ,cos^-1x,tan^-1 x,cot^-1x,sec^-1x or cos ec^-1 x are called inverse trigonometric functions.

Def 30:
The functions f(x) = sinh x, cosh x, coth x, sech x or cosech x are called hyperbolic functions.

Def 30:
The functions f(x) = sinh^-1x, cosh^-1x, coth^-1x, sech^-1x or cosech^-1x are called Inverse hyperbolic functions.

Function	Domain	Range
ax	R	(0, ∞)
log a x	(0, ∞)	R
[X]	R	Z
[X]	R	[0, ∞)
√ x	[0, ∞)	[0, ∞)
sin x	R	[-1, 1]
cos x	R	[-1, 1]
tan x	R – {(2n +1)\(\frac{\pi}{2}\): n ∈ Z}	R
cot x	R – {nπ: n ∈ Z}	R
sec x	R – {(2n +1)\(\frac{\pi}{2}\): n ∈ Z}	(-∞,-1] ∪ [1, ∞)
cos ecx	R – {nπ: n ∈ Z}	(-∞,-1] ∪ [1, ∞)
Sin-1x	[-1 , 1]	[-π/2, π/2]
Cos-1x	[ -1, 1]	[0, π]
Tan-1x	R	(-π/2, π/2)
Cot-1x	R	(0, π)
Sec-1x	(-∞ -1] ∪ [1, ∞)	[0, π/2) ∪ (π/2, π]
Cosec-1x	(-∞ -1] ∪ [1, ∞)	[-π/2,0) ∪ (0, π/2]
sinh x	R	R
cosh x	R	[1, ∞)
tanh x	R	(-1,1)
coth x	(-∞,0) ∪ (0, ∞)	(-∞,-1) ∪ (1, ∞)
sech x	R	(0, 1]
cosech x	(-∞,0) ∪ (0, ∞)	(-∞,0) ∪ (0, ∞)
Sinh-1x	R	R
Cosh-1x	[1, ∞)	[0, ∞)
Tanh-1x	(-1, 1)	R
Coth-1x	(-∞,-1) ∪ (1, ∞)	(-∞,0) ∪ (0, ∞)
Sech-1x	(0, 1]	[0, ∞)
Coseh-1x	(-∞,0) ∪ (0, ∞)	(-∞,0) ∪ (0, ∞)