Students get through Maths 1B Important Questions Inter 1st Year Maths 1B The Straight Line Important Questions which are most likely to be asked in the exam.
Intermediate 1st Year Maths 1B The Straight Line Important Questions
Question 1.
Find the equation of the straight line passing through the point (2, 3) and making non-zero intercepts on the axes of coordinates whose sum is zero. [Mar 12]
Solution:
Equation of the line in the intercept form is
\(\frac{x}{a}\) + \(\frac{y}{b}\) = 1
Given b = -a
Equation of the line is \(\frac{x}{a}\) – \(\frac{y}{a}\) = 1
⇒ x – y = a
This line passes through (2, 3)
2 – 3 = a ⇒ a = -1
Equation of the line is
x – y = -1 or x – y + 1 = 0
![]()
Question 2.
Find the equation of the straight line passing through the points (at12, 2at1 ) and (at22, 2at1 ).
Solution:
Equation of the given points.
(x – x1) (y – y2) = (y – y1) (x1 – x2)
( x -at12) (2at1 – 2at2)
= (y – 2at1) (at, — at2)
(x – at12) .2a(t1 – t2) = (y – 2at1) a. (t12 – t22)
2x – 2at12 = y(t1 + t2) – 2at12 + 2at1t2 = 0
2x – (t1 + t2)y + 2at1t2 = 0
Question 3.
Find the equation of the straight line passing through A (-1, 3) and i) parallel ii) perpendicular to the straight line passing through B(2, – 5) and C(4, 6). [Mar 11]
Solution:
Slope of BC = \(\frac{-5-6}{2-4}\) = \(\frac{-11}{-2}\) = \(\frac{11}{2}\)
i) The required line is parallel to BC and passes through A(- 1, 3)
Equation of the parallel line is
y – 3 = \(\frac{11}{2}\)(x + 1)
2y – 6 = 11x + 11
11x – 2y + 17 = 0
ii) The required line is perpendicular to BC.
Slope of the required line = –\(\frac{1}{m}\) = –\(\frac{2}{11}\)
This line passes through A (-1, 3)
Equation of the required line is
y – 3 = –\(\frac{2}{11}\)(x + 1)
11y – 33 = -2x – 2
2x + 11y – 31 = 0
![]()
Question 4.
Prove that the points (1, 11), (2, 15) and (-3, -5) are collinear and find the equation of the straight line containing them.
Solution:
A(1, 11), B(2, 15) and C (-3, -5) are the given points.
Equation of AB is
(y – y1) (x1 – x2) = (x – x1) (y1 – y2)
(y – 11) (1 -2) = (x – 1) (11 – 15)
-(y – 11) = -4 (x – 1)
-y + 11 = – 4x + 4
4x – y + 7 = 0
C (-3, -5) .
4x – y + 7 = 4(-3) + 5 + 7
= -12 + 12 = 0
C lines on AB ⇒ A, B, C are collinear.
Equation of the line containing them is 4x – y + 7 = 0
Question 5.
A straight line passing through A(1, -2) makes an angle tan-1 \(\frac{4}{3}\) with the positive direction of the X – axis in the anticlock-wise sense. Find the points on the straight line whose distance from A is 5.
Solution:
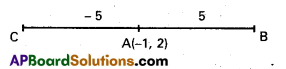
Given α = tan-1 \(\frac{4}{3}\) ⇒ tan α = \(\frac{4}{3}\)
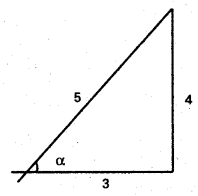
cos α = \(\frac{3}{5}\), sin α = \(\frac{4}{5}\)
(x1, y1) = (1, -2) = x1 = 1, y1 = -2
Case i) .
r = 5
x = x1 + r cos α = 1 + 5 . \(\frac{4}{5}\) = 1 + 4 = 5
y = y1 + r sin α= – 2 + 5 . \(\frac{3}{5}\) = -2 + 3 = 1
Co-ordinates of B are (5, 1)
Case ii) r = -5
x = x1 + r cos α = 1 – 5 . \(\frac{4}{5}\) = 1 – 4 = -3
y = y1 + r sin α = -2 – 5 . \(\frac{3}{5}\) = -2 – 3 = -5
Co-ordinates of C are (- 3, – 5)
Question 6.
A straight line parallel to the line y = \(\sqrt{3} x\) passes through Q(2, 3) and cuts the line 2x + 4y – 27 = 0 at P. Find the length of PQ.
Solution:
PQ is parallel to the straight line y = \(\sqrt{3} x\)
tan α = \(\sqrt{3}\) = tan 60°
α = 60°
Q(2, 3) is a given point
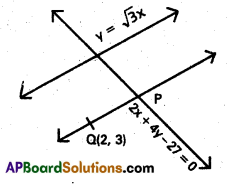
Co-ordinates of any point P are
(x1 + r cos α, y1 + r sin α)
(2 + r cos 60°, 3 + r sin 60°)
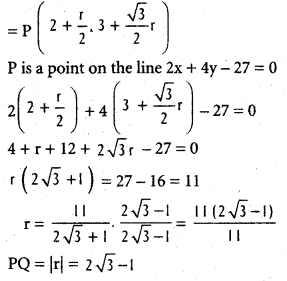
![]()
Question 7.
Transform the equation
3x + 4y+ 12 = 0 into
i) slope—intercept form
ii) Intercept form and
in) normal form
Solution:
The given equation is 3x + 4y + 12=0
i) Slope-intercept form
4y = -3x – 12
y = (-\(\frac{3}{4}\))x + (-3)
Slope = –\(\frac{3}{4}\) , y – intercept = -3.
ii) Intercept form
-3x – 4y = 12
–\(\frac{3 x}{12}\) – \(\frac{4 y}{12}\) = 1
\(\frac{x}{(-4)}\) + \(\frac{y}{(-3)}\) = 1
x – intercept = -4, y – intercept = -3
iii) Normal form
-3x – 4y = 12
Dividing with \(\sqrt{9+16}\) = 5
(-\(\frac{3}{5}\))x + (-\(\frac{4}{5}\))y = \(\frac{12}{5}\)
Let cos α = \(\frac{-3}{5}\) and sin α = –\(\frac{4}{5}\)
p = \(\frac{12}{5}\) so that
x cos α + y sin α = p
α lies in third quadrant so that
α = π + tan-1(\(\frac{4}{3}\))
Question 8.
If the area of the triangle formed by the straight line x = 0, y = 0 and 3x + 4y = a (a > 0) is 6, find the value of a. [May 11]
Solution:
Equation of the line is 3x + 4y = a
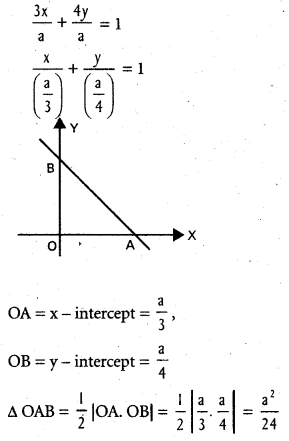
Given \(\frac{a^{2}}{2 a}\) = 6 ⇒ a2 = 144
a = ±12
But a > 0
a = 12
![]()
Question 9.
Find the value of k, if the lines 2x – 3y + k = 0, 3x – 4y -13 = 0 and 8x – 11y – 33 = 0 are concurrent.
Solution:
Let L1, L2, L3 be the straight lines whose equations are respectively
2x – 3y + k = 0 ………………. (1)
3x – 4y – 13 = 0 ……………….. (2)
8x – 11y – 33 = 0 ………………. (3)
Solving (2) and (3) for x and y
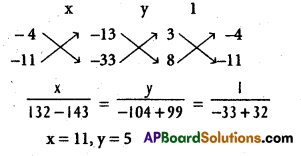
Point of the lines (2) and (3) is (11, 5)
The given lines L1, L2, L3 are concurrent
∴ L1 contain (11, 5)
∴ 2(11) – 3(5) + k = 0
k = -7
Question 10.
If the straight lines ax + by + c = 0, bx + cy + a = 0 and cx + ay + b = 0 are concurrent, then prove that a3 + b3 + c3 = 3abc.
Solution:
The equation of the given lines are
ax + by +c = 0 ………………… (1)
bx + cy + a = 0 ……………….. (2)
cx + ay + b = 0 ……………….. (3)
Solving (1) and (2) point of intersection is got by
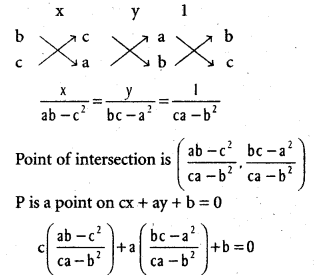
c(ab – c2) +a (bc – a2) + b(ca – b2) = 0
abc – c3 + abc – a3 + abc – b3 = 0
∴ a3 + b3 + c3 = 3abc.
Question 11.
A variable straight line drawn through the point of intersection of the straight lines \(\frac{x}{a}\) + \(\frac{y}{b}\) = 1 and \(\frac{x}{b}\) + \(\frac{y}{a}\) = 1 meets the co-ordinate axes at A and B. Show that the locus of the mid point of \(\overline{\mathrm{AB}}\) is 2(a + b) xy = ab(x + y)
Solution:
Equations of the given lines are \(\frac{x}{a}\) + \(\frac{y}{b}\) = 1
and \(\frac{x}{b}\) + \(\frac{y}{a}\) = 1
Solving the point of intersection P(\(\frac{a b}{a+b}\), \(\frac{a b}{a+b}\))
Q (x0, y0) is any point on the locus
⇔ The line with x – intercept 2x0, y – intercept 2y0, passes through P
⇔ P lies on the straight line \(\frac{x}{2 x_{0}}\) + \(\frac{y}{2 y_{0}}\) = 1
i.e., \(\frac{a b}{a+b}\)(\(\frac{1}{2 x_{0}}\) + \(\frac{1}{2 y_{0}}\)) = 1
⇒ \(\frac{a b}{a+b}\) . \(\frac{x_{0}+y_{0}}{2 x_{0} y_{0}}\) = 0
ab(x0 + y0) = 2(a + b) x0y0
Q(x0, y0) lies on the curve
2(a + b)xy = ab(x + y)
Locks the mid of point of
AB is 2(a + b)xy = ab(x +y)
![]()
Question 12.
If a, b, c are in arithmetic progression, then show that the equation ax + by + c = 0 represents a family of concurrent lines and find the point of concurrency.
Solution:
a, b, c are in A.P.
2b = a + c
a – 2b + c = 0
a.1 + b(-2) + c = 0
Each number of family of straight lines
ax + by + c = 0
passes through the fixed point (1,-2)
∴ Set of lines ax + by + c = 0 for parametric values of a, b and c is a family of concurrent lines.
∴ Point of concurrency is (1, -2).
Question 13.
Find the value of k, if the angle between the straight lines 4x – y + 7 = 0 and kx – 5y – 9 = 0 is 45°.
Solution:

Squaring and cross multiplying
2(4k + 5)2 = 17(k2 + 25)
2(16k2 + 40k + 25) = 17k2 + 425
32k2 + 80k + 50 = 17k2 + 425
15k2 + 80k – 375 = 0
3k2 + 16k – 75 = 0
(k – 3) (3k + 25) = 0
k = 3 or -25/3
Question 14.
Find the equation of the straight line passing through (x0, y0) and (i) parallel (ii) perpendicular to the straight line
ax + by + c = 0.
Solution:
Equation of the given line is ax + by + c = 0
i) Equation of the parallel line is ax + by = k ………………… (1)
This line passes through P(x0, y0) ⇒ ax0 + by0 = k ……………… (2)
Subtracting (2) from (1) equation of the required line is a(x – x0) + b(y – y0) = 0
ii) Equation of the perpendicular line is bx – ay = k.
This line passes through P(x0, y0) ⇒ bx0 – ay0 = k
Subtracting, equation of the required line is b(x – x0) – a(y – y0) = 0
![]()
Question 15.
Find the equation of the straight line perpendicular to the line 5x – 2y = 7 and passing through the point of intersection of the lines 2x + 3y = 1 and 3x + 4y = 6.
Solution:
Given lines are L1 = 2x + 3y – 1 = 0
L2 = 3x + 4y – 6 = 0
Equation of the line passing through the intersection of L1 = 0, L2 = 0 is
L1 + kL2 = 0
(2x + 3y – 1) + k(3x + 4y – 6) = 0
(2 + 3k)x + (3 + 4k)y – (1 + 6k) = 0 …………………. (1)
This line is perpendicular to 5x – 2y = 7 ………………… (2)
a1a2 + b1b2 = 0
5(2 + 3k) – 2(3 + 4k) = 0
10 + 15k – 6 – 8k = 0
7k = -4 ⇒ k = – 4/7
Substituting in (1) equation of the required lines
(2 – \(\frac{12}{7}\))x + (3 – \(\frac{16}{7}\))x – (1 – \(\frac{24}{7}\)) = 0
\(\frac{2}{7}\)x + \(\frac{5}{7}\)y + \(\frac{17}{7}\) = 0 ⇒ 2x + 5y + 17 = 0
Question 16.
If 2x – 3y – 5 = 0 is the perpendicular bi-sector of the line segment joining (3, – 4) and (α, β) find α + β.
Solution:
(α, β) is the reflection of (3, -4) is the line
2x – 3y – 5 = 0
\(\frac{\alpha-3}{2}\) = \(\frac{\beta+4}{-3}\) = \(\frac{-2(6+12-5)}{4+9}\) = -2
α – 3 = -4 ⇒ α = -1
β + 4 = 6 ⇒ β = 2
α + β = -1 + 2 = 1
![]()
Question 17.
If the four straight lines ax + by + p = 0, ax + by + q = 0, cx + dy + r = 0 and cx + dy + s = 0 form a parallelogram, show that the area of the parallelogram so formed is \(\left|\frac{(p-a)(r-s)}{b c-a d}\right|\).
Solution:
Let L1, L2, L3, L4 be the lines given by
L1 = ax + by + p = 0
L2 = ax + by + q = 0
L3 = cx + dy + r = 0
L4 = cx + dy + s = 0
L1 and L2 are parallel: L3 and L4 are parallel
Area of the parallelogram = \(\frac{\mathrm{d}_{1} \mathrm{~d}_{2}}{\sin \theta}\)
d1 = distance between L1 and L2 = \(\frac{|p-a|}{\sqrt{a^{2}+b^{2}}}\)
d2 = distance between L3 and L4 = \(\frac{|r-s|}{\sqrt{c^{2}+d^{2}}}\)

Question 18.
The hypotenuse of a right angled isosceles triangle has its ends at the points (1, 3) and (-4, 1). Find the equations of the legs of the triangle.
Sol:
LetA =(1, 3)and B = (-4, 1) and ABC b a right isosceles triangle with \(\stackrel{\leftrightarrow}{A B}\) as hypotenuse.
We require, therefore, the equations of
\(\stackrel{\leftrightarrow}{A C}\) and \(\stackrel{\leftrightarrow}{B C}\)
Slope of \(\stackrel{\leftrightarrow}{A B}\) is \(\frac{1-3}{-4-1}\) = \(\frac{2}{5}\)
Since the slope of \(\stackrel{\leftrightarrow}{A B}\) is \(\), neither \(\frac{2}{5}\) nor \(\stackrel{\leftrightarrow}{A C}\) is vertical.
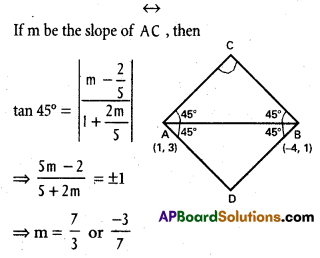
Taking the slope of \(\stackrel{\leftrightarrow}{A C}\) as \(\frac{7}{3}\), the slope of \(\stackrel{\leftrightarrow}{B C}\) would be –\(\frac{3}{7}\). Therefore, the equations of \(\stackrel{\leftrightarrow}{A C}\) and \(\stackrel{\leftrightarrow}{B C}\) are respectively.
y – 3 = \(\frac{7}{3}\) (x – 1) and y – 1 = – \(\frac{3}{7}\) (x + 4),
which become 7x – 3y + 2 = 0 and 3x + 7y + 5 = 0
If the lines drawn through A and B respectively parallel to \(\stackrel{\leftrightarrow}{B C}\) and \(\stackrel{\leftrightarrow}{A C}\) meet at D, then ∆ABD is also right isosceles, having \(\stackrel{\leftrightarrow}{A B}\) as its hypotenuse.
Therefore, the equations of \(\stackrel{\leftrightarrow}{A D}\) and \(\stackrel{\leftrightarrow}{B D}\) are respectively,
3(x – 1) + 7(y – 3) = 0 and 7(x + 4) – 3(y – 1) = 0
⇒ 3x + 7y – 24 = 0 and 7x – 3y + 31 = 0.
Therefore, the two pairs of legs required are
7x – 3y + 2 = 0, 3x + 7y + 5 = 0 and
3x + 7y – 24 = 0, 7x – 3y + 31 = 0.
Note : ADBC is square.
![]()
Question 19.
A line is such that its segment between the lines 5x – y + 4 = 0 and 3x + 4y – 4 = 0 is . bisected at the point (1, 5). Obtain its equation.
Solution:
Let the required line meet 3x + 4y – 4 = 0 at A and 5x – y + 4 = 0 at B, so that AB is the segment between the given lines, with its mid-point at C = (1, 5).
The equation 5x – y + 4 = 0 can be written as
y = 5x + 4 so that any point on \(\stackrel{\leftrightarrow}{B X}\) is (t, 5t + 4) for all real t.
∴ B = (t, 5t + 4) for some t. Since (1, 5) is the mid-point of \(\stackrel{\leftrightarrow}{A B}\)
A = [2 – t, 10 – (5t + 4)]
= [2 – t, 6 – 5t]
Since A lies on 3x + 4y – 4 = 0,
3(2 – 1) + 4(6 – 5t) – 4 = 0
⇒ -23t + 26 = 0
⇒ t = \(\frac{26}{23}\)
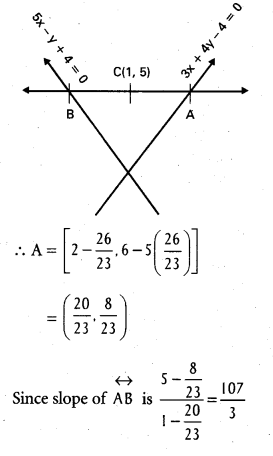
equation of \(\stackrel{\leftrightarrow}{A B}\) is y – 5 = \(\frac{107}{3}\) (x – 1)
⇒ 3y – 15 = 107x – 107
⇒ 107x – 3y – 92 = 0.
Question 20.
An equilateral triangle has its incentre at the origin and one side as x + y – 2 = 0. Find the vertex opposite to x + y – 2 = 0.
Solution:
Let ABC be the equilateral triangle and
x + y – 2 = 0 represent side \(\stackrel{\leftrightarrow}{B C}\).
Since O is the incentre of the triangle, \(\stackrel{\leftrightarrow}{A D}\) is the bisector of ∠BAC .
Since the triangle is equilateral, \(\stackrel{\leftrightarrow}{A D}\) is the perpendicular bisector of \(\stackrel{\leftrightarrow}{B C}\).
Since O is also the centroid, AO : OD = 2 : 1. [The centroid, circumcentre incentre and orthocentre coincide]
Let D = (h, k).
Since D is the foot of the perpendicular from O onto \(\stackrel{\leftrightarrow}{B C}\), D is given by
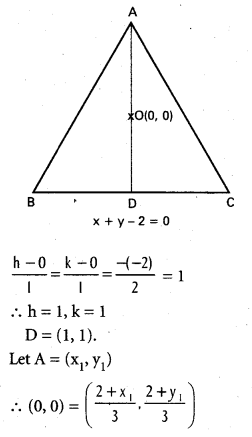
∴ x1 = -2, y1 = -2.
∴ A = (-2, -2), the required vertex.
![]()
Question 21.
Find the orthocentre of the triangle whose vertices are (-5,-7) (13, 2) and (-5, 6)
Solution:
Let A(-5, -7), B(13,2) and C (-5, 6) be the vertices of a triangle. Let \(\stackrel{\leftrightarrow}{A D}\) be the perpendicular drawn from A to \(\stackrel{\leftrightarrow}{B C}\) and \(\stackrel{\leftrightarrow}{B E}\) be the perpendicular drawn from B to \(\stackrel{\leftrightarrow}{A C}\).
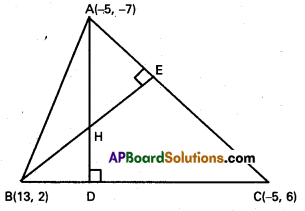
Now slope of \(\stackrel{\leftrightarrow}{B C}\) = \(\frac{6-2}{-5-13}\) = \(\frac{-2}{9}\)
Since \(\stackrel{\leftrightarrow}{A D}\) ⊥ \(\stackrel{\leftrightarrow}{B C}\) , slope of \(\stackrel{\leftrightarrow}{A D}\) = \(\frac{9}{2}\) and so, the equation of \(\stackrel{\leftrightarrow}{A D}\) is
9x – 2y = – 45 + 14 = -31 ………………… (1)
Equation of \(\stackrel{\leftrightarrow}{A C}\) is x = -5 which is a vertical line and therefore equation of \(\stackrel{\leftrightarrow}{B E}\) is y = 2. ……………… (2)
Point of intersection of the lines (1) and (2) is (-3, 2) which is the orthocentre of ∆ ABC.
Question 22.
If the equations of the sides of a triangle are 7x + y – 10 = 0, x – 2y + 5 = 0 and x + y + 2 = 0, find the orthocentre of the triangle.
Solution:
Let ∆ ABC be the given triangle
Let the equations x – 2y + 5 = 0 ……………… (1)
7x + y – 10 = 0 ……………… (2)
and x + y + 2 = 0 ……………….. (3)
represent the sides \(\overleftrightarrow{\mathrm{AB}}\), \(\overleftrightarrow{\mathrm{BC}}\), and \(\overleftrightarrow{\mathrm{CA}}\)
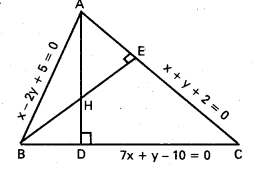
Let \(\overleftrightarrow{\mathrm{AD}}\) and \(\overleftrightarrow{\mathrm{BE}}\) be the altitudes drawn from A and B respectively to the sides \(\overleftrightarrow{\mathrm{BC}}\) & \(\overleftrightarrow{\mathrm{CA}}\)
Solving the equations (1) and (3), we obtain A =(-3,1).
Since \(\overleftrightarrow{\mathrm{AD}}\) ⊥ \(\overleftrightarrow{\mathrm{BC}}\), the equations of \(\overleftrightarrow{\mathrm{AD}}\) is
x – 7y = -3 – 7 = -10 …………………… (4)
Solving the equation (1) and (2), we obtain B = (1, 3).
Since \(\overleftrightarrow{\mathrm{BE}}\) ⊥ \(\overleftrightarrow{\mathrm{AC}}\) , the equation of BE is
x – y = 1 – 3 = -2 …………… (5)
Point of intersection of the lines (4) and (5) is H(\(\frac{-2}{3}\), \(\frac{4}{3}\)) which is the orthocentre of ∆ ABC.
![]()
Question 23.
Find the circumcentre of the triangle whose vertices are (1, 3), (-3, 5) and (5, -1).
Solution:
Let the vertices of the triangle be
A(1, 3), B(-3, 5) and (5,-1).
The midpoints of the sides \(\overline{\mathrm{BC}}\), \(\overline{\mathrm{CA}}\) are respectively D(1, 2) and E(3, 1).
Let S be the point of intersection of the perpendicular bisectors of the sides \overline{\mathrm{BC}} and \overline{\mathrm{CA}}
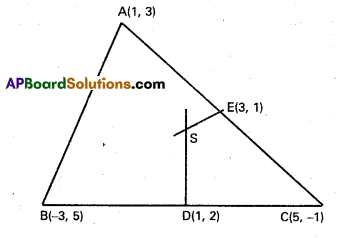
Since the slope of \(\overleftrightarrow{\mathrm{BC}}\) = \(\frac{5+1}{-3-5}\) = \(\frac{-3}{4}\), the slope \(\overleftrightarrow{\mathrm{SD}}\) is \(\frac{4}{3}\) and therefore its equation is 4x – 3y = 4 – 6 = -2 …………….. (1)
Slope of \(\overleftrightarrow{\mathrm{AC}}\) = \(\frac{3+1}{1-5}\) = -1 ⇒ Slope of –\(\sqrt{3x}\) = 1
∴ Equation of \(\overleftrightarrow{\mathrm{SE}}\) is x – y = 3 – 1 = 2 ………………….. (2),
Solving the equations (1) and (2),we obtain S = (-8, -10) which is the circumcentre of ∆ ABC.
Question 24.
Find the circumcentre of the triangle whose sides are 3x – y – 5 = 0, x + 2y – 4 = 0 and 5x + 3y + 1 = 0. [May 11, 05; Mar. 06]
Solution:
Let the given equations 3x – y – 5 = 0, x + 2y – 4 = 0 and 5x + 3y + 1 = 0 represent the sides \(\overleftrightarrow{\mathrm{BC}}\), \(\overleftrightarrow{\mathrm{CA}}\) and \(\overleftrightarrow{\mathrm{AB}}\) respectively of ∆ ABC.
Solving the above equations two by two, we obtain the vertices A(-2, 3), B(1, -2) and (2, 1) of the given triangle.
The midpoints of the sides \(\overline{\mathrm{BC}}\) and \(\overline{\mathrm{CA}}\) are respectively D = (\(\frac{3}{2}\), \(\frac{-1}{2}\)) and E = (0, 2).
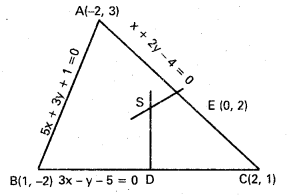
Equation of \(\overleftrightarrow{\mathrm{SD}}\) the perpendicular bisector of \(\overline{\mathrm{BC}}\) is x + 3y = 0 and the equation of \(\overleftrightarrow{\mathrm{SE}}\) the perpendicular bisector of \(\overline{\mathrm{AC}}\) is 2x – y + 2 = 0. Solving these two equations, we obtain the point of intersection of the lines \(\overleftrightarrow{\mathrm{SD}}\) and \(\overleftrightarrow{\mathrm{SE}}\) which is S(\(\frac{-6}{7}\), \(\frac{2}{7}\)) the circumcentre of ∆ ABC.
![]()
Question 25.
Find the incentre of the triangle formed by the straight lines y = \(\sqrt{3}\)x, y = –\(\sqrt{3}\)x and y = 3.
Solution:
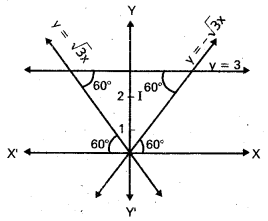
The straight lines y = \(\sqrt{3x}\) and y = –\(\sqrt{3x}\) respectively make angles 60° and 120° with the positive direction of X – axis.
Since y = 3 is a horizontal line, the triangle formed by the three given lines is equilateral. So in-centre is same and centroid.
Vertices of the triangle and O(0, 0), A(\(\sqrt{3}\), 3) and D(\(\sqrt{3}\), 3).
∴ Incentre is (\(\frac{0+\sqrt{3}-\sqrt{3}}{3}\), \(\frac{0+3+3}{3}\)) = (0, 2)
Question 26.
Find the equation of the straight line whose distance from the origin is 4, If the normal ray from the origin to the straight line makes an angle of 135° with the positive direction of the x-axis.
Solution:
The equation of the given line is
x cos α + y sin α = p where p = 4 and α = 135°
∴ x(\(\frac{-1}{\sqrt{2}}\)) + y(\(\frac{1}{\sqrt{2}}\)) = 4 ⇒ or x – y + 4\(\sqrt{2}\) = 0
(i). Transform the equation x + y + 1 = 0 in to normal from.
Solution:
x + y + 1 = 0
⇔ (\(\frac{-1}{\sqrt{2}}\))n + (\(\frac{-1}{\sqrt{2}}\)) y = \(\frac{1}{\sqrt{2}}\)
⇔ x cos \(\frac{5\pi}{42}\) + y sin \(\frac{5\pi}{4}\) = \(\frac{1}{\sqrt{2}}\)
Hence the normal form of the equation of the given straight line is x cos \(\frac{5\pi}{4}\) + y sin \(\frac{5\pi}{4}\) = \(\frac{1}{\sqrt{2}}\) and the distance of the line from the origin is = \(\frac{1}{\sqrt{2}}\)
ii) A straight line passing through A(1, -2) makes and angle Tan-1\(\frac{4}{3}\) with the positive direction of the x – axis in the anti-clock wise sense. Find the points of the straight line whose distance from A is 5.
Solution:
The paramatic equation of the lines A (1, -2)
Slope is \(\frac{4}{3}\) (∵ tan θ = \(\frac{4}{3}\))
are x = 1 + r cos θ = 1 + r(\(\frac{3}{5}\)) and y
= -2 + r sinθ
= -2 + r (\(\frac{4}{5}\))
The points on the above line a + a distance of (r) = 5 correspond to r = ±5 in the above equation and are
∴ (4, 2) and (-2, -6)
![]()
Question 27.
Trans form the equation 3x + 4y + 12 = 0 in to (i) slope – intercept from (ii) intercept form (iii) normal form.
Solution:
(i) slop – intercept form
3x + 4y + 12 = 0
⇔ 4y = -3x – 12
⇔ y = (\(\frac{-3}{4}\)) x + (-3)
∴ Slope = (\(\frac{-3}{4}\)) and y – intercept = -3,
ii) Intercept form :
3x = 4y + 12 = 0
⇔ \(\frac{-3y}{12}\) – \(\frac{-4y}{12}\) = 1
⇔ \(\frac{x}{(-4)}\) + \(\frac{y}{(-3)}\) = 1
∴ x-intercept of the line is -4, and tan y-intercept is -3.
iii) Normal form
3x = 4y + 12 = 0
⇔ -3x + -4y – 12 = 0
⇔ (\(\frac{-3}{5}\))x + (\(\frac{-4}{5}\))y = \(\frac{12}{5}\)
⇔ x cos α + y sin α = p ⇒ p\(\frac{12}{5}\) and cos α = \(\frac{-3}{5}\), sin α = \(\frac{-4}{5}\) determine the angle α in (0, 2π).
Question 28.
Find the angle between the lines 2x + y + 4 = 0 and y – 3x = 7.
Solution:
The angle between the given lines
= cos-1 \(\frac{-6+1}{\sqrt{5 \times 10}}\)
= cos-1 [latex]\frac{5}{\sqrt{2}}[/latex] = cos-1(\(\frac{1}{\sqrt{2}}\)) = \(\frac{\pi}{4}\)
![]()
Question 29.
Find Q(h,k) in the foot of the perpendicular from p(x1, y1) on the straight lines ax + by + c = 0 then (h – x1) ; a = (k – y1); b = -(ax1 + by1 + c); (a2 + b2)
Solution:
Equation of \(\stackrel{\leftrightarrow}{P Q}\) which is normal to the given straight line
L : ax + by + c = 0
bx – ay = bx1 – ay1
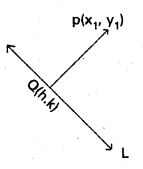
∴ Q ∈ \(\stackrel{\leftrightarrow}{P Q}\) we have
bh – ak = bx1 – ay1
∴ b(h – x1) = a(k – y1)
or (h – x1) a = (k – y1); b.
But, this implus that h = aλ + x1, and k = bλ + y1
for some λ ∈ R. sine Q(h, k) in point on L.
a(aλ + x1) + b(bλ + y1) + c = 0
i.e., λ = \(\frac{\left(a x_{1}+b y_{1}+c\right.}{\left(a^{2}+b^{2}\right)}\)
∴ (h – x1) ; a = (k – y1); b
= – (ax1 + by1 + c); (a2 + b2)
Question 30.
Find the distance between the parallel straight lines 3x + 4y – 3 = 0 and 6x + 8y -1 = 0.
Solution:
The equation of the given straight lines is 3x + 4y – 3 = 0 and 6x + 8y – 1 = 0.
formula : \(\frac{c_{1}-c_{2}}{\sqrt{a^{2}+b^{2}}}\) = \(\frac{-6+1}{\sqrt{6^{2}+8^{2}}}\) = \(\frac{5}{10}\) = \(\frac{1}{2}\)
Question 31.
Find the condition for the points (a, o) (h, k) and (o, b) when ab ≠ 0 to be collinear. [Mar 10]
Solution:
The equation of the line passing through (a, o) and (o, b) is \(\frac{x}{a}\) + \(\frac{y}{b}\) = 1
The given points are collinear ⇒ (h, k) lies on the above line ⇒ \(\frac{h}{a}\) + \(\frac{k}{b}\) = 1
⇒ hb + ka = ab
![]()
Question 32.
Find the area of the triangle formed by the straight lines x cos a + y sin a = p and the axes of co-ordinates. [Mar 10]
Solution:
The area of the triangle formed by the line ax + by + c = 0
and the co-ordinate axes is \(\frac{c^{2}}{2|a b|}\)
∴ Area of the triangle = \(\frac{p^{2}}{2|\cos \alpha \cdot \sin \alpha|}\)
= \(\frac{p^{2}}{|\sin 2 \alpha|}\)