Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Theory of Equations Solutions Exercise 4(d) will help students to clear their doubts quickly.
Intermediate 2nd Year Maths 2A Theory of Equations Solutions Exercise 4(d)
I.
Question 1.
Find the algebraic equation whose roots are 3 times the roots of x3 + 2x2 – 4x + 1 = 0
Solution:
Given equation is f(x) = x3 + 2x2 – 4x + 1 = 0
We require an equation whose roots are 3 times the roots of f(x) = 0
i,e., Required equation is f(\(\frac{x}{3}\)) = 0
⇒ \(\left(\frac{x}{3}\right)^{3}+2\left(\frac{x}{3}\right)^{2}-\frac{4 x}{3}+1=0\)
⇒ \(\frac{x^{3}}{27}+\frac{2}{9} x^{2}-\frac{4}{3} x+1=0\)
Multiplying with 27, required equation is x3 + 6x2 – 36x + 27 = 0
Question 2.
Find the algebraic equation whose roots are 2 times the roots of x5 – 2x4 + 3x3 – 2x2 + 4x + 3 = 0
Solution:
Given equation is f(x) = x5 – 2x4 + 3x3 – 2x2 + 4x + 3 = 0
We require an equation whose roots are 2 times the roots of f(x) = 0
Required equation is f(\(\frac{x}{2}\)) = 0
⇒ \(\left(\frac{x}{2}\right)^{5}-2\left(\frac{x}{2}\right)^{4}+3\left(\frac{x}{2}\right)^{3}-2\left(\frac{x}{2}\right)^{2}+4\left(\frac{x}{2}\right)\) + 3 = 0
⇒ \(\frac{x^{5}}{32}-2 \cdot \frac{x^{4}}{16}+3 \cdot \frac{x^{3}}{8}-2 \cdot \frac{x^{2}}{4}+4 \cdot \frac{x}{2}+3=0\)
Multiplying with 32, the required equation is
⇒ x5 – 4x4 + 12x3 – 16x2 + 64x + 96 = 0
![]()
Question 3.
Find the transformed equation whose roots are the negative of the roots of x4 + 5x3 + 11x + 3 = 0
Solution:
Given f(x) = x4 + 5x3 + 11x + 3 = 0
We want an equation whose roots are -α1, -α2, -α3, -α4
Required equation f(-x) = 0
⇒ (-x)4 + 5(-x)3 + 11(-x) + 3 = 0
⇒ x4 – 5x3 – 11x + 3 = 0
Question 4.
Find the transformed equation whose roots are the negatives of the roots of x7 + 3x5 + x3 – x2 + 7x + 2 = 0
Solution:
Given f(x) = x7 + 3x5 + x3 – x2 + 7x + 2 = 0
We want an equation whose roots are -α1, -α2, ………., -αn
Required equation is f(-x) = 0
⇒ (-x)7 + 3(-x)5 + (-x)3 – (-x)2 + 7(-x) + 2 = 0
⇒ -x7 – 3x5 – x3 – x2 – 7x + 2 = 0
⇒ x7 + 3x5 + x3 + x2 + 7x – 2 = 0
Question 5.
Find the polynomial equation whose roots are the reciprocals of the roots of x4 – 3x3 + 7x2 + 5x – 2 = 0
Solution:
Given equation is f(x) = x4 – 3x3 + 7x2 + 5x – 2 = 0
Required equation is f(\(\frac{1}{x}\)) = 0
i.e., \(\frac{1}{x^{4}}-\frac{3}{x^{3}}+\frac{7}{x^{2}}+\frac{5}{x}-2=0\)
Multiplying with x4
⇒ 1 – 3x + 7x2 + 5x3 – 2x4 = 0
⇒ 2x4 – 5x3 – 7x2 + 3x – 1 = 0
Question 6.
Find the polynomial equation whose roots are the reciprocals of the roots of x5 + 11x4 + x3 + 4x2 – 13x + 6 = 0
Solution:
Given equation is f(x) = x5 + 11x4 + x3 + 4x2 – 13x + 6 = 0
Required equation is f(\(\frac{1}{x}\)) = 0
\(\frac{1}{x^5}+\frac{11}{x^4}+\frac{1}{x^3}+\frac{4}{x^2}-\frac{13}{x}+6=0\)
Multiplying by x5
⇒ 1 + 11x + x2 + 4x3 – 13x4 + 6x5 = 0
⇒ 6x5 – 13x4 + 4x3 + x2 + 11x + 1 = 0
![]()
II.
Question 1.
Find the polynomial equation whose roots are the squares of the roots of x4 + x3 + 2x2 + x + 1 = 0
Solution:
Given equation is f(x) = x4 + x3 + 2x2 + x + 1 = 0
Required equation f(√x) = 0
⇒ x2 + x√x + 2x + √x + 1 = 0
⇒ √x(x + 1) = -(x2 + 2x + 1)
Squaring both sides,
⇒ x(x + 1)2 = (x2 + 2x + 1)2
⇒ x(x2 + 2x + 1) = x4 + 4x2 + 1 + 4x3 + 4x + 2x2
⇒ x3 + 2x2 + x = x4 + 4x3 + 6x2 + 4x + 1
⇒ x4 + 3x3 + 4x2 + 3x + 1 = 0
Question 2.
Form the polynomial equation whose roots are the squares of the roots of x3 + 3x2 – 7x + 6 = 0
Solution:
Given equation is f(x) = x3 + 3x2 – 7x + 6 = 0
Required equation is f(√x) = 0
⇒ x√x + 3x – 7√x + 6 = 0
⇒ √x(x – 7) = -(3x + 6)
Squaring on both sides,
⇒ x(x – 7)2 = (3x + 6)2
⇒ x(x2 – 14x + 49) = 9x2 + 36 + 36x
⇒ x3 – 14x2 + 49x – 9x2 – 36x – 36 = 0
⇒ x3 – 23x2 + 13x – 36 = 0
![]()
Question 3.
Form the polynomial equation whose roots are cubes of the roots of x3 + 3x2 + 2 = 0
Solution:
Given equation is x3 + 3x2 + 2 = 0
Put y = x3 so that x = y1/3
∴ y + 3y2/3 + 2 = 0
∴ 3y2/3 = -(y + 2)
Cubing on both sides,
27y2 = -(y + 2)3 = -(y3 + 6y2 + 12y + 8)
∴ y3 + 6y2 + 12y + 8 = 0
⇒ y3 + 33y2 + 12y + 8 = 0
Required equation is x3 + 33x2 + 12x + 8 = 0
III.
Question 1.
Find the polynomial equation whose roots are the translates of those of the equation x4 – 5x3 + 7x2 – 17x + 11 = 0 by -2.
Solution:
Given equation is f(x) = x4 – 5x3 + 7x2 – 17x + 11 = 0
The required equation is f(x + 2) = 0
(x + 2)4 – 5(x + 2)3 + 7(x + 2)2 – 17(x + 2) + 11 = 0
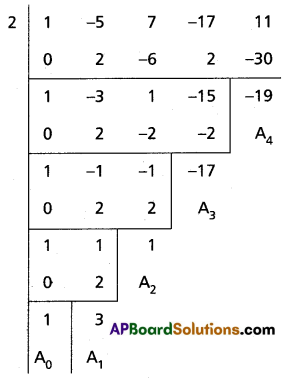
Required equation is x4 + 3x3 + x2 – 17x – 19 = 0
Question 2.
Find the polynomial equation whose roots are the translates of those of x5 – 4x4 + 3x2 – 4x + 6 = 0 by -3.
Solution:
Given equation is f(x) = x5 – 4x4 + 3x2 – 4x + 6 = 0
Required equation is f(x + 3) = 0
(x + 3)5 – 4(x + 3)4 + 3(x + 3)2

Required equation is x5 + 11x4 + 42x3 + 57x2 – 13x – 60 = 0
Question 3.
Find the polynomial equation whose roots are the translates of the roots of the equation x4 – x3 – 10x2 + 4x + 24 = 0 by 2.
Solution:
Given f(x) = x4 – x3 – 10x2 + 4x + 24 = 0
Required equation is f(x – 2) = 0
(x – 2)4 – (x – 2)3 – 10(x – 2)2 + 4(x – 2) + 24 = 0
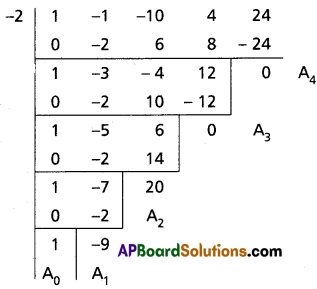
Required equation is x4 – 9x3 + 20x2 = 0
![]()
Question 4.
Find the polynomial equation whose roots are the translates of the equation 3x5 – 5x3 + 7 = 0 by 4.
Solution:
Given f(x) = 3x5 – 5x3 + 7 = 0
Required equation is f(x – 4) = 0
3(x – 4)5 – 5(x – 4)3 + 7 = 0
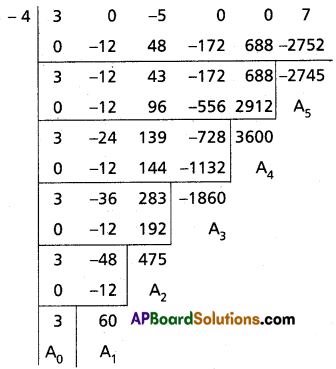
Required equation is x5 – 60x4 + 475x3 – 1860x2 + 3600x – 2745 = 0
Question 5.
Transform each of the following equations into ones in which of the coefficients of the second highest power of x is zero and also find their transformed equations.
(i) x3 – 6x2 + 10x – 3 = 0
Solution:
Given equation is x3 – 6x2 + 10x – 3 = 0
To remove the second term diminish the roots by \(-\frac{a_1}{n a_0}=\frac{6}{3}=2\)
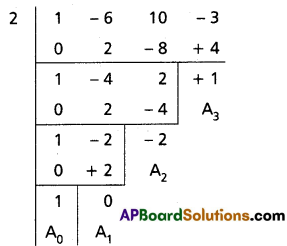
Required equation is x3 – 2x + 1 = 0
(ii) x4 + 4x3 + 2x2 – 4x – 2 = 0
Solution:
Given equation is x4 + 4x3 + 2x2 – 4x – 2 = 0
Diminishing the roots by \(-\frac{a_1}{n a_0}=\frac{-4}{4}=-1\)
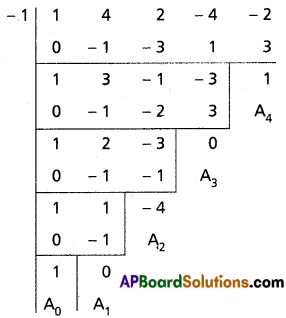
Required equation is x4 – 4x2 + 1 = 0
(iii) x3 – 6x2 + 4x – 7 = 0
Solution:
Given equation is x3 – 6x2 + 4x – 7 = 0
Diminishing the roots by \(-\frac{a_1}{n a_0}=\frac{6}{3}=2\)
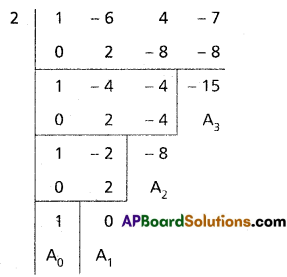
Required equation is x3 – 8x – 15 = 0
(iv) x3 + 6x2 + 4x + 4 = 0
Solution:
Given equation is x3 + 6x2 + 4x + 4 = 0
To remove the second term diminish the roots by \(\frac{-a_1}{n a_0}=-\frac{6}{3}=-2\)
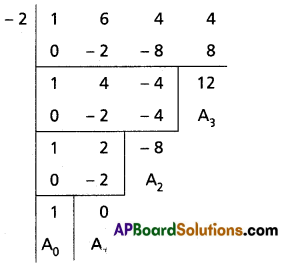
Required equation is x3 – 8x + 12 = 0
![]()
Question 6.
Transform each of the following equations into ones in which the coefficients of the third highest power of x are zero.
Hint: To remove the rth term in an equation f(x) = 0 of degree n diminish the roots by ‘h’ such that \(f^{(n-r+1)}(h)=0\)
(i) x4 + 2x3 – 12x2 + 2x – 1 = 0
Solution:
Let f(x) = x4 + 2x3 – 12x2 + 2x – 1
To remove the 3rd term, diminish the roots by h such that f”(h) = 0
f'(x) = 4x3 + 6x2 – 24x + 2
f”(x) = 12x2 + 12x – 24
f”(h) = 0
⇒ 12h2 + 12h – 24 = 0
⇒ h2 + h – 2 = 0
⇒ (h + 2) (h – 1) = 0
⇒ h = -2 or 1
Case (i):

Transformed equation is x4 – 6x3 + 42x – 53 = 0
Case (ii):
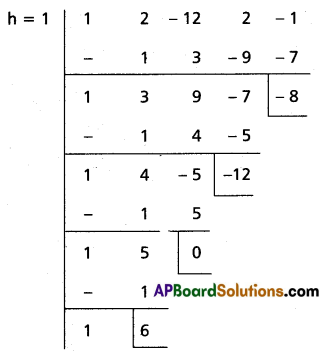
Transformed equation is x4 – 6x3 – 12x – 8 = 0
∴ The required equation is x4 – 6x3 + 42x – 53 = 0
or x4 + 6x3 – 12x – 8 = 0
(ii) x3 + 2x2 + x + 1 = 0
Solution:
Let f(x) = x3 + 2x2 + x + 1
To remove the 3rd term, diminish the roots by h such that f'(h) = 0, f'(x) = 3x2 + 4x + 1
f'(h) = 0
⇒ 3h2 + 4h + 1 = 0
⇒ (3h + 1) (h + 1)
⇒ h = -1, \(-\frac{1}{3}\)
Case (i):
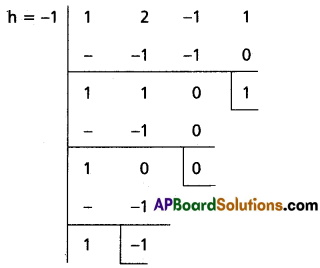
Transformed equation is x3 – x2 + 1 = 0
Case (ii):
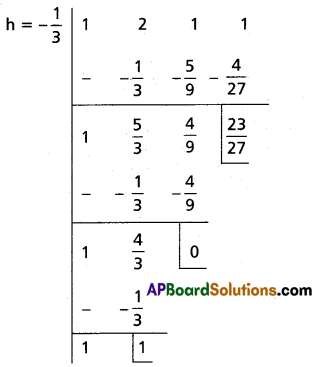
Transformed equation is x3 + x2 + \(\frac{23}{27}\) = 0
⇒ 27x3 + 27x2 + 23 = 0
∴ The required equation is x3 – x2 + 1 = 0 or 27x3 + 27x2 + 23 = 0
![]()
Question 7.
Solve the following equations.
(i) x4 – 10x3 + 26x2 – 10x + 1 = 0
Solution:
This is a standard reciprocal equation.
Dividing with x2
\(x^2-10 x+26-\frac{10}{x}+\frac{1}{x^2}=0\)
\(\left(x^2+\frac{1}{x^2}\right)-10\left(x+\frac{1}{x}\right)+26=0\) …….(1)
put a = x + \(\frac{1}{x}\)
\(x^2+\frac{1}{x^2}=\left(x+\frac{1}{x}\right)^2-2\) = a2 – 2
Substituting in (1)
a2 – 2 – 10a + 26 = 0
⇒ a2 – 10a + 24 = 0
⇒ (a – 4)(a – 6) = 0
⇒ a = 4 or 6
Case (i): a = 4
x + \(\frac{1}{x}\) = 4
⇒ x2 + 1 = 4x
⇒ x2 – 4x + 1 = 0
⇒ x = \(\frac{4 \pm \sqrt{16-4}}{2}=\frac{4 \pm 2 \sqrt{3}}{2}\)
⇒ x = 2 ± √3
Case (ii): a = 6
x + \(\frac{1}{x}\) = 6
⇒ x2 + 1 = 6x
⇒ x2 – 6x + 1 = 0
⇒ x = \(\frac{6 \pm \sqrt{36-4}}{2}\)
⇒ x = \(\frac{2(3 \pm 2 \sqrt{2)}}{2}\)
⇒ x = 3 ± 2√2
∴ The roots are 3 ± 2√2, 2 ± √3
(ii) 2x5 + x4 – 12x3 – 12x2 + x + 2 = 0
Solution:
Given f(x) = 2x5 + x4 – 12x3 – 12x2 + x + 2 = 0
This is an odd-degree reciprocal equation of the first type.
∴ -1 is a root.
Dividing f(x) with x + 1

Dividing f(x) by (x + 1), we get
2x4 – x3 – 11x2 – x + 2 = 0
Dividing by x2
\(2 x^2-x-11-\frac{1}{x}+\frac{2}{x^2}=0\)
\(2\left(x^2+\frac{1}{x^2}\right)-\left(x+\frac{1}{x}\right)-11=0\) ……..(1)
Put a = x + \(\frac{1}{x}\) so that
\(x^2+\frac{1}{x^2}=a^2-2\)
Substituting in (1), the required equation is
⇒ 2(a2 – 2) – a – 11 = 0
⇒ 2a2 – 4 – a – 11 = 0
⇒ 2a2 – a – 15 = 0
⇒ (a – 3) (2a + 5) = 0
⇒ a = 3 or \(-\frac{5}{2}\)
Case (i): a = 3
x + \(\frac{1}{x}\) = 3
⇒ x2 + 1 = 3x
⇒ x2 – 3x + 1 = 0
⇒ x = \(\frac{3 \pm \sqrt{9-4}}{2}=\frac{3 \pm \sqrt{5}}{2}\)
Case (ii): a = \(-\frac{5}{2}\)
⇒ \(x+\frac{1}{x}=-\frac{5}{2}\)
⇒ \(\frac{x^2+1}{x}=-\frac{5}{2}\)
⇒ 2x2 + 2 = -5x
⇒ 2x2 + 5x + 2 = 0
⇒ (2x + 1) (x + 2) = 0
⇒ x = \(-\frac{1}{2}\), -2
∴ The roots are -1, \(-\frac{1}{2}\), -2, \(\frac{3 \pm \sqrt{5}}{2}\)