Inter 2nd Year Maths 2A Complex Numbers Solutions Ex 1(c)

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Complex Numbers Solutions Exercise 1(c) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2A Complex Numbers Solutions Exercise 1(c)

I.

Question 1.
Express the following complex numbers in modulus-amplitude form.
(i) 1 – i
Solution:
1 – i
Let 1 – i = r(cos θ + i sin θ)
Equating real and imaginary parts
r cos θ = 1, r sin θ = -1
⇒ θ lies in IV quadrant
Squaring and adding
r² (cos²θ + sin²θ) = 1 + 1 = 2
⇒ r² = 2
⇒ r = √2
tan θ = – 1
⇒ θ = \(-\frac{\pi}{4}\)
∴ 1 – i = √2(cos(\(-\frac{\pi}{4}\)) + i sin(\(-\frac{\pi}{4}\)))

(ii) 1 + i√3
Solution:
1 + i√3 = r (cos θ + i sin θ)
Equating real and imaginary parts
r cos θ = 1 ………(1)
r sin θ = √3 ……..(2)
θ lies in the I quadrant
Squaring and adding (1) and (2)
r² (cos²θ + sin²θ) = 1 + 3
⇒ r² = 4
⇒ r = 2
Dividing (2) by (1)
\(\frac{r \sin \theta}{r \cos \theta}\) = √3
⇒ tan θ = √3
⇒ θ = \(\frac{\pi}{3}\)
∴ 1 + i√3 = 2(cos \(\frac{\pi}{3}\) + i sin \(\frac{\pi}{3}\))

(iii) -√3 + i
Solution:
-√3 + i = r(cos θ + i sin θ)
Equating real and imaginary parts
r cos θ = -√3 …….(1)
r sin θ = 1 …….(2)
⇒ θ lies in II quadrant
Squaring and adding (1), (2)
r² (cos²θ + sin²θ) = 3 + 1 = 4
⇒ r² = 4
⇒ r = 2
Dividing (2) by (1)
\(\frac{r \sin \theta}{r \cos \theta}=-\frac{1}{\sqrt{3}}\)
⇒ tan θ = \(-\frac{1}{\sqrt{3}}\) and θ lies in II quadrant
⇒ θ = 180° – 30° = 150° = \(\frac{5 \pi}{6}\)
∴ -√3 + i = 2(cos \(\frac{5 \pi}{6}\) + i sin \(\frac{5 \pi}{6}\))

(iv) -1 – i√3
Solution:
1 – i√3 = r (cos θ + i sin θ)
Equating real and imaginary parts
r cos θ = -1, r sin θ = -√3
Squaring and adding
r² (cos²θ + sin²θ) = 1 + 3
⇒ r² = 4
⇒ r = 2
∴ cos θ = \(-\frac{1}{2}\), sin θ = \(-\frac{\sqrt{3}}{2}\)
⇒ θ = -120° = \(-\frac{2 \pi}{3}\)
∴ -1 – i√3 = 2[cos(\(-\frac{2 \pi}{3}\)) + i sin(\(-\frac{2 \pi}{3}\))]

Question 2.
Simplify -2i(3 + i) (2 + 4i) (1 + i) and obtain the modulus of that complex number.
Solution:
-2i(3 + i) (2 + 4i) (1 + i)
= (-6i – 2i²) (2 + 2i + 4i + 4i²)
= (2 – 6i) (-2 + 6i)
= -4 + 12i – 36i² + 12i
= 32 + 24i
= 8(4 + 3i)
Modulus = |8(4 + 3i)|
= 8\(\sqrt{(4)^{2}+(3)^{2}}\)
= 8(5)
= 40

Question 3.
(i) If z ≠ 0, find Arg z + Arg \((\bar{z})\).
Solution:
If z = x + iy, then Arg(z) = \(\tan ^{-1}\left(\frac{y}{x}\right)\)
and \((\bar{z})\) = x – iy, then Arg (z) = \(\tan ^{-1}\left(\frac{-y}{x}\right)\) = –\(\tan ^{-1}\left(\frac{y}{x}\right)\)
∴ Arg (z) + Arg \((\bar{z})\) = \(\tan ^{-1}\left(\frac{y}{x}\right)\) + (-\(\tan ^{-1}\left(\frac{y}{x}\right)\)) = 0

(ii) If z₁ = -1 and z₂ = -i, then find Arg(z₁z₂)
Solution:
z₁ = -1
⇒ z₁ = cos π + i sin π
⇒ Arg z₁ = π
z₂ = -i
⇒ z₂ = \(\cos \left(-\frac{\pi}{2}\right)+i \sin \left(-\frac{\pi}{2}\right)\)
⇒ Arg z₂ = \(-\frac{\pi}{2}\)
∴ Arg (z₁z₂) = Arg z₁ + Arg z₂
= π – \(\frac{\pi}{2}\)
= \(\frac{\pi}{2}\)

(iii) If z₁ = -1, z₂ = i then find Arg\(\left(\frac{\mathbf{z}_{1}}{\mathbf{z}_{2}}\right)\)
Solution:
z₁ = -1 = cos π + i sin π
⇒ Arg z₁ = π
z₂ = i = cos \(\frac{\pi}{2}\) + i sin \(\frac{\pi}{2}\)
⇒ Arg z₂ = \(\frac{\pi}{2}\)
∴ Arg\(\left(\frac{\mathbf{z}_{1}}{\mathbf{z}_{2}}\right)\) = Arg z₁ – Arg z₂
= π – \(\frac{\pi}{2}\)
= \(\frac{\pi}{2}\)

Question 4.
(i) If (cos 2α + i sin 2α) (cos 2β + i sin 2β) = cos θ + i sin θ, then find the value of θ.
Solution:
cos θ + i sin θ
= (cos 2α + i sin 2α) (cos 2β + i sin 2β)
= cos 2α . cos 2β + i sin 2α . cos 2β + i cos 2α sin 2β + i² sin 2α . sin 2β
= (cos 2α . cos 2β – sin 2α . sin 2β) + i(sin 2α cos 2β + cos 2α sin 2β)
= cos 2(α + β) + i sin 2(α + β)
∴ θ = 2(α + β)

(ii) If √3 + i = r (cos θ + i sin θ), then find the value of θ in radian measure.
Solution:
Given that
√3 + i = r(cos θ + i sin θ)
⇒ r cos θ = √3, r sin θ = 1
⇒ r² (cos²θ + sin²θ) = 3 + 1
⇒ r² = 4
⇒ r = 2
∴ cos θ = \(\frac{\sqrt{3}}{2}\) and sin θ = \(\frac{1}{2}\)
⇒ θ = \(\frac{\pi}{6}\)

(iii) If x + iy = cis α . cis β then find the value of x² + y².
Solution:
Given x + iy = cis α . cis β
⇒ x + iy = (cos α + i sin α) (cos β + i sin β)
⇒ x + iy = cos(α + β) + i sin(α + β)
Equating real and imaginary parts
x = cos(α + β) and y = sin(α + β)
∴ x² + y² = cos²(α + β) + sin²(α + β) = 1

(iv) If \(\frac{z_{2}}{z_{1}}\), (z₁ ≠ 0) is an imaginary number, then find the value of \(\left|\frac{2 z_{1}+z_{2}}{2 z_{1}-z_{2}}\right|\)
Solution:
\(\frac{z_{2}}{z_{1}}\), (z₁ ≠ 0) is purely imaginary.
We can suppose that \(\frac{z_{2}}{z_{1}}\) = iy, where y ∈ R – {0}

(v) If (√3 + i)¹⁰⁰ = 2⁹⁹ (a + ib), then show that a² + b² = 4.
Solution:

Question 5.
(i) If z = x + iy and |z| = 1, find the locus of z.
Solution:
Given z = x + iy
Also |z| = 1
⇒ |x + iy| = 1
⇒ \(\sqrt{x^{2}+y^{2}}=1\)
⇒ x² + y² = 1
∴ Locus of z is x² + y² = 1

(ii) If the amplitude of (z – 1) is \(\frac{\pi}{2}\), then find the locus of z.
Solution:
Given z = x + iy
z – 1 = x + iy – 1 = (x – 1) + iy
Since Amplitude (z – 1) is \(\frac{\pi}{2}\)
Real part of z – 1 is zero.
∴ x – 1 = 0
∴ Locus of z is x – 1 = 0

(iii) If the Arg \(\overline{\mathbf{z}}_{1}\) and Arg z₂ are \(\frac{\pi}{5}\) and \(\frac{\pi}{3}\) respectively, find (Arg z₁ + Arg z₂)
Solution:
Arg \(\overline{\mathbf{z}}_{1}\) = \(\frac{\pi}{5}\)
⇒ Arg \(\overline{\mathbf{z}}_{1}\) = -Arg z₁ = \(-\frac{\pi}{5}\)
Arg z₂ = \(\frac{\pi}{3}\)
∴ Arg z₁ + Arg z₂ = \(-\frac{\pi}{5}+\frac{\pi}{3}\) = \(\frac{2 \pi}{15}\)

(iv) If z = \(\frac{1+2 i}{1-(1-i)^{2}}\) then find Arg(z).
Solution:
Given z = \(\frac{1+2 i}{1-(1-i)^{2}}\)
= \(\frac{1+2 i}{1-(1-2 i+i)^{2}}\)
= \(\frac{1+2 i}{1+2 i}\)
= 1
= cos 0° + i sin 0°
∴ Arg (z) = 0°

II.

Question 1.
Simplify the following complex numbers and find their modulus.
(i) \(\frac{(2+4 i)(-1+2 i)}{(-1-i)(3-i)}\)
(ii) \(\frac{(1+i)^{3}}{(2+i)(1+2 i)}\)
Solution:

Question 2.
(i) If (1 – i) (2 – i) ( 3 – i) …… (1 – ni) = x – iy then prove that 2 . 5 . 10 …….. (1 + n²) = x² + y².
Solution:
Given (1 – i) (2 – i) (3 – i) (1 – ni) = x – iy
|1 – i| |2 – i| |3 – i| …… |1 – ni| = |x – iy|
\(\sqrt{1+1} \sqrt{4+1} \sqrt{9+1} \ldots \sqrt{1+n^{2}}=\sqrt{x^{2}+y^{2}}\)
∴ 2 . 5 . 10 ……. (1 + n²) = x² + y²

(ii) If the real part of \(\frac{z+1}{z+i}\) is 1, then find the locus of z.
Solution:

(iii) If |z – 3 + i | = 4 determine the locus of z.
Solution:
Let z = x + iy
Given |z – 3 + i| = 4
⇒ |x + iy – 3 + i | = 4
⇒ (x – 3) + i(y + 1) = 4
⇒ \(\sqrt{(x-3)^{2}+(y+1)^{2}}\) = 4
⇒ (x – 3)² + (y + 1)² = 16
⇒ x² – 6x + 9 + y² + 2y + 1 = 16
⇒ x² + y² – 6x + 2y – 6 = 0
∴ The locus of z is x² + y² – 6x + 2y – 6 = 0

(iv) If |z + ai| = |z – ai| then find the locus of z.
Solution:
Let z = x + iy
Given |z + ai | = |z – ai|
⇒ |x + iy + ai| = |x + iy – ai|
⇒ |x + i(y + a)| = |x + i(y – a)|
⇒ \(\sqrt{x^{2}+(y+a)^{2}}=\sqrt{x^{2}+(y-a)^{2}}\)
⇒ x² + (y + a)² = x² + (y – a)²
⇒ (y + a)² – (y – a)² = 0
⇒ 4ay = 0
⇒ y = 0
∴ The locus of z is y = 0

Question 3.
If z = (x + iy) and if the point P in the Argand plane represents z, then describe geometrically the locus of P satisfying the equation.
(i) |2z – 3| = 7
Solution:
|2z – 3| = 7
Let z = x + iy
Given |2z – 3| = 7
⇒ |2(x + iy) – 3| = 7
⇒ |(2x – 3) + i(2y)| = 7
⇒ \(\sqrt{(2 x-3)^{2}+(2 y)^{2}}\) = 7
⇒ 4x² – 12x + 9 + 4y² = 49
⇒ 4x² + 4y² – 12x – 40 = 0
⇒ x² + y² – 3x – 10 = 0
∴ The locus of z is x² + y² – 3x – 10 = 0
This equation represents a circle.
Centre = (\(\frac{3}{2}\), 0)
Radius = \(\sqrt{\frac{9}{4}-(-10)}\) = \(\frac{7}{2}\) units

(ii) |z|² = 4 Re(z + 2)
Solution:
|z|² = 4 Re (z + 2)
Given |z|² = 4 Re (z + 2)
⇒ |x + iy|² = 4 Re (x + iy + z)
⇒ (\(\sqrt{x^{2}+y^{2}}\)) = 4(x + 2)
⇒ x² + y² = 4x + 8
∴ The locus of z is x² + y² – 4x – 8 = 0
This equation represents a circle. Center = (2, 0)
Radius = \(\sqrt{4-(-8)}\) = 2√3 units.

(iii) |z + i|² – |z – i|² = 2
Solution:
Given |z + i|² – |z –  i|² = 2
⇒ |x + iy + i|² – |x + iy – i|² = 2
⇒ |x + i(y + 1)|² – |x + i(y – 1)|² = 2
⇒ \(\left[\sqrt{x^{2}+(y+1)^{2}}\right]^{2}\) – \(\left[\sqrt{x^{2}+(y-1)^{2}}\right]^{2}\) = 2
⇒ x² + (y + 1 )² – [x² + (y – 1)²] = 2
⇒ x² + (y + 1)² – x² – (y – 1)² = 2
⇒ 4y = 2
⇒ 2y – 1 = 0
The locus of P is 2y – 1 = 0
This equation represents a straight line parallel to the x-axis.

(iv) |z + 4i| + |z – 4i| = 10
Solution:
Given |z + 4i| + |z – 4i| = 10
⇒ |x + iy + 4i| + |x + iy – 4i| = 10
⇒ |x + i(y + 4)| + |x + i(y – 4)| = 10
⇒ \(\sqrt{x^{2}+(y+4)^{2}}+\sqrt{x^{2}+(y-4)^{2}}\)
⇒ \(\sqrt{x^{2}+(y+4)^{2}}\) = 10 – \(\sqrt{x^{2}+(y-4)^{2}}\)
⇒ x² + (y + 4)² = 100 + x² + (y – 4)² – 20 \(\sqrt{x^{2}+(y-4)^{2}}\)
⇒ 16y – 100 = – 20\(\sqrt{x^{2}+(y-4)^{2}}\)
⇒ 4y – 25 = -5\(\sqrt{x^{2}+(y-4)^{2}}\)
⇒ (4y – 25)² = 25[x² + (y – 4)²]
⇒ 16y² – 200y + 625 = 25x² + 25y² – 200y + 400
⇒ 25x² + 9y² = 225
∴ The locus of P is 25x² + 9y² = 225
⇒ \(\frac{x^{2}}{9}+\frac{y^{2}}{25}\) = 1
This equation represents an ellipse.
Center = (0, 0)
a² = 9, b² = 25
We know a² – b²(1 – e²)
⇒ 9 = 25(1 – e²)
⇒ 1 – e² = \(\frac{9}{25}\)
⇒ e = 1 – \(\frac{9}{25}\) = \(\frac{16}{25}\)
∴ Eccentricity = \(\frac{4}{5}\) and major axis parallel to y-axis.

Question 4.
(i) If z₁, z₂ are two non-zero complex numbers satisfying |z₁ + z₂| = |z₁| + |z₂|, show that Arg z₁ – Arg z₂ = 0.
Solution:

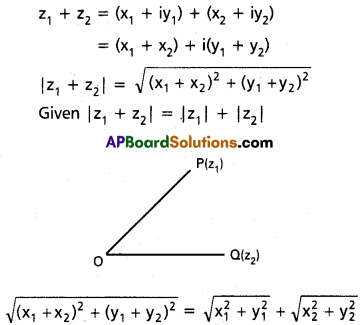
(ii) z = x + iy and the point P represents z in the Argand plane and \(\left|\frac{z-a}{z+\bar{a}}\right|\) = 1, Re(a) ≠ 0, then find the locus of P.
Solution:
Let z = x + iy and a = α + iβ
\(\frac{z-a}{z+\bar{a}}=\frac{(x+i y)-(\alpha+i \beta)}{(x+i y)+(\alpha-i \beta)}\)
\(\left|\frac{z-a}{z+\bar{a}}\right|\) = 1
⇒ \(\frac{|z-a|}{|z+\bar{a}|}\) = 1
⇒ |z – a| = |z + \(\overline{\mathrm{a}}\)|
⇒ |(x – α)| + i(y – β)| = |(x + α) + i(y – β)|
⇒ \(\sqrt{(x-\alpha)^{2}+(y-\beta)^{2}}=\sqrt{(x+\alpha)^{2}+(y-\beta)^{2}}\)
⇒ (x – α)² + (y – β)² = (x + α)² + (y – β)²
⇒ (x – α)² = (x + α)²
⇒ (x + α)² – (x – α)² = 0
⇒ 4αx = 0
Re(a) ≠ 0
⇒ a ≠ 0
⇒ x = 0
Locus of P is x = 0 i.e., Y-axis