Use these Inter 1st Year Maths 1B Formulas PDF Chapter 5 Three Dimensional Coordinates to solve questions creatively.
Intermediate 1st Year Maths 1B Three Dimensional Coordinates Formulas
→ Distance from the origin to P(x, y, z) = OP = \(\sqrt{x^{2}+y^{2}+z^{2}}\)
→ Distance between the points P(x1, y1 z1) and Q (x2, y2, z2) is
→ PQ = \(\sqrt{\left(x_{1}-x_{2}\right)^{2}+\left(y_{1}-y_{2}\right)^{2}+\left(z_{1}-z_{2}\right)^{2}}\)
→ Translation of axes : If the origin is shifted to the point (h, k, l) under translation of axes, then x = x’ + h, y = y’ + k, z = z’ + l where (x, y, z) are the old co-ordinates and (x’, y’, z’) are the new co-ordinates.
Coordinates of a Point In Space (3-D):
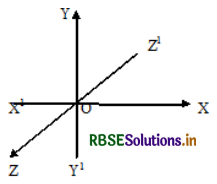
Let \(\overline{X^{\prime} O X}, \overline{Y^{\prime} O Y}\) and \(\overline{Z^{\prime} O Z}\) be three mutually perpendicular straight lines in space, intersecting at O. This point O is called origin.
Axes :
The three fixed straight lines \(\overline{X^{\prime} O X}, \overline{Y^{\prime} O Y}\) and \(\overline{Z^{\prime} O Z}\) are respectively called X-axis ,Y-axis and Z-axis. The three lines taken together are called rectangular coordinate axes.
Coordinate Planes:
The plane containing the axes of Y and Z is called yz-plane. Thus yoz is the yz plane. Similarly the plane zox containing the axes of z and x is called ZX-plane and the plane xoy is called the xy-plane and contains x axis and y axis.
The above three planes are together called the rectangular co ordinate plane.
Octants:
The three co ordinate planes divide the whole space into 8 parts called octants.
![]()
Coordinates of A Point:
Let P be any point in the space. Draw through P , three planes parallel to the three co ordinate planes meeting the axes of X,Y,Z in the points A,B and C respectively. Then if OA = x, OB = y and OC = z, the three numbers x,y,z taken in this order are called the co ordinates of the point P and we refer the point as (x,y,z) . Any one of these x,y,z will be positive of negative according as it is measured from O along the corresponding axis, in the positive or negative direction.
Another method of finding coordinates of a point.
The coordinates x,y,z of a point P are the perpendicular distances of P from the three co ordinate planes YZ,ZX and XY respectively.
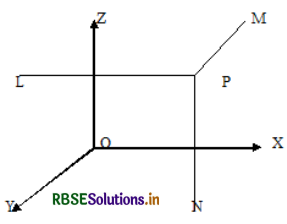
From fig PN = z, PL = x and PM = y
Therefore point P =(x,y,z)
Note. On YZ- plane, a point has x coordinate as zero and similarly on zx-plane y coordinates and on xy-plane z coordinates are zero.
For any point on the
- X-axis, Y,Z coordinates are equal to zero,
- Y-axis, X,Z coordinates are equal to zero,
- Zaxis, X,Y coordinates are equal to zero.
Distance Between The Points:
The distance between the points and is given by PQ = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}+\left(z_{2}-z_{1}\right)^{2}}\)
Note:
If is the origin and is a point in space, then
OP = \(\sqrt{(x-0)^{2}+(y-0)^{2}+(z-0)^{2}}=\sqrt{x^{2}+y^{2}+z^{2}}\)
Section Formula:
P(x1, y1, z1) and Q(x2, y2, z2) be two points in space and let R be a point on the line segment joining P and Q such that it divides \(\overline{P Q}\) internally in the ratio m: n . Then the coordinate of are \(\left(\frac{m x_{2}+n x_{1}}{m+n}, \frac{m y_{2}+n y_{1}}{m+n}, \frac{m z_{2}+n z_{1}}{m+n}\right)\)
(ii) P(x1, y1, z1) and Q(x2, y2, z2) be two points in space and let R be a point on the line segment joining P and Q such that it divides \(\overline{P Q}\) externally in the ratio m: n . Then the coordinate of are \(\left(\frac{m x_{2}-n x_{1}}{m-n}, \frac{m y_{2}-n y_{1}}{m-n}, \frac{m z_{2}-n z_{1}}{m-n}\right)\), m ≠ n
Mid Point:
The mid point of the linesegment joining the points P(x1, y1, z1) and Q(x2, y2, z2) is
\(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}, \frac{z_{1}+z_{2}}{2}\right)\)
Centroid of a triangle:
The coordinates of the centriod of the triangle with vertices A(x1, y1, z1) B(x2, y2, z2) and C(x3, y3, z3) is \(\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}+\frac{z_{1}+z_{2}+z_{3}}{3}\right)\)
Centroid of a tetrahydron:
The coordinates of the centriod of the tetrahedron with vertices A(x1, y1, z1) B(x2, y2, z2), C(x3, y3, z3) and D(x4, y4, z4) is \(\left(\frac{x_{1}+x_{2}+x_{3}+x_{4}}{4}, \frac{y_{1}+y_{2}+y_{3}+y_{4}}{4}, \frac{z_{1}+z_{2}+z_{3}+z_{4}}{4}\right)\)
![]()
Translation of Axes :
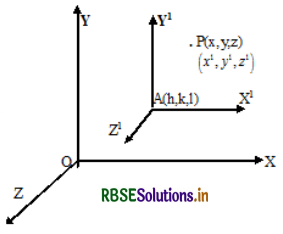
Let P(x,y,z) and A(h,k,l) be two points is space w.r.t the frame of reference OXYZ. Now treating A as the origin, let \(\overline{A X^{1}}, \overline{A Y^{1}}, \overline{A Z^{1}}\) be the new axes parallel to
\(\overline{O X}, \overline{O Y}, \overline{O Z}\) respectively. If (x’, y’, z’) are the coordinates of P w.r.t
AX1Y1Z1 then x1 = x – h, y1 = y – k, z1 = z – l.
Example: Origin is shifted to the point (1,2 -3). Find the new coordinates of (1,0,-1)
Answer:
(x, y, z) = (1,0,-1) and( h, k, l) = (1,2 -3).
Now new coordinates are X = x – h = 1 -1 = 0
Y = y – k = 0 – 2 = -2
Z = z – l = -1 + 3 = 2
herefore new coordinates are ( 0,-2, 2)