Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Quadratic Expressions Solutions Exercise 3(c) will help students to clear their doubts quickly.
Intermediate 2nd Year Maths 2A Quadratic Expressions Solutions Exercise 3(c)
I.
Question 1.
Solve the following inequations by the algebraic method.
(i) 15x2 + 4x – 4 ≤ 0
Solution:
15x2 + 4x – 4 ≤ 0
⇒ 15x2 – 6x + 10x – 4 ≤ 0
⇒ 3x(5x – 2) + 2(5x – 2) ≤ 0
⇒ (3x + 2) (5x – 2) ≤ 0
Co-efficient of x2 = 15 > 0,
Given Expression is ≤ 0
⇒ x lies between \(\frac{-2}{3}\) and \(\frac{2}{5}\)
i.e., \(\frac{-2}{3} \leq x \leq \frac{2}{5}\)
(ii) x2 – 2x + 1 < 0
Solution:
x2 – 2x + 1 < 0
⇒ (x – 1)2 < 0
There is no real value of ‘x’ satisfying this inequality
Solution set = Φ (or) Solution does not exist.
![]()
(iii) 2 – 3x – 2x2 ≥ 0
Solution:
-(2x2 + 3x – 2) ≥ 0
⇒ -(2x2 + 4x – x – 2) ≥ 0
⇒ -[2x(x + 2) – 1(x + 2)] ≥ 0
⇒ -(2x – 1) (x + 2) ≥ 0
Co-efficient of x2 = -2 < 0,
The given expression is ≥ 0
⇒ x lies between -2 and \(\frac{1}{2}\)
i.e., -2 ≤ x ≤ \(\frac{1}{2}\)
(iv) x2 – 4x – 21 ≥ 0
Solution:
x2 – 4x – 21 ≥ 0
⇒ x2 – 7x + 3x – 21 ≥ 0
⇒ x(x – 7) + 3(x – 7) ≥ 0
⇒ (x + 3) (x – 7) ≥ 0
Co-efficient of x2 = 1 > 0,
The given expression is ≥ 0
x does not lie between -3 and 7
i.e., {x/x ∈ (-∞, -3] ∪ [7, ∞)}
II.
Question 1.
Solve the following inequations by graphical method.
(i) x2 – 7x + 6 > 0
Solution:
f(x) = x2 – 7x + 6
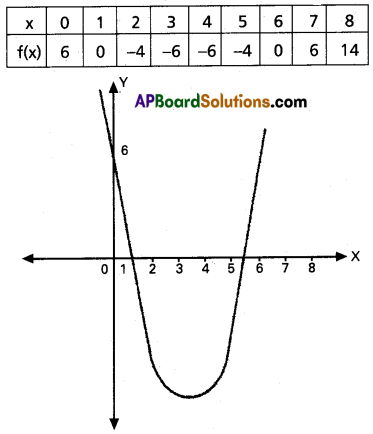
f(x) > 0 ⇒ y > 0
Solutions are given by x < 1 and x > 6
(ii) 4 – x2 > 0
Solution:
Let f(x) = 4 – x2
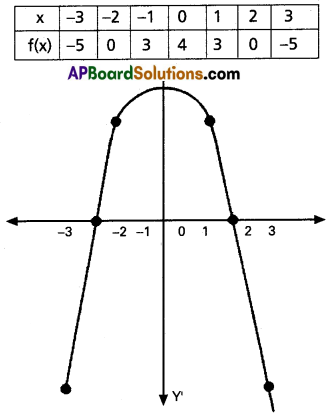
f(x) > 0 ⇒ y > 0
Solution set = {x/-2 < x < 2}
(iii) 15x2 + 4x – 4 < 0
Solution:
Let f(x) = 15x2 + 4x – 4
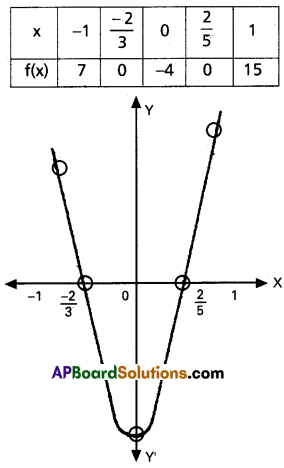
f(x) ≤ 0 ⇒ y ≤ 0
Solution set = \(\left\{x / \frac{-2}{3} \leq x \leq \frac{2}{5}\right\}\)
(iv) x2 – 4x – 21 ≥ 0
Solution:
Let f(x) = x2 – 4x – 21
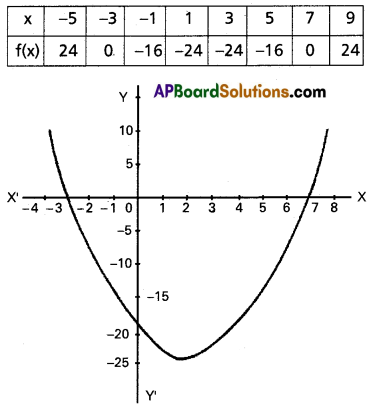
f(x) ≥ 0 ⇒ y ≥ 0
Solution set = {x/x ∈ (-∞, -3] ∪ [7, ∞)}
![]()
Question 2.
Solve the following inequations.
(i) \(\sqrt{3 x-8}\) < -2
Solution:
L.H.S. is positive and R.H.S. is negative.
∴ The given inequality holds for no real x.
Solution set = Φ (or) Solution does not exist.
(ii) \(\sqrt{-x^{2}+6 x-5}\) > 8 – 2x
Solution:
\(\sqrt{-x^{2}+6 x-5}\) > 8 – 2x
⇔ -x2 + 6x – 5 > 0
and (i) 8 – 2x < 0 (or) (ii) 8 – 2x ≥ 0
We have -x2 + 6x – 5 = -(x2 – 6x + 5) = -(x – 1) (x – 5)
Hence -x2 + 6x – 5 ≥ 0 ⇔ x ∈ [1, 5]
(i) -x2 + 6x – 5 ≥ 0 and 8 – 2x < 0
⇔ x ∈ [1, 5] and x > 4
⇔ x ∈ [4, 5] ………(1)
(ii) -x2 + 6x – 5 ≥ 0 and 8 – 2x ≥ 0
∵ \(\sqrt{\left(-x^{2}+6 x-5\right)}\) > 8 – 2x
⇔ -x2 + 6x – 5 > (8 – 2x)2 and 8 – 2x ≥ 0
⇔ -x2 + 6x – 5 > 64 + 4x2 – 32x and x ≤ 4
⇔ -5x2 + 38x – 69 > 0 and x ≤ 4
⇔ 5x2 – 38x + 69 < 0 and x ≤ 4
⇔ 5x2 – 15x – 23x + 69 < 0 and x ≤ 4
⇔ (5x – 23)(x – 3) < 0 and x ≤ 4
⇔ x ∈ (3, \(\frac{23}{5}\)) and x ≤ 4
⇔ x ∈ (3, \(\frac{23}{5}\)) ∩ (-∞, 4)
⇔ x ∈ (3, 4)
Hence the solution set of the given equation is x ∈ (4, 5) ∪ (3, 4)
⇒ x ∈ (3, 5) (or) 3 < x ≤ 5.