Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Measures of Dispersion Solutions Exercise 8(a) will help students to clear their doubts quickly.
Intermediate 2nd Year Maths 2A Measures of Dispersion Solutions Exercise 8(a)
I.
Question 1.
Find the mean deviation about the mean for the following data.
(i) 38, 70, 48, 40, 42, 55, 63, 46, 54, 44
Solution:
The arithmetic mean of the given data
\(\bar{x}=\frac{38+70+48+40+42+55+63+46+54+44}{10}\)
= \(\frac{500}{10}\)
= 50
The absolute values of the deviations are
\(\left|x_i-\bar{x}\right|\), |50 – 38|, |50 – 70|, |50 – 48|, |50 – 40|, |50 – 42|, |50 – 55|, |50 – 63|, |50 – 46|, |50 – 54|, |50 – 44|
= 12, +20, 2, 10, 8, +5, +13, 4, +4, 6
∴ The mean deviation from the mean

(ii) 3, 6, 10, 4, 9, 10
Solution:
The arithmetic mean of the given data
\(\bar{x}=\frac{3+6+10+4+9+10}{6}\)
= \(\frac{42}{6}\)
= 7
The absolute values of the deviations are
\(\left|x_i-\bar{x}\right|\), |3 – 7|, |16 – 7|, |10 – 7|, |4 – 7|, |9 – 7|, |10 – 7|
= 4, 1, 3, 3, 2, 3
∴ The mean deviation from the mean

![]()
Question 2.
Find the mean deviation about the median for the following data.
(i) 13, 17, 16, 11, 13, 10, 16, 11, 18, 12, 17
Solution:
Given ungrouped data are
13, 17, 16, 11, 13, 10, 16, 11, 18, 12, 17
Expressing the data in the ascending order of magnitude, we have
10, 11, 11, 12, 13, 13, 16, 16, 17, 17, 18
∴ Median = 13 = b(say)
The absolute values are
|13 – 10|, |13 – 11|, |13 – 11|, |13 – 12|, |13 – 13|, |13 – 13|, |13 – 16|, |13 – 16|, |13 – 17|, |13 – 17|, |13 – 18|
= 3, 2, 2, 1, 0, 0, 3, 3, 4, 4, 5
∴ Mean deviation from the median
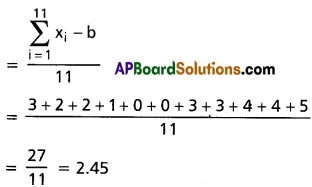
(ii) 4, 6, 9, 3, 10, 13, 2
Solution:
Given ungrouped data are 4, 6, 9, 3, 10, 13, 2
Expressing the data in the ascending order of magnitude, we have
2, 3, 4, 6, 9, 10, 13
∴ Median = 6 = b (say)
The absolute values are
|6 – 2|, |6 – 3|, |6 – 4|, |6 – 6|, |6 – 9|, |6 – 10|, |6 – 13|
= 4, 3, 2, 0, 3, 4, 7
∴ Mean deviation from the median = \(\frac{\sum_{i=1}^7\left|x_i-b\right|}{7}\)
= \(\frac{4+3+2+0+3+4+7}{7}\)
= 3.285
Question 3.
Find the mean deviation about the mean for the following distribution.
(i)
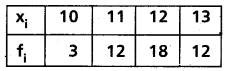
Solution:

(ii)

Solution:

![]()
Question 4.
Find the mean deviation about the median for the following frequency distribution.
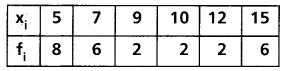
Solution:
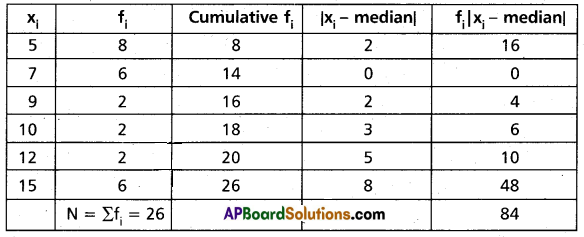
\(\frac{N}{2}\) = 13
∴ Median = 7
Hence mean deviation from the median = \(\frac{1}{N} \sum f_i \mid x_i-\text { Median } \mid\)
= \(\frac{1}{26}\) (84)
= 3.23
II.
Question 1.
(i) Find the mean deviation about the median for the following continuous distribution.

Solution:
Construct the table
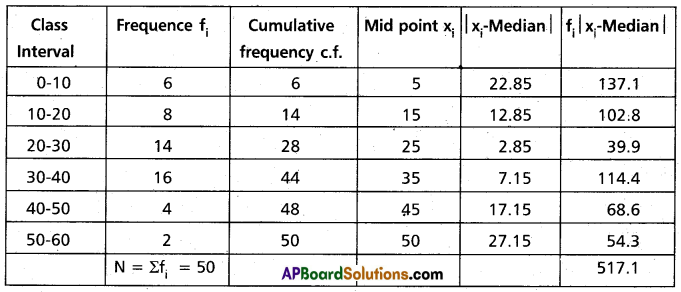
\(\frac{N}{2}\) = 25
Observation lies in the class-interval 20-30.
This is the median class.

(ii)

Solution:
Construct the table
\(\frac{N}{2}=\frac{100}{2}\) = 50
Observation lies in the interval 40-50
This is the median class
∴ Median = \(L+\left\{\frac{\frac{N}{2}-\text { P.C.f }}{f}\right\} \times i\)
= 40 + \(\left\{\frac{50-32}{28}\right\} \times 10\)
= 40 + 6.43
= 46.43
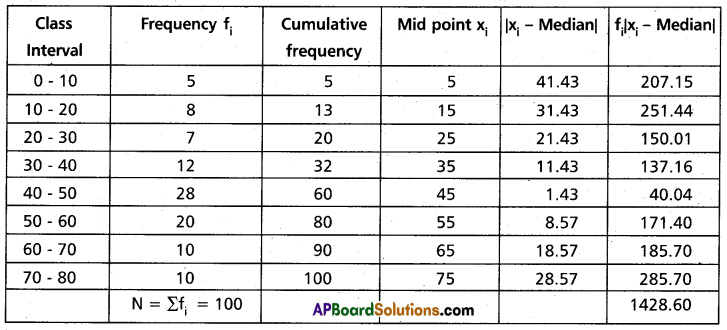
∴ Median deviation about median = \(\frac{1}{N} \sum_{i=1}^8 f_i \mid x_i-\text { median } \mid\)
= \(\frac{1}{100}\) (1428.6)
= 14.286
![]()
Question 2.
Find the mean deviation about the mean for the following continuous distribution.

Solution:
Taking the assumed mean a = 130 and h = 10 construct the table
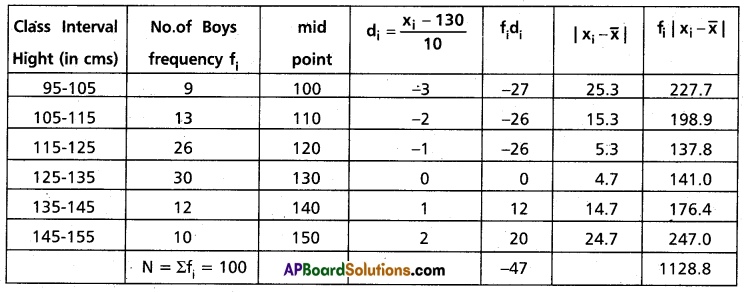
\(\bar{x}=a+\left(\frac{\sum f_i d_i}{N}\right) h\)
= 130 + \(\left(\frac{-47}{100}\right) 10\)
= 130 – 4.7
= 125.3
Mean deviation about the mean = \(\frac{1}{N} \sum_{i=1}^6 f_i\left|x_i-\bar{x}\right|\)
= \(\frac{1}{100}\) (1428.8)
= 14.288
Question 3.
Find the variance for the discrete data given below.
(i) 6, 7, 10, 12, 13, 4, 8, 12
Solution:
Given data are 6, 7, 10, 12, 13, 4, 8, 12
Mean \(\bar{x}=\frac{6+7+10+12+13+4+8+12}{8}\)
= \(\frac{72}{8}\)
= 9
Construct the table
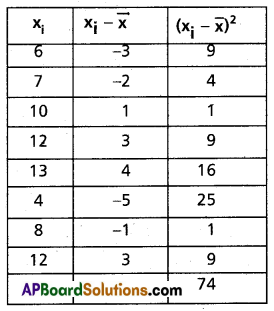
Variance σ2 = \(\frac{1}{n} \Sigma\left(x_i-\bar{x}\right)^2\)
= \(\frac{1}{8}\) (74)
= 9.25
(ii) 350, 361, 370, 373, 376, 379, 385, 387, 394, 395
Solution:
Given data are 350, 361, 370, 373, 376, 379, 385, 387, 394, 395
Mean \(\bar{x}=\frac{350+361+370+373+376+379+385+387+394+395}{10}\) = 377
Construct the table
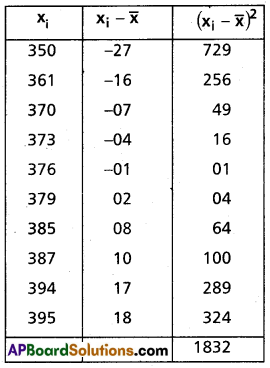
Variance = \(\frac{1}{n} \sum_{i=1}^{10}\left(x_i-\bar{x}\right)^2\)
= \(\frac{1}{10}\) (1832)
= 183.2
![]()
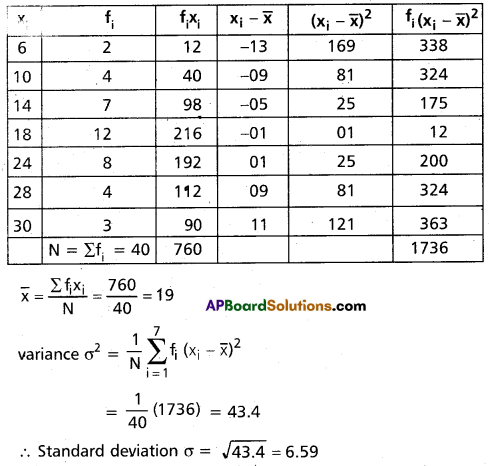
Question 4.
Find the variance and standard deviation of the following frequency distribution.

Solution:
III.
Question 1.
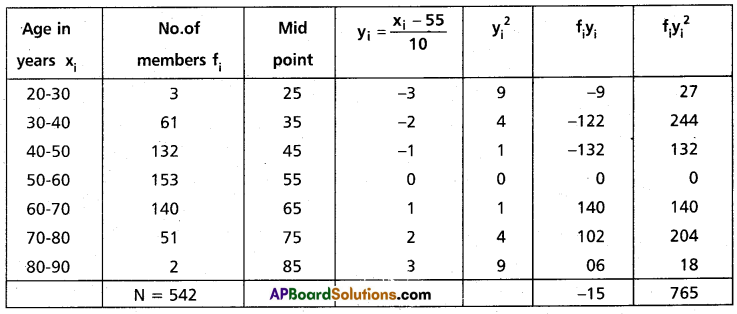
Find the mean and variance using the step deviation method, of the following tabular data, giving the age distribution of 542 members.

Solution:
If we take assumed mean A = 55 then yi = \(\frac{x_i-55}{10}\)
Here h = 10
Construct the table
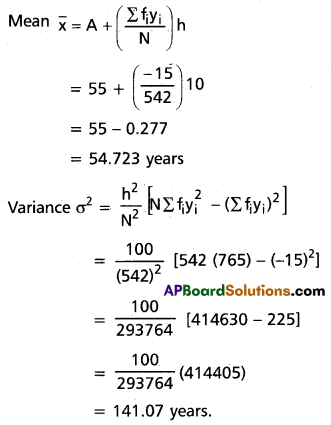
Question 2.
The coefficient of variation of the two distributions are 60 and 70 and their standard deviations are 21 and 16 respectively. Find their arithmetic means.
Solution:
Given coefficient of variance C.V = 60
Standard deviation s = 21
We know C.V = \(\frac{\sigma}{x} \times 100\)
⇒ \(\bar{x}=\frac{\sigma}{C . V} \times 100\)
= \(\frac{21}{60}\) × 100
= 35
Arithmetic mean = 35
Given co-efficient of variance C.V = 70
Standard deviation σ = 16
We know C.V = \(\frac{\sigma}{x} \times 100\)
⇒ \(\bar{x}=\frac{\sigma}{C . V} \times 100\)
= \(\frac{16}{70}\) × 100
= 22.85
![]()
Question 3.
From the prices of Shares X and Y given below, for 10 days of trading, find out which share is more stable.

Solution:
For share x
\(\bar{x}=\frac{35+54+52+53+56+58+52+50+51+49}{10}\)
= \(\frac{510}{10}\)
= 51
For share y
\(\bar{y}=\frac{108+107+105+105+106+107+104+103+104+101}{10}\)
= \(\frac{1050}{10}\)
= 105

C.V of share x = \(\frac{\sigma_{\mathrm{x}}}{\mathrm{x}} \times 100\)
= \(\frac{5.92}{51}\) × 100
= 11.61
C.V of share y = \(\frac{\sigma_{\mathrm{y}}}{\mathrm{y}} \times 100\)
= \(\frac{2}{105}\) × 100
= 1.91
since \(\bar{x}<\bar{y}\) and C.V of share x > C.V of shares y
∴ Y share is more stable.
Question 4.
The mean of 5 observations is 4.4. Their variance is 8.24. If three of the observations are 1, 2, and 6. Find the other two observations.
Solution:
Let x and y be the required two observations.
Given, that the mean of 5 observations = 4.4
⇒ \(\frac{1+2+6+x+y}{5}\) = 4.4
⇒ 9 + x + y = 22
⇒ x + y = 13 ……..(1)
Also thin variance = 8.24
⇒ \(\frac{1}{5}\) [(1 – 4.4)2 + (2 – 4.4)2 + (6 – 4.4)2 + (x – 4.4)2 + (y – 4.4)2] = 8.24
⇒ (-3.4)2 + (-2.4)2 + (1.6)2 + x2 – 8.8x + 19.36 + y2 – 8.8y + 19.36 = 41.2
⇒ x2 + y2 – (8.8) (x + y) = 41.2 – 11.56 – 5.76 – 2.56 – 19.36 – 19.36
⇒ x2 + y2 – (8.8) (13) = -17.4
⇒ x2 + y2 = -17.4 + 114.4
⇒ x2 + y2 = 97
We know (x + y)2 = x2 + y2 + 2xy
⇒ 169 = 97 + 2xy
⇒ 2xy = 72
⇒ xy = 36
(x – y)2 = (x + y)2 – 4xy
⇒ (x – y)2 = 169 – 144 = 25
⇒ x – y = 5 ……..(2)
(1) + (2) ⇒ 2X = 18
⇒ X = 9
(1) – (2) ⇒ 2Y = 8
⇒ Y = 4
∴ The other two observations are 4, 9.
![]()
Question 5.
The arithmetic mean and standard deviation of a set of 9 items are 43 and 5 respectively. If an item of value 63 is added to that set, find the new mean and standard deviation of 10 item set given.
Solution:
Given the arithmetic mean of 9 items is 43
∴ \(\bar{x}=\frac{1}{9} \sum_{i=1}^9 x_i=43\)
⇒ Σxi = 387
If an item of value 63 is added to that set then
Σyi = Σxi + 63
= 387 + 63
= 450
∴ \(\bar{y}=\frac{1}{10} \sum y_i\)
= \(\frac{1}{10}\) (450)
= 45
∴ New mean = 45
Given the standard deviation of 9 items is 5
⇒ σ = 5
⇒ σ2 = 25
⇒ \(\frac{1}{9} \sum_{i=1}^9\left(x_i-\bar{x}\right)^2\)
⇒ \(\sum_{i=1}^9\left(x_i-43\right)^2\) = 225 ……(1)
New variance σ2 = \(\frac{1}{10} \sum_{i=1}^{10}\left(y_i-45\right)^2\)
= \(\frac{1}{10}\)[(x1 – 45)2 + (x2 – 45)2 + …….. + (x9 – 45)2 + (63 – 45)2]
Since first 9 items are same i.e, xi = yi, i = 1, 2, 3, …….., 9
= \(\frac{1}{10}\) [(xi – 43 – 2)2 + (x2 – 43 – 2)2 + …… + (x9 – 43 – 2)2 + 324]
= \(\frac{1}{10}\) [(xi – 43)2 + 4 – 2 . 2 . (x1 – 43) + (x2 – 43)2 + 4 – 2 . 2 . (x2 – 43) + …. (x9 – 43)2 + 4 – 2 . 2 . (x9 – 43) + 324]
= \(\frac{1}{10}\) [(xi – 43)2 + (x2 – 43)2 + ……. + (x9 – 43)2 + 36 – 4{x1 – 43 + x2 – 43 + …….. + x9 – 43} + 324]
= \(\frac{1}{10}\) [225 + 36 – 4(x1 + x2 + …. + x9 – 387) + 324]
= \(\frac{1}{10}\) [225 + 36 – 4(387 – 387) + 324]
= \(\frac{1}{10}\) [585]
= 58.5
New standard deviation σ = √58.5 = 7.65