Students get through Maths 2B Important Questions Inter 2nd Year Maths 2B Differential Equations Important Questions which are most likely to be asked in the exam.
Intermediate 2nd Year Maths 2B Differential Equations Important Questions
Question 1.
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = ex – y + x2 e-y [Mar. 06; May 05]
Solution:

Question 2.
x\(\frac{\mathrm{dy}}{\mathrm{dx}}\) – y = 2x2 sec22x [May 11]
Solution:
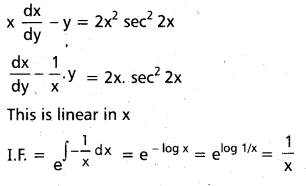
![]()
Question 3.
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) + y tan x = sin x. [T.S. Mar. 16]
Solution:
I.F. = \(e^{\int \tan x d x}\) = elog sec x = sec x
y.sec x = \(\int\) sin x . sec x dx = \(\int\) tan x dx
= log sec x + c
Question 4.
cos x . \(\frac{\mathrm{dy}}{\mathrm{dx}}\) + y sin x = sec2x [Mar. 14]
Solution:
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) + tan x . y = sec3x
I.F. = e\(\int\)tan x dx = elog sec x = sec x
y . sec x = \(\int\) sec4x dx = \(\int\) (1 + tan2 x) sec2 x
dx = tan x + \(\frac{\tan ^{3} x}{3}\) + c
Question 5.
(x + y + 1)\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 1.
Solution:
\(\frac{\mathrm{dx}}{\mathrm{dy}}\) = x + y + 1
\(\frac{\mathrm{dx}}{\mathrm{dy}}\) = x + y + 1
I.F. = e\(\int\) -dy = e-y
x . e-y = \(\int\) e-y (y + 1)dy
= – (y + 1) . e-y + \(\int\) e-y . dy
= – (y + 1) e-y – e-y
= – (y + 2) e-y + c
x = – (y + 2) + c. e-y
![]()
Question 6.
Find the order and degree of r
\(\frac{\mathrm{d}^{3} \mathrm{~y}}{\mathrm{dx}^{3}}\) – 3 (\(\frac{\mathrm{dy}}{\mathrm{dx}}\)) – ex = 4. [Mar. 14]
Solution:
The equation is a polynomial in \(\frac{\mathrm{dy}}{\mathrm{dx}}\) and \(\frac{\mathrm{d}^{3} \mathrm{~y}}{\mathrm{dx}^{3}}\).
The exponent of \(\frac{\mathrm{d}^{3} \mathrm{~y}}{\mathrm{dx}^{3}}\) is 2.
Hence the degree is 2.
\(\frac{\mathrm{d}^{3} \mathrm{~y}}{\mathrm{dx}^{3}}\) is the highest order derivative occuring in the equation.
Order of the equation is 3.
Question 7.
x\(\frac{1}{2}\)(\(\frac{\mathrm{d}^{2} \mathrm{~y}}{\mathrm{dx}^{2}}\))\(\frac{1}{3}\) + x . \(\frac{\mathrm{dy}}{\mathrm{dx}}\) + y = 0 has order 2 and degree 1. Prove. [T.S. Mar. 15]
Solution:
The given equation can be written as
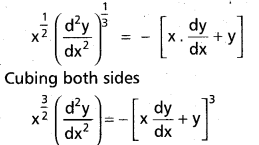
∴ The order of the equation is 2 and its degree is 1.
Question 8.
Find the order and degree of \(\left(\frac{d^{2} y}{d x^{2}}+\left(\frac{d y}{d x}\right)^{3}\right)^{\frac{6}{5}}\) = 6y [Mar. 16; May 11]
Solution:
Given equation is \(\left(\frac{d^{2} y}{d x^{2}}+\left(\frac{d y}{d x}\right)^{3}\right)^{\frac{6}{5}}\) = 6y
i.e., \(\frac{\mathrm{d}^{2} \mathrm{~y}}{\mathrm{dx}^{2}}\) + (\(\frac{\mathrm{dy}}{\mathrm{dx}}\))3 = (6y)\(\frac{5}{6}\)
Order = 2, degree = 1
![]()
Question 9.
Solve \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(\frac{x(2 \log x+1)}{\sin y+y \cos y}\) [Mar. 08]
Solution:
Given equation can be written as
(sin y + y cos y) dy = x(2 log x + 1) dx
\(\int\) sin y dy + \(\int\) y cos y dy = \(\int\) 2x log x dx + \(\int\) x dx
\(\int\) sin y dy + y sin y – \(\int\) sin y dy = x2 log x – \(\int\) x2 . \(\frac{1}{x}\) dx + \(\int\) x dx + c
y sin y = x2 log x + c
Question 10.
(xy2 + x) dx + (yx2 + y) dy = 0. [A.P. Mar. 15, 07]
Solution:
(xy2 + x) dx + (yx2 + y) dy = 0
x(y2 + 1) dx + y (x2 + 1) dy = 0
Dividing with (1 + x2) (1 + y2)
\(\frac{x d x}{1+x^{2}}\) + \(\frac{y d x}{1+y^{2}}\) = 0
Integrating
\(\int \frac{x d x}{1+x^{2}}+\int \frac{y d y}{1+y^{2}}=0\)
\(\frac{1}{2}\)[(log (1 + x2) + log (1 + y2)] = log c
log (1 + x2) (1 + y2) = 2 log c = log c2
Solution is(1 + x2) (1 + y2) = k when k = c2.
Question 11.
sin-1 (\(\frac{\mathrm{dy}}{\mathrm{dx}}\)) = x + y [Mar. 07]
Solution:
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = sin (x + y)
x + y = t
1 + \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(\frac{\mathrm{dt}}{\mathrm{dx}}\)
\(\frac{\mathrm{dt}}{\mathrm{dx}}\) – 1 = sin t
\(\frac{\mathrm{dt}}{\mathrm{dx}}\) = 1 + sin t
\(\frac{d t}{1+\sin t}\) = dx
Integrating both sides we get
\(\int \frac{d t}{1+\sin t}=\int d x\)
\(\int \frac{1-\sin t}{\cos ^{2} t} d t=x+c\)
\(\int\) sec2 t dt = \(\int\) tan t . sec t dt = x + c
tan t – sec t = x + c
⇒ tan (x + y) – sec (x + y) = x + c
![]()
Question 12.
(x2 – y2) \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = xy [May 11]
Solution:

= log y + c
\(\frac{-x^{2}}{2 y^{2}}\) = (log y + c)
-x2 = 2y2 (c + log y)
⇒ Solution is x2 + 2y2 (c + log y) = 0.
Question 13.
Solve : x dy = (y + x cos2 \(\frac{y}{x}\)) dx.
Solution:
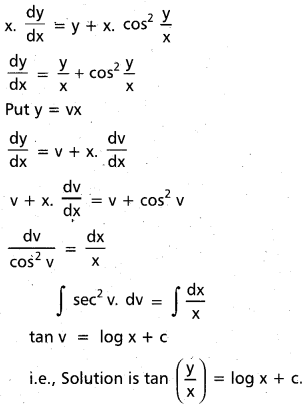
Question 14.
(2x + y + 1) dx + (4x + 2y – 1) dy = 0 [T.S. Mar. 15]
Solution:

2v + log (v – 1) = 3x + c
2v – 3x + log (v – 1) = c
2(2x + y) – 3x + log (2x + y – 1) = c
4x + 2y – 3x + log (2x + y – 1) = c
Solution is x + 2y + log (2x + y – 1) = c
![]()
Question 15.
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) + y tan x = cos3x [May 11]
Solution:
I.F. = e\(\int\) tan x dx = elog sec x = sec x
y . sec x = \(\int\) sec x. cos3 x dx
= \(\int\) cos2x dx
= \(\frac{1}{2}\) \(\int\) (1 + cos 2x) dx
= \(\frac{1}{2}\) (x + \(\frac{sin2x}{2}\)) + c
\(\frac{2 y}{\cos x}\) = x + sin x . cos x + c
Solution is 2y = x cos x + sin x . cos2 x + c . cos x^
Question 16.
(1 + x2) \(\frac{\mathrm{dy}}{\mathrm{dx}}\) + y = etan-1 x [May 07] [A.P. Mar. 16] [T.S. Mar. 15]
Solution:
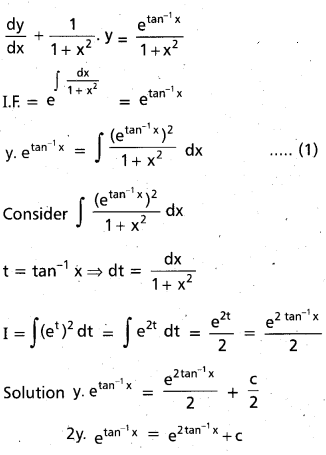
Question 17.
Solve (1 + y2)dx = (tan-1y – x)dy. [A.P. Mar. 15]
Solution:
Given \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(\frac{\tan ^{-1} y-x}{1+y^{2}}\)
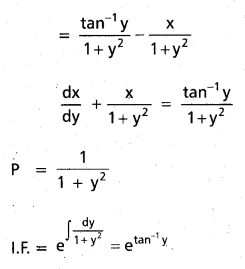

Question 18.
(x2 – y2)dx – xy dy = 0 [May 06]
Solution:
(x2 – y2)dx – xy dy = 0
(x2 – y2)dx = xy . dy
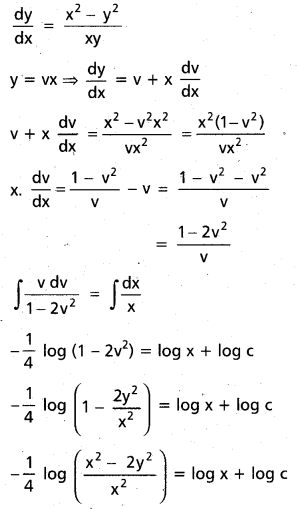
–\(\frac{1}{4}\) [log (x2 – 2y2) – log x2] = log x + log c
–\(\frac{1}{4}\) log (x2 – 2y2) + \(\frac{1}{4}\) . 2 log x = log x + log c
–\(\frac{1}{4}\) log (x2 – 2y2) = \(\frac{1}{2}\) log x + log c
– log (x2 – 2y2) = – 2 log x – 4 log c
log (x2 – 2y2) = – 2 log x + log k where
k = \(\frac{1}{c^{4}}\) = log \(\frac{\mathrm{k}}{\mathrm{x}^{2}}\)
x2 – 2y2 = \(\frac{\mathrm{k}}{\mathrm{x}^{2}}\)
Solution is x2 (x2 – 2y2) = k
![]()
Question 19.
\(\frac{d y}{d x}=\frac{3 y-7 x+7}{3 x-7 y-3}\) [T.S. Mar. 16]
Solution:
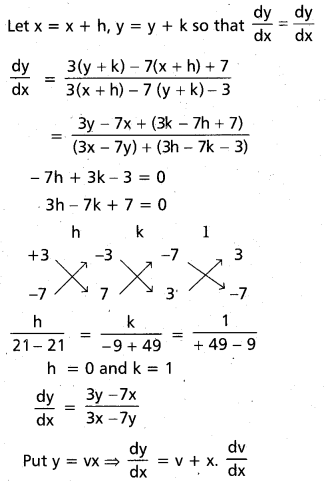

= 3ln (v – 1) – 3ln (v + 1) – 7ln (v + 1) – 7ln (v – 1)
14ln x – ln c = – 10 ln (v + 1) – 4 ln (v – 1)
ln (v + 1)5 + ln (v – 1)2 + ln x7 = ln c
(v + 1)5 . (v – 1)2 . x7 = c
(\(\frac{y}{x}\) + 1)5 (\(\frac{y}{x}\) – 1)2 . x7 = c
(y – x)2 (y + x)5 = c
[y – (x – 1)]2 (y + x – 1)5 = c
Solution is [y – x + 1]2 (y + x – 1)5 = c.
![]()
Question 20.
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) (x2y3 + xy) = 1 [Mar. 11]
Solution:
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = xy + x2y3
This is Bernoulli’s equation
x-2 . \(\frac{\mathrm{dx}}{\mathrm{dy}}\) – \(\frac{1}{x}\) . y = y3
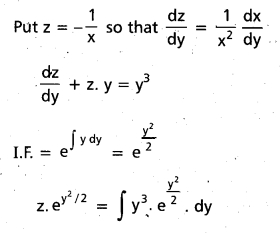
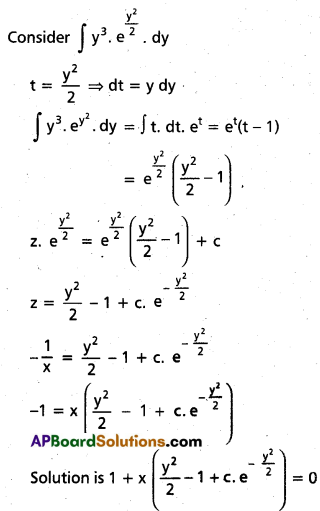
Question 21.
Form the differential equation corresponding to y = A cos 3x + B sin 3x, where A and B are parameters. [AP Mar. 15]
Solution:
We have y = A cos 3x + B sin 3x
Differentiating w.r.to x
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = -3A sin 3x + 3B cos 3x
Differentiating again w.r.to. x
\(\frac{\mathrm{d}^{2} \mathrm{~y}}{\mathrm{dx}^{2}}\) = -9A cos 3x – 9B sin 3x
= – 9(A cos 3x + B sin 3x)
= -9y .
is \(\frac{\mathrm{d}^{2} \mathrm{~y}}{\mathrm{dx}^{2}}\) + 9y = 0.
Alternate method:
Eliminating A, B from the equation
y = A cos 3x + B sin 3x
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = – 3A sin 3x + 3B sin cos 3x
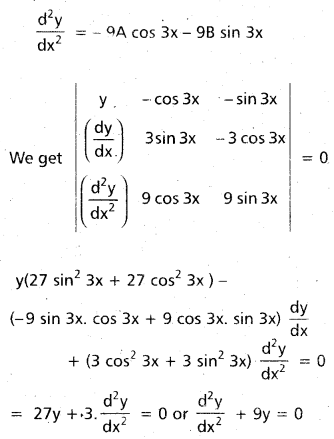
This is the required differential equation.
Question 22.
Solve (x2 + y2) dx = 2xy dy [A.P. Mar. 16]
Solution:
Given equation can be written as

log cx(1 – v2 = log 1
cx (1 – v2) = 1
cx (1 – \(\frac{\mathrm{y}^{2}}{\mathrm{x}^{2}}\)) = 1
c(x2 – y2) = x is the required solution.
![]()
Question 23.
Give the solution of x sin2 \(\frac{y}{x}\) dx = y dx – x dy which passes through the point (1, \(\frac{\pi}{4}\)). [Mar. 14]
Solution:
The given equation can be written as
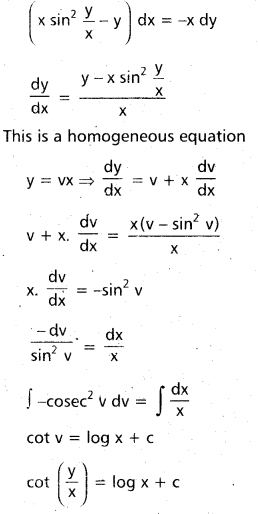
The given curve passes through (1, \(\frac{\pi}{4}\))
cot \(\frac{\pi}{4}\) = log 1 + c
1 = 0 + c ⇒ c = 1
Solution is cot \(\frac{y}{x}\) = log x + 1
Question 24.
Find the order and degree of the differential equation \(\frac{\mathrm{d}^{2} \mathrm{y}}{\mathrm{dx}^{2}}\) = – p2y.
Solution:
The given equation is a polynomial equation in \(\frac{\mathrm{d}^{2} \mathrm{y}}{\mathrm{dx}^{2}}\)
Hence the degree is 1
\(\frac{\mathrm{d}^{2} \mathrm{y}}{\mathrm{dx}^{2}}\) is the highest order derivative occuring in the equation.
Its order is 2.
Question 25.
Find the order and degree of
(\(\frac{\mathrm{d}^{3} \mathrm{y}}{\mathrm{dx}^{3}}\))2 – 3 (\(\frac{\mathrm{dy}}{\mathrm{dx}}\))2 – ex = 4 [Mar. 14]
Solution:
The equation is a polynomial in \(\frac{\mathrm{dy}}{\mathrm{dx}}\) and \(\frac{\mathrm{d}^{3} \mathrm{y}}{\mathrm{dx}^{3}}\).
The exponent of \(\frac{\mathrm{d}^{3} \mathrm{y}}{\mathrm{dx}^{3}}\) is 2.
Hence the degree is 2.
\(\frac{\mathrm{d}^{3} \mathrm{y}}{\mathrm{dx}^{3}}\) is the highest õrder derivative occuring in the equation.
Order of the equation is 3.
![]()
Question 26.
x\(\frac{1}{2}\)(\(\frac{\mathrm{d}^{2} \mathrm{y}}{\mathrm{dx}^{2}}\))\(\frac{1}{3}\) + x . \(\frac{\mathrm{dy}}{\mathrm{dx}}\) + y = 0 has order 2 and degree 1. Prove. [T.S. Mar. 15]
Solution:
The given equation can be written as
x\(\frac{1}{2}\)(\(\frac{\mathrm{d}^{2} \mathrm{y}}{\mathrm{dx}^{2}}\))\(\frac{1}{3}\) = -[x . \(\frac{\mathrm{dy}}{\mathrm{dx}}\) + y]
Cubing both sides
x\(\frac{3}{2}\)(\(\frac{\mathrm{d}^{2} \mathrm{y}}{\mathrm{dx}^{2}}\)) = -[x . \(\frac{\mathrm{dy}}{\mathrm{dx}}\) + y]3
∴ The order of the equation is 2 and its degree is 1.
Question 27.
Find the order and degree of \(\left(\frac{d^{2} y}{d x^{2}}+\left(\frac{d y}{d x}\right)^{3}\right)^{\frac{6}{5}}\) = 6y [A.P. Mar. 16; May 11]
Solution:
Given equation is \(\left(\frac{d^{2} y}{d x^{2}}+\left(\frac{d y}{d x}\right)^{3}\right)^{\frac{6}{5}}\) = 6y
i.e., \(\frac{\mathrm{d}^{2} \mathrm{y}}{\mathrm{dx}^{2}}\) + (\(\frac{\mathrm{dy}}{\mathrm{dx}}\))3 = (6y)\(\frac{5}{6}\)
Order = 2; degree = 1
Question 28.
Find the order of the differential equation corresponding to y = c(x – c)2, where c is an arbitrary constant.
Solution:
The given differential equation is
y = c(x – c)2
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 2c(x – c)
∴ Order of the differential equation is 1.
![]()
Question 29.
Find the order of the differential equation corresponding to y = Aex + Be3x + Ce5x; (A, B, C being parameters) is a solution.
Solution:
Required differential equation is obtained by eliminating A, B, C from y,
\(\frac{\mathrm{dy}}{\mathrm{dx}}\), \(\frac{\mathrm{d}^{2} \mathrm{y}}{\mathrm{dx}^{2}}\), \(\frac{\mathrm{d}^{3} \mathrm{y}}{\mathrm{dx}^{3}}\)
Highest order deviation = \(\frac{\mathrm{d}^{3} \mathrm{y}}{\mathrm{dx}^{3}}\)
Order of the differential equation = 3.
Question 30.
Form the differential equation corresponding to y = cx – 2c2, where c is a parameter.
Solution:
Given y = cx – 2c2 ………………. (1)
Differentiating (1) w.r.to
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = c
Substituting in (1), required differential equation is
y = x . (\(\frac{\mathrm{dy}}{\mathrm{dx}}\)) – 2(\(\frac{\mathrm{dy}}{\mathrm{dx}}\))2
Question 31.
Form the differential equation corresponding to y = A cos 3x + B sin 3x, where A and B are parameters. [A.P. Mar. 15]
Solution:
We have y = A cos 3x + B sin 3x
Differentiating w.r.to x
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = -3A sin 3x + 3B cos 3x
Differentiating again w.r.to. x
\(\frac{\mathrm{d}^{2} \mathrm{y}}{\mathrm{dx}^{2}}\) = -9A cos 3x – 9B sin 3x
= -9(A cos 3x + B sin 3x)
= -9y
is \(\frac{\mathrm{d}^{2} \mathrm{y}}{\mathrm{dx}^{2}}\) + 9y = 0
![]()
Alternate Method:
Eliminating A, B from the equation
y = A cos 3x + B sin 3x
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = -3A sin 3x = 3B sin cos 3x
\(\frac{\mathrm{d}^{2} \mathrm{y}}{\mathrm{dx}^{2}}\) = -9A cos 3x – 9B sin 3x
We get \(\left|\begin{array}{ccc}
y & -\cos 3 x & -\sin 3 x \\
\left(\frac{d y}{d x}\right) & 3 \sin 3 x & -3 \cos 3 x \\
\left(\frac{d^{2} y}{d x^{2}}\right) & 9 \cos 3 x & 9 \sin 3 x
\end{array}\right|\) = 0
y(27 sin2 3x + 27 cos2 3x) – (-9 sin 3x. cos 3x + 9 cos 3x. sin 3x) \(\frac{\mathrm{dy}}{\mathrm{dx}}\) + (3 cos2 3x + 3 sin2 3x) \(\frac{\mathrm{d}^{2} \mathrm{y}}{\mathrm{dx}^{2}}\) = 0
= 27y + 3 .\(\frac{\mathrm{d}^{2} \mathrm{y}}{\mathrm{dx}^{2}}\) = 0 or \(\frac{\mathrm{d}^{2} \mathrm{y}}{\mathrm{dx}^{2}}\) + 9y = 0
This is the required differential equation.
Question 32.
Form the differential equation corresponding to the family of circles of radius r given by (x – a)2 + (y – b)2 = r2, where a and b are parameters.
Solution:
We have (x – a)2 + (y – b)2 = r2 ………………… (1)
Differentiating (1) w.r.to x
2(x – a) + 2(y – b) \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 0 ……………….. (2)
Differentiating (2) w.r.to. x
1 + (y – b) \(\frac{\mathrm{d}^{2} \mathrm{y}}{\mathrm{dx}^{2}}\) + (\(\frac{\mathrm{dy}}{\mathrm{dx}}\))2 = 0 ……………… (3)
From (2) (x – a) = -(y – b) \(\frac{\mathrm{dy}}{\mathrm{dx}}\)
Substituting in (1), we get

i.e., \(r^{2}\left(\frac{d^{2} y}{d x^{2}}\right)^{2}=\left(1+\left(\frac{d y}{d x}\right)^{2}\right)^{3}\)
Which is the required differential equation.
Question 33.
Form the differential equation corresponding to the family of circles passing through the origin and having centres on Y-axis.
Solution:
The equation of the family of all circles passing through the origin and having centres on Y—axis is
x2 + y2 + 2hy = 0 …………………. (1)
Where h is a parameter
Differentiating (1) w.r. to x
2x + 2y . \(\frac{\mathrm{dy}}{\mathrm{dx}}\) + 2h . \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 0
or x + y . \(\frac{\mathrm{dy}}{\mathrm{dx}}\) + h . \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 0
-(x + y . \(\frac{\mathrm{dy}}{\mathrm{dx}}\)) = h. \(\frac{\mathrm{dy}}{\mathrm{dx}}\)
h = \(\frac{-\left(x+y \cdot \frac{d y}{d x}\right)}{\frac{d y}{d x}}\)
Substituting in (1)
We get x2 + y2 – 2y \(\frac{\left(x+y \cdot \frac{d y}{d x}\right)}{\frac{d y}{d x}}\) = 0
x2 . \(\frac{\mathrm{dy}}{\mathrm{dx}}\) + y2 . \(\frac{\mathrm{dy}}{\mathrm{dx}}\) – 2xy – 2y2 . \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 0
or (x2 – y2) \(\frac{\mathrm{dy}}{\mathrm{dx}}\) – 2xy = 0
This is the required differential equation.
![]()
Question 34.
Express the following differential equations in the form f(x) dx + g(y) dy = 0.
i) \(\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{1+\mathrm{y}^{2}}{1+\mathrm{x}^{2}}\)
Solution:
⇒ \(\frac{d y}{1+y^{2}}=\frac{d x}{1+x^{2}}\)
\(\frac{d x}{1+x^{2}}-\frac{d y}{1+y^{2}}\) = 0
ii) y – x \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = a (y2 + \(\frac{\mathrm{dy}}{\mathrm{dx}}\))
Solution:
y – x . \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = ay2 + a. \(\frac{\mathrm{dy}}{\mathrm{dx}}\)
y – ay2 = (x + a) . \(\frac{\mathrm{dy}}{\mathrm{dx}}\)
\(\frac{d x}{x+a}=\frac{d y}{y-a y^{2}}\)
iii) \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = ex-y + x2 e-y
Solution:
Multiplying in the ey
ey . \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = ex + x2
ey . dy = (ex + x2) dx
(ex + x2) dx – ey . dy = 0
iv) \(\frac{\mathrm{dy}}{\mathrm{dx}}\) + x2 = x2 e3y
Solution:
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = x2 . e3y – x2 = x2(e3y – 1)
\(\frac{d y}{e^{3 y}-1}\) = x2 dx ⇒ x2 dx – \(\frac{d y}{e^{3 y}-1}\) = 0
or x2dx + \(\frac{1}{\left(1-e^{3 y}\right)}\) . dy = 0
Question 35.
Find the general solution of
x + y\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 0.
Solution:
Given equation is x + y . \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 0
x . dx + y . dy = 0
Integrating \(\frac{x^{2}}{2}\) + \(\frac{y^{2}}{2}\) = c
or x2 + y2 = 2 c = c’
Question 36.
Find the general solution of \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = ex+y.
Solution:
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = ex+y = ex . ey
\(\frac{d y}{e^{y}}\) = ex dx
\(\int\) e-y dy = \(\int\) ex dx
e – e-y = ex
or ex + e-y = c is the required solution.
![]()
Question 37.
Solve y2 – x \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = a(y + \(\frac{\mathrm{dy}}{\mathrm{dx}}\))
Solution:
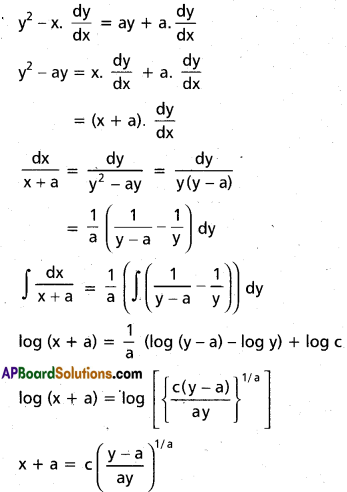
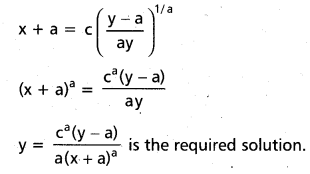
Question 38.
Solve \(\frac{d y}{d x}=\frac{y^{2}+2 y}{x-1}\)
Solution:
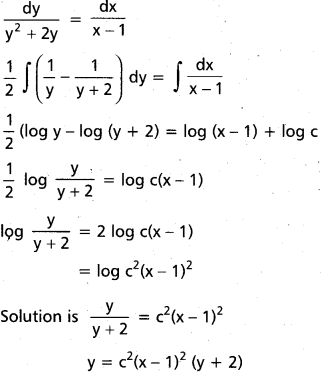
Question 39.
Solve \(\frac{d y}{d x}=\frac{x(2 \log x+1)}{\sin y+y \cos y}\) [Mar. 08]
Solution:
Given equation can be written as
(sin y + y cos y) dy = x(2 log x + 1) dx
\(\int\) sin y dy + \(\int\) y cos y dy = \(\int\) 2x log x dx + \(\int\) x dx
\(\int\) sin y dy + y sin y – \(\int\) sin y dy = x2 log x – \(\int\) x2 . \(\frac{1}{x}\) dx + \(\int\) x dx + c
y sin y = x2 log x + c
![]()
Question 40.
Find the equation of the curve whose slope, at any point, (x, y) is \(\frac{y}{x^{2}}\) and which satisfies the condition y = 1 when x = 3.
Solution:

Question 41.
Solve y(1 + x) dx + x(1 + y) dy = 0
Solution:
The given equation can be written as
\(\frac{(1+x)}{x}\) dx + \(\frac{(1+y)}{y}\) . dy = 0
\(\int\) (1 + \(\frac{1}{x}\))dx + \(\int\) (1 + \(\frac{1}{y}\)) dy = 0
x + log x + y + log y = c
x + y + log (xy) = c is the required solution.
Question 42.
Solve \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = sin (x + y) + cos (x + y)
Solution:
Put x + y = t

x = log (1 + tan \(\frac{t}{2}\)) + c
But t = x + y
Solution is x = log (1 + tan \(\frac{x+y}{2}\)) + c
Question 43.
Solve (x – y)2 \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = a2
Solution:
Put x – y = t
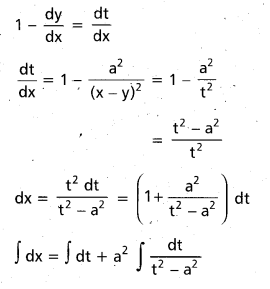
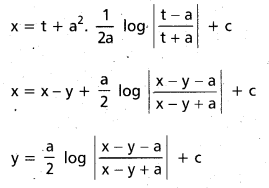
![]()
Question 44.
Solve \(\sqrt{1+x^{2}} \sqrt{1+y^{2}}\) dx + xy dy = 0
Solution:
Given equation can be written as

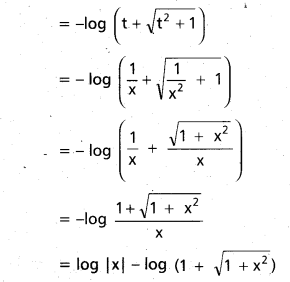

Question 45.
Solve \(\frac{d y}{d x}=\frac{x-2 y+1}{2 x-4 y}\)
Solution:
Put x – 2y = t
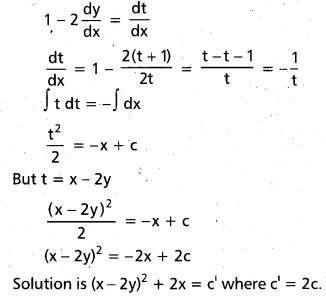
Question 46.
Solve \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(\sqrt{y-x}\)
Solution:
Put y – x = t2

Question 47.
Solve \(\frac{\mathrm{dy}}{\mathrm{dx}}\) + 1 = ex+y
Solution:
Put t = x + y
\(\frac{\mathrm{dt}}{\mathrm{dx}}\) = 1 + \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = et
\(\int \frac{d t}{e^{t}}=\int d x\)
\(\int\) e-t dt = \(\int\) dx
-e-t = x + c
x + e-t + c = 0
Solution is x + e-(x+y) + c = 0
![]()
Question 48.
Solve \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = (3x + y + 4)2
Solution:
Put t = 3x + y + 4
\(\frac{\mathrm{dt}}{\mathrm{dx}}\) = 3 + \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 3 + t2
\(\frac{\mathrm{dt}}{\mathrm{t}^{3}+3}\) = dx
\(\int \frac{d t}{t^{2}+3}=\int d x\)
\(\frac{1}{\sqrt{3}}\) tan-1 (\(\frac{t}{\sqrt{3}}\)) = x + c
Solution is \(\frac{1}{\sqrt{3}}\) tan-1 (\(\frac{3 x+y+4}{\sqrt{3}}\)) = x + c
Question 49.
Solve \(\frac{\mathrm{dy}}{\mathrm{dx}}\) – x tan (y – x) = 1
Solution:
Put y – x = t
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) – 1 = \(\frac{\mathrm{dt}}{\mathrm{dx}}\)
\(\frac{\mathrm{dt}}{\mathrm{dx}}\) = x tan t + 1 – 1 = x tan t
\(\frac{\mathrm{dt}}{\tan \mathrm{t}}\) = x dx
\(\int\) cot dt = \(\int\) x dx
log |sin | = \(\frac{x^{2}}{2}\) + c
Solution is log |sin (y – x)| = \(\frac{x^{2}}{2}\) + c
Question 50.
Show that f(x, y) = 1 + ex/y is a homogeneous function of x and y.
Solution:
f(kx, xy) = 1 + ekx/ky = 1 + ex/y = f(x, y)
f(x, y) is a homogeneous function degree 0.
Question 51.
Show that f(x, y) = x\(\sqrt{x^{2}+y^{2}}\) – y2 is a homogeneous function of x and y.
Solution:
f(kx, ky) = kx\(\sqrt{k^{2} x^{2}+k^{2} y^{2}}\) – k2y2.
= k2 (x\(\sqrt{x^{2}+y^{2}}\) – y2) = k2 f(x, y)
f(x, y) is a homogeneous function of degree 2.
![]()
Question 52.
Show that f(x, y) = x – y log y + y log x is a homogeneous function of x and y.
Solution:
f(kx, ky) = kx – ky. log ky + ky log (kx)
= k(x – y log (ky) + y log kx)
= k(x – y log k – y log y + y log k + y log x)
= k(x – y log y + y log x)
= k. f(x, y)
f(x, y) is a homogeneous function of degree 1.
Question 53.
Express (1 + ex/y)dx + ex/y (1 – \(\frac{x}{y}\)) dy = 0 in the form \(\frac{\mathrm{dx}}{\mathrm{dy}}\) = F (\(\frac{x}{y}\))
Solution:
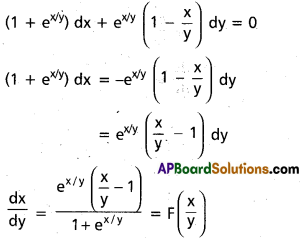
Question 54.
Express (x\(\sqrt{x^{2}+y^{2}}\) – y2) dx + xy dy = 0 in the form \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = F (\(\frac{x}{y}\))
Solution:
Given equation is
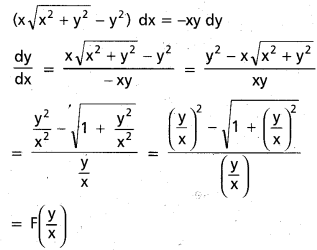
Question 55.
Express \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(\frac{y}{x+y e^{\frac{-2 x}{y}}}\) in the form \(\frac{\mathrm{dx}}{\mathrm{dy}}\) = F (\(\frac{x}{y}\))
Solution:
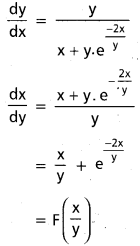
![]()
Question 56.
Solve \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(\frac{y^{2}-2 x y}{x^{2}-x y}\)
Solution:
The given equation is a homogeneous equation.
Put y = vx

\(\log v \sqrt{2 v-3}=-3 \log \frac{x}{c}=\log \frac{c^{3}}{x^{3}}\)

Question 57.
Solve (x2 + y2) dx = 2xy dy [A.P. Mar. 16]
Solution:
Given equation can be written as
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(\frac{x^{2}+y^{2}}{2 x y}\)
This is a homogeneous function
Put y = vx
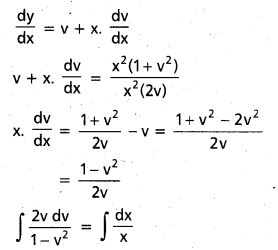
-log (1 – v2) = log x + log c
= log cx
log cx + log (1 – v2) = 0
log cx(1 – v2) = log 1
cx (1 – v2) = 1
cx (1 – \(\frac{\mathrm{y}^{2}}{\mathrm{x}^{2}}\)) = 1
c(x2 – y2) = x is the required solution.
![]()
Question 58.
Solve xy2 dy – (x3 + y3) dx = 0.
Solution:
Given equation is xy2 dy = (x3 + y2) dx
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(\frac{x^{3}+y^{3}}{x y^{2}}\)
This is a homogeneous equation.
Put y = vx

Question 59.
Solve \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(\frac{x^{2}+y^{2}}{2 x^{2}}\)
Solution:
This is a homogeneous equation.
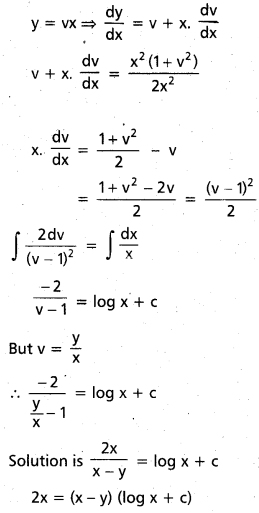
Question 60.
Solve x sec (\(\frac{y}{x}\)) . (y dx + x dy) = y cosec (\(\frac{y}{x}\)) . (x dy – y dx)
Solution:
This given equation can be written as

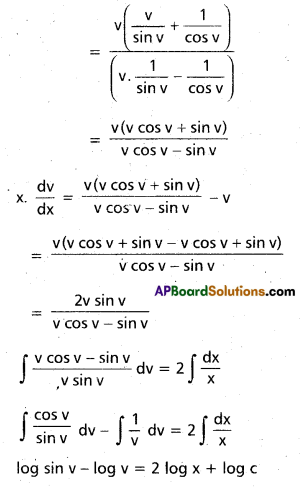
log(\(\frac{\sin v}{v}\)) = log cx2
\(\frac{\sin v}{v}\) = cx2
\(\frac{x}{y}\) sin (\(\frac{y}{x}\)) = cx2
Solution is sin(\(\frac{y}{x}\)) = cxy.
![]()
Question 61.
Give the solution of x sin2 \(\frac{y}{x}\) dx = y dx – x dy which passes through the point (1, \(\frac{\pi}{4}\)). [Mar. 14]
Solution:
The given equation can be written as
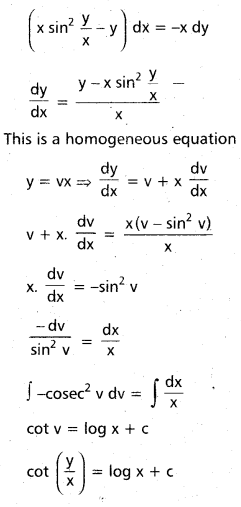
The given curve passes through (1, \(\frac{\pi}{4}\))
cot \(\frac{\pi}{4}\) = log 1 + c
1 = 0 + c ⇒ c = 1
Solution is cot \(\frac{y}{x}\) = log x + 1
Question 62.
Solve (x3 – 3xy2) dx + (3x2y – y3) dy = 0
Solution:
(x3 – 3xy2) dx = -(3x2y – y3) dy


Question 63.
Transform the following two differential equations Into linear form.
x log x \(\frac{\mathrm{dy}}{\mathrm{dx}}\) + y = 2 log x
Solution:
Given equation can be written as
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) + \(\frac{1}{x \log x}\) . y = \(\frac{2}{x}\)
This is of the form \(\frac{\mathrm{dy}}{\mathrm{dx}}\) + Py = Q
![]()
Question 64.
(x + 2y3) \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = y
Solution:
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(\frac{x+2 y^{3}}{y}\) = \(\frac{x}{y}\) + 2y2
\(\frac{\mathrm{dx}}{\mathrm{dy}}\) – \(\frac{1}{y}\) . x = 2y2
This is of the form \(\frac{\mathrm{dx}}{\mathrm{dy}}\) + Px = Q.
Question 65.
(cos x) \(\frac{\mathrm{dy}}{\mathrm{dx}}\) + y sin x = tan x
Solution:
Given equation can be written as
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) + y(tan x) = (tan x) (sec x)
P = tan x ⇒ \(\int\) P dx = \(\int\) tan x dx = log sec x
I.F. = e\(\int\) log sec x = sec x
Question 66.
Solve (2x – 10y3) \(\frac{\mathrm{dy}}{\mathrm{dx}}\) + y = o
Solution:
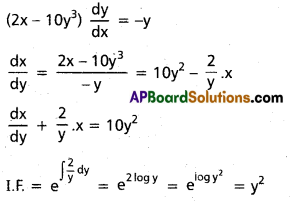
Question 67.
Solve (1 + x2) \(\frac{\mathrm{dy}}{\mathrm{dx}}\) + 2xy – 4x2 = 0
Solution:
Given equation can be written as
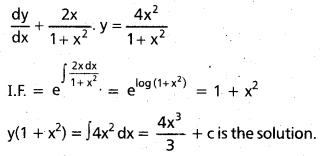
![]()
Question 68.
Solve \(\frac{1}{x}\) \(\frac{\mathrm{dy}}{\mathrm{dx}}\) + y . ex = e(1 – x)ex
Solution:
Given equation can be written as
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) + (x.ex) . y = x . e(1 – x)ex
I.F. = e\(\int\).ex dx = e(x – 1) ex
y . e(x – 1) ex = \(\int\) x dx
= \(\frac{\mathrm{x}^{2}}{2}\) + c
2y. e(x – 1) ex = x2 + 2c is the required solution.
Question 69.
Solve sin2 x. \(\frac{\mathrm{dy}}{\mathrm{dx}}\) + y = cot x
Solution:
Given equation can be written as
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) + y cosec2 x = cot x . cosec2 x
I.F. = e\(\int\) cosec2 x dx = e-cot x
y . e-cot x = \(\int\) e-cot x . cosec2 x. cot x dx ……………… (1)
Consider \(\int\) e-cot x . cosec2 x . cot x dx
Put -cot x = t ⇒ cosec2 x dx = dt
(1) becomes y . et = \(\int\) -t. et dt
= -(t – 1) et + c
y . e-cot x = -(-cot x – 1) e-cot x + 1
= (cot x + 1) e-cot x + c is the required solution.
![]()
Question 70.
Find the solution of the equation
x(x – 2) \(\frac{\mathrm{dy}}{\mathrm{dx}}\) – 2(x – 1)y = x3(x – 2)
which satisfies the condition that y = 9 when x = 3.
Solution:
The given equation can be written as

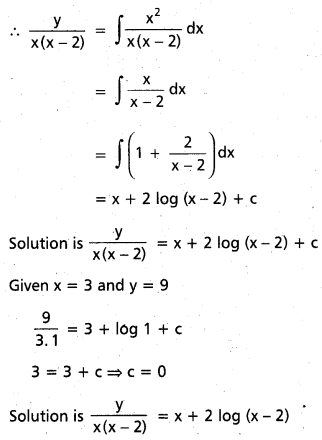
Question 71.
Solve (1 + y2)dx = (tan-1y – x)dy. [A.P. Mar. 15]
Solution:
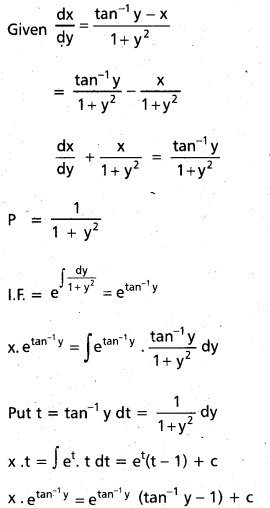
is the solution.