Inter 1st Year Maths 1A Mathematical Induction Solutions Ex 2(a)

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Mathematical Induction Solutions Exercise 2(a) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Mathematical Induction Solutions Exercise 2(a)

Using mathematical induction, prove each of the following statements for all n ∈ N.

Question 1.
1² + 2² + 3² + …… + n² = \(\frac{n(n+1)(2 n+1)}{6}\)
Solution:
Let p(n) be the given statement:
1² + 2² + 3² + ….. + n² = \(\frac{n(n+1)(2 n+1)}{6}\)
Since 1² = \(\frac{(1)(1+1)(2 \times 1+1)}{6}\)
⇒ 1 = 1 the formula is true for n = 1
i.e., p(1) is true.
Assume the statement p(n) is true for n = k
i.e., 1² + 2² + 3² + …… + 1k² = \(\frac{k(k+1)(2 k+1)}{6}\)
We show that the formula is true for n = k + 1
i.e., We show that p(k + 1) = \(\frac{(k+1)(k+2)(2 k+3)}{6}\)
(Where p(k) = 1² + 2² + 3² + … + k²)
We observe that
p(k + 1) = 1² + 2² + 3² + …… + (k)² + (k + 1)² = p(k) + (k + 1)²
Since p(k) = \(\frac{k(k+1)(2 k+1)}{6}\)
We have p(k + 1) = p(k) + (k + 1)²

∴ The formula holds for n = k + 1
∴ By the principle of mathematical induction, p(n) is true for all n ∈ N
i.e., the formula 1² + 2² + 3² + ……. + n² = \(\frac{n(n+1)(2 n+1)}{6}\) for all n ∈ N

Question 2.
2.3 + 3.4 + 4.5 + …… up to n terms = \(\frac{n\left(n^{2}+6 n+11\right)}{3}\)
Solution:
The nth term in the given series is (n + 1) (n + 2)
Let p(n) be the statement:
2.3 + 3.4 + 4.5 + …… + (n + 1) (n + 2) = \(\frac{n\left(n^{2}+6 n+11\right)}{3}\)
and let S(n) be the sum on the left-hand side.
Since S(1) = 2.3 = \(\frac{(1)(1+6+11)}{3}\) = 6
∴ The statement is true for n = 1
Assume that the statement p(n) is true for n = k
i.e., S(k) = 2.3 + 3.4 + …… + (k + 1) (k + 2) = \(\frac{k\left(k^{2}+6 k+11\right)}{3}\)
We show that the statement is true for n = k + 1
i.e., We show that S(k + 1) = \((k+1)\left[\frac{(k+1)^{2}+6(k+1)+11}{3}\right]\)
We observe that
S(k + 1) = 2.3 + 3.4 + 4.5 + + (k + 1) (k + 2) + (k + 2) (k + 3)
= S(k) + (k + 2) (k + 3)

∴ The statement holds for n = k + 1
∴ By the principle of mathematical induction,
p(n) is true for all n ∈ N
i.e., 2.3 + 3.4 + 4.5 + ……. + (n + 1) (n + 2) = \(\frac{n\left(n^{2}+6 n+11\right)}{3}\)

Question 3.
\(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\ldots+\frac{1}{(2 n-1)(2 n+1)}=\frac{n}{2 n+1}\)
Solution:
Let p(n) be the statement:
\(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\ldots+\frac{1}{(2 n-1)(2 n+1)}=\frac{n}{2 n+1}\)
and let S(n) be the sum on the L.H.S.
Since S(1) = \(\frac{1}{1.3}=\frac{1}{1(2+1)}=\frac{1}{1.3}\)
∴ P(1) is true.
Assume that the statement p(n) is true for n = k
i.e., S(k) = \(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\ldots+\frac{1}{(2 k-1)(2 k+1)}\) = \(\frac{k}{2 k+1}\)
We show that the statement p(n) is true for n = k + 1
i.e., we show that s(k + 1) = \(\frac{k+1}{2(k+1)+1}\)
We observe that

∴ The statement holds for n = k + 1
∴ By the principle of mathematical induction,
p(n) is true for all n ∈ N
i.e., \(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\ldots+\frac{1}{(2 n-1)(2 n+1)}=\frac{n}{2 n+1}\)

Question 4.
4³ + 8³ + 12³ + …… up to n terms = 16n²(n + 1)².
Solution:
4, 8, 12,….. are in A.P., whose nth term is (4n)
Let p(n) be the statement:
4³ + 8³ + 12³ + ………. + (4n)³ = 16n²(n + 1)²
and S(n) be the sum on the L.H.S.
S(1) = 4³ = 16(1²) (1 + 1)² = 16(4) = 64 = 4³
∴ p(1) is true
Assume that the statement p(n) is true for n = k
i.e., S(k) = 4³ + 8³ + (12)³ + …… + (4k)³ = 16k²(k + 1)²
We show that the statement is true for n = k + 1
i.e., We show that S(k + 1) = 16(k + 1)² (k + 2)²
We observe that
S(k + 1) = 4³ + 8³ + 12³ + …… + (4k)³ + [4(k + 1)]³
= S(k) + [4(k + 1)]³
= 16k² (k + 1)² + 4³ (k + 1)³
= 16(k + 1)² [k² + 4(k + 1)]
= 16(k + 1)² [k² + 4k + 4]
= 16(k + 1)² (k + 2)²
= 16(k + 1)² \((\overline{k+1}+1)^{2}\)
∴ The formula holds for n = k + 1
∴ By the principle of mathematical induction,
p(n) is true for all n ∈ N
(i.e.,) 4³ + 8³ + 12³ + …… + (4n)³ = 16n²(n + 1)²

Question 5.
a + (a + d) + (a + 2d) + ……. up to n terms = \(\frac{n}{2}\) [2a + (n – 1)d]
Solution:
Let p(n) be the statement:
a + (a + d) + (a + 2d) + …… + [a + (n – 1)d] = \(\frac{n}{2}\) [2a + (n – 1)d]
and let the sum on the L.H.S. is denoted by S(n)
Since S(1) = a = \(\frac{1}{2}\) [2a + (1 – 1)d] = a
∴ p(1) is true.
Assume that the statement is true for n = k
(i.e.,) S(k) = a + (a + d) + (a + 2d) + ……. + [a + (k – 1)d] = \(\frac{k}{2}\) [2a + (k – 1 )d]
We show that the statement is true for n = k + 1
(i.e.,) we show that S(k + 1) = \(\left(\frac{k+1}{2}\right)[2 a+k d]\)
We observe that
S(k + 1) = a + (a + d) + (a + 2d) + …… + [a + (k – 1)d] + (a + kd)
= S(k) + (a + kd)
= \(\frac{k}{2}\) [2a + (k – 1)d] + (a + kd)
= \(\frac{k[2 a+(k-1) d]+2(a+k d)}{2}\)
= \(\frac{1}{2}\) [2ak + k(k – 1)d + 2a + 2kd]
= \(\frac{1}{2}\) [2a(k + 1) + k(k – 1 + 2)d]
= \(\frac{1}{2}\) (k + 1)(2a + kd)
∴ The statement holds for n = k + 1
∴ By the principle of mathematical inductions,
p(n) is true for all n ∈ N
(i.e.,) a + (a + d) + (a + 2d) + …… + [a + (n – 1)d] = \(\frac{n}{2}\) [2a + (n – 1)d]

Question 6.
a + ar + ar² + ……… up to n terms = \(\frac{a\left(r^{n}-1\right)}{r-1}\); r ≠ 1
Solution:
Let p(n) be the statement:
a + ar + a.r² + …… + a. r^n-1 = \(\frac{a\left(r^{n}-1\right)}{r-1}\), r ≠ 1
and let S(n) be the sum on the L.H.S
Since S(1) = a = \(\frac{a\left(r^{1}-1\right)}{r-1}\) = a
∴ p(1) is true
Assume that the statement is true for n = k
(i.e) S(k) = a + ar + ar² + ……… + a . r^k-1 = \(\frac{a\left(r^{k}-1\right)}{r-1}\)
We show that the statement is true for n = k + 1
(i.e) S(k + 1) = \(\frac{a\left(r^{k+1}-1\right)}{r-1}\)
Now S(k + 1) = a + ar + ar² + ……. + a r^k-1 + ar^k
= S(k) + a . r^k

∴ The statement holds for n = k + 1
∴ By the principle of mathematical induction,
p(n) is true for all n ∈ N
(i.e) a + ar + ar² + ……. + a.r^n-1 = \(\frac{a\left(r^{n}-1\right)}{r-1}\), r ≠ 1

Question 7.
2 + 7 + 12 + ……. + (5n – 3) = \(\frac{n(5 n-1)}{2}\)
Solution:
Let p(n) be the statement:
2 + 7 + 12 + ……. + (5n – 3) = \(\frac{n(5 n-1)}{2}\)
and let S(n) be the sum on the L.H.S
Since S(1) = 2 = \(\frac{1(5 \times 1-1)}{2}=\frac{4}{2}\) = 2
∴ p(1) is true
Assume that the statement is true for n = k
(i.e) S(k) = 2 + 7 + 12 + …….. + (5k – 3) = \(\frac{k(5 k-1)}{2}\)
We have to show that S(k + 1) = \(\frac{(k+1)(5 k+4)}{2}\)
We observe that S(k + 1) = 2 + 7 + 12 + ……. + (5k – 3) + (5k + 2)
= S(k) + (5k + 2)
= \(\frac{k(5 k-1)}{2}\) + (5k + 2)
= \(\frac{5 k^{2}-k+2(5 k+2)}{2}\)
= \(\frac{1}{2}\) [5k² + 9k + 4]
= \(\frac{1}{2}\) (k + 1) (5k + 4)
= \(\frac{1}{2}\) (k + 1) [5(k + 1) – 1]
∴ p(k + 1) is true
∴ By the principle of mathematical induction,
p(n) is true for all n ∈ N.
(i.e.,) 2 + 7 + 12 + …… + (5n – 3) = \(\frac{n(5 n-1)}{2}\)

Question 8.
\(\left(1+\frac{3}{1}\right)\left(1+\frac{5}{4}\right)\left(1+\frac{7}{9}\right) \ldots \ldots\left(1+\frac{2 n+1}{n^{2}}\right)\) = (n + 1)²
Solution:
Let p(n) be the statement:
\(\left(1+\frac{3}{1}\right)\left(1+\frac{5}{4}\right)\left(1+\frac{7}{9}\right) \ldots \ldots\left(1+\frac{2 n+1}{n^{2}}\right)\) = (n + 1)²
and let S(n) be the product on the LHS
since S(1) = 1 + 3 = 4 = (1 + 1)² = 4
∴ P(a) 4 time for n = 1
Assume that p(n) is true for n = k

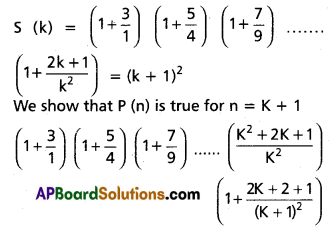
= (k + 1)² + 2k + 3
= k² + 2k + 1 + 2k + 3
= k² + 4k + 4
= (k + 2)²
= (k + 1 + 1)²
∴ P(n) is true for n = k + 1
By the principle of Mathematical Induction,
p(n) is true & n ∈ N

Question 9.
(2n + 7) < (n + 3)²
Solution:
Let p (n) be the statement
When n = 1, 9 < 16
∴ p(n) is true for n = 1
Assume p (n) is true for n = k
(2k + 7) < (k + 3)²
We show that p(n) is true for n = k + 1
2(k + 1) + 7 = 2k + 7 + 2
< (k + 3)² + 2
< k² + 6k + 9 + 2 + 2k + 5 – 2k – 5
< (k + 4)² – (2k + 5)
< (k + 4)²
< (k + 1 + 3)²
∴ p(n) is true for n = k + 1
By the principle of Mathematical Induction
p(n) is true ∀ n ∈ N

Question 10.
1² + 2² + …… + n² > \(\frac{n^{3}}{3}\)
Solution:
Let P(n) by the statement
when n = 1, 1 > \(\frac{1}{3}\)
∴ p(n) is true for n = 1
Assume p (n) is true for n = k
1² + 2² + …… + k² > \(\frac{k^{3}}{3}\)
We show that p(n) is true for n = k + 1

∴ p(n) is true for n = k + 1
By the principle of Mathematical Induction,
p(n) is true ∀ n ∈ N

Question 11.
4ⁿ – 3n – 1 is divisible by 9.
Solution:
Let p(n) be the statement:
4ⁿ – 3n – 1 is divisible by 9
Since 4¹ – 3(1) – 1 = 0 is divisible by 9.
The statement is true for n = 1
Assume that p(n) is true for n = k
(i.e) 4^k – 3k – 1 is divisible by 9
Then 4^k – 3k – 1 = 9t, for some t ∈ N ……..(1)
Show that the statement p(n) is true for n = k + 1
(i.e.,) we show that S(k + 1) = 4^k+1 – 3(k+1) – 1 is divisible by 9
From (1), we have
4^k = 9t + 3k + 1
∴ S(k + 1) = 4 . 4^k – 3(k + 1) – 1
= 4(9t + 3k + 1) – 3k – 3 – 1
= 4(9t) + 9k
= 9[4t + k]
Hence s(k + 1) is divisible by 9
Since 4t + k is an integer
∴ 4^k+1 – 3(k+1) – 1 is divisible by 9
∴ The statement is true for n = k + 1
∴ By the principle of mathematical induction,
p(n) is true for all n ∈ k
(i.e.,) 4ⁿ – 3n – 1 is divisible by 9

Question 12.
3 . 5²ⁿ⁺¹ + 2³ⁿ⁺¹ is divisible by 17.
Solution:
Let p(n) be the statement:
3. 5²ⁿ⁺¹ + 2³ⁿ⁺¹ is divisible by 17
Since 3 . 5²⁽¹⁾⁺¹ + 2³⁽¹⁾⁺¹
= 3 . 5³ + 2⁴
= 3(125) + 16
= 375 + 16
= 391
= 17(23) is divisible by 17
∴ The statement is true for n = 1
Assume that the statement is true for n = k
(i.e) 3 . 5^2k+1 + 2^3k+1 is divisible by 17
Then 3 . 5^2k+1 + 2^3k+1 = 17t, for some t ∈ N ……..(1)
Show that the statement p(n) is true for n = k + 1
(i.e.,) We have to show that
\(\text { 3. } 5^{2(k+1)+1}+2^{3(k+1)+1}\) is divisible by 17
From (1) we have

Here 25t + 2^3k+1 is an integer
∴ \(\text { 3. } 5^{2(k+1)+1}+2^{3(k+1)+1}\) is divisible by 17
∴ The statement is true for n = k + 1
∴ By the principle of mathematical induction,
p(n) is true for all n ∈ N
(i.e.,) 3 . 5²ⁿ⁺¹ + 2³ⁿ⁺¹ is divisible by 17.

Question 13.
1.2.3 + 2.3.4 + 3.4.5 + ……. upto n terms = \(\frac{n(n+1)(n+2)(n+3)}{4}\)
Solution:
The nth term of the given series is (n) (n + 1) (n + 2)
Let p(n) be the statement:
1.2.3 + 2.3.4 + 3.4.5 +……. + (n) (n+1) (n+2) = \(\frac{n(n+1)(n+2)(n+3)}{4}\)
and S(n) be the sum on the L.H.S.
∵ S(1) = 1.2.3 = \(\frac{(1)(1+1)(1+2)(1+3)}{4}\) = 1.2.3
∴ p(1) is true
Assume that the statement p(n) is true for n = k
(i.e) S(k) = 1.2.3 + 2.3.4 + 3.4.5 + ……. + k(k + 1) (k + 2) = \(\frac{k(k+1)(k+2)(k+3)}{4}\)
We show that the statement is true for n = k + 1
(i.e) We show that S(k + 1) = \(\frac{(k+1)(k+2)(k+3)(k+4)}{4}\)
We observe that
S(k + 1) = 1.2.3 + 2.3.4 + …… + k(k + 1) (k + 2) + (k + 1) (k + 2) (k + 3)
= S(k) + (k + 1) (k + 2) (k + 3)
= \(\frac{k(k+1)(k+2)(k+3)}{4}\) + (k + 1)(k + 2)(k + 3)
= (k + 1)(k + 2)(k + 3) \(\left(\frac{k}{4}+1\right)\)
= \(\frac{(k+1)(k+2)(k+3)(k+4)}{4}\)
∴ The statement holds for n = k + 1
∴ By the principle of mathematical induction,
p(n) is true for all n ∈ N
(i.e.,) 1.2.3 + 2.3.4 + 3.4.5 + ……. + (n)(n + 1)(n + 2) = \(\frac{n(n+1)(n+2)(n+3)}{4}\)

Question 14.
\(\frac{1^{3}}{1}+\frac{1^{3}+2^{3}}{1+3}+\frac{1^{3}+2^{3}+3^{3}}{1+3+5}\) + …. up to n terms = \(\frac{n}{24}\) [2n² + 9n + 13]
Solution:
The nth term of the given series is \(\frac{1^{3}+2^{3}+3^{3}+\ldots .+n^{3}}{1+3+5+\ldots+(2 n-1)}\)
Let p(n) be the statement :

and let S(n) be the sum on the L.H.S.
∵ S(1) = \(\frac{1^{3}}{1}=\frac{1}{24}(2+9+13)=1=\frac{1^{3}}{1}\)
∴ p(1) is true
Assume that p(k) is true
(i.e.,) S(k) = \(\frac{1^{3}}{1}+\frac{1^{3}+2^{3}}{1+3}+\ldots+\frac{1^{3}+2^{3}+\ldots \pm k^{3}}{1+3+\ldots+(2 k-1)}\) = \(\frac{k}{24}\) [2k² + 9k + 13]
We show that p(k + 1) is true
(i.e,) we show that


∴ The statement holds for n = k + 1
∴ By the principle of mathematical induction,
p(n) is true for all n
(i.e.,) \(\frac{1^{3}}{1}+\frac{1^{3}+2^{3}}{1+3}+\ldots+\frac{1^{3}+2^{3}+\ldots \ldots+n^{3}}{1+3+\ldots+(2 n-1)}\) = \(\frac{n}{24}\) [2n² + 9n + 13]

Question 15.
1² + (1² + 2²) + (1² + 2² + 3²) + ……. up to n terms = \(\frac{n(n+1)^{2}(n+2)}{12}\)
Solution:
The nth term of the given series is (1² + 2² + 3² + …… + n²)
Let p(n) be the statement:
1² + (1² + 2²) + (1² + 2² + 3²) + ……. + (1² + 2² + …… + n²) = \(\frac{\mathrm{n}(\mathrm{n}+1)^{2}(\mathrm{n}+2)}{12}\)
and the sum on the LH.S. is denoted by S(n).
Since S(1) = 1² = \(\frac{1(1+1)^{2}(1+2)}{12}\) = 1 = 1²
∴ p(1) is true.
Assume that the statement is true for n = k
(i.e.,) S(k) = 1² + (1² + 2²) + ……. + (1² + 2² + ……. + k²)
= \(\frac{k(k+1)^{2}(k+2)}{12}\)
We show that S(k + 1) = \(\frac{(k+1)(k+2)^{2}(k+3)}{12}\)
We observe that


∴ The statement holds for n = k + 1.
∴ By the principle of mathematical induction,
p(n) is true for all n ∈ N.
(i.e.,) 1² + (1² + 2²) + (1² + 2² + 3²) + …….. (1² + 2² + ………. + n²) = \(\frac{n(n+1)^{2}(n+2)}{12}\)