Use these Inter 1st Year Maths 1B Formulas PDF Chapter 9 Differentiation to solve questions creatively.
Intermediate 1st Year Maths 1B Differentiation Formulas
→ f'(x) = \({Lt}_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\)
→ Δy = f(x + Δx) – f(x)
→ \(\frac{d}{d x}\) (u ± v) = \(\frac{d u}{d x} \pm \frac{d v}{d x}\)
→ \(\frac{d}{d x}\)(uv) = u\(\frac{d v}{d x}\) + v\(\frac{d u}{d x}\)
→ \(\frac{d}{d x}\)(uvw) = uv\(\frac{d w}{d x}\) + uw\(\frac{d v}{d x}\) + vw\(\frac{d u}{d x}\)
→ \(\frac{d}{d x}\left(\frac{u}{v}\right)=\frac{v \frac{d u}{d x}-u \frac{d v}{d x}}{v^{2}}\)
→ \(\frac{d}{d x}\)(xn) = nxn-1
→ \(\frac{d}{d x}\)(x) = 1
→ \(\frac{d}{d x}\)(sin x) = cos x
→ \(\frac{d}{d x}\)(cos x) = -sin x
→ \(\frac{d}{d x}\)(tan x) = sec2x
→ \(\frac{d}{d x}\)(cot x) = -cosec2x
![]()
→ \(\frac{d}{d x}\)(sec x) = sec x tan x
→ \(\frac{d}{d x}\)(cosec x) = -cosec x cot x
→ \(\frac{d}{d x}\)(sin-1x) = \(\frac{1}{\sqrt{1-x^{2}}}\)
→ \(\frac{d}{d x}\)(cos-1x) = –\(\frac{1}{\sqrt{1-x^{2}}}\)
→ \(\frac{d}{d x}\)(tan-1x) = \(\frac{1}{1+x^{2}}\)
→ \(\frac{d}{d x}\)(cot-1x) = –\(\frac{1}{1+x^{2}}\)
→ \(\frac{d}{d x}\)(sec-1x) = \(\frac{1}{|x| \sqrt{x^{2}-1}}\)
→ \(\frac{d}{d x}\)(cosec-1x) = \(\frac{-1}{|x| \sqrt{x^{2}-1}}\)
→ \(\frac{d}{d x}\)(ex) = ex
→ \(\frac{d}{d x}\)(ax) = axlog a
→ \(\frac{d}{d x}\)(log x) = \(\frac{1}{x}\)
→ \(\frac{d}{d x}\)|x| = \(\frac{|x|}{x}\)
→ \(\frac{d}{d x}\)(log |x|) = \(\frac{1}{x}\)
→ \(\frac{d}{d x}\)(xx) = xx(1 + log x)
→ \(\frac{d}{d x}\)(sinh x) = cosh x
→ \(\frac{d}{d x}\)(cosh x) = sinh x
→ \(\frac{d}{d x}\)(tanh x) = sech2x
→ \(\frac{d}{d x}\)(coth x) = -cosech2x
→ \(\frac{d}{d x}\)(sech x) = -sech x tanh x
→ \(\frac{d}{d x}\)(cosech x) =-cosech x coth x
→ \(\frac{d}{d x}\)(sinh-1x) = \(\frac{1}{\sqrt{1+x^{2}}}\)
→ \(\frac{d}{d x}\)(cosh-1x) = \(\frac{1}{\sqrt{x^{2}-1}}\)
→ \(\frac{d}{d x}\)(tanh-1x) = \(\frac{1}{1-x^{2}}\)
→ \(\frac{d}{d x}\)coth-1x) = \(\frac{1}{1-x^{2}}\)
![]()
→ \(\frac{d}{d x}\)(sech-1x) = \(\frac{-1}{|x| \sqrt{1-x^{2}}}\)
→ \(\frac{d}{d x}\)(cosech-1x) = \(\frac{-1}{|x| \sqrt{x^{2}+1}}\)
→ \(\frac{\mathrm{d} y}{\mathrm{dx}}=\frac{\mathrm{d} y}{\mathrm{du}} \cdot \frac{\mathrm{d} u}{\mathrm{dx}}\)
→ \(\frac{d}{d x}\left(\frac{1}{x^{n}}\right)=\frac{-n}{x^{n+1}}\)
Parametric Differentiation
If x =g (t) and y =h (t) are two functions of t then y may be expressed as a function of x, say y = f(x), by eliminating the real variable t. Such a variable t is called a parameter. Also, x and y are said to be defined parametrically. The equations x =g (t), y =h (t) are called the parametric equations of y = f(x).
The process of finding \(\frac{d y}{d x}\) when x and y are defined parametrically, is called parametric differentiation.
Theorem:
Let x = g(t) and y = h(t) be two differentiable functions of t such that g-1 exists.
Then \(\frac{d y}{d x}=\left(\frac{d y}{d t}\right) /\left(\frac{d x}{d t}\right)\)
Implicit Differentiation
Let y be an implicit function of x defined by a relation of the type f(x, y) = 0. Then the method of finding the derivative \(\frac{d y}{d x}\) of such an implicitly defined function is called implicit differentiation.
In this method, we differentiate f(x, y) = 0 w.r.t x (treating y as a function of x) to get an equation of the type F(x,y, \(\frac{d y}{d x}\)) = 0.
By solving this equation we find \(\frac{d y}{d x}\).
Logarithmic Differentiation
If a given function is of the form y = f(x) g(x) where f(x) and g(x) are differentiable functions of x, we apply logarithms to transform it into a suitable form so as to find . This method of finding \(\frac{d y}{d x}\) is called logarithmic differentiation.
This method is also useful in finding the derivatives of functions which are products of a number of functions.
Theorem:
If y = f(x) g(x) where f(x) and g(x) are differentiable functions then \(\frac{d y}{d x}\) = f (x)g(x)[\(\frac{g(x)}{f(x)}\)f'(x) + g'(x)log f(x)]
Proof:
y = f(x)g(x), f(x) > 0
logy = g(x) log f(x)
Differentiating both sides w.r.t x,
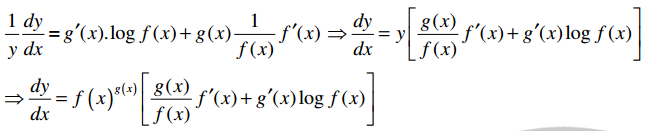
Method of Substitution:
In the case of inverse trigonometric functions with typical arguments direct differentiation of the function to find the derivative may become quite tedious and cumbersome. In such cases the derivative can be easily found by using proper trigonometric substitutions and transformations. The application of this method is illustrated in the following examples.
Derivative Of One Function W.R.T Another Function
Let f(x) and g(x) be two differentiable functions with a common domain of differentiability then the derivative of u = f(x) w.r.t v = g(x) is given by
\(\frac{d u}{d v}=\left(\frac{d u}{d x}\right) /\left(\frac{d v}{d x}\right)=\frac{f^{\prime}(x)}{g^{\prime}(x)}\)
![]()
Second Order Derivatives:
If y = f(x) is a differentiable function of x then its derivative f ‘(x) is a function of x. If f ‘(x) is a differentiable function then its derivative is called the second order derivative of f(x). It is denoted by f ”(x) and f”(x) = \({Lt}_{h \rightarrow 0} \frac{f^{\prime}(x+h)-f^{\prime}(x)}{h}\)
f ”(x) is also denoted by f”(x) = \({Lt}_{h \rightarrow 0} \frac{f^{\prime}(x+h)-f^{\prime}(x)}{h}\) or \(\frac{d^{2} f}{d x^{2}}\) or D2y or y” or y2.
Derivatives of Inverse Trignometric Functions
If y = sin-1x, x ∈ (-1, 1) then \(\frac{d y}{d x}=\frac{1}{\sqrt{1-x^{2}}}\)
Proof:
y = sin-1x ⇒ x = sin y
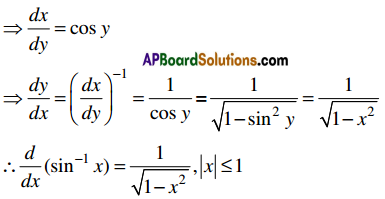
Theorem:
y = cos-1x, x ∈(-1, 1) then \(\frac{d y}{d x}=\frac{-1}{\sqrt{1-x^{2}}}\)
Theorem:
y = Tan-1x, x ∈(-1, 1) then \(\frac{d y}{d x}=\frac{1}{1+x^{2}}\)
Proof:
y = Tan-1x ⇒ x = tan y where x ∈ R and y ∈ \(\left(\frac{-\pi}{2}, \frac{\pi}{2}\right)\)
x = tan y ⇒ \(\frac{d y}{d x}\) = sec2y = 1 + tan2y = 1 + x2 > 0
∴ \(\frac{d y}{d x}=\left(\frac{d x}{d y}\right)^{-1}=\frac{1}{1+x^{2}}\), x ∈ R
Theorem:
y = Cot-1x, x ∈ R then \(\frac{d y}{d x}=\frac{-1}{1+x^{2}}\)
Theorem:
y = Sec-1x, x ∈ (-∞, -1) ∪ (1, ∞) then \(\frac{d y}{d x}=\frac{1}{|x| \sqrt{x^{2}-1}}\)
Theorem:
\(\frac{d}{d x}\)(Cosec-1x) = \(\frac{-1}{|x| \sqrt{x^{2}-1}}\), |x| > 1
Derivatives of Hyperbolic Functions
1. \(\frac{d}{d x}\)(sinh x) = cosh x, x ∈ R
\(\frac{d}{d x}\)(sinh x) = \(\frac{d}{d x}\left(\frac{e^{x}-e^{-x}}{2}\right)\)
= \(\frac{1}{2}\)[\(\frac{d}{d x}\)(ex) – \(\frac{d}{d x}\)(e-x] = \(\frac{1}{2}\)[ex + e-x]
= cosh x, exists for all x.
2. \(\frac{d}{d x}\)(cosh x) = sinh x, x ∈ R
\(\frac{d}{d x}\)(cosh x) = \(\frac{d}{d x}\left(\frac{e^{x}+e^{-x}}{2}\right)\)
= \(\frac{1}{2}\)[\(\frac{d}{d x}\)(ex) + \(\frac{d}{d x}\)(e-x] = \(\frac{1}{2}\)[ex – e-x] = sinh x, ∀x
3. \(\frac{d}{d x}\)(tanh x) = sech2x, x ∈ R
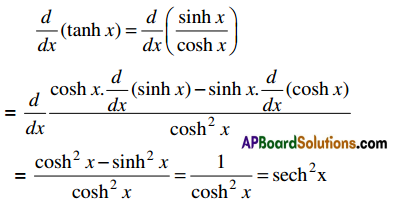
4. \(\frac{d}{d x}\)(Coth x) = -cosec2x, x ∈ R

= \(\frac{-1}{\sinh ^{2} x}\) = -cosech2x exists for all x ≠ 0
![]()
Derivatives of Inverse Hyperbolic Functions:
1. \(\frac{d}{d x}\)(sinh-1x) = \(\frac{1}{\sqrt{1+x^{2}}}\), x ∈ R
Let y = sinh-1x, x, y ∈ R
Then x = sinh y, sinh y is differentiable for all y ∈ R
\(\frac{d x}{d y}\) = cosh y and cosh y > 0 ∀ x ∈ R
\(\frac{d y}{d x}=\left(\frac{d x}{d y}\right)^{-1}=\frac{1}{\cosh y}=\frac{1}{\sqrt{1+\sinh ^{2} y}} .=\frac{1}{\sqrt{1+x^{2}}}\) exists
\(\frac{d}{d x}\)(sinh-1x) = \(\frac{1}{\sqrt{1+x^{2}}}\), x ∈ R
2. \(\frac{d}{d x}\)(cosh-1x) = \(\frac{1}{\sqrt{x^{2}-1}}\), x ∈ (1, ∞)
3. \(\frac{d}{d x}\)(tanh-1x) = \(\frac{1}{1-x^{2}}\), |x| < 1
Let y = Tanh-1x, x ∈ (-1, 1), y ∈ R
Then x = tanhy. Tanh y is differetniable on R
∴ \(\frac{d x}{d y}\) = sech2 ⇒ \(\frac{d y}{d x}=\frac{1}{{sech}^{2} y}=\frac{1}{1-\tanh ^{2} y}=\frac{1}{1-x^{2}}\) exists for all x ∈ (-1, 1)
4. \(\frac{d}{d x}\)(coth-1x) = \(\frac{1}{1-x^{2}}\), |x| > 1
5. \(\frac{d}{d x}\)(sech-1x) = \(\frac{-1}{x \sqrt{1-x^{2}}}\), x ∈ (0, 1)
6. \(\frac{d}{d x}\)(cosech-1x) = \(\frac{-1}{x \sqrt{1+x^{2}}}\), x ≠ 0
Let y = cosech-1x, x ∈ R – {0}, y ∈ R- {0}.
Then x = cosech y, cosech y is differentiable on R – {0}.
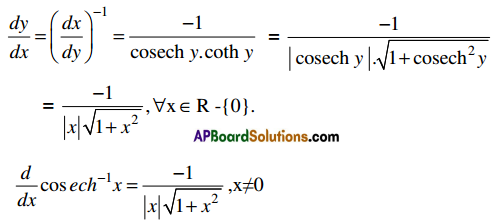
Partial Differentiation
Let u = f (x, y) be a function of two independent varaibles x and y.
(i) If \({Lt}_{h \rightarrow 0} \frac{f(x+h, y)-f(x, y)}{h}\) exists then the limit is called the partial derivatie of u with respect to x. It is denoted by \(\frac{\partial u}{\partial x}\) or ux or \(\frac{\partial f}{\partial x}\) or fx.
(ii) If \({Lt}_{k \rightarrow 0} \frac{f(x, y+k)-f(x, y)}{k}\) exists then the limit is called the partial derivative of u with respect to x. It is denoted by \(\frac{\partial u}{\partial y}\) or ux or \(\frac{\partial f}{\partial y}\) or fx.
∴ \(\frac{\partial u}{\partial x}={Lt}_{h \rightarrow 0} \frac{f(x+h, y)-f(x, y)}{h}\) and \(\frac{\partial u}{\partial y}=\underset{k \rightarrow 0}{L t} \frac{f(x, y+k)-f(x, y)}{k}\)
Note :
- The partial derivative of u w.r.t. x is the ordinary derivative of u w.r.t. x treating the other variable y (and its functions) as constant
- The partial derivative of u w.r.t. y is the ordinary derivative of u w.r.t. y treating the other variable x (and its functions) as constant.
Differentiation of Composite Functions
1. If V = g(U) and U = f(x, y) then (i) \(\frac{\partial V}{\partial x}=\frac{d V}{d U} \cdot \frac{\partial U}{\partial x}\) (ii) \(\frac{\partial V}{\partial y}=\frac{d V}{d U} \cdot \frac{\partial U}{\partial y}\)
2. If Z = f(x, y) and x = g(t); y = h(t) then \(\frac{d Z}{d t}=\frac{\partial Z}{\partial x} \cdot \frac{d x}{d t}+\frac{\partial Z}{\partial y} \frac{d y}{d t}\) is called the total differential coefficient of Z w.r.t. t.
3. If f(x, y) = c where c is constant, then \(\frac{d y}{d x}=-\frac{\partial f}{\partial x} / \frac{\partial f}{\partial y}\).
Partial Derivatives Of Second Order:
Definition : If U = f(x, y) then \(\frac{\partial \mathbf{U}}{\partial \mathrm{x}}, \frac{\partial \mathbf{U}}{\partial \mathbf{y}}\) are called the partial derivatives of first order and they are functions of x, y. The partial derivatives of \(\frac{\partial U}{\partial x}\) and \(\frac{\partial U}{\partial y}\), if they exist, are called the second order partial derivatives . They are denoted by
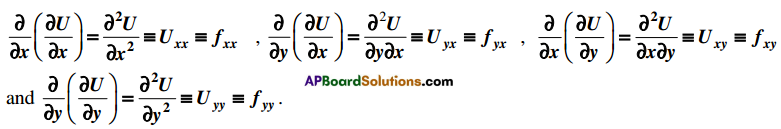
Homogeneous Functions:
A function u = f (x, y) is said to be a homogeneous function of degree n in the variables in x and y if f(kx, ky) = knf(x, y) for all k or f (x, y) = xn f\(\left(\frac{y}{x}\right)\) or f (x, y) = yn f\(\left(\frac{y}{x}\right)\).
Euler’S Theorem:
If u = f (x, y) is a homogeneous function of degree n in the variables x,y then x\(\frac{\partial \boldsymbol{U}}{\partial x}\) + y \(\frac{\partial \boldsymbol{U}}{\partial y}\) = nU
Proof:
Since u = f (x, y) is a homogeneous function of degree n, we have U = xng (y / x) where g (y / x) is function of y/x.
\(\frac{\partial \boldsymbol{U}}{\partial x}\) = xn.g'(y / x)\(\left(\frac{-y}{x^{2}}\right)\) + nxn-1 .g (y / x) ………(1)
and \(\frac{\partial \boldsymbol{U}}{\partial y}\) = xn .g'(y / x) \(\left(\frac{1}{x}\right)\)
x\(\frac{\partial \boldsymbol{U}}{\partial x}\) + y\(\frac{\partial \boldsymbol{U}}{\partial y}\) = x(x\(\left(\frac{-y}{x^{2}}\right)\)) + nxng(y/x) + yxn-1.g’9y/x)
= n.xn.g (y / x) == nU.
Note :
If U = f (x, y, z) is a homogeneous function of degree n in x,y,z then
x\(\frac{\partial U}{\partial x}\) + y\(\frac{\partial U}{\partial y}\) + z\(\frac{\partial U}{\partial z}\) = nU
![]()
Theorem:
If U = f (x, y) is a homogeneous function of degree n in x,y then x2\(\frac{\partial^{2} U}{\partial x^{2}}\) + 2xy\(\frac{\partial^{2} U}{\partial x \partial y}\) + y2\(\frac{\partial^{2} U}{\partial y^{2}}\) = n(n – 1)U .
Proof:
Since U = f (x, y) is a homogeneous function of degree n, by Euler’s theorem, we have
