Use these Inter 1st Year Maths 1A Formulas PDF Chapter 4 Addition of Vectors to solve questions creatively.
Intermediate 1st Year Maths 1A Addition of Vectors Formulas
Scalar :
A physical quantity that has only magnitude is called a scalar quantity. All the real numbers will be taken as scalars.
Vector :
A physical quantity that has both magnitude and direction.
e.g. : Velocity acceleration, force, momentum.
Position vector :
Let ‘O’ and ‘P be any points in space. Then OP is called the position vector of the point ‘P w.r.t. origin ‘O’.
Note : \(\overline{A B}\) = Position vector of B- position vector of A’
= \(\overline{O B}-\overline{O A}\)
Coinitial vector:
Vectors having the same initial point are called coinitial vectors.
e.g. : \(\overline{O A}, \overline{O B}, \overline{O C}\) etc.
Unit vector:
A vector whose magnitude is one-unit is called unit vector.
Unit vector in the direction of a is denoted by â = \(\frac{\bar{a}}{|a|}\).
For any non-zero vector \(\bar{a}=|\bar{a}|\) â.
![]()
Like vectors :
If two vectors are parallel and having the same direction then they are called like vectors.
Unlike vectors :
If two vectors are parallel and having Opposite direction then they are called unlike vectors.
The position vector of any point C on \(\overline{A B}\) can be taken as λ\(\bar{a}\) + µ\(\bar{a}\), where λ + µ = 1
Angle between vectors:
Let \(\overline{O A}=\bar{a}\) = a, \(\overline{O B}=\bar{a}\) = b be any two non – zero vectors, then angle AOB is defined as angle between vectors \(\bar{a}, \bar{b}\) and is denoted by \((\bar{a}, \bar{b})\) where 0 ≤ \((\bar{a}, \bar{b})\) ≤ 180°.
Addition of vectors (or) Parallelogram Law:
If \(\bar{a}, \bar{b}\) are the adjacent sides of a parallelogram the diagonals which is coinitial with \(\bar{a}, \bar{b}\) is given by \(\bar{a}+ \bar{b}\) and its magnitude is given by
\(|\bar{a}+\bar{b}|=\sqrt{|\bar{a}|^{2}+|\bar{b}|^{2}+2|\bar{a}||\bar{b}| \cos (\bar{a}, \bar{b})}\)
Triangle law:
If two vectors are represented in magnitude and direction by the two sides of a triangle taken in the same order, then their sum is represented by the third side taken in the reverse order.
Note : Addition of vectors is of 2 types :
- Commutative
- Associative.
(ie) (i) \(\bar{a}+\bar{b}=\bar{b}+\bar{a}\) and (ii) \((\bar{a}+\bar{b})+\bar{c}=\bar{a}+(\bar{b}+\bar{c})\)
Rule: \(|\bar{a}| \sim|\bar{b}| \leq|\bar{a}-\bar{b}| \leq|\bar{a}+\bar{b}| \leq|\bar{a}|+|\bar{b}|\)
Parallel (or) Collinear vector:
- Two vectors a, b are parallel or collinear, then a = λ. b, where ‘λ’ is a scalar.
- If \(\bar{a}\) = (a1, a2, a3), b = (b1, b2, b3) are parallel or collinear, then
\(\frac{a_{1}}{b_{1}}=\frac{a_{2}}{b_{2}}=\frac{a_{3}}{b_{3}}\)
Note : Zero vector is parallel to any vector. - If three points with position vectors a, b, c are to be collinear. The necessary and sufficient condition is that there exists scalars \(\bar{a}, \bar{b}, \bar{c}\) not all zero, such that
l\(\bar{a}\) + m\(\bar{b}\) + n\(\bar{c}\) = 0, l + m + n = 0. - If \(\bar{a}, \bar{b}, \bar{c}\) are non-zero, non-collinear vectors such that l\(\bar{a}\) + m\(\bar{b}\) + n\(\bar{c}\) = 0, then l = 0, m = 0, n = 0.
Linear combination of vectors :
A linear combination of the system of vectors \(\bar{a}_{1}, \bar{a}_{2}, \ldots, \bar{a}_{n}\) is a vector.
r = x1\(\bar{a}_{1}\) + x2\(\bar{a}_{2}\) + x3\(\bar{a}_{3}\) + ………………. + xn\(\bar{a}_{n}\)
where x1 x2, x3, ………………., xn are scalars.
Coplanar vectors:
If three or more vectors lie in the same plane (or) parallel to the same plane then they are called coplanar vectors. If one vector can be expressed as a linear combination of the remaining vectors, then the vectors are coplanar vectors.
If \(\bar{a}\) = x\(\bar{b}\) + y\(\bar{c}\), where x, y, are scalars, then \(\bar{a}, \bar{b}, \bar{c}\) are coplanar.
![]()
Linearly dependent system of vectors :
A system of vectors \(\bar{a}_{1}, \bar{a}_{2}, \bar{a}_{3}, \ldots \ldots, \bar{a}_{n}\) is said to
be linearly dependent, if there exists a system of scalars x1, x2, x3, ……………….., xn not all zero
such that
x1\(\bar{a}_{1}\) + x2\(\bar{a}_{2}\) + x3\(\bar{a}_{3}\) + ………………. + xn\(\bar{a}_{n}\) = \(\bar{0}\)
- The null vector is linearly dependent.
- Two collinear vectors are linearly dependent.
\(\bar{a}\) = λ\(\bar{b}\) ⇒ (1)\(\bar{a}\) + (-λ)\(\bar{b}\) = 0 - Any three coplanar vectors are linearly dependent.
\(\bar{a}\) = x\(\bar{b}\) + y\(\bar{c}\) ⇒ (1)\(\bar{a}\) + (-x)\(\bar{b}\) + (-y)\(\bar{c}\) = 0 - Any four vectors in space from a linearly dependent set of vectors.
Linearly independent system of vectors:
A system of vectors \(\bar{a}_{1}, \bar{a}_{2}, \bar{a}_{3}, \ldots \ldots, \bar{a}_{n}\) is said to be linearly independent, if x1\(\bar{a}_{1}\) + x2\(\bar{a}_{2}\) + x3\(\bar{a}_{3}\) + ………………. + xn\(\bar{a}_{n}\) = \(\bar{0}\) implies
- Two non-zero, non-collinear vectors are linearly independent.
- Any three non-coplanar vectors are linearly independent. If a, b, c are three non-coplanar vectors and \(\bar{r}\) be any other vector. Then there exists unique scalars x, y, z such that
\(\bar{r}\) = x\(\bar{a}\) + y\(\bar{b}\) + z\(\bar{c}\).
Right handed system of vectors:
Three non-coplanar vectors \(\bar{a}, \bar{b}, \bar{c}\) are said to form a – right-handed system, if the rotation is form \(\bar{a}\) to \(\bar{b}\) in anti-clockwise direction, through an angle less than 180° as seen from the terminal point of c.
If \(\bar{a}, \bar{b}, \bar{c}\) from RHS and \(\bar{b}, \overline{,}, \bar{a}\) and \(\bar{c}, \bar{a}, \bar{b}\) also from RHS.
Left-handed system of vectors:
Three non-coplanar vectors \(\bar{a}, \bar{b}, \bar{c}\) are said to form a left handed system. If the rotation is from \(\bar{a}\) to \(\bar{b}\) in clockwise direction through an angle less than 180° as seen from terminal point of c.
If \(\bar{a}, \bar{b}, \bar{c}\) are in RHS, then
\(\bar{b}, \overline{,}, \bar{a}\); \(\bar{c}, \bar{a}, \bar{b}\) also from R.H.S.
and \(-\bar{a}, \bar{b}, \bar{c} ; \bar{a},-\bar{b}, \bar{c} ; \bar{a}, \bar{b},-\bar{c}\) form L.H.S.
Direction cosines of a vector and direction ratios of a vector:
If α, β, γ are the angles made by a line with +ve directions of x, y, z axes respectively, then cos α, cos β, cos γ are known as the direction cosines of that line.
Generally the direction cosines are denoted by l, m, n and l2 + m2 + n2 = 1.
Any numbers proportional to the direction cosines are known as direction ratios.
→ Unit vector in the direction of \(\bar{a}\) = \(\frac{\bar{a}}{|\bar{a}|}\)
→ Unit vector parallel to the resultant of the vectors \(\frac{\bar{a}+\bar{b}+\bar{c}}{|\bar{a}+\bar{b}+\bar{c}|}\) is ± \(\frac{\bar{a}+\bar{b}+\bar{c}}{|\bar{a}+\bar{b}+\bar{c}|}\)
→ The vector parallel to the resultant of the vectors \(\frac{\bar{a}+\bar{b}+\bar{c}}{|\bar{a}+\bar{b}+\bar{c}|}\) and having magnitude λ is ±λ \(\frac{\bar{a}+\bar{b}+\bar{c}}{|\bar{a}+\bar{b}+\bar{c}|}\)
→ The position vector of the point which divides the line segment joining the points A and B whose position vectors are \(\bar{a}, \bar{b}\) respectively, internally in the ratio, l:m is \(\frac{m \overline{\mathrm{a}}+l \bar{b}}{l+m}\) externally in the ratio l: m is \(\frac{m \bar{a}-l \bar{b}}{m-l}\), m ≠ l.
→ The ratio in which the line joining the points A(x1 y1, z1) and B(x2, y2, z2) is divided by
- xy – plane is – z1: z2
- yz – plane is -x1 : x2
- zx – plane is -y1: y2
![]()
→ If ‘c’ is the mid-point of line AB, the position vector of ‘c’ is \(\overline{O C}=\frac{\overline{O A}+\overline{O B}}{2}\)
= \(\frac{\bar{a}+\bar{b}}{2}\)
→ If \(\bar{a}, \bar{b}\) are two unit vectors, then the unit vector along the bisector of the angle between \(\bar{a}, \bar{b}\) is given by
\(\bar{c}=\frac{\bar{a}+\bar{b}}{|\bar{a}+\bar{b}|}\)
or
\(\bar{c}=\frac{\bar{a}-\bar{b}}{|\bar{a}-\bar{b}|}\)
→ The Vector \(\bar{a}\) = (a1, a2, a3), \(\bar{b}\) = (b1, b2, b3), \(\bar{c}\) = (c1, c2, c3) are coplanar or linearly dependent iff \(\left|\begin{array}{lll}
a_{1} & a_{2} & a_{3} \\
b_{1} & b_{2} & b_{3} \\
c_{1} & c_{2} & c_{3}
\end{array}\right|\) = 0
→ The Vector \(\bar{a}\) = (a1, a2, a3), \(\bar{b}\) = (b1, b2, b3), \(\bar{c}\) = (c1, c2, c3) are non-coplanar or linearly independent iff \(\left|\begin{array}{lll}
a_{1} & a_{2} & a_{3} \\
b_{1} & b_{2} & b_{3} \\
c_{1} & c_{2} & c_{3}
\end{array}\right|\) ≠ 0
→ The necessary and sufficient condition for four points with position vectors \(\bar{a}, \bar{b}, \bar{c}, \bar{d}\) are coplanar is that there exists scalars l, m, n, p not all zero such that
l\(\bar{a}\) + m\(\bar{b}\) + n\(\bar{c}\) + p\(\bar{da}\) = \(\bar{0}\), l + m + n + p = 0.
→ If \(\bar{a}, \bar{b}, \bar{c}\) are three non-zero, non – coplanar vectors and x, y, z are three scalars such that x\(\bar{a}\) + y\(\bar{b}\) + z\(\bar{c}\) = 0, then x = 0, y = 0, z = 0.
Note : Collinearity implies coplanarity but coplanarity does not imply collinearity.
→ If \(\bar{a}\) = (a1, a2, a3), \(\bar{b}\) = (b1, b2, b3), \(\bar{c}\) = (c1, c2, c3) and if \(\left|\begin{array}{lll}
a_{1} & a_{2} & a_{3} \\
b_{1} & b_{2} & b_{3} \\
c_{1} & c_{2} & c_{3}
\end{array}\right|\) > 0 then \(\bar{a}, \bar{b}, \bar{c}\) are in R.H.S
→ If \(\bar{a}\) = (a1, a2, a3), \(\bar{b}\) = (b1, b2, b3), \(\bar{c}\) = (c1, c2, c3) and if \(\left|\begin{array}{lll}
a_{1} & a_{2} & a_{3} \\
b_{1} & b_{2} & b_{3} \\
c_{1} & c_{2} & c_{3}
\end{array}\right|\) < 0 then \(\bar{a}, \bar{b}, \bar{c}\) are in L.H.S
![]()
→ If \(\bar{r}\) = x\(\bar{i}\) + y\(\bar{j}\) + z\(\bar{k}\), then |\(\bar{r}\)| = r = \(\sqrt{x^{2}+y^{2}+z^{2}}\) .
→ If l, m, n are the direction cosines of a line, then l2 + m2 + n2 = 1.
→ If a vector makes angles α, β, γ with co-ordinate axes, then
- cos2 α + cos2 β + cos2 γ = 1
- sin2 α + sin2 β + sin2 γ =2
→ The direction ratios of a vector \(\bar{r}\) = a\(\bar{i}\) + b\(\bar{j}\) + c\(\bar{k}\) are a, b, c.
→ If A = (x1, y1 z1), B = (x2, y2, z2) then the direction ratios of a vector
AB are x2 – x1, y2 – y1, z2 – z1
→ If a, b, c are the direction ratios of a vector then direction cosines of a vector are
\(\pm \frac{a}{\sqrt{a^{2}+b^{2}+c^{2}}}, \pm \frac{b}{\sqrt{a^{2}+b^{2}+c^{2}}}, \pm \frac{c}{\sqrt{a^{2}+b^{2}+c^{2}}}\)
→ If a, b, c are the direction ratios of a line then λa, λb, λc also become the direction ratios of that line where ‘λ’ is a non-zero scalar.
→ If \(\bar{r}\) = x\(\bar{i}\) + y\(\bar{j}\) + z\(\bar{k}\), then the direction cosines of a vector are \(\frac{a}{|\vec{r}|}, \frac{b}{|\vec{r}|}, \frac{c}{|\vec{r}|}\)
→ If \(\bar{r}\) = x\(\bar{i}\) + y\(\bar{j}\) + z\(\bar{k}\) makes angles α, γ with co-ordinate axes respectively, then
cos α = \(\frac{a}{|\vec{r}|}\),
cos β = \(\frac{b}{|\vec{r}|}\)
cos γ = \(\frac{c}{|\vec{r}|}\).
- The direction cosines of x- axis are 1, 0, 0.
- The direction cosines of y – axis are 0, 1,0.
- The direction cosines of z- axis are 0, 0, 1.
→ If a vector make equal angles with co-ordinate axes then direction cosines of a vector are \(\pm \frac{1}{\sqrt{3}}, \pm \frac{1}{\sqrt{3}}, \pm \frac{1}{\sqrt{3}}\)
→ If l, m, n are direction cosines of a vector OP and ‘O’ is the origin OP = r, then P = (lr, mr, nr).
→ If 1, m, n are direction cosines of a vector, then the maximum value of lmn is \(\frac{1}{3 \sqrt{3}}\)
→ The maximum value of l + m + n = \(\frac{1}{3 \sqrt{3}}\)
→ The vector equation of a straight-line passing through the point whose position vector is a and parallel to the vector \(\bar{b}\) is \(\bar{r}=\bar{a}+t \bar{b}\), where ‘t’ is parameter.
→ In cartesian form its equation is \(\frac{x-a_{1}}{b_{1}}=\frac{y-a_{2}}{b_{2}}=\frac{z-a_{3}}{b_{3}}\)
where \(\bar{a}\) = (a1, a2, a3), \(\bar{b}\) = (b1, b2, b3).
![]()
→ The vector equation of a straight-line passing through the point whose position vectors are
a and b is \(\bar{r}\) = (1 – t)\(\bar{a}\) (or) \(\bar{r}=\bar{a}+t(\bar{b}-\bar{a})\); where’t’ is a parameter.
→ In cartesian form \(\frac{x-a_{1}}{b_{1}-a_{1}}=\frac{y-a_{2}}{b_{2}-a_{2}}=\frac{z-a_{3}}{b_{3}-a_{3}}\)
where \(\bar{a}\) = (a1, a2, a3), \(\bar{b}\) = (b1, b2, b3).
→ Vector equation of the plane through the points whose position vectors are \(\bar{a}, \bar{b}, \bar{c}\) is \(\bar{r}=(1-s-t) \bar{a}+s \bar{b}+t \bar{c}\), where s and t are parameters (or)
\(\bar{r}=\bar{a}+s(\bar{b}-\bar{a})+t(\bar{c}-\bar{a})\).
where \(\bar{a}\) = (a1, a2, a3), \(\bar{b}\) = (b1, b2, b3), \(\bar{c}\) = (c1, c2, c3)
→ The vector equation of the plane through the point whose position vector is \(\bar{a}\) and parallel to the vectors \(\bar{b}\) and \(\bar{c}\) is \(\bar{r}=\bar{a}+s \bar{b}+t \bar{c}\), where ‘s’ and ‘t’ are parameter.
In cartesian form it is \(\left|\begin{array}{ccc}
x-a_{1} & y-a_{2} & z-a_{3} \\
b_{1} & b_{2} & b_{3} \\
c_{1} & c_{2} & c_{3}
\end{array}\right|\) = 0
→ Vector equation of the plane through the point’s whose position vectors are a, b and parallel to vector c is
\(\bar{r}=(1-s) \bar{a}+s \bar{b}+t \bar{c}\)
or
\(\bar{r}=\bar{a}+s(\bar{b}-\bar{a})+t \bar{c}\)
In cartesian form it is \(\left|\begin{array}{ccc}
x-a_{1} & y-a_{2} & z-a_{3} \\
b_{1}-a_{1} & b_{2}-a_{2} & b_{3}-a_{3} \\
c_{1} & c_{2} & c_{3}
\end{array}\right|\) = 0
Scalar:
A quantity which has only magnitude but no directions is called scalar quantity.
Ex: Length, mass, time ………….
Vector:
A quantity which has both magnitude and direction is called a vector quantity
Ex: Displacement, Velocity, Force ………………
A vector can also be denoted by a single letter \(\vec{a}, \vec{b}, \vec{c}\) …….. or bold letter a, b, c
Length of \(\vec{a}\) is dinded by |\(\vec{a}\)|. Length of \(\vec{a}\) is called magnitude of \(\vec{a}\).
![]()
Zero vector (Null Vector):
The vector of length O and having any direction is called null vector. It is denoted by \(\bar{O}\)
Note:
- If A is any point in the space then \(\overrightarrow{A A}=\vec{O}\)
- A non zero vector is called a proper vector.
Free vector:
A vector which is independent of its position is called free vector
Localised vector:
If \(\vec{a}\) is a vector P is a point then the ordere of pair, (P,a) is called localized vector at P
Multiplication of a vector by a scalar:
- Let m be any scalar and \(\vec{a}\) be any vector then the vector m \(\vec{a}\) is defined as
- Length of m \(\vec{a}\) is |m| times of length of \(\vec{a}\) i.e. |m\(\vec{a}\)| = |m||a|
- The line of support of m\(\vec{a}\) is same or parallel to that of \(\vec{a}\)
The sense the direction of m\(\vec{a}\) is same as that of \(\vec{a}\) if m is positive, the direction of m\(\vec{a}\) is opposite to that \(\vec{a}\) if m is negative
Note:
- o\(\vec{a}\) = o
- m\(\vec{0}\) = \(\vec{0}\)
- (mn)\(\vec{a}\) = m(n\(\vec{a}\)) = n(m\(\vec{a}\))
- (-1)\(\vec{a}\)
Negative of a vector:
\(\vec{a}\) ,\(\vec{b}\) are two vectors having same length but their directions are opposite to each other then each vector is called the negative of the other vector.
Here \(\vec{a}\) = –\(\vec{b}\) and \(\vec{b}\) = –\(\vec{a}\)
Unit vector:
A vector whose magnitude is unity is called unit vector.
Note: If \(\vec{a}\) is any vector then unit vector is \(\frac{\vec{a}}{|\vec{a}|}\) this is denoted by â {read as ‘a’ cap}
Collinear or parallel vectors:
Two or more vectors are said to the collinear vectors if the have same line of support. The vectors are said to be parallel if they have parallel lines of support.
Like parallel vectors:
Vectors having same direction are called like parallel vectors.
Unlike parallel vectors:
Vectors having different direction are called unlike parallel vectors.
Note:
- If \(\vec{a}\), \(\vec{b}\) are two non-zero collinear or parallel vectors then there exists a non zero scalar m such that \(\vec{a}\) = m\(\vec{b}\)
- Conversly if there exists a relation of the type \(\vec{a}\) = m\(\vec{b}\) between two non zero two non zero vectors a, b then a, b must be parallel or collinear.
Cointialvectors:
The vectors having the same initial point are called co-initial vectors.
Co planar vectors:
Three or more vectors are said to be coplanar if they lie on a plane parallel to same plane. Other wise the vectors are non coplanar vectors.
![]()
Angle between two non-zero vectors:
Let \(\overline{O A}=\vec{a}\) and \(\overline{O B}=\vec{b}\) be two non-zero vectors. Then the angle between \(\vec{a}\) and \(\vec{b}\) is defined as that angle AOB where O ≤ ∠AOB ≤ 180°
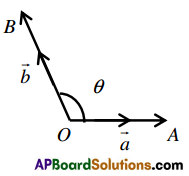
The angle between \(\vec{a}\) and \(\vec{b}\) is denoted by (\(\vec{a}\), \(\vec{b}\))
Note:
- If \(\vec{a}\) and \(\vec{b}\)are any two vectors such that (\(\vec{a}\), \(\vec{b}\)) = 0 then o ≤ 0 ≤ 180° {this is the range of θ i.e. angle beween vectors}
- \((\vec{a}, \vec{b})=(\vec{b}, \vec{a})\)
- \((\vec{a},-\vec{b})=(-\vec{a}, \vec{b})\) = 180° – \((\vec{a}, \vec{b})\)
- \((-\vec{a},-\vec{b})=(\vec{a}, \vec{b})\)
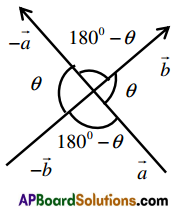
- If k > 0; 1 > 0 then \((k \vec{a}, l \vec{b})=(\vec{a}, \vec{b})\)
- If \((\vec{a}, \vec{b})\) = 0 then \(\vec{a}, \vec{b}\) are like parallel vectors
- If \((\vec{a}, \vec{b})\) = 180° then \(\vec{a}, \vec{b}\) are unlike parallel vectors
- If \((\vec{a}, \vec{b})\) = 90° then \(\vec{a}, \vec{b}\) are orthogonal or perpendicular vectors.
Addition of vectors:
Let \(\vec{a}\) and \(\vec{b}\) be any two given vectors. If three points O, A, B are taken such that \(\overline{O A}=\vec{a}\), \(\overrightarrow{A B}=\vec{b}\) then vectors \(\) is called the vector sum or resultant of the given vectors a and b we write \(\overline{O B}=\overline{O A}+\overline{A B}=\vec{a}+\vec{b}\)
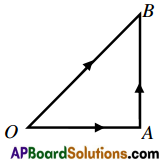
Triangular law of vectors:
Trianglular law states that if two vectors are represented in magnitude and direction by two sides of a triangle taken in order, then their sum or resultant is represented in magnitude and direction by the third side of the triangle taken in opposite direction.
Position vector:
Let O be a fixed point in the space called origin. If P is any point in the space then \(\) is called position vector of P relative to O.
Note:
If \(\vec{a}\) and \(\vec{b}\) be two non collinear vectors, then there exists a unique plane through a,b this plane is called plane generated by a, b. If \(\overline{O A}=\vec{a} ; \overline{O B}=\vec{b}\) then the plane generated by \(\vec{a}\), \(\vec{b}\) is denoted by \(\overline{A O B}\).
- Two non zero vectors a, b are collinear if m\(\vec{a}\) + n\(\vec{b}\) = 0 for some scalars m,n not both zero
- Let \(\vec{a}, \vec{b}, \vec{c}\) be the position vectors of the points A, B, C respectively. Then A, B, C are collinear iff m\(\vec{a}\) + n\(\vec{b}\) + p\(\vec{c}\) = 0 for some scalars m, n, p not all zero such that m + n + p = 0
- Let \(\vec{a}, \vec{b}\) be two non collinear vectors, If \(\vec{r}\) is any vector in the plane generated by a,b then there exist a unique pair of real numbers x, y such that \(\vec{r}\) = x\(\vec{a}\) + y\(\vec{b}\).
- Let \(\vec{a}, \vec{b}\) be two non collinear vectors. If \(\vec{r}\) is any vector such that \(\vec{r}\) = xa + yb for some real numbers then \(\vec{r}\) lies in the plane generated by a, b.
- Three vectors \(\vec{a}, \vec{b}, \vec{c}\) coplanar iff x\(\vec{a}\) + y\(\vec{b}\) + z\(\vec{c}\) = 0 for some scalars x, y, z not all zero.
- Let \(\vec{a}, \vec{b}, \vec{c}, \vec{d}\) be the position vectors of the points A, B, C, D in which no three of them are collinear. Then A, B, C, D are coplanar iff m\(\vec{a}\) + n\(\vec{b}\) + p\(\vec{c}\) + q\(\vec{d}\) = 0 for some scalars m,n,p,q not all zero such that m + n + p + q = 0
- If \(\vec{a}, \vec{b}, \vec{c}\) are three non coplanar vectors and \(\vec{r}\) is any vector then there exist a unique traid of real numbers. x, y, z such that \(\vec{r}\) = x\(\vec{a}\) + y\(\vec{b}\) + z\(\vec{c}\).
![]()
Right handed system of orthonormal vectors
A triced of three non-coplanar vectors\(\vec{i}, \vec{j}, \vec{k}\) is said to be a right hand system of orthonormal triad of vectors if
- \(\vec{i}, \vec{j}, \vec{k}\) from a right handed system
- \(\vec{i}, \vec{j}, \vec{k}\) are unit vectors
- (i, j) = 900 = \((\vec{j}, \vec{k})=(\vec{k}, i)\)
Right handed system:
Let \(\overline{O A}=\vec{a}, \overline{O B}=\vec{b}\) and \(\overrightarrow{O C}=\vec{c}\) be three non coplanar vectors. If we observe from the point C that a rotation from OA to OB through an angle not greater than 1800 is in the anti clock wise direction then the vectors a,b, c are said to form ‘Right handed system’.
Left handed system:
If we observe from C that a rotation from OA to OB through an angle not greater than 1800 is in the clock -wise direction then the vectors a,b, c are said to form a “Left handed system”.
If \(\vec{r}=x \vec{i}+y \vec{j}+z \vec{k}\) then \(|\vec{r}|=\sqrt{x_{2}+y_{2}+z_{2}}\).
Direction Cosines:
If a given directed line makes angles α, β, γ, with positive direction of axes of x,y, and z respectively then cos α,cos β,cos γ are called direction cosines of the line and these are denoted by l,m,n.
Direction ratios:
Thre real numbers a,b,c are said to be direction ratios of a line if a:b:c = l:m:n where l,m,n are the direction cosines of the line.
Linear combination:
Let \(\vec{a}_{1}, \bar{a}_{2}, \overline{a_{3}} \ldots \ldots \overline{a_{n}}\) be n vectors and l1,l2,l3….ln be n scalars then \(l_{1} \bar{a}_{1}+l_{2} \overline{a_{2}}+l_{3} \overline{a_{3}}+\ldots+l_{n} \overline{a_{n}}\) is called a. linear combination of \(\vec{a}_{1}, \bar{a}_{2} \ldots \ldots . \overline{a_{n}}\)
Linear dependent vectors:
The vectors \(\bar{a}_{1}, \overline{a_{2}} \ldots \ldots \overline{a_{n}}\) are said to be linearly dependent if there exist scalars l1,l2,l3….ln not all zero such that \(_{1} \vec{a}_{1}+l_{2} \overline{a_{2}}+\ldots+l_{n} \overline{a_{n}}]\) = 0
Linear independent The vectors a1, a2, a3 ……………. an are said to be linearly independt if l1, l2, l3 ……………. ln are scalars, \(l_{1} \vec{a}_{1}+l_{2} \overline{a_{2}}+\ldots l_{n} \overline{a_{n}}\) = 0
⇒ l1 = 0 l2 = o…. ln = o
- Let \(\vec{a}, \vec{b}\) be the position vectors of A, B respectively the position vector of the point P which divides \(\overline{A B}\) in the ratio m:n is \(\frac{m \vec{b}+n \vec{a}}{m+n}\). Conversely the point P with position vector \(\frac{m \vec{b}+n \vec{a}}{m+n}\) lies on the lines \(\overline{A B}\) and divides \(\overline{A B}\) in the ratio m:n.
- The medians of a triangle are concurrent. The point of concurrence divides each median in the ratio 2:1
- Let ABC be a triangle and D be a point which is not in the plane of \(\overline{A B C}\) the lines joining O, A, B,C with the centroids of triangle ABC, triangle BCD, triangle CDA and triangle DAB respectively are concurrent and the point of concurrence divides each line segment in the ratio 3:1
- The equation of the line passing through the point A = (x1, y1, z1) and parallel to the vector b = (l, m, n) is \(\frac{x-x_{1}}{l}=\frac{y-y_{1}}{m}=\frac{z-z_{1}}{n}\) = t
- The equation of the line having through the points A(x1, y1, z1), B(x2, y2, z2) is \(\frac{x-x_{1}}{x_{2}-x_{1}}=\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{z-z_{1}}{z_{2}-z_{1}}\) = t
- The unit vector bisecting the angle between the vectors \(\vec{a}, \vec{b}\) is \(\frac{\hat{a}+\hat{b}}{|\hat{a}+\hat{b}|}\)
- The internal bisector the angle between \(\vec{a}, \vec{b}\) is \(\frac{\overline{O P}}{O P}=\frac{\hat{a}+\hat{b}}{|\hat{a}+\hat{b}|}\) are concurrent
![]()
Theorem 1:
The vector equation of a line parallel to the vector \(\vec{b}\) and passing through the point A with position vector \(\vec{a}\) is \(\vec{r}=\vec{a}+t \vec{b}\) where t is a scalar.
Proof:
Let \(\overline{O A}=t \vec{a}\) be the given point and \(\overline{O P}=\vec{r}\) be any point on the line
\(\overline{A P}=t \vec{b}\) where ‘t’ is a scalar
\(\vec{r}-\vec{a}=t \vec{b} \Rightarrow \vec{r}=\vec{a}+t \vec{b}\)
Theorem 2:
The vector equation of the line passing through the points A, B whose position vectors \(\vec{a}, \vec{b}\) respectively is \(\vec{r}=\vec{a}(1-t)+t \vec{b}\) where t is a scalar.
Proof:
let P a a point on the line joining of A, B

Theorem 3:
The vector equation of the plane passing through the point A with position vector \(\vec{b}, \vec{c}\) and parallel to the vectors \(\vec{a}\) is \(\vec{r}=\vec{a}+s \vec{b}+t \vec{c}\) where s,t are scalars
Proof:
Given that \(\overline{O A}=\vec{a}\)
Let \(\overline{O P}=\vec{r}\) be the position vector of P
\(\overrightarrow{A P}, \vec{b}, \vec{c}\) are coplanar
∴ \(\overrightarrow{A P}=s \vec{b}+t \vec{c} \Rightarrow \vec{r}-\vec{a}=s \vec{b}+t \vec{c}\)
∴ \(\vec{r}=\vec{a}+s \vec{b}+t \vec{c}\)
Theorem 4:
The vector equation of the plane passing through the points A, B with position vectors \(\vec{a}, \vec{b}\) and parallel to the vector \(\vec{c}\) is \(\vec{r}=(1-s) \vec{a}+s \vec{b}+t \vec{c}\)
Proof:
Let P be a point on the plane and \(\overline{O P}=\vec{r}\)
\(\overline{O A}=\vec{a} \overline{O B}=\vec{b}\) be the given points \(\overline{A P}, \overrightarrow{A B}, \vec{C}\) are coplanar
\(\overrightarrow{A P}=s \overrightarrow{A B}+t \vec{C}\)
\(\vec{r}-\vec{a}=s(\vec{b}-\vec{a})+t \vec{c}\)
\(\vec{r}=(1-s) \vec{a}+s \vec{b}+t \vec{c}\)
![]()
Theorem 5:
The vector equation of the plane passing through the points A, B, C having position vectors \(\vec{a}, \vec{b}, \vec{c}\) is \(\vec{r}=(1-s-t) \vec{a}+s \vec{b}+t \vec{c}\) where s,t are scalars
Proof:
Let P be a point on the plane and \(\overline{O P}=\vec{r}\)
\(\overline{O A}=\vec{a} \overline{O B}=\vec{b}, \overline{O C}=\bar{c}\)
Now the vectors \(\overline{A B}, \overline{A C}, \overline{A P}\) are coplanar.
Therefore, \(\overline{A P}=s \overline{A B}+t \overline{A C}\), t,s are scalars.
\(\bar{r}-\bar{a}=s(\bar{b}-\bar{a})+t(\bar{c}-\bar{a})\)
\(\vec{r}=(1-s-t) \vec{a}+s \vec{b}+t \vec{c}\)