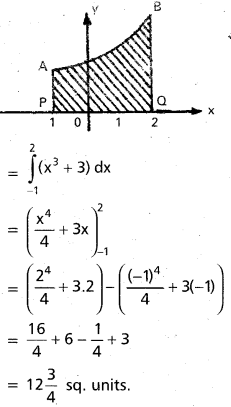
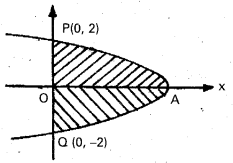
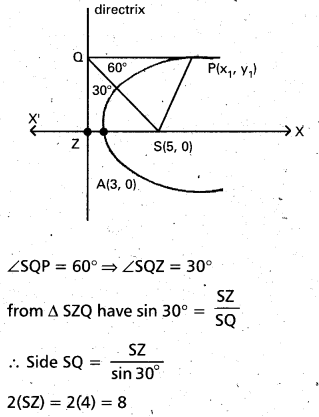
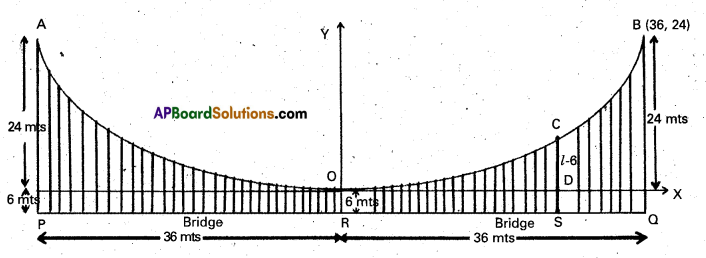
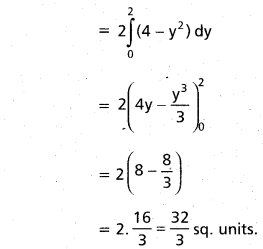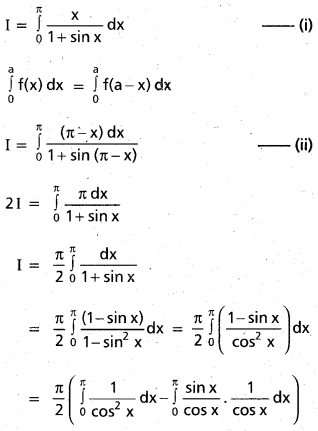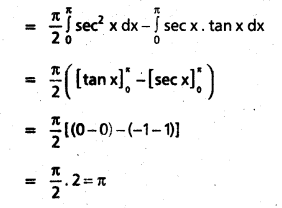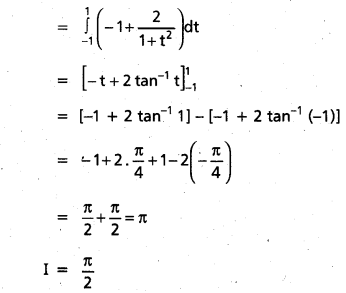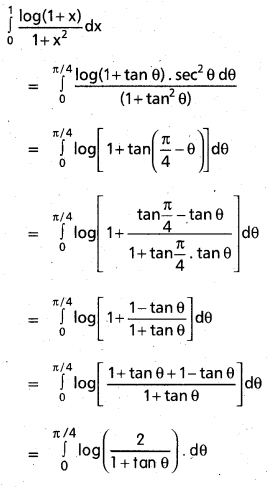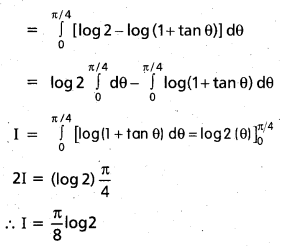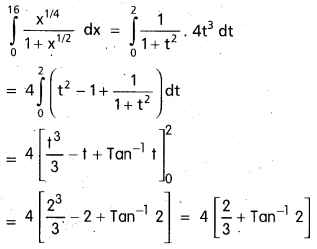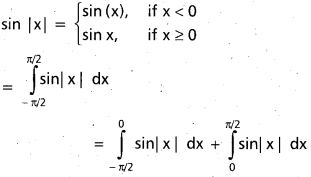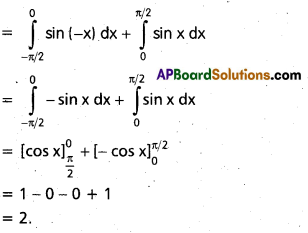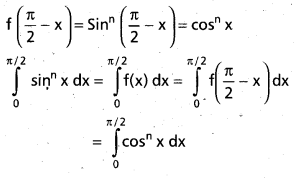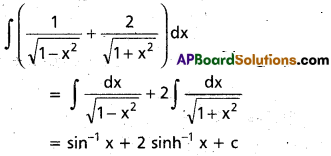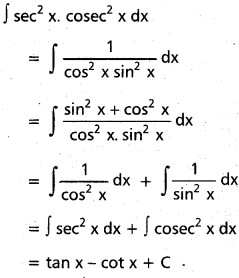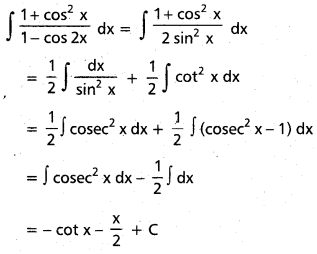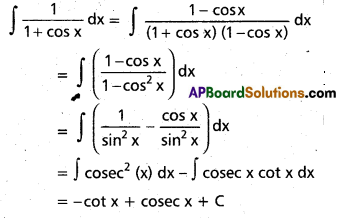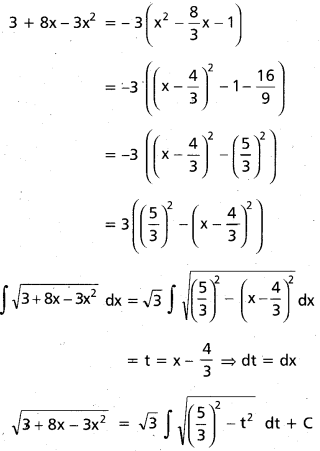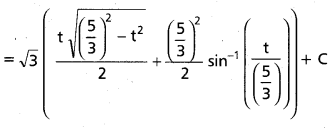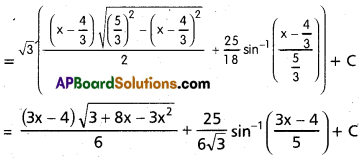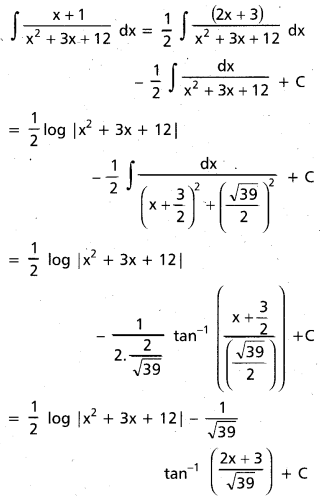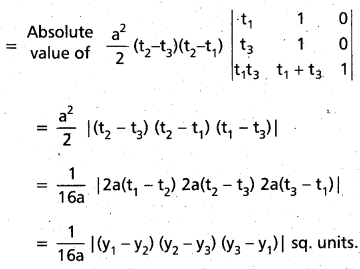Students can go through Telangana & Andhra Pradesh BIEAP TS AP Inter 2nd Year Physics Notes Pdf Download in English Medium and Telugu Medium to understand and remember the concepts easily. Besides, with our AP Sr Inter 2nd Year Physics Notes students can have a complete revision of the subject effectively while focusing on the important chapters and topics.
Students can also go through AP Inter 2nd Year Physics Study Material and AP Inter 2nd Year Physics Important Questions for exam preparation.
AP Intermediate 2nd Year Physics Notes
- Chapter 1 Waves Notes
- Chapter 2 Ray Optics and Optical Instruments Notes
- Chapter 3 Wave Optics Notes
- Chapter 4 Electric Charges and Fields Notes
- Chapter 5 Electrostatic Potential and Capacitance Notes
- Chapter 6 Current Electricity Notes
- Chapter 7 Moving Charges and Magnetism Notes
- Chapter 8 Magnetism and Matter Notes
- Chapter 9 Electromagnetic Induction Notes
- Chapter 10 Alternating Current Notes
- Chapter 11 Electromagnetic Waves Notes
- Chapter 12 Dual Nature of Radiation and Matter Notes
- Chapter 13 Atoms Notes
- Chapter 14 Nuclei Notes
- Chapter 15 Semiconductor Electronics: Material, Devices and Simple Circuits Notes
- Chapter 16 Communication Systems Notes
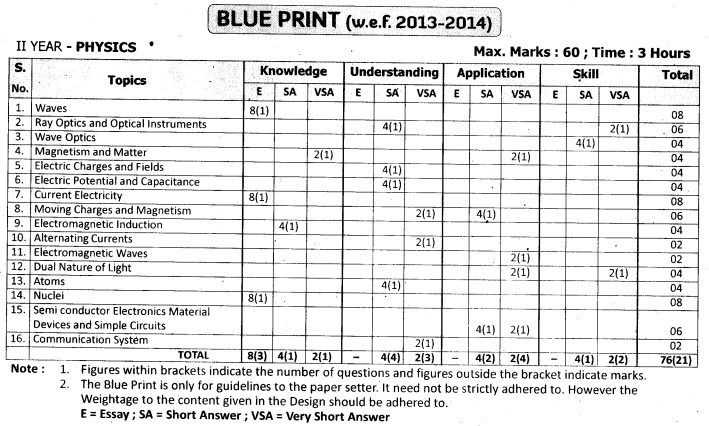
These TS AP Intermediate 2nd Year Physics Notes provide an extra edge and help students to boost their self-confidence before appearing for their final examinations. These Inter 2nd Year Physics Notes will enable students to study smartly and get a clear idea about each and every concept discussed in their syllabus.