Andhra Pradesh BIEAP AP Inter 2nd Year Physics Study Material 3rd Lesson Wave Optics Textbook Questions and Answers.
AP Inter 2nd Year Physics Study Material 3rd Lesson Wave Optics
Very Short Answer Questions
Question 1.
What is Fresnel distance?
Answer:
“Fresnel distance is the minimum distance a beam of light has to travel before its deviation from straight line path becomes significant”.
Fresnel distance (ZF) = \(\frac{\mathrm{a}^2}{\lambda}\) ; Where a = width of the aperture, λ = wave length.
Question 2.
Give the justification for the validity of ray optics.
Answer:
The distances are much smaller than ZF, and the spreading due to diffraction is smaller compared to the size of the beam.
When the distance is approximately ZF, and much more than ZF, the spreading due to diffraction dominates over that due to ray optics (size of the aperture (a)]
Z = \(\frac{\mathrm{a}^2}{\lambda}\)
From this equation, ray optics is valid in the limit of wavelength tending to zero.
![]()
Question 3.
What is polarisation of light ?
Answer:
The vibrations of the light confined only one direction. This phenomenon is called polarisation.
(or)
The phenomenon due to which the transverse vibrations of electric field vector of a light wave become confined to one plane, is called polarisation.
Question 4.
What is Malus’ law.
Answer:
Malus’ law : It states that the intensity of polarised light transmitted through the analyser varies as a square of cosine of the angle between the plane of transmission of analyser and polariser.
I ∝ cos2 θ; I = I0 cos2 θ.
Question 5.
Explain Brewster’s law.
Answer:
Brewster’s law : The tangent of the polarising angle is equal to the refractive index of the medium.
μ = tan iB, where iB = polarising angle and μ = refractive index. Note : r + iB = 90°
Question 6.
When does a monochromatic beam of light incident on a reflective surface get completely transmitted ?
Answer:
Let the light emitted by laser source passes through polariser, and incident on the surface of the reflective surface with Brewster’s angle (iB). Now rotate the polariser at particular alignment the light incident on the surface is completely transmitted.
Short Answer Questions
Question 1.
Explain Doppler effect in light. Distinguish between red shift and blue shift. (T.S. Mar. ’18, ’16)
Answer:
Dopper effect in light: The change in the apparent frequency of light, due to relative motion between source of light and observer. This phenomenon is called Doppler effect.
The apparent frequency of light increases when the distance between observer and Source of light is decreasing and the apparent frequency of light decreases, if the distance between source of light and observer increasing.
Doppler shift can be expressed as \(\frac{\Delta v}{v}\) = \(\frac{-v_{\text {radial }}}{\mathrm{C}}\)
Applications of Doppler effect in light:
- It is used in measuring the speed of a star and speed of galaxies.
- Measuring the speed of rotation of the sun.
Red shift: The apparent increase in wave length in the middle of the visible region of the spectrum moves towards the red end of the spectrum is called red shift.
Blue shift: When waves are received from a source moving towards the observer, there is an apparent decrease in wave length, this is called blue shift.
![]()
Question 2.
What is total internal reflection. Explain the phenomenon using Huygen’s principle.
Answer:
Total internal reflection: When a light ray travels from denser medium to rarer medium, the angle of incidence is greater than critical angle then it reflects into the same medium. This phenomenon is called total internal reflection.
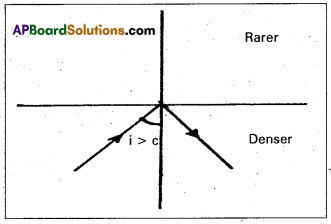
Huygen’s principle : According to Huygen’s principle, every point on the wavefront AB is a source of secondary wavelets and time during which wavelets from B reaches at C, Let \(\tau\) be the time taken by the wave front to advance from B to C.
Then distance BC = υ\(\tau\)
In order to construct the reflected wavefront, we draw a sphere of radius ux from point A.
Let CE represent the tangent drawn from C to this sphere.
AE = BC = υ\(\tau\)
Consider the triangles EAC and BAC are congruent.
∴ Angles i and r would be equal. This is the law of reflection.
Question 3.
Derive the expression for the intensity at a point where interference of light occurs. Arrive at the conditions for maximum and zero intensity. (A.P. & T.S. Mar. ’16)
Answer:
Let y1 and y2 be the displacements of the two waves having same amplitude a and Φ is the phase difference between them.
y1 = a sin ωt …… (1)
y2 = a sin (ωt + ϕ)) …… (2)
The resultant displacement y = y1 + y2
y = a sin ωt + a sin (ωt + ϕ)
y = a sin ωt + a sin ωt cos ϕ + a cos ωt sin ϕ
y = a sin ωt [1 + cos ϕ] + cos ωt (a sin ϕ)
Let R cos θ = a(1 + cos ϕ) —– (4)
R sin θ = a sin ϕ —– (5)
y = R sin ωt . cos θ + R cos ωt . sin θ
y = R sin(ωt + θ) —– (6)
where R is the resultant amplitude at P, squaring equations (4) and (5), then adding
R2 (cos2 θ + sin θ] = a2[1 + cos2 ϕ + 2 cos ϕ + sin2 ϕ]
R2[1] = a2[1 + 1 + 2 cos ϕ]
I = R2 = 2a2 [1 + cos ϕ] = 2a2 × 2 cos2 \(\frac{\phi}{2}\); I = 4a2 cos2 \(\frac{\phi}{2}\) —— (7)
i) Minimum intensity (Imax)
c0s2 \(\frac{\phi}{2}\) = 1
ϕ = 2nπ Where n = 0, 1, 2, 3 …….
ϕ = 0, 2π, 4π, 6π
∴ Imax = 4a2.
ii) Minimum intensity (Imin)
cos2 \(\frac{\theta}{2}\) = 0
ϕ = (2n + 1)π where n = 0, 1, 2, 3, …….
ϕ = π, 3π, 5π, 7π
Imin = 0
Question 4.
Does the principle of conservation of energy hold for interference and diffraction phenomena ? Explain briefly. (Mar. ’14)
Answer:
Yes, law of conservation of energy is obeyed. In case of constructive interference, intensity becomes maximum. Hence bright fringes are formed on the screen where as in the case of destructive interference, intensity becomes minimum. Hence dark fringes are formed on the screen.
This establishes that in the interference and diffraction pattern, the intensity of light is simply being redistributed i.e., energy is being transferred from dark fringe to bright fringe. No energy is being created (or) destroyed in the process. Hence energy is redistributed.
Thus the principle of conservation of energy is being obeyed in the process of interference and diffraction.
![]()
Question 5.
How do you determine the resolving power of your eye ? (A.P. Mar. ’19)
Answer:
Make black strips of equal width separated by white strips. All the black strips having same width, while the width of white strips should increase from left to right.
Now watch the pattern with one eye. By moving away (or) closer to the wall, find the position where you can just see some two black strips as separate strips.
All black strips to the left of this strips would merge into one another and would not be distinguishable on the other hand, the black strips to the right of this would be more and more clearly visible.
Note the width d of the white strips and measure the distance D of the wall from eye.
Then resolution of your eye = \(\frac{\mathrm{d}}{\mathrm{D}}\).
Question 6.
Discuss the intensity of transmitted light when a polaroid sheet is rotated between two crossed polaroids.
Answer:
Let I0 be the intensity of polarised light after passing through the first polariser P1. Then the intensity of light after passing through second polariser P2 will be I = I0cos2θ.
Where θ is the angle between pass axes P1 and P2. Since P1 and P2 are crossed the angle between the pass axes of P2 and P3 will be \(\left(\frac{\pi}{2}-\theta\right)\)
Hence the intensity of light emerging from P3 will be
I = I0cos2 θ. cos2 \(\left(\frac{\pi}{2}-\theta\right)\)
= I0 cos2 θ . sin2 θ
I = \(\frac{I_0}{4}\) sin2 2θ
The transmitted intensity will be maximum when θ = \(\frac{\pi}{4}\)
Long Answer Questions
Question 1.
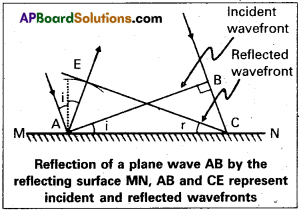
What is Huygen’s Principle? Explain the optical phenomenon of refraction using Huygen’s principle.
Answer:
Huygens principle: Every point on a wave front is the source of secondary wavelets.
Refraction of a plane wave using Huygen’s principle:
Let the surface PP’ separating the two medium of refractive index μ1 and μ2. Let υ1 and υ2 be the velocities of light in medium 1 and medium 2.
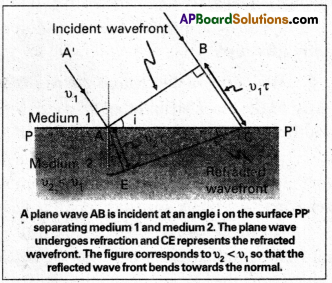
According to Huygen’s principle, every point on incident wave front AB is a source of secondary wavelets. By the time wavelét from point B reaches at point C, the wavelet from point A would have reached at point E. Let t be the time taken from B to C is equal to time taken from A to D.

μ1 sin i = μ2 sin r
This is the Snell’s law of refraction.
Second law of refraction: Since incident ray, refracted ray and the normal all the lie on the same plane PP’ at the point of incidence. This proves the second law of refraction.
Question 2.
Distinguish between Coherent and Incoherent addition of waves. Develop the theory of constructive interferences.
Answer:
Coherent sources : The two sources which maintain zero (or) any constant phase relation between themselves are known as Coherent sources.
Incoherent sources : If the phase difference changes with time, the two sources are known as incoherent sources.
Theory of constructive and destructive interference :
Let the waves of two coherent sources be
y1 = a sin ωt —— (1)
y2 = a sin (ωt + ϕ) —– (2)
where a is amplitude and ϕ is the phase difference between two displacements.
According to superposition principle, y = y1 + y2
y = a sin ωt + a sin (ωt + ϕ)= a sin ωt + a sin ωt cos ϕ + a cos ωt sin ϕ
y = a sin ωt [1 + cos ϕ] + cos ωt [a sin ϕ] —– (3)
Let A cos θ = a(1 + cos ϕ] —– (4)
A sin θ = a sin ϕ —– (5)
Substituting equations (4) and (5) in equation (3)
y = A sin ωt. cos θ + A cos ωt sin θ
y = A sin (ωt + θ) —— (6)
Where A is resultant amplitude. Squaring equations (4) and (5), then adding
A2 [cos2 θ + sin2 θ] = a2[1 + cos2 ϕ + 2 cos ϕ + sin2 ϕ]
A2 [1] = a2 [1 + 1 + 2 cos ϕ]
I = A2 = 2a2 [1 + cos ϕ] ( ∵ I = A2)
I = 2a2 × 2 cos2 \(\frac{\phi}{2}\)
I = 4a2 cos2 \(\frac{\phi}{2}\)
I = 4I0 cos2 \(\frac{\phi}{2}\) —— (7) (∵ I0 = a2)
Case (i) For constructive interference : Intensity should be maximum.
cos \(\frac{\phi}{2}\) = 1 ⇒ ϕ = 2nπ
Where n = 0, 1, 2, 3….. ⇒ ϕ = 0, 2π, 4π, 6π ….. Imax = 4I0
Case (ii) For destructive interference : Intensity should be minimum
i.e., cos ϕ = 0 ⇒ ϕ = (2n + 1) π ; where n = 0, 1, 2, 3……. ; ϕ = π, 3π, 5π ⇒ Imin = 0.
![]()
Question 3.
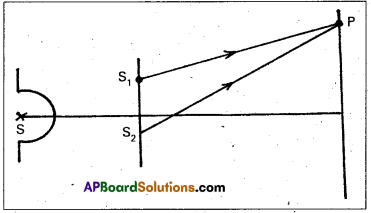
Describe Young’s experiment for observing interference and hence arrive at the expression for ‘fringe width’. ‘
Answer:
Interference : The modification of intensity obtained by the super position of two (or) more light waves is called interference.
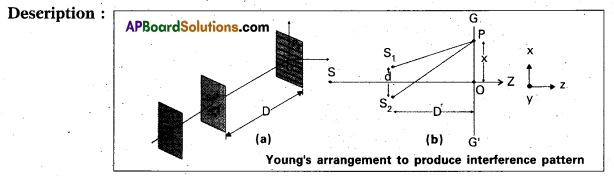
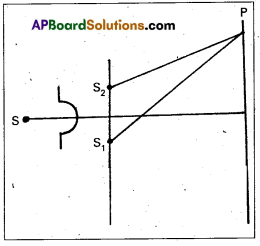
- Thomas Young experimentally observed the phenomenon of interference of light using two coherent sources.
- A small pin hole ‘S’ illuminated by monochromatic source of light which produces a spherical wave.
- S1 and S2 are two narrow pin holes equidistant from S.
- Screen is placed at a distance D.
- The points at which any two crests (or) any two troughs are superimposed, constructive interference takes place bright fringe will be observed on the screen.
- The points at which crest of one wave and trough of another wave are super imposed, destructive interference takes place dark fringe will be observed on the screen.
- Thus on the screen alternately bright and dark frings are observed.
Expression for fringe width :
i) It is the distance between two successive bright (or) dark fringes, denoted by p.
ii) The path difference (δ) = d sin θ
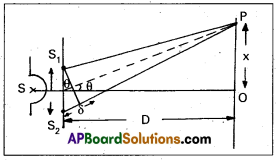
If θ is very small then from figure sin θ ≈ tan θ = \(\frac{x}{D}\)
iii) For bright fringes path difference S2P – S1P = nλ
∴ d sin θ = nλ,
d × \(\frac{x}{D}\) = nλ
x = \(\frac{n \lambda \mathrm{D}}{\mathrm{d}}\) —– (1) where n = 0, 1, 2, 3,…….
This equation represents the position of bright fringe.
When n = 0, x0 = 0
n = 1, x1 = \(\frac{\lambda \mathrm{D}}{\mathrm{d}}\) and n = 2, x2 = \(\frac{2 \lambda \mathrm{D}}{\mathrm{d}}\)
The distance between any two consecutive bright fringes is
x2 – x1 = \(\frac{2 \lambda \mathrm{D}}{\mathrm{d}}-\frac{\lambda \mathrm{D}}{\mathrm{d}}\) ⇒ β = \(\frac{\lambda \mathrm{D}}{\mathrm{d}}\) ——- (2)
iv) For dark fringes path difference S2P – S1P = (2n + 1) \(\frac{\lambda}{2}\) ∴ d sin θ = (2n + 1)\(\frac{\lambda}{2}\)
d × \(\frac{x}{D}\) = (2n + 1) \(\frac{\lambda}{2}\) = \(\frac{(2 \mathrm{n}+1) \lambda \mathrm{D}}{2 \mathrm{~d}}\) ——- (3) where n =0, 1, 2, 3, ………
This equation (3) represents, position of dark fringe.
When n = 0, x0 = \(\frac{\lambda \mathrm{D}}{2 \mathrm{~d}}\) ⇒ n = 1, x1 = \(\frac{3 \lambda \mathrm{D}}{2 \mathrm{~d}}\) ; n = 2, x2 = \(\frac{5 \lambda \mathrm{D}}{2 \mathrm{~d}}\) ……
The distance between any two consecutive dark fringes is x2 – x1 = \(\frac{5 \lambda \mathrm{D}}{2 \mathrm{~d}}-\frac{3 \lambda \mathrm{D}}{2 \mathrm{~d}}\) = \(\frac{5 \lambda \mathrm{D}-3 \lambda \mathrm{D}}{2 \mathrm{~d}}\)
β = \(\frac{\lambda \mathrm{D}}{\mathrm{d}}\) —– (4)
Hence fringe width is same for bright and dark fringes.
Question 4.
What is diffraction ? Discuss diffraction pattern obtainable from a single slit.
Answer:
Diffraction : The phenomenon of bending of light at the edges of an obstacle and light enters into the geometrical shadow is known as diffraction of light.
Example : The silver lining surrounding the profile of a mountain just before sunrise.
Diffraction of light at a single slit:
- Consider a narrow slit AB of width d. A parallel beam of light of wave length λ falling normally on a single slit.
- Let the diffracted light be focussed by means of a convex lens on a screen.
- The secondary wavelets travelling normally to the slit, i.e., along the direction of OP0.
Thus P0 is a bright central image.
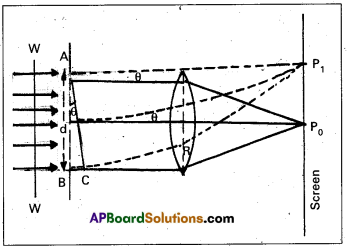
- The secondary wavelets travelling at an angle θ with the normal are focussed at a point P1 on the screen.
- In order to find out intensity at P1, draw a perpendicular AC on BR.
- The path difference between secondary wavelets = BC
= AB sin θ = a sin θ (∵ sin θ = 0)
Path difference (λ) ≈ a θ —– (1) - Experimental observations shown in figure, that the intensity has a central maximum at θ = 0 and other secondary maxima at θ ≈ \(\left(\mathrm{n}+\frac{1}{2}\right) \frac{\lambda}{\mathrm{a}}\) and has minima at θ = \(\approx \frac{n \lambda}{a}\)
- From equation (1), θ = \(\frac{\lambda}{\mathrm{a}}\). Now we divide the slit into two equal halves, each of size \(\frac{a}{2}\).
- We can show that the intensity is zero for θ = \(\frac{n \lambda}{a}\) where n = 1, 2, 3….
- It is alsó to see why there are maxima at θ = \(\left(\mathrm{n}+\frac{1}{2}\right) \frac{\lambda}{\mathrm{a}}\)
- Consider θ = \(\frac{3 \lambda}{2 \mathrm{a}}\) which is midway between two of the dark fringes.
- If we take the first two thirds of the slit, the path difference between two ends is
\(\frac{2}{3} a \times \theta\) = \(\frac{2 \mathrm{a}}{3} \times \frac{3 \lambda}{2 \mathrm{a}}\) = λ —– (2)
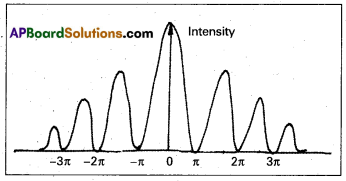
- The first two third of the slit can be divided into two halves which have a \(\frac{\lambda}{2}\) path difference. The contribution of two halves cancel and only remaining one third of the slit contributes to the intensity minima.
Question 5.
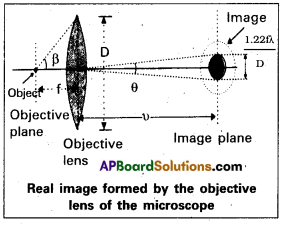
What is resolving power of Optical Instruments? Derive the condition under which images are resolved.
Answer:
Resolving power : The resolving power of a lens is its ability to resolve two points that are to each other.
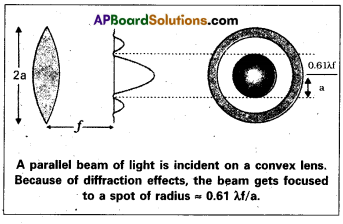
Resolving power of optical instruments:
- Consider a parallel beam of light falling on a convex lens. Due to diffraction effect, the beam focussed to a spot of finite area.
- Taking into account the effects duè to diffraction, the pattern on the focal plane would consist of a central bright region (circular) surrounded by a concentric dark and bright rings.
- The radius of the central bright region is given by r0 = \(\frac{1.22 \lambda \mathrm{f}}{2 \mathrm{a}}\) = \(\frac{0.61 \lambda \mathrm{f}}{\mathrm{a}}\)
where f is focal length of the lens
2a = diameter of the lens.
Derive the condition under which images are resolved : The size of the spot is very small, it plays an important role in determining the limit of resolution.
For the two stars to be Just resolved
f Δ θ ≈ r0 ≈ \(\frac{0.61 \lambda \mathrm{f}}{\mathrm{a}}\)
Δ θ ≈ \(\frac{0.61 \lambda}{\mathrm{a}}\) —– (1)
Thus Δθ will be small, if the diameter (2a) of the objective is large. This implies that the telescope will have better resolving power if a is large.
In case of microscope, the object is placed slightly beyond f. The corresponding minimum seperation (dMin) between the object and the objective lens is given by
dMin = \(\frac{1.22 \lambda}{2 \mu \sin \beta}\)
Where μ = Refractive index
μ sin β = Numerical aperture.
Textual Exercises
Question 1.
Monochromatic light of wavelength. 589 nm is incident from air on a water surface. What are the wavelength, frequency and speed of (a) reflected, and (b) refracted light ? Refractive index of water is 1.33.
Solution:
λ = 589 nm = 589 × 10-9 m
a) Reflected light: (Wavelength, frequency, speed same as incident light)
λ = 589 nm, v = 5.09 × 1014 Hz
c = 3 × 108 m/s ⇒ υ = \(\frac{c}{\lambda}=\frac{3 \times 10^8}{589 \times 10^{-9}}\) = 5.093 × 1014 Hz.
b) Refracted light: (frequency same as the incident frequency)
y = 5.093 × 1014 Hz
υ = \(\frac{\mathrm{c}}{\mu}=\frac{3 \times 10^8}{1.33}\) = 2.256 × 108 m/s ⇒ λ = \(\frac{v}{v}=\frac{2.26 \times 10^8}{5.09 \times 10^{14}}\) = 443 m.
![]()
Question 2.
What is the shape of the wavefront in each of the following cases :
(a) Light diverging from a point source.
(b) Light emerging out of a convex lens when a point source is placed at its focus.
(c) The portion of the wavefront of light from a distant intercepted by the Earth.
Soution:
a) It is spherical wavefront.
b) It is plane wavefront.
c) Plane wavefront (a small area on the surface of a large sphere is nearly planar.
Question 3.
(a) The refractive index of glass is 1.5. What is the speed of light in glass ? (Speed of light in vacuum is 3.0 × 108 m s-1)
(b) Is the speed of light in glass independent of the colour of light ? If not, which of the two colours red and violet travels slower in a glass prism ?
Solution:
a) Here, µ = \(\frac{\mathbf{c}}{v}\) ⇒ υ = \(\frac{\mathrm{c}}{\mu}\) = \(\frac{3 \times 10^8}{1.5}\) = 2 × 108 m/s
b) No, the refractive index and speed of light in a medium depend on wavelength i.e. colour of light. We know that µv > µr.
Therefore vviolet < vred. Hence violet component of white light travels slower than the red component.
Question 4.
In a Young’s double-slit experiment, the slits are separated by 0.28 mm and the screen is placed 1.4 m away. The distance between the central bright fringe and the fourth bright fringe is measured to be 1.2 cm. Determine the wavelength of light used in the experiment.
Solution:
d = 0.28 mm = 0.28 × 10-3 m, D = 1.4 m, β = 1.2 × 10-2 m, n = 4
![]()
⇒ λ = 600 nm.
Question 5.
In Young’s double-slit experiment using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. What is the intensity of light at a point where path difference is λ/3 ?
Solution:
Let I1 = I2 = I. If ϕ is phase difference between the two light waves, then resultant intensity,
IR = I1 + I2 + \(2 \sqrt{\mathrm{I}_1 \mathrm{I}_2}\) . cos ϕ
When path difference = λ, Phase difference ϕ = 0° ∴ IR = I + I + \(2 \sqrt{I I}\). cos 0° = 4I = k
When path difference = \(\frac{\lambda}{3}\), phase difference ϕ = \(\frac{2 \pi}{3}\) rad.
∴ IR = I + I + \(2 \sqrt{\mathrm{II}} \cdot \cos \frac{2 \pi}{3}\) ⇒ I’R = 2I + 2I\(\left(\frac{-1}{2}\right)\) = I = \(\frac{\mathrm{k}}{4}\)
Question 6.
A beam of light consisting of two wavelengths, 650 nm and 520 nm, is used to obtain interference fringes in a Young’s double-slit experiment.
(a) Find the distance of the third bright fringe on the screen from the central maximum for wavelength 650 nm.
(b) What is the least distance from the central maximum where the bright fringes due to both’the wavelengths coincide ?
Solution:
Here λ1 = 650 nm = 650 × 10-9 m, λ2 = 520 nm = 520 × 10-9 m .
Suppose d = Distance between two slits; D = Distance of screen from the slits
a) For third bright fringe, n = 3 ⇒ x = nλ, \(\frac{\mathrm{D}}{\mathrm{d}}\) = 3 × 650 \(\frac{\mathrm{D}}{\mathrm{d}}\) nm
b) Let nth fringe due to λ2 = 520 nm coincide with (n – 1)th bright fringe due to λ1 = 650 nm
∴ nλ2 = (n – 1) λ1 ; n × 520 = (n – 1) 650; 4n = 5n – 5 or n = 5 .
∴ The least distance required, x = nλ2 \(\frac{\mathrm{D}}{\mathrm{d}}\) = 5 × 520 \(\frac{\mathrm{D}}{\mathrm{d}}\) = 2600 \(\frac{\mathrm{D}}{\mathrm{d}}\) nm.
Question 7.
In a double-slit experiment the angular width of the fringe is found to be 0.2° on a screen placed 1 m away. The wavelength of light used is 600 nm. What will be the angular width of the fringe if the entire experimental apparatus is immersed in water ? Take refractive index of water to be 4/3.
Solution:
Here, θ1 = 0.2°, D = 1m, λ1 = 600 nm, θ2 = ?, μ = 4/3
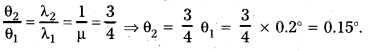
Question 8.
What is the Brewster angle for air to glass transition ? (Refractive index of glass = 1.5.)
Solution:
Here, ip = ? μ = 1.5; As tan ip = μ = 1.5 ∴ ip = tan-1 (1.5); ip = 56.3
Question 9.
Light of wavelength 5000 A falls on a plane reflecting surface. What are the wavelength and frequency of the reflected light ? For what angle of incidence is the reflected ray normal to the incident ray ?
Solution:
Given λ = 5000 A = 5 × 10-7 m
The wavelength and frequency of reflected light remains the same.
∴ Wavelength of reflected light, λ = 5000 A
Frequency of reflected light, υ = \(\frac{\mathrm{c}}{\lambda}=\frac{3 \times 10^8}{5 \times 10^{-7}}\) = 6 × 1014 Hz
The reflected ray is normal to incident if angle of incidence i = 45.
![]()
Question 10.
Estimate the distance for which ray optics is good approximation for an aperture of 4 mm and wavelength 400 nm.
Solution:
Here, a = 4 mm = 4 × 10-3 m; λ = 400 nm = 400 × 10-9 m = 4 × 10-7 m
Ray optics is good approximation upto distances equal to Fresnels’ distance (ZF)
ZF = \(\frac{a^2}{\lambda}=\frac{\left(4 \times 10^{-3}\right)^2}{4 \times 10^{-7}}\) = 40 m
Additional Exercises
Question 11.
The 6563 A Hα line emitted by hydrogen in a star is found to be red-shifted by 15 A. Estimate the speed with which the star is receding from the Earth.
Solution:
Given λ’ – λ= 15A = 15 × 10-10 m; λ = 6563 A = 6563 × 10-10 m; v = ?
Since λ’ – λ = \(\frac{v \lambda}{c}\) ∴ v = \(\frac{c\left(\lambda^{\prime}-\lambda\right)}{\lambda}\) ⇒ v = \(\frac{3 \times 10^8 \times 15 \times 10^{-10}}{6563 \times 10^{-10}}\) = 6.86 × 105 m/s
Question 12.
Explain how Corpuscular theory predicts the speed of light in a medium, say, water, to be greater than the speed of light in vacuum. Is the prediction confirmed by experimental determination of the speed of light in water ? If not, which alternative picture of light is consistent with experiment ?
Solution:
In Newton’s corpuscular picture of refraction, particles of light incident from a rarer to a denser medium experience a force of attraction normal to the surface. This results in an increase in the normal component of velocity but the component along the surface remains unchanged. This means
c sin i = v sin r or \(\frac{\mathrm{v}}{\mathrm{c}}=\frac{\sin \mathrm{i}}{\sin \mathrm{r}}\) = μ; Since μ > 1, ∴ v > c
The prediction is opposite to the experimental result: (v < c) . The wave picture of light is consistent with experiment.
Question 13.
You have learnt in the text how Huygens’ principle leads to the laws of reflection and refraction. Use the same principle to deduce directly that a point object placed in front of a plane mirror produces a virtual image whose distance from the mirror is equal to the object distance from the mirror.
Solution:
In figure, P is a point object placed at a distance r from a plane mirror M1 M2. with P as centre and OP = r as radius, draw a spherical arc; AB. This is the spherical wave front from the object, incident on M1 M2. If mirrors were not present, the position of wave front AB would be A’B’ where PP’ = 2r. In the presence of the mirror, wave front AB would appear as A”PB”, according to Huygen’s construction. As is clear from the fig. A’B’ and
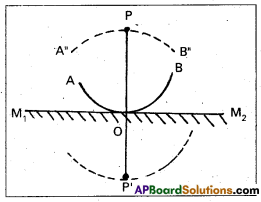
A”B” are two spherical arcs located symmetrically on either side of M1 M2. Therefore, A’PB’ can be treated as reflected image of A”PB”. From simple geometry, we find OP = OP’, which was to be proved.
Question 14.
Let us list some of the factors, which could possibly influence the speed of wave propagation :
- nature of the source
- direction of propagation
- motion of the source and/or observer
- wavelength
- intensity of the wave On which of these factors, if any, does
(a) the speed of light in vacuum
(b) the speed of light in a medium (say, glass or water), depend ?
Solution:
a) The speed of light in vacuum is a universal constant, independent of all the factorslisted and anything else.
b) Dependence of the speed of light in a medium
- Does not depend on the nature of the source.
- Independent of the direction of propagation for isotropic media.
- Independent of the motion of the source relative to the medium but depends on the motion of the Observer relative to the medium.
- Depends on wavelength.
- Independent of intensity.
Question 15.
For sound waves, the Doppler formula for frequency shift differs slightly between the two situations :
(i) source at rest; observer moving and
(ii) source moving; observer at rest. The exact Doppler formulas for the case of light waves in vacuum are, however, strictly identical for these situations. Explain why this should be so. Would you expect the formulas to be strictly identical for the two situations in case of light travelling in a medium ?
Solution:
Sound waves require a material medium for propagation. That is why situation (i) and (ii) are not identical physically though relative motion between the source and the observer is the same in the two cases. Infact, relative motion of the observer relative to the medium is different in two situations. That is why Doppler’s formulae for sound are different in the two cases.
For light waves travelling in vacuum, there is nothing to distinguish between the two situations. That is why the formulae are strictly identical.
For light propagating in a medium, situation (i) and (ii) are not identical. The formulae governing the two situations would obviously be different.
Question 16.
In double-slit experiment using light of wavelength 600 nm, the angular width of a fringe formed on a distant screen is 0.1°. What is the spacing between the two slits ?
Solution:
Here λ = 600 nm = 6 × 10-7 m, θ = 0.1° = \(\frac{0.1^{\circ}}{180^{\circ}} \times \pi \mathrm{rad}\), d = ?
Since θ = \(\frac{\lambda}{\mathrm{d}}\) ⇒ d = \(\frac{\lambda}{\theta}\) = \(\frac{6 \times 10^{-7} \times 180^{\circ}}{0.1^{\circ} \times \pi}\) = 343 × 10-4 m.
Question 17.
Answer the following questions :
(a) In a single slit diffraction experiment, the width of the slit is made double the original width. How does this affect the size and density of the central diffraction band ?
(b) In what way is diffraction from each slit related to the interference pattern in a double-slit experiment ?
(c) When a tiny circular obstacle is placed in the path of light from a distant source, a bright spot is seen at the centre of the shadow of the obstacle. Explain why ?
(d) Two students are separated by a 7m partition wall in a room 10 m high. If both light and sound waves Can bend around obstacles, how is it that the students are unable to see each other even though they can converse easily.
(e) Ray optics is based on the assumption that light travels in a straight line.fDiffraction effects (observed when light propagates through small apertures/slits or around small obstacles) disprove this assumption. Yet the ray optics assumption is so commonly used in understanding location and several other properties of images in optical instruments. What is the justification ?
Solution:
a) The size of centred diffraction band reduces by half according to the relation : size \(\frac{\lambda}{\mathrm{d}}\). Intensity increase four fold.
b) The intensity of interference fringes in a double slit arrangement is modulated by diffraction pattern Of each slit.
c) Waves diffracted from the edge of the circular obstacle interfer constructively at the centre of the shadow producing a bright spot.
d) For diffraction the size of the obstacle should be comparable to wavelength if the size of the obstacle is much too large compared to wavelength, diffraction is by a small angle. Here the size partition of wall is of the order of few metres. The wavelength of light is about 5 × 10-7 m, while sound waves of say 1 kHZ frequency have wavelength of about 0.3 m. Thus sound waves can bend around the partition while light waves cannot.
e) Typical sizes of apertures involved in ordinary optical instruments are much larger than the wavelength.
![]()
Question 18.
Two towers on top of two hills are 40 km apart. The line joining them passes 50 m above a hill halfway between the towers. What is the longest wavelength of radio waves, which can be sent between the towers without appreciable diffraction effects ?
Solution:
We want \(\frac{(5.0)^2}{\lambda}\) > > \(\frac{40,000}{2}\) ⇒ i.e. λ = < < \(\frac{(5.0)^2}{20,000}\) = \(\frac{250}{20,000}\) = 0.125 m = 12.5 cm
Question 19.
A parallel beam of light of wavelength 500 nm falls on a narrow slit and the resulting diffraction pattern is observed on a screen 1 m away. It is observed that the first minimum is at a distance of 2.5 mm from the centre of the screen. Find the width of the slit.
Solution:
Here λ = 500 nm = 5 × 10-7 m, D = 1 m, y = 2.5 mm = 2.5 × 10-3 m, d = ?
sin θ = \(\frac{\lambda}{d}=\frac{y}{D}\) ∴ d = \(\frac{\lambda \mathrm{D}}{\mathrm{y}}=\frac{5 \times 10^{-7} \times 1}{2.5 \times 10^{-3}}\) = 2 × 10-4 m = 0.2 mm
Question 20.
Answer the following questions :
(a) When a low flying aircraft passes overhead, we sometimes notice a slight shaking of the picture on our TV screen. Suggest a possible explanation.
(b) As you have learnt in the text, the principle of linear superposition of wave displacement is basic to understanding intensity distributions in diffraction and interference patterns. What is the justification of this principle ?
Solution:
a) Interference of the direct signal received by the antenna with the (weak) signal reflected by the passing air craft.
b) Super position principle follows from the linear character of the equation governing wave motion. It is true so ions as wave have small amplitude.
Question 21.
In deriving the single slit diffraction pattern, it was stated that the intensity is zero at angles of nλ/a. Justify this by suitable dividing the slit to bring out the cancellation.
Solution:
Divide the signal slit into n smaller slits of width a’ = \(\frac{\mathrm{a}}{\mathrm{n}}\). Each of the smaller slits sends zero intensity in the direction θ. The combination gives zero intensity as well.