AP Inter 2nd Year Physics Important Questions Chapter 13 Atoms

Students get through AP Inter 2nd Year Physics Important Questions 13th Lesson Atoms which are most likely to be asked in the exam.

AP Inter 2nd Year Physics Important Questions 13th Lesson Atoms

Very Short Answer Questions

Question 1.
What is the physical meaning of negative energy of an electron’ ?
Answer:
The ‘negative energy of an electron’ indicates that the electron is bound to the nucleus due to force of attraction.

Question 2.
Sharp lines are present in the spectrum of a gas. What does this indicate ?
Answer:
Sharp lines in the spectrum of gas, indicates bright lines against dark background.

Question 3.
Name a physical quantity whose dimensions are the same as those of angular momentum.
Answer:
Planck’s constant.

Question 4.
What is the difference between α – particle and helium atom ?
Answer:
Alpha particle

1. It is a + 2e charged Helium nucleus.
2. It contains 2 protons and 2 neutrons.

Helium atom

1. It has no charge.
2. It contains 2 protons, 2 electrons and 2 neutrons.

Question 5.
Among alpha, beta and gamma radiations, which get affected by the electric field ?
Answer:
Alpha and Beta radiations are get affected by the electric field.

Question 6.
What do you understand by the phrase ground state atom ?
Answer:
If the electron is present in the ground state, it is called ground state atom.

Question 7.
Why does the mass of the nucleus not have any significance in scattering in Rutherford’s experiment ?
Answer:
The size of the atom is 10^-10 m and size of the nucleus is 10^-15 m. Hence atom has large empty space. So the mass of nucleus has no significance in Rutherford’s scattering experiment.

Question 8.
The Lyman series of hydrogen spectrum lies in the ultraviolet region. Why ? [A.P. Mar. 15]
Answer:
The calculated values of wavelengths lie in the ultraviolet region of the spectrum will agree with the values of wavelengths observed experimentally by Lyman.

Question 9.
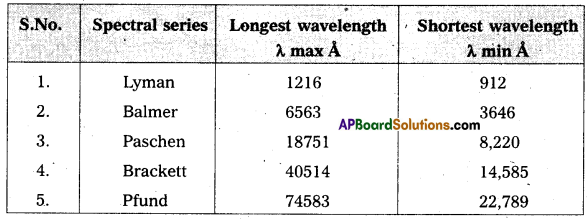
Write down a table giving longest and shortest wavelengths of different spectral series.
Answer:
Wavelength limits of some spectral series of hydrogen.

Question 10.
Give two drawbacks of Rutherford’s atomic model.
Answer:
Drawbacks of Rutherford’s atomic model:

1. As the revolving electron loses energy continuously, it must spiral inwards and eventually fall into the nucleus. But matter .is stable, we cannot expect the atom collapse.
2. The atoms should emit continuous spectrum, but what we observe is only a line spectrum.

Question 11.
If the kinetic energy of revolving electron in an orbit is K, what is its potential energy and total energy ?
Answer:
For an electron revolving round the nucleus, total energy is always negative and it is numerically equal to kinetic energy.
∴ Total energy = -Kinetic energy = -K
Potential energy is always negative and PE = 2 × TE = -2K

Short Answer Questions

Question 1.
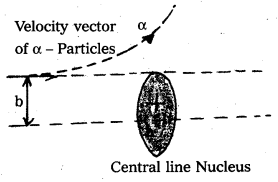
What is impact parameter and angle of scattering ? How are they related to each other ?
Answer:

1. Impact parameter (b) : Impact parameter is defined as the perpendicular distance of the initial velocity vector of the alpha particle from the central line of the nucleus, when the particle is far away from the nucleus of the atom.
2. Scattering angle (θ) : The scattering angle (θ) is the angle between the asymtotic direction of approach of the α – particle and the asymtotic direction in which it receeds.
3. The relation between b and θ is b = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{Ze}^2}{\mathrm{E}}\) cot \(\frac{\theta}{2}\) where E = K.E of α – particle = \(\frac{1}{2}\) mυ².

Question 2.
Explain the distance of closest approach and impact parameter.
Answer:
Distance of closest approach :

1. Suppose an α-particle with initial kinetic energy (K.E) is directed towards the centre of the nucleus of an atom.
2. On account of Coulomb’s repulsive force between nucleus and alpha particle, kinetic energy of alpha particle goes on decreasing and in turn, electric potential energy of the particle goes on increasing.
3. At certain distance d’ from the nucleus, K. E of α-particle reduces to zero. The particle stops and it cannot go closer to the nucleus. It is repelled by the nucleus and therefore it retraces its path, turning through 180°.
4. Therefore, the distance d is known as the distance of closest of approach.
   
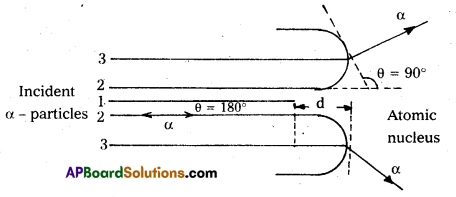
   The closest distance of approach,
   d = \(\frac{1}{4 \pi \varepsilon_0} \times \frac{Z e^2}{\left(\frac{1}{2} m v^2\right)}\)
5. Impact parameter (b) : Impact parameter is defined as the ⊥^r distance of the initial velocity vector of the α – particle from the central line of the nucleus, when the particle is far away from the nucleus of the atom.
   

Question 3.
Describe Rutherford atom model. What are the draw backs of this model ?
Answer:
Rutherford atom model: The essential features of Rutherford’s nuclear model of the atom or planetary model of the atom are as follows :

1. Every atom consists of tiny central core, called the atomic nucleus, in which the entire positive charge and almost entire mass of the atom are concentrated.
2. The size of nucleus is of the order of 10^-15m, which is very small as compared to the size of the atom which is of the order of 10^-10 m.
3. The atomic nucleus is surrounded by certain number of electrons. As atom on the whole is electrically neutral, the total negative charge of electrons surrounding the nucleus is equal to total positive charge on the nucleus.
4. These electrons revolve around the nucleus in various circular orbits as do the planets around the sun. The centripetal force required by electron for revolution is provided by the electrostatic force of attraction between the electrons and the nucleus.

Drawbacks : According to classical E.M. theory,

1. the revolving electron loses energy continuously, it must spiral inwards and eventually fall into the nucleus. As matter is stable, we cannot expect the atoms to collapse.
2. since the frequency of radiation emitted is the same as the frequency of revolution, the atom should radiate a continuous spectrum, but what we observe is only a line spectrum.

Question 4.
What are the limitations of Bohr’s theory of hydrogen atom ? [A.P. Mar. 17; Mar. 14]
Answer:
Limitations of Bohr’s theory of Hydrogen atom :

1. This theory is applicable only to simplest atom like hydrogen, with z = 1. The theory fails in case of atoms of other elements for which z > 1.
2. The theory does not explain why orbits of electrons are taken as circular, while elliptical orbits are also possible.
3. Bohr’s theory does not say anything about the relative intensities of spectral lines.
4. Bohr’s theory does not take into account the wave properties of electrons.

Question 5.
Write a short note on Debroglie’s explanation of Bohr’s second postulate of quantization. [T.S. Mar. 17]
Answer:
Debroglie’s explanation of Bohr’s second postulate of quantization :

1. The second postulate of Bohr atom model says that angular momentum of electron orbiting around the nucleus is quantized i.e., mυr = \(\frac{\mathrm{nh}}{2 \pi}\) where n = 1, 2, 3,….
2. According to Debroglie, the electron in its circular orbit, as proposed by Bohr, must be seen as a particle wave.
3. When a string fixed at two ends is plucked, a large number of wavelengths are excited and standing wave is formed.
4. It means that in a string, standing waves form when total distance travelled by a wave down the string and back is an integral number of wavelengths.
5. According to Debroglie, a stationary orbit is that which contains an integral number of Debrogile waves associated with the revolving electron.
6. For an electron revolving in n^th circular orbit of radius r_n, total distance covered = circumference of the orbit = 2πr_n
   ∴ For permissible orbit, 2πr_n = nλ
7. According to Debrogile, λ = \(\frac{h}{m v_n}\)
   Where υ_n is speed of electron revolving in n^th orbit
   ∴ 2πr_n = \(\frac{\mathrm{nh}}{\mathrm{m} v_{\mathrm{n}}}\)
   mυ_nr_n = \(\frac{\mathrm{nh}}{2 \pi}=\mathrm{n}\left(\frac{\mathrm{h}}{2 \pi}\right)\)
   i.e., angular momentum of electron revolving in n^th orbit must be an integral multiple of \(\frac{\mathrm{h}}{2 \pi}\), which is the quantum condition proposed by Bohr in second postulate.

Question 6.
Explain the different types of spectral series in hydrogen atom. [T.S. Mar. 16, A.P. Mar. 15]
Answer:
The atomic hydrogen emits a line spectrum consisting of five series.

1. Lyman series : v = Rc \(\left(\frac{1}{1^2}-\frac{1}{n^2}\right)\) where n = 2, 3, 4
2. Balmer series : v = Rc \(\left(\frac{1}{2^2}-\frac{1}{n^2}\right)\) where n = 3, 4, 5.
3. Paschen series : v = Rc \(\left(\frac{1}{3^2}-\frac{1}{n^2}\right)\) where n = 4, 5, 6
4. Brackett series: v = Rc \(\left(\frac{1}{4^2}-\frac{1}{n^2}\right)\) where n = 5, 6, 7
5. Pfund series: v = Rc \(\left(\frac{1}{5^2}-\frac{1}{n^2}\right)\) where n = 6, 7, 8

Long Answer Questions

Question 1.
State the basic postulates of Bohr’s theory of atomic spectra. Hence obtain an expression for the radius of orbit and the energy of orbital electron in a hydrogen atom. [A.P. Mar. 16]
Answer:
a) Basic postulates of Bohr’s theory are

1. The electron revolves round a nucleus in an atom in various orbits known as stationary orbits. The electrons cannot emit radiation when moving in their own stationary levels.
2. The electron can revolve round the nucleus only in allowed orbits whose angular momentum is the integral multiple of \(\frac{\mathrm{h}}{2 \pi}\)
   i.e., mυ_nr_n = \(\frac{\mathrm{nh}}{2 \pi}\) …………… (1)
   where n = 1, 2, 3 …………..
   If an electron jumps from higher energy (E₂) orbit to the lower energy (E₁) orbit, the difference of energy is radiated in the form of radiation.
   i.e., E = hv = E₂ – E₁ ⇒ v = \(\frac{E_2-E_1}{h}\) …………… (2)

b) Energy of emitted radiation: In hydrogen atom, a single electron of charge – e, revolves around the nucleus of charge e in a circular orbit of radius r_n.
1) K.E. of electron : For the electron to be in circular orbit, centripetal force = The electrostatic force of attraction between the electron and nucleus.

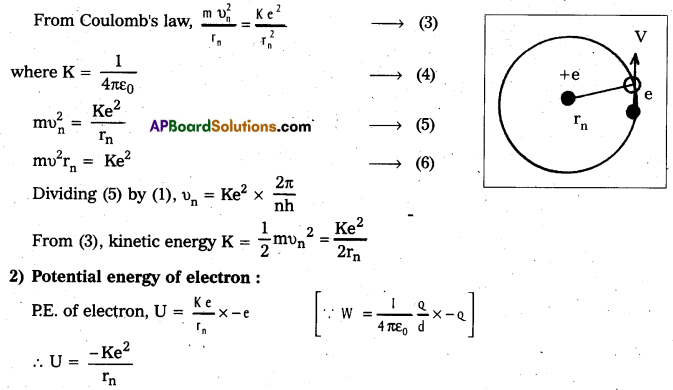
3) Radius of the oribit: Substituting the value of (6) in (2),
\(\frac{\mathrm{m}}{\mathrm{r}_{\mathrm{n}}}\left(\frac{\mathrm{n}^2 \mathrm{~h}^2}{4 \pi^2 \mathrm{r}_{\mathrm{n}}^2 \mathrm{~m}^2}\right)=\frac{\mathrm{Ke}^2}{\mathrm{r}_{\mathrm{n}}^2}\)
r_n = \(\frac{n^2 h^2}{4 \pi^2 m K e^2}\) ……………. (1)
∴ r_n = 0.53 n²

4) Total energy (E_n) : Revolving electron possess K.E. as well as P.E.

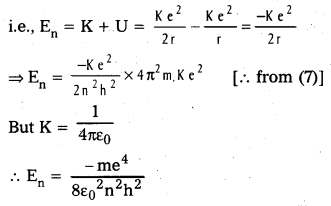
Problems

Question 1.
The radius of the first electron orbit of a hydrogen atom is 5.3 x HTum. What is the radius of the second orbit ?
Solution:
∴ r_n ∝ n²
\(\) ⇒ r₂ = 4r₁
∴ r₂ = 4 × 5.3 × 10^-11 = 2.12 × 10^-10m.

Question 2.
The total energy of an electron in the first excited state of the hydrogen atom is -3.4eV. What is the potential energy of the electron in this state?
Solution:
In 1^st orbit, E = -3.4 eV
Total energy E = \(\frac{\mathrm{KZe}^2}{2 \mathrm{r}}-\frac{\mathrm{KZe}^2}{\mathrm{r}}\)
\(\frac{\mathrm{KZe}^2}{\mathrm{r}}\) = U(say)
E = \(\frac{\mathrm{U}}{2}\) – u = \(\frac{\mathrm{-U}}{2}\)
U = -2E
∴ U = -2 × -3.4 = 6.8 eV.

Question 3.
The total energy of an electron in the first excited state of hydrogen atom is -3.4eV. What is the kinetic energy of the electron in this state ?
Solution:
In Hydrogen like atom, we know that
K = – Total energy E
Here E = – 3.4eV
∴ K = -(-3.4) = 3.4 eV . . ,

Question 4.
Prove that the ionisation energy of hydrogen atom is 13.6 eV.
Solution:
n = 1 corresponds to ground state.
E = \(\frac{-13.6}{\mathrm{n}^2}\) eV
E = \(\frac{-13.6}{\mathrm{1}^2}\) eV
E = -13.6 eV
The minimum energy required to free the electron from the ground state of hydrogen atom = 13.6 eV.
∴ Ionisation energy of hydrogen atom = 13.6 eV

Question 5.
Calculate the ionization energy for a lithium atom.
Solution:
For 3^Li7 atom, Z = 3, n = 2 [∵Li = 1s² 2s¹]
E_n = \(\frac{13.6 \mathrm{Z}^2}{\mathrm{n}^2}\) eV
= \(\frac{13.6 \times(3)^2}{4}\) = 30.6 eV
∴ Ionization energy of Lithium = 30.6eV

Question 6.
The wavelength of the first member of Lyman series is 1216 A. Calculate the wavelength of second member of Balmer series.
Solution:

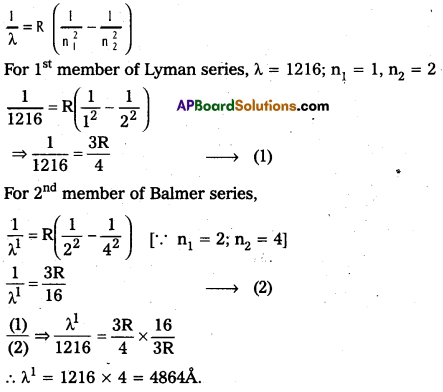
Textual Examples

Question 1.
In the Rutherford’s nuclear model of the atom, the nucleus (radius about 10^-15m) is analogous to the sun about which the electron move in orbit (radius ≈ 10^-10m) like the earth orbits around the sun. If the dimensions of the solar system had the same proportions as those of the atom, would the earth be closer to or farther away from the sun than actually it is ? The radius of earth’s orbit is about 1.5 × 10¹¹m. The radius of sun is taken as 7 × 10⁸ m.
Solution:
The ratio of the radius of electron’s orbit to the radius of nucleus is (10^-10 m)/(10^-15 m) = 105, that is, the radius of the electron’s orbit is 10⁵ times larger than the radius of nucleus. If the radius of the earth’s orbit around the sun were 10⁵ times larger than the radius of the sun, the radius of the earth’s orbit would be 10⁵ × 7 × 10⁸ m = 7 × 10¹³ m. This is more than 100 times greater than the actual orbital radius of earth. Thus, the earth would be much farther away from the sun.

It implies that an atom contains a much greater fraction of empty space than our solar system does.

Question 2.
In a Geiger-Marsden experiment, what is the distance of closest approach to the nucleus of a 7.7 MeV α-particle before it comes momentarily to rest and reverses its direction?
Solution:
The key idea here is that throughout the scattering process, the total mechanical energy of the system consisting of an α-particle and a gold nucleus is conserved. The system’s initial mechanical energy is E_i; before the particle and nucleus interact, and it is equal to its mechanical energy E_f when the α-particle momentarily stops. The initial energy E_t is just the kinetic energy K of the incoming α-particle. The final energy E_f is just the electric potential energy U of the system. The potential energy U can be calculated from Equation.
F = \(\frac{1}{4 \pi \varepsilon_0} \frac{(2 \mathrm{e})(\mathrm{Ze})}{\mathrm{r}^2}\)
Let d be the centre-to-centre distance between the α-particle and the gold nucleus when the α-particle is at its stopping point. Then we can write the conservation of energy
E_i = E_f as
K = \(\frac{1}{4 \pi \varepsilon_0} \frac{(2 \mathrm{e})(\mathrm{Ze})}{\mathrm{d}}=\frac{2 \mathrm{Ze}^2}{4 \pi \varepsilon_0 \mathrm{~d}}\)
Thus the distance of closest approach d is given by
d = \(\frac{2 \mathrm{Ze}^2}{4 \pi \varepsilon_0 \mathrm{~K}}\)
The maximum kinetic energy found in α-particles of natural origin is 7.7 MeV or 1.2 × 10^-12 J. Since 1/4πε₀ = 9.0 × 10⁹N m²/C². Therefore with e = 1.6 × 10^-19C, we have,
d = \(\frac{(2)\left(9.0 \times 10^9 \mathrm{Nm}^2 / \mathrm{C}^2\right)\left(1.6 \times 10^{-19} \mathrm{C}\right)^2 \mathrm{Z}}{1.2 \times 10^{-12} \mathrm{~J}}\)
= 3.84 × 10^-16 Zm
The atomic number of foil material gold is Z = 79, so that
d (Au) = 3.0 × 10^-14m = 30 fm. (1 fm (i.e. fermi) = 10^-15m.)
The radius of gold nucleus is, therefore, less than 3.0 × 10^-14 m. This is not in very good agreement with the observed result as the actual radius of gold nucleus is 6 fm. The cause of discrepancy is that the distance of closest approach is considerably larger than the sum of the radii of the gold nucleus and the a-particle. Thus, the α-particle reverses its motion without ever actually touching the gold nucleus.

Question 3.
It is found experimentally that 13.6 eV energy is required to separate a hydrogen atom into a proton and an electron. Compute the orbital radius and the velocity of the electron in a hydrogen atom.
Solution:
Total energy of the electron in hydrogen atom is – 13.6 eV = -13.6 × 1.6 × 10^-19J
= -2.2 × 10^-18 J.
Thus from equation, E = – \(\frac{\mathrm{e}^2}{8 \pi \varepsilon_0 \mathrm{r}}\) we have
– \(\frac{\mathrm{e}^2}{8 \pi \varepsilon_0 \mathrm{r}}\) = 2.2 10^-18 J
This gives the orbital radius
r = – \(\frac{\mathrm{e}^2}{8 \pi \varepsilon_0 \mathrm{r}}\) = \(\frac{\left(9 \times 10^9 \mathrm{Nm}^2 / \mathrm{C}^2\right)\left(1.6 \times 10^{-19} \mathrm{C}\right)^2}{(2)\left(-2.2 \times 10^{-18} \mathrm{~J}\right)}\)
= 5.3 × 10^-11 m.
The velocity of the revolving electron can be computed from Equation r = –\(\frac{e^2}{4 \pi \varepsilon_0 r m v^2}\)
with
m = 9.1 × 10^-31kg,
υ = \(\frac{\mathrm{e}}{\sqrt{4 \pi \varepsilon_0 \mathrm{mr}}}\) = 2.2 × 10⁶ m/s

Question 4.
According to the classical electromagnetic theory, calculate the initial frequency of the light emitted by the electron revolving around a proton in hydrogen atom.
Solution:
From Examjple 3 we know that velocity of electron moving around a proton in hydrogen atom in an orbit of radius 5.3 × 10^-11 m is 2.2 × 10^-6 m/s. Thus, the frequency of the electron moving around the proton is
v = \(\frac{v}{2 \pi \mathrm{r}}=\frac{2.2 \times 10^6 \mathrm{~m} \mathrm{~s}^{-1}}{2 \pi\left(5.3 \times 10^{-11} \mathrm{~m}\right)}\)
≈ 6.6 × 10¹⁵ Hz.
According to the classical electromagnetic theory we know that the frequency of the electromagnetic waves emitted by the revolving electrons is equal to the frequency of its revolution around the nucleus. Thus the initial frequency of the light emitted is 6.6 × 10¹⁵Hz.

Question 5.
A 10 kg satellite circles earth once every 2 h in an orbit having a radius of 8000 km. Assuming that Bohr’s angular momentum postulate applies to satellites just as it does to an electron in the hydrogen atom, find the quantum number of the orbit of the satellite.
Solution:
From equation, we have
mυ_nr_n = nh/2π
Here m = 10 kg and r_n = 8 × 10⁶ m. We have the time period T of the circling satellite as 2h. That is T = 7200 s.
Thus the velocity υ_n = 2π r_n/T
The quantum number of the orbit of satellite
n = (2π r_n)² × m(T × h)
Substituting the values,
n = (2π × 8 × 10⁶m)² × 10/(7200 s × 6.64 × 10^-34 J s)
= 5.3 × 10⁴⁵
Note that the quantum number for the satellite motion is extremely large. In fact for such large quantum numbers the results of quantisation conditions tend to those of classical physics.

Question 6.
Using the Rydberg formula, calculate the wavelengths of the first four spectral lines in the Lyman series of the hydrogen spectrum.
Solution:
The Rydberg formula is
hc/λ_if = \(\left(\frac{1}{n_{\mathrm{f}}^2}-\frac{1}{\mathrm{n}_{\mathrm{i}}^2}\right)\)
The wavelengths of the first four lines in the Lyman series correspond to transitions from n_i = 2, 3, 4, 5 to n_f = 1. We know that
\(\frac{\mathrm{me}^4}{8 \varepsilon_0^2 \mathrm{~h}^2}\) = 13.6 eV = 21.76 × 10^-19 J
Therefore,

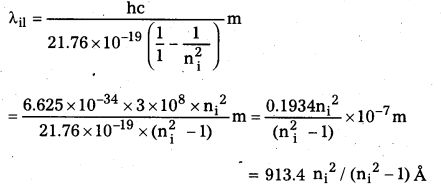
Substituting, n_i = 2, 3, 4, 5 we get λ₂₁ = 1218 Å, λ₃₁ = 1028 Å, λ₄₁ = 974.3 Å, and λ₅₁ = 951.4 Å.