AP Inter 2nd Year Physics Study Material Chapter 7 Moving Charges and Magnetism

Andhra Pradesh BIEAP AP Inter 2nd Year Physics Study Material 7th Lesson Moving Charges and Magnetism Textbook Questions and Answers.

AP Inter 2nd Year Physics Study Material 7th Lesson Moving Charges and Magnetism

Very Short Answer Questions

Question 1.
What is the importance of Oersted’s experiment?
Answer:
The importance of Oersted’s experiment is every current-carrying conductor produces a magnetic field around it which is perpendicular to the current-carrying conductor.

Question 2.
State Ampere’s law and Biot-Savart’s law. (T.S. Mar. ’19)
Answer:
Ampere’s law: The line integral of the intensity of magnetic induction around a closed path is equal to µ₀ times the total current enclosed in it.
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d} l}\) = \(\mu_0 \mathrm{i}\)

Biot – Savart’s laws: Biot – Savart’s states that the intensity of magnetic induction (dB) due to a small element is directly proportional to the

1. current (i)
2. length of the element (dl)
3. sine angle between radius vector (r) and dl and
4. Inversely proportional to the square of the point from current element.
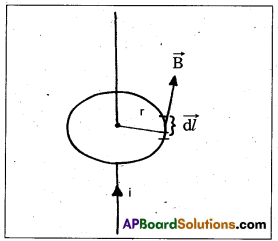
   ∴ dB ∝ \(\frac{\mathrm{i} \mathrm{d} l \sin \theta}{\mathrm{r}^2}\)
   dB = \(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{i} d l \sin \theta}{r^2}\)

Question 3.
Write the expression for the magnetic induction at any point on the axis of a circular current-carrying coil. Hence, obtain an expression for the magnetic induction at the centre of the circular coil.
Answer:

1. Intensity of magnetic induction field on the axis of the circular coil B = \(\frac{\mu_0 n i r^2}{2\left(r^2+x^2\right)^{3 / 2}}\)
2. At the centre of the coil B = \(\frac{\mu_0 \mathrm{ni}}{2 \mathrm{r}}\)

Question 4.
A circular coil of radius V having N turns carries a current “i”. What is its magnetic moment ?
Answer:
Magnetic moment (M) = N i A
M = N i (πr²) (∵ A = πr²)
∴ M = n N i r²

Question 5.
What is the force on a conductor of length L carrying a current “i” placed in a magnetic field of induction B ? When does it become maximum ?
Answer:

1. Force on a conductor (F) = B i L sin θ
2. If θ = 90°, F_Max = B i L
   i.e., the direction of current and magnetic field are perpendicular to each other, then force is maximum.

Question 6.
What is the force on a charged particle of charge “q” moving with a velocity “v” in a uniform magnetic field of induction B ? When does it become maximum ?
Answer:

1. Force on a charged particle (F) = B q v sin θ.
2. If θ = 90°, F_Max = B q v.

Question 7.
Distinguish between ammeter and voltmeter. (A.P. Mar. ’15)
Answer:
Ammeter

1. It is used to measure current.
2. Resistance of an ideal Ammeter is zero.
3. It is connected in series in the circuits.

Voltmeter

1. It is used to measure P.D between two points.
2. Resistance of ideal voltmeter is infinity.
3. It is connected in parallel in the circuits.

Question 8.
What is the principle of a moving coil galvanometer ?
Answer:
Moving coil galvanometer is based on the fact that when a current carrying coil is placed in a uniform magnetic field, it experiences a torque.
∴ current in the coil (i) ∝ deflecting angle (θ).

Question 9.
What is the smallest value of current that can be measured with a moving coil galvanometer ?
Answer:
Moving coil galvanometer is sensitive galvanometer, it is used to measure very small current upto 10^-9A.

Question 10.
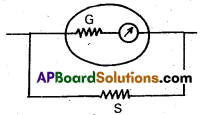
How do you convert a moving coil galvanometer into an ammeter ? (A.P. Mar. ’19)
Answer:
A small resistance is connected in parallel to the moving coil galvanometer, then it converts to Ammeter.
S = \(\frac{\mathrm{G}}{\frac{\mathrm{i}}{\mathrm{i}_{\mathrm{g}}}-1}\)

Question 11.
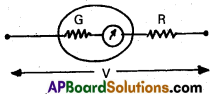
How do you convert a moving coil galvanometer into a voltmeter? (T.S. & A.P. Mar. ’16, T.S. Mar. ’15 Mar. ’14)
Answer:
A high resistance is connected in series to the moving coil galvanometer, then it converts to voltmeter.
R = \(\frac{\mathrm{v}}{\mathrm{i}_{\mathrm{g}}}-\mathrm{G}\)

Question 12.
What is the relation between the permittivity of free space e₀, the permeability of free space m₀ and the speed of light in vacuum ?
Answer:
Speed of light in vacuum (C) = \(\frac{1}{\sqrt{\mu_0 \varepsilon_0}}\)
Here μ₀ = m₀ = permeability in vacuum
ε₀ = permittivity in vacuum.

Question 13.
A current carrying circular loop lies on a smooth horizontal plane. Can a uniform magnetic field be set up in such a manner that the loop turns about the vertical axis ?
Answer:
Torque \((\tau)\) = \(\overrightarrow{\mathrm{M}}\) × \(\overrightarrow{\mathrm{B}}\) = i\(\overrightarrow{\mathrm{A}}\) × \(\overrightarrow{\mathrm{B}}\) (M = n i A)
where i is current, \(\overrightarrow{\mathrm{A}}\) is area vector, \(\overrightarrow{\mathrm{B}}\) is magnetic field. Area vector \(\overrightarrow{\mathrm{A}}\) acts normal to the loop, so torque \(\vec{\tau}\) cannot act along the vertical axis. The magnetic field is not set up to turn the loop around it self.

Question 14.
A current carrying circular loop is placed in a uniform external magnetic field. If the loop is free to turn, what is its orientation when it is achieves stable equilibrium ?
Answer:
The plane of the loop is perpendicular to the direction of magnetic field because the torque on the loop in this orientation is zero.

Question 15.
A wire loop of Irregular shape carrying current is placed In an external magnetic field. If the wire is flexible, what shape will the loop change to ? Why?
Answer:
For a given perimeter, a circle has maximum area among all geometrical shapes. So to maximise tie magnetic flux through it will assume a circular shape with its plane normal to the field.

Short Answer Questions

Question 1.
State and explain Biot-Savart law. (T.S. Mar. ’16, Mar. ’14)
Answer:
Consider a very small element of length dl of a conductor carrying current

Magnetic induction due to small element at a point P distance r form the element. Magnetic induction (dB) is directly proportional to

1. 1. current (i)
   2. Length of the element (dl)
   3.  sine angle between r and dl and
   4. Inversely proportional to the square of the distance from small element to point R
      
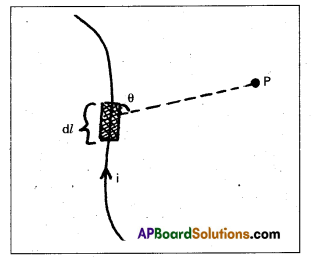
      dB ∝ \(\frac{\mathrm{id} l \sin \theta}{\mathrm{r}^2}\)
      dB = \(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{id} l \sin \theta}{\mathrm{r}^2}\)
      where μ = permeability in free space.
      \(\frac{\mu_0}{4 \pi}\) = 10^-7 Wb m^-1 A^-1

Question 2.
State and explain Ampere’s law.
Answer:
Ampere’s law : The line integral of the intensity of magnetic induction field around closed path is equal to μ₀ times the net current (i) enclosed by the path.
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d} l}\) = μ₀i
Proof: Consider a long” straight conductor carrying current i as shown in figure. Magnetic induction at a distance r from the conductor is given by

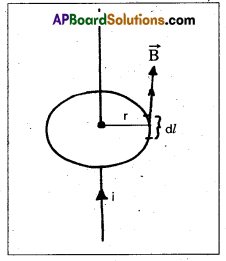
B = \(\frac{\mu_0 \mathrm{i}}{2 \pi \mathrm{r}}\) (from Biot-Savart’s law)
The value of B is same at all points on the circle.
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d} l}\) = \(\oint \mathrm{Bd} l \cos \theta\)
= \(\mathrm{B} \oint \mathrm{d} l\) = B × 2πr (∵ θ = 0° Angle between \(\overrightarrow{\mathrm{B}}\) & \(\overrightarrow{\mathrm{d} l}\) is zero)
= \(\frac{\mu_0 \mathrm{i}}{2 \pi \mathrm{r}}\) × 2πr
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d} l}\) = μ₀i.
This proves Ampere’s circuital laws.

Question 3.
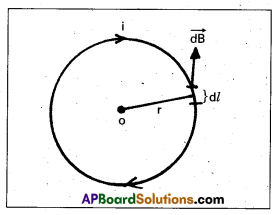
Find the magnetic induction due to a long current carrying conductor.
Answer:
Consider a long straight conductor carrying a current i. Let P be a point at a distance r from the conductor. Let r be the radius of the circle passing through point p.

(∵ \(\oint \mathrm{d} l\) = 2πr = circumference of the circle)
Magnetic induction is same at all points on the circle. Consider a small element of length dl.
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d} l}\) = \(\oint \mathrm{Bd} l \cos \theta\)
Angle between B and dl is zero i.e. θ = 0
= B\(\oint \mathrm{dl}\)
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d} l}\) = B (2πr) ——> (1)
According to Ampere’s laws
\(\oint \vec{B} \cdot \overrightarrow{d l}\) = µ₀i ——-> (2)
From equations (1) and (2), B (2πr) = µ₀ i
B = \(\frac{\mu_0 \mathrm{i}}{2 \pi \mathrm{r}}\)

Question 4.
Derive an expression for the magnetic induction at the centre of a current carrying circular coil using Biot-Savart law.
Answer:
Consider a circular coil of radius r and carry a current i. Consider a small element ‘dl’. Let O is the centre of the coil. By using Biot – Savart’s law
dB = \(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{i} d l \sin \theta}{\mathrm{r}^2}\)
Here angle \(\overrightarrow{\mathrm{d} t}\) and \(\overrightarrow{\mathrm{r}}\) is 90° (i.e. θ = 90°)
dB = \(\frac{\mu_0}{4 \pi} \frac{\mathrm{id} l}{\mathrm{r}^2}\) — (1)

As the field due to all elements of the circular loop have the same direction.
The resultant magnetic field can be obtained by integrating equation (1)
\(\int \mathrm{dB}\) = \(\int \frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{id} l}{\mathrm{r}^2}\)
B = \(\frac{\mu_0 \mathrm{i}}{4 \pi \mathrm{r}^2} \int \mathrm{d} l\) ∵ (\(\int\)dl = 2πr)
= \(\frac{\mu 0 \mathrm{i}}{4 \pi \mathrm{r}^2}\) × 2πr
B = \(\frac{\mu_0 \mathrm{i}}{2 \mathrm{r}}\)
If the circular coil has n turns.
B = \(\frac{\mu_0 \mathrm{ni}}{2 \mathrm{r}}\)

Question 5.
Derive an expression for the magnetic induction a point on the axis of a current carrying circular coil using
Answer:

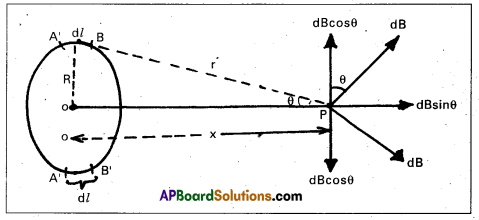
Consider a circular coil of radius R and carrying a current i. Let P is a point on the axis at a distance x from the centre O. Let r be the distance of small element (dl) from P.
From Biot – savart’s law
dB = \(\frac{\mu_0}{4 \pi} \frac{\text { id } l \sin \theta}{r^2}\) = \(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{id} l}{\mathrm{r}^2}\) —– (1) (∵ θ = 90° Angle between \(\overrightarrow{\mathrm{d} l}\) and \(\overrightarrow{\mathrm{r}}\))
dB can be resolved into two components dB cos θ and dB sinθ. If we consider another element diametrically opposite to AB.
This also resolved into dB cosθ and dB sinθ.
The components along the axis will add up and perpendicular to the axis will cancel.
∴ Resultant magnetic induction at P is
B = \(\int \frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{id} l \sin \theta}{\mathrm{r}^2}\)
= \(\frac{\mu_0 i}{4 \pi^2} \int d / \sin \theta\) (∵ sin θ = \(\frac{R}{r}\))
= \(\frac{\mu_0 \mathrm{i}}{4 \pi \mathrm{r}^2}\) × 2πR × \(\frac{\mathrm{R}}{\mathrm{r}}\) (∵ \(\int dl\) = 2πr)
B = \(\frac{\mu_0 \mathrm{iR}^2}{2 \mathrm{r}^3}\) —–> (3)
From figure r = \(\sqrt{\mathrm{R}^2+\mathrm{x}^2}\)
B = \(\frac{\mu_0 i R^2}{2\left(R^2+x^2\right)^{3 / 2}}\) —–> (4)
If the coil contains N turns,
B = \(\frac{\mu_0 N i R^2}{2\left(R^2+x^2\right)^{3 / 2}}\) —–> (5)

Question 6.
Obtain an expression for the magnetic dipole moment of current loop.
Answer:
We know that magnetic induction on the axial line of a circular coil is B = \(\frac{\mu_0 N \mathrm{iR}^2}{2\left(\mathrm{R}^2+\mathrm{x}^2\right)^{3 / 2}}\)
where N = Number of turns in the coil
R = Radius of the coil
x = Distance from centre of the coil
i = Current in a coil
If x >> R, Then B = \(\frac{\mu_0 \mathrm{Ni} \mathrm{R}^2}{2 \mathrm{x}^3}\)
Multiplying and dividing with 2π
B = \(\frac{\mu_0 \mathrm{Ni} \mathrm{R}^2}{2 \mathrm{x}^3} \times \frac{2 \pi}{2 \pi}\)
B = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 \mathrm{Ni}\left(\pi \mathrm{R}^2\right)}{\mathrm{x}^3}\) (∵ A = πR²)
B = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 \mathrm{Ni} \mathrm{A}}{\mathrm{x}^3}\) —– (1)
We know that magnetic induction field on the axial line of a bar magnet
B = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 \mathrm{M}}{\mathrm{x}^3}\) —– (2)
Comparing the equations (1) and (2)
Magnetic moment (M) = N i A

Question 7.
Derive an expression for the magnetic dipole moment of a revolving electron. (Ã.P. Mar. ’16)
Answer:
Consider an electron revolving in a circular orbit of radius r with speed v and frequency υ.
If the electron cross a point P on the circle in every revolution, then distance travelled by electron to complete one revolution = 2πr.
No. of revolutions in one second (υ) = \(\frac{\mathrm{v}}{2 \pi r}\)
The electric current (i) = \(\frac{\text { charge }}{\text { time }}\) = charge × frequency
i = e × \(\frac{\mathrm{v}}{2 \pi \mathrm{r}}\)
∴ Magnetic dipole moment (M) = I A (∵ N = 1)
M = \(\frac{\mathrm{ev}}{2 \pi \mathrm{r}} \times \pi \mathrm{r}^2\) (∵ A = πr²)
M = \(\frac{\text { evr }}{2}\)

Question 8.
Explain how crossed E and B fields serve as a velocity selector.
Answer:
When a charged particle q moving with a velocity v in presence of both electric and magnetic fields.
The force experienced due to electric field F_E = q\(\overrightarrow{\mathrm{E}}\)
The force experienced due to magnetic field F_B = q \(\left(\begin{array}{l}
\vec{v} \times \vec{B}
\end{array}\right)\)
Consider electric and magnetic fields are perpendicular to each other and also perpendicular to the velocity of the particle.
E = E\(\hat{j}\), B = B\(\hat{k}\), v = v\(\hat{i}\)
F_E = qE\(\hat{j}\), F_B = q (v\(\hat{i}\) × B\(\hat{k}\)) = – qvB\(\hat{j}\)
∴ F = F_E + F_B
F = q (E – υB) \(\hat{j}\)

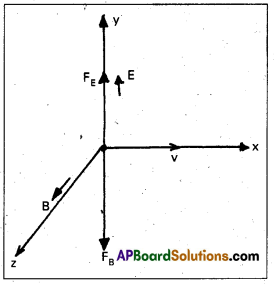
Thus electric and magnetic forces are in opposite directions.
We adjust E and B such that, the forces are equal
F_E = F_B
qE’ = q υ B
υ = \(\frac{E}{B}\)
This condition can be used to select charged particles of a particular velocity. The crossed field E and B serve as a velocity selector.

Question 9.
What are the basic components of a cyclotron ? Mention its uses ?
Answer:
Cyclotron is a device used to accelerate positively charged particles like protons, α – particles, deutrons etc.

Cyclotron mainly consists of

1. Two hollow D-shaped metallic chambers D₁ and D₂
2. High frequency oscillator
3. Strong electro magnet
4. Vacuum chamber.

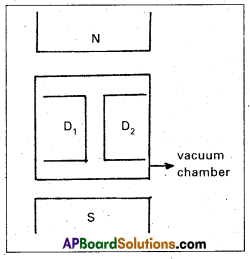
Uses of cyclotron :

1. It is used for producing radioactive material for medical purposes i.e. diagnostics and treatment of chronic diseases.
2. It is used to improve the quality of solids by adding ions.
3. It is used to synthesise fresh substances.
4. It is used to bombard the atoms with highly accelerated particles to study the nuclear reactions.

Long Answer Questions

Question 1.
Deduce an expression for the force on a current carrying conductor placed in a magnetic field. Derive an expression for the force per unit length between two parallel current carrying conductors.
Answer:
Expression for the Force acting on a current carrying conductor :
Consider a straight conductor (wire) of length ‘l’, area of cross section ‘A’, carrying a current ’i’, ‘which is placed in a uniform magnetic field of induction B’ as shown in fig.
We know the external magnetic field exerts a force on the conductor.
The electrons in effect move with an average velocity called drift velocity V_d‘. The direction of conventional current will be opposite to the direction of drift velocity.

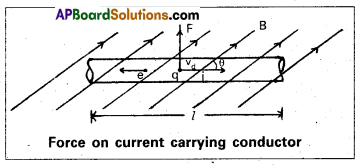
Let us assume that the current flows through the conductor from left ‘B’ in the plane of the paper makes an angle ‘θ’ with the direction of current ‘i’ as shown in fig.

If F’ is the force acting on the charge ‘q’ in B
∴ F = q V_d B sin θ
If ‘n’ represents number of moving electrons per unit volume (∵ n = \(\frac{\mathrm{N}}{\mathrm{V}}\))
∴ Current i = nqV_dA
If ‘N’ is the number of electrons in the length ‘l’
N = nlA .
Total force on conductor F = F’.N (∵ N = nV = n × A × l)
= (q V_dB sin θ) (nlA)
= (nqV_dA) (IB sin θ)
∴ F = ilB sin θ
Case (i) : If θ = 0°, F_Min = 0
Case (ii) : If θ = 90°, F_Max = Bil

Expression for the force between two Parallel conductors carrying conductors:
Consider two straight parallel conductors .‘AB and ‘CD’ carrying currents ‘i₁’ and “i₂’ and which are separated by a distance ‘r’ as shown in fig.

If B₁ and B₂ are magnetic inductions produced by the current carrying conductors AB and CD. Magnetic induction B₁ at a distance ‘r’ from the conductor ‘AB’ can be written as B₁ = \(\frac{\mu_0 i_1}{2 \pi r}\)
If ‘F is force acting on CD’ due to magnetic induction B₁ then
F_CD = i₂lB₁
Where l = length of the conductor
F_CD = \(\mathrm{i}_2 l\left(\frac{\mu_0 \mathrm{i}_1}{2 \pi \mathrm{r}}\right)\) = \(\frac{\mu_0 \mathrm{i}_1 \mathrm{i}_2 l}{2 \pi \mathrm{r}}\) — (1)

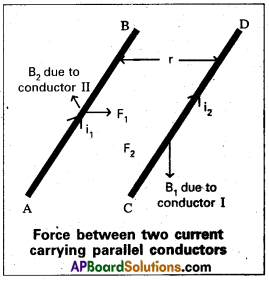
The direction of the force can be determined by using Flemings left hand rule.
Similarly we can find the force acting on the conductor AB due to magnetic induction B₂.
F_AB = i₁lB₂
∴ F_AB = \(\mathrm{i}_1 l\left(\frac{\mu_0 \mathrm{i}_2}{2 \pi \mathrm{r}}\right)\) —– (2) [∵ B₂ = \(\frac{\mu_0 i_2}{2 \pi r}\)]
From the equations (1) and (2) F_AB = F_CD = \(\frac{\mu_0 \mathrm{i}_1 \mathrm{i}_2 l}{2 \pi \mathrm{r}}\)
∴ Force between two parallel, straight conductors carrying currents
F = \(\frac{\mu_0 \mathrm{i}_1 \mathrm{i}_2 l}{2 \pi \mathrm{r}}\)
Force per unit length \(\frac{\mathrm{F}}{l}\) = \(\frac{\mu_0 \mathrm{i}_1 \mathrm{i}_2}{2 \pi \mathrm{r}}\)

Question 2.
Obtain an expression for the torque on a current carrying loop placed in a uniform magnetic field. Describe the construction and working of a moving coil galvanometer.
Answer:
Torque acting on a coil carrying a current kept in a uniform magnetic field : Let a rectangular current loop ABCD of length l = AB = CD and width b = AD = BC carrying a current “i” be suspended in a magnetic field of flux density B.
The normal ON drawn to the plane of the coil makes an angle ‘θ’ with the magnetic field B.

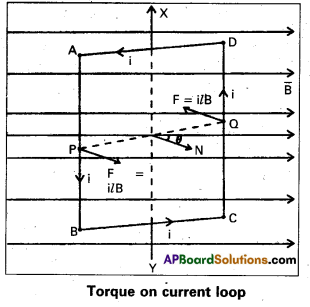
Force on arm AD = i\(\overline{\mathrm{b}}\) × \(\overrightarrow{\mathrm{B}}\) acting upwards along the axis of suspension
Force on arm BC = i\(\overline{\mathrm{b}}\) × \(\overrightarrow{\mathrm{B}}\) acting downwards along the axis of suspension
Hence these two forces cancel.

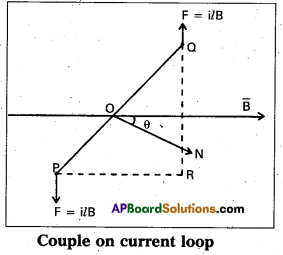
Force on arm AB = ilB acting perpendicular to the plane as shown.
Force on arm CD = ilB acting perpendicular to the plane as shown.
These two forces constitute a couple on the coil.
Moment of the couple = (Force) × (Perpendicular distance between the forces) = i/B (PQ sin θ)
Torque = ilB b sinθ
But l × b = Area of coil
∴ Torque = iAB sin θ
If the loop has n’ turns the torque on the coil
\(\tau\) = n i AB sinθ
If “ϕ’ is the deflection of the coil, that is the angle between the plane of the coil and magnetic field B
\(\tau\) = n i AB cos ϕ

Moving coil galvanometer:
Principle : When a current carrying coil is placed in the uniform magnetic field, it experiences a torque.

Construction: .

1. It consists of a coil wound on a non metallic frame.
2. A rectangular coil is suspended between two concave shaped magnetic poles with the help of phosphour Bronze wire.
3. The lower portion of the coil ‘is connected to a spring.
4. A small plane mirror M is fixed to the phosphour Bronze wire to measure the deflection of the coil.
5. A small soft iron cylinder is placed with in the coil without touching the coil. ‘The soft iron cylinder increases the induction field strength.
6. The concave shaped magnetic poles render the field radial. So maximum torque acting on it.
7. The whole of the apparatus is kept inside a brass case provided with a glass window.
   

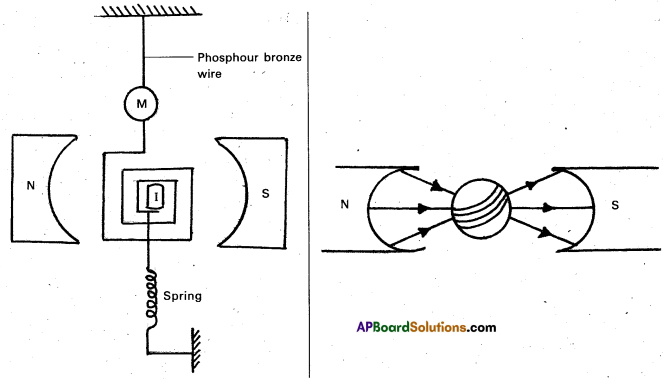
Theory:
Consider a rectangular coil of length l and breadth b and carrying current i suspended in the induction field strength B.
Deflecting torque \((\tau)\) = B i A N —–> (5)

where A = Area of the coil
N = Total number of turns.
The restoring torque developed in the suspension = C θ —-> (2)
Where C is the couple per unit twist and θ is the deflection made by the coil. When the coil is in equilibrium position
Deflecting torque = Restoring torque
B i A N = C θ
i = \(\left(\frac{C}{\mathrm{BAN}}\right) \theta\)
Where K = \(\frac{\mathrm{C}}{\mathrm{BAN}}\) = Galvanometer constant
i = K θ —-> (3)
i ∝ θ
Thus deflection of the coil is directly proportional to the current flowing through it.
The deflection in the coil is measured using lamp and scale arrangement.

Question 3.
How can a galvanometer be converted fo an ammeter ? Why is the parallel resistance smaller that the galvanometer resistance ?
Answer:
Conversion of Galvanometer into Ammeter :
Galvanometer is converted into an ammeter by connecting a suitable resistance is parallel to it.
This arrangement decreases the effective resistance.

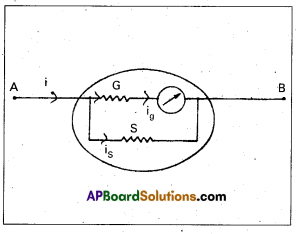
Ammeter is used for measuring the current in an electric circuit and it is connected in series in circuit.
The inclusion of the ammeter in the circuit should not alter the current or total resistance of the circuit so it has very low resistance.
The resistance of An ideal Ammeter is zero.
Let G and S be the Galvanometer and shunt resistances respectively.
Let ‘i’ be the total current, divided at A into i_g and i_s as shown in fig.
From Kirchhoff’s I^st law i = i_g + i_s
As ‘G’ and ‘S’ are parallel
PD. across Galvanometer = P.D. across shunt
i_g G = i_s S
S = \(\frac{\mathrm{i}_{\mathrm{g}}}{\mathrm{i}_{\mathrm{s}}} \mathrm{G}\)
= \(\frac{\mathrm{Gi}_{\mathrm{g}}}{\mathrm{i}-\mathrm{i}_{\mathrm{g}}}\) [∵ i_s = i – i_g]
S = \(\frac{\mathrm{G}}{\frac{\mathrm{i}}{\mathrm{i}_{\mathrm{g}}}-1}\)
If \(\frac{\mathrm{i}}{\mathrm{i}_g}\) = n ⇒ i_g = \(\frac{i}{n}\)
∴ The current flowing through the galvanometer be \(\left(\frac{1}{n}\right)^{\text {th }}\) of total current.
∴ S = \(\frac{\mathrm{G}}{\mathrm{n}-1}\)
If ‘R is the effective resistance between points ‘A’ and ‘B’ then

Hence current through galvanometer is proportional to the total current. Since ‘S’ is small major portion of the current flows through it and a small portion of current flows through G. So shunt protects the galvanometer from high currents. Parallel resistance is smaller than Galvanometer resistance because to protect the Galvanometer from high (large) current (or) to pass. Large currents through shunt and small current passes through the galvanometer.

Question 4.
How can a galvanometer be converted to a voltmeter ? Why is the series resistance greater that the galvanometer resistance ?
Answer:
Conversion of Galvanometer into, Voltmeter: A galvanometer-is converted into voltmeter by connecting a high resistance (R) in series with it. Voltmeter is used to measure the RD. between any two points in circuit and it is connected in parallel to the component of the circuit.

Let V be the potential difference to be measured between the points ‘A’ and ‘B’.
∴ V = (R + G) i_g [∴ V = iR]

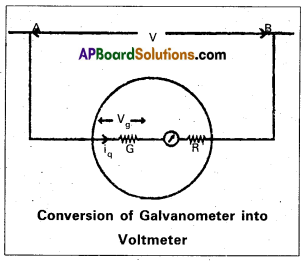
Where G = Galvanometer Resistance
i_g = Current passing through the galvanometer
\(\frac{\mathrm{V}}{\mathrm{i}_g}\) = R + G
∴ R = \(\frac{\mathrm{V}}{\mathrm{i}_g}\) – G —- (1)
The value of ‘R’ can be calculated by using the above formula. If V_g is the maximum P.D. across the galvanometer then V_g = i_g G
∴ i_g = \(\frac{V_g}{G}\) —— (2)
Substitute ‘i_g‘ in Equ (1)
R = \(\frac{V G}{V_g}\) – G = G\(\left(\frac{V}{V_g}-1\right)\)
If \(\frac{V}{V_g}\) = n ⇒ R = G(n – 1)
Note: n = \(\frac{V}{V_g}\) is the ratio of maximum voltage to be measured to the maximum voltage across the galvanometer
Series resistance is greater than galvanometer resistance because the current in external resistance and potential difference will be decreased and to increase the resistance of the galvanometer.

Question 5.
Derive an expression for the force acting between two very long parallel current-carrying conductors and hence define the Ampere.
Answer:
Force between two parallel conductors carrying current:

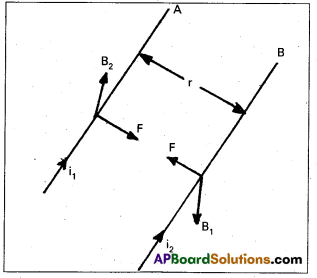
Let two long parallel conductors A and B seperated by a distance r carry currents i₁ and i₂ in the same directions.
The current i₁ produces magnetic induction around the conductor A and the current i₂ produces magnetic induction B₂ around the conductor B.
If l is the length of each conductor,
The magnetic induction B₁ at distance r from conductor A is
B₁ = \(\frac{\mu_0 \mathrm{i}_1}{2 \pi \mathrm{r}}\) — (1)
The force on conductor B is given by
F₂ = i₂ l B₁ —- (2)
The direction of force is given by Fleming left hand rule
F₂ = i₂l × \(\frac{\mu_0 \mathrm{i}_1}{2 \pi \mathrm{r}}\) = \(\frac{\mu_0 \mathrm{i}_1 \mathrm{i}_2 l}{2 \pi \mathrm{r}}\) —- (3)
The direction of force F₂ is towards conductor A. Similary the magnetic induction B₂ at distance r from conductor B is
B₂ = \(\frac{\mu_0 \mathrm{i}_2}{2 \pi \mathrm{r}}\) — (4)
The force on conductor A is given by
F₁ = i₁lB₂ —- (5)
Substituting B₂ value in equation (5)
F₁ = \(\frac{\mathrm{i}_1 l \times \mu_0 \mathrm{i}_2}{2 \pi \mathrm{r}}\)
F₁ = \(\frac{\mu_0 \mathrm{i}_1 \mathrm{i}_2 l}{2 \pi \mathrm{r}}\) — (6)
It can be seen that | F₁| = | F₂| = \(\frac{\mu_0 \mathrm{i}_1 \mathrm{i}_2 l}{2 \pi \mathrm{r}}\)
The force per unit length of the conductor is given by
\(\frac{F}{l}\) = \(\frac{\mu_0 \mathrm{i}_1 \mathrm{i}_2}{2 \pi \mathrm{r}}\) —–>(7)

Definition of Ampere:
If i₁ = i₂ = 1A, r = 1m
F/l = \(\frac{4 \pi \times 10^{-7} \times 1 \times 1}{2 \pi \times 1}\) = 2 × 10^-7 Nm^-1
“When two infinitely long parallel conductors, carrying the same current are seperated by 2 × 10^-7 Nm^-1, then the current flowing through each conductor is said to be one Ampere”.

Problems

Question 1.
A current of 10A passes through two very long wires held parallel to each other and separated by a distance of 1m. What is the force per unit length between them ? (T.S. Mar. ’19 & A.P. & T.S. Mar. ’15)
Solution:
i₁ = i₂ = 10A
r = 1m
\(\frac{\mathrm{F}}{l}\) = \(\frac{\mu_0 \mathrm{i}_1 \mathrm{i}_2}{2 \pi \mathrm{r}}\)
= \(\frac{4 \pi \times 10^{-7} \times 10 \times 10}{2 \pi \times 1}\)
\(\frac{\mathrm{F}}{\mathrm{l}}\) = 2 × 10^-5 Nm^-1.

Question 2.
A moving coil galvanometer can measure a current of 10^-6 A. What is the resistance of the shunt required if it is to measure 1A ?
Solution:
Galvanometer current (i_g) = 10^-6A
i = 1A
S = \(\frac{\mathrm{G}}{\frac{\mathrm{i}}{\mathrm{i}_{\mathrm{g}}}-1}\)
= \(\frac{\mathrm{G}}{\frac{1}{10^{-6}}-1}\)
S = \(\frac{G}{10^6-1}\)
S = \(\frac{\mathrm{G}}{99,999} \Omega\)
Where G = Galvanometer resistance.

Question 3.
A circular wire loop of radius 30 cm carries a current of 3.5 A. Find the magnetic field at a point on its axis 40 cm away from the centre.
Solution:
Radius (r) = 30 cm = 30 × 10^-2m
Current (i) = 3.5 A
x = 40 cm = 40 × 10^-2m

Textual Exercises

Question 1.
A circular coil of wire consisting of 100 turns, each of radius 8.0 cm carries a current of 0.40 A. What is the magnitude of the magnetic field B at the centre of the coil ?
Solution:
Here, n = 100, r = 8cm = 8 × 10^-2 m and I = 0.40 A
The magnetic field B at the centre
B = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 \pi \mathrm{In}}{\mathrm{r}}\) = \(\frac{10^{-7} \times 2 \times 3.14 \times 0.4 \times 100}{8 \times 10^{-2}}\) = 3.1 × 10^-4T
The direction of magnetic field depends on the direction of current if the direction of current is anticlockwise. According to Maxwell’s right hand rule, the direction of magnetic field at the centre of coil will be perpendicular outwards to the plane of paper.

Question 2.
A long straight wire carries a current of 35 A. What is the magnitude of the field B at a point 20 cm from the wire ?
Solution:
Here, I = 35 A and r = 20 cm = 0.2 m
The wire is along and it is considered as an infinite length wire. The magnetic field
B = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 \mathrm{I}}{\mathrm{r}}\) = \(\frac{10^{-7} \times 2 \times 35}{0.2}\) = 3.5 × 10^-5T

Question 3.
A long straight wire in the horizontal plane carries a current of 50 A in north to south direction. Give the magnitude and direction of B at a point 2.5 m east of the wire.
Solution:
Given I = 50A and r = 2.5 m
The magnitude of magnetic field

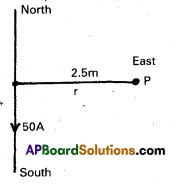
B = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 I}{r}\) = 10^-7 × \(\frac{2 \times 50}{2.5}\)
= 4 × 10^-6T
The direction of magnetic field at point P is given by Maxwell’s right hand rule.

Question 4.
A horizontal overhead power line carries a current of 90 A in east to west direction. What is the magnitude and direction of the magnetic field due to the current 1.5 m below the line ?
Solution:

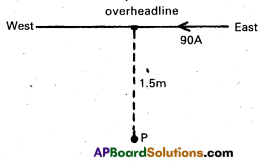
Given I = 90 A and r = 1.5m
The magnitude of magnetic field
B = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 \mathrm{I}}{\mathrm{r}}\) = \(\frac{10^{-7} \times 2 \times 90}{1.5}\)
= 1.2 × 10^-5 T
The direction of magnetic flux is given by Maxwell’s right hand rule. So, the direction of magnetic field at point P due to the following current is perpendicularly outwards to the plane of paper.

Question 5.
What is the magnitude of magnetic force per unit length on a wire carrying a current of 8A and making an angle of 300 with the direction of a uniform magnetic field of 0.15.T?
Solution:
According to the question
I = 8 A, θ = 30°, B = 0.15 T, l = 1 m
The magnitude of magnetic force

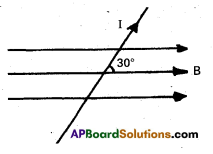
f = I(l × B) = I l B sin θ
= 8 × 1 × 0.15 × sin 30°
= \(\frac{8 \times 0.15}{2}\) = 4 × 0.15 = 0.6 N/m

Question 6.
A 3.0 cm wire carrying a current of 10 A is placed inside a solenoid perpendicular to its axis. The magnetic field inside the solenoid is given to be 0.27 T. What is the magnetic force on the wire ?
Solution:
Here, the angle between the magnetic field and the direction of flow of current is 90°. Because the magneitc field due to a solenoid is along the axis of solenoid and the wire is placed perpendicular to the axis.

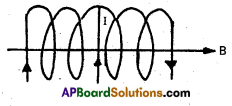
Given, l = 3 cm = 3 × 10^-2 m, I = 10A, B = 0.27 T
f = I l B sin 90°
= 10 × 3 × 10^-2 × 0.27 = 8.1 × 10^-2 N
According to right hand palm rule, the direction of magnetic force is perpendicular to plane of paper inwards.

Question 7.
Two long and parallel straight wires A and B carrying currents of 8.0 A and 5.0 A in the same direction are separated by a distance of 4.0 cm. Estimate the force on a 10 cm section of wire A.
Solution:
Given I₁ = 8A, I₂ = 5A and r = 4 cm = 0.4m
F = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 \mathrm{I}_1 \mathrm{I}_2}{\mathrm{r}}\) = \(\frac{10^{-7} \times 2 \times 8 \times 5}{0.04}\) = 2 × 10^-4N
The force on A of length 10 cm is F¹ = F × 0.1 (∵ 1m = 100 cm)
F¹ = 2 × 10^-4 × 0.1
F¹ = 2 × 10^-5N.

Question 8.
A closely wound solenoid 80 cm long has 5 layers of windings of 400 turns each. The diameter of the solenoid is 1.8 cm. It the current carried is 8.0 A, estimate the magnitude of B inside the solenoid near its centre.
Solution:
The length of solenoid, l = 80 cm = 0.8 m
Number of layers = 5
Number of turns per layer = 400

Diameter of solenoid = 1.8 cm
Current in solenoid = I = 8 A
∴ The total number of turns N = 400 × 5 = 2000
and no. of turns / length, n = \(\frac{2000}{0.8}\) = 2500
The magnitude of magnetic field inside the solenoid
B = μ₀nl = 4 × 3 .14 10^-7 × 2500 × 8
= 2. 5 × 10^-2 T
The direction of magnetic field is along the axes of solenoid.

Question 9.
A square coil of side 10 cm consists of 20 turns and carries current of 12 A. The coil is suspended vertically and the normal to the plane of the coil makes an angle of 30° with the direction of a uniform horizontal magnetic field of magnitude 0.80 T. What is the magnitude of torque experienced by the coil ?
Solution:
Given, side of square coil = 10 cm = 0.1 m
Number of turns (n) = 20
current in square coil I = 12 A
Angle made by coil θ = 30°
Magnetic filed B = 0.80 T

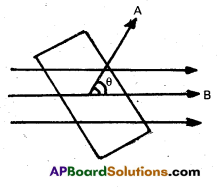
The magnitude of torque experienced by the coil
\(\tau\) = NIAB sinθ
= 20 × 12 × (10 × 10^-2)² × 0.80 × sin 30°
= 0.96 N – m

Question 10.
Two moving coil meters, M₁ and M₂ have the following particulars :
R₁ = 10 Ω, n₁ = 30,
A₁ = 3.6 × 10^-3 m², B₁ = 0.25 T
R₂ = 14Ω, n₂ = 42,
A₂ = 1.8 × 10^-3 m², B₂ = 0.50 T, K₁ = K₂
(The spring constants are identical for the two meters).
Determine the ratio of (a) current sensitivity and (b) voltage sensitivity of M₂ and M₁.
Solution:
Given, R₁ = 10 Ω, N₁ = 30, A₁ = 3.6 × 10^-3 m², B₁ = 0.25 T
R₂ = 140Ω, n₂ = 42, A₂ = 1.8 × 10^-3 m², B₂ = 0.50 T, K₁ = K₂

Question 11.
In a chamber, a uniform magnetic field of 6.5 G (1 G = 10^-4 T) is maintained. An electron is shot into the field with a speed of 4.8 × 10⁶ m s^-1 normal to the field. Explain why the path of the electron is a circle. Determine the radius of the circular orbit.
(e = 1.5 × 10^-19 C, m_e = 9.1 × 10^-31 kg)
Solution:
Given, magnetic field B = 6.5 G = 6.5 × 10^-4 T
Charge e = -1.6 × 10^-19 C
Speed of electron V = 4.8 × 10⁶ m/s
Mass of electron m_e = 9.1 × 10^-31 kg
Angle between magnetic field and electron (θ) = 90°
The force on charge particle entering in the magnetic field
F = q (V × B) = e (V × b)
The electron attains a circular path and necessarily centripetal force is provided by magnetic force.
e (V × B) = \(\frac{m V^2}{r}\)
e V B sin 90° = \(\frac{\mathrm{m} \mathrm{V}^2}{\mathrm{r}}\)
r = \(\frac{\mathrm{mV}}{\mathrm{e} \mathrm{B} \times 1}\) = \(\frac{9.1 \times 10^{-31} \times 4.8 \times 10^6}{1.6 \times 10^{-19} \times 6.5 \times 10^{-4}}\) = 4.2 × 10^-2m = 4.2 cm

Question 12.
From Exercise 11 data, obtain the frequency of revolution of the electron in its circular orbit. Does the answer depend on the speed of the electron ? Explain.
Solution:
Given
B = 6.5 G = 6.5 × 10^-4T, V = 4.8 × 10⁶ m/s, e = 1.6 × 10^-19C
m_e = 9.1 × 10^-3 kg
\(\frac{\mathrm{mV}^2}{\mathrm{r}}\) = q V B ⇒ \(\frac{\mathrm{mV}}{\mathrm{r}}\) = qB
If angular velocity of electron is ω, then
V = r ω
ω = \(\frac{\mathrm{qB}}{\mathrm{m}}\)
2πn = \(\frac{\mathrm{qB}}{\mathrm{m}}\) ⇒ n = \(\frac{\mathrm{qB}}{2 \pi \mathrm{m}}\)
Frequency of revolution of electron in orbit
υ = \(\frac{\mathrm{Bq}}{2 \pi \mathrm{m}}\) = \(\frac{\mathrm{Be}}{2 \pi \mathrm{m}_{\mathrm{e}}}\) = \(\frac{6.5 \times 10^{-4} \times 1.6 \times 10^{-19}}{2 \times 3.14 \times 9.1 \times 10^{-31}}\) = 18.18 × 10⁶ Hz.

Question 13.
(a) Circular coil of 30 turns and radius 8.0 cm carrying a current of 6.0 A is suspended vertically in a uniiorm horizontal magnetic field of magnitude 1.0 T. The field lines make an angle of 60° with the normal of the coil. Calculate the magnitude of the counter torque that must be applied to prevent the coil form turning.
(b) Would your answer change, If the circular coil in (a) were replaced by a planar coil of some irregular shape that encloses the same area ? (All other particular are also unaltered.)
Answer:
a) Given, no. of turns (n) = 30, radius (r) = 8 cm = 0.08 m
Current in coil (I) = 6A, Magnetic field (B) = 1.0 T,
Angle made by field with the normal of the coil, θ = 60°
\(\tau\) = n I A Bsinθ
= 30 × 6 × π (0.08)² × 1 × sin 60°
= 30 × 6 × 3.14 × 0.08 × 0.08 × \(\frac{\sqrt{3}}{2}\)
\(\tau\) = 3.133 N – m

b) From the formula, it is clear that the torque on the loop does not depend on the shape if area remains constant. So, the torque remains constant.

Additional Exercises

Question 1.
Two concentric circular coils X and Y of radii 16 cm and 10 cm, respectively, lie in the same vertical plane containing the north to south direction. Coil X has 20 turns and carries a current of 16 A; coil Y has 25 turns and carries a current of 18 A. The sense of the current in X Is anticlockwise, and clockwise In Y, for an observer looking at the coils facing west. Give the magnitude and direction of the net magnetic field due to the coils at their centre.
Solution:
For coil X
Radius of coil, r_x = 16 cm = 0.16 m
No. of turns n_x = 20
Current in the coil I_x = 16A (Anti clockwise) .
For coil Y
Radius of coil, r_y = 10 cm = 0.1 m
No. of turns n_y = 25
Current in the coil I_y = 18 A (clockwise)
The magnitude of the magnetic field at the centre of coil X
B_x = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 I_x \cdot \pi n_x}{r_x}\) = \(\frac{10^{-7} \times 2 \times 16 \times 3.14 \times 20}{0.16} \mathrm{~T}\)
B_x = 4π × 10^-4T
The magnitude field at the centre B =B_y – B_x
= (9π – 4π) × 10^-4 = 5π × 10^-4
= 1.6 × 10^-3T (towards west)

Question 2.
A magnetic field of 1oo G (1 G = 10^-4 T) is required which is uniform in a region of linear dimension about 10 cm and area of cross-section about 10^-3 m². The maximum current carrying capacity of a given coil of wire is 15 A and the number of turns per unit length that can be wound round a côre is at most 1000 turns m^-1. Suggest some appropriate design particulars of a solenoid for the required purpose. Assume the core is not ferromagnetic.
Solution:
Magnetic field B = 100 G = 100 × 10^-4T = 10^-2 T
Maximum current I = 15A, n = 1000/m.
The magnitude of magnetic field B = μ₀ nI
nI = \(\frac{\mathrm{B}}{\mu_0}\) = \(\frac{10^{-2}}{4 \times 3.14 \times 10^{-7}}\)
⇒ nI = 7961 ≈ 8000
Here; the product of n I is 8000. So,
Current I = 8A and no. of turns = 1000
The other design is I = 10A and n = 800/m. This is the most appropriate design as the requirement.

Question 3.
For a circular coil of radius R and N turns carrying current I, the magnitude of the magnetic field at a point on its axis at a distance x from Its centre is given by,
B = \(\frac{\mu_0 \mathbf{I R}^2 \mathbf{N}}{2\left(\mathbf{x}^2+\mathbf{R}^2\right)^{3 / 2}}\)
a) Show that this reduces to the familiar result for field at the centre of the coil.
Solution:
Given, magnetic field at distance x :
B = \(\frac{\mu_0 \mathrm{NIR}^2}{2\left(\mathrm{x}^2+\mathrm{R}^2\right)^{3 / 2}}\) (∵ x = 0)
∴ The magnetic field at the centre B = \(\frac{\mu_0 \mathrm{~N} \mathrm{I} \mathrm{R}^2}{2 \mathrm{R}^3}\)
B = \(\frac{\mu_0 \mathrm{~N} \mathrm{I}}{2 \mathrm{R}}\)
This result is same as the magnetic field due to current loop at its centre.

b) Consider two parallel co-axial circular coils of equal radius R, and number of turns N, carrying equal currents in the same direction, and separated bya distance R. Show that the field on the axis around the mid-point between the coils is uniform over a distance that is small as compared to R, and is given by, B = 072\(\frac{\mu_0 \mathrm{NI}}{\mathrm{R}}\) approximately.
ISuch an arrangement to produce a nearly uniform magnetic field over a small region is known as Helmholtz coils.] :
Solution:
Radius of two parallel co-axial coils = R, number of turns = N Current = I
Let the mid points between the coils is at point O and P be the pomt around the mid point O.
Suppose, the distance between OP = d which is very less than R (d < < R)
For the Coil A,
O_AP = \(\frac{R}{2}\) + d
the magnetic field at point P due to coil A.


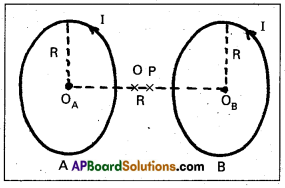
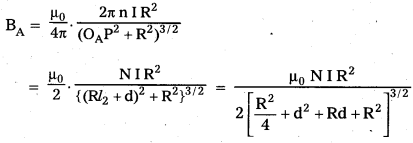
as according to the question d < <R, so neglect turn d².

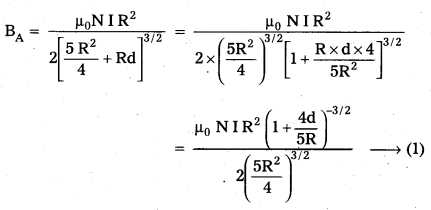
The direction of B_A is along PO_B. According to Maxwell’s right hand rule
for the coil B, O_BP = (Rl₂ – d)
The magnetic field at point P due to coil B

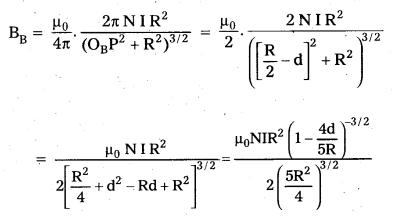
The direction of magnetic field B_B is towards PO_B. So, the resultant magnetic field at P due to coil A and coil B is

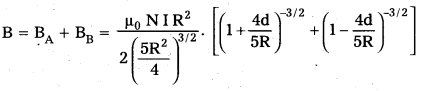
Now, use binomial theorem and neglect higher power as d < < R

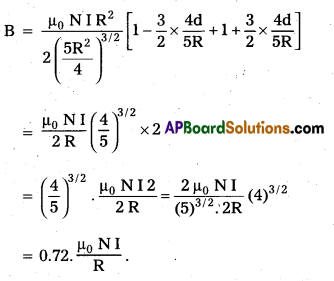
Question 4.
A toroid has a core (non-ferromagnetic) of inner radius 25 cm and outer radius 26 cm, around whIch 3500 turns of a wire are wound. If the current in the wire Is 11 A, what is the magnetic field (a) outside the toroid, (b) inside the core of the toroid, and (c) in the empty space surrounded by the toroid.
Solution:
a) For outside the toroid, the magnetic field is zero, because the magnetic field due to toroid is only inside it and along the length of toroid.

b) Inner radius of toroid, r₁ = 25 cm = 0.25 m
Outer radius of toroid, r₂ = 26 cm = 0.26 m
Number of turns N = 3500
current in the wire, I = 11A
The mean radius of toroid r = \(\left(\frac{\mathrm{r}_1+\mathrm{r}_2}{2}\right)\) = \(\frac{2}{2}\)(0.25 + 0.26) = 0.51
∴ length of toroid = 2πr = 2π × 0.51
the magnetic field strength due to toroid is B = µ₀ n I
where n is number of turns per unit length
n = \(\frac{N}{I}\)
B = 4π × 10^-7 × \(\frac{3500}{\pi \times 0.51}\) × 11 = 3.02 × 10^-2 T

c) The magnetic field in the empty space surrounded by toroid is also zero, because the
magnetic field due to toroid is only along its length.

Question 5.
Answer the following questions.
a) A magnetic field that varies in magnitude form point to point but has a constant direction (east to west) is set up in a chamber. A charged particle enters the chamber and travels undeflected along a straight path with constant speed. What can you say about the initial velocity of the particle?
Answer:
The magnetic field is in constant direction from east to west. According to the question, a charged particle travels undeflected along a striaght path with constant speed. It is only possible, if the magnetic force experienced by the charged particle is zero. The magnitude of magnetic force on a moving charged particle in a magnetic field is given by F = qvB sin θ. Here F = 0, if and only if sinθ. This indicates the angle between the velocity and magnetic fled is 0° or 180°. Thus, the charged particle moves parallel or antiparallel to the magnetic field B.

b) A charged particle enters an environment of a strong and non-uniform magnetic field varying from point to point both in magnitude and direction, and comes out of it following a complicated trajectory Would its final speed equal the initial speed lilt suffered no collisions with the environment?
Answer:
Yes, the final speed be equal to its initial speed as the magnetic force acting on the charged particle only changes the direction of velocity of charged particle but cannot change the magnitude of velocity of charged particle.

c) An electron travelling west to east enters a chamber having a uniform electrostatic field in north to south direction. Specify the direction in which a uniform magnetic field should be set up to prevent the electron from deflecting from its straight line path.
Solution:
B should be in a vertically downward direction.

Question 6.
An electron emitted by a heated cathode and accelerated through a potential difference of 2.0 kV, enters a region with uniform magnetic field of 0.15 T. Determine the trajectory of the electron if the field (a) is transverse to its initial velocity, (b) makes an angle of 30° with the initial velocity.
Solution:
a) Since magnetic field is perpendicular to initial velocity of electron therefore, the electron will move in circular path.
B = 0.15 T,PD = 200 V
K. E. of electron = eV = \(\frac{1}{2}\)mv²
V² = \(\frac{2 \mathrm{ev}}{\mathrm{m}}\)
V = \(\sqrt{\frac{2 \times 1.6 \times 10^{-19} \times 2000}{9.1 \times 10^{-31}}}\)
V = \(\frac{8}{3}\) (e = charge of electron)
V = 2.66 × 10⁷ m/s
Also
BqV = \(\frac{\mathrm{m} \mathrm{V}^2}{\mathrm{Br}}\)
∴ r = \(\frac{\mathrm{mv}}{\mathrm{Bq}}\)
or r = \(\frac{9.1 \times 10^{-31} \times 2.66 \times 10^7}{0.15 \times 1.6 \times 10^{-19}}\)
= \(\frac{91 \times 83.86 \times 10^{-5}}{15 \times 1.6}\) = 10^-3 m = 1 mm

b) When magnetic field makes an angle 30° with the initial velocity i.e. θ = 30°
Then V¹ = V sin θ = \(\sqrt{\frac{2 \mathrm{ev}}{\mathrm{m}}}\) = sin 30°
V¹ = \(\frac{8}{3}\) × 10⁷ × \(\frac{1}{2}\) = \(\frac{4}{3}\) × 10⁷ m/s
The radius of the helical path is
r = \(\frac{\mathrm{m} \mathrm{V}^{\prime}}{\mathrm{Be}}\)
= \(\frac{9 \times 10^{-31} \times\left(\frac{4}{3} \times 10^7\right)}{0.15 \times 1.6 \times 10^{-19}}\) = 0.5 mm

Question 7.
A magnetic field set up using Helmholtz coils (described in Exercise 16) is uniform in a small region and has a magnitude of 0.75 T. In the same region, a uniform electrostatic field is maintained in a direction normal to the common axis of the coils. A narrow beam of (single species) charged particles all accelerated through 15 kV enters this region in a direction perpendicular to both the axis of the coils and the electrostatic field. If the beam remains undeflected when the electrostatic field is 9.0 × 10^-5 V m^-1, make a simple guess as to what the beam contains. Why is the answer not unique ?
Solution:
B = 0.75 T, E = 9 × 10⁵ Vm^-1
V = \(\frac{E}{B}\) = \(\frac{9 \times 10^5}{0.75}\) = 12 × 10⁶ m/s
K. E of charged particle
= \(\frac{1}{2} \mathrm{mv}^2\) = eV
or \(\frac{\mathrm{e}}{\mathrm{m}}\) = \(\frac{v^2}{2 v}\) = \(\frac{144 \times 10^{12}}{2 \times 15000}\) = 4.8 × 10⁷C kg^-1
Particle is deuteron; the answer is not unique because only the ratio of charge to mass is determined. Other possibe answers are He⁺⁺, Li⁺⁺⁺ etc.
∴ He⁺⁺ and Li⁺⁺⁺ also have the same value of
e/m (∵ e/m = \(\frac{2 \mathrm{e}}{2 \mathrm{~m}}\) = \(\frac{3 \mathrm{e}}{3 \mathrm{~m}}\))

Question 8.
A straight horizontal conducting rod of length 0.45 m and mass 6 g is suspended by two vertical wires at its ends. A current of 5.0 A is set up in the rod through the wires.

a) What magnetic field should be set up normal to the conductor in order that the tension in the wires is zero?
Solution:
Rod carrying current placed in uniform magnetic field expëriences a force Bu which is balanced by weigth of rod
F = B I l
mg = B I l
B = \(\frac{\mathrm{m} \mathrm{g}}{\mathrm{I} l}\) = \(\frac{60 \times 9.8}{1000 \times 0.45 \times 5}\) = 0.26 T

b) What will be the total tension in the wires if the direction of current is reversed keeping the magnetic field same as before? (Ignore the mass of the wires.) g = 9.8 m s^-2.
Solution:
Force due to magnetic field = B I l
= 0.26 × 5 × 0.45 = 5.85 N
Weight of rod = \(\frac{60}{1000}\) × 9.8 = 0.588 N
Total force = 0.588 + 0.585 = 1.173 N

Question 9.
The wires which connect the battery of an automobile to its starting motor carry a current of 300 A (for a short time). What is the force per unit length between the wires if they are 70 cm long and 1.5 cm apart? Is the force attractive or repulsive?
Solution:
F = \(\frac{\mu_0}{4 \pi} \times \frac{2 I_1 I_2}{r}\)
= 10^-7 × \(\frac{2 \times 300 \times 300 \times 100}{1.5 \times 10^{-2}}\) = 1.2 Nm^-1 (Repulsive force)

Question 10.
A uniform magnetic field of 1.5 T exists in a cylindrical region of radius 10.0 cm, its direction parallel to the axis along east to west. A wire carrying current of 7.0 A in the north to south direction passes through this region. What is the magnitude and direction of the force on the wire if,

a) the wire intersects the axis,
Solution:
F = BI 1 sin 900 = 1.5 × 7 × \(\frac{20}{100}\) = 2.1 N acting vertically downwards.

b) The wire is turned form N-S to north-east-northwest direction,
Solution:
Now θ = 45°, and length of the wire in the cylindrical region of the magnetic field is l, and is given by
l = l₁ sin 45°
l₁ = \(\frac{l}{\sin 45^{\circ}}\) = \(\sqrt{2 l}\)
So force F₁ = BI l sin 45°
= 1.5 × 7.0 × \(\sqrt{2} l\) × \(\frac{l}{\sqrt{2}}\)
= 10.5 × 0.2 = 2.1 N

c) The wire in the N-S direction is lowered from the axis by a distance of 6.0 cm?
Solution:
When the wire is lowered through a distance 6.0 cm and reaches at CD then length of wire in magnetic field
l₂ = 2x
x.x = 4 × (10 + 6) = 64
x = 8 cm
∴ l₂ = 8 × 2 = 16 cm = \(\frac{16}{100}\)m
∴ Force on the wire
F₂ = BI l₂
= \(\frac{1.5 \times 7 \times 16}{100}\) = 1.68 N (Vertically downwards)

Question 11.
A uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop in the different cases shown in Fig. ? What is the force on each case ? Which case corresponds to stable equilibrium?

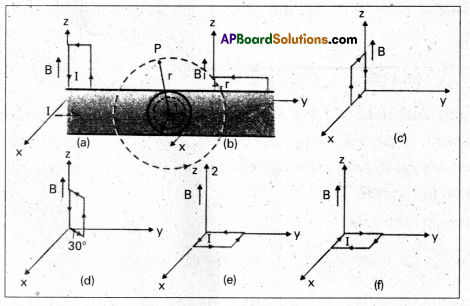
Solution:
a) Torque = 300, G = 3000 × 10^-4 T
Area A = 10 × 5 = 50 cm² = \(\frac{50}{100 \times 100}\)m²
\(\tau\) = BIA = \(\frac{3}{10}\) × 12 × \(\frac{50}{100 \times 100}\) = 18 × 10^-2 Nm along Y-axis
b) Same as in (a)
c) 1.8 × 10^-2 Nm along x – direction
d) 1.8 × 10^-2 Nm at an angle 240° with the +x direction :
e) Zero
f) Zero
Force is zero in each case. Case (e) corresponds to stable and case (f) to unstable equilibrium.

Question 12.
A circular coil of 20 turns and radius 10 cm is placed in a uniform magnetic field of 0.10 T normal to the plane of the coil. 1f the current in the coil is 5.0 A, what is the
(a) total torque on the coil,
(b) total force on the coil,
(c) average force on each electron in the coil due to the magnetic field?
(The coil is made of copper wire of cross-sectional area 10^-5 m², and the free electron density in copper is given to be about 10²⁹ m^-3.)
Solution:
n = 20, r = 10 cm, B = 0.10 T, I = 50 A
a) Torque acting on the coil = nBIA sinθ = 0
b) Force acting on the coil = BIl sinθ = 0
e) Force on each electron
n = No. of electrons per unit volume
A = Area of cross – section of wire
F = Be V = \(\frac{\mathrm{BI}}{\mathrm{nA}}\) = \(\frac{0.1 \times 5}{10^{29} \times 10^{-5}}\) = 5 × 10^-25N

Question 13.
A solenoid 60 cm long and of radius 7.0 cm has 3 layers of windings of 300 turns each. A 2.0 cm long wire of mass 2.5 g lies inside the solenoid (near its centre) normal to its axis; both the wire and the axis of the solenoid are in the horizontal plane. The wire is connected through two lead parallel to the axis of the solenoid to an external battery which supplies a current of 6.0 A in the wire. What value of current (with appropriate sense of circulation) in the windings of the solenoid can support the weight of the wire ? g = 9.8 m s^-2.
Solution:
B = μ₀n I
Force acts on the wire normal to its length
∴ F = BI¹ l
= μ₀n I I¹ l and n = \(\frac{\frac{900}{60}}{100}\) = 1500
= μ₀n I I¹ l = mg
I = \(\frac{2.5 \times 9.8}{1000 \times 4 \pi \times 10^{-7} \times 1500 \times 6 \times \frac{1}{15}}\) = 108 A.

Question 14.
A galvanometer coil has a resistance of 12 Ω and the metre shows full scale deflection for a current of 3 mA How will you convert the metre into a voltameter of range 0 to 18V ?
Solution:
Here G = 12Ω, Ig = 3mA = 3 × 10^-3A, V = 18V
R = \(\frac{v}{I_g}\) – G = \(\frac{18}{3 \times 10^{-3}}\) – 12 = (6000 – 12)Ω = 5988 Ω.

Question 15.
A galvanometer coil has a resistance of 15 Ω and the meter shows full scale deflection for a current of 4 mA. How will you convert the meter into an ammeter of range 0 to 6 A?
Solution:
Here G = 15Ω, I_g = 4 mA = 0.004 A, I = 6A
shunt S = \(\frac{\mathrm{I}_{\mathrm{g}} \mathrm{G}}{\mathrm{I}-\mathrm{I}_{\mathrm{g}}}\) = \(\frac{0.004 \times 15}{6-0.004}\) = \(\frac{0.06}{5.996}\) = ≈ 10 × 10^-3Ω = 10 m Ω
So shunt resistance = 10 m \(\simeq\) 10 mΩ