Students get through AP Inter 2nd Year Chemistry Important Questions 2nd Lesson Solutions which are most likely to be asked in the exam.
AP Inter 2nd Year Chemistry Important Questions 2nd Lesson Solutions
Very Short Answer Questions
Question 1.
Define molarity. [AP IPE ’15] [TS Mar. ’17 ’11]
Answer:
Molarity : The number of moles of solute dissolved in one litre of solution is called molarity.
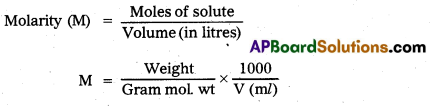
Units : moles / kg.
Question 2.
Define molality. [AP IPE 2015, May ’11]
Answer:
Molality : The number of moles of solute present in one kilogram of solvent is called molality.
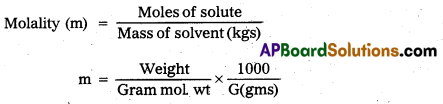
Units : moles / kg.
![]()
Question 3.
Define mole fraction. (AP IPE 2015, Mar. ’14)
Answer:
Mole fraction : The ratio of number of moles of the one component of the solution to the total number of moles of all the components of the solution is called mole fraction.
Mole fraction of solute Xs = \(\frac{n_{\mathrm{s}}}{\mathbf{n}_0+\mathrm{n}_{\mathrm{s}}}\)
Mole fraction of solvent X0 = \(\frac{\mathrm{n}_{\mathrm{s}}}{\mathrm{n}_0+\mathrm{n}_{\mathrm{s}}}\)
[ns = number of moles of solute
n0 = number of moles of solvent]
→ It has no units.
Question 4.
State Raoult’s law. (AP Mar. ’17, ’14 IPE ‘16, 14 (AP, TS)
Answer:
Raoult’s law for volatile solute: For a solution of volatile liquids, the partial vapour pressure of each component of the solution is directly proportional to its mole fraction present in solution.
Raoults law for non-válatlle solute : The relative lowering of vapour pressure of dilute solution containing non-volatile solute is equal to the mole fraction of solute.
Question 5.
State Henrýs law. (TS IPE ’16)
Answer:
At constant temperature, the solubility of a gas in a liquid -is directly proportional to the partial pressure of the gas present above the surface of liquid.
The partial pressure of the gas in vapour phase is proportional to the mole fraction of the gas in the solution.
P = KH × X
KH = Henry’s constant
P = Partial pressure
X = Mole fraction of gas
![]()
Question 6.
What is Ebullioscopic constant ?
Answer:
Ebullioscopic constant : The elevation of boiling point observed in one molal solution containing non-volatile solute is called Ebullioscopic constant (or) molal elevation constant.
Question 7.
What are isotonic solutions ?
Ans. Isotonic solutions : Solutions having same osmotic pressure at a given temperature are called isotonic solutions.
e.g.: Blood is isotonic with 0.9% (\(\frac{\mathrm{W}}{\mathrm{V}}\)) NaCl [Saline]
Question 8.
What is Cryoscopic constant?
Answer:
Cryoscopic constant : The depression in freezing point observed in one molal solution containing non-volatile solute is called cryoscopic constant (or) molal depression constant.
Question 9.
Define osmosis and osmotic pressure. (IPE 15, (AP) ‘16 (TS), (AP))
Answer:
Osmosis : The spontaneous flow of solvent particles from a solution of lower concentration in to higher concentration through semi permeable membrane is called osmosis.
Osmotic pressure : The pressure required to prevent the flow of solvent particles from pure
solvent into solution through semipermeable membrane is called osmotic pressure.
π = (nRT) / V Here π = Osmotic pressure; V = Volume of solution;
n = No. of moles of solute; R = Universal gas constant: T = Absolute temperature
Question 10.
What is Van’t Hoff’s factor ‘i’ and how is it related to ‘α’ in the case of a binary electrolyte (1:1)?
Answer:
Van’t Hoff’s factor (i): ‘It is defined as the ratio of the observed value of colligative property to the theóretical value of colligative property”.
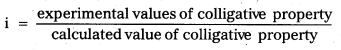
Solute dissociation or ionization process: If a solute on ionization gives ‘n ions and ‘α’ is degree of ionization at the given concentration, we will have [1 + (n – 1) α] particles.
(1 – α) \(\rightleftharpoons\) nα
Total 1 – α + nα = [1 + (n – 1)α]
∴ i = \(\frac{[1+(n-1) \alpha]}{1}\)
α = \(\frac{\mathrm{i}-1}{\mathrm{n}-1}\)
αionization = \(\frac{\mathrm{i}-1}{\mathrm{n}-1}\)
Solute association process:
If ‘n’A molecules combine to give A, we have
nA \(\rightleftharpoons\) An
If ‘α’ is degree of association at the given concentration.
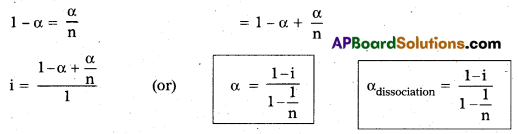
![]()
Question 11.
What is relative lowering of vapour pressure? [IPE ’16, (TS)]
Answer:
Relating lowering of vapour pressure : The ratio of lowering of vapour pressure of a solution containing non-volatile solute to the vapour pressure of pure solvent is called relative lowering of vapour pressure.
R.L.V.P. = \(\frac{\mathrm{P}_0-\mathrm{P}_{\mathrm{S}}}{\mathrm{P}_0}\)
P0 – PS = lowering of vapour pressure
Po = Vapour pressure of pure solvent
Question 12.
What is vapour pressure of a liquid?
Answer:
The pressure exerted by vapour over liquid when it is in equilibrium with the liquid is called vapour pressure.
Question 13.
What is elevation of boiling point? (IPE 16, (TS) )
Answer:
The boiling point of a solution containing non-volatile solute is higher than the boiling point of pure solvent. The difference in boiling points between solution and pure solvent is called elevation of boiling point.
Question 14.
What is depression of freezing point?
Answer:
The freezing point of a solution containing non-volatile solute is always lower than the freëzing point of puré solvent. The difference in freezing points between solution and pure solvent is called depression of freezing point.
Question 15.
Calculate the amount of benzoic acid (C6H5COOH) required for preparing 250 ml of
0.15 M solution in methanol.
Answer:
Given
Molarity = 0.15 M
Volume V = 250 ml
Molecular weight of benzoic acid (C6H5COOH) = 122
Molarity (M) = \(\frac{\text { Weight }}{\mathrm{GMw}} \times \frac{1000}{\mathrm{~V}(\mathrm{~m} l)}\)
0.15 = \(\frac{\mathrm{W}}{122} \times \frac{1000}{250}\)
W = \(\frac{122 \times 0.15}{4}\) = 4.575 gms.
Question 16.
Calculate the mole fraction of H2SO4 in a solution containing 98% H2SO4 by mass. (T.S. Mar. ’18; A.P Mar. ‘17, IPE ‘15, (AP))
Answer:
Given a solution containing – 98% H2SO4 by mass.
It means 98 gms of H2SO4 and 2 gms of H2O mixed to form a solution.

![]()
Question 17.
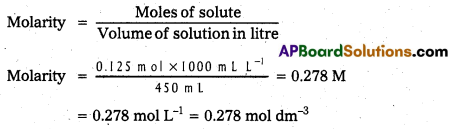
Calculate the molarity of a solution containing 5g of NaOH in 450 ml solution. (T.S. Mar. ’19, ’17 )
Solution:
Moles of NaOH = \(\frac{5 \mathrm{~g}}{40 \mathrm{~g} \mathrm{~mol}^{-1}}\) = 0.125 mol
Volume of the solution in litres = 450 mL / 1000 mL L-1
Using equation
Question 18.
200 cm3 of an aqueous solution of a protein contains 1.26 g of the protein. The osmotic pressure of such a solution at 300 K is found to be 2.57 × 10-3 bar. Calculate the molar masš of the protein.
Sólution:
The various quantities known to us are as follows : π = 2.57 × 10-3 bar.
V = 200 cm3 = 0.200 litre
T = 300 K
R = 0.083 L bar moL-1 K-1
Substituting these values in equation,
we get M2 = \(\frac{\mathrm{w}_2 \mathrm{RT}}{\pi \mathrm{V}}\)
M2 = \(\frac{1.26 \mathrm{~g} \times 0.083 \mathrm{~L} \mathrm{bar} \mathrm{K}^{-1} \mathrm{~mol}^{-1} \times 300 \mathrm{~K}}{2.57 \times 10^{-3} \mathrm{bar} \times 0.200 \mathrm{~L}}\)
= 61.022 g mol-1
Question 19.
Calculate the molality of 10g of glucose in 90g of water.
Answer:

Question 20.
Calculate the mass percentage of benzene (C6H6) and carbon tetrachloride (Ccl4) if 22g of benzene is dissolved in 122g of carbon tetrachloride.
• Then, calculate the mass percentage from the formula
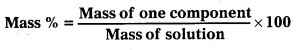
Solution:
Mass of benzene = 22g; Mass of CCl4 = 122g
Mass of solution = 22 + 122 = 144g
Mass % of benzene = \(\frac{22}{144}\) × 100 = 15.28%
Mass of CCl4 = 100 – 15.28 = 84.72%
Note: Mass percent of CCl4 can also be calculated by using the formula as:
Mass % of CCl4 = \(\frac{122}{144}\) × 100 = 84.72%
![]()
Question 21.
What are colligative properties? Give their names.
Answer:
The properties of a solution which depend on number of solute particles but not on the nature are called colligative properties.
Names:
- Lowering of vapour pressure
- Elevation of boiling point.
- Depression of freezing point.
- Osmotic pressure.
Question 22.
Calculate the weight of Glucose required to prepare 500 ml of 0.1 M solution. (IPE ‘16, (TS))
Answer:
Molarity = 0.1; Molecular weight of glucose = 180; Volume of solution = 500 ml
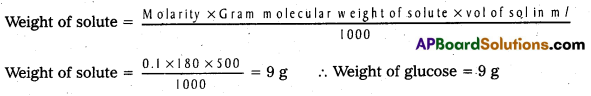
Short Answer Questions
Question 1.
What is an ideal solution?
Answer:
A solution of two or more components which obeys Raoult’s law at all concentrations and at all temperatures is called ideal solution. In ideal solution there should not be any association between solute and solvent, (Le.) no chemical interaction between solute and solvent of solution.
Ex : The following mixtures form ideal solutions.
- Benzene + Toluéne ‘
- n – hexane + n – heptane
- ethyl bromide + ethyl iodide
Question 2.
What is relative lowering of vapour pressure? How is it useful to determine the molar mass of a solute?
Answer:
Raoult’s law for volatile solute: For a solution of volatile liquids, the partial vapour pressure of each component of the solution is directly proportional to its mole fraction present in solution.
Raoult’s law for non-volatile solute : The relative lowering of vapour pressure of dilute solution containing non-volatile solute is equal to the mole fraction of solute.
Relative lowering of vapour pressure \(\frac{\mathrm{P}_0-\mathrm{P}_{\mathrm{s}}}{\mathrm{P}_0}\) = Xs (mole fraction of solute)
\(\frac{\mathrm{P}_0-\mathrm{P}_{\mathrm{s}}}{\mathrm{P}_0}\) = \(\frac{\mathbf{n}_{\mathrm{s}}}{\mathrm{n}_0+\mathrm{n}_{\mathrm{s}}}\)
For very much dilute solutions ns < < < ….. n0
∴ \(\frac{\mathrm{P}_0-\mathrm{P}_{\mathrm{s}}}{\mathrm{P}_0}\) = \(\frac{\mathrm{n}_{\mathrm{s}}}{\mathrm{n}_0}\) = \(\frac{\mathrm{w}}{\mathrm{m}}\) × \(\frac{\mathrm{M}}{\mathrm{W}}\)
W = Weight of solute
m = Molar mass of solute
w = Weight of solvent
M = Molar mass of solvent
Molar mass of solute m = \(\frac{w \times M}{W} \times \frac{P_0}{P_0-P_5}\)
![]()
Question 3.
The vapour pressure of a solution containing non volatile solute Is less than the vapour pressure of pure of solvent. Give reason.
Answer:
In pure solvent the surface is occupied by solvent molecules only. Number of molecules evapoarating will be more, hence vapour pressure is more. In case of solution the surface is occupied by both solute and solvent molecules. The number of molecules evaporating will be less in case of solution containing non volatile solute. Hence the vapour pressure of solution containing non volatile solute is less than the vapour pressure of pure solvent.
Question 4.
An antifreeze solution is prepared from 222.6g of ethylene glycol [(C2H6O2)] and 200g of water (solvent). Calculate the molality of the solution.
Solution:
Weight of Ethylene glycol = 222.6 gms
G.mol wt = 62

Question 5.
Vapour pressure of water at 293K is 17.535 mm Hg. Calculate the vapour pressure of the solution at 293K when 25g of glucose is dissolved in 450g of water? (BMP)
Answer:
Raoult’s law formula

Question 6.
The vapour pressure of pure benzene at a certain temperature is 0.850 bar. A non-volatile, non-electrolyte solid weighing 0.5g when added to 39.0 g of benzene (molar mass 78 g mol-1). Vapour pressure-of the solution, then, is 0.845 bar. What is the molar mass of the solid substance? (IPE 2016 (AP))
Solution:
The various quantities known to us are as follows.
\(\mathrm{p}_1^0\) = 0.850 bar
P = 0.845bar
M1 = 78 g mol-1
w2 = 0.5 g
w1 = 39 g
Substituting these values in equation \(\frac{\mathrm{P}^0-\mathrm{P}}{\mathrm{P}_1^0}\) = \(\frac{\mathrm{w}_2 \times \mathrm{M}_1}{\mathrm{M}_2 \times \mathrm{w}_1}\) we get
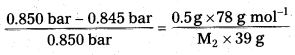
Therefore, M2 = 170 g mol-1
![]()
Question 7.
Vapour pressure of pure water at 298 K is 23.8 mm Hg. 50g urea (NH2CONH2) is dissolved in 850 g of water. Calculate the vapour pressure of water for this solution and its relative lowering.
• Consider Raoults law and formula for relative lowering in vapour pressure,
\(\frac{\mathbf{p}_{\mathbf{A}}^0-\mathbf{p}_{\mathrm{s}}}{\mathbf{p}_{\mathbf{A}}^0}\) = \(\frac{\mathbf{n}_{\mathbf{B}}}{\mathbf{n}_{\mathbf{A}}}\) = \(\frac{\mathbf{W}_{\mathrm{B}}}{\mathbf{M}_{\mathrm{B}}}\) × \frac{\mathbf{M}_{\mathbf{A}}}{\mathbf{W}_{\mathbf{A}}}\(\)
Where, \(\frac{\mathbf{p}_{\mathrm{A}}^0-\mathbf{p}_{\mathrm{s}}}{\mathbf{p}_{\mathrm{A}}^0}\) is called relative lowering in vapour pressure.
Solution:
Step 1: Calculation of vapour pressure of water for this solution.
According to Raoult’s law,
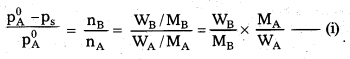
(Pure water) \(\mathrm{p}_{\mathrm{A}}^0\) = 23.8 mm; .
WB (urea) = 50 g; WA (water) = 850 g
MB (urea) = 60 g mol-1; MA (water) = 180 g mol-1
Placing the values in eq. (i)

Step II: Calculation of relative lowering of vapour pressure
Relative lowering in vapour pressure = \(\frac{\mathrm{p}_{\mathrm{A}}^0-\mathrm{p}_{\mathrm{s}}}{\mathrm{p}_{\mathrm{A}}^0}\) = \(\frac{(23.8-23.38) \mathrm{mm}}{(23.8 \mathrm{~mm})}\) = 0.0176
Question 8.
A solution of sucrose in water is labelled as 20% w/W. What would be the mole fraction of each component in the solution? (IPE ‘2014)
Answer:
20% \(\frac{w}{W}\) Sucrose in water solution means
20 gms of Sucrose and 80 gms of water.
Number of moles of sucrose (ns) = \(\frac{20}{342}\) = 0.0584
Number of moles of water (n0) = \(\frac{80}{18}\) = 4.444
Mole fraction of sucrose Xs = \(\frac{n_s}{n_0+n_s}\)
= \(\frac{0.0584}{4.444+0.0584}\) = \(\frac{0.0584}{4.50284}\) = 0.01296
Mole fraction of water Xo = \(\frac{\mathbf{n}_0}{\mathrm{n}_0+\mathrm{n}_{\mathrm{s}}}\) = \(\frac{4.444}{4.50284}\) = 0.9869
Xs + X0 = 1
X0 = 1 – Xs = 1 – 0.01296 = 0.987
Question 9.
Calculate the vapour pressure of a solution containing 9g of glucose in 162g of water at 293K. The vapour pressure of water of 293K is 17.535mm Hg. (IPE ‘15, ’14, BOARD MODEL PAPER)
Solution:
Weight of solute (w) = 9g; Weight of solvent (W) = 162g
Molecular weight of solute (mw) = 180; molecular weight of solvent Mw = 18
Vapour pressure of pure solvent = 17.535 vapour pressure of solution Ps = ?
\(\frac{P_0-P_3}{P_0}\) = \(\frac{W}{m w} \times \frac{M W}{W}\)
⇒ \(\frac{17.535-P_s}{17.535}\) = \(\frac{9}{180} \times \frac{18}{162}\)
17.535 – Ps = 17.535 × \(\frac{9}{180}\) × \(\frac{18}{162}\)
⇒ 17.535 – Ps = 0.0972
∴ Ps = 17.535 – 0.0972 = 17.4378 mm