AP Inter 2nd Year Physics Important Questions Chapter 10 Alternating Current

Students get through AP Inter 2nd Year Physics Important Questions 10th Lesson Alternating Current which are most likely to be asked in the exam.

AP Inter 2nd Year Physics Important Questions 10th Lesson Alternating Current

Very Short Answer Questions

Question 1.
A transformer converts 200 V ac into 2000 V ac. Calculate the number of turns in the ‘ secondary if the primary has 10 turns. [T.S. Mar. 16]
Answer:
\(\frac{\mathrm{V}_{\mathrm{s}}}{\mathrm{V}_{\mathrm{p}}}=\frac{\mathrm{N}_{\mathrm{s}}}{\mathrm{N}_{\mathrm{p}}}\)
V_p = 200V, V_s = 2000V, N_p = 10
N_s = \(\frac{\mathrm{V}_{\mathrm{s}}}{\mathrm{V}_{\mathrm{p}}}\) × N_p = \(\frac{2000}{200}\) × 10
N_s = 100.

Question 2.
What type of transformer is used in a 6V bed lamp ? [A.P. Mar. 17]
Answer:
Step down transformer is used in 6V bed lamp.

Question 3.
What is the phenomenon involved in the working of a transformer ? [Mar. 16(A.P.) Mar. 14]
Answer:
Transformer works on the principle of mutual induction.

Question 4.
What is transformer ratio ?
Answer:
The ratio of secondary e.m.f to the primary e.m.f. (or) number of turns in secondary to the number of turns in the primary is called the transformer ratio.
Transformer ratio = \(\frac{\mathrm{V}_{\mathrm{s}}}{\mathrm{V}_{\mathrm{p}}}=\frac{\mathrm{N}_{\mathrm{s}}}{\mathrm{N}_{\mathrm{p}}}\)

Question 5.
Write the expression for the reactance of i) an inductor and (ii) a capacitor.
Answer:

Inductive reactance (X_L) = ωL
Capacitive reactance (X_C) = \(\frac{1}{\omega C}\)

Question 6.
What is the phase difference between A.C emf and current in the following: Pure resistor, pure inductor and pure capacitor. [T.S. Mar. 15]
Answer:

In pure resistor A.C. e.m.f and current are in phase with each other.
In pure inductor, current lags behind the e.m.f. by an angle of \(\frac{\pi}{2}\) (or) 90°.
In pure capacitor, current leads the e.m.f by an angle \(\frac{\pi}{2}\) (or) 90°.

Question 7.
Define power factor. On which factors does power factor depend ?
Answer:
The ratio of true power and apparent power (virtual power) in an a.c circuit is called as power factor of the circuit.
Power factor (cosΦ) = \(\frac{\mathrm{P}}{\mathrm{P}_{\mathrm{rms}}}\) [∵ P_rms = V_rms I_rms]
Power factor depends on r.m.s voltage, r.m.s current and average power (P).

Question 8.
What is meant by wattless component of current ?
Answer:
Average power (P) = V_rms(I_rms sinΦ) cos\(\frac{\pi}{2}\)
The average power consumed in the circuit due to (I_rms sinΦ) component of current is zero. This component of current is known as wattless current. (I_rms sinΦ) is the wattless component of current.

Question 9.
When does a LCR series circuit have minimum impedance ?
Answer:
In LCR series circuit, Impendence (Z) = \(\sqrt{R^2+\left(\frac{1}{\omega C}-\omega L\right)^2}\)
At a particular frequency, ωL = \(\frac{1}{\omega C}\)
The impedance is minimum (Z = R)
This frequency is called resonant frequency.

Question 10.
What is the phase difference between voltage and current when the power factor in LCR series circuit is unity ?
Answer:
In LCR series circuit power factor (cosΦ) = 1
Phase difference between voltage and current is zero. (Φ = 0)

Short Answer Questions

Question 1.
State the principle on which a transformer works. Describe the working of a transformer with necessary theory.
Answer:
Transformer is a device to convert a low alternating current of high voltage into high alternating current of low voltage and vice versa.
Principle : It works on the principle of mutual induction between two coils.
Working : When an alternating emf is applied across the primary coil, the input voltage changes with time. Hence the magnetic flux through the primary also changes with time.
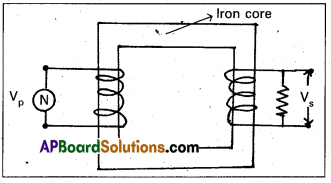
AP Inter 2nd Year Physics Important Questions Chapter 10 Alternating Current 1
This changing magnetic flux will be linked with secondary through the core. An emf is induced in the secondary.

Theory: Let N₁ and N₂ be the number of turns in the primary and secondary. Let V_P and V_S be the emf s across the primary and secondary.
\(\frac{V_S}{V_p}=\frac{\text { Output emf }}{\text{Input emf}}=\frac{-N_2 \frac{d \phi}{d t}}{-N_1 \frac{d \phi}{d t}}=\frac{N_2}{N_1}\)
∴ \(\frac{\mathrm{V}_{\mathrm{S}}}{\mathrm{V}_{\mathrm{P}}}=\frac{\mathrm{N}_2}{\mathrm{~N}_1}\) = Transformer ratio
Efficiency of transformer :
It is the ratio of output power to the input power.
η = \(\frac{\text { Outputpower }}{\text { Input power }}\) × 100

Problems

Question 1.
A light bulb is rated at 100W for a 220 V supply. Find
(a) the resistance of the bulb;
(b) the peak voltage of the source; and
(c) the rms current through the bulb. [A.P. Mar. 15]
Solution:
(a) We are given P = 100 W and V = 220V The resistance of the bulb is
R = \(\frac{\mathrm{V}^2}{\mathrm{P}}=\frac{(220 \mathrm{~V})^2}{100 \mathrm{~W}}\) = 484 Ω

(b) The peak voltage of the source is υ_m = \(\sqrt{2}\)V = 311 V

Question 2.
A pure inductor of 25.0 mH is connected to a source of 220 V. Find the inductive reactance and rms current in the circuit if the frequency of the source is 50 Hz.
Solution:
The inductive reactance,
X_L = 2πvL = 2 × 3.14 × 50 × 25 × 10^-3 = 7.85 Ω
The rms current in the circuit is I = \(\frac{\mathrm{V}}{\mathrm{X}_{\mathrm{L}}}=\frac{220 \mathrm{~V}}{7.85 \Omega}\) = 28 A

Question 3.
The instantaneous current and instantaneous voltage across a series circuit containing resistance and inductance are given by i = \(\sqrt{2}\) sin (100t – π/4)A and υ = 40 sin (100t) V. Calculate the resistance ?
Solution:
i = \(\sqrt{2}\) sin (100t – π/4)A (∵i = i₀sin(ωt – Φ))
υ = 40 sin(100t)V (∵ V = V₀sin(ωt ))
i₀ = \(\sqrt{2}\) , V₀ = 40, ω = 100, Φ = π/4
R = \(\frac{\mathrm{V}_0}{\mathrm{i}_0}\) cosΦ = \(\frac{40}{\sqrt{2}}\) cos\(\frac{\pi}{4}\), R = \(\frac{40}{\sqrt{2}} \times \frac{1}{\sqrt{2}}\), R = 20 Ω

Question 4.
In an AC circuit, a condenser, a resistor and a pure inductor are connected in series across an alternator (AC generator). If the voltages across them are 20 V, 35 V and 20 V respectively, find the voltage supplied by the alternator.
Solution:
V_C = 20V, V_R = 35V, V_L = 20V
V = \(\sqrt{V_R^2+\left(V_L^2-V_C^2\right)}\) ; V = \(\sqrt{(35)^2+\left(20^2-20^2\right)}\) ; V = \(\sqrt{35^2}\); V = 35 Volt.

Question 5.
What is step up transformer ? How it differs from step down transformer ?
Solution:
The ratio of number of turns in the secondary coil to the number of turns in the primary coil is called transformer ratio.
T = \(\frac{N_S}{N_p}=\frac{\text {No. of turns in the secondary }}{\text {No. of turns in the primary }}\)
If N_S > N_P, then the transformer is called step up transformer.
If N_S < N_P, then the transformer is called step down transformer.

Textual Examples

Question 1.
A light bulb is rated at 100W for a 220 V supply. Find
(a) the resistance of the bulb;
(b) the peak voltage of the source; and
(c) the rms current through the bulb. [A.P. Mar. 15]
Solution:
(a) We are given P = 100 W and V = 220V.
The resistance of the bulb is
R = \(\frac{\mathrm{V}^2}{\mathrm{P}}=\frac{(220 \mathrm{~V})^2}{100 \mathrm{~W}}\) = 484 Ω

(b) The peak voltage of the source is υ_m = \(\sqrt{2}\)V = 311 V

Question 3.
A lamp is connected in series with a capacitor. Predict your observations for dc and ac connections. What happens in each case if the capacitance of the capacitor is reduced ?
Solution:
When a dc source is connected to a capacitor, the capacitor gets charged and after charging no current flows in the circuit and the lamp will not glow. There will be no change even if C is reduced. With ac source, the capacitor offers capacitative reactance (1/ωC) and the current flows in the circuit. Consequently, the lamp will shine. Reducing C will increase reactance and the lamp will shine less brightly than before.

Question 4.
A 15.0 μF capacitor is connected to a 220 V, 50 Hz source. Find the capacitive reactance and the current (rms and peak) in the circuit. If the frequency is doubled, what happens to the capacitive reactance and the current ?
Solution:
The capacitive reactance is
X_c = \(\frac{1}{2 \pi v C}=\frac{1}{2 \pi(50 \mathrm{~Hz})\left(15.0 \times 10^{-6} \mathrm{~F}\right)}\)
= 212 Ω
The rms current is I = \(\frac{\mathrm{V}}{\mathrm{X}_{\mathrm{C}}}=\frac{220 \mathrm{~V}}{212 \Omega}\)
= 1.04 A
The peak current is
i_m = \(\sqrt{2}\)I = (1.41)(1.04A) = 1.47A
This current oscillates between + 1.47A and – 1.47 A, and is ahead of the voltage by π/2.
If the frequency is doubled, the capacitive reactance is halved and consequently, the current is doubled.

Question 5.
A light bulb and an open coil inductor are connected to an ac source through a key as shown in the figure.
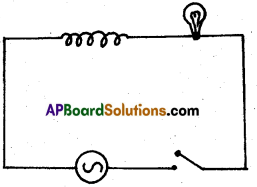
AP Inter 2nd Year Physics Important Questions Chapter 10 Alternating Current 2
The switch is closed and after sometime, an iron rod is inserted into the interior of the inductor. The glow of the light bulb (a) increases; (b) decreases; (c) is unchanged, as the iron rod is inserted. Give your answer with reasons.
Solution:
As the iron rod is inserted, the magnetic field inside the coil magnetizes the iron increasing the magnetic field inside it. Hence, the inductance of the coil increases. Consequently, the inductive reactance of the coil increases. As a result, a larger fraction of the applied ac voltage appears across the inductor, leaving less voltage across the bulb. Therefore, the glow of the light bulb decreases.

Question 6.
A resistor of 200Ω and a capacitor of 15.0 μF are connected in series to a 220V, 50 Hz ac source,
(a) Calculate the current in the circuit;
(b) Calculate the voltage (rms) across the resistor and the capacitor. Is the algebraic sum of these voltages more than the source voltage ? If yes, resolve the paradox.
Solution:
Given
R = 200Ω. C = 15.0 μF = 15.0 × 10^-6F
V = 220V, v = 50Hz
(a) In order to calculate the current, we need the impedance of the circuit. It is
Z = \(\sqrt{\mathrm{R}^2+\mathrm{X}_{\mathrm{C}}^2}=\sqrt{\mathrm{R}^2+(2 \pi v C)^{-2}}\)
= \(\sqrt{(200 \Omega)^2+\left(2 \times 3.14 \times 50 \times 10^{-6} \mathrm{~F}\right)^{-2}}\)
= \(\sqrt{(200 \Omega)^2+(212 \Omega)^2}\) = 291.5Ω
Therefore, the current in the circuit is
I = \(\frac{\mathrm{V}}{\mathrm{Z}}=\frac{220 \mathrm{~V}}{291.5 \Omega}\) = 0.755A

(b) Since the current is the same throughout the circuit, we have
V_R = IR = (0.755 A) (200Ω) = 151V
V_C = IX_C = (0.755A) (212.3Ω) = 160.3V
The algebraic sum of the two voltages, V_R and V_C is 311.3 V which is more than the source voltage of 220 V. How to resolve this paradox ? As you have learnt in the text, the two voltages are not in the same phase. Therefore, they cannot be added like ordinary numbers. The two voltages are out of phase by ninety degrees. Therefore, the total of these voltages must be obtained using the Pythagorean theorem:
V_R+C = \(\sqrt{\mathrm{V}_{\mathrm{R}}^2+\mathrm{V}_{\mathrm{C}}^2}\) = 220 V
Thus, if the phase difference between two voltages is properly taken into account, the total voltage across the resistor and the capacitor is equal to the voltage of the source.

Question 7.
a) For circuits used for transporting electric power, a low power factor implies large power loss in transmission. Explain.
b) Power factor can often be improved by the use of a capacitor of appropriate capacitance in the circuit. Explain.
Solution:
a) We know that P = IV cosΦ where cosΦ is the power factor. To supply a given power at a given voltage, if cosΦ is small, we have to increase current accordingly. But this will lead to large power loss (I^R) in transmission.

b) Suppose in a circuit, current I lags the voltage by an angle Φ.
Then power factor cosΦ = R/Z
We can improve the power factor (tending to 1) by making Z tend to R. Let us understand, with the help of a phasor diagram in the figure how this can be achieved. Let us resolve I into two components, I_P
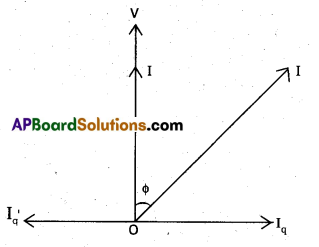
AP Inter 2nd Year Physics Important Questions Chapter 10 Alternating Current 3
along the applied voltage V and I_q perpendicular to the applied voltage. I_q is called the wattless component since corresponding to this component of current, there is no power loss. I_P is known as the power component because it is in phase with the voltage and corresponds to power loss in the circuit.

It’s clear from this analysis that if we want to improve power factor, we must completely neutralize the lagging wattless current I_q by an equal leading wattless current I’_q. This can be done by connecting a capacitor of appropriate value in parallel so that I_q and I’_q cancel each other and P is effectively I_P V.

Question 8.
A sinusoidal voltage of peak value 283 V , and frequency 50 Hz is applied to a series LCR circuit in which R = 3Ω. L = 25.48 mH. and C = 796μF. Find
(a) the impedance of the circuit;
(b) the phase difference between the voltage across the source and the current;
(c) the power dissipated in the circuit; and
(d) the power factor.
Solution:
a) To find the impedance of the circuit, we first calculate X_L and X_C.
X_L = 2πvL
= 2 × 3.14 × 50 × 25.48 × 10^-3Ω = 8Ω
X_C = \(\frac{1}{2 \pi v \mathrm{C}}\)
= \(\frac{1}{2 \times 3.14 \times 50 \times 796 \times 10^{-6}}\) = 4Ω
Therefore,
z = \(\sqrt{\mathrm{R}^2+\left(\mathrm{X}_{\mathrm{L}}-\mathrm{X}_{\mathrm{C}}\right)^2}=\sqrt{3^2+(8-4)^2}\)
= 5Ω

b) Phase difference, Φ = tan^-1\(\frac{\mathrm{X}_{\mathrm{C}}-\mathrm{X}_{\mathrm{L}}}{\mathrm{R}}\)
= tan^-1\(\left(\frac{4-8}{3}\right)\) = -53.1°

c) The power dissipated in the circuit is
P = I²R
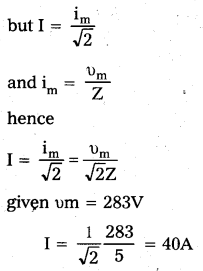
AP Inter 2nd Year Physics Important Questions Chapter 10 Alternating Current 4
Therefore, P = (40A)² × 3Ω = 4800W
= 4.8 kW

d) Power factor = cos Φ = cos 53.1° = 0.6.

Question 9.
Suppose the frequency of the source in the previous example can be varied,
(a) What is the frequency of the source at which resonance occurs ?
(b) Calculate the impedance, the current, and the power dissipated at the resonant condition.
Solution:
(a) The frequency at which the resonance occurs is
ω₀ = \(\frac{1}{\sqrt{\mathrm{LC}}}=\frac{1}{\sqrt{25.48 \times 10^{-3} \times 796 \times 10^{-6}}}\)
= 222.1 rad/s
v_r = \(\frac{\omega_0}{2 \pi}=\frac{221.1}{2 \times 3.14}\) Hz = 35.4Hz

b) The impedance Z at resonant condition is equal to the resistance
Z = R = 3Ω
The rms current at resonance is ,
as V = \(\frac{v_{\mathrm{m}}}{\sqrt{2}}\)
I = \(\frac{\mathrm{V}}{\mathrm{Z}}=\frac{\mathrm{V}}{\mathrm{R}}=\left(\frac{283}{\sqrt{2}}\right) \frac{1}{3}\) = 66.7 A
The power dissipated at resonance is
P = I² × R = (66.7)² × 3 = 13.35 kW
You can see that in the present case, power dissipated at resonance is more than the power dissipated in Example 8.

Question 10.
At an airport, a person is made to walk through the doorway of a metal detector, for security reasons. If she/he is carrying anything made of metal, the metal detector emits a sound. On what principle does this detector work ?
Solution:
The metal detector works on the principle of resonance in ac circuits. When you walk through a metal detector, you are, in fact, walking through a coil of many turns. The coil is connected to a capacitor tuned so that the circuit is in resonance. When you walk through with metal in your pocket, the impedance of the circuit changes – resulting in significant change in current in the circuit. This change in current is detected and the electronic circuitry causes a sound to be emitted as an alarm.

Question 11.
Show that in the free oscillations of an LC circuit, the sum of energies stored in the capacitor and the inductor is constant in time.
Solution:
Let q₀ be the initial charge tin a capacitor. Let the charged capacitor be connected to an inductor of inductance L. this LC circuit will sustain an oscillation with frequency
\(\omega\left(2 \pi v=\frac{1}{\sqrt{\mathrm{LC}}}\right)\)
At an instant t, charge q on the capacitor and the current i are given by :
q(t) = q₀ cos ωt
i(t) = -q₀ co sin ωt
Energy stored in the capacitor at time ‘t’ is
U_E = \(\frac{1}{2}\) C V² = \(\frac{1}{2} \frac{\mathrm{q}^2}{\mathrm{C}}=\frac{\mathrm{q}_0^2}{2 \mathrm{C}}\) cos² (ωt)
Energy stored in the inductor at time ‘t’ is
U_M = \(\frac{1}{2}\) L i²
= \(\frac{1}{2}\) L q₀² ω²sin² (ωt)
= \(\frac{Q_0^2}{2 C} \sin ^2(\omega t)\) [∵ ω = 1/ \(\sqrt{L C}\)]
Sum of energies
U_E + U_M = \(\frac{\mathrm{q}_0^2}{2 \mathrm{C}}\) [cos² ωt + sin²ωt) = \(\frac{\mathrm{q}_0^2}{2 \mathrm{C}}\)
This sum is constant in time as q₀ and C, both are time-independent.