Andhra Pradesh BIEAP AP Inter 2nd Year Chemistry Study Material 2nd Lesson Solutions Textbook Questions and Answers.
AP Inter 2nd Year Chemistry Study Material 2nd Lesson Solutions
Very Short Answer Questions
Question 1.
Define the term solution.
Answer:
Solution : Solution is a homogeneous mixture of two (or) more components whose composition may be varied with certain limits.
Question 2.
Define molarity. [T.S. Mar.17] [Mar. 11]
Answer:
Molarity : The number of moles of solute dissolved in one litre of solution is called molarity.
Molarity (M) = \(\frac{\text { Moles of solute }}{\text { Volume (in litres) }}\)
M = \(\frac{\text { Weight }}{\text { Gram mol wt }} \times \frac{1000}{V(\mathrm{ml} l)}\)
Units: moles / litre.
![]()
Question 3.
Define molality [A.P. Mar. 15] [May 11]
Answer:
Molality: The number of moles of solute present in one kilogram of solvent is called molality.
Molality (M) = \(\frac{\text { Moles of solute }}{\text { Mass of solvent (kgs) }}\)
m = \(\frac{\text { Weight }}{\text { Gram mol wt }} \times \frac{1000}{\mathrm{G}(\mathrm{gms})}\)
Question 4.
Give an example of a solid solution in which the solute is solid.
Answer:
Example of a solid solution in which the solute is solid, is copper dissolved in gold.
Question 5.
Define mole fraction. . [T.S. Mar. 18] [Mar. 14]
Answer:
Mole fraction : The ratio of number of moles of the one component of the solution to the total number of moles of all the components of the solution is called mole fraction.
Mole fraction of solute Xs = \(\frac{\mathbf{n}_{\mathrm{S}}}{\mathbf{n}_{0}+\mathbf{n}_{\mathrm{s}}}\)
Mole fraction of solvent X0 = \(\frac{\mathbf{n}_{\mathrm{S}}}{\mathbf{n}_{0}+\mathbf{n}_{\mathrm{s}}}\)
[ns =number of moles of solute]
[n0 = number of moles of solvent]
It has no units.
Question 6.
Define mass percentage solution.
Answer:
The mass percentage of a component of a solution is defined as the
mass % =  × 100
× 100
![]()
Question 7.
What is ppm of a solution ?
Answer:
ppm – parts per million : It is a convenient method of expressing concentration when a solute is present in trace quantities. Parts per million is defined as the
ppm = 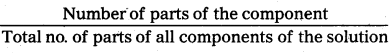 × 106
× 106
Question 8.
What role do the molecular interactions play in a solution of alcohol and water ?
Answer:
In a solution of alcohol and water the molecular interactions present are hydrogen bondings. When these components are mixed then new hydrogen bonds develop between alcohol and water. The formed forces are weaker. Due to the decrease of magnitude of attractive forces, the solution shows positive deviation from Raoult’s law. This leads to increase of vapour pressure of solution and decrease in its boiling point.
Question 9.
State Raoult’s law. [A.P. & T.S. Mar. 18; 16; A.P. Mar. 17] [Mar. 14]
Answer:
Raoult’s law for volatile solute: For a solution of volatile liquids, the partial vapour pressure of each component of the solution is directly proportional to its mole fraction present in solution.
Raoult’s law for non-volatile solute : The relative lowering of vapour pressure of dilute solution containing non-volatile solute is equal to the mole fraction of solute.
Question 10.
State Henry’s law.
Answer:
At constant temperature, the solubility of a gas in a liquid is directly proportional to the partial pressure of the gas present above the surface of liquid. .
(Or)
The partial pressure of the gas in vapour phase is proportional to the mole fraction of the gas in the solution.
P = KH × x KH = Henry’s constant
P = Partial pressure
x = Mole fraction of gas
![]()
Question 11.
What is Ebullioscopic constant ?
Answer:
Ebullioscopic constant : The elevation of boiling point observed in one molal solution containing non-volatile solute is called Ebullioscopic constant (or) molal elevation constant.
Question 12.
What is Cryoscopic constant ?
Answer:
Cryoscopic constant : The depression in freezing point observed in one molal solution containing non-volatile solute is called cryoscopic constant (or) molal depression constant.
Question 13.
Define osmotic pressure. [A.P. Mar. 18; 16]
Answer:
Osmotic pressure : The pressure required to prevent the in flow of solvent molecules into the solution when these are. separated by semi-permeable membrane.
Question 14.
What are isotonic solutions ? [T.S. Mar. 19; 16; A.P. Mar. 17, 15]
Answer:
Isotonic solutions : Solutions having same osmotic pressure at a given temperature are called isotonic solutions.
e.g.: Blood is isotonic with 0.9% \(\left(\frac{\mathrm{W}}{\mathrm{V}}\right)\) NaCl [Saline]
Question 15.
Amongst the following compounds, identify which are insoluble, partially soluble and highly soluble in water, (i) phenol (ii) toluene (iii) formic acid (iv) ethylene glycol (v) chloroform (vi) pentanol.
Answer:
- Phenol is partially soluble in water.
- Toluene is insoluble in water.
- Formic acid is highly soluble in water.
- Ethylene glycol is highly soluble in water.
- Chloroform is insoluble in water.
- Pentanol is partially soluble in water.
![]()
Question 16.
Calculate the mass percentage of aspirin (C9H8O4) in acetonitrile (CH3CN) when 6.5 gm of C9H8O4 is dissolved in 450g of CH3CN.
Answer:
Given
The Mass of aspirin = 6.5 gms
Mass of acetonitrile = 450 gms
Mass of solution = 6.5 + 450
= 456.5 gms
Mass % = \(\frac{6.5}{456.5}\) × 100 = 1.424 %
Question 17.
Calculate the amount of benzoic acid (C6H5COOH) required for preparing 250 ml of 0.15 M solution in methanol.
Answer:
Given
Molarity = 0.15 M
Volume V = 250 ml
Molecular weight of benzoic acid (C6H5COOH) = 122
Molarity (M) = \(\frac{\text { Weight }}{\text { GMw }} \times \frac{1000}{V(\mathrm{~m} l)}\)
0.15 = \(\frac{\mathrm{W}}{122} \times \frac{1000}{250}\)
W = \(\frac{122 \times 0.15}{4}\) = 4.575 gms
Question 18.
The depression in freezing point of water observed for the same amount of acetic acid, dichloro-acetic acid and trichloro acetic acid increases in the order given above. Explain briefly.
Answer:
Given acids are CH3COOH, CHCl2COOH, CCl3 COOH.
The depression in freezing point of a solute in water depends upon the number of ions (or) particles in aqueous solution.
The given three acids are arranged in the order of their acidic strengths (increasing order)
CH3COOH < CHCl2COOH < CCl3COOH
Due to the presence of three chlorine atoms CCl3COOH is more acidic than CHCl2 COOH and followed by CH3COOH.
∴ The order of depression in freezing point is
CH3COOH < CHCl2COOH < CCl3COOH
![]()
Question 19.
What is Van’t Hoffs factor ‘i’ and how is it related to ‘a’ in the case of a binary electrolyte (1:1)?
Answer:
Van’t Hoffs factor (i) : “It is defined as the ratio of the observed value of colligative property to the theoretical value of colligative property”.
i = 
Solute dissociation or ionization process : If a solute on ionization gives ‘n’ ions and ‘a’ is degree of ionization at the given concentration, we will have [1 + (n – 1) α] particles.
(1 – α) ⇌ nα
Total 1 – α + nα = [1 + (n – 1) α]
∴ i = \(\frac{[1+(n-1) \alpha]}{1}\)
α = \(\frac{\mathrm{i}-1}{\mathrm{n}-1}\)
αionization = \(\frac{\mathrm{i}-1}{\mathrm{n}-1}\)
Solute association process :
If ‘n’A molecules combine to give An, we have
nA ⇌ An
If ‘α’ is degree of association at the given concentration.
1 – α = \(\frac{\alpha}{n}\)
= 1 – α + \(\frac{\alpha}{n}\)
i = \(\frac{1-\alpha+\frac{\alpha}{n}}{1}\)
(or) α = \(\frac{1-\mathrm{i}}{1-\frac{1}{n}}\)
α dissociation = \(\frac{1-\mathrm{i}}{1-\frac{1}{n}}\)
Question 20.
What is relative lowering of vapour pressure ? [A.P. Mar. 19]
Answer:
Relating lowering of vapour pressure: The ratio of lowering of vapour pressure of a solution containing non-volatile solute to the vapour pressure of pure solvent is called relative lowering of vapour pressure.
R.L.V.P. = \(\frac{\mathrm{P}_{0}-\mathrm{P}_{\mathrm{S}}}{\mathrm{P}_{0}}\)
P0 – PS = lowering of vapour pressure
P0 = Vapour pressure of pure solvent
![]()
Question 21.
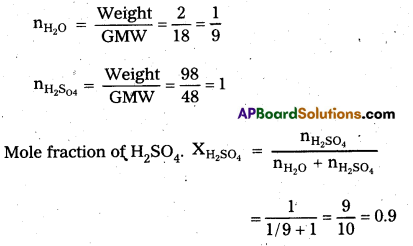
Calculate the mole fraction of H2SO4 in a solution containing 98% H2SO4 by mass. [A.P. Mar. 17]
Answer:
Given a Solution containing – 98% H2SO4 by mass.
It means 98 gms of H2SO4 and 2 gms of H2O mixed to form a solution.
Short Answer Questions
Question 1.
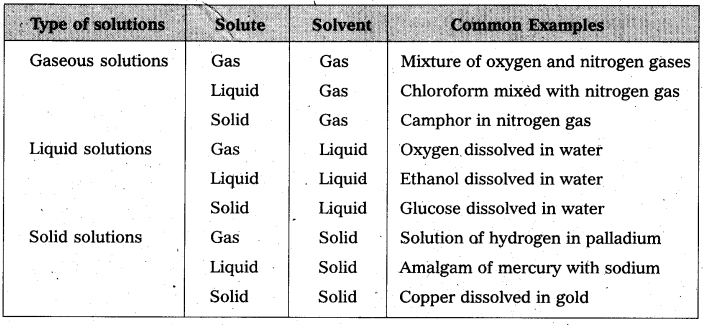
How many types of solutions are formed? Give an example for each type of solution.
Answer:
Solutions are classified into three types on the basis of the solvent present in that solution.
Question 2.
Define mass percentage, volume percentage and mass to volume percentage solutions.
Answer:
i) Mass percentage : The mass percentage of a component of a solution is defined as the
mass % =  × 10
× 10
ii) Volume percentage \(\left(\frac{\mathbf{v}}{\mathbf{V}}\right)\) : It is defined as the volume % of a component
=  × 100
× 100
iii) Mass to volume percentage \(\left(\frac{\mathbf{w}}{\mathbf{V}}\right)\) : It is defined as the mass of solute dissolved in 100 ml of the solution.
It is commonly used in medicine and pharmacy.
![]()
Question 3.
Concentrated nitric acid used in the laboratory work is 68% nitric acid by mass in aqueous solution. What should be the molarity of such a sample of the acid if the density of the solution is 1.504g mL-1?
Answer:
Given 68% HNO3 by mass that means
68gms mass of HNO3 present in 100 gms of solution.
Molecular weight of HNO3 = 63
Number of moles of HNO3 = \(\frac{\text { weight }}{\text { GMW }}=\frac{68}{63}\) = 1.079
Given density of the solution = 1.504 gm/ml

Question 4.
A solution of glucose in water is labelled as 10% w/w. What would be the molarity of the solution?
Answer:
Given 10% \(\left(\frac{\mathrm{W}}{\mathrm{w}}\right)\) glucose in water solution
Weight of glucose = 10 gms
GMW of glucose (C6H12O6) = 180
Weight of water = 100 – 10 = 90 gms.
Molarity (m) = \(\frac{\text { Weight }}{\text { GMW }} \times \frac{1000}{\text { W (gms) }}\)
= \(\frac{10}{180} \times \frac{1000}{90}\) = \(\frac{100}{18 \times 9}\)
= 0.617 moles / kg
Molarity = \(\frac{\text { Weight }}{\text { GMW }} \times \frac{1000}{V(\mathrm{~m} l)}\)
Weight of solution = 100 gms
Assuming that Density of solution = 1.2 gm/ml
Volume = \(\frac{100}{1.2}\) = 83.33 ml
Molarity (M) = \(\frac{10}{180} \times \frac{1000}{83.33}\) ml
= \(\frac{1000}{18 \times 83.33}\) = 0.67 M
Question 5.
A solution of sucrose in water is labelled as 20% w/w. What would be the mole fraction of each component in the solution ?
Answer:
20% \(\left(\frac{\mathrm{W}}{\mathrm{w}}\right)\) Sucrose in water solution means
20 gms of Sucrose and 80 gms of water.
Number of moles of sucrose (ns) = \(\frac{20}{342}\) = 0.0584
Number of moles of water (n0) = \(\frac{80}{18}\) = 4.444
Mole fraction of sucrose Xs = \(\frac{n_{s}}{n_{0}+n_{s}}\)
= \(\frac{0.0584}{4.444+0.0584}\) + \(\frac{0.0584}{4.50284}\) = 0.01296
Mole fraction of water X0 = \(\frac{n_{s}}{n_{0}+n_{s}}\) = \(\frac{4.444}{4.50284}\) = 0.9869
(Or)
Xs + X0 = 1
X0 = 1 – Xs = 1 – 0.01296 = 0987
![]()
Question 6.
How many ml of 0.1 M HCl is required to react completely with 1.0 g mixture of Na2CO3 and NaHCO3 containing equal-molar amounts of both?
Answer:
Given 1gm mixture of Na2CO3 and NaHCO3
Let the mass of Na2CO3 = a gms
Mass of NaHCO3 = (1 – a) gms
Number of moles of Na2CO3 = \(\frac{\mathrm{wt}}{\text { GMW }}=\frac{\mathrm{a}}{106}\)
Number of moles of NaHCO3 = \(\frac{\mathrm{wt}}{\mathrm{GMW}}=\frac{1-\mathrm{a}}{84}\)
Given that the mixture contains Equi molar amounts of Na2CO3 and NaHCO2
∴ \(\frac{a}{106}\) = \(\frac{1-a}{84}\)
84 a =106 – 106 a
190 a = 106
a = 0.558gms
∴ Weight of Na2CO3 = 0.558 gms
Weight of NaHCO3 = 1 – 0.558 = 0.442gms
Na2CO3 + 2 HCl → 2 NaCl + H2O + CO2
106 gms – 73 gms
0.558 g – ? \(\frac{73 \times 0.558}{106}\) = 0.384 gms
NaHCO3 + HCl → NaCl + H2O + CO2
84 gms — 36.5 gins
0.442gms — ?
= \(\frac{36.5 \times 0.442}{84}\) = 0.1928
∴ The weight of HC1 required = 0.384 + 0.192 = 0.576 gms
Molarity (M) = \(\frac{\mathrm{Wt}}{\text { GMWt }} \times \frac{1000}{\mathrm{~V}(\mathrm{~m} l)}\)
0.1 = \(\frac{0.576}{36.5} \times \frac{1000}{V}\)
V = \(\frac{0.576 \times 1000}{36.5 \times 0.1}=\frac{576}{3.65}\) = 157.80 ml
Question 7.
A solution is obtained by mixing 300g of 25% solution and 400g of 40% solution by mass. Calculate the mass percentage of the resulting solution.
Answer:
Given a solution is obtained by mixing 300 gms of 25% solution and 400 gms of 40% solution by mass.
Weight of solute in 1st solution = 300 × \(\frac{25}{100}\) = 75 gms
Weight of solute in 2nd solution = 400 × \(\frac{40}{100}\) = 160 gms
Total weight of solute = 75 + 160 = 235 gms
Total weight of solution = 300 + 400 = 700 gms
Mass % of solute in resulting solution = \(\frac{235}{700}\) × 100 = 33.5%
![]()
Question 8.
An antifreeze solution is prepared from 222.6g of ethylene glycol [(C2H6O2)] and 200g of water (solvent). Calculate the molality of the solution.
Solution:
Weight of Ethylene glycol = 222.6 gms .
G.mol wt =62
Weight of solvent = 200 gms
Molality (m) = \(\frac{\mathrm{Wt}}{\mathrm{GMWt}} \times \frac{1000}{\mathrm{a}(\mathrm{gms})}\)
= \(\frac{222.6}{62} \times \frac{1000}{200}=\frac{222.6}{62 \times 0.2}\) = 17.95 m
Molarity (M) = \(\frac{\mathrm{Wt}}{\mathrm{GMWt}} \times \frac{1000}{\mathrm{~V}(\mathrm{~m} l)}\)
= \(\frac{222.6}{62} \times \frac{1000}{394.2}\) = 9.1 M
Mass of solution = 200 + 222.6
= 422.6 gms
Volume = \(\frac{\text { Weight }}{\text { Density }}\) = \(\frac{422.6}{1.072}\) = 394.2 ml
Question 9.
Why do gases always tend to be less soluble in liquids as the temperature is raised?
Answer:
Gas dissolved in a liquid is an exothermic reaction (H <O).
According to Lechatelier’s principle,
- If the reaction is exothermic the solubility of gas, decrease with increases in temperature.
- So gases always tend to be less soluble in liquids to as the temperature is raised.
Question 10.
What is meant by positive deviations from Raoults law and how is the sign of ∆mix H related to positive deviation from Raoult’s law?
Answer:
- When the vapour pressure of a solution is higher than the predicted value by Raoult’s law, it is called positive deviation.
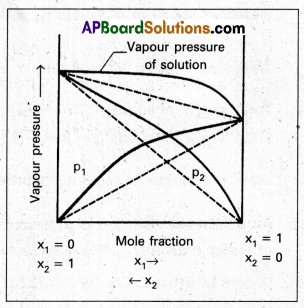
- In this case inter molecular interactions between solute and solvent particles (1 and 2) are weaker than those between solute and solvent particles (1 and 2) are weaker than those between solute and solute (1 – 1) and solvent – solvent (2 – 2)
- Hence the molecules of 1 or 2 will escape more easily from the surface of solution than in their pure state.
∴ The vapour pressure of the solution will be higher. - The vapour pressure diagram showing positive deviation as follows.
Eg. : Ethyl alcohol and water, Acetone and benzene.
![]()
Question 11.
What is meant by negative deviation from Raoult’s law and how is the sign of ∆mixH related to negative deviation from Raoult’s law?
Answer:
- When the vapour pressure of a solution is lower than the predicted value by Raoult’s law, it is called negative deviation.
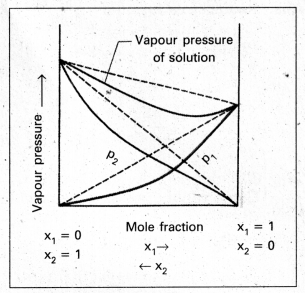
- In case of negative deviation the inter molecular attractive forces between 1 – 1 and 2 – 2 are weaker than those between 1 -2.
- It leads to decrease in vapour pressure resulting in negative deviation.
- The vapour pressure diagram showing negative deviation as follows.
- Eg.: HNO3 and water, HCl and water.
Question 12.
The vapour pressure of water is 12.3 k Pa at 300 K. Calculate the vapour pressure of 1 molal solution of a non-volatile solute in it.
Answer:
Given molality of solution = 1 m
Vapour pressure of water P0 = 12.3 kPa
Number of moles of water = \(\frac{100}{18}\)
= 55.55 (n0)
Mole fraction of solute (Xs) = \(\frac{\mathrm{n}_{\mathrm{s}}}{\mathrm{n}_{0}+\mathrm{n}_{\mathrm{s}}}\)
= \(\frac{1}{55.55+1}\)
= \(\frac{1}{56.55}\) = 0.0177
Mole fraction of water (X0) = 1 – Xs
= 1 – 0.0177 = 0.9823
Vapour pressure of solution (Ps) = P0X0
= 12.3 × 0.9823 = 12.08 kPa
Question 13.
Calculate the mass of a non-volatile solute (molar mass 40g mol-1) which should be dissolved in 114g Octane to reduce its vapour pressure to 80%. [T.S. Mar. 16]
Answer:
Raoult’s law formula
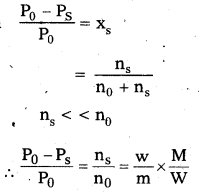
Given vapour pressure reduced to 80%, when non-volatile solute is dissolved in octane.
P0 = 1 atm
Ps = 0.8 atm
W = 114 gms
M = 114 gm/mole
w = ? ; m = 40
\(\frac{\mathrm{P}_{0}-\mathrm{P}_{\mathrm{s}}}{\mathrm{P}_{0}}=\frac{\mathrm{n}_{\mathrm{s}}}{\mathrm{n}_{0}}=\frac{\mathrm{w}}{\mathrm{m}} \times \frac{\mathrm{M}}{\mathrm{W}}\)
\(\frac{1-0.8}{1}=\frac{w}{40} \times \frac{114}{114}\)
w = 8 gms
![]()
Question 14.
A 5% solution (by mass) of cane sugar in water has freezing point of 271K. Calculate the freezing point of 5% glucose in water If freezing point of water is 273.15 K.
Answer:
Given 5% solution of cane sugar
w = 5gms; W = 95gms
m = 342; ∆Tf = 273.15 – 271 = 2.15
∆Tf = \(\frac{\mathrm{K}_{\mathrm{f}} \times \mathrm{w}}{\mathrm{m} \times \mathrm{W}}\)
2.15 =\(\frac{\mathrm{K}_{\mathrm{f}} \times 5}{342 \times 95}\) ……………… (1)
5% solution of glucose
w = 5gms; W = 95gms
m = 180, ∆Tf = ?
∆Tf = \(\frac{K_{f} \times 5}{180 \times 95}\) ………………… (2)
Dividing equation (2) by Equation (1)
\(\frac{\Delta \mathrm{T}_{\mathrm{f}}}{2.15}=\frac{\mathrm{K}_{\mathrm{f}} \times 5}{180 \times 95} \times \frac{342 \times 95}{\mathrm{~K}_{\mathrm{f}} \times 5}\)
∆Tf = \(\frac{342 \times 2.15}{180}\) = 4.085 K
∴ The freezing point temperature for 5% glucose solution
= 273.15 – 4.085 = 269.07 K
Question 15.
If the osmotic pressure of glucose solution is 1.52 bar at 300 K. What would be its concentration if R = 0.083L bar mol-1 K-1 ?
Answer:
π = CRT
R = 0.0836.bar. mole-1 K-1
T = 300 K
π = 1.52 bar
C = \(\frac{\pi}{\mathrm{RT}}=\frac{1.52}{0.083 \times 300}=\frac{1.52}{24.9}\) = 0.061 M
Question 16.
Vapour pressure of of water at 293K is 17.535 mm Hg. Calculate the vapour pressure of the solution at 293K when 25g of glucose is dissolved in 450g of water? [A.P. Mar.19]
Answer:
Raoult1s law formula

Question 17.
How is molar mass related to the elevation in boiling point of a solution?
Answer:
The expression for elevation of boiling point is
∆Tb = \(\frac{\mathrm{K}_{\mathrm{b}} \times 1000 \times \mathrm{w}}{\mathrm{m} \times \mathrm{w}}\) = Kb = molal elevation constant
w = Weight of solute
W = Weight of solvent
m = molar mass of solute
Molar mass of solute m = \(\frac{K_{\mathrm{b}} \times 1000 \times \mathrm{w}}{\Delta \mathrm{T}_{\mathrm{b}} \times \mathrm{w}}\)
∴ Molar mass of solute (m) and elevation of boiling point (∆Tb) are inversely related.
![]()
Question 18.
What is an ideal solution ?
Answer:
A solution of two or mote components which obeys Raoult’s law at all concentrations and at all temperatures is called ideal Solution. In ideal solution there should not be any association between solute and solvent, (i.e.) no chemical interaction between solute and solvent of solution.
Ex : The following mixtures form ideal solutions.
- Benzene + Toluene
- n – hexane + n – heptane
- ethyl bromide + ethyl iodide
Question 19
What is relative lowering of vapour pressure ? How is it useful to determine the molar mass of a solute ? [T.S. Mar. 15]
Answer:
Raoult’s law for volatile solute: For a solution of volatile liquids, the partial vapour pressure of each component of the solution is directly proportional to its mole fraction present in solution.
Raoult’s law for non-volatile solute : The relative lowering of vapour pressure of dilute solution containing non-volatile solute is equal to the mole fraction of solute.
Relative lowering of vapour pressure \(\frac{\mathrm{P}_{0}-\mathrm{P}_{\mathrm{s}}}{\mathrm{P}_{0}}\) = Xs (mole fraction of solute)
\(\frac{\mathrm{P}_{0}-\mathrm{P}_{\mathrm{s}}}{\mathrm{P}_{0}}=\frac{\mathrm{n}_{\mathrm{s}}}{\mathrm{n}_{0}+\mathrm{n}_{\mathrm{s}}}\)
For very much dilute solutions ns < < < …………… n0
∴ \(\frac{\mathrm{P}_{0}-\mathrm{P}_{\mathrm{s}}}{\mathrm{P}_{0}}=\frac{\mathrm{n}_{\mathrm{s}}}{\mathrm{n}_{0}}=\frac{\mathrm{w}}{\mathrm{m}} \times \frac{\mathrm{M}}{\mathrm{W}}\)
W = Weight of solute
w = Weight of solvent
m = Molar mass of solute
M = Molar mass of solvent
Molar mass of solute m = \(\frac{W \times M}{W} \times \frac{P_{0}}{P_{0}-P_{s}}\)
Question 20.
How is molar mass related to the depression in freezing point of a solution ?
Answer:
The expression for depression in Freezing point is
∆Tf = \(\frac{\mathrm{K}_{\mathrm{f}} \times 1000 \times \mathrm{w}}{\mathrm{m} \times \mathrm{W}}\)
Kf = molal depression constant
W = Weight of solvent
w = Weight of solute
m = molar mass of solute
Molar mass of solute (m) = \(\frac{\mathrm{K}_{\mathrm{f}} \times 1000 \times \mathrm{w}}{\Delta \mathrm{T}_{\mathrm{f}} \times \mathrm{W}}\)
∴ Molar mass ôf solute (m) and depression in freezing point (∆Tf) are inversely related.
Long Answer Questions
Question 1.
An aqueous solution of 2% non volatile solute exerts a pressure of 1.004 bar at the normal boiling point of the solvent. What is the molecular mass of the solute ?
Answer:
Relative lowering of vapour pressure = \(\frac{\mathrm{P}_{0}-\mathrm{P}_{\mathrm{s}}}{\mathrm{P}_{0}}=\frac{\mathrm{n}_{\mathrm{s}}}{\mathrm{n}_{0}}\)
P0 = 1.013 bar, Ps = 1.004 bar
w = 2gms
W = 98gms
M = 18
m = ?
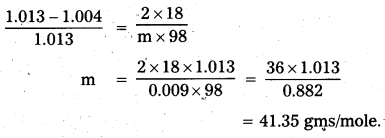
![]()
Question 2.
Heptane and Octane form an ideal solution. At 373 K the vapour pressure of the two liquid components are 105.2 kPa and 46.8 kPa respectively. What will be the vapour pressure of a mixture of 26.0 g heptane and 35g of octane?
Answer:
Number of moles of octane n0 = \(\frac{\text { Weight }}{\text { GMwt }}=\frac{35}{114}\) = 0.307
Number of moles of heptane ns = \(\frac{\text { Weight }}{\text { GMwt }}=\frac{26}{100}\) = 0.26
no 0.307
Mole fraction of octane X0 = \(\frac{\mathrm{n}_{0}}{\mathrm{n}_{0}+\mathrm{n}_{\mathrm{s}}}=\frac{0.307}{0.307+0.26}\) = 0.541
Mole fraction of heptane Xs = \(\frac{\mathrm{n}_{\mathrm{s}}}{\mathrm{n}_{0}+\mathrm{n}_{\mathrm{s}}}=\frac{0.26}{0.307+0.26}\) = 0.459
Given vapour pressure of heptane P1 = 105.2 kPa
vapour pressure of Octane P2 = 46.8 kPa
26 gms of heptane and 35 gms of octane are mixed.
In that mixture
The vapour pressure of heptane (P11) = P1 × Xs
= 105.2 × 0.459 = 48.28 kPa
The vapour pressure of Octane (P22) = P2 × X0
= 46.8 × 0.541
= 25.32 kPa
Total pressure of the mixture (P) = P11 + P22
= 25.32 + 48.28
= 73.6 kPa
Question 3.
A solution containing 30g of non-volatile solute exactly in 90g of water has a vapour pressure of 2.8 kPa at 298 K. Further 18g of water is then added to the solution and the new vapour pressure becomes 2.9 kPa at 298 K. Calculate (i) The molar mass of the solute and (ii) Vapour pressure of water at 298 K.
Answer:
Calculation of molar mass of solute
Case – I:

Case – II :

Calculation of vapour pressure of water :
According to Raoult’s law
PA = \(\mathrm{P}_{\mathrm{A}}^{0} \mathrm{X}_{\mathrm{A}}\)
2.8 = \(P_{A}^{0} \times \frac{M}{6+M}\)
M = 23
2.8 = \(\mathrm{P}_{\mathrm{A}}^{0} \times \frac{23}{6+23}\)
\(\mathrm{P}_{\mathrm{A}}^{0}=\frac{2.8 \times 29}{23}=\frac{81.2}{23}\) = 3.53 k.pa
Question 4.
Two elements A and B from compounds having formula AB2 and AB4. When dissolved in 20g of Benzene (C6H6), 1g of AB2 lowers the freezing point by 2.3 K whereas 1.0g of AB4 lowers it by 1.3 K. The molar depression constant for benzene is 5.1 K kg mol-1. Calculate atomic masses of A and B.
Answer:
Calculation of molecular masses of compounds AB2 and AB4
For AB2 compounds
m = \(\frac{\mathrm{K}_{\mathrm{f}} \times 1000 \times \mathrm{W}}{\Delta \mathrm{T}_{\mathrm{f}} \times \mathrm{W}}=\frac{5.1 \times 1000 \times 1}{2.3 \times 20}\) = 110.87 gms/mole
For AB4 compound
m = \(\frac{5.1 \times 1000 \times 1}{1: 3 \times 20}\) = 196.15 gms/mole
Calculation of the atomic masses of elements
Atomic mass of element A = x
Atomic mass of element B = y
Molecular mass of AB2 = x + 2y
Molecular mass of AB4 = x + 4y
a + 2b = 110.87 ……………….. (1)
a + 4b = 196.15 ………………. (2)
Equation (2) – Eqiation (1)
x + 4y – x – 2y
196.15 – 110.87
2y = 85.28
y = 42.64
x + 2y = 110.87
x + 85.28 = 110.87
x = 25.59
Atomic mass of element A = 25.59 u
B = 42.64 u
![]()
Question 5.
Calculate the depression in the freezing point of water when 10g of CH3CH2CHClCOOH is added to 250g of water. Ka = 1.4 × 10-3, Kf = 1.86 K kg mol-1.
Answer:
Calculation of degree of dissociation :
Mass of solute = 10 gms
Molar mass of solute (CH3 – CH2 – CH – Cl – COOH) = 122.5 g/mole
Molality = \(\frac{10}{122.5} \times \frac{1000}{250}\) = 0.326 m

Calculation of depression in freezing point
∆Tf = i × Kf × m = 1.065 × 1.86 × 0.326 = 0.65 K
Question 6.
19.5g of CH2FCOOH is dissolved in 500g of water. The depression In freezing point of water observed is 1.0°C. Calculate the Van’t Hoff factor and dissociation constant of fluoroacetic acid.
Answer:
Calculation of Vant Hoff factor of acid:
∆Tf = 1°C
Kf = 1.86 K kg/mole-1
∆Tf = i Kf m
m = \(\frac{19.5}{78} \times \frac{1000}{500}\) = 0.5 m
i = \(\frac{1}{1.86 \times 0.5}\) = 1.0753
Calculation of degree of dissociation of the acid :

Question 7.
100 g of liquid A(molar mass 140g mol-1) was dissolved in 1000 g of liquid B(molar mass 180g mol-1). The vapour pressure of pure liquid B was found to be 500 torr. Calculate the vapour pressure of pure liquid A and its vapour pressure in the solution if the total vapour pressure of the solution is 475 torr.
Answer:
Calculation of vapour pressure of pure liquid A (\(\mathrm{P}_{\mathrm{A}}^{0}\))
Number of moles of liquid A
nA = \(\frac{\mathrm{w}}{\mathrm{m}}=\frac{100}{140}\) = 0.7143
Number of moles of liquid B
nB = \(\frac{\mathrm{w}}{\mathrm{m}}=\frac{1000}{180}\) = 5.5556
Mole fraction of A
XA = \(\frac{\mathrm{n}_{\mathrm{A}}}{\mathrm{n}_{\mathrm{A}}+\mathrm{n}_{\mathrm{B}}}=\frac{0.7143}{0.7143+5.5556}=\frac{0.7143}{6.2699}\)
= 0.1139
Mole fraction of B (XB) = 1 – 0.1139 = 0.8861
Vapour pressure of liquid (\(\mathrm{P}_{\mathrm{B}}^{0}\)) = 500 torr
Total vapour pressure of solution (P) = 475 torr
According to Raoult’s law
P = P\(\mathrm{P}_{\mathrm{A}}^{0}\) XA + P\(\mathrm{P}_{\mathrm{B}}^{0}\) XB
475 = P\(\mathrm{P}_{\mathrm{A}}^{0}\) (0.1139) + 500(0.8861)
475 = P\(\mathrm{P}_{\mathrm{A}}^{0}\) (0.1139) + 443.05
\(\mathrm{P}_{\mathrm{A}}^{0}\) = \(\frac{475-443.05}{0.1139}=\frac{31.95}{0.1139}\) = 280.5 torr
Calculation of vapour pressure of A in the solution (PA)
PA = P\(\mathrm{P}_{\mathrm{A}}^{0}\) XA = 280.5 × 0.1139
PA = 32 torr.
![]()
Question 8.
Determine the amount of CaCl2 (i = 2.47) dissolved in 2.5 litre of water such that its osmotic pressure is 0.75 atm at 27°C.
Answer:
Varit Hoffs equation
Osmotic pressure (π) = i CRT
i = 2.47 .
V = 2.5 lit
R = 0.0821 lit. atm.k-1. mol-1
T = 27 + 273 = 300 K
π = 0.75 atm
π = i(\(\frac{n_{B}}{V}\))RT
nB = \(\frac{\pi \mathrm{V}}{\mathrm{iRT}}=\frac{0.75 \times 2.5}{2.47 \times 0.0821 \times 300}\) = 0.0308
The amount of CaCl2 dissolved = nB × mB
= 0.0308 × 111 = 3.42 gms
Question 9.
Determine the osmotic pressure of a solution prepared by dissolving 25 mg of K2SO4 in two litre of water at 25°C assuming that it is completely dissociated.
Answer:
The amount of K2SO4 dissolved = 25 mg
Volume = 2 lit; T = 25°C = 298 K
Molecular weight of K2SO4 = 174 gms / mole
![]()
Total ions produced on dissociation = 3
i = 3
π = i CRT = \(\mathrm{i}\left(\frac{\mathrm{n}}{\mathrm{V}}\right) \mathrm{RT}=\mathrm{i}\left(\frac{\mathrm{w}}{\mathrm{m}}\right) \times \frac{\mathrm{RT}}{\mathrm{V}}\)
= \(\frac{3 \times 0.025 \times 0.0821 \times 298}{174 \times 2}\) = 5.27 × 10-3 atm.
![]()
Question 10.
Benzene and Toluene form ideal solution over the entire range of composition. The vapour pressure of pure benzene and toluene at 300 K are 50.71 mm of Hg and 32.06 mm of Hg respectively. Calculate the mole fraction of benzene in vapour phase if 80g of benzene is mixed with 100g of toluene.
Answer:
Molecular weight of benzene (C6H6) = 78
Molecular weight of Toluene (C7H8) = 92
nC6H6 = \(\frac{80}{78}\) = 1.026
nC7H8= \(\frac{100}{92}\) = 1.087
XC6H6 = \(\frac{1.026}{1.026+1.087}=\frac{1.026}{2.113}\) = 0.4855
XC7H8 = 1 – 0.4855 = 0.5145
According to Raoult’s law
Partial pressure of benzene in solution
PC6H6 = PC6H6 × XC6H6
= 50.71 × 0.4855 = 24.61 mm
Partial pressure of Toluene in solution
PGH8 = ![]() × XC7H8 = 32.06 × 0.5145 = 16.49 mm
× XC7H8 = 32.06 × 0.5145 = 16.49 mm
Total vapour pressure of solution (P) = 24.61 + 16.49 = 41.1 mm
Mole fraction of benzene in vapour phase is
= \(\frac{\mathrm{X}_{\mathrm{C}_{6} \mathrm{H}_{6}} \times \mathrm{P}_{\mathrm{C}_{6} \mathrm{H}_{6}}^{0}}{\mathrm{P}_{\text {total }}}=\frac{0.4855 \times 50.71}{41.1}=\frac{24.61}{41.1}\) = 0.5987
Textual Examples
Question 1.
Calculate the mole fraction of ethylene glycol (C2H6O2) In a solution containing 20% of C2H6O2 by mass.
Solution:
Assume that we have 100g of solution (one can start with any amount of solution because the results obtained will be the same). Solution will contain 20g of ethylene glycol and 80g of water.
Molar mass of C2H6O2 = 12 × 2 + 1 × 6 + 16 × 2 = 62 g mol-1

Question 2.
Calculate the molarity of a solution containing 5g of NaOH in 500 mL solution. [T.S Mar.17]
Solution:
Moles of NaOH = \(\frac{5 \mathrm{~g}}{40 \mathrm{~g} \mathrm{~mol}^{-1}}\) = 0.125 mol
Volume of the solution in litres = 450 mL / 1000 mL L-1
Using equation

= 0.278 mol L-1 = 0.278 mol dm-3
Question 3.
Calculate molality of 2.5 of ethanoic acid (CH3COOH) In 75g of benzene. [T.S. Mar. 15]
Solution:
Molar mass of C2H4O2: 12 × 2 + 1 × 4 + 16 × 2 = 60g mol-1
Moles of C2H4O2 = \(\frac{2.5 \mathrm{~g}}{60 \mathrm{~g} \mathrm{~mol}^{-1}}\) = 0.0417 mol
Mass of benzene in kg = 75g/1000 g kg-1 = 75 × 10-3 kg
Molality of C2H4O2 = \(\frac{\text { Moles of } \mathrm{C}_{2} \mathrm{H}_{4} \mathrm{O}_{2}}{\mathrm{~kg} \text { of benzene }}=\frac{0.0417 \times \mathrm{mol} \times 1000 \mathrm{~g} \mathrm{~kg}^{-1}}{75 \mathrm{~g}}\)
= 0.556 mol kg-1
![]()
Question 4.
If N2 gas is bubbled through water at 293 K, how many mililmoles of N2 gas would dissolve in 1 litre of water ? Assume that N2 exerts a partial pressure of 0.987 bar. Given that Henrys law constant for N2 at 293 K is 76.48 k bar.
Solution:
The solubiity of gas is related to the mole fraction in aqueous solution.
The mole fraction of the gas in the solution is calculated by applying Henrys law. Thus:
x (nitrogen) = \(\frac{\mathrm{p} \text { (nitrogen) }}{\mathrm{K}_{\mathrm{H}}}=\frac{0.987 \mathrm{bar}}{76.480 \mathrm{bar}}\) = 1.29 × 10-5
As 1 Litre of water contains 55.5 mol of it, therefore if n represents number of moles of N2 in solution.
x(Nitrogen) = \(\frac{\mathrm{n} \mathrm{mol}}{\mathrm{n} \mathrm{mol}+55.5 \mathrm{~mol}}=\frac{\mathrm{n}}{55.5}\) = 1.29 × 10-5
(n in denominator is neglected as it is << 55.5)
Thus n = 1.29 × 10-5 55.5 mol 7.16 × 10-4 mol
= \(\frac{7.16 \times 10^{-4} \mathrm{~mol} \times 1000 \mathrm{mmol}}{1 \mathrm{~mol}}\) = 0.716 m mol
Question 5.
Vapour pressure of chloroform (CHCl3) and dichloromethane (CH2Cl2) at 298 K are 200 mm Hg and 415 mm Hg respectively. (i) Calculate the vapour pressure of the solution prepared by mixing 25.5 g of CHCl3 and 40 g of CH2Cl2 at 298 K and (ii) mole fractions of each component in vapour phase.
Solution:
i) Molar mass of CH2Cl2 = 12 × 1 + 1 × 2 + 35.5 × 2 = 85 g mol-1
Molar mass of CHCl3 = 12 × 1 + 1 × 1 +35.5 × 3 = 119.5 g mol-1
Moles of CH2Cl2 = \(\frac{40 \mathrm{~g}}{85 \mathrm{~g} \mathrm{~mol}^{-1}}\) = 0.47 mol
Moles of CHCl3 = \(\frac{25.5 \mathrm{~g}}{119.5 \mathrm{~g} \mathrm{~mol}^{-1}}\) = 0.2 13 mol
Total number of moles = 0.47 + 0.2 13 = 0.683 mol
XCH2Cl2 = \(\frac{0.47 \mathrm{~mol}}{0.683 \mathrm{~mol}}\) = 0.688
XCHCl3 = 1.00 – 0.688 = 0.3 12
Using equation :
ptotal = \(\mathrm{p}_{1}^{0}+\left(\mathrm{p}_{2}^{0}-\mathrm{p}_{1}^{0}\right)\) x2 = 200 + (415 – 200) × 0.688
= 200 + 147.9 = 347.9mm Hg
ii) Using the relation, y1 = p1/ptotal we can calculate the mole fraction of the components in gas phase (y1)
PCH2Cl2 = 0.688 × 415 mm Hg = 285.5 mm Hg
PCHCl3 = 0.3 12 × 200 mm Hg = 62.4 mm Hg
yCH2Cl2 = 285.5 mm Hg/347.9 mm Hg = 0.82
yCHCl3 = 62.4 mm Hg/347.9 mm Hg = 0.18
Note : Since CH2Cl2 is a more volatile component than CHCl3, [\(\mathrm{p}_{\mathrm{CH}_{2} \mathrm{Cl}_{2}}^{0}\) = 415 mm Hg and
\(\mathrm{p}_{\mathrm{CHCl}_{3}}^{0}\) = 200 mm Hg] and the vapour phase is also richer in CH2Cl2 [yCH2Cl2 = 0.82 and yCHCl3 = 0.18], it may thus be concluded that at equilibrium, vapour phase will be always rich in the component which is more volatile.
![]()
Question 6.
The vapour pressure of pure benzene at a certain temperature is 0.850 bar. A non-volatile, non-electrolyte solid weighing 0.5g when added to 39.0 g of benzene (molar mass 78 g mol-1), vapour pressure of the solution, then, is 0.845 bar. What is the molar mass of the solid substance ? [A.P. Mar. 18; 16]
Solution:
The various quantities known to us are as follows.
\(\mathrm{p}_{1}^{0}\) = 0.850 bar
P = 0.845bar
M1 = 78 g mol-1
w2 = 0.5 g
w1 = 39 g
Substituting these values in equation \(\frac{\mathrm{P}^{0}-\mathrm{P}}{\mathrm{P}_{1}^{0}}=\frac{\mathrm{w}_{2} \times \mathrm{M}_{1}}{\mathrm{M}_{2} \times \mathrm{w}_{1}}\) we get
\(\frac{0.850 \mathrm{bar}-0.845 \mathrm{bar}}{0.850 \mathrm{bar}}=\frac{0.5 \mathrm{~g} \times 78 \mathrm{~g} \mathrm{~mol}^{-1}}{\mathrm{M}_{2} \times 39 \mathrm{~g}}\)
Therefore, M2 = 170 g mol-1.
Question 7.
18g of glucose, C6H12O6, is dissolved in 1 kg of water in a saucepan. At what temperature will water boil at 1.013 bar ? Kb for water is 0.52 K kg mol-1.
Solution:
Moles of glucose = 18g/180 g mol-1 = 0.1 mol
Number of kilograms of solvent = 1 kg
Thus molality of glucose solution = 0.1 mol kg-1
For water, change in boiling point
∆Tb = Kb × m = 0.52 K kg mol-1 × 0.1 mol kg-1 = 0.052 K .
Since water boils at 373.15 K at 1.013 bar pressure, therefore, the boiling point of solution will be 373.15 + 0.052 = 373.202 K.
Question 8.
The boiling point of benzene is 353.23 K. When 1.80 g of a non-volatile solute was dissolved in 90 g of benzene, the boiling point is raised to 354.11 K. Calculate the molar mass of the solute. Kb for benzene is 2.53 K kg mol-1.
Solution:
The elevation of (∆Tb) in.the boiling point = 354.11 K – 353.23 K. = 0.88 K
Substituting these values in expression we get, M2 = \(\frac{1000 \times \mathrm{w}_{2} \times \mathrm{K}_{\mathrm{b}}}{\Delta \mathrm{T}_{\mathrm{b}} \times \mathrm{w}_{1}}\)
M2 = \(\frac{2.53 \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1} \times 1.8 \mathrm{~g} \times 1000 \mathrm{~g} \mathrm{~kg}^{-1}}{0.88 \mathrm{~K} \times 90 \mathrm{~g}}\)
Therefore, molar mass of the solute, M2 = 58 g mol-1.
![]()
Question 9.
45 g of ethylene glycol (C2H6O2) is mixed with 600 g of water. Calculate (a) the freezing point depression and (b) the freezing point of the solution.
Solution:
Depression in freezing point is related to the molality, therefore, the molality of the solution with respect to ethylene glycol = \(\frac{\text { moles of ethylene glycol }}{\text { mass of water in kilogram }}\)
Moles of ethylene glycol = \(\frac{45 \mathrm{~g}}{62 \mathrm{~g} \mathrm{~mol}^{-1}}\) = 0.73 mol
Mass of water in kg = \(\frac{600 \mathrm{~g}}{1000 \mathrm{~g} \mathrm{~kg}^{-1}}\) = 0.6 kg
Hence molality of ethylene glycol = \(\frac{0.73 \mathrm{~mol}}{0.60 \mathrm{~kg}}\) = 1.2 mol kg-1
Therefore freezing point depression,
∆Tf = 1.86 K kg mol-1 × 1.2 mol kg-1 = 2.2 K
Freezing point of the aqueous solution 273.15 K – 2.2 K = 270.95 K
Question 10.
1.00 g of a non-electrolyte solute dissolved in 50g of benzene lowered the freezing point of benzene by 0.40 K. The freezing point depression constant of benzene is 5.12 K kg mol-1. Find the molar mass of the solute.
Solution:
Substituting the values of various terms involved in equation
M2 = \(\frac{\mathrm{K}_{\mathrm{f}} \times \mathrm{w}_{2} \times 1000}{\Delta \mathrm{T}_{\mathrm{f}} \times \mathrm{w}_{1}}\) we get
M2 = \(\frac{5.12 \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1} \times 1.00 \mathrm{~g} \times 1000 \mathrm{~g} \mathrm{~kg}^{-1}}{0.40 \times 50 \mathrm{~g}}\) = 256 g mol-1
Thus, molar mass of the solute = 256 g mol-1
Question 11.
200 cm3 of an aqueous solution of a protein contains 1.26 g of the protein. The osmotiç pressure of such a solution at 300 K is found to be 2.57 × 10-3 bar. Calculate the molar mass of the protein.
Solution:
The various quantities known to us are as follows : π = 2.57 × 10-3 bar.
V = 200 cm3 = 0.200 litre
T = 300K
R = 0.083 L bar mol-1 K-1
Substituting these values in equation,
we get M2 = \(\frac{w_{2} R T}{\pi V}\)
M2 = \(\frac{1.26 \mathrm{~g} \times 0.083 \mathrm{~L} \mathrm{bar} \mathrm{K}^{-1} \mathrm{~mol}^{-1} \times 300 \mathrm{~K}}{2.57 \times 10^{-3} \mathrm{bar} \times 0.200 \mathrm{~L}}\)
= 61.022 g mol-1
![]()
Question 12.
2 g of benzoic acid (C6H5COOH) dissolved in 25g of benzene shows a depression in freezing point equal to 1.62 K. Molal depression constant for benzene is 4.9 K kg mol-1. What is the percentage association of acid if it forms dimer in solution ?
Solution:
The given quantities are :
w2 = 2g; Kf = 4.9 K kg mol-1; w1 = 25 g
∆Tf = 1.62 K
Substituting these values, in equation, we get:
M2 = \(\frac{\mathrm{K}_{\mathrm{f}} \times \mathrm{w}_{2} \times 1000}{\Delta \mathrm{T}_{\mathrm{f}} \times \mathrm{w}_{1}}\)
M2 = \(\frac{4.9 \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1} \times 2 \mathrm{~g} \times 1000 \mathrm{~g} \mathrm{~kg}^{-1}}{25 \mathrm{~g} \times 1.62 \mathrm{~K}}\) = 241.98 g mol-1
Thus, experimental molar mass of benzoic acid in benzene is = 241.98 g mol-1
Now consider the following equilibrium for the acid :
2 C6H5COOH ⇌ (C6H5COOH)2
If x represents the degree of association of the solute then we would have (1 – x) mol of benzoic acid left in unassociated form and correspondingly \(\frac{x}{2}\) as associated moles of benzoic acid at equilibrium.
Therefore, total number of particles at equilibrium is :
1 – x + \(\frac{x}{2}\) = 1 – \(\frac{x}{2}\).
Thus, total number of moles of particles at equilibrium equals van’t Hoff factor i.
But i = \(\frac{\text { Normal molar mass }}{\text { Abnormal molar mass }}=\frac{122 \mathrm{~g} \mathrm{~mol}^{-1}}{241.98 \mathrm{~g} \mathrm{~mol}^{-1}}\)
or = \(\frac{x}{2}\) = 1 – \(\frac{122}{241.98}\) = 1 – 0.504 = 0.496
or x = 2 × 0.496 = 0.992
Therefore, degree of association of benzoic acid in benzene is 99.2%.
Question 13.
0.6 mL of acetic acid (CH3COOH), having density 1.06 g mL-1, is dissolved in 1 litre of water. The depression in freezing point observed for this strength of acid was 0.0205°C. Calculate the van’t Hoff factor and the dissociation constant of acid.
Answer:
Number of moles of acetic acid = \(\frac{0.6 \mathrm{~mL} \times 1.06 \mathrm{~g} \mathrm{~mL}^{-1}}{60 \mathrm{~g} \mathrm{~mol}^{-1}}\)
= 0.0106 mol = n
Molality = \(\frac{0.0106 \times \mathrm{mol}}{1000 \mathrm{~mL} \times 1 \mathrm{~g} \mathrm{~mL}^{-1}}\) = 0.0106 mol kg-1
Using equation ∆Tf = \(\frac{\mathrm{K}_{\mathrm{f}} \times \mathrm{w}_{2} \times 1000}{\mathrm{M}_{2} \times \mathrm{w}_{1}}\)
∆Tf = 1.86 K kg mol-1 × 0.0106 mol kg-1 = 0.0197 K
van’t Hoff factor (i) = \(\frac{\text { Observed freezing point }}{\text { Calculated freezing point }}=\frac{0.0205 \mathrm{~K}}{0.0197 \mathrm{~K}}\) = 1.041
Acetic acid is a weak electrolyte and will dissociate into two ions: acetate and hydrogen ions per molecule of acetic acid. If x is the degree of dissociation of acetic acid, then we would have n (1 — X) moles of undissociated acetic acid, mc moles of CH3COO– and nx moles of H+ ions.

Intext Questions
Question 1.
Calculate the mass percentage of benzene (C6H6) and carbon tetrachlodie (CCl4) if 22g of benzene is dissolved in 122g of carbon tetrachioride.
Then, calculate the mass percentage from the formula
Mass % = ![]() × 100
× 100
Solution:
Mass of benzene = 22g; Mass of CCl4 = 122g
Mass of solution = 22 + 122 = 144g
Mass % of benzene = \(\frac{22}{144}\) × 100 = 15.28%
Mass of CCl4 = 100 – 15.28 = 84.72%
Note: Mass percent of CCl4 can also be calculated by using the formula as:
Mass % of CCCl4 = \(\frac{122}{144}\) × 100 = 84.72%
![]()
Question 2.
Calculate the mole fraction of benzene in solution containing 30% by mass in carbon tetrachloride.
• Then calculate the mole fraction by using the formula
Mole fraction of a component = \(\frac{\text { Number of moles of the component }}{\text { Total number of moles of all components }}\)
xA = \(\frac{\mathbf{n}_{\mathbf{A}}}{\mathbf{n}_{\mathbf{A}}+\mathbf{n}_{\mathbf{B}}}\)
Solution:
For 100 g of the solution
Mass of benzene = 30 g
Mass of carbon tetrachioride = 100 – 30 = 70g
Molar mass of benzene (C6H6) (12 × 6) + (6 × 1) = 72 + 6 = 78 g mol-1
Moles of benzene, nC6H6 = \(\frac{\text { Mass }}{\text { Molar mass }}=\frac{30}{78}\) = 0385 mol
Molar mass of carbon tetrachioride (CCl4) = 12 + (35.5 × 4)
= 12 + 142.0 = 154 g mol-1
Moles of CCl4,nCCl4 = \(\frac{70 \mathrm{~g}}{\left(154 \mathrm{~mol}^{-1}\right)}\) = (154 mol-1)
Mole fraction of benzene, XC6H6 = \(\frac{\mathrm{n}_{\mathrm{C}_{6} \mathrm{H}_{6}}}{\mathrm{n}_{\mathrm{C}_{6} \mathrm{H}_{6}}+\mathrm{n}_{\mathrm{CC}_{4}}}=\frac{0.385 \mathrm{~mol}}{(0.385+0.454) \mathrm{mol}}\) = 0.459
Question 3.
Calculate the molarity of each of the following solution:
a) 30g of CO(NH3)2. 6H2O in 4.3 L of solution.
b) 30 mL of 0.5 MH2SO4 diluted to 500 mL.

So, first find molar mass by adding atomic masses of different elements, then find moles of solute and then molarity.
b)Use molarity equation for dilution.
M1V1
(Before dilution)
M2V2
(After dilution)
Solution:
a) Molar mass of CO(NO3)2. 6H2O = (58.7) + 2(14 + 48) + (6 × 18) g mol-1
= 58.7 + 124 + 108 = 290.7 = 291g mol-1
Mole of CO(NO3)2 6 H2O = \(\frac{30 \mathrm{~g}}{291 \mathrm{~g} \mathrm{~mol}^{-1}}\) = 0.103
Volume of solution = 4.3 L
Molarity (M) = \(\frac{0.103 \mathrm{~mol}}{4.3 \mathrm{~L}}\) = 0.024 mol L-1 = 0.024 M
b) Volume of undiluted H2SO4 solution (V1) = 30 mL
Molarity of undiluted H2SO4 solution (M1) = 0.5 M
Volume of diluted H2SO4 solution (V2) = 500 mL
We know that M1V1 = M2V2
∴ M2 = \(\frac{\mathrm{M}_{1} \mathrm{~V}_{1}}{\mathrm{~V}_{2}}=\frac{(0.5 \mathrm{M})(30 \mathrm{~mL})}{500 \mathrm{~mL}}\) = 0.03 M
Question 4.
Calculate the mass of urea (NH2CONH2) required in making 2.5 kg of 0.25 molar aqueous solution.

So, find the molar mass of solute by adding atomic masses of different element present in it and mass by using the formula,
Molality = ![]()
Mass of solvent in kg
Solution:
Molality of the solution = 0.25 m = 0.25 mol kg-1
Molar mass of urea (NH2CONH2) = (14 × 2) + (1 × 4) + 12 + 16
= 60 g mol-1
Mass of solvent (water) = 2.5 kg
Molality = ![]()
(0.25 mol kg-1) = \(\frac{\text { Mass of urea }}{\left(60 \mathrm{~g} \mathrm{~mol}^{-1}\right) \times(2.5 \mathrm{~kg})}\)
Mass of urea = (0.25 mol kg-1) × (60 g mol-1) × (2.5 kg) = 37.5 g
![]()
Question 5.
Calculate a) molality b) molarity and c) mole fraction of KI if the density of 20% (mass / mass) aqueous Kl is 1.202 g mL-1.
• As density and % by mass is given, so find the mass of solute and solvent (as x % solution contains x g solute in (100 – x) g solvent).
Find volume of the solution, by using,
Volume = \(\frac{\text { Mass }}{\text { Density }}\)
Recall the formulae of molality, molarity and mole fraction, to calculate them.
Molality = 
Solution:
a) Molality
Weight of KI in 100 g of water = 20 g
Weight of water in the solution = 100 – 20 = 80 g = 0.08 kg
Molar mass of KI = 39 + 127 = 166 g mol-1
Molarity of the solution (m) = \(\frac{\text { Number of moles of KI }}{\text { Mass of water in } \mathrm{kg}}\)
= \(\frac{(20 \mathrm{~g}) /\left(166 \mathrm{~g} \mathrm{~mol}^{-1}\right)}{(0.08 \mathrm{~kg})}\) = 1.506 mol kg-1 = 1.506 m
b) Molarity
Weight of the solution = 100 g
Density of the solution = 1.202g m-1

c) Mole fraction of KI

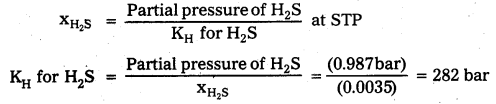
Question 6.
H2S, a toxic gas with rotten egg like smell, is used for the qualitative analysis. If the solubility of H2S in water at STP is 0.195m, calculate Henry’s law constant.
Solution:
a) Calculation of mole fraction of H2S 0.195 m means that 0.195 mole of H2S are dissolves in 1000 g of water.
Number of moles of water in 1000g, (nH2O) = \(\frac{(1000 \mathrm{~g})}{\left(18 \mathrm{~g} \mathrm{~mol}^{-1}\right)}\) = 55.55 mol
Mole fraction H2S (xH2S) = \(\frac{\mathrm{n}_{\mathrm{H}_{2} \mathrm{~s}}}{\mathrm{n}_{\mathrm{H}_{2} \mathrm{~s}}+\mathrm{n}_{\mathrm{H}_{2} \mathrm{O}}}\)
= \(\frac{(0.195 \mathrm{~mol})}{(0.195+55.55) \mathrm{mol}}=\frac{(0.195 \mathrm{~mol})}{(55.745 \mathrm{~mol})}\) = 0.0035
b) Calculation of Henry’s law constant:
According to Henry’s law
Question 7.
Henrys law constant for CO2 in water is 1.67 × 108 Pa at 298 K. Calculate the quantity of CO2 in 500 mL of soda water when packed under 2.5 atm CO2 pressure at’298 K.
Solution:
Step I : Calculation of number of moles of CO2
According to Henrys law,
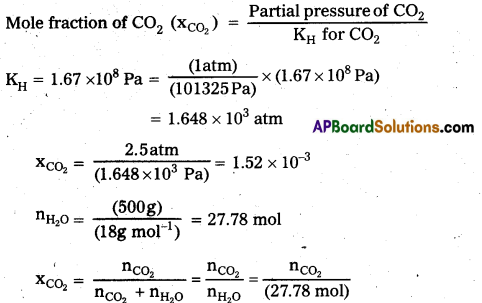
nCO2 = xCO2 × (27.78 mol) (1.52 10-3) × (27.78 mol) = 0.0422 mol
Note: nCO2 is considered negligible due to its little solubility in water.
Step II : Calculation of mass of dissolved CO2 in water
Mass of CO2 = No. of moles CO2 × Molar mass of CO2
= (0.0422 mol) × (44 g mol-1) = 1.857 g
![]()
Question 8.
The vapour pressure of pure liquids A and B are 450 and 700 mm Hg respectively, at 350 K. Find out the composition of the liquid mixture if total vapour pressure is 600 mm Hg. Also find the composition of the vapour phase.
. Apply Raoults law pT = \(\mathbf{p}_{\mathrm{A}}^{0} \mathbf{x}_{\mathrm{A}}+\mathbf{p}_{\mathrm{B}}^{0} \mathbf{x}_{\mathrm{B}}=\mathbf{p}_{\mathrm{B}}^{0} \mathbf{x}_{\mathrm{A}}+\mathbf{p}_{\mathrm{B}}^{0}\left(1-\mathbf{x}_{\mathrm{A}}\right)\) to calculate mole fraction of A(xA) and B(xB).
In vapour phase, partial pressure are used instead of number of moles.
Solution:
Step I: ComposItion In liquid phase
Vapour pressure of pure liquid A (\(p_{A}^{0}\)) = 450 mm
Vapour pressure of pure liquid B (\(p_{B}^{0}\)) = 700 mm
Total vapour pressure of the solution (p) = 600 mm
According to Raoult’s law,
p = \(\mathbf{p}_{\mathrm{A}}^{0} \mathbf{x}_{\mathrm{A}}+\mathbf{p}_{\mathrm{B}}^{0} \mathbf{x}_{\mathrm{B}}=\mathbf{p}_{\mathrm{B}}^{0} \mathbf{x}_{\mathrm{A}}+\mathbf{p}_{\mathrm{B}}^{0}\left(1-\mathbf{x}_{\mathrm{A}}\right)\)
(600 mm) = 450 mm × xA + 700 mm (1 – xA)
=700 mm + xA + (450 – 700)mm
= 700 – xA (250 mm)
xA = \(\frac{(600-700)}{-(250 \mathrm{~mm})}\) = 0.40
Mole fraction of A(xA) = 0.40
Molefraction of B(xB) = 1 – 0.40 = 0.60
Step II: Composition in vapour phase
PA = \(\mathrm{p}_{\mathrm{A}}^{0} \mathrm{x}_{\mathrm{A}}\) = (450 mm) × 0.40 = 180 mm
PB = \(\mathrm{p}_{\mathrm{B}}^{0} \mathrm{x}_{\mathrm{B}}\) = (700 mm) × 0.60 = 420 mm
Mole fraction of A in vapour phase = \(\frac{\mathrm{p}_{\mathrm{A}}}{\mathrm{p}_{\mathrm{A}}+\mathrm{p}_{\mathrm{B}}}\)
= \(\frac{(180) \mathrm{mm}}{(180+420) \mathrm{mm}}\) = 0.30
Mole fraction of B in vapour phase = \(\frac{\mathrm{p}_{\mathrm{B}}}{\mathrm{p}_{\mathrm{A}}+\mathrm{p}_{\mathrm{B}}}=\frac{(420) \mathrm{mm}}{(180+420) \mathrm{mm}}\) = 0.70
Question 9.
Vapour pressure of pure water at 298 K Is 23.8 mm Hg. 50g urea (NH2CONH2) is dissolved in 850 g of water. Calculate the vapour pressure of water for this solution and Its relative lowering.
Consider Raoult’s law and formula for relative lowering in vapour pressure,
\(\frac{\mathbf{p}_{\mathrm{A}}^{0}-\mathbf{p}_{\mathrm{s}}}{\mathbf{p}_{\mathrm{A}}^{0}}=\frac{\mathbf{n}_{\mathrm{B}}}{\mathbf{n}_{\mathrm{A}}}=\frac{\mathbf{W}_{\mathrm{B}}}{\mathbf{M}_{\mathrm{B}}} \times \frac{\mathbf{M}_{\mathrm{A}}}{\mathbf{W}_{\mathrm{A}}}\)
Where, \(\frac{\mathbf{p}_{\mathrm{A}}^{0}-\mathbf{p}_{\mathrm{s}}}{\mathbf{p}_{\mathrm{A}}^{0}}\) is called relative lowering in vapour pressure.
Solution:
Step I : Calculation of vapour pressure of water for this solution.
According to Raoult’s law,
\(\frac{\mathrm{p}_{\mathrm{A}}^{0}-\mathrm{p}_{\mathrm{s}}}{\mathrm{p}_{\mathrm{A}}^{0}}=\frac{\mathrm{n}_{\mathrm{B}}}{\mathrm{n}_{\mathrm{A}}}=\frac{\mathrm{W}_{\mathrm{B}} / \mathrm{M}_{\mathrm{B}}}{\mathrm{W}_{\mathrm{A}} / \mathrm{M}_{\mathrm{A}}}=\frac{\mathrm{W}_{\mathrm{B}}}{\mathrm{M}_{\mathrm{B}}} \times \frac{\mathrm{M}_{\mathrm{A}}}{\mathrm{W}_{\mathrm{A}}}\) ………………. (1)
(Pure water) \(\mathrm{p}_{\mathrm{A}}^{0}\) = 23.8 mm;
WB (urea) = 50 g; WA (water) = 850 g
MB (urea) = 60 g mol-1; MA (water) = 180 g mol-1
Placing the values in eq. (i)
\(\frac{\mathrm{p}_{\mathrm{A}}^{0}-\mathrm{p}_{\mathrm{s}}}{\mathrm{p}_{\mathrm{A}}^{0}}=\frac{(50 \mathrm{~g}) \times\left(18 \mathrm{~g} \mathrm{~mol}^{-1}\right)}{\left(60 \mathrm{~g} \mathrm{~mol}^{-1}\right) \times(850 \mathrm{~g})}=0.01762\)
\(\frac{23.8-\mathrm{p}_{\mathrm{s}}}{238}\) = 0.01762; 23.8 – ps = 0.4194
ps = 23.3806 ≈ 23.38 mm Hg
Step II : Calculation of relative lowering of vapour pressure
Relative lowering in vapour pressure = \(\frac{\mathrm{p}_{\mathrm{A}}^{0}-\mathrm{p}_{\mathrm{s}}}{\mathrm{p}_{\mathrm{A}}^{0}}=\frac{(23.8-23.38) \mathrm{mm}}{(23.8 \mathrm{~mm})}\) = 0.0176
![]()
Question 10.
Boiling point of water 750 mm Hg is 99.63°C. How much sucrose is to be added to 500 g of water such that it boils at 100°C.
[Kb for water is 0.52 K kg mol-1]
i) Since boiling point is changing, apply the formula for elevation In boiling point,
∆Tb = Kbm
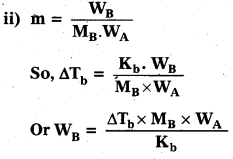
iii) Find ∆Tb as ∆Tb = Tb = Tb – \(T_{b}^{0}\)
Tb = Boiling point of solution
Tb = Boiling point of pure solvent
Solution:
Mass of water (WA) = 500 g = 0.5 kg
Elevation in boiling point (∆Tb) = 100°C – 99.63°C = 037°C = 0.37 K
Molal elevation constant (Kb) = 0.52 K kg mol-1
Molar mass sucrose C12H22O11
(MB) = (12 × 12) + (22 × 1) + (16 × 11)
= 342 g mol-1
WB = \(\frac{\mathrm{M}_{\mathrm{B}} \times \Delta \mathrm{T}_{\mathrm{B}} \times \mathrm{W}_{\mathrm{A}}}{\mathrm{K}_{\mathrm{b}}}\)
= \(\frac{\left(342 \mathrm{~g} \mathrm{~mol}^{-1}\right) \times(0.37 \mathrm{~K}) \times(0.5 \mathrm{~kg})}{\left(0.52 \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1}\right)}\) = 121.7 g
Question 11.
Calculate the mass of ascorbic acid (Vitamin C, C6H8O6) to be dissolved in 75g of acetic acid to lower its melting point by 1.5°C. Kf = 3.9 K kg mol-1.
. Since, lowering of melting point is given apply the formula for lowering of melting point, i.e.,
∆Tf = Kf.m
∆Tf = \(\frac{\mathbf{K}_{f} \cdot \mathbf{W}_{\mathbf{B}}}{\mathbf{M}_{\mathbf{B}} \times \mathbf{W}_{\mathbf{A}}}\) or WB = \(\frac{\Delta \mathbf{T}_{\mathrm{f}^{*}} \mathbf{M}_{\mathrm{B}} \cdot \mathbf{W}_{\mathrm{A}}}{\mathbf{K}_{\mathrm{f}}}\)
Solution:
Mass of ascorbic acid (WA) = 75 g = 0.075 kg
Depression in melting point (∆Tf) = 1.5° C = 1.5 K
Molar mass of ascorbic acid (MB) = (12 × 6) + (8 × 1) + (16 × 6) = 176 g mol-1
Molal depression constant (Kf) = 3.9 K kg mol-1
WB = \(\frac{\left(176 \mathrm{~g} \mathrm{~mol}^{-1}\right) \times(1.5 \mathrm{~K}) \times(0.075 \mathrm{~kg})}{\left(3.9 \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1}\right)}\) = 5.08 g
![]()
Question 12.
Calculate the osmotic pressure in Pascals exerted by a solution prepared by dissolving 1.0 g of polymer of molar mass 1,85,000 in 450 mL of water at 37°C.
Use the formula for osmotic pressure (π) = CRT and C = \(\frac{\mathbf{n}}{\mathbf{V}}\) and n = \(\frac{\mathbf{W}_{\mathbf{B}}}{\mathbf{M}_{\mathbf{B}}}\)
Solution:
Mass of polymer (WB) = 1.0 g
Molar mass of polymer (MB) = 185000 g mol-1
Volume of solution (V) = 450 mL = 0.450 L
Temperature (T) = 37 + 273 = 310 K
Solution constant (R) = 8.314 × 103 Pa L K-1 mol-1
Osmotic pressure (π) = CRT
= \(\frac{\mathrm{W}_{\mathrm{B}} \times \mathrm{R} \times \mathrm{T}}{\mathrm{M}_{\mathrm{B}} \times \mathrm{V}}\)
π = \(\frac{(1.0 \mathrm{~g}) \times\left(8.314 \times 10^{3} \mathrm{~Pa} \mathrm{~L} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\right) \times(310 \mathrm{~K})}{\left(185000 \mathrm{~g} \mathrm{~mol}^{-1}\right) \times(0.450 \mathrm{~L})}\)
= 30.96 Pa