AP Inter 2nd Year Physics Important Questions Chapter 14 Nuclei

Students get through AP Inter 2nd Year Physics Important Questions 14th Lesson Nuclei which are most likely to be asked in the exam.

AP Inter 2nd Year Physics Important Questions 14th Lesson Nuclei

Very Short Answer Questions

Question 1.
The half life of ⁵⁸Co is 72 days. Calculate Its average life. [Board model Paper]
Answer:
T_half = 0.693 × T_Mean ⇒ T_Mean = \(\frac{T_{\text {half }}}{0.693}=\frac{72}{0.693}\) = 103.8 days.

Question 2.
Why do all electrons emitted during p-decay not have the same energy?
Answer:
When a neutron is converted into a proton, an electron and neutron are emitted along with it.
\({ }_1^1 \mathrm{n} \longrightarrow{ }_1^1 \mathrm{H}+{ }_{-1}^0 \mathrm{e}+\mathrm{v}\)
In β – decay proton remains in the nucleus, but electron and neutron are emitted with constant energy. The energy of neutron is not constant. So, ail electrons do not have same energy.

Question 3.
Neutrons are the best projectiles to produce nuclear reactions. Why ?
Answer:
Neutrons are uncharged particles. So they do not get deflected by the electric and magnetic fields. Hence Neutrons are considered as best projectiles in nuclear reaction.

Question 4.
Neutrons cannot produce ionization. Why ?
Answer:
Because neutrons are uncharged particles and cannot produce ionization.

Question 5.
What are delayed neutrons ?
Answer:
Neutrons are emitted in the fission products after, sometime are called delayed neutrons.

Question 6.
What are thermal neutrons ? What is their importance ?
Answer:
Neutrons having kinetic energies approximately 0.025 eV are called as slow neutrons or thermal neutrons. ²³⁵U undergoes fission only when bombarded with thermal neutrons.

Question 7.
What is the value of neutron multiplication factor in a controlled reaction and in an uncontrolled chain reaction ?
Answer:
In controlled chain reaction K = 1
In uncontrolled chain reaction K > 1

Question 8.
What is the role of controlling rods in a nuclear reactor ?
Answer:
In nuclear reactor, controlling rods are used to absorb the neutrons. Cadmium, boron materials are used in the form of rods in reactor. These control the fission rate.

Question 9.
Why are nuclear fusion reactions called thermo nuclear reactions ?
Answer:
Nuclear fusion occurs at very high temperatures. So it is called as thermo nuclear reaction.

Question 10.
Define Becquerel and Curie.
Answer:
Becquerel: 1 disintegration or decay per second is called Becquerel. It is SI unit of activity.
1 disintegration or decay
i.e., Becquerel = \(\frac{1 \text { disintegration or decay }}{\text { second }}\)
Curie : 3.7 × 10¹⁰ decays per second is called Curie.
1 Curie : 1 Ci = \(\frac{3.7 \times 10^{10} \text { decays }}{\text { second }}\) = 3.7 × 10¹⁰Bq.

Question 11.
What is a chain reaction ?
Answer:
Chain reaction : The neutrons produced in the fission of a nucleus can cause fission in other neighbouring nuclei producing more and more neutrons to continue the fission until the whole fissionable material is disintegrated. This is called chain reaction.

Question 12.
What is the function of moderator in a nuclear reactor ?
Answer:
They are used to slow down the fast moving neutrons produced during the fission process.
e.g.: Heavy water, Beryllium.

Question 13.
What is the energy released in the fusion of four protons to form a helium nucleus ?
Answer:
26.7 MeV energy is released.

Short Answer Questions

Question 1.
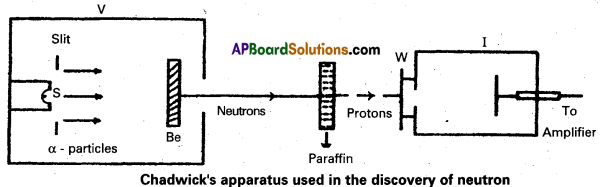
Write a short note on the discovery of neutron.
Answer:

1. Bothe and Becker found that when beryllium is bombarded with a – particles of energy 5 MeY which emitted a highly penetrating radiation.
2. The equation for above process can be written as
   \({ }_4^9 \mathrm{Be}+{ }_2^4 \mathrm{He} \rightarrow{ }_6^{13} \mathrm{C}\) + γ – (radiation energy)
3. The radiations are not effected by electric and magnetic fields.
4. In 1932, James Chadwick, had subjected nitrogen and argon to the beryllium radiation. He interpreted the experimental results by assuming that the radiation is of a new kind of particles which has no charge and its mass is equal to proton. These neutral particles were named as neutrons. Thus the neutron was discovered.
5. The experimental results can be represented by the following equation.
   \({ }_4^9 \mathrm{Be}+{ }_2^4 \mathrm{He} \rightarrow{ }_6^{12} \mathrm{C}+{ }_0^1 \mathrm{n}+\mathrm{Q}\)
   

Question 2.
What are nuclear forces ? Write their properties.
Answer:
The forces which hold the nucleons together in nucleus are called nuclear forces.
Properties of Nuclear forces:

1. Nuclear forces are attractive forces between proton and proton (P – N, proton and neutron (P – N) and neutron and neutron (N – N).
2. Nuclear forces are independent of charge. It was found that force between proton and proton is same as force between neutron and neutron.
3. These forces are short range forces i.e., these forces will act upto a small distance only. Generally the range of nuclear forces is upto few Fermi (10^-15 m).
4. These forces are non central forces, i.e., they do not act along the line joining the two nucleons.
5. These forces are exchange forces. The force between two nucleons is due to exchange of n-mesons.
6. These forces are spin dependent. These forces are strong when the spin of two nucleons are in same direction and they are weak when they are in opposite direction.
7. Nuclear forces are saturated forces i.e., the force between nucleons will extend upto the immediate neighbouring nucleons only.
8. These are the strongest forces in nature. They are nearly 10³⁸ times stronger than gravitational forces and nearly 100 times stronger than Coulombic forces.

Question 3.
Define half life period and decay constant for a radioactive substance. Deduce the relation between them.
Answer:
Half life period (T) : Time taken for the number of radio active nuclei to disintegrate to half of its original number of nuclei is called Half life period.

Decay constant (λ) : The ratio of the rate of radioactive decay to the number of nuclei present at that instant.
It is a proportional constant and is denoted by ‘λ’.
∴ λ = \(\frac{-\left(\frac{d N}{d t}\right)}{N}\)

Relation between half the period and decay constant:

1. The radioactive decay law N = N₀ e^-λt states that the number of radioactive nuclei in a radioactive sample decreases exponentially with time. Here A is called decay constant.
2. If N₀ is the number of nuclei at t = 0 and N is the radioactive nuclei at any instant of time’t’.
3. Substituting N = \(\frac{\mathrm{N}_0}{2}\) at t = T in N = N₀ e^-λt
4. \(\frac{\mathrm{N}_0}{2}\) = N₀ e^-λT
   e^λT = 2
   λT= ln 2
   T = \(\frac{\ln 2}{\lambda}=\frac{2.303 \log _{10}^2}{\lambda}\)
   ∴ T = \(\frac{0.693}{\lambda}\)

Question 4.
What is nuclear fission ? Give an example to illustrate it.
Answer:
Nuclear fission : The process of dividing a heavy nucleus into two or more smaller and stable nuclei due to nuclear reaction is called nuclear fission.
Ex: The fission reaction is \({ }_{92}^{235} \mathrm{U}+{ }_0^1 \mathrm{n} \rightarrow{ }_{56}^{141} \mathrm{Ba}+{ }_{36}^{92} \mathrm{Kr}+3{ }_0^1 \mathrm{n}+\mathrm{Q}\)
Where Q is the energy released.
Q = (Total mass of reactants – Total mass of product) C²
= [(Mass of \({ }_{92}^{235} \mathrm{U}\) + Mass of \({ }_0^1 \mathrm{n}\)) – (Mass of \({ }_{56}^{141} \mathrm{Ba}\) + Mass of \({ }_{36}^{92} \mathrm{Kr}\) + Mass of three neutrons)] C²
= (235.043933 – 140.9177 – 91.895400 – 2 × 1.008665) amu × C².
= 0.2135 × 931.5 MeV = 198.9 MeV = 200 MeV

Question 5.
What is nuclear fusion ? Write the conditions for nuclear fusion to occur.
Answer:
Nuclear fusion : The process of combining lighter nuclei to produce a larger nucleus is known as nuclear fusion.
E.g : Hydrogen nuclei (₁H¹) are fused together to form heavy Helium (₂He⁴) along with 25.71 MeV energy released.
Conditions for nuclear fusion :

1. Nuclear fusion occurs at very high temperatures such as 10⁷ kelvin and very high pressures. These are obtained under the explosion of an atom bomb.
2. Higher density is also desirable so that collisions between light nuclei occur quite frequently.

Question 6.
Distinguish between nuclear fission and nuclear fusion.
Answer:
Nuclear fission

1. In this process heavy nucleus is divided into two fragments along with few neutrons.
2. These reactions will takes place even at room temperature.
3. To start fission atleast one thermal neutron from outside is compulsory.
4. Energy released per unit mass of participants is less.
5. In this process neutrons are liberated.
6. This reaction can be controlled.
   Ex: Nuclear reactor.
7. Atom bomb works on principle of fission reaction.
8. The energy released in fission can be used for peaceful purpose.
   Ex: Nuclear reactor and Atomic power stations.

Nuclear fusion

1. In this process lighter nuclei will join together to produce heavy nucleus.
2. These reactions will takes place at very high temperature such as 107 Kelwin.
3. No necessary of external neutrons.
4. Energy released per unit mass of participants is high. Nearly seven times more than fission reaction.
5. In this process positrons are liberated.
6. There is no control on fusion reaction.
7. Hydrogen bomb works on the principle of fusion reaction.
8. The energy released in fusion cannot be used for peaceful purpose.

Long Answer Questions

Question 1.
Define mass defect and binding energy. How does binding energy per nucleon vary with mass number ? What is its significance ?
Answer:
1. Mass defect (∆M) : The difference in mass of a nucleus and its constituents is called the mass defect. The nuclear mass M is always less than the total mass, Em, of its constituents.
Mass defect, (∆M) = [Zm_p + (A – Z)m_n – M]

2. Binding energy: The energy required to break the nucleus into its constituent nucleons is called the binding energy.
Binding Energy, (E_b) = ∆MC² = [Zm_p + (A – Z)m_n – M] 931.5 MeV
Nuclear binding energy is an indication of the stability of the nucleus.
Nuclear binding energy per nucleon E_bn = \(\frac{E_{\mathrm{b}}}{\mathrm{A}}\)

3. The following graph represents how the binding energy per nucleon varies with the mass number A.

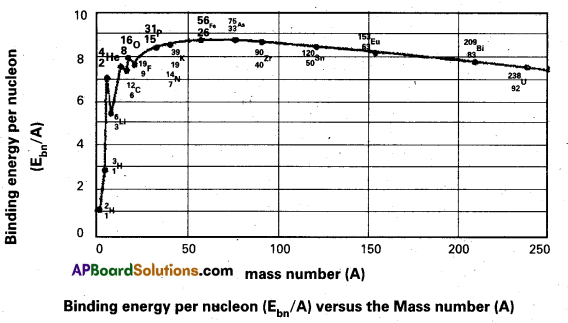
4. From the graph that the binding energy is highest in the range 28 < A < 138. The binding energy of these nuclei is very close to 8.7 MeV

5. With the increase in the mass number the binding energy per nucleon decreases and consequently for the heavy nuclei like Uranium it is 7.6 MeV

6. In the region of smaller mass numbers, the binding energy per nucleon curve shows the characteristic minima and maxima.

7. Minima are associated with nuclei containing an odd number of protons and neutrons such as \({ }_3^6 \mathrm{Li},{ }_5^{10} \mathrm{~B},{ }_7^{14} \mathrm{~N}\) and the maxima are associated with nuclei having an even number of protons and neutrons such as \({ }_2^4 \mathrm{He},{ }_6^{12} \mathrm{C},{ }_8^{16} \mathrm{O}\).

Significance:
8. The curve explains the relationship between binding energy per nucleon and stability of the nuclei.

9. Uranium has a relatively low binding energy per nucleon as 7.6 MeV Hence to attain greater stability Uranium breaks up into intermediate mass nuclei resulting in a phenomenon called fission.

10. On the other hand light nuclei such as hydrogen combine to form heavy nucleus to form helium for greater stability, resulting in a phenomenon called fusion.

11. Iron is the most stable having binding energy per nucleon 8.7 MeV, and it neither undergoes fission per fusion.

Question 2.
What is radioactivity ? State the law of radioactive decay. Show that radioactive decay is exponential in nature. [T.S. Mar. 16]
Answer:
1. Radioactivity : The nuclei of certain elements disintegrate spontaneously by emitting alpha (α), beta (β) and gamma (δ) rays. This phenomenon is called Radioactivity or Natural radioactivity.

2. Law of radioactivity decay : “The rate of radioactive decay \(\left(\frac{d N}{d t}\right)\) (or) the number of
nuclei decaying per unit time at any instant, is directly proportional to the number of nuclei (N) present at that instant is called law of radioactivity decay”.

3. Radioactive decay is exponential in nature : Consider a radioactive substance. Let the number of nuclei present in the sample at t = 0, be N₀ and let N be the radioactive nuclei remain at an instant t.
\(\frac{\mathrm{dN}}{\mathrm{dt}}\) ∝ N ⇒ \(\frac{\mathrm{dN}}{\mathrm{dt}}\) = – λN
dN = – λ Ndt …………………….. (1)
The proportionality constant λ is called decay constant or disintegration constant. The negative sign indicates the decrease in the number of nuclei.

4. From eq. (1) \(\frac{\mathrm{dN}}{\mathrm{N}}\) = – λ dt ……………… (2)

5. Integrating on both sides
\(\int \frac{\mathrm{dN}}{\mathrm{N}}=-\lambda \int \mathrm{dt}\)
ln N = – λt + C …………….. (3)
Where C = Integration constant.

6. At t = O; N = N₀. Substituting in eq. (3), we get ln N₀ = C
∴ ln N = -λt + ln N₀
ln N – ln N₀ = – λt
ln (\(\frac{\mathrm{N}}{\mathrm{N}_0}\)) = – λt
∴ N = N₀ e^-λt
The above equation represents radioactive decay law.

7. It states that the number of radioactive nuclei in a radioactive sample decreases exponentially with time.

Sample Problems

Question 1.
The half life of radium is 1600 years. How much time does lg of radium take to reduce to 0.125g. [IPE 2016 (TS)]
Answer:
Half – life of radium = 1600 years;
\(\frac{N}{N_0}=\frac{1}{2^n} \Rightarrow \frac{0.125}{1}=\frac{1}{2^n} \Rightarrow \frac{125}{1000}=\frac{1}{2^n} \Rightarrow \frac{1}{8}=\frac{1}{2^n} \Rightarrow \frac{1}{2^3}=\frac{1}{2^n} \Rightarrow n=3\)
∴ Time taken = Half life × no. of Half lives = 1600 × 3 = 4800 years

Question 2.
Plutonium decays with a half-life of 24,000 years. If plutonium is stored for 72,000 years, what fraction of it remains ?
Answer:
Half life of plutonium, T = 24000 years; Stored time of plutonium, t = 72000 years
no. of half lives, n = \(\frac{t}{T}=\frac{72000}{24000}\) = 3; Fraction of plutonium remains = \(\frac{N}{N_0}=\frac{1}{2^n}=\frac{1}{2^3}=\frac{1}{8}\)

Question 3.
Explain the principle and working of a nuclear reactor with the help of a labelled diagram. [A.P. & T.S. Mar. 17, A.P. Mar. 16 15, Mar. 14]
Answer:
Principle : A nuclear reactor works on the principle of achieving controlled chain reaction in natural Uranium ²³⁸U enriched with ²³⁵U, consequently generating large amounts of heat.
A nuclear reactor consists of (1) Fuel (2) Moderator (3) Control rods (4) Radiation shielding (5) Coolant.

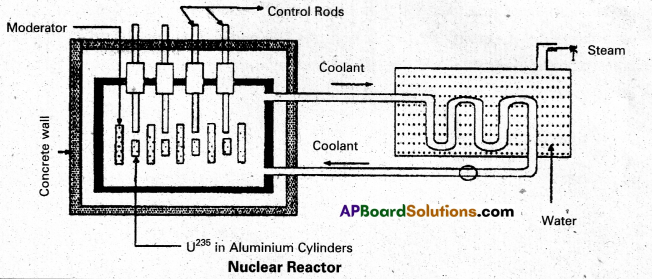
1. Fuel and clad : In reactor the nuclear fuel is fabricated in the form of thin and long cylindrical rods. These group of rods treated as a fuel assembly. These rods are surrounded by coolant, which is used to transfer of heat produced in them. A part of the nuclear reactor which is used to store the nuclear fuel is called the core of the reactor. Natural uranium, enriched uranium, plutonium and uranium – 233 are used as nuclear fuels.

2. Moderator : The average energy of neutrons released in fission process is 2 MeV. They are used to slow down the velocity of neutrons. Heavy water or graphite are used as moderating materials in reactor.

3. Control Rods : These are used to control the fission rate in reactor by absorbing the neutrons. Cadmium and boron are used as controlling the neutrons, in the form of rods.

4. Shielding : During fission reaction beta and gamma rays are emitted in addition to neutrons. Suitable shielding such as steel, lead, concrete etc., are provided around the reactor to absorb and reduce the intensity of radiations to such low levels that do not harm the operating personnel.

5. Coolant : The heat generated in fuel elements is removed by using a suitable coolant to flow around them. The coolants used are water at high pressures, molten sodium etc.

Working : Uranium fuel rods are placed in the aluminium cylinders. The graphite moderator is placed in between the fuel cylinders. To control the number of neutrons, a number of control rods of cadnium or beryllium or boron are placed in the holes of graphite block. When a few ²³⁵U nuclei undergo fission fast neutrons are liberated. These neutrons pass through the surrounding graphite moderator and loose their energy to become thermal neutrons. These thermal neutrons are captured by ²³⁵U. The heat generated here is used for heating suitable coolants which is turn heat water and produce steam. This steam is made to rotate steam turbine and there by drive a generator of production for electric power.

Question 4.
Explain the source of stellar energy. Explain the carbon – nitrogen cycle, proton – proton cycle occuring in stars.
Answer:
Scientists proposed two types of cyclic processes for the sources of energy in the sun and stars. The first is known as carbon-nitrogen cycle and the second is proton-proton cylce.

1. Carbon-Nitrogen Cycle : According to Bethe carbon-nitrogen cycle is mainly responsible for the production of solar energy. This cycle consists of a chain of nuclear reactions in which hydrogen is converted into Helium, with the help of Carbon and Nitrogen as catalysts. The nuclear reactions are as given below.

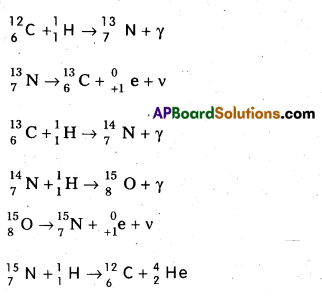
2. Proton – Proton Cycle: A star is formed by the condensation of a large amount of matter at a point in space. Its temperature rises to 2,00,000°C as the matter contracts under the influence of gravitational attraction. At this temperature the thermal energy of the protons is sufficient to form a deuteron and a positron. The deuteron then combines with another proton to form lighter nuclei of helium \({ }_2^3 \mathrm{He}\). Two such helium nuclei combine to form a helium nucleus latex]{ }_2^4 \mathrm{He}[/latex] and two protons releasing a total amount of energy 25.71 MeV The nuclear fusion reactions are given below.

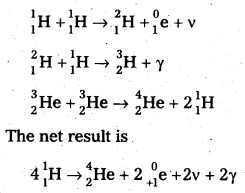
Problems

Question 1.
Compare the radii of the nuclei of mass numbers 27 and 64.
Solution:
A₁ = 27; Asub>2 = 64
\(\frac{\mathrm{R}_1}{\mathrm{R}_2}=\left[\frac{\mathrm{A}_1}{\mathrm{~A}_2}\right]^{1 / 3}\) [∵ R = R₀A^1/3]
\(\frac{\mathrm{R}_1}{\mathrm{R}_2}=\left[\frac{27}{64}\right]^{\frac{1}{3}}=\frac{3}{4}\)
∴ R₁ : R₂ = 3 : 4

Question 2.
Find the energy required to split \({ }_8^{16} \mathrm{O}\) nucleus into four α-particles. The mass of an a-particle is 4.002603u and that of oxygen is 15.994915u.
Solution:
The energy required to split O = [Total mass of the products – Total mass of the reactants] c²
Mass of four \({ }_2^4 \mathrm{He}\) – Mass of \({ }_8^{16} \mathrm{O}\)] × c²
= [(4 X 4.002603) – 15.994915] u × c²
= [16.010412 – 15.994915] u × c²
= (0.015497) 931.5 MeV = 14.43 MeV

Question 3.
A certain substance decays to 1/232 of its initial activity in 25 days. Calculate its half-life.
Solution:
Fraction of substance decays
= \(\frac{\text { Quantity remains }}{\text { Initial quantity }}\)
= \(\frac{1}{2^n}=\frac{1}{32}=\frac{1}{2^5}\)
∴ n = 5
Duration of time = 25 days
We know (n) = \(\frac{\text { Duration of time }}{\text { Half life time }}\)
∴ Half life time = \(\frac{\text { Duration of time }}{\mathrm{n}}\)
\(\frac{25}{5}\) = 5 days

Question 4.
One gram of radium is reduced by 2 milli- gram in 5 years by a-decay. Calculate the half¬life of radium.
Solution:
Initial (original) mass (N₀) = 1 gram
Reduced mass – 2 mg = 0.002 grams
Final mass (N)= 1 – 0.002 = 0.998 grams
t = 5 years
e^-λt = \(\frac{\mathrm{N}}{\mathrm{N}_0}\) ⇒ e^λt = \(\frac{\mathrm{N}_0}{\mathrm{~N}}\) ⇒ λt = log_e[latex]\frac{\mathrm{N}_0}{\mathrm{~N}}[/latex]
λt = 2.303 log [latex]\frac{\mathrm{N}_0}{\mathrm{~N}}[/latex]
λt = 2.303 log [latex]\frac{1}{0.998}[/latex]
= 2.303 log (1.002)
= 2.303 × 0.000868
= 0.001999
λ = \(\frac{0.001999}{5}\) = 0.0003998
T = \(\frac{0.693}{\lambda}=\frac{0.693}{0.0003998}\) = 1733.3 years

Question 5.
If one microgram of \({ }_92^{235} \mathrm{U}\) is completely destroyed in an atomhomb, how much energy will be released ?
Solution:
m = 1 μg = 1 × 10^-6 g = 1 × 10^-6 × 10^-3 kg
= 10^-9 kg
c = 3 × 10⁸ m/s
E = mc² = 1 × 10^-9 × 9 × 10⁶ = 9 × 10⁷ J

Question 6.
200 MeV energy is released when one nucleus of ²³⁵U undergoes fission. Find the number of fissions per second required for producing a power of 1 megawatt.
Solution:
E = 200 MeV
P = 1 × 10⁶ W
P = \(\frac{\mathrm{nE}}{\mathrm{t}} \Rightarrow \frac{\mathrm{n}}{\mathrm{t}}=\frac{\mathrm{P}}{\mathrm{E}}=\frac{10^6}{200 \times 10^6 \times 1.6 \times 10^{-19}}\)
= \(\frac{1}{32}\) × 10¹⁸
∴ P = 0.03125 × 10¹⁸
= 3.125 × 10⁶

Textual Examples

Question 1.
Given the mass of iron nucleus as 55.85u and A = 56, find the nuclear density ?
Solution:
m_Fe = 55.85, u = 9.27 × 10^-26 kg
Nuclear density = \(\frac{\text { mass }}{\text { volume }}\)
= \(\frac{9.27 \times 10^{-26}}{(4 \pi / 3)\left(1.2 \times 10^{-15}\right)^3} \times \frac{1}{56}\)
= 2.29 × 10¹⁷ kg m^-3
The density of matter in neutron stars (an astrophysical object) is comparable to this density. This shows that matter in these objects has been compressed to such an extent that they resemble a big nucleus.

Question 2.
Calculate the energy equivalent of 1 g of substance.
Solution:
Energy, E = 10^-3 × (3 × 10⁸)² J
E = 10^-3 × 9 × 10¹⁶ = 9 × 10¹³ J
Thus, if one gram of matter is converted to energy, there is a release of an enormous amount of energy.

Question 3.
Find the energy equivalent of one atomic mass unit, first in Joules and then in MeV. Using this, express the mass defect of \({ }_8^{16} \mathrm{O}\) in MeV/c².
Solution:
1 u = 1.6605 × 10^-27 kg
To convert it into energy units, we multiply it by c² and find, that energy. equivalent
= 1.6605 × 10^-27 × 2.9979 × 10⁸ kg m²/s²
= 1.4924 × 10^-10 J
= \(\frac{1.4924 \times 10^{-10}}{1.602 \times 10^{-19}}\) eV
= 0.9315 × 10⁹ eV = 931.5 MeV
or, 1 u = 931.5 MeV/c².
For \({ }_8^{16} \mathrm{O}\), ∆M = 0.13691 u = 0.13691 × 931.5 MeV/c² = 127.5 MeV/c²
The energy needed to separate \({ }_8^{16} \mathrm{O}\) into hs constituents is thus 127.5 MeV/c².

Question 4.
The half-life of \({ }_{92}^{238} \mathrm{U}\) undergoing a – decay is 4.5 × 10⁹ years. What is the activity of 1 g sample of \({ }_{92}^{238} \mathrm{U}\) ?
Solution:
T_1/2 = 4.5 × 10⁹ y
= 4.5 × 10⁹ y × 3.16 × 10⁷ s/y.
= 1.42 × 10¹⁷ s
One k mol of any isotope contains Avogadro’s number of atoms, and so 1 g of \({ }_{92}^{238} \mathrm{U}\) contains
\(\frac{1}{238 \times 10^{-3}}\) k mol × 6.025 × 10²⁶ atoms/kmol
= 25.3 × 10²⁰ atoms.
The decay rate R is
R = λN
= \(\frac{0.693}{\mathrm{~T}_{1 / 2}}\) N = \(\frac{0.693 \times 25.3 \times 10^{20}}{1.42 \times 10^{17}}\) S^-1
= 1.23 × 10⁴ S^-1
= 1.23 × 10⁴ Bq

Question 5.
Tritium has a half-life of 12.5 y undergoing beta decay. What fraction of sample of pure tritium will remain undecayed after 25 y.
Solution:
By definition of half-life, half of the initial i sample will remain undecayed after 12.5 y. In the next 12.5 y, one-half of these nuclei would have decayed. Hence, one fourth of the sample of the initial pure s tritium will remain undecayed.

Question 6.
We are given the following atomic masses:
\({ }_{92}^{238} \mathrm{U}\) = 238.05079 u
\({ }_{2}^{4} \mathrm{He}\) = 4.00260 u
\({ }_{90}^{234} \mathrm{Th}\) = 234.04363 u
\({ }_{1}^{1} \mathrm{H}\) = 1.00783 u
\({ }_{91}^{237} \mathrm{Pa}\) = 237.05121 u
Here the symbol Pa is for the element protactinium (Z = 91).
a) Calculate the energy released during the alpha decay of \({ }_{92}^{238} \mathrm{U}\).
b) Show that \({ }_{92}^{238} \mathrm{U}\) cannot spontaneously emit a proton.
Solution:
a) The alpha decay of \({ }_{92}^{238} \mathrm{U}\) is given by

The energy released in this process is given by
Q = (M_U – M_Th – M_He) c²
Substituting the atomic masses as given in the data, we find
Q = (238.05079 – 234.04363 – 4.00260)u × c²
= (0.00456 u) c²
= (0.00456 u) (931.5 MeV/u)
= 4.25 MeV

b) If \({ }_{92}^{238} \mathrm{U}\) spontaneously emits a proton, the decay process would be
\({ }_{92}^{238} \mathrm{U} \rightarrow{ }_{91}^{237} \mathrm{~Pa}+{ }_1^1 \mathrm{H}\)
The Q for this process to happen is
= (M_U – M_Pa – M_H)c²
(238.05079 – 237.05121 – 1.00783) u × c²
=(- 0.00825 u) c²
= – (0.00825 u) (931.5 MeV/u)
= -7.68 MeV
Thus, the Q of the process is negative and therefore it cannot proceed spontaneously. We will have to supply an energy of 7.68 MeV to a \({ }_{92}^{238} \mathrm{U}\) nucleus to make it emit a proton.