Students get through AP Inter 2nd Year Physics Important Questions 1st Lesson Waves which are most likely to be asked in the exam.
AP Inter 2nd Year Physics Important Questions 1st Lesson Waves
Very Short Answer Questions
Question 1.
Write the formula for the speed of sound in solids and gases.
Answer:
Speed of sound in solids,
Vs = \(\sqrt{Y / \rho}\) [y = Young’s modulus of solid, ρ = density of solid]
Speed of sound in gases,
Vs = \(\sqrt{\gamma P / \rho}\) [γP = Adiabatic Bulk modulus of gas, ρ = density of gas] .
Question 2.
What does a wave represent?
Answer:
A wave represents the transport of energy through a medium from one point to another without translation of the medium.
![]()
Question 3.
Distinguish between transverse and longitudinal waves.
Answer:
Transverse waves
- The particles of the medium vibrate perpendicular to the direction of wave propagation.
- Crests and troughs are formed alternatively.
Longitudinal waves
- The particles of the medium vibrate parallel to the direction of wave propagation.
- Compressions and rare factions are formed alternatively.
Question 4.
What are the parameters used to describe a progressive harmonic wave ?
Answer:
Progressive wave equation is given y = a sin (ωt – kx)
Where ω = 2πv = \(\frac{2 \pi}{T}\); k = \(\frac{2 \pi}{\lambda}\)
Parameters:
- a = Amplitude
- λ = Wavelength
- T = Time period
- v = Frequency
- k = Propagation constant
- ω = Angular frequency.
Question 5.
What is the principle of superposition of waves ? .
Answer:
When two or more waves are acting simultaneously on the particle of the medium, the resultant displacement is equal to the algebraic sum of individual displacements of all the waves. This is the principle of superposition of waves.
If y1, y2, ……………… yn be the individual displacements of the particles,then resultant displacement
y = y1 + y2 + ……………… + yn.
![]()
Question 6.
Under what conditions will a wave be reflected ?
Answer:
- When the medium ends abruptly at any point.
- If the density and rigidity modulus of the medium changes at any point.
Question 7.
What is the phase difference between the incident and reflected waves when the wave is reflected by a rigid boundary ?
Answer:
Phase difference between the incident and reflected waves when the wave is reflected by a rigid boundary is radian or 180°.
Question 8.
What is a stationary or standing wave ?
Answer:
When two identical progressive (Transeverse or longitudinal) waves travelling opposite directions in a medium along the same straight line, which are superimposed then the resultant wave is called stationary waves or standing wave.
Question 9.
What do you understand by the terms node’ and ‘antinode’ ?
Answer:
Node : The points at which the amplitude is zero, are called nodes.
Antinodes: The points at which the amplitude is maximum, are called antinodes.
Question 10.
What is the distance between a node and an antinode in a stationary wave ?
Answer:
The distance between node and antinode is \(\frac{\lambda}{4}\).
![]()
Question 11.
What do you understand by ‘natural frequency’ or ‘normal mode of vibration’ ?
Answer:
When a body is set into vibration and then left to itself, the vibrations made by it are called natural or free vibrations. Its frequency is called natural frequency or normal mode of vibration.
Question 12.
What are harmonics ?
Answer:
The frequencies in which the standing waves can be formed are called harmonics..
(Or)
The integral multiple of fundamental frequencies are called harmonics.
Question 13.
A string is stretched between two rigid supports. What frequencies of vibration are possible in such a string ?
Answer:
The possible frequencies of vibrations in a stretched string between two rigid supports is given by
vn = (n + \(\frac{1}{2}\)) \(\frac{v}{2l}\) where n = 0, 1, 2, 3, ……….
Question 14.
If the air column in a long tube, closed at one end, is set in vibration, what harmonics are possible in the vibrating air column ?
Answer:
The possible harmonics in the vibrating air column of a long closed tube is given by
vn = [2n +1]\(\frac{v}{4 l}\) where n = 0, 1, 2, 3,
![]()
Question 15.
If the air column in a tube, open at both ends, is set in vibration; what harmonics are possible ?
Answer:
The possible harmonics in vibrating air column of a long open tube is given by no
vn = \(\frac{\mathrm{nv}}{21}\)
where n = 1, 2, 3, ……………….
Question 16.
What are ‘beats’ ?
Answer:
Beats : When two sound notes of nearly frequency travelling in the same direction and interfere to produce waxing and waning of sound at regular intervals of time is called “Beats”.
Short Answer Questions
Question 1.
What are transverse waves ? Give illustrative examples of such waves.
Answer:
Transverse waves: In a wave motion, the vibration of the particles and the direction of the propagation of the waves are perpendicular to each other, the waves are said to be transverse waves.
Illustration:
- Waves produced in the stretched strings are transverse.
- When a stretched string is plucked, the waves travel along the string.
- But the particles in the string vibrate in the direction perpendicular to the propagation of the wave.
- They can propagate only in solids and on the surface of the liquids.
- Ex : Light waves, surface water waves.
![]()
Question 2.
What are longitudinal waves ? Give illustrative example of such waves.
Answer:
Longitudinal waves : In a wave motion, the direction of the propagation of the wave and vibrations of particles are in the same direction, the waves are said to be longitudinal waves.
Illustration:
- Longitudinal waves may be easily illustrated by releasing a compressed spring.
- A series of compressions and rarefactions (expansions) propagate along the spring.

C = Compression; R = Rarefaction. - They can travel in solids, liquids and gases.
- Ex : Sound waves.
Question 3.
What are ‘beats’ ? When do they occur ? Explain their use, if any.
Answer:
Two sound waves of nearly same frequency are travelling in the same direction and interfere to produce a regular waxing (maximum) and waning (minimum) in the intensity of the resultant sound waves at regular intervals of time is called beats.
It two vibrating bodies have slightly difference in frequencies, beats can occur.
No. of beats can be heard, ∆υ = υ1 ~ υ2
Importance:
1. It can be used to tune musical instruments.
2. Beats are used to detect dangerous gases.
Explanation for tuning musical instruments with beats:
Musicians use. the beat phenomenon in tuning their musical instruments. If an instrument is sounded against a standard frequency and tuned until the beats disappear. Then the instrument is in tune with the standard frequency.
![]()
Question 4.
What is ‘Doppler effect’ ? Give illustrative examples.
Answer:
Doppler effect: The apparent change in the frequency heard by the observer due to relative motion between .the observer and the source of sound is called doppler effect.
Examples:
- The frequency of whistling, engine heard by a person standing on the platform appears to increase, when the engine is approaching the platform and it appears to decrease when the engine is moving away from the platform.
- Due to Doppler effect the frequency of sound emitted by the siren of an approaching ambulance appears to increase. Similarly the frequency of sound appears to drop when it is moving away.
Sample Problem on Doppler effect:
Two trucks heading in opposite direction with speeds of 60 kmph and 70 kmph respectively, approach each other. The driver of the first truck sounds his horn of frequency 400Hz. What frequency does the driver of the second truck hear ? (Velocity of sound = 330m/s). After the two trucks have passed each other, what frequency does the driver of the second truckhear?
Answer:
Speed of first truck = 60 kmph
= 60 × \(\frac{5}{18}\) = 16.66 m/s;
Speed of second truck = 70 kmph 5
= 70 × \(\frac{5}{18}\) = 19.44 m/s
Frequency of horn of first truck = 400 Hz;
Velocity of sound, (V) =330 m/s
Frequency of sound heard by the driver of the second truck when approaching each other,
v1 = \(\left(\frac{V+V_0}{V-V_s}\right) v=\left(\frac{330+19.44}{330-16.66}\right)\) × 400 = 446 Hz
Frequency of sound heard by the driver of the second truck when approaching each other,
V11 = \(\left(\frac{\mathrm{V}-\mathrm{V}_0}{\mathrm{~V}+\mathrm{V}_{\mathrm{s}}}\right) \mathrm{v}=\left(\frac{330-19.44}{330+16.66}\right)\) × 400 = 358.5 Hz
Long Answer Questions
Question 1.
Explain the formation of stationary waves in stretched strings and hence deduce the laws of transverse wave in stretched strings. [IPE]
Answer:
A string is a metal wire whose length is large when compared to its thickness. A stretched string is fixed at both ends, when it is plucked at mid point, two reflected waves of same amplitude and frequency at the ends are travelling in opposite direction and overlap along the length. Then the resultant waves are known as the standing waves (or) stationary waves. Let two transverse progressive waves of same amplitude a, wave length λ and frequency v, travelling in opposite direction be given by
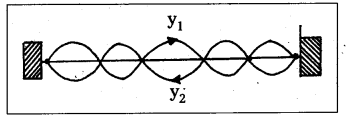
y1 = a sin (kx – ωt) and y2 = a sin (kx + ωt)
where ω = 2πv and k = \(\frac{2 \pi}{\lambda}\)
The resultant wave is given by y = y1 + y2
y = a sin (kx – ωt) + a sin (kx + ωt)
y = (2a sin kx) cos ωt
2a sin kx = Amplitude of resultant wave.
It depends on ‘kx’. If x = 0, \(\frac{\lambda}{2}, \frac{2 \lambda}{2}, \frac{3 \lambda}{2}\) ……………… etc, the amplitude = zero
These positions are known as “Nodes”.
If x = \(\frac{\lambda}{4}, \frac{3 \lambda}{4}, \frac{5 \lambda}{4}\) …………… etc., the amplitude = maximum (2a)
These positions are called “Antinodes”.
If the string vibrates in ‘P’ segments and T is its length, then length of each segment = \(\frac{l}{\mathrm{P}}\)
Which is equal to \(\frac{\lambda}{2}\)
∴ \(\frac{l}{\mathrm{P}}=\frac{\lambda}{2} \Rightarrow \lambda=\frac{2 l}{\mathrm{P}}\)
Harmonic frequency v = \(\frac{v}{\lambda}=\frac{v \mathrm{P}}{2 l}\)
v = \(\frac{v \mathrm{P}}{2 l}\) ………………. (1)
If’ T’ is tension (stretching force) in the string and ‘μ’ is linear density then velocity of transverse wave (v) in the string is
v = \(\sqrt{\frac{\mathrm{T}}{\mu}}\) …………… (2)
From the Eqs (1) and (2) :
Harmonic frequency v = \(\frac{\mathrm{P}}{2 l} \sqrt{\frac{\Gamma}{\mu}}\)
If P = 1 then it is called fundamental frequency (or) first harmonic frequency
∴ Fundamental Frequency v = \(\frac{1}{2 l} \sqrt{\frac{\mathrm{T}}{\mu}}\) …………….. (3)
Laws of Transverse Waves Along Stretched String:
Fundamental frequency of the vibrating string v = \(\frac{1}{2 l} \sqrt{\frac{\mathrm{T}}{\mu}}\)
First Law : When the tension (T) and linear density (μ) are constant, the fundamental frequency (v) of a vibrating string is inversely proportional to its length.
∴ v ∝ \(\frac{1}{l}\) ⇒ vl = constant, when ‘T’ and ‘μ’ are constant. .
Second Law: When the length (l) and its, linear density (m) are constant the fundamental frequency of a vibrating string is directly proportional to the square root of the stretching force (T).
∴ v ∝ \(\sqrt{T}\) ⇒ \(\frac{v}{\sqrt{T}}\) = constant, when ‘l’ and ‘m’ are constant.
JT .
Third Law: When the length (l) and the tension (T) are constant, the fundamental frequency of a vibrating string is inversely proportional to the square root of the linear density (m).
∴ v ∝ \(\frac{1}{\sqrt{\mu}}\) ⇒ \(v \sqrt{\mu}\) = constant, when ‘l’ and T are constant.
![]()
Question 2.
Explain the formation of stationary waves in an air column enclosed in open pipe. Derive the equations for the frequencies of the harmonics produced. [A.P. 17; IPE 2015, 2016 (TS)]
Answer:
A pipe, which is opened at both ends is called open pipe. When a sound wave is sent through a open pipe, which gets reflected by the earth. Then incident and reflected waves are in same frequency, travelling in the opposite directions are super-imposed stationary waves are formed.
Harmonics in open pipe : To form the stationary wave in open pipe, which has two anti nodes at two ends of the pipe with a node between them.
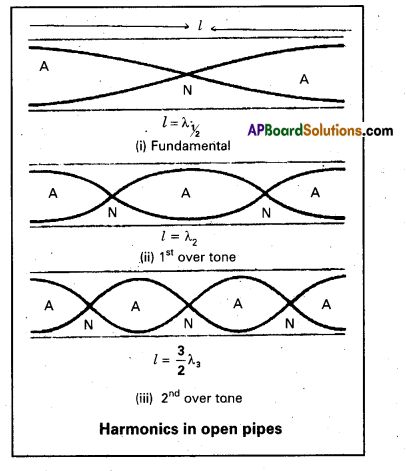
∴ The vibrating length (l) = half of the wavelength \(\left(\frac{\lambda_1}{2}\right)\)
l = \(\frac{\lambda_1}{2}\) ⇒ λ1 = 2l
fundamental frequency v1 = \(\frac{\mathrm{v}}{\lambda_1}\) where v is velocity,of sound in air, v1 = \(\frac{v}{21}\) = v
For second harmonic (first overtone) will have one more node and antinode than the fundamental.
If λ2 is wavelength of second harmonic l = \(\frac{2 \lambda_2}{2}\) ⇒ λ2 = \(\frac{21}{2}\)
If ‘v2’ is frequency of second harmonic then v2 = \(\frac{v}{\lambda_2}=\frac{v \times 2}{2 l}\) = 2v
v2 = 2v ……………… (2)
Similarly for third harmonic (second overtone) will have three nodes and four antinodes as shown in above figure.
If λ3 is wave length of third harmonic l = \(\frac{3 \lambda_3}{2}\)
λ3 = \(\frac{2l}{3}\)
If ‘v2‘ is frequency of third harmonic then
v3 = \(\frac{v}{\lambda_3}=\frac{v \times 3}{2 l}\) = 3V
v3 = 3v …………… (3)
Similarly we can find the remaining or higher harmonic frequencies i.e., v3, v4 etc., can be determined in the same way.
Therefore the ratio of the harmonic frequencies in open pipe can be written as given below.
v : V1 : v2 = 1 : 2 : 3
Question 3.
How are stationary waves formed in closed pipes ? Explain the various modes of vibrations and obtain relations for their frequencies. [IPE 2015, 2016(A.P.), (T.S) A.P. & T.S. Mar. 15]
Answer:
A pipe, which is closed at one end and the other is opened is called closed pipe. When a sound wave is sent through a closed pipe, which gets reflected at the closed end of the pipe. Then incident and reflected waves are in same frequency, travelling in the opposite directions are superimposed stationary waves are formed.
To form the stationary wave in closed pipe, which has atleast a node at closed end and antinode at open end of the pipe, it is known as first harmonic in closed pipe. Then length of the pipe (l) is equal to one fourth of the wave length.
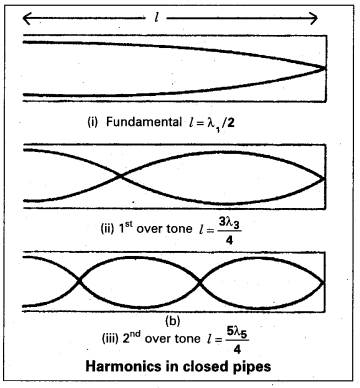
∴ l = \(\frac{\lambda_1}{4}\) ⇒ λ1 = 4l
If ‘v1‘ is fundamental frequency then
v1 = \(\frac{v}{\lambda_1}\) where ‘υ’ is velocity of sound in air
v1 = \(\frac{v}{4 l}\) = v …………….. (1)
To form the next harmonic in closed pipe, two nodes and two antinodes should be formed. So that there is possible to form third harmonic in closed pipe. Since one more node and antinode should be included.
Then length of the pipe is equal to \(\frac{3}{4}\) of the wavelength.
∴ l = \(\frac{3 \lambda_3}{4}\) where ‘λ3‘ is wave length of third harmonic
λ3 = \(\frac{4l}{3}\)
where ‘X3’ is wave length of third harmonic.
If ‘v3‘ is third harmonic frequency (first overtone)
∴ v3 = \(\frac{v}{\lambda_3}=\frac{3 v}{41}\)
v3 = 3v …………….. (2)
Similarly the next overtone in the close pipe is only fifth harmonic, it will have three nodes and 3 antinodes between the closed end and open end.
Then length of the pipe is equal to \(\frac{5}{4}\) of wave length (λ5)
∴ l = \(\frac{5 \lambda_5}{4}\) where ‘λ5‘ is wave length of fifth harmonic.
λ5 = \(\frac{4l}{5}\)
If ‘v5‘ is frequency of fifth harmonic (second overtone)
v5 = \(\frac{v}{\lambda_5}=\frac{5 v}{4 l}\)
v5 = 5v …………….. (3)
∴ The frequencies of higher harmonics can be determined by using the same procedure. Therefore from the Eq (1), (2) and (3) only odd harmonics are formed.
Therefore the ratio of the frequencies of harmonics in closed pipe can be written as
v1 : v3 : v5 = v : 3v : 5v
v1 : v3 : v5 = 1 : 3 : 5
![]()
Question 4.
What is Doppler effect ? Obtain an expression for the apparent frequency of sound heard when the source is in motion with respect to an observer at rest. [Mar. 17, BMP, 2016 (AP) Mar. 14, (TS)]
Answer:
Doppier effect: The apparent change in the frequency heard by the observer due to the relative motion between the observer and the source of sound is called doppier effect. When a whistling railway engine approaches an observer standing on the platform, the frequency of sound appears to increase. When it moves away the frequency appear to decrease.
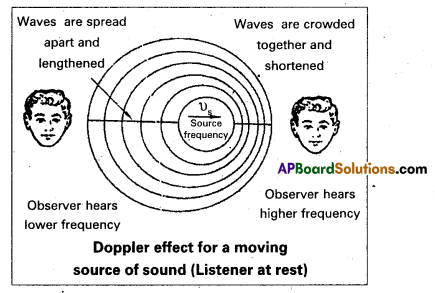
Expression for apparent frequency when source is in motion and listener at rest:
Let S = Source of sound
O = Listener
Let ‘S’ be the source, moving with a velocity ‘υs‘ towards the stationary listener.
The distance travelled by the source in time period T = υs. T Therefore the successive compressions and rarefactions are drawn closer to listener.
∴ Apparent wavelength λ’ = λ – υsT.
λ’ = λ – \(\frac{v_s}{v}\) [∵ υ = \(\frac{1}{T}\)]
= \(\frac{\lambda v-v_s}{v}=\frac{v-v_s}{v}\) [∵ υ = vλ]
If “v'” is apparent frequency heard by the listener then v’ = \(\frac{v}{\lambda^{\prime}}\) where ‘υ’ is Velocity of sound in air
v’ = \(\frac{v . v}{v-v_S}\)
Therefore the apparent frequency is greater than the actual frequency.
Similarly, if the source is away from the stationary listener then apparent frequency v’ = \(\frac{v . v}{v+v_s}\), which is less than the actual frequency.
Limitation : Doppler effect is applicable when the velocities of the source and listener are much less than that of sound velocity.
Problems
Question 1.
A stretched wire of length 0.6 m is observed to vibrate with a frequency of 30 Hz in the fundamental mode. If the string has a linear mass of 0.05 kg / m find (a) the velocity of propagation of transverse waves in the string (b) the tension in the string. [IPE 2016 (T.S)
Answer:
v = 30 Hz; I = 0.6 m; μ = 0.05 kg m-1
υ = ?; T = ?
a) υ = 2vl = 2 × 30 × 0.6 = 36 m/s
b) T = υ2μ = 36 × 36 × 0.05 = 64.8 N .
Question 2.
A string has a length of 0.4m and a mass of 0.16g. If the tension in the string is 70N, what are the three lowest frequencies it produces when plucked ?
Solution:
I = 0.4 m; M = 0.16g = 0.16 × 10-3 kg;
μ = \(\frac{\mathrm{M}}{1}=\frac{0.16 \times 10^{-3}}{0.4}\) = 0.4 × 10-3 kg/m;
T = 70 N; vn = \(\frac{\mathrm{P}}{21} \sqrt{\frac{\mathrm{T}}{\mu}}\)
v1 = \(\frac{1}{21} \sqrt{\frac{\mathrm{T}}{\mu}}=\frac{1}{2 \times 0.4} \sqrt{\frac{70}{0.4 \times 10^{-3}}}\) = 523 Hz
v2 = 2v1 = 2 × 523 = 1046 Hz
v3 = 3v1 = 3 × 523 = 1569 Hz
![]()
Question 3.
A closed organ pipe 70 cm long is sounded. If the velocity of sound is 331 m/s, what is the fundamental frequency of vibration of the air column ?
Solution:
l = 70 cm = 70 × 10-2m; v = 331 m/s ;
v = ?
v = \(\frac{v}{4 l}=\frac{331}{4 \times 70 \times 10^{-2}}\) = 118.2 Hz.
Question 4.
A steel cable of diameter 3 cm is kept under a tension of lOkN. The density of steel is 7.8 g/ cm3. With what speed would transverse waves propagate along the cable ?
Solution:
T = 10 kN = 104 N
D = 3 cm; r = \(\frac{D}{2}=\frac{3}{2}\) cm
= \(\frac{3}{2}\) × 10-2m;

Question 5.
A train sounds its whistle as it approaches and crosses a level crossing. An observer at the crossing measures a frequency of 219 Hz as the train approaches and a frequency of 184 Hz as it leaves. If the speed of sound is taken to be 340 m/s, find the speed of the train and the frequency of its whistle. [T.S. Mar. 17]
Solution:
When a whistling train away from rest observer, ![]()
v’ = \(\left[\frac{v}{v-v_s}\right] v\) ……………… (1)
When a whistling train away from rest observer, ![]()
v” = \(\left[\frac{v}{v+v_s}\right] v\) ……………… (2)
Here v’ = 219 Hz; v” = 184 Hz;
v = 340 m/s

![]()
Question 6.
A rocket is moving at a speed of 200 m s-1 towards a stationary target. While moving, it emits a wave of frequency 1000 Hz. Some of the sound reaching the target gets reflected back to the rocket as an echo. Calculate (1) the frequency of the sound as detected by the target and (2) the frequency of the echo as detected by the rocket. [A.P. Mar. 16]
Solution:
1) The observer is at rest and the source is moving with a speed of 200 m s-1. Since this is comparable with the velocity of sound 330 ms-1, we must use Eq.
v = v0 \(\left[\frac{1+v_{\mathrm{S}}}{v}\right]^{-1}\) and not the approximate
v = v0 [1 – \(\frac{v_s}{v}\)]
Since the source is approaching a stationary target, υ0 = 0, and υs must be replaced by -υs. Thus, we have
v = v0 [1 – \(\frac{v_s}{v}\)]-1
v = 1000 Hz × [1 – 200 m s-1/330 m s-1]-1
≃ 2540Hz
2) The target is now the source (because it is the source of echo) and the rocket’s detector is now the detector or observer (because it detects echo). Thus, υs = 0 and υ0 has a positive value. The frequency of the sound emitted by the source (the target) is v, the frequency intercepted by the target and not v0, Therefore, the frequency as registered by the rocket is
v’ = \(v\left(\frac{v+v_0}{v}\right)\)
= 2540 Hz × \(\left(\frac{200 \mathrm{~m} \mathrm{~s}^{-1}+330 \mathrm{~m} \mathrm{~s}^{-1}}{330 \mathrm{~m} \mathrm{~s}^{-1}}\right)\)
≃ 4080Hz
Textual Examples
Question 1.
Given below are some examples of wave motion. State in each case if the wave motion is transverse, longitudinal or a combination of both.
a) Motion of kink in a longitudinal spring produced by displacing one end of the spring sideways.
b) Waves produced in a cylinder containing a liquid by moving its piston back and forth.
c) Waves produced by a motorboat sailing in water.
d) Ultrasonic waves in air produced by a vibrating quartz crystal.
Solution:
a) Transverse and longitudinal
b) Longitudinal
c) Transverse and longitudinal
d) Longitudinal.
![]()
Question 2.
A wave travelling along a string is des-cribed by, y(x, t) = 0.005 sin (80.0 x – 3.01), in which the numerical constants are in SI untis (0.005 m, 80.0 rad m-1, and 3.0 rad s-1). Calculate (a) the amplitude, (b) the wavelength, and (c) the period and frequency of the wave. Also, calculate the displacement y of the wave at a distance x = 30.0 cm and time t = 20 s ?
Solution:
On comparing this displacement equation with Eq. y (x, t)n = a sin(kx – ωt + Φ)
y(x, t) = a sin (kx – ωt).
We find
a) the amplitude of the wave is
0. 005 m = 5 mm.
b) the angular wave number k and angular frequency ω are k = 80.0 m-1 and ω = 3.0 s-1
We then relate the wavelength λ to k through Eq.
λ = \(\frac{2 \pi}{K}\)
= \(\frac{2 \pi}{80.0 \mathrm{~m}^{-1}}\) = 7.85 cm
c) Now we relate T to ω by the relation
T = \(\frac{2 \pi}{\omega}\)
= \(\frac{2 \pi}{3.0 \mathrm{~s}^{-1}}\)
= 2.09 s
and frequency, v = \(\frac{1}{T}\) = 0.48 Hz
The displacement y at x = 30.0 cm and time t= 20s is given by
y = (0.005 m) sin (80.0 × 0.3 – 3.0 × 20)
= (0.005 m) sin (-36 + 12π)
= (0.005 m) sin (1.699)
= (0.005 m) sin (97°) ≃ 5 mm
Question 3.
A steel wire 0.72 m long has a mass of 5.0 × 10-3 kg. If the .wire is under a tension of 60 N, what is the speed of transverse waves on the wire ? [A.P. Mar. 19]
Solution:
Mass per unit length of the wire,
μ = \(\frac{5.0 \times 10^{-3} \mathrm{~kg}}{0.72 \mathrm{~m}}\) = 6.9 × 10-3 kg m-1
Tension, T = 60 N
The speed of wave on the wire is given by
υ = \(\sqrt{\frac{\mathrm{T}}{\mu}}=\sqrt{\frac{60 \mathrm{~N}}{6.9 \times 10^{-3} \mathrm{~kg} \mathrm{~m}^{-1}}}\) = 93 m s-1
![]()
Question 4.
Estimate the speed of sound in air at standard temperature and pressure. The mass of 1 mole of air is 29.0 × 10-3 kg.
Solution:
We know that 1 mole of any gas occupies 22.4 litres at STP Therefore, density of air at STP is:
ρ0 = (mass of one mole of air) / (Volume of one mole of air at STP)
= \(\frac{29.0 \times 10^{-3} \mathrm{~kg}}{22.4 \times 10^{-3} \mathrm{~m}^3}\) = 1.29 kgm-3
According to Newton’s formula for the speed of sound in a medium, we get for the speed of sound in air at STP,
υ = \(\left[\frac{1.01 \times 10^5 \mathrm{~N} \mathrm{~m}^{-2}}{1.29 \mathrm{~kg} \mathrm{~m}^{-3}}\right]^{1 / 2}\) = 280 m s-1
Question 5.
A pipe, 30.0 cm long is open at both ends. Which harmonic mode of the pipe resonates a 1.1 kHz source ? Will resonance with the same source be observed if one end of the pipe is closed ? Take the speed of sound in air as 330 m s-1.
Solution:
The first harmonic frequency is given by
v1 = \(\frac{v}{\lambda_1}=\frac{v}{2 L}\) (open pipe)
Where L is the length of the pipe. The frequency of its nth; harmonic is
vn = \(\frac{n v}{2 L}\) for n = 1, 2, 3, ……………… (open pipe)
First few modes of an open pipe are shown in Fig.
For L = 30.0 cm. υ = 330 m s-1
vn = \(\frac{\mathrm{n} \times 330\left(\mathrm{~m} \mathrm{~s}^{-1}\right)}{0.6(\mathrm{~m})}\) = 550 s-1
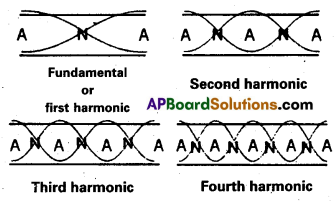
Clearly, for a source of frequency 1.1 kHz the air column will resonate at υ2, i.e. the second harmonic.
Now if one end of the pipe is closed (Fig.), the fundamental frequency is
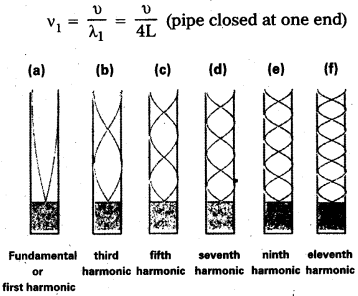
and only to odd numbered harmonics are present :
v3 = \(\frac{3 v}{4 L}/latex], v5 = [latex]\frac{5 v}{4 L}\) and s0 0n.
For L = 30 cm and υ = 330 m s-1;, the fundamental frequency of the pipe closed at one end is 275 Hz and the source frequency corresponds to its fourth harmonic. Since this harmonic is not a possible mode, no resonance will be observed with the source, the moment one end is closed.
![]()
Question 6.
Two sitar strings A and B playing the note ‘Dha’ are slightly put of tune and produce beats of frequency 5 Hz. The tension of the string B is slightly increased and the beat frequency is found to decrease to 3 Hz. What is the original frequency of B if the frequency of A is 427 Hz ?
Solution:
Increase in the tension of a string increases its frequency. It the original frequency of B (vB) were greater than that of A(vA) .further increase in vB should have resulted in an increase in the beat frequency. But the beat frequency is found to decrease. This shows that vB < vA. Since vA – vB = 5 Hz, and va = 427 Hz, we get vB = 422 Hz.
Question 7.
A rocket is moving at a speed of 200 m s-1 towards a stationary target. While moving, it emits a wave of frequency 1000 Hz. Some of the sound reaching the target gets reflected back to the rocket as an echo. Calculate (1) the frequency of the sound as detected by the target and (2) the frequency of the echo as detected by the rocket. [A.P. Mar. 16]
Solution:
1) The observer is at rest and the source is moving with a speed of 200 ms-1. Since this is comparable with the velocity of sound 330 ms-1, we must use Eq.
v = v0 \(\left[\frac{1+\mathrm{v}_{\mathrm{S}}}{\mathrm{v}}\right]^{-1}\) and not the approximate
v = v0 \(\left[1-\frac{v_s}{v}\right]\)
Since the source is approaching a stationary target, υ0 = 0, and υs must be replaced by -υs. Thus, we have
v = v0 \(\left(1-\frac{v_{\mathrm{S}}}{v}\right)^{-1}\)
v = 1000 Hz × [1 – 200 m s-1/330 m s-1]-1
≃ 2540Hz
![]()
2) The target is now the source (because it is the source of echo) and the rocket’s detector is now the detector or observer (because it detects echo). Thus, υs = 0 and υ0 has a positive value. The frequency of the sound emitted by the source (the target) is v0, the frequency intercepted by the target and not v0, Therefore, the frequency as registered by the rocket is
v’ = \(v\left(\frac{v+v_0}{v}\right)\)
= 2540 Hz × \(\left(\frac{200 \mathrm{~m} \mathrm{~s}^{-1}+330 \mathrm{~m} \mathrm{~s}^{-1}}{330 \mathrm{~m} \mathrm{~s}^{-1}}\right)\)
≃ 4080Hz