Students get through AP Inter 2nd Year Physics Important Questions 2nd Lesson Ray Optics and Optical Instruments which are most likely to be asked in the exam.
AP Inter 2nd Year Physics Important Questions 2nd Lesson Ray Optics and Optical Instruments
Very Short Answer Questions
Question 1.
What is optical density and how is it different from mass density?
Answer:
Optical density: Optical density is defined as the ratio of the speed of light in media. Mass density: Mass per unit volume is defined as mass density.
The mass density of an optically denser medium is less than that of an optically rarer medium.
Question 2.
What are the laws of reflection through curved mirrors?
Answer:
- “The angle of reflection equals to the angle of incidence”.
- “The incident ray, reflected ray and the normal to the reflecting surface at the point of incidence lie in the same plane”.
![]()
Question 3.
Define ‘power’ of a convex lens. What is its unit ? [A.P. Mar. 17, T.S. Mar. 16]
Answer:
Power of a lens : Power of a lens is defined as its bending ability and is measured as reciprocal of focal length in metre.
∴ Power of a lens = \(\frac{1}{f(\text { in metres) }}=\frac{100}{\mathrm{f}(\text { in cms) }}\)
Unit → Dioptre (D)
Problems
Question 1.
A concave mirror of focal length 10 cm is placed at a distance 35 cm from a wall. How far from the wall should an object be placed so that its real image is formed on the wall ?
Answer:
f = 10 cm, υ = 35 cm
\(\frac{1}{f}=\frac{1}{v}+\frac{1}{-u}\) (using sign convention)
\(\frac{1}{u}=\frac{1}{v}-\frac{1}{f}=\frac{1}{35}-\frac{1}{10}\)
\(\frac{1}{u}=\frac{10-35}{35 \times 10}=\frac{-1}{14}\)
U = – 14 cm.
Distance of the object from the wall = 35 – 14 = 21cm.
Question 2.
A concave mirror produces an image of a long vertical pin, placed 40cm from the mirror, at the position of the object. Find the focal length of the mirror. [T.S. Mar. 17, 16]
Answer:
Give u = υ = 40cm
\(\frac{1}{\mathrm{f}}=\frac{1}{v}+\frac{1}{u}\)
\(\frac{1}{f}=\frac{1}{40}+\frac{1}{40}\)
\(\frac{1}{\mathrm{f}}=\frac{2}{40}\)
f = 20 cm.
![]()
Question 3.
A small angled prism of 4° deviates a ray through 2.48°. Find the refractive index of the prism.
Answer:
A = 4°, Dm = 2.48°
Dm = A (μ – 1)
μ – 1 = \(\frac{\mathrm{D}_{\mathrm{m}}}{\mathrm{A}}=\frac{2.48}{4}\) = 0.62
μ = 1 + 0.62
μ = 1.62
Question 4.
What is ‘dispersion’? Which colour gets relatively more dispersed ? [Mar. 14]
Answer:
Dispersion : The phenomenon of splitting of white light ipto its constituent colours, on passing through a prism is called dispersion of light.
The deviation is maximum for violet colour.
Question 5.
The focal length of a concave lens is 30 cm. Where should an object be placed so that its image is 1/10 of its size ?
Solution:
f = 30 cm, h1 = h, h2 = \(\frac{\mathrm{h}}{10}\)

Question 6.
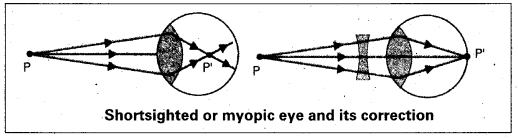
What is myopia ? How can it be corrected ? [T.S. Mar. 15]
Answer:
Myopia (or) Near sightedness :
The light from a distant object arriving at the eye-lens may get converged at a point infront of the retina. This type of defect is called myopia.
To correct this, we interpose a concave lens between the eye and the object.
![]()
Question 7.
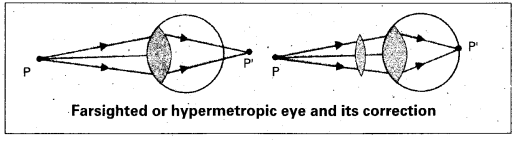
What is hypermetropia ? How can it be corrected ? [A.P. Mar. 16]
Answer:
Hypermetropia (or) Farsightedness :
The light from a distant object arriving at the eye-lens may get converged at a point behind the retina. This type of defect is called Hypermetropia.
To correct this, we interpose a convex lens (Convergent lens) between the eye and the object.
Question 8.
Draw neat labelled ray diagram of simple microscope. [PE 2015 (A.P.)]
Answer:
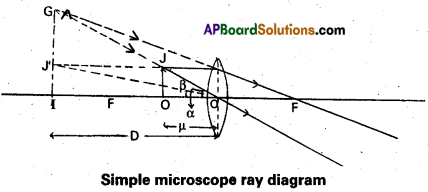
u = object distance
D = distance of near point.
Short Answer Questions
Question 1.
Define focal length of a concave mirror. Prove that the radius of curvature of a concave mirror is double its focal length. [A.P. Mar. 17]
Answer:
Focal length of concave mirror:
The distance between the focus F and the pole P of the mirror is called the focal length of the concave mirror.
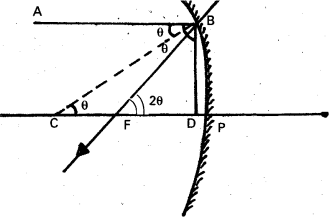
Consider a ray AB parallel to principal axis incident on a concave mirror at B and is re-flected along BF. The line CB is normal to the mirror.
Let θ be the angle of incidence, ∠ABC = ∠BCP = θ
Draw BD ⊥ CP
In right angled ∆le
Tan θ = \(\frac{\mathrm{BD}}{\mathrm{CD}}\) ……………. (1)
From ∆le BFD, Tan 2θ = \(\frac{\mathrm{BD}}{\mathrm{FD}}\) ……………. (2)
Dividing eq (2) by eq (1), \(\frac{{Tan} 2 \theta}{{Tan} \theta}=\frac{\mathrm{CD}}{\mathrm{FD}}\) ………………….. (3)
If θ is very small, then tan θ ≈ θ and tan 2θ ≈ 2θ since the aperture of the lens is small
∴ The point B lies very close to p.
CD ≈ CP and FD ≈ FP
From eq (3), \(\frac{2 \theta}{\theta}=\frac{\mathrm{CP}}{\mathrm{FP}}=\frac{\mathrm{R}}{\mathrm{f}} \Rightarrow 2=\frac{\mathrm{R}}{\mathrm{f}}\)
R = 2f
![]()
Question 2.
Define critical angle. Explain total internal reflection using a neat diagram. [T.S. Mar. 15]
Answer:
Critical angle:
When light ray travelling from denser medium to rarer medium, then the angle of incidence for which angle of refraction in air is 90a is called critical angle.
C = sin-1 \(\left(\frac{1}{\mu}\right)\)
Total internal reflection:
When a light ray travels from denser to rarer medium, the angle of incidence is greater than the critical angle, then it reflects into the same medium is called total internal reflection.
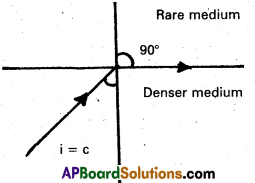
Explanation:
Consider an object in the denser medium. A ray OA incident on XY bends away from the normal. As the angle of incidence is increased, the angle of refraction goes on increasing. For certain angle of incidence, the refracted ray parallel to XY surface (r = 90°).
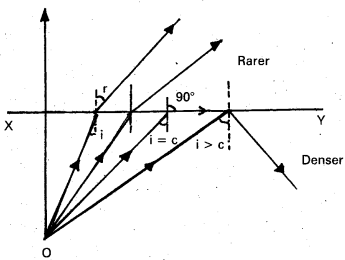
When the angle of incidence is further increased, the ray is not refracted but is totally reflected back in the denser medium. This phenomenon is called total internal reflection.
Question 3.
Explain the formation of a mirage. [A.P. Mar. 16]
Answer:
In a desert, the sand becomes very hot during the day time and it rapidly heats the layer of air which is in its contact. So density of air decreases. As a result the successive upward layers are denser than lower layers.
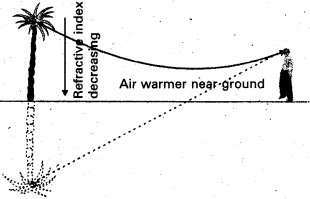
When a beam of light travelling from the top of a tree enters a rarer layer, it is refracted away from the normal. As a result at the surface of layers of air, each time the angle of incidence increases and ultimately a stage is reached, when the angle of incidence becomes greater than the critical angle between the two layers, the incident ray suffers total internal reflection.
So it appears as inverted image of the tree is formed and the same looks like a pool of water to the observer.
![]()
Question 4.
Explain the formation of a rainbow. [A.P. Mar. 15]
Answer:
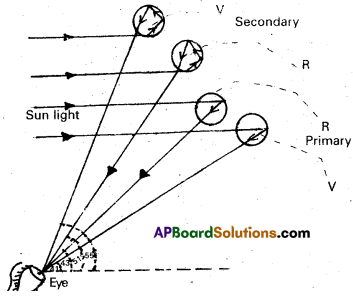
Figure shows how sun light is broken into its segments in the process and a rainbow appears. The dispersion of the violet and the red rays after internal reflection in the drop is shown in figure.
The red rays emerge from the drops of water at one angle (43°) and the violet rays emerge at another angle (41°). The large number of water drops in the sky makes a rain-bow. The rainbow appears semicircular for an observer on earth.
Question 5.
Why does the setting sun appear red ? [T.S. Mar. 17, Mar. 14]
Answer:
As sunlight travels through the earths atmosphere, gets scattered by the large number of molecules present. This scattering of sun light is responsible for the colour of the sky, during sunrise and sunset etc.
The light of shorter wave length is scattered much more than light of larger wave-length. Scattering ∝ \(\frac{1}{\lambda^4}\).
Most of blue light is scattered, hence the bluish colour of sky predominates.
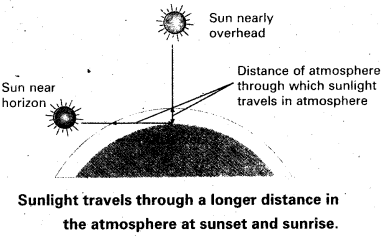
At sunset (or) sunrise, sun rays must pass through a larger atmospheric distance. More of the blue colour is scattered away only red colour which is least scattered ap-pears to come from sun. Hence it appears red.
Question 6.
With a neat labelled diagram explain the formation of image in a simple microscope. [T.S. Mar. 16, A.P. Mar. 15]
Answer:
Simple microscope: It consists a single short focus convex lens. It increases the visual angle to see an object clearly. It is also called magnifying glass (or) reading glass.
Working : The object is adjusted within the principal focus Of the convex lens to form the image at the near point. The image is formed on same side of the object and it is virtual, erect and magnified as shown in fig.
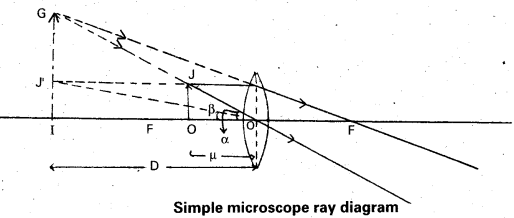
Magnifying power : The ratio of the angle subtended by the image at the eye to the angle subtended by the object at the eye is called magnifying power of a simple microscope.
It is denoted by ‘m’.
m = \(\frac{\alpha}{\beta} \simeq \frac{{Tan} \alpha}{{Tan} \beta}\)
![]()
Question 7.
What is the position of the object for a simple microscope ? What is the maximum magnifi-cation of a simple microscope for a realistic focal length ?
Answer:
When an object is placed between principal focus and optical centre of a convex lens, a virtual and erect image will be formed on the same side of the object.
Magnifying power: It is defined as the ratio of the angle subtended at the eye by the image to the angle subtended by the object at the eye.
m = \(\frac{\alpha}{\beta} \simeq \frac{{Tan} \alpha}{{Tan} \beta}\)
From figure OJ = IJ’, ∠IO’G = α and ∠IO’J’ = β
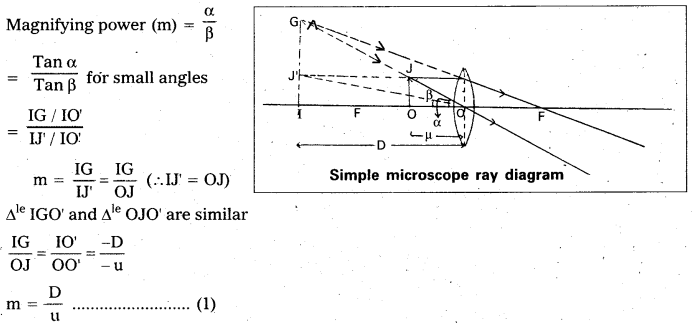
The above equation can be written as
m = 1 + \(\frac{\mathrm{D}}{\mathrm{f}}\) …………… (2)
This shows that smaller the focal length of the lens, greater will be the magnifying power of microscope.
Long Answer Questions
Question 1.
Draw a neat labelled diagram of a compound microscope and explain its working. Derive an expression for its magnification.
Answer:
Description : It consists of two convex lenses separated by a distance. The lens near the object is called objective and the lens near the eye is called eye piece. The objective lens has small focal length and eye piece has of larger focal length. The distance of the object can be adjusted by
means of a rack and pinion arrangement.
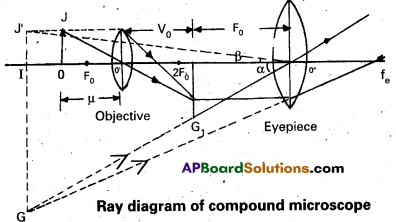
Working: The object OJ is placed outside the principal focus of the objective and the real image is formed on the other side of it. The image I1 G1 is real, inverted and magnified.
This image acts as the object for the eyepiece. The position of the eyepiece is so adjusted that the image due to the objective is between the optic centre and principal focus to form the final image at the near point. The final image IG is virtual, inverted and magnified.
Magnifying Power: It is defined as the ratio of the angle subtended by the final image at the eye when formed at near point to the angle subtended by the object at the eye when imagined to be at near point.
Imagining that the eye is at the optic centre, the angle subtended by the final image is a. When the object is imagined to be taken at near point it is represented by IJ’ and OJ – IJ’.
The angle made by I J’ at the eye is β. Then by the definition of magnifying power
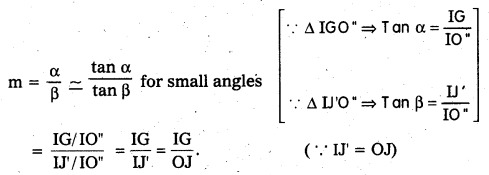
Dividing and multiplying by I1 G1 on the right side, we get
m = \(\left(\frac{\mathrm{IG}}{\mathrm{I}_1 \mathrm{G}_1}\right)\left(\frac{\mathrm{I}_1 \mathrm{G}_1}{\mathrm{OJ}}\right)\)
Magnifying power of the objective (m0) = I1 G1 / OJ = Height of the image due to the objective / Height of its object.
Magnifying power of the eye piece (me) = IG/I1G1 = Height of the final image / Height of the object for the eyepiece.
∴ m = m0 × me ……………… (1)
To find m0: In figure OJ O’ and I1 G1 O’ are similar triangles. \(\left(\frac{\mathrm{I}_1 \mathrm{G}_1}{\mathrm{OJ}}\right)=\frac{\mathrm{O}^{\prime} \mathrm{I}_1}{\mathrm{O}^{\prime} \mathrm{O}}\)
Using sign convention, we find that O’I1 = + v0 and O’O = -u where v0 is the image distance due to the objective and u is the object distance for the objective or the compound microscope. I1G1 is negative and OJ is positive.
∴ m0 = \(\frac{\mathrm{v}_0}{\mathrm{U}}\) (∵ \(\frac{\mathrm{I}_1 \mathrm{G}_1}{\mathrm{OJ}}\) = m0)
To find me : The eyepiece behaves like a simple microscope. So the magnifying power of the eye piece.
∴ me = (1 + \(\frac{\mathrm{D}}{\mathrm{f}_{\mathrm{e}}}\))
Where fe is the focal length of the eyepiece.
Substituting m0 and me in equation (1),
m = \(+\frac{\mathrm{v}_0}{\mathrm{u}}\left(1+\frac{\mathrm{D}}{\mathrm{f}_{\mathrm{e}}}\right)\)
When the object is very close to the principal focus F0 of the objective, the image due to the objective becomes very close to the eyepiece,
u ≈ -f0 and v0 ≈ L
Where L is the length of the microscope. Then
m ≈ \(-\frac{L}{f_0}\left(1+\frac{D}{f_e}\right)\)
![]()
Question 2.
a) Define Snell’s Law. Using a neat labelled diagram derive an expression for the refractive index of the material of an equilateral prism.
b) A ray of light, after passing through a medium, meets the surface separating the medium from air at an angle of 45° and is just not refracted. What is the refractive index of the medium ?
Answer:
a) Snell’s law:
The ratio of the sine of the angle of incidence to the sine of angle of refraction is constant, called the refractive index of the medium.
\(\frac{\sin i}{\sin r}\) = μ (constant).
Let ABC be the glass prism. Its angle of prism is A. The refractive index of the material of the prism is p. Let AB and AC be the two refracting surfaces PQ = incident ray, RS = emergent ray.
Let angle of incidence = i1
angle of emergence = i2
angle of refraction = r1
angle of refraction at R = r2
After travelling through the prism it falls on AC and emerges as RS.
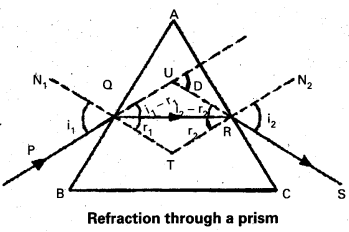
The D angle of deviation.
From the ∆ QRT
r1 + r2 + ∠T = 180° ……………….. (1)
From the quadrilateral AQTR
∠A + ∠T = 180°
∠T = 180° – A ………………. (2)
From the equations (1) and (2)
r1 + r2 + ∠T = 180° we get
r1 + r2 + 180° – A = 180°
r1 + r1 = A ………………. (3)
from the ∆ QUR
i1 – r1 + i2 – r2 + 180° – D = 180°
i1 + i2 = (r1 + r2) = D
i1 + i2 – A = D [∵r1 + r2 = A]
i1 + i2 = A + D ……………… (4)
Minimum deviation : Experimentally it is found that as the angle of incidence increased the angle of deviation decreases till it reaches a minimum value and then it increases. This least value of deviation is called angle of minimum deviation ‘δ’ as shown in the fig.
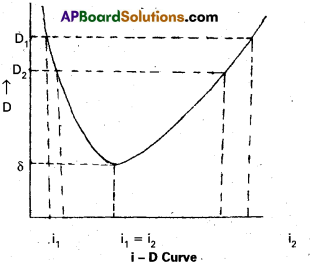
When D decreases the two angles i1 and i2 become closer to each other at the angle of minimum deviation, the two angles of incidence are same i.e, i 1 = i2.
As i1 = i2, r1 = r2
∴ i1 = i2 = i, r1 = r2 = r
substituting this in (1) and (2) we get
2r = A ⇒ r = A/2
i + i = A + δ ⇒ i = \(\frac{\mathrm{A}+\delta}{2}\)
According to Snell’s law μ = ![]()
μ = 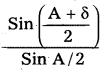
Note :The minimum deviation depends on the refractive index of the prism material and the angle of the prism.
b) Given that i = C = 45°
μ = \(\frac{1}{\sin \mathrm{c}}\) ⇒ μ = \(\frac{1}{\sin 45^{\circ}}\)
μ = \(\frac{1}{1 / \sqrt{2}}=\sqrt{2}\)
μ = 1.414
Textual Examples
Question 1.
Suppose that the lower half of the concave mirror’s reflecting surface in figure is covered with an opaque (non- reflective) material. What effect will this have on the image of an object p’ iced in front of the mirror ?
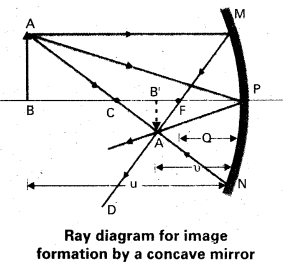
Solution:
You may think that the image will now show only half of the object, but taking the laws of reflection to be true for all points of the remaining part of the mirror, the image will be that of the whole object. However, as the area of the re-fleeting surface has been reduced, the intensity of the image will be low (in this case, half).
![]()
Question 2.
A mobile phone lies along the principal axis of a concave mirror, as shown in Fig. Show by suitable diagram, the formation of its image. Explain why the magnification is not uniform. Will the distortion of image depend on the location of the phone with respect to the mirror ?
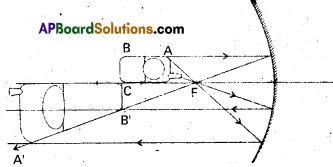
Solution:
The ray diagram for the formation of the image of the phone is shown in fig. The image of the part which is on the plane perpendicular to principal axis will be on the same plane. It will be of the same size, i.e., B’C = BC. You can yourself realise why the image is distorted.
Question 3.
An object is placed at (i) 10 cm. (ii) 5 cm in front of a concave mirror of radius of curvature 15cm. Find the position, nature, and magnification of the image in each case.
Solution:
The focal length f = – 15/2 cm = – 7.5 cm
i) The object distance u = – 10 cm. Then
Eq. \(\frac{1}{v}+\frac{1}{\mathrm{u}}=\frac{1}{\mathrm{f}}\) gives
\(\frac{1}{v}+\frac{1}{-10}=\frac{1}{-7.5}\)
or υ = \(\frac{10 \times 7.5}{-2.5}\) = -30 cm
The image is 30 cm from the mirror on the same side as the object.
Also, magnification
m = –\(\frac{v}{u}=-\frac{(-30)}{(-10)}\) = -3
The image is magnified, real and inverted.
ii) The object distance u = -5cm. Then
from Eq. \(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\)
\(\frac{1}{v}+\frac{1}{-5}=\frac{1}{-7.5}\)
or υ = \(\frac{5 \times 7.5}{(7.5-5)}\) = 15 cm
This image is formed at 15 cm behind the mirror. It is a virtual image.
Magnification m = – \(\frac{v}{u}=-\frac{15}{(-5)}\) = 3
The image is magnified, virtual and erect.
![]()
Question 4.
Suppose while sitting in a parked car, you notice a jogger approaching towards you in the side view mirror of R = 2 m. If the jogger is running at a speed of 5ms-1, how fast the image of the jogger appear to move when the jogger is (a) 39 m, (b) 29m, (c) 19 m and (d) 9 m away.
Solution:
From the mirror equation, Eq. \(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\)
we get
υ = \(\frac{\mathrm{fu}}{\mathrm{u}-\mathrm{f}}\)
For convex mirror, since R = 2m, f = 1 m.
Then for u = -39 m. v = \(\frac{(39) \times 1}{-39-1}\)
= \(\frac{39}{40}\)
Since the jogger moves at a constant speed of 5ms”1, after Is the position of the image u (for u = – 39 + 5 = – 34) is (34/35) m.
The shift in the position of image in 1 s is
\(\frac{39}{40}-\frac{34}{35}=\frac{1365-1360}{1400}=\frac{5}{1400}\)
Therefore, the average speed of the im-age when the jogger is between 39 m and 34 m from the mirror, is (1/280) ms-1. Similarly, it can be seen that for u = – 29 m, -19 m and -9 m, the speed with which the image appears to move is \(\frac{1}{150}\)ms-1, \(\frac{1}{60}\) ms-1 and \(\frac{1}{10}\) ms-1 respectively.
Question 5.
The earth takes 24 h to rotate once about its axis. How much time does the sun take to shift by 1° when viewed from the earth ?
Solution:
Time taken for 360° shift = 24h
Time taken for 1° shift = 24/360
h = 4 min.
Question 6.
Light from a point source in air falls on a spherical glass surface (n = 1.5 and radius of curvature = 20 cm). The distance of the light source from the glass surface is 100 cm. At what position the image is formed ?
Solution:
We use the relation given by Eq.
\(\frac{\mathrm{h}_2}{v}-\frac{\mathrm{h}}{\mathrm{u}}=\frac{\mathrm{h}_2-\mathrm{h}_1}{\mathrm{R}}\) Here
u = – 100 cm, υ = ?. R = + 20 cm, n1 = 1, and n2 = 1.5. We then have
\(\frac{1.5}{v}+\frac{1}{100}=\frac{0.5}{20}\)
or υ = + 100 cm
![]()
Question 7.
A magician during a show makes a glass lens with n = 1.47 disappear in a trough of liquid. What is the refractive index of the liquid ? Could the liquid be water ?
Answer:
The refractive index of the liquid must be equal to 1.47 in order to make the lens disappear. This means n1 = n2. This gives 1/f = 0 or f → ∞. The lens in the liquid will act like a plane sheet of glass. No, the liquid is not water. It could be glycerine.
Question 8.
(i) If f = 0.5 m for a glass lens, what is the power of the lens ? (ii) The radii of curvature 6f the faces of a double convex lens are 10 cm and 15cm. Its focal length is 12 cm. What is the refractive index of glass ? (iii) A convex lens has 20 cm focal length in air. What is focal length in water ?
(Refractive index of air-water = 1.33. Refractive index for air – glass = 1.5.)
Solution:
i) Power = + 2 dioptre.
ii) Here, we have f = + 12 cm,
R1 = + 10 cm, R2 = – 15 cm.
Refractive index of air is taken as unity.
We use the lens formula of Eq. \(\frac{\mathrm{h}_1}{\mathrm{DB}}+\frac{\mathrm{h}_1}{\mathrm{DB}}=\frac{\mathrm{h}_1}{\mathrm{f}}\). The sign convention has to be applied for f, R1 and R2.
Substituting the values, we have
\(\frac{1}{12}\) = (n – 1) (\(\frac{1}{10}\) – \(\frac{1}{-15}\))
This gives n = 1.5.
iii) For a glass lens in air, n2 = 1.5, n: = 1, f = + 20cm. Hence, the lens formula gives.
\(\frac{1}{20}=0.5\left[\frac{1}{R_1}-\frac{1}{R_2}\right]\)
For the same glass lens in water. n2 = 1.5, n1 = 1.33. Therefore,
\(\frac{1.33}{f}=(1.5-1.33)\left[\frac{1}{R_1}-\frac{1}{R_2}\right]\)
Combining the above two equations, we find f = + 78.2 cm.
Question 9.
Find the position of the image formed by the lens combination given in the fig.
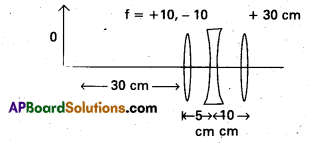
Solution:
Image formed by the first lens
\(\frac{1}{v_1}-\frac{1}{\mathrm{u}}=\frac{1}{\mathrm{f}_1}\)
\(\frac{1}{v_1}-\frac{1}{-30}=\frac{1}{10}\)
or v1 = 15 cm
The image formed by the first lens serves as the object for the second. This is at a distance of (15 – 5) cm = 10 cm to the right of the second lens. Though the image is reeil, it serves as a virtual object for the second lens, which means that the rays appear to come from it for the second lens.
\(\frac{1}{v_3}-\frac{1}{10}=\frac{1}{-10}\) or v2 ∞
The virtual image is formed at an infinite distance to the left of the second lens. This acts as an object for the third lens.
\(\frac{1}{v_3}-\frac{1}{\mathrm{u}_3}=\frac{1}{\mathrm{f}_3} \text { or } \frac{1}{v_3}-\frac{1}{\infty}+\frac{1}{30}\)
or v3 = 30 cm
The final image is formed 30 cm to the right of the third lens.
![]()
Question 10.
What focal length should the reading spectacles have for a person for whom the least distance of distinct vision is 50 cm ?
Solution:
The distance of normal vision is 25cm. So if a book is at u= – 25 cm. Its image should be formed at υ = – 50 cm. There-fore, the desired focal length given by
\(\frac{1}{\mathrm{f}}=\frac{1}{v}-\frac{1}{\mathrm{u}} \text { or } \frac{1}{\mathrm{f}}=\frac{1}{-50}-\frac{1}{-25}=\frac{1}{50}\)
or f = + 50 cm (convex lens).
Question 11.
a) The far point of a myopic person is 80 cm in front of the eye. What is ,. the power of the lens required to enable him to see very distant objects clearly ?
b) In what way does the corrective lens help the above person ? Does the lens magnify very distant objects ? Explain carefully.
c) The above person prefers to remove his spectacles while reading a book. Explain why?
Solution:
a) Solving as in the previous example, we find that the person should use a concave lens of focal length = – 80 cm. i.e:, of power = – 1.25 dioptres.
b) No. The concave lens, in fact, reduces the size of the object, but the angle subtended by the image (at the far point) at the eye. The eye is able to see distant objects not because the corrective lens magnifies the object, but because it brings the (i.e., it produces virtual image of the object) at the far point of the eye which then can be focussed by the eye-lens on the retina.
c) The myopic person may have a normal near point, i.e., about 25 cm (or even less). In order to read a book with the spectacles, such a person must keep the book at a distance greater than 25cm so that the image of the book by the concave lens is produced not closer than 25cm. The angular size of the book (dr its image) at the greater distance is evidently less than the angular size when the book is placed at 25 cm and no spectacles are needed. Hence, the person prefers to remove the spectacles while reading.
![]()
Question 12.
a) The near point of a hypermetropic person is 75 cm from the eye. What is the power of the lens required to enable the person to read clearly a book held at 25cm from the eye ?
b) In what way does the corrective lens help the above person ? Does the lens magnify objects held near the eye ?
c) The above person prefers to remove the spectacles while looking at the sky. Explain why?
Solution:
a) u = – 25 cm, υ = – 75 cm
1/f = 1/25 – 1/75, i.e., f = 37.5 cm.
The corrective lens- needs to have a converging power of +2.67 dioptres.
b) The corrective lens produces a virtual image (at 75 cm) of an object at 25 cm. The angular size of this image is the same as that of the object. In this sense the lens does not magnify the object but merely brings the object to the near point of the hypermetric eye, which then gets focussed on the retina. However, the angular size is greater than that of the same object at the near point (75 cm) viewed without the spectacles.
c) A hypermetropic eye may have normal far point i.e., it may have enough converging power to focus parallel rays from infinity on the retina of the shortened eyeball. Wearing spectacles of converging lenses (used for near vision) will amount to more converging power than needed for parallel rays. Hence the person prefers not to use the spectacles for far objects.