SCERT AP 9th Class Social Studies Guide Pdf 20th Lesson ప్రజాస్వామ్యం – రూపుదిద్దుకుంటున్న భావన Textbook Questions and Answers.
AP State Syllabus 9th Class Social Solutions 20th Lesson ప్రజాస్వామ్యం – రూపుదిద్దుకుంటున్న భావన
9th Class Social Studies 20th Lesson ప్రజాస్వామ్యం – రూపుదిద్దుకుంటున్న భావన Textbook Questions and Answers
Improve your learning (మీ అభ్యసనాన్ని మెరుగుపడుచుకోండి)
ప్రశ్న 1.
జవాబుదారీ, బాధ్యతాయుత, చట్టబద్ధ ప్రభుత్వం ఉండేలా ప్రజాస్వామ్యం ఎలా చూస్తుంది? (AS1)
జవాబు:
- ప్రజాస్వామ్యం అంటే అంతిమంగా ప్రజల నుంచి అధికారం పొంది, దానికి జవాబుదారీగా ఉండే ప్రభుత్వం.
- దీనిలో ప్రజాప్రతినిధులను ఎప్పటికప్పుడు కొంతకాలానికి ఎన్నుకుంటారు.
- ఎన్నికైన ప్రజాప్రతినిధులు వివిధ రకాలుగా ప్రజలకు జవాబుదారీగా ఉంటారు.
- ప్రజలు ఎన్నుకున్న శాసనసభలలో ప్రభుత్వ పక్ష ప్రతినిధులు తమ పనిని వివరించాలి, పనుల ప్రణాళికను ఈ శాసనసభలే ఆమోదించాలి.
- ప్రభుత్వం చేసిన పనికి సంబంధించిన సమాచారాన్ని ఏ పౌరుడైనా అడగవచ్చు. ఆ సమాచారాన్ని ఇవ్వవలసిన బాధ్యత ప్రభుత్వానిది. అన్నిటికీ మించి నిర్దిష్ట కాలం తరువాత మళ్ళీ ఎన్నికలుంటాయి.
- ప్రజాప్రతినిధులు మళ్ళీ ప్రజల మద్దతును పొందవలసి ఉంటుంది.
- వాళ్ళు చేసిన పనిని వివరించమని అడిగి అది సంతృప్తికరంగా లేనప్పుడు ప్రజలు వాళ్లను తిరస్కరించవచ్చు.
ప్రశ్న 2.
సామాజిక వైవిధ్యతలను కలుపుకుని వెళ్లే స్వభావాన్ని ప్రజాస్వామ్యాలు ఏ స్థితిలో ప్రదర్శిస్తాయి? (AS1)
జవాబు:
- ప్రజల పాలన అని. అన్నప్పుడు వయోజనులైన అందరూ అని అర్థం.
- వాళ్ళు పురుషులు కావచ్చు, స్త్రీలు కావచ్చు, ధనికులు కావచ్చు,. పేదవాళ్ళు కావచ్చు. నల్లవాళ్లు కావచ్చు, తెల్లవాళ్లు కావచ్చు, హిందువులు లేదా క్రిస్టియన్లు లేదా ముస్లింలు లేదా నాస్తికులు కావచ్చు. ఏ భాష మాట్లాడే వాళ్లేనా కావచ్చు. ఈ భావన ఏర్పడటానికి చాలాకాలం పట్టింది.
- సూచికగా ఎన్నికలలో ఓటు చేసే హక్కును తీసుకుందాం.
- మొదట్లో ఆస్తి ఉన్న కొంతమంది పురుషులకు మాత్రమే ఓటుహక్కు ఉండేది.
- క్రమేపీ కొన్ని దేశాలలో ఈ హక్కును పేదవాళ్ళకు కల్పించారు. ఆ తరువాత అది మహిళలకు లభించింది.
- చివరికి అన్ని మతాల, జాతుల వాళ్ళకు ఓటు హక్కు లభించింది.
- 1920 నుంచి అమెరికాలో శ్వేతజాతి మహిళలకు ఓటుహక్కు లభించింది.
- 1965 లో నల్లజాతీయులైన పౌరుల ఓటు హక్కుపై వివక్షతను తొలగించింది.
- న్యూజీలాండ్ 1893లోనే అన్ని వర్గాల ప్రజలకు ఓటుహక్కు కల్పించిన మొదటి దేశం.
- సార్వజనీన ఓటుహక్కు కల్పించిన తొలి పెద్ద దేశం యూనియన్ ఆఫ్ సోవియట్ సోషలిస్ట్ రిపబ్లిక్.
రాజకీయ సమానత్వం, అందరినీ కలుపుకోవటం అన్న మౌలిక సూత్రంపై ప్రజాస్వామ్యం ఆధారపడి ఉంది. ప్రజాస్వామ్యంలో వయోజనులైన ప్రతి ఒక్క పౌరునికి ఒక ఓటుహక్కు ఉండాలి. ప్రతి ‘ఓటుకు సమాన విలువ ఉండాలి.
![]()
ప్రశ్న 3.
కింద వ్యాఖ్యానాలను సమర్ధించటానికి వ్యతిరేకించటానికి మీ వాదనలు పేర్కొనండి : (AS2)
అ. పారిశ్రామిక దేశాలు ప్రజాస్వామ్య విధానాన్ని అనుసరించగలవు, కానీ పేద దేశాలు ధనిక దేశాలు కావాలంటే నియంతృత్వం ఉండాలి.
జవాబు:
పేద దేశాలు ధనిక దేశాలు కావాలంటే నియంతృత్వం కన్నా ప్రజాస్వామ్యం ఉంటేనే బాగుంటుంది.
కారణం ప్రజాస్వామ్య దేశాలలో ప్రభుత్వ కార్యక్రమాల రూపకల్పనలోను, ప్రభుత్వ విధానాలు, చట్టాలు తయారు చేయటంలో, వాటిని అమలు చేయటంలో ప్రజలు భాగస్వాములు కావాలి. ప్రజలందరూ బహిరంగంగా పాల్గొని తమ అవసరాలు, అభిప్రాయాలు స్పష్టంగా పేర్కొనేలా బహిరంగ చర్చలు జరపాలి తరువాత చట్టాలు, విధానాలు రూపొందించాలి ఆ విధంగా ప్రజల సంక్షేమ పథకాలు అమలు చేయటం వల్ల ప్రజలు ఆర్థికంగా, సామాజికంగా, రాజకీయంగా సమాన అవకాశాలు పొందుతారు. అందువలన పేద దేశాలు కూడా ధనిక దేశాలుగా మారతాయి.
పారదర్శకత (దాపరికం లేని పరిపాలన), అమలు జరిగినపుడు,. అవినీతి, అన్యాయం, లంచగొండితనం వంటివి లేనప్పుడు పేదదేశాలు ప్రజాస్వామ్యాన్ని అమలు చేసినప్పటికీ ధనిక దేశాలుగా మారతాయి.
అందువల్ల పేద దేశాలు ధనిక దేశాలు కావాలంటే నియంతృత్వం కన్నా ప్రజాస్వామ్యమే మేలు.
ఆ. పౌరుల మధ్య ఆదాయాలలో అసమానతలను ప్రజాస్వామ్యం తగ్గించలేదు.
జవాబు:
- సమాజం ధనిక – పేదలుగా, పైకులాలు – దళితులుగా విభజింపబడి ఉంటే రాజకీయ సమానత్వం అర్థరహితం అవుతుంది.
- ఉన్నత హెూదా, సంపద ఉన్నవాళ్ళు తమకు అనుకూలంగా ఓటు వేయమని మిగిలిన వాళ్లని తేలికగా ప్రభావితం చేయగలుగుతారు.
- చాలా కుటుంబాలలో ఆ కుటుంబానికి పెద్ద అయిన పురుషుడు మహిళలతో సహా కుటుంబ సభ్యులందరూ ఎవరికి ఓటు వేయాలో నిర్ణయిస్తారు.
- అమెరికా వంటి అనేక దేశాలలో అనేక ప్రసార సాధనాలు ధనిక కార్పొరేట్ సంస్థలు లేదా వ్యక్తుల చేతుల్లో ఉంటాయి.
- దేనిని ఎక్కువగా ప్రసారం చేస్తారు ? దేనిని విస్మరిస్తారు ? అన్న దానిని బట్టి వీళ్ళు ప్రజాభిప్రాయాన్ని తీర్చిదిద్దుతారు. ప్రభావితం చేస్తారు.
- సంపన్నులకు, శక్తిమంతులకు శాసనసభ్యులు, మంత్రులు అందుబాటులో ఉంటారు. కాబట్టి వాళ్ళు విధానాలను, కార్యక్రమాలను ప్రభావితం చేయగలుగుతారు.
- ఇంకోవైపున పేదలకు నిరక్షరాస్యులకు ప్రభుత్వ వర్గాలు ఈ విధంగా అందుబాటులో ఉండవు కాబట్టి అనేక దేశాల ప్రభుత్వాలు ధనికులకు అనుకూలంగా, పేదల ప్రయోజనాలకు విరుద్దంగా ఉండే విధానాలను అనుసరిస్తుంటాయి.
- కాబట్టి రాజకీయ సమానత్వంతో పాటు సామాజిక, ఆర్థిక సమానత్వం ఉంటే తప్ప పౌరుల మధ్య ఆదాయాలలో అసమానతలను ప్రజాస్వామ్యం తగ్గించలేదు.
ఇ. పేద దేశాలలోని ప్రభుత్వాలు పేదరికం తగ్గించటం, ఆరోగ్యం , విద్యల పై తక్కువ ఖర్చు చేసి, పరిశ్రమలకు, మౌలిక సదుపాయాలకు ఎక్కువ ఖర్చు చేయాలి.
జవాబు:
పేద దేశాలలోని ప్రభుత్వాలు పేదరికం తగ్గించటం, ఆరోగ్యం , విద్యలపై తక్కువ ఖర్చుచేసి, పరిశ్రమలకు మౌలిక సదుపాయాలకు ఎక్కువ ఖర్చు చేయడానికి కారణం.
అర్థశాస్త్ర పరిభాషలో వ్యయాలు రెండు రకాలు :
- ఉత్పాదక వ్యయం
- అనుత్పాదక వ్యయం
ఉత్పాదక వ్యయం అనగా పరిశ్రమలు, వ్యవసాయంపై చేసే వ్యయం.
అనుత్పాదక వ్యయం అనగా రోడ్లు, భవనాలపై చేసే వ్యయం.
అందువలన పేద దేశాలు ఉత్పాదక వ్యయం మీద ఎక్కువ ఖర్చు చేస్తాయి. అనుత్పాదక వ్యయంపై చేసే వ్యయం వలన అదనపు రాబడులు ఏమీరావు.
ఈ. ప్రజాస్వామ్యంలో పౌరులందరికీ ఒక ఓటు ఉంటుంది కాబట్టి ఆధిపత్యానికి, ఘర్షణలకు తావు ఉండదు.
జవాబు:
ప్రజాస్వామ్యంలో పౌరులందరికీ ఒక ఓటు ఉంటుంది. పౌరుల మధ్య ఓటు హక్కు విషయంలో ఏ విధమైన వ్యత్యాసం ఉండదు. ప్రతి ఓటుకీ సమాన విలువ ఉంటుంది.
పురుషులు, స్త్రీలు, ధనికులు, పేదలు, నల్లవాళ్ళు, తెల్లవాళ్ళు, హిందువులు, క్రిస్టియన్లు లేదా ముస్లింలు లేదా నాస్తికులు అయినా, ఏ భాష మాట్లాడేవారైనా ఎవరికైనా ఓటుహక్కు ఉంటుంది కాబట్టి ఏ విధమైన వ్యత్యాసం ఉండదు. కావున ఏ విధమైన ఆధిపత్యానికీ, ఘర్షణలకూ తావు ఉండదు.
ప్రశ్న 4.
ప్రజాస్వామ్యాన్ని అంచనా వేయటంలో కింద ఉన్న వాటిల్లో ఏది వర్తించదు? (AS1)
ప్రజాస్వామ్యంలో :
అ. స్వేచ్ఛాయుత ఎన్నికలు
ఆ. వ్యక్తి గౌరవం
ఇ. అధిక సంఖ్యాకుల పాలన
ఈ. చట్టం ముందు అందరూ సమానులు
జవాబు:
ఆ. వ్యక్తి గౌరవం .
![]()
ప్రశ్న 5.
ప్రజాస్వామ్యంలో రాజకీయ, సామాజిక అసమానతలపై అధ్యయనం ఈ కింది విషయాన్ని వెల్లడి చేస్తోంది. (AS1)
అ. ప్రజాస్వామ్యం, అభివృద్ధి కలిసి ఉంటాయి.
ఆ. ప్రజాస్వామ్యంలో అసమానతలు ఉంటాయి.
ఇ. నియంతృత్వంలో అసమానతలు ఉండవు
ఈ. ప్రజాస్వామ్యం కంటే నియంతృత్వం మంచిది.
జవాబు:
(ఆ) ప్రజాస్వామ్యంలో అసమానతలు ఉంటాయి.
ప్రశ్న 6.
ఆరు దేశాలకు సంబంధించిన సమాచారం దిగువన ఉంది. ఈ సమాచారాన్ని బట్టి ఆయా దేశాలను ఏ రకంగా వర్గీకరిస్తారు? ఒక్కొక్కదాని ఎదురుగా “ప్రజాస్వామికం’ లేదా ‘అప్రజాస్వామికం’ లేదా ‘ఖచ్చితంగా చెప్పలేం’ అని రాయండి. (AS1)
దేశం (అ) : దేశ అధికారిక మతాన్ని అంగీకరించని ప్రజలకు ఓటు హక్కు ఉండదు.
దేశం (ఆ) : ఒకే పార్టీ గత ఇరవై సంవత్సరాలుగా ఎన్నికలలో గెలుస్తోంది.
దేశం (ఇ) : గత ఎన్నికలలో అధికారంలో ఉన్న పార్టీ ఓడిపోయింది.
దేశం (ఈ) : సైన్యాధిపతి ఆమోదం లేకుండా సైన్యానికి సంబంధించిన చట్టాన్ని పార్లమెంటు చేయలేదు.
దేశం (ఉ) : న్యాయవ్యవస్థ అధికారాలను తగ్గిస్తూ పార్లమెంటు చట్టం చేయలేదు.
దేశం (ఊ) : దేశానికి సంబంధించి ముఖ్య ఆర్థిక నిర్ణయాలన్నీ కేంద్ర బ్యాంకు అధికారులు తీసుకుంటారు, వీటిని మంత్రులు మార్చలేరు.
జవాబు:
దేశం (అ) : ప్రజాస్వామికం
దేశం (ఆ) : ప్రజాస్వామికం
దేశం (ఇ) : ప్రజాస్వామికం
దేశం (ఈ) : అప్రజాస్వామికం
దేశం (ఉ) : ప్రజాస్వామికం
దేశం (ఊ) : అప్రజాస్వామికం
ప్రశ్న 7.
కింద ఉన్న ప్రతి వాక్యంలో ప్రజాస్వామిక, అప్రజాస్వామిక అంశాలు ఉన్నాయి. ప్రతి వాక్యానికి ఆ రెండింటినీ వేరుగా రాయండి. (AS1)
అ. ప్రపంచ వాణిజ్య సంస్థ నిర్ణయించిన నియంత్రణలకు లోబడి పార్లమెంటు కొన్ని చట్టాలు చేయాలని మంత్రి చెప్పారు. – ప్రజాస్వామికం
ప్రపంచ వాణిజ్య సంస్థ నిర్ణయించిన నియంత్రణలకు లోబడి పార్లమెంటు . కొన్ని చట్టాలు చేయవలసిన అవసరం లేదు అని మంత్రి చెప్పారు. – అప్రజాస్వామికం
ఆ. పెద్ద ఎత్తున రిగ్గింగ్ జరిగిందని నివేదికలు వచ్చిన నియోజకవర్గంలో మళ్ళీ ఎన్నికలను నిర్వహించవలసిందిగా ఎన్నికల సంఘం ఆదేశించింది. – ప్రజాస్వామికం
పెద్ద ఎత్తున రిగ్గింగ్ జరిగిందని నివేదికలు వచ్చిన నియోజకవర్గంలో మళ్ళీ ఎన్నికలు నిర్వహించవలసిందిగా ఎన్నికల సంఘం ఆదేశించలేదు. – అప్రజాస్వామికం
పార్లమెంటులో మహిళల ప్రాతినిధ్యం ఏనాడూ 10 శాతం మించలేదు. ఈ కారణంగా పార్లమెంటులో మూడవ వంతు సీట్లు మహిళలకు కేటాయించాలని మహిళా సంఘాలు ఉద్యమం మొదలు పెట్టాయి. – ప్రజాస్వామికం
పార్లమెంటులో మహిళల ప్రాతినిధ్యం ఏనాడూ 10 శాతం మించలేదు. ఈ కారణంగా పార్లమెంటులో మూడవ వంతు సీట్లు మహిళలకు కేటాయించాలని మహిళా సంఘాలు ఉద్యమం మొదలు పెట్టలేదు. అసలు ఆ ప్రస్తావన కూడా తేలేదు. – అప్రజాస్వామికం
ప్రశ్న 8.
ప్రజాస్వామ్యానికి వ్యతిరేకంగా ఉన్న కింది వాదనలకు మీ ప్రతిస్పందన రాయండి : (AS4)
అ. దేశంలో అత్యంత క్రమశిక్షణ ఉండి, అవినీతిలేని వ్యవస్థ సైన్యం ఒక్కటే. కాబట్టి దేశాన్ని సైన్యం పరిపాలించాలి.
జవాబు:
సైన్యం పరిపాలిస్తే బాగుంటుంది కానీ ప్రజల సమస్యలు సైన్యానికి అంతగా తెలియవు. తెలిసిన వాటిని చేయాలి అనే దృఢ సంకల్పం సైన్యానికి ఉండకపోవచ్చు. కారణం. సైన్యం అనేది ఉద్యోగస్వామ్యం మాత్రమే. ప్రజాసమస్యలు ప్రజాస్వామ్యంలోనే చక్కగా పరిష్కరింపబడతాయి. కానీ నాయకులలో అవినీతి, బంధుప్రీతి, లంచగొండితనం వంటి అంశాలు లేకపోతే ప్రజాస్వామ్యంలో దేశం త్వరితగతిన అభివృద్ధి చెందడానికి అవకాశం ఉంటుంది. ప్రజాస్వామ్యంలో నాయకులు ప్రజలనుండి వస్తారు కాబట్టి ప్రజాసమస్యలు బాగా పరిష్కరింపబడతాయి.
ఆ. అధిక సంఖ్యాకుల పాలన అంటే ఏమీ తెలియని ప్రజల పాలన. తక్కువ సంఖ్యలో ఉన్నప్పటికీ మనకు కావలసింది విజ్ఞుల పాలన.
జవాబు:
అధిక సంఖ్యాకుల పాలన ఆంటే ప్రజలందరి పాలన. అనగా ప్రత్యక్ష ప్రజాస్వామ్యం. ప్రజలందరు ప్రభుత్వ కార్యకలాపాలలో భాగస్వాములు కావడం.
తక్కువ సంఖ్యలో ఉన్నప్పటికీ మనకి కావలసింది విజ్ఞుల పాలన. అనగా ప్రాతినిధ్య ప్రజాస్వామ్యం. ప్రజలు విజ్ఞులైన నాయకులను ఎన్నుకొని వారి ద్వారా పరిపాలింపబడడం. ఇలాంటి విధానం వలన సమయం ధనం ఆదా కావడానికి అవకాశం ఉంటుంది.
ఇ. ఆధ్యాత్మిక విషయాలలో మతగురువుల మార్గదర్శనం కోరుకున్నప్పుడు రాజకీయాల్లో కూడా మార్గదర్శనం చేయమని ఎందుకు అడగకూడదు? దేశాన్ని మతగురువులు పరిపాలించాలి.
జవాబు:
ఆధ్యాత్మిక విషయాలలో మత గురువులు. కానీ వారు రాజనీతిలో కాని రాజకీయాలలోకాని, సంక్షేమ పథకాల రూపకల్పనలో, కాని, వాటిని అమలు చేయడంలో కాని మత గురువులకు అవగాహన ఉండవలసిన అవసరం ఉండదు. కాబట్టి దాని పట్ల వారికి సరైన అవగాహన ఉండకపోవచ్చు. పైగా మత గురువులు మతపరమైన విషయాలపట్ల చూపించిన ప్రతిభ రాజకీయ, ప్రజాపాలన విషయాలలో చూపించకపోవచ్చును, మతం అనేది మత్తుమందు లాంటిది. రాజకీయాలు ఆ విధమైనవి కావు.
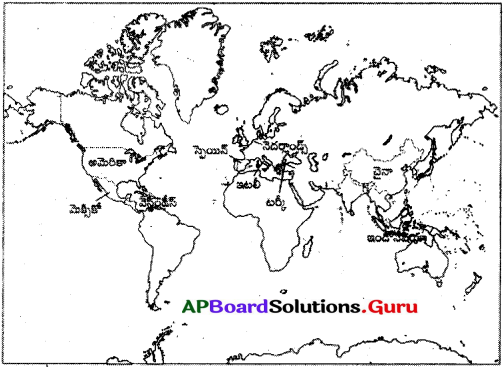
ప్రశ్న 9.
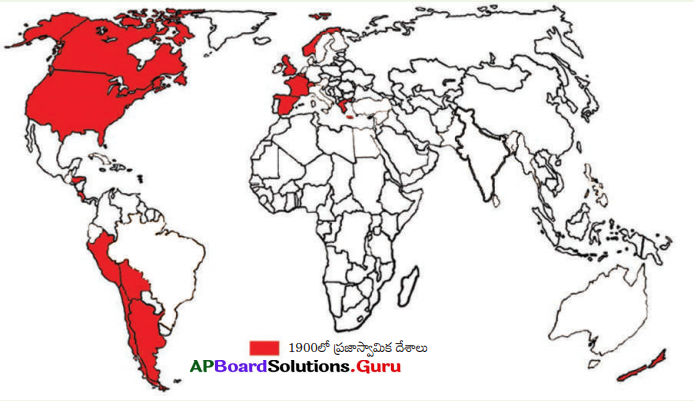
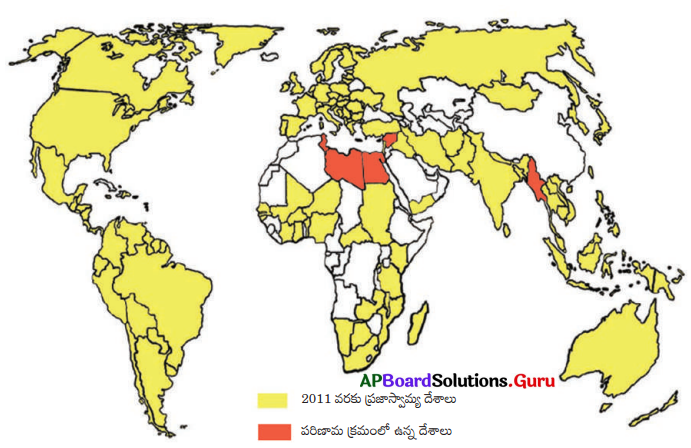
ప్రపంచ పటంలో ఈ క్రింది దేశాలను గుర్తించండి. (AS5)
అ) శ్రీలంక
ఆ) బెల్జియం
ఇ) రష్యా
ఈ) అమెరికా (యు.ఎస్.ఎ)
ప్రశ్న 10.
‘పౌరుల గౌరవం, స్వేచ్ఛ’ అనే శీర్షిక కింద గల మొదటి రెండు పేరాలు చదివి దిగువ ప్రశ్నకు సమాధానం ఇవ్వండి :
ప్రజాస్వామిక దేశంలో పౌరుల గౌరవం, స్వేచ్ఛ గురించి మీ సొంతమాటల్లో రాయండి. (AS2)
జవాబు:
వ్యక్తి గౌరవాన్ని, స్వేచ్ఛని కాపాడటంలో వివిధ రకాల ప్రభుత్వాలలో ప్రజాస్వామ్యం మెరుగైనది.
ప్రతి వ్యక్తికీ తోటి మానవుల నుంచి గౌరవం పొందాలని ఉంటుంది.
తనకు తగినంత మర్యాద ఇవ్వటం లేదని భావించినందువల్లనే తరచు వ్యక్తుల మధ్య ఘర్షణలు తలెత్తుతుంటాయి. • గౌరవం, స్వేచ్ఛల పట్ల నిబద్దతే ప్రజాస్వామ్యానికి పునాది. ప్రపంచ వ్యాప్తంగా ఈ విషయాన్ని కనీసం సూత్రబద్దంగానైనా ప్రజాస్వామిక దేశాలు గుర్తించాయి.
దీనిని వివిధ ప్రజాస్వామ్యాలలో వివిధ స్థాయిలలో సాధించారు. ఆధిపత్యం, పరాధీనత ఆధారంగా తరతరాలుగా నడిచిన సమాజాలలో అందరూ సమానం అని అంగీకరించటం అంత తేలికైన విషయం కాదు.
ప్రశ్న 11.
ప్రజలు ప్రజాస్వామ్యం కొరకు పోరాడడానికి గల కారణాలను తెల్పండి.
జవాబు:
తరతరాలుగా రాచరిక, నియంతృత్వ పరిపాలనపై ప్రజల గౌరవానికి, స్వేచ్ఛకు విలువ లేకుండా, ప్రజల భాగస్వామ్యంతో పరిపాలన కొనసాగించడంపై ప్రజలు ఎదిరించారు. పౌరుల హక్కులకు భంగం వాటిల్లినప్పుడు, బాధ్యత లేని పరిపాలన కొనసాగినప్పుడు ప్రజలు, రాచరిక పునాదులపై నడిచే ప్రభుత్వాలను, సైనిక పాలనలను సైతం ప్రజలు తిరస్కరించారు. సమానత్వ సూత్రంపై నడిచే, ప్రజల సంక్షేమం, ఉపాధి మెరుగుపరిచే ప్రజాస్వామ్యంపై ప్రజలు ఇష్టత చూపించారు. కుల ఆధారిత అసమానతలు, అత్యాచారాలు, వ్యక్తికి చట్టపర నైతిక విలువలు లేని పాలనను కాదని ప్రజాస్వామ్యం కావాలన్నారు.
![]()
ప్రశ్న 12.
మన పాఠశాలల్లో ప్రజాస్వామ్యం అమలు జరుగుతుందనడానికి కొన్ని ఉదాహరణలు ఇవ్వండి. (AS6)
జవాబు:
మన పాఠశాలల్లో ప్రజాస్వామ్యం జరుగుతుంది అనడానికి కొన్ని ఉదాహరణలు :
- మన పాఠశాలల్లో కులమతాలు, ధనిక, పేదాయని భేదం లేకుండా అందరికీ యూనిఫారమ్స్ ధారణ ద్వారా సమానత్వం లభిస్తుంది.
- అదేవిధంగా తరగతులు, ఆర్థిక స్తోమతతో సంబంధం లేకుండా అందరికీ మధ్యాహ్న భోజనం అందించబడుతుంది.
- అన్ని మతాల పండుగలకు ప్రాధాన్యతనిస్తూ ఆ రోజులలో సెలవును మంజూరు చేయడమే కాకుండా స్థానిక ప్రాంత పండుగలకు కూడా ప్రాధాన్యత ఇవ్వడం జరుగుతుంది.
- తరగతి నాయకుడి ఎన్నిక కూడా ప్రజాస్వామ్య పద్ధతిలో మెజార్టీ విద్యార్ధుల అభిప్రాయం మేరకు, ఎన్నిక ప్రకారం ఎంపిక చేయడం జరుగుతుంది.
- పేదవారికి, వెనుకబడిన వారికి ఆర్థికంగా చేయూత నందించుటకుగాను స్కాలర్ షిప్స్, ఆర్థిక పథకాలు అందించడం జరుగుతుంది.
9th Class Social Studies 20th Lesson ప్రజాస్వామ్యం – రూపుదిద్దుకుంటున్న భావన InText Questions and Answers
9th Class Social Textbook Page No.247
ప్రశ్న 1.
పరిపాలనలో భాగస్వాములు కావటం ప్రజలకు ఎందుకు ఇష్టం ఉండదు? సరైన అవగాహన లేకపోవటం వల్లనా, ఆసక్తి లేకనా, లేక తమ అభిప్రాయానికి విలువ ఉండదని భావించటం వల్లనా?
జవాబు:
- ప్రజాస్వామ్యం అంటే ప్రజలు కేవలం ఎన్నికల్లో పాల్గొని, పాలకులను ఎన్నుకోవటం మాత్రమే కాదు.
- ప్రభుత్వ విధానాలు, చట్టాలు తయారు చేయటంలో, వాటిని అమలు చేయటంలో కూడా ప్రజలు భాగస్వాములు కావాలి.
- ప్రజలందరూ బహిరంగంగా పాల్గొని తమ అవసరాలు, అభిప్రాయాలు స్పష్టంగా పేర్కొనేలా బహిరంగ చర్చలు జరిపిన తరువాత ,చట్టాలు, విధానాలు రూపొందించినప్పుడు ఇది సాధ్యమవుతుంది.
- స్వతంత్ర పౌర సంఘాలుగా ఏర్పడి చట్టాలు, విధానాలు సమర్థంగా అమలు అయ్యేలా చూడటంలో ప్రజలు భాగస్వాములు కావాలి.
- అనేక దేశాలలో ఎన్నికైనా ప్రభుత్వాలు కూడా ప్రజల భాగస్వామ్యాన్ని ప్రోత్సహించవు. పైగా దానిని అడ్డుకుంటాయి.
- ప్రజలు కూడా దేశ వ్యవహారాలలో అంత ఆసక్తి చూపకుండా ఉదాసీనంగా ఉండిపోతారు.
- కారణం ప్రజలందరికి పరిపాలన పట్ల అవగాహన లేకపోవడం, ఆసక్తి చూపకపోవడం.
- ఒకవేళ ఆసక్తి చూపినా పాలకులు వారి అభిప్రాయాలను పరిగణనలోనికి తీసుకోకపోవడం.
9th Class Social Textbook Page No.248
ప్రశ్న 2.
ప్రపంచంలో అనేక ప్రభుత్వాలు ప్రజలకు పౌరహక్కులను ఇచ్చాయి. అయితే ప్రజల ఫోనులను టాపింగ్ చేయటం, వాళ్ళ ఉత్తరాలు చదవటం, వాళ్ళ కార్యకలాపాలపై నిఘా ఉంచటం వంటి చర్యలు చేపడతాయి. ఇది సరైనదేనా?
జవాబు:
- ప్రజాస్వామ్యానికి పౌరహక్కులు ఉండాలి.
- తెలుసుకోటానికి, చర్చించటానికి, స్వతంత్ర అభిప్రాయాలు ఏర్పరచుకోటానికి, వాటిని వ్యక్తపరచటానికి సంఘాలుగా ఏర్పడి తమ భావాల అమలుకు పోరాడటానికి పౌరులకు స్వేచ్ఛ ఉన్నప్పుడే వాళ్ళు నిర్ణయాలు తీసుకోవటంలో భాగస్వాములు అవుతారు.
- అంతేకాని ప్రజల ఫోనులను టాపింగ్ చేయటం, వాళ్ళ ఉత్తరాలు చదవటం, వాళ్ల కార్యకలాపాలపై నిఘా ఉంచడం వంటి చర్యల వల్ల వాళ్ళ భావ ప్రకటన స్వేచ్ఛను హరించివేయడమే అవుతుంది.
- ప్రజాస్వామ్య వ్యవస్థలో ఇది సరైనదికాదు.
![]()
ప్రశ్న 3.
ప్రజాస్వామికంగా, ప్రజలందరి ప్రయోజనాల కోసం పనిచేసే ప్రభుత్వాలు ఉన్నప్పటికీ అనేక దేశాలలో తీవ్రస్థాయిలో అసమానతలు ఎందుకు కొనసాగుతున్నాయి?
జవాబు:
- అనేక దేశాల ప్రభుత్వాలు ధనికులకు అనుకూలంగా, పేదల ప్రయోజనాలకు విరుద్ధంగా ఉండే విధానాలను అనుసరిస్తూ ఉంటాయి.
- ప్రజాస్వామికంగా ప్రజలందరి ప్రయోజనాల కోసం పనిచేసే ప్రభుత్వాలు ఉన్నప్పటికీ అనేక దేశాలలో తీవ్ర స్థాయిలో అసమానతలు ఉండటానికి కారణాలు.
అ) తరతరాలుగా వస్తున్న వారసత్వపు సంపద.
ఆ) ఉన్నత వర్గాలకు చెందినవారు మంచి విద్య, ఉద్యోగావకాశాలు పొందడం.
ఇ) సంపద మరికొంత సంపదను సముపార్జించి పెట్టడం.
ఈ) ఉన్న వర్గాలకు చెందినవారు పారిశ్రామిక, వాణిజ్య వర్గాలపై ఆధిపత్యం చెలాయించడం.
ఉ) ఆలోచనా విధానాలలోనూ మార్పులు రావడం.
9th Class Social Textbook Page No.250
ప్రశ్న 4.
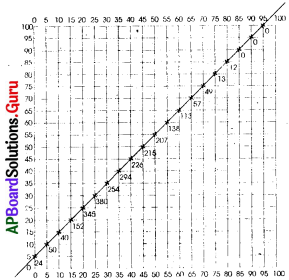
మన దేశంలోని ఎన్నికలను ఉదాహరణగా తీసుకుందాం. ఒక ప్రాంతంలో ఉంటున్న వాళ్ళలో 1000 మందికి ఓటు హక్కు ఉందని అనుకుందాం. సాధారణంగా ఎన్నికల్లో 60 శాతం ఓటర్లు మాత్రమే తమ ఓటు హక్కుని ఉపయోగించుకుంటారు. అంటే ఎన్నికల్లో 600 మంది ఓటు వేస్తారు. ఎన్నికల్లో 10 మంది అభ్యర్థులు పోటీ చేస్తున్నారని అనుకుందాం. గెలిచిన అభ్యర్థికి 250 ఓట్లు, రెండవ అభ్యర్థికి 200 ఓట్లు, మిగిలిన 8 మందికి కలిపి 150 ఓట్లు పడ్డాయని అనుకుందాం. 250 . ఓట్లు వచ్చిన వ్యక్తి గెలిచినట్లు ప్రకటిస్తారు. ఆ ప్రాంతంలో నివసిస్తున్న ప్రజల ప్రయోజనాలకు, దృక్పథాలకు గెలిచిన అభ్యర్థి ఏ మేరకు ప్రాతినిధ్యం వహిస్తారు? గెలిచిన అభ్యర్థికి ఓటర్లలో 25 శాతం మద్దతు మాత్రమే ఉంది. ఇది న్యాయమైన ప్రజాస్వామిక ఏర్పాటేనా? నిర్ణయాలు తీసుకునే సంస్థలకు ప్రజల ప్రతినిధులను ఎన్నుకోటానికి మరో విధానం ఏమైనా ఉందా?
జవాబు:
మన దేశంలోని ఎన్నికలను ఉదాహరణగా తీసుకుందాం. ఒక ప్రాంతంలో ఉంటున్న వాళ్ళలో 1000కి ఓటుహక్కు ఉందని అనుకుందాం. సాధారణంగా ఎన్నికల్లో 60 శాతం ఓటర్లు మాత్రమే తమ ఓటుహక్కుని ఉపయోగించుకుంటారు. అనగా ఎన్నికల్లో 600 మంది ఓటు వేస్తారు. అయితే ఎన్నికల్లో 10 మంది అభ్యర్థులు పోటీచేస్తున్నారని అనుకుందాం. గెలిచిన అభ్యర్థికి 250 ఓట్లు, రెండవ అభ్యర్థికి 200 ఓట్లు, మిగిలిన 8 మందికి కలిపి 150 ఓట్లు పడ్డాయని అనుకుందాం. కానీ 250 ఓట్లు వచ్చిన వ్యక్తి గెలిచినట్లు ప్రకటిస్తారు. అయితే అతను ఆ 250 మందికి మాత్రమే ప్రతినిధిగా కాకుండా ప్రజలందరికి ప్రతినిధిగా వ్యవహరిస్తాడు.
ప్రజలందరికి అభిప్రాయాలను తెలుసుకుంటాడు. ప్రజలందరికి ప్రాతినిధ్యం వహిస్తాడు. ప్రజలందరికి సంక్షేమ పథకాలను వర్తింపచేస్తాడు. ప్రజలందరికి అవసరాలు తీర్చటానికి కృషి చేస్తాడు. అందువల్ల ఇది న్యాయమైన ప్రజాస్వామిక వ్యవస్థగానే కొనసాగుతుంది. నిర్ణయాలు తీసుకునే సంస్థలకు ప్రజల ప్రతినిధులను ఎన్నుకోటానికి మరో విధానం.
- ప్రజలకు ఓటు చేసే హక్కుతో పాటు తిరస్కరించే అధికారం కూడా ఇవ్వాలి.
- ఎక్కువమంది ప్రజలు తిరస్కరించిన అభ్యర్థి గెలిచినట్లు ప్రకటించరాదు.
- అనుకూలమైన ఓట్లతో పాటు వ్యతిరేకమైన ఓట్లను కూడా పరిగణనలోనికి తీసుకోవాలి.
9th Class Social Textbook Page No.254
ప్రశ్న 5.
సామాజిక, మత, భాషాపర వైవిధ్యతలను కలుపుకుని వెళ్ళటానికి ఈ రెండు (బెల్జియం, శ్రీలంక) దేశాలు అనుసరించిన మార్గాలను చర్చించండి.
జవాబు:
బెల్జియం, శ్రీలంకలు రెండు ప్రజాస్వామిక దేశాలే అయినప్పటికీ రెండు దేశాలు అధికారాన్ని పంచుకోవటంలో భిన్నమైన మార్గాలు అవలంబించాయి.
1) బెల్జియం :
వివిధ ప్రాంతాల ప్రజల ప్రయోజనాలు, భావనలను మన్నించినపుడే దేశం ఐక్యంగా ఉంటుందని బెల్జియం నాయకులు గుర్తించారు. ఈ అవగాహన కారణంగా అధికారాన్ని పంచుకోటానికి అందరికీ ఆమోదయోగ్యమైన ఏర్పాట్లు చేసుకున్నారు.
2) శ్రీలంక :
అధిక సంఖ్యలో ఉన్న ప్రజలు అధికారాన్ని పంచుకోటానికి ఇష్టపడక తమ ఆధిపత్యాన్ని ఇతరులపై రుద్దాలని ప్రయత్నించినపుడు దేశ సమైక్యత దెబ్బ తింటుందని, అంతర్యుద్ధాలు, పౌర యుద్ధాల కారణంగా దేశం వందల సంవత్సరాలు వెనుకబడుతుందని శ్రీలంక నిరూపించింది.
ప్రాజెక్టు
ప్రశ్న 1.
మీ ఉపాధ్యాయుని సహాయంతో తరగతి ప్రతినిధిని ఎన్నుకోటానికి తరగతిలో ఎన్నికలు నిర్వహించండి.