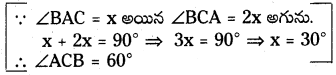Category: Class 9

SCERT AP 9th Class Maths Solutions Chapter 7 త్రిభుజాలు InText Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 7th Lesson త్రిభుజాలు InText Questions

ఇవి చేయండి

1. కింద కొన్ని ప్రవచనాలు ఇవ్వబడ్డాయి. అవి సత్యమో, కాదో సరిచూడుము. [పేజీ నెం. 15]
i) రెండు వృత్తములు ఎల్లప్పుడూ సర్వసమానము.
ii) ఒకే పొడవు కలిగిన రెండు రేఖాఖండములు ఎల్లప్పుడూ సర్వసమానము.
iii) రెండు లంబకోణ త్రిభుజములు కొన్నిసార్లు సర్వసమానము.
iv) భుజముల కొలతలు సమానముగాగల రెండు సమబాహు త్రిభుజములు ఎల్లప్పుడూ సర్వసమానము.
సాధన.
i) అసత్యము
ii) సత్యము
iii) సత్యము
iv) సత్యము

2. ఇచ్చిన పటములు సర్వసమానమో కాదో సరిచూచుటకు కావలసిన కనీస కొలతలు ఎన్ని ? [పేజీ నెం. 150]
i) రెండు దీర్ఘచతురస్రములు
సాధన.
పొడవు మరియు వెడల్పుల కొలతలు అవసరము.

ii) రెండు సమచతుర్భుజాలు
సాధన.
ఒక భుజము మరియు ఒక అంతర కోణము అవసరము.

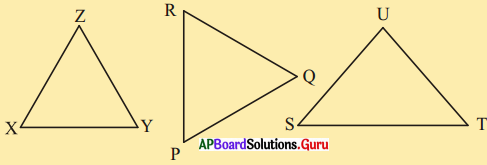
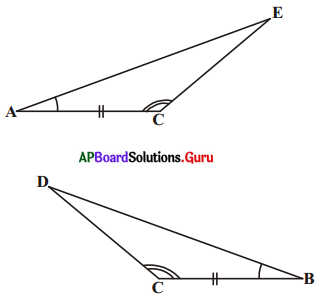
3. ఈ కింది త్రిభుజములు సర్వసమానములు అవునో కాదో తెలుపుము. దానికి కారణములను వివరించుము. [పేజీ నెం. 153]

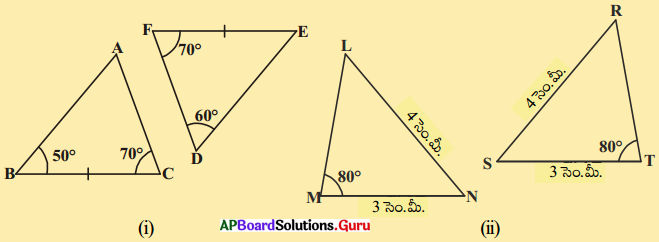
సాధన.
i) ΔABC, ΔDEF లలో
∴ ∠B = ∠E
(∵ త్రిభుజంలోని కోణాల మొత్తం ధర్మమును అనుసరించి ∠E = 180° – (70° + 60°) = 50°)
BC = EF
∠C = ∠F
∴ భు-కో-భు సర్వసమాన నియమం ప్రకారం,
ΔABC ≅ ΔDEF

ii) ΔMNL మరియు ΔTSR లలో
MN = ST
NL = RS
∠M = ∠T
భు-కో-భు సర్వసమాన నియమం ప్రకారం,
∴ ΔMNL ≅ ΔTSR

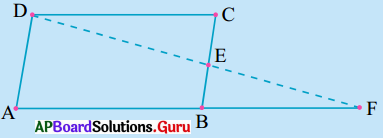
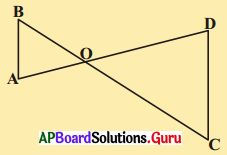
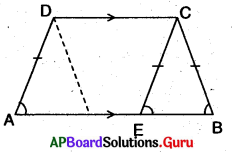
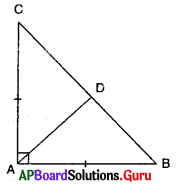
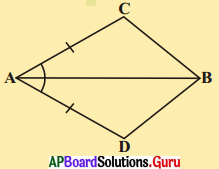
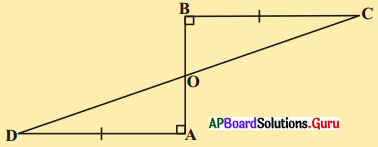
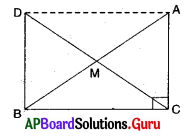
4. ఇచ్చిన పటంలో AB, DC రేఖాఖండములను Pబిందువు సమద్విఖండన చేసిన ΔAPC ≅ ΔBPD అని చూపుము.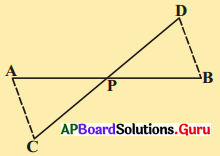
సాధన.
దత్తాంశం నుండి, AB, DC రేఖాఖండములను P బిందువు సమద్విఖండన చేయును.
ΔAPC మరియు ΔBPD లలో
AP = BP (∵ AB ను P సమద్విఖండన చేయును)
CP = DP (∵ CD ను P సమద్విఖండన చేయును)
∠APC = ∠BPD
ΔAPC ≅ ΔBPD (∵ భు.కో.భు. నియమం ప్రకారం)

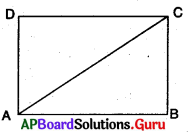
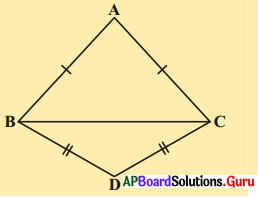
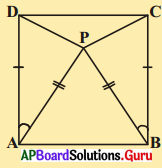
5. కింది పటంలో ΔABC మరియు ΔDBC లు \(\overline{\mathrm{AB}}\) = \(\overline{\mathrm{BD}}\) మరియు \(\overline{\mathrm{AC}}\) = \(\overline{\mathrm{CD}}\) అయ్యేటట్లున్న రెండు త్రిభుజములు అయిన ΔABC ≅ ΔDBC అని చూపండి. [పేజీ నెం. 164]

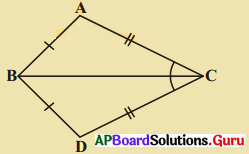
సాధన.
దత్తాంశము \(\overline{\mathrm{AB}}\) = \(\overline{\mathrm{BD}}\) మరియు \(\overline{\mathrm{AC}}\) = \(\overline{\mathrm{CD}}\)
ΔABC మరియు ΔDBC లలో
AB = BD (∵ దత్తాంశము)
AC = DC (∵ దత్తాంశము)
BC = BC (∵ ఉమ్మడి భుజము)
భు-భు-భు నియమము ప్రకారం
ΔABC ≅ ΔDBC

6. త్రిభుజము ABC గీసి వాటి భుజాల పొడవులు కొలవండి. దానిలో AB + BC, BC + AC మరియు AC + AB లను కనుగొని వాటి మూడు భుజాలతో పోల్చండి. మీరు ఏమి గమనిస్తారు ? ఈ కృత్యమును వివిధ త్రిభుజములను తీసుకుని చెయ్యండి. [పేజీ నెం. 171]
సాధన.

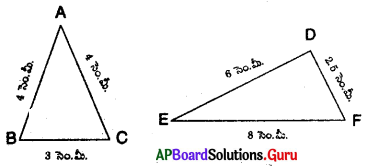
AB + BC = 4 + 3 = 7
⇒ 7 > 4 = AC
BC + CA > AB;
3 + 4 > 4
CA + AB > BC;
4 + 4 > 3

DE + EF > DF
EF + DF > DE
FD + DE > EF
∴ ఒక త్రిభుజములో ఏవైనా రెండు భుజాల పొడవుల మొత్తము మూడవ భుజము పొడవు కన్నా ఎక్కువ.

సిద్ధాంతాలు

1. (కో.భు.కో. సర్వసమానత్వ నియమము)
ఒక త్రిభుజములోని రెండు కోణములు, వాటి మధ్య భుజము వరుసగా వేరొక త్రిభుజములోని రెండు కోణములు, వాటి మధ్య భుజమునకు సమానమైన ఆ రెండు త్రిభుజములు సర్వసమానములు. [పేజీ నెం.154]
దత్తాంశము : ΔABC, ΔDEF లలో
∠B = ∠E, ∠C = ∠F మరియు \(\overline{\mathrm{BC}}=\overline{\mathrm{EF}}\)
సారాంశము : ΔABC ≅ ΔDEF
ఉపపత్తి : దీనికి మూడు సందర్భములున్నవి.
\(\overline{\mathrm{AD}}\) మరియు \(\overline{\mathrm{DE}}\) లకు సందర్భములు \(\overline{\mathrm{AB}}\) > \(\overline{\mathrm{DE}}\) లేదా \(\overline{\mathrm{DE}}\) > \(\overline{\mathrm{AB}}\) లేదా \(\overline{\mathrm{DE}}\) = \(\overline{\mathrm{AE}}\). మనము ఈ మూడు సందర్భములలో AABC, ADEF ల సంబంధాన్ని పరిశీలిద్దాం.
సందర్భం i : \(\overline{\mathrm{AD}}\) = \(\overline{\mathrm{DE}}\) అనుకొనుము. అయిన మనం ఏమి గమనింపవచ్చును ?
ΔABC, ΔDEF లను తీసుకొనుము.

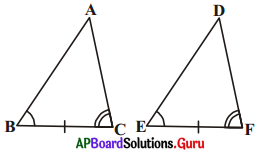
\(\overline{\mathrm{AB}}\) = \(\overline{\mathrm{DE}}\) (ఊహించినది)
∠B = ∠E (దత్తాంశము)
\(\overline{\mathrm{BC}}=\overline{\mathrm{EF}}\) (దత్తాంశము)
కావున ΔABC ≅ ΔDEF
(భు. కో.భు. సర్వసమాన స్వీకృతం నుండి)

సందర్భం (ii) : రెండవ సందర్భము AB > DE అనుకొనుము.
PB = DE అగునట్లు AB పై P బిందువును తీసుకొనుము.
ఇప్పుడు ΔPBC, ΔDEF

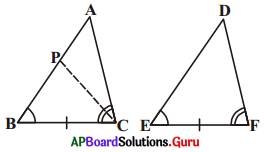
\(\overline{\mathrm{PB}}\) లేదా \(\overline{\mathrm{DE}}\) (నిర్మాణ ప్రకారం)
∠B = ∠E (దత్తాంశము)
\(\overline{\mathrm{BC}}=\overline{\mathrm{EF}}\) (దత్తాంశము)
కావున ΔPBC ≅ ΔDEF
(భు.కో. భు. సర్వసమాన స్వీకృతం)
త్రిభుజములు సర్వసమానము. కావున వాటి సదృశ భాగాలు సమానం.
కావున ∠PCB = ∠DFE
కాని ∠ACB = ∠DFE (దత్తాంశము)
అందువలన, ∠ACB = ∠PCB
(పై సమాచారం నుండి)
కాని, ఇది సాధ్యమా ?
ఇది సాధ్యమవ్వాలంటే P బిందువు Aతో ఏకీభవించాలి.
(లేదా) \(\overline{\mathrm{BA}}=\overline{\mathrm{ED}}\)
అప్పుడు ΔABC = ΔDEF
(భు.కో. భు. సర్వసమానత్వ స్వీకృతము నుండి)
(గమనిక : పై నిరూపణ నుండి మనం ∠B = ∠E, ∠C = ∠Fమరియు \(\overline{\mathrm{BC}}=\overline{\mathrm{EF}}\) అయిన \(\overline{\mathrm{AB}}=\overline{\mathrm{DE}}\) అవుతాయి. అయితే ఆ రెండు త్రిభుజాలు సర్వసమాన త్రిభుజాలు ).

సందర్భం (iii) : మూడవ సందర్భం \(\overline{\mathrm{AB}}\) < \(\overline{\mathrm{DE}}\)
ME = AB అగునట్లు ΔDEF లో DE పై M అనే బిందువును తీసుకొనుము. సందర్భం (ii) లో చెప్పిన వాదనను కొనసాగించిన \(\overline{\mathrm{AB}}\) = \(\overline{\mathrm{DE}}\) అని చెప్పవచ్చును. అప్పుడు. ΔABC ≅ ΔDEF. కింది పటములను పరిశీలించి దీనిని నీవు చేయుటకు ప్రయత్నించుము.

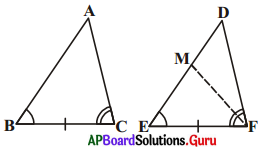
రెండు త్రిభుజములలో రెండు జతల కోణములు, ఒక జత భుజములు సమానము. ఇక్కడ ఆ భుజము సమానముగానున్న సదృశకోణాల జతల మధ్య భుజము కాదు. అయిననూ త్రిభుజములు సర్వసమానంగా ఉంటాయా? అవి రెండూ సర్వసమానంగా ఉంటాయని మీరు గమనించవచ్చును. ఎందుకో మీరు కారణము చెప్పగలరా ?
ఒక త్రిభుజములోని కోణములు మొత్తము 180°. రెండు జతల కోణాలు సమానమైన మూడవజత కోణాలు కూడా సమానమవుతాయి. (180° – సమాన కోణాల మొత్తము).
రెండు త్రిభుజములలో రెండు జతల కోణములు మరియు ఒక జత సదృశ భుజాలు సమానమైన ఆ రెండు త్రిభుజాలు సర్వసమాన త్రిభుజములు. దీనిని మనం కో.కో. భు. సర్వసమాన నియమం అంటాము.

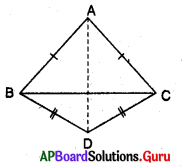
2. ఒక సమద్విబాహు త్రిభుజములో సమానభుజములకు ఎదురుగానున్న కోణములు సమానము. [పేజీ నెం. 159]

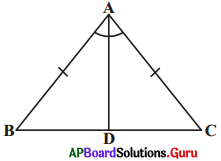
సాధన.
ఈ ఫలితాన్ని మనము అనేక పద్ధతులలో రుజువు చేయవచ్చును. ఇక్కడ ఆ నిరూపణలలో ఒకటి ఇవ్వబడినది.
దత్తాంశము : సమద్విబాహు త్రిభుజము ABC లో
AB = AC.
సారాంశము : ∠B = ∠C.
నిర్మాణము : ∠A యొక్క కోణసమద్విఖండన రేఖ గీయుము. ఇది భుజము BC ని D బిందువు వద్ద ఖండించును.
ఉపపతి : ΔBAD మరియు ΔCAD లలో
AB = AC (దత్తాంశము)
∠BAD = ∠CAD (నిర్మాణం ప్రకారం)
AD = AD (ఉమ్మడి భుజం)
కావున ΔBAD ≅ ΔCAD
(భు.కో. భు. సర్వసమానత్వ స్వీకృతం)
అందువలన ∠ABD = ∠ACD
(సర్వసమాన త్రిభుజ సదృశ భుజాలు సమానం)
అనగా ∠B = ∠C (సమాన కోణాలు)

3. ఒక త్రిభుజములో సమాన కోణాలకు ఎదురుగా ఉండే భుజాలు సమానము. [పేజీ నెం. 160]
సాధన.
దీనిని మీరు ఇంతకు ముందు మనం చెప్పుకున్న సిద్ధాంతానికి విపర్యయము. కో. భు. కో. సర్వసమానత్వ నియమాన్ని ఉపయోగించి రుజువు చేయండి.

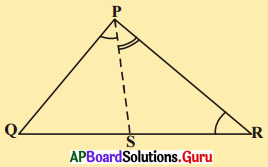
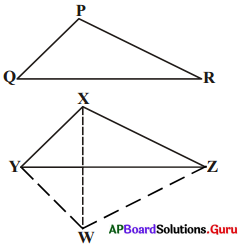
4. (భు. భు.భు. సర్వసమానత్వ నియమం) : నిర్మాణముల ద్వారా భు.భు. భు సర్వసమానత్వ నియమము వర్తిస్తుంది. భు.భు. భు సర్వసమానత్వ నియమం నిరూపణ : [పేజీ నెం. 163]
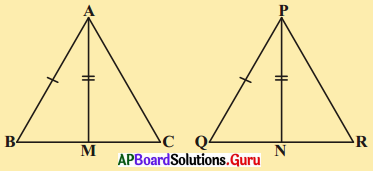
దత్తాంశము : ΔPQR మరియు ΔXYZ లలో
PQ = XY, QR = YZ మరియు PR = XZ.
సారాంశము : ΔPQR ≅ ΔXYZ
నిర్మాణము : ∠ZYW = ∠PQR మరియు WY = PQ అగునట్లు.YWని గీయుము. XW మరియు WZలను కలుపుము.
ఉపపత్తి : ΔPQR మరియు ΔWYZ లలో
QR = YZ (దత్తాంశము)
∠PQR = ∠ZYW (నిర్మాణం)
PQ = YW (నిర్మాణం)
∴ ΔPQR ≅ ΔXYZ
(భు.కో. భు. సర్వసమానత్వ స్వీకృతం)

⇒ ∠P = ∠W మరియు PR = WZ
(సర్వసమాన త్రిభుజాల సదృశ భాగాలు)
PQ = X (దత్తాంశము) మరియు
PQ = YW (నిర్మాణం)
∴ XY = YW
అదేవిధంగా, XY = YW
ΔXYW లలో XY = YW
⇒ ∠YWX = ∠YXW
(ఒక త్రిభుజంలో సమాన భుజాలకు ఎదురుగా ఉన్న కోణాలు సమానంగా ఉంటాయి.)
ఇదేవిధంగా, ∠ZWX = ∠ZXW
∴ ∠YWX + ∠ZWX = ∠YXW + ∠ZXW
⇒ ∠W = ∠X
ఇప్పుడు, ∠W = ∠P
∴ ∠P = ∠X
ΔPQR మరియు ΔXYZ లలో
PQ = XY
∠P = ∠X
PR = XZ
∴ ΔPQR ≅ ΔXYZ
(భు.కో. భు. సర్వసమానత్వ స్వీకృతం)

5. (లం.క.భు. సర్వసమానత్వ నియమం) :
రెండు లంబకోణ త్రిభుజములలో ఒక త్రిభుజములోని కర్ణము, భుజములు వరుసగా రెండవ త్రిభుజములోని కర్ణము, భుజములకు సమానమైన ఆ రెండు త్రిభుజములు సర్వసమాన త్రిభుజములు.
లం.క.భు. అనగా లంబకోణము – కర్ణము – భుజము.
ఇప్పుడు నిరూపణ చేద్దాం. [పేజీ నెం. 165]
దత్తాంశము : రెండు లంబకోణ త్రిభుజములు ΔABC మరియు ΔDEF లలో
∠B = 90° మరియు
∠E = 90°, AC = DF
మరియు BC = EF.
సారాంశము : ΔABC ≅ ΔDEF
నిర్మాణము : EG = AB అగునట్లు DE ని G వద్దకు పొడిగించండి. G, F లను కలపండి.

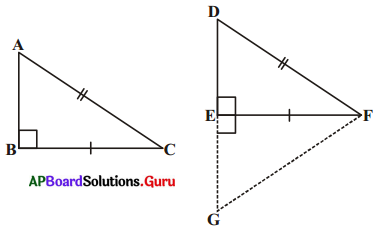
ఉపపత్తి : ΔABC మరియు ΔGEF లలో
AB = GE (నిర్మాణం ప్రకారం)
∠B = ∠FEG (ప్రతి కోణము లంబకోణము (90°))
BC = EF (దత్తాంశము)
ΔABC ≅ ΔGEF
(భు.కో. భు. సర్వసమానత్వ స్వీకృతం)
కావున ∠A = ∠G ……….. (1)
(సర్వసమాన త్రిభుజాల సదృశ కోణాలు)
AC = GF ……….. (2)
(సర్వసమాన త్రిభుజాల సదృశ కోణాలు)
ఇంకా AC = GF మరియు AC = DF
((2) మరియు దత్తాంశం)
∴ DF = GF (పై వాటి నుండి)
కావున ∠D = ∠G …… (3)
(సమాన భుజాల కెదురుగానున్న కోణాలు సమానం)
మరల ∠A = ∠D …… (4) ((1), (3) ల నుండీ)
ΔABC, ΔDEF లలో ∠A = ∠D ((4) నుండి)
∠B = ∠E (దత్తాంశము)
కావున ∠A + ∠B = ∠D + ∠E (కలుపగా)
కాని ∠A + ∠B + ∠C = 180°మరియు
(త్రిభుజకోణాల మొత్తం ధర్మం)
∠D + ∠E + ∠F = 180°
(త్రిభుజకోణాల మొత్తం ధర్మం)
180 – ∠C = 180 – ∠F
(∠A + ∠B 180° – ∠C మరియు ∠D + ∠F = 180° – ∠F)
కావున ∠C = ∠F ………. (5)
(కొట్టివేత నియమాల ప్రకారం)
ఇప్పుడు ΔABC, ΔDEF లలో
BC = EF (దత్తాంశం)
∠C = ∠F ((5) నుండి)
AC = DF (దత్తాంశం)
ΔABC ≅ ΔDER
(భు.కో.భు. సర్వసమానత్వ స్వీకృతం)

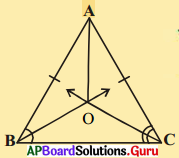
6. ఒక త్రిభుజములో రెండు భుజములు అసమానముగా నున్న పెద్ద భుజానికి ఎదురుగానున్న కోణము పెద్దది.

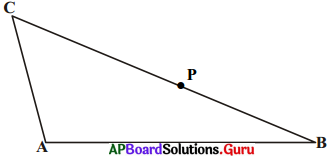
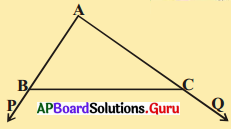
పటములో చూపినట్లు CA = CP అయ్యే విధంగా BC పై P బిందువును తీసుకొని ఈ సిద్ధాంతమును రుజువు చేయవచ్చును. [పేజీ నెం.170]

7. ఒక త్రిభుజములో పెద్ద కోణానికి ఎదురుగానున్న భుజము పొడవైనది.
ఈ సిద్ధాంతమును మనం విరోధాభాస పద్ధతి ద్వారా నిరూపించవచ్చు. [పేజీ నెం. 171]

8. ఒక త్రిభుజములో ఏవైనా రెండు భుజాల పొడవుల మొత్తము మూడవ భుజము పొడవుకన్నా ఎక్కువ.
కింది పటంలో ΔABC లో AD = AC అగునట్లు భుజము BA బిందువు D వద్దకు పొడిగించబడినది. ∠BCD > ∠BDC అని BA + AC > BC ? అని మీరు చూపించగలరా ?

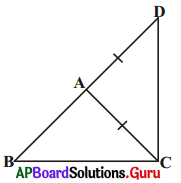
పై సిద్ధాంతమునకు నిరూపణను రాబట్టగలరా ? [పేజీ నెం. 171]

కృత్యం

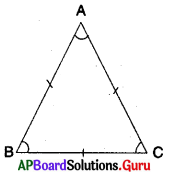
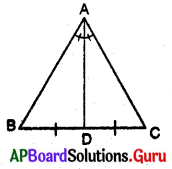
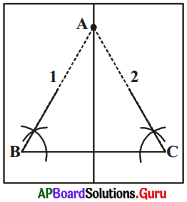
1. i) వృత్తలేఖిని ఉపయోగించి త్రిభుజమును నిర్మించుటకు, ఏదేని కొంత కొలతతో రేఖాఖండము AB ని గీయుము. వృత్తలేఖిని తీసుకొని దానికి సరిపడినంత’ కొలత తీసుకొని బిందువులు A, B ల వద్ద ఉంచి చాపములు గీయుము. అప్పుడు మీకు ఏ రకమైన త్రిభుజము ఏర్పడుతుంది ? అపుడు ఏర్పడినది ఒక సమద్విబాహు త్రిభుజము. అందువలన పటంలోని ΔABC, AC = BC కలిగిన ఒక సమద్విబాహు త్రిభుజము. ఇప్పుడు కోణములు ∠A, ∠B ల విలువలను కొలవండి. మీరు ఏమి గమనిస్తారు ? [పేజీ నెం. 159]

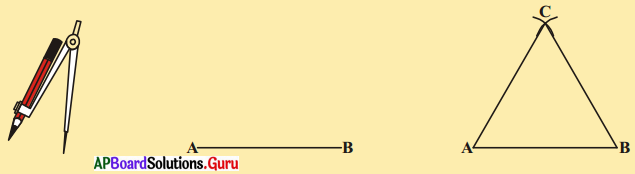
ii) ఒక సమద్విబాహు త్రిభుజమును కత్తిరించుము.
సర్వసమాన భాగములు ఒకదానిపై ఒకటి ఏకీభవించునట్లు ఆ త్రిభుజమును మడవండి. ∠A, ∠B ల గురించి మీరు ఏమి గమనించారు ?
అటువంటి ప్రతీ త్రిభుజములో, సమాన భుజములకు ఎదురుగా ఉండే కోణములు సమానంగా ఉండడాన్ని మీరు గమనిస్తారు.

2.

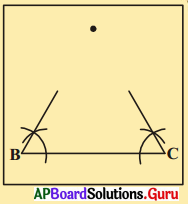
1. ఒక ఉల్లి పొర కాగితంపై 6 సెం.మీ. పొడవుగల రేఖాఖండము BC ని గీయండి.
2. B మరియు C బిందువుల వద్ద నుండి 60° కోణము చేయునట్లు రెండు కిరణములను గీయండి. వాటి ఖండన బిందువునకు, A అని పేరు పెట్టండి.
3. B, C బిందువులు ఒకదానిపై ఒకటి ఏకీభవించునట్లు కాగితాన్ని మడత పెట్టండి. మీరు ఏమి గమనిస్తారు ? AB, AC లు సమానంగా ఉన్నాయా ? [పేజీ నెం. 160]

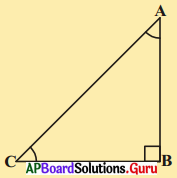
3. కర్ణము 5 సెం.మీ. .మరియు ఒక భుజము కొలత 3 సెం.మీ. ఉండేటట్లు ఒక లంబకోణ త్రిభుజాన్ని నిర్మించండి. ఇటువంటి ఎన్ని వేర్వేరు త్రిభుజాలను మీరు నిర్మించగలరు ? మీరు నిర్మించిన త్రిభుజాన్ని మీ తరగతిలోని, ఇతర విద్యార్థుల త్రిభుజాలతో పోల్చి చూడండి. ఈ త్రిభుజాలు సర్వసమాన త్రిభుజాలు అవుతాయా? ఈ త్రిభుజాలను కత్తిరించి సమానభుజాలు ఒకదానిపై ఒకటి ఉంటేటట్లు అమర్చండి. అవసరమైతే త్రిభుజాలను తిప్పండి. మీరు ఏమి పరిశీలిస్తారు ? రెండు లంబకోణ త్రిభుజాలు సర్వ సమానమని మీరు గమనిస్తారు. రెండు లంబకోణ త్రిభుజములలో ఒక త్రిభుజము లంబకోణంలోని కర్ణము, భుజము వరుసగా రెండవ త్రిభుజంలోని కర్ణము, భుజములకు సమానం. [పేజీ నెం. 165]

4. ABC త్రిభుజాన్ని గీసి CA ని A’ బిందువు’ వరకు పొడిగించండి. (కొత్త స్థానం)
కావున A’C > AC (పొడవులను పోల్చిన)
A’, B లను కలిపి త్రిభుజము A’BC ని ఏర్పరచండి. ఇప్పుడు మీరు ∠A’BC మరియు ∠ABC గురించి ఏమి చెప్పగలరు ?
ఆ రెండు కోణములను పోల్చండి. మీరు ఏమి గమనించారు ?
స్పష్టంగా, ∠A’BC > ∠ABC

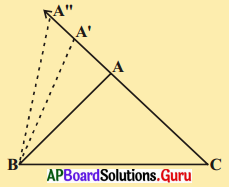
ఇదే విధంగా CA ను పొడిగించి దానిపై అనేక బిందువులను గుర్తించండి. BC భుజంగా గుర్తించిన బిందువులను కలుపుతూ త్రిభుజాలను గీయండి. భుజం AC పొడవు పెరుగుతున్నప్పుడు (బిందువు Aకు వివిధ స్థానాలు తీసుకొంటున్నప్పుడు) దానికి ఎదురుగానున్న కోణము అనగా ∠B కూడా పెరుగుతుంది. [పేజీ నెం. 169]

5. ఒక విషమబాహు త్రిభుజాన్ని నిర్మించుము. (ఒక త్రిభుజములో మూడు భుజాల పొడవులు వేర్వేరుగా ఉంటాయి.) భుజాల పొడవులను కొలవండి.

కోణాలను కొలవండి. మీరు ఏమి గమనించారు ?
ΔABC పటంలో BC ఎక్కువ పొడవుగల భుజం మరియు AC తక్కువ పొడవుగల భుజం. అదేవిధంగా ∠A పెద్దకోణం మరియు ∠B చిన్నకోణం.
కింద ఇచ్చిన త్రిభుజాలలో ప్రతి త్రిభుజానికి భుజాలు మరియు కోణాలను కొలవండి. భుజాన్ని దాని ఎదురుగా ఉండే కోణాన్ని వేరొక జతతో పోల్చినప్పుడు వాటి మధ్య ఏ సంబంధాన్ని మీరు గమనిస్తారు ? [పేజీ నెం. 169]

6. AB రేఖాఖండమును గీయుము. A కేంద్రంగా కొంత వ్యాసార్ధముతో చాపమును గీసి దానిపై వేర్వేరు బిందువులు P, Q, R, S, T లను గుర్తించుము

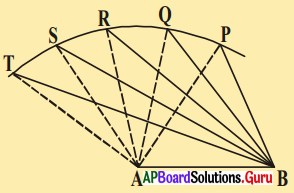
ఈ బిందువులన్నింటిని A, B బిందువులతో కలుపుము (పటం చూడండి). మనం P బిందువు నుండి T బిందువువైపు కదులుతున్నప్పుడు LA క్రమంగా పెద్దదవుతుంది. దానికి ఎదురుగా ఉండే భుజం కొలత ఎలా ఉంటుంది ? దాని ఎదురుగా ఉండే భుజం కొలత కూడా పెరుగుతూ ఉండడాన్ని గమనించవచ్చును.
అనగా ∠TAB > ∠SAB > ∠RAB > ∠QAB > ∠PAB మరియు TB > SB > RB > QB > PB.
ఇప్పుడు వేరువేరు కోణముల కొలతలు గల ఒక త్రిభుజమును గీయుము. భుజాల పొడవులను కొలుచుము. (పటం చూడండి.).

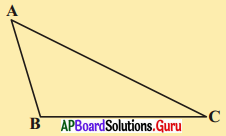
పెద్ద కోణానికి ఎదురుగావున్న భుజము పొడవుగా ఉండడాన్ని గమనించవచ్చును. పటంలో, పెద్ద కోణము ∠B మరియు దాని ఎదురుగానున్న పొడవైన భుజము AC.
ఈ కృత్యమును వివిధ త్రిభుజములతో చేయుము. పై సిద్ధాంతము విపర్యయము సత్యమని గ్రహిస్తాము.
కింద ఇవ్వబడిన ప్రతి త్రిభుజం యొక్క కోణాలను, భుజాల పొడవులను కొలవండి. ప్రతి త్రిభుజంలోని ఒక్కొక్క భుజమునకు మరియు వాటి ఎదురుగానున్న కోణాలకు మధ్యగల సంబంధం ఏమై ఉంటుందనుకొంటున్నారు ?

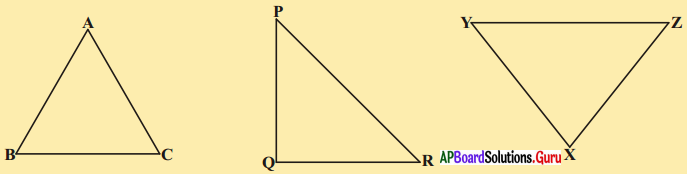
ఈ విధంగా మనకు కింది సిద్ధాంతము వస్తుంది. [పేజీ నెం. 170]

ఉదాహరణలు

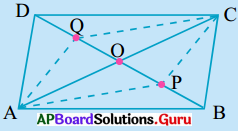
1. ఇచ్చిన పటంలో AB మరియు CD లు ‘O’ వద్ద ఖండించుకొనుచున్నాయి. OA = OB మరియు OD = OC అయిన
(i) ΔAOD = ΔBOC మరియు
(ii) AD || BC అని నిరూపించండి. [పేజీ నెం. 152]

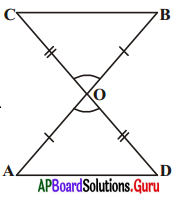
సాధన.
i) ΔAOD, ΔBOC లలో
OA = OB (దత్తాంశము)
OD = OC (దత్తాంశము)
∠AOD, ∠BOC లు ఒక జత శీర్షాభిముఖ కోణములను ఏర్పరచును.
అందువలన ∠AOD = ∠BOC.
కావున ΔAOD ≅ ΔBOC
(భు. కో. భు. సర్వసమానత్వ నియమం ప్రకారం)

ii) AOD, BOC సర్వసమానత్వ త్రిభుజాలలో సదృశభాగాలు సమానము.
కావున ∠OAD = ∠OBC మరియు ఇవి AD, BC రేఖాఖండములకు ఒక జత ఏకాంతర కోణములను ఏర్పరచును.
∴ AD || BC

2. AB ఒక రేఖాఖండము సరళరేఖ l దీనికి లంబ సమద్విఖండనరేఖ. ఈ రేఖపై P ఒక బిందువు అయిన ఈ P బిందువు A, B బిందువుల నుండి సమాన దూరంలో ఉంటుందని చూపుము. [పేజీ నెం. 153]
సాధన.
l ⊥ AB మరియు ఈ రేఖ l, రేఖాఖండము AB మధ్యబిందువు C గుండాపోవును.
మనము PA = PB అని చూపాలి.

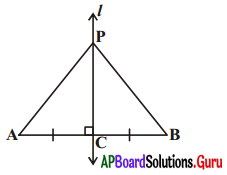
ΔPCA మరియు ΔPCB లను తీసుకొనుము.
AC = BC (AB నకు C మధ్యబిందువు)
∠PCA = ∠PCB = 90° (దత్తాంశము)
PC = PC (ఉమ్మడి బిందువు)
కావున, ΔPCA ≅ ΔPCB (భు. కో. భు. నియమం)
అందువలన PA = PB (సర్వసమాన త్రిభుజాల సదృశ భుజాలు కావున)

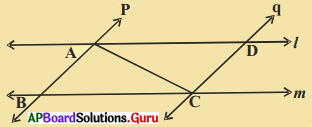
3. ఇచ్చిన పటంలో AB || DC మరియు AD || BC అయిన ΔABC ≅ ΔCDA అని చూపుము. [పేజీ నెం. 155]

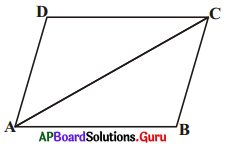
సాధన.
ΔABC, ΔCDA లను తీసుకొనుము.
∠BAC = ∠DCA (ఏకాంతర కోణములు)
AC = CA (ఉమ్మడి భుజం)
∠BCA = ∠DAC (ఏకాంతర కోణములు)
ΔABC ≅ ΔCDA
(కో.భు.కో. సర్వసమానత్వం ప్రకారం)

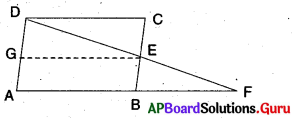
4. ఇచ్చిన పటంలో AL || DC, BC మధ్య బిందువు E అయిన ΔEBL ≅ ΔECD అని చూపండి. [పేజీ నెం. 156]

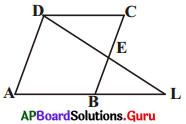
సాధన.
ΔEBL మరియు ΔECD లలో
∠BEL = ∠CED (శీర్షాభిముఖ కోణాలు)
BE = CE (BC మధ్య బిందువు E కావున)
∠EBL = ∠ECD (ఏకాంతర కోణములు)
ΔEBL ≅ ΔECD (కో.భు. కో. సర్వసమానత్వం)

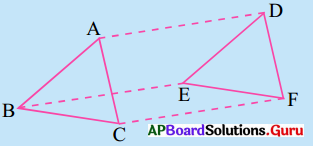
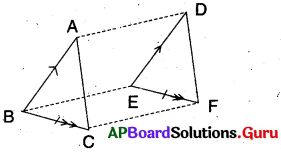
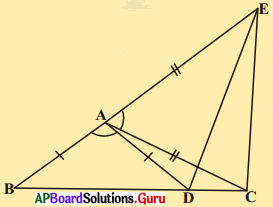
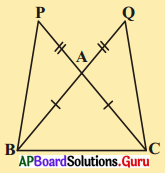
5. కింది పటంలోని సమాచారమును ఉపయోగించుకొని (i) ΔDBC ≅ ΔEAC (ii) DC = EC అని రుజువు చేయుము. [పేజీ నెం.156]

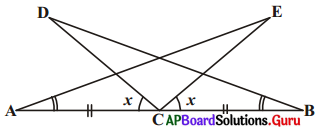
సాధన.
∠ACD = ∠BCE = x అనుకొనుము.
∠ACE = ∠DCE + ∠ACD
= ∠DCE + x ……… (i)
∴ ∠BCD = ∠DCE + ∠BCE
= ∠DCE + x …… (ii)
(i), (ii) ల నుండి, ∠ACE = ∠BCD
ΔDBC మరియు ΔEAC లలో

∠ACE = ∠BCD (పైన నిరూపించబడినది)
BC = AC (దత్తాంశము)
∠CBD = ∠EAC (దత్తాంశము)
ΔDBC ≅ ΔEAC (కో. భు.కో. ప్రకారం)
ΔDBC ≅ ΔEAC కావున
DC = EC
(సర్వసమాన త్రిభుజాల సదృశభుజాలు సమానం)

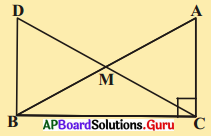
6. AB, CD లు సమాంతరాలు. AD మధ్య బిందువు O అయిన (i) ΔAOB ≅ ΔDOC (ii) BC కూడా మధ్య బిందువు O అని నిరూపించుము. [పేజీ నెం. 156]

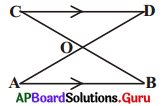
సాధన.
i) ΔAOB మరియు ΔDOC లలో
∠ABO = ∠DCO
(AB || CD, BC తిర్యగ్రేఖ ఏకాంతర కోణాలు)
∠AOB = ∠DOC (శీర్షాభిముఖ కోణాలు)
OA = OD (దత్తాంశము)
∴ ΔAOB ≅ ΔDOC (కో.కో.భు. నియమం ప్రకారం)

ii) OB = OC
(సర్వసమాన త్రిభుజాల సదృశభుజాలు సమానం)
కావున BC మధ్య బిందువు O.

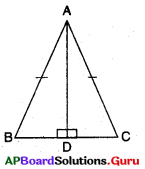
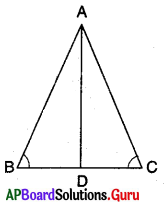
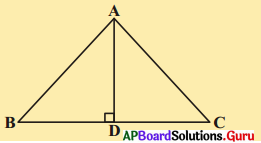
7. ΔABC లో ∠A యొక్క కోణసమద్విఖండనరేఖ AD, BC భుజానికి లంబంగానున్నది. అయిన AB = AC అని ΔABC సమద్విబాహు త్రిభుజమని చూపండి. [పేజీ నెం. 160]

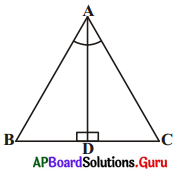
సాధన.
ΔABD మరియు ΔACD లో
∠BAD = ∠CAD (దత్తాంశము)
AD = AD (ఉమ్మడి భుజం)
∠ADB = ∠ADC = 90° (దత్తాంశము)
కావున ΔABD ≅ ΔACD (కో.భు.కో. నియమం)
దాని వలన AB = AC
(సర్వసమాన త్రిభుజాల సదృశ భుజాలు)
లేదా ΔABC సమద్విబాహు త్రిభుజము.

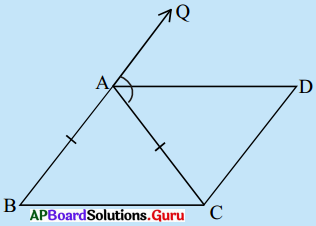
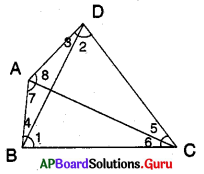
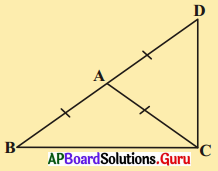
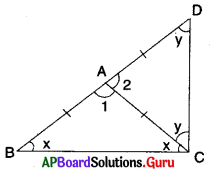
8. ఇచ్చిన పటంలో AB = BC మరియు AC = CD. అయిన ∠BAD = ∠ADB = 3 : 1 అని చూపండి. [పేజీ నెం. 160]

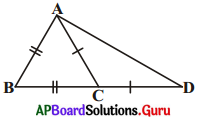
సాదన.

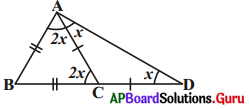
∠ADB = x అనుకొసుము.
∠ACD లో AC = CD
⇒ ∠CAD = ∠CDA = x
మరియు బాహ్యకోణం ∠ACB = ∠CAD + ∠CDA
= x + x = 2x
⇒ ∠BAC = ∠ACB = 2x.
(∵ ΔABC లో, AB = BC)
∴ ∠BAD = ∠BAC + ∠CAD
= 2x + x = 3x
మరియు \(\frac{\angle \mathrm{BAD}}{\angle \mathrm{ADB}}=\frac{3 \mathrm{x}}{\mathrm{x}}=\frac{3}{1}\)
అనగా ∠BAD : ∠ADB = 3 : 1.
అందుచేత ఇది నిరూపించబడినది.

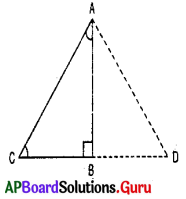
9. ఇచ్చిన పటంలో AD అనేది BC మరియు EF లు రెండింటికీ లంబము. ఇంకా ∠EAB = ∠FAC, అయిన ΔABD మరియు ΔACD లు సర్వ సమానమని చూపుము.
ఇంకా AB = 2x + 3, AC = 3y + 1, BD = x మరియు DC = y + 1 అయిన x, y విలువలు కనుగొనండి. [పేజీ నెం. 161]

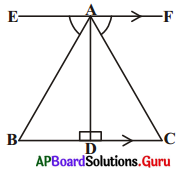
సాధన.
AD ⊥ EF
⇒ ∠EAD = ∠FAD = 90°
∠EAB = ∠FAC (దత్తాంశము)
⇒∠EAD – ∠EAB = ∠FAD – ∠FAC
⇒ ∠BAD = ∠CAD
ΔABD మరియు ΔACD లలో
∠BAD = ∠CAD (పైన నిరూపించబడినది)
∠ADB = ∠ADC = 90° [AD ⊥ BC దత్తాంశము]
మరియు AD = AD
∴ ΔABD ≅ ΔACD (కో.భు.కో. నియమం)
ఇది నిరూపించబడినది.
∠ABD = ∠ACD
⇒ AB = AC మరియు BD = CD
(సర్వసమాన త్రిభుజాల సదృశభాగాలు)
⇒ 2x + 3 = 3y + 1 మరియు x = y + 1
⇒ 2x + 3y = – 2 మరియు x – y = 1
సమీకరణాలను సాధించగా 2(1 + y) – 3y = -2
x = 1+ y
2 + 2y – 3y = -2
– y = – 2 – 2
– y = -4
సమీకరణాలు సాధించగా y = 4 లో
x = 1 + y
x = 1 + 4
x = 5

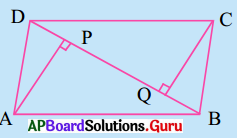
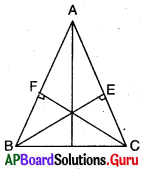
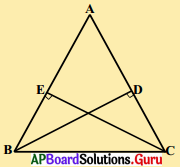
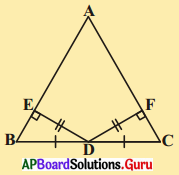
10. ΔABC లో సమాన భుజాలు AB, AC ల మధ్యబిందువులు వరుసగా E మరియు F (పటాన్ని చూడుము), BF = CE అని చూపండి. [పేజీ నెం. 162]

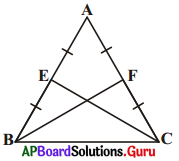
సాధన.
ΔABF మరియు ΔACE లలో
AB = AC (దత్తాంశము)
∠A = ∠A (ఉమ్మడి కోణము)
AF = AE (సమానభుజాలలో సగాలు)
కావున ΔABF ≅ ΔACE (భు.కో.భు. నియమం)
∴ BF = CE
(సర్వసమాన త్రిభుజాలలోని సదృశ భుజాలు సమానం)

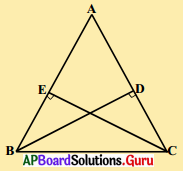
11. ఒక సమద్విబాహు త్రిభుజము ABC లో AB = AC, D మరియు E బిందువులు BC పై BE = CD అయ్యేటట్లున్న బిందువులు (పటాన్ని చూడండి) అయిన AD = AE అని చూపండి. [పేజీ నెం. 162]

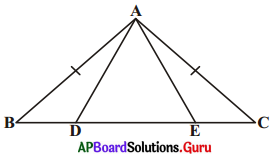
సాధన.
ΔABD మరియు ΔACE లలో
AB = AC (దత్తాంశము) ………… (1)
∠B = ∠C (సమాన భుజాలకు ఎదురుగానున్న సమాన కోణాలు) …….(2)
ఇంకా BE = CD
కావున BE – DE = CD – DE
అనగా BD = CE …………. (3)
కావున ΔABD ≅ ΔACE
((1), (2), (3) ల నుండి మరియు భు.కో.భు. నియమం).
దీని నుండి AD = AE
(సర్వసమాన త్రిభుజాల సదృశ భుజాలు)

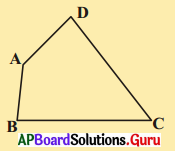
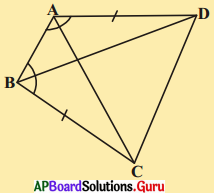
12. ABCD చతుర్భుజములో AB = CD, BC = AD అయిన ΔABC ≅ ΔCDA అని నిరూపించండి. [పేజీ నెం. 164]

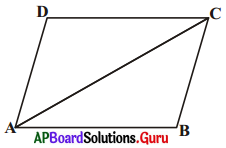
సాధన.
ΔABC మరియు ΔCDA లలో
AB = CD (దత్తాంశము)
AD = BC (దత్తాంశము)
AC = CA (ఉమ్మడి భుజం)
ΔABC ≅ ΔCDA
(భు.భు.భు. సర్వసమానత్వ నియమం)

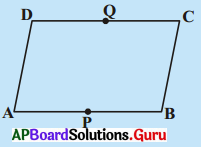
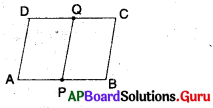
13. AB ఒక రేఖాఖండము. P మరియు Q అనే బిందువులు ABకి రెండు వైపులలో A, Bలకు సమానదూరంలో ఉన్నాయి. (పటాన్ని చూడండి) అయిన PQ రేఖ ABకి లంబసమద్విఖండనరేఖ అని చూపండి. [పేజీ నెం. 166]
సాధన.
PA = PB మరియు QA = QB అని ఇవ్వబడినది.
మీరు PQ, AB కి లంబమని మరియు దానిని సమద్విఖండన చేస్తుందని చూపాలి. PQ, AB ని C బిందువు వద్ద ఖండించుననుకొనుము.
ఈ పటంలో రెండు సర్వసమాన త్రిభుజాల గురించి మీరు ఆలోచించగలరా ?

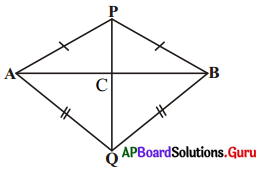
ΔPAQ మరియు ΔPBQ తీసుకోండి.
ఈ త్రిభుజములలో
AP = BP (దత్తాంశము)
AQ = BQ (దత్తాంశము)
PQ = PQ (ఉమ్మడి భుజం)
కావున ΔPAQ ≅ ΔPBQ
(భు. భు. భు. సర్వసమానత్వ నియమం)
∴ ∠APQ = ∠BPQ
(సర్వసమాన త్రిభుజాల సదృశ కోణాలు).
ΔPAC మరియు ΔPBC లలో
AP = BP (దత్తాంశము)
∠APC = ∠BPC
(∠APQ = ∠BPQ పైన నిరూపించబడినది)
PC = PC (ఉమ్మడి భుజం)
కావున ΔPAC ≅ ΔPBC (భు. కో.భు. నియమం)
AC = BC ……….. (1)
(సర్వసమాన త్రిభుజాల సదృశ భుజాలు)
మరియు ∠ACP = ∠BCP
(సర్వసమాన త్రిభుజాల సదృశ కోణాలు)
ఇంకా ∠ACP + ∠BCP = 180° (రేఖీయద్వయం)
కావున 2∠ACP = 180°
లేదా ∠ACP = 90° ………… (2)
(1), (2) ల నుండి PQ, AB కి లంబసమద్విఖండన రేఖ అని చెప్పవచ్చును.
[గమనించవలసిన విషయమేమంటే ΔPAQ, ΔPBQ ల సర్వసమానత్వం రుజువు చేయకుండా ΔPAC = ΔPBC అని నిరూపించలేము.
AP = BP (దత్తాంశము)
PC = PC (ఉమ్మడి భుజము)
మరియు ∠PAC = ∠PBC (AAPB లో సమాన భుజాలకు ఎదురుగానున్న సమానకోణాలు)
దీని నుండి ఇవి రెండూ సర్వసమానం కాదు ఎందుకంటే ఈ ఫలితము భు. భు, కో. నియమాన్ని ఇస్తుంది. కాని త్రిభుజాల సర్వసమానత్వానికి ఈ నియమం ఎల్లప్పుడూ నిజంకాదు. ఇంకా కోణం జత సమానభుజాల జతల మధ్యకోణము కాదు.]

14. l, mరేఖలు A బిందువు వద్ద ఖండించుకొంటున్నాయి. P బిందువు ఈ రేఖలకు సమాన దూరంలో ఉంది. (పటం చూడండి). AP రేఖ l, m ల మధ్య ఏర్పడిన కోణాన్ని సమద్విఖండన చేస్తుందని చూపండి. [పేజీ నెం. 167]
సాధన.
l, m రేఖలు A బిందువు వద్ద ఖండించుకొంటున్నాయి.
PB, l కు లంబము అనుకొనుము. PC ⊥ m.

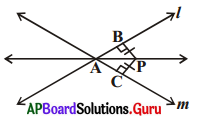
PB = PC అని ఇవ్వబడినది.
∠PBA = ∠PCA = 90° అని చూపాలి.
ΔPAB, ΔPAC లలో
PB = PC (దత్తాంశము)
∠PBA = ∠PCA = 90° (దత్తాంశము)
PA = PA (ఉమ్మడి భుజం)
కావున ΔPAB ≅ ΔPAC (లం.క.భు. నియమం)
కావున ∠PAB = ∠PAC
(సర్వసమాన త్రిభుజాల సదృశకోణాలు)

15. ΔABC లో AD = AC అగునట్లు భుజం BC పై D ఒక బిందువు (పటం చూడండి).

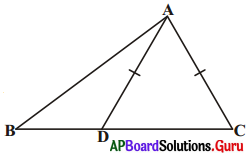
అయిన AB > AD అని చూపండి. [పేజీ నెం.171]
సాధన.
ΔDAC లలో
AD = AC (దత్తాంశము)
కానీ, ∠ADC = ∠ACD
(సమాన భుజాలకు ఎదురుగానున్న కోణాలు)
ఇప్పుడు, ∠ADC, ΔABD కి బాహ్య కోణము.
కావున ∠ADC > ∠ABD
లేదా ∠ACD > ∠ABD
లేదా ∠ACB > ∠ABC
అప్పుడు AB > AC
(ΔABC లో పెద్దకోణానికి ఎదుటి భుజం)
లేదా AB > AD (AD = AC కావున)

AP SCERT 9th Class Maths Textbook Solutions Chapter 8 చతుర్భుజాలు Ex 8.3 Textbook Exercise Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 8th Lesson చతుర్భుజాలు Exercise 8.3

ప్రశ్న 1.
సమాంతర చతుర్భుజము ఎదుటి కోణాలు (3x – 2)° మరియు (x + 48)° అయిన సమాంతర చతుర్భుజములో ప్రతీ కోణాన్ని కనుగొనండి.
సాధన.
సమాంతర చతుర్భుజము ఎదుటి కోణాలు
(3x – 2)° మరియు (x + 48)°
సమాంతర చతుర్భుజంలో ఎదుటి కోణాలు సమానము.
3x – 2 = x + 48
3x – x = 48 + 2
2x = 50
x = \(\frac {50}{2}\) = 25°
∴ ఇచ్చిన కోణాలు (3x – 2)° (x + 48)°
= 3x – 2 = (3 × 25 – 2)° = (75 – 2)° = 73°
x + 48° = (25 + 48)° = 73°
సమాంతర చతుర్భుజంలోని వరుస కోణాలు సంపూరకాలు కావున మిగిలిన రెండు కోణాలు (180° – 73°) మరియు (180° – 73°) = 107° మరియు 107°
∴ నాలుగు కోణాలు 78°, 107°, 73° మరియు 107°.

ప్రశ్న 2.
సమాంతర చతుర్భుజములో ఒక కోణం, అతి చిన్న కోణమునకు రెట్టింపు కన్నా 24° తక్కువ అయిన సమాంతర చతుర్భుజంలో అన్ని కోణాలను కనుగొనుము.
సాధన.
సమాంతర చతుర్భుజములోని అతి చిన్న కోణం = x
దాని ఆసన్న కోణము = (180 – x)°
లెక్క ప్రకారము (180 – x)° = (2x – 24)°
(∵ ఎదుటి కోణాలు సమానము)
180 + 24 = 2x + x
3x = 204
x = \(\frac {204}{3}\) = 68°
∴ మిగిలిన కోణాలు 68°; (2 × 68 – 24)°
68°; (2 × 68 – 24)°
= 68°, 112°, 68°, 112°

ప్రశ్న 3.
కింది పటంలో ABCD ఒక సమాంతర చతుర్భుజము. BC యొక్క మధ్య బిందువు E. AB మరియు DE లను F వరకు పొడిగించిన, AF = 2AB అని నిరూపించండి.

సాధన.

ABCD ఒక సమాంతర చతుర్భుజము.
E, BC యొక్క మధ్య బిందువు.
G, AD యొక్క మధ్య బిందువు.
G మరియు E లను కలుపుము.
∆AFD లో AD మరియు DF ల మధ్య బిందువులను కలుపగా
GE // AF మరియు GE = \(\frac {1}{2}\) AF
కాని GE = AB [∵ ABEG సమాంతర చతుర్భుజంలో AB, GE లు ఒక జత ఎదుటి భుజాలు]
∴ \(\frac {1}{2}\)AF = AB
∴ AF = 2AB

ప్రశ్న 4.
కింది పటంలో ABCDఒక సమాంతర చతుర్భుజము. AB, DCల యొక్క మధ్య బిందువు P మరియు Qలు అయిన PBCQ ఒక సమాంతర చతుర్భుజమని చూపండి.

సాధన.

ABCD ఒక సమాంతర చతుర్భుజము
P,Qలు AB, CDల మధ్య బిందువులు.
P, Qలను కలుపుము.
AB = CD (సమాంతర చతుర్భుజ ఎదుటి భుజాలు)
\(\frac {1}{2}\)AB = \(\frac {1}{2}\)CD
PB = QC మరియు PB//QC.
చతుర్భుజం PBCQ లో PB = QC; PB//QC
కావున ☐PBCQ ఒక సమాంతర చతుర్భుజము.

ప్రశ్న 5.
ABC ఒక సమద్విబాహు త్రిభుజము మరియు AB = AC. బాహ్యకోణం QAC నకు AD సమద్విఖండనరేఖ అయితే
(i) \(\angle \mathrm{DAC}=\angle \mathrm{BCA}\)
(ii) ABCD ఒక సమాంతర చతుర్భుజమని చూపండి.

సాధన.
∆ABC ఒక సమద్విబాహు త్రిభుజము; AB = AC
\(\angle \mathrm{QAC}\) యొక్క కోణ సమద్విఖండన రేఖ AD.
(i) ∆ABC లో, AB = AC ⇒ \(\angle \mathrm{B}=\angle \mathrm{ACB}\)
(సమాన భుజాలకు ఎదుటి కోణాలు)
\(\angle \mathrm{QAC}=\angle \mathrm{B}+\angle \mathrm{ACB}\)
\(\angle \mathrm{QAC}=\angle \mathrm{BCA}+\angle \mathrm{BCA}\)
(∵ \(\angle \mathrm{QAC}=\angle \mathrm{B}\))
⇒ \(\frac {1}{2}\) \(\angle \mathrm{OAC}\) = \(\frac {1}{2}\) [2\(\angle \mathrm{BCA}\)]
⇒ \(\angle \mathrm{DAC}=\angle \mathrm{BCA}\) [∵ \(\angle \mathrm{QAC}\) యొక్క కోణ సమద్విఖండన రేఖ AD]

(ii) సమస్య (i) నుండి \(\angle \mathrm{DAC}=\angle \mathrm{BCA}\)
ఈ కోణాలు, AD మరియు BC రేఖలను AC అను తిర్యగ్రేఖ ఖండించడం వలన ఏర్పడిన ఏకాంతర కోణాలు.
∴ AD // BC
చతుర్భుజం ABCD లో AB // DC; BC / AD
∴ ABCD ఒక సమాంతర చతుర్భుజము.

ప్రశ్న 6.
ABCD ఒక సమాంతర చతుర్భుజము AP మరియు CQలు శీర్షాలు A మరియు Cల నుండి కర్ణం BD పైకి గీచిన లంబాలు (పటంలో చూడండి) అయిన (i) ∆APB ≅ ∆CQD (ii) AP = CO అని చూపండి.

సాధన.
ABCD ఒక సమాంతర చతుర్భుజము మరియు
BD ఒక కర్ణము.
AP ⊥ BD మరియు CQ ⊥ BD
(i) ∆APB మరియు ∆CQD లలో
AB = CD (∵ సమాంతర చతుర్భుజము ABCD యొక్క ఎదుటి భుజాలు)
\(\angle \mathrm{APB}=\angle \mathrm{CQD}\) = 90°
\(\angle \mathrm{PBA}=\angle \mathrm{QDC}\) (ఒకదాని తరువాత ఒకటి ఏర్పడు అంతర కోణాలు)
∴ ∆APB ≅ ∆CQD (కో.కో.భు. నియమం ప్రకారం)

(ii) సమస్య (i) నుంచి ∆APB ≅ ∆CQD
⇒ AP = CQ (CPCT)

ప్రశ్న 7.
∆ABC మరియు ∆DEF లలో AB//DE; BC= EF మరియు BC//EF. శీర్షాలు A, B మరియు Cలు వరుసగా D, E మరియు F లకు కలుపబడినవి (పటం చూడండి) అయిన
(i) ABED ఒక సమాంతర చతుర్భుజము
(ii) BCFE ఒక సమాంతర చతుర్భుజము.
(iii) AC = DF
(iv) ∆ABC ≅ ∆DEF అని చూపండి.

సాధన.

దత్తాంశము నుండి AB//DE; BC = EF
చతుర్భుజం ☐BCFE లో
BC = EF మరియు BC//EF
కావున ☐BCFE ఒక సమాంతర చతుర్భుజము.
చతుర్భుజము ☐ABED లో
AB//ED మరియు AB = ED
కావున ☐ABED ఒక సమాంతర చతుర్భుజము
∆ABC మరియు ∆DEF లలో
AB = DE
BC = EF
\(\angle \mathrm{ABC}=\angle \mathrm{DEF}\) (సమాంతర భుజాల రెండు కోణాలు)
∴ ∆ABC ≅ ∆DEF
⇒ AC = DF (∵ CPCT)
(లేక)
AD = BE = CF ((i) మరియు (ii) ల నుండి)
ACFD ఒక సమాంతర చతుర్భుజము.
ఆ విధముగా AC = DF (∵ సమాంతర చతుర్భుజపు ఎదుటి భుజాలు)

ప్రశ్న 8.
ABCDఒక సమాంతర చతుర్భుజము. AC మరియు BD లు ‘O’ వద్ద ఖండించుకున్నాయి. P, Qలు BD కర్ణంపై త్రిథాకరించబడిన బిందువులైన CQ//AP మరియు AC కర్ణం, PQను సమద్విఖండన చేయునని చూపండి (పటం చూడండి).

సాధన.
☐ABCD ఒక సమాంతర చతుర్భుజము.
BD దాని యొక్క కర్ణము.
P మరియు Qలు BD పై సమత్రిఖండన బిందువులు.
∆APB మరియు ∆CQD లలో
AB = CD(∵ //^gm ABCD యొక్క ఎదుటి భుజాలు)
BP = DQ (దత్తాంశము)
\(\angle \mathrm{ABP}=\angle \mathrm{CDQ}\) (AB, DC సమాంతర రేఖలను BD అను తిర్యగ్రేఖ ఖండించగా ఏర్పడు ఏకాంతర కోణాలు)
∴ ∆APB ≅ ∆CQD (భు.కో.భు. నియమము)
అదే విధముగా ∆AQD మరియు ∆CPB లలో
AD = BC (//^gm ABCD యొక్క ఎదుటి భుజాలు)
DQ = BP (దత్తాంశము)
\(\angle \mathrm{ADQ}=\angle \mathrm{CBP}\)
(AD మరియు BC సమాంతర రేఖలను \(\overline{\mathrm{BD}}\) తిర్యగ్రేఖ ఖండించగా ఏర్పడిన ఏకాంతర కోణాలు)
∴ ∆AQD ≅ ∆CPB
చతుర్భుజము ☐APCQ లో
AP = CQ(∵ ∆APB, ∆CQDల యొక్క CPCT)
AQ = CP(∵ ∆AQD, ∆CPBల యొక్క CPCT)
∴ ☐APCQ ఒక సమాంతర చతుర్భుజము.
∴ CQ// AP (//^gm APCQ యొక్క ఎదుటి భుజాలు) మరియు AC, PQ ను సమద్విఖండన చేస్తుంది.
[∵ //^gm APCQ యొక్క కర్ణాలు)

ప్రశ్న 9.
ABCD ఒక చతురస్రము. E, F, G మరియు Hలు వరుసగా AB, BC, CD మరియు DA లపై గల బిందువులు AE = BF – CG = DH అయినచో EFGH ఒక చతురస్రమని చూపండి.
సాధన.

దత్తాంశం నుండి ABCD ఒక చతురస్రము.
AB, BC, CD మరియు DA భుజాల మధ్య బిందువులు E, F, G, మరియు H లు మరియు AE = BF = CG = DH.
∆ABC లో E, F లు AB మరియు BC ల మధ్య బిందువులు.
∴ EF // AC మరియు EF = \(\frac {1}{2}\) AC
అదే విధముగా GH//AC మరియు GH = AC
GF//BD మరియు GF = \(\frac {1}{2}\)BD
HE//BD మరియు HE = \(\frac {1}{2}\)BD
కాని AC = BD (∵ చతురస్రము యొక్క కర్ణాలు)
∴ EF = FG = GH = HE
∴ EFGH ఒక రాంబస్ మరియు AC ⊥ BD (∵ రాంబస్ యొక్క కర్ణాలు)
∴ //^gm OIEJ లో \(\angle \mathrm{IOJ}=\angle \mathrm{E}\) [∵ ఎదుటి కోణాలు]
∴ \(\angle \mathrm{E}\)= 90°
చతుర్భుజం EFGH లో అన్ని భుజాలు సమానము మరియు ఒక కోణం 90° కావున EFGH ఒక చతురస్రము.

SCERT AP 9th Class Maths Solutions Chapter 7 త్రిభుజాలు Ex 7.4 Textbook Exercise Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 7th Lesson త్రిభుజాలు Exercise 7.4

ప్రశ్న 1.
ఒక లంబకోణ త్రిభుజములో కర్ణము అతి పొడవైన భుజమని నిరూపించండి.
సాధన.

ΔABC లో ∠B లంబకోణము అయిన
∠A + ∠C = 90°
∠A మరియు ∠C లు రెండూ అల్పకోణాలే.
∠A < ∠B ⇒ BC < AC
అదే విధముగా,
∠C < ∠B ⇒ AB < AC
∴ కర్ణము AC త్రిభుజములో పొడవైన భుజము.

ప్రశ్న 2.
కింది పటంలో ΔABC లో భుజాలు AB, AC లు వరుసగా P, Q బిందువులకు పొడిగించబడినవి. ఇంకనూ ∠PBC < ∠QCB. అయిన AC > AB అని చూపండి.

సాధన.
పటం నుండి,
∠PBC = ∠A + ∠ACB
∠QCB = ∠A + ∠ABC
దత్తాంశం నుండి, ∠PBC < ∠QCB
⇒ ∠A + ∠ACB < ∠A + ∠ABC
⇒ ∠ACB < ∠ABC
⇒ AB < AC
∴ AC > AB

ప్రశ్న 3.
కింది పటంలో ∠B < ∠A మరియు ∠C < ∠D అయిన AD < BC అని చూపండి.

సాధన.
దత్తాంశం నుండి, ∠B < ∠A; ∠C < ∠D
∠B < ∠A ⇒ AO < OB [ΔAOB లో] ….. (1)
∠C < ∠D ⇒ OD < OC [ΔCOD లో] …… (2)
(1) & (2) లను కలుపగా,
AO + OD < OB + OC
AD < BC

ప్రశ్న 4.
చతుర్భుజం ABCD లో AB అతి చిన్న భుజం మరియు CD అతి పొడవైన భుజం (క్రింది పటమును చూడండి). అయిన ∠A > ∠Cమరియు ∠B > ∠D అని చూపండి.

సాధన.

చతుర్భుజం ABCD లో AB అతి చిన్న భుజం మరియు CD అతి పొడవైన భుజము.
పటం నుండి, ΔBCD లో,
∠1 > ∠2 [∵ DC > BC …… (1)
ΔBDA లో, ∠4 > ∠3 [∵ AD > AB] …… (2)
(1) మరియు (2) లను కూడగా,
∠1 + ∠4 > ∠2 + ∠3
∠B > ∠D
అదే విధముగా,
ΔABC లో, ∠6 < ∠7 [∵ AB < BC) ……. (3)
ΔACD లో, ∠5 < ∠8 ……….. (4)
(3) మరియు (1) లను కూడగా,
∠6 + ∠5 < ∠7 + ∠8
∠C < ∠A ⇒ ∠A > ∠C
∴ ∠A > ∠C మరియు ∠B > ∠D

ప్రశ్న 5.
క్రింది పటంలో PR > PQ మరియు ∠QPR కోణ సమద్విఖండన రేఖ PS అయిన ∠PSR > ∠PSQ అని చూపండి.

సాధన.
దత్తాంశం నుండి,
PR > PQ; ∠QPS = ∠RPS
PR > PQ అయిన ∠Q > ∠R
∠Q + ∠QPS > ∠R + ∠RPS
⇒ 180° – (∠Q + ∠QPS) < 180° – (∠R + ∠RPS)
⇒ ∠PSQ < ∠PSR
∴ ∠PSR > ∠PSQ

ప్రశ్న 6.
ఒక త్రిభుజము రెండు భుజాల కొలతలు 4 సెం.మీ. మరియు 6 సెం.మీ. అయిన మూడవ భుజం కొలతగా ఉండడానికి సాధ్యమయ్యే అన్ని ధనాత్మక పూర్ణ సంఖ్యల విలువలు కనుగొనండి. అటువంటి ఎన్ని త్రిభుజాలు సాధ్యమవుతాయి ?
సాధన.
ఒక త్రిభుజము యొక్క రెండు భుజాల కొలతలు 4 సెం.మీ. మరియు 6 సెం.మీ.
∴ మూడవ భుజము > మిగిలిన రెండు భుజాల మధ్య భేదము
మూడవ భుజము > 6 – 4
మూడవ భుజము > 2
అదే విధముగా, మూడవ భుజము < మిగిలిన రెండు భుజాల మొత్తము
మూడవ భుజము. < 6 + 4
మూడవ భుజము < 10
∴ మూడవ భుజం కొలతగా ఉండడానికి సాధ్యమయ్యే ధనాత్మక పూర్ణ సంఖ్యలు 3 సెం.మీ., 4 సెం.మీ., 5 సెం.మీ., 6 సెం.మీ., 7 సెం.మీ., 8 సెం.మీ., 9 సెం.మీ.
∴ అటువంటి త్రిభుజాలు ‘7’ సాధ్యమవుతాయి.

ప్రశ్న 7.
5 సెం.మీ., 8 సెం.మీ., 1 సెం.మీ. కొలతతో ఒక త్రిభుజాన్ని నిర్మించడానికి ప్రయత్నించండి. ఈ నిర్మాణం సాధ్యమా ? కాదా ? మీ వివరణను రాయండి.
సాధన.
5 సెం.మీ. మరియు 1 సెం.మీ. భుజాల మొత్తము 6 సెం.మీ. ఇది మూడవ భుజము కొలత కన్నా తక్కువగా వున్నది. కావున ఇది అసాధ్యము.

AP SCERT 9th Class Maths Textbook Solutions Chapter 8 చతుర్భుజాలు Ex 8.2 Textbook Exercise Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 8th Lesson చతుర్భుజాలు Exercise 8.2

ప్రశ్న 1.
ABCD ఒక సమాంతర చతుర్భుజము మరియు ABEF ఒక దీర్ఘచతురస్రము అయిన ∆AFD ≅ ∆BEC అని చూపండి.

సాధన.
☐ABCD ఒక సమాంతర చతుర్భుజము.
☐ABEF ఒక దీర్ఘచతురస్రము.
∆AFD మరియు ∆BEC లలో
AF = BE (∵ ☐ABEF దీర్ఘచతురస్రపు ఎదుటి భుజాలు)
AD = BC (∵ ☐ABCD సమాంతర చతుర్భుజపు ఎదుటి భుజాలు)
DF = CE (∵ AB = DC = DE + EC
AB = EF = DE + DF)
∴ ∆AFD ≅ ∆BEC (భు. భు. భు నియమం)

ప్రశ్న 2.
రాంబలో కర్ణాలు దానిని నాలుగు సర్వసమాన త్రిభుజాలుగా విభజిస్తాయని నిరూపించండి.
సాధన.

☐ABCD ఒక రాంబస్.
AC మరియు BD లు ‘O’ వద్ద ఖండించుకొనును అనుకొనుము.
∆AOB మరియు ∆COD లలో
\(\angle \mathrm{OAB}=\angle \mathrm{OCD}\) (ఏకాంతర కోణాలు)
AB = CD (రాంబస్ నిర్వచనం)
\(\angle \mathrm{OBA}=\angle \mathrm{ODC}\)……. (1) (ఏకాంతర కోణాలు)
∴ ∆AOB ≅ ∆COD (కో.భు.కో. నియమం)
⇒ AO = OC (CPCT)
మరియు ∆AOD ≅ ∆COD ……… (2) [∵ AO = OC; AD = CD; OD = OD భు.భు.భు. నియమం]
అదే విధముగా,
∆AOD ≅ ∆COB …. (3) అని నిరూపించవచ్చును.
(1), (2) మరియు (3) ల నుండి,
∆AOB ≅ ∆BOC ≅ ∆COD ≅ ∆AOD
∴ రాంబస్ కర్ణాలు రాంబను 4 సర్వసమాన త్రిభుజాలుగా విభజించును.

ప్రశ్న 3.
ABCD చతుర్భుజములో \(\angle \mathrm{C}\) మరియు \(\angle \mathrm{D}\)ల యొక్క సమద్విఖందన రేఖలు O వద్ద ఖండించుకుంటే \(\angle \mathrm{COD}\) = \(\frac {1}{2}\) (\(\angle \mathrm{A}\) + \(\angle \mathrm{B}\)) అని చూపండి.
సాధన.

AP SCERT 9th Class Maths Textbook Solutions Chapter 8 చతుర్భుజాలు Ex 8.1 Textbook Exercise Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 8th Lesson చతుర్భుజాలు Exercise 8.1

ప్రశ్న 1.
కింది ప్రవచనాలు ‘సత్యమో’ లేదా ‘అసత్యమో’ తెలపండి.
(i) ప్రతి సమాంతర చతుర్భుజము ఒక ట్రెపీజియం అగును.
(ii) అన్ని సమాంతర చతుర్భుజాలు, చతుర్భుజాలే.
(iii) అన్ని ట్రెపీజియమ్ లు, సమాంతర చతుర్భుజాలే.
(iv) చతురస్రము అనేది రాంబస్ అవుతుంది.
(v) ప్రతి రాంబస్ కూడా ఒక చతురస్రము.
(vi) అన్ని సమాంతర చతుర్భుజాలు, దీర్ఘచతురస్రాలే.
సాధన.
(i) సత్యము
(ii) సత్యము
(iii) అసత్యము
(iv) సత్యము
(v) అసత్యము
(vi) అసత్యము

ప్రశ్న 2.
కింది పట్టికలో చతుర్భుజ ధర్మాలు ఆయా పటాలకు వర్తిస్తే “అవును” అనీ, వర్తించకపోతే “కాదు” అనీ రాయండి.

సాధన.

ప్రశ్న 3.
ABCD ట్రెపీజియంలో AB || CD, AD = BC అయితే \(\angle \mathrm{A}\) = \(\angle \mathrm{B}\) మరియు \(\angle \mathrm{C}\) = \(\angle \mathrm{D}\) అవుతాయని చూపండి.
సాధన.
ABCD ట్రెపీజియంలో AB || CD; AD = BC, DC = AE అగునట్లుగా AB పై ‘E’ బిందువును గుర్తించుము.

E మరియు C లను కలుపుము.
AECD చతుర్భుజంలో
∴ AE // DC మరియు AE = DC
∴ AECDఒక సమాంతర చతుర్భుజము.
∴ AD//EC
\(\angle \mathrm{DAE}=\angle \mathrm{CEB}\) (ఆసన్న కోణాలు) ……….. (1)
ΔCEB లో CE = CB (∵ CE = AD)
∴ \(\angle \mathrm{CEB}=\angle \mathrm{CBE}\) (సమాన భుజాలకెదురుగా వున్న కోణాలు) …….. (2)
(1) మరియు (2) ల నుండి,
\(\angle \mathrm{DAE}=\angle \mathrm{CBE}\) ⇒ \(\angle \mathrm{A}\) = \(\angle \mathrm{B}\)
\(\angle \mathrm{D}\) = \(\angle \mathrm{AEC}\) (∵ సమాంతర చతుర్భుజంలోని ఎదురు కోణాలు)
= \(\angle \mathrm{ECB}+\angle \mathrm{CBE}\) [∵ ΔBCE యొక్క బాహ్య కోణము \(\angle \mathrm{AEC}\))
= \(\angle \mathrm{ECB}+\angle \mathrm{CEB}\) [∵ \(\angle \mathrm{CBE}=\angle \mathrm{CEB}\)
= \(\angle \mathrm{ECB}+\angle \mathrm{ECD}\) [∵ \(\angle \mathrm{ECD}=\angle \mathrm{CEB}\) ఏకాంతర కోణాలు]
= \(\angle \mathrm{BCD}\) = \(\angle \mathrm{C}\)
∴ \(\angle \mathrm{C}\) = \(\angle \mathrm{D}\)

ప్రశ్న 4.
చతుర్భుజములో కోణాల నిష్పత్తి 1 : 2 : 3 : 4 అయిన ప్రతీ కోణం కొలతను కనుగొనండి.
సాధన.
చతుర్భుజములోని కోణాల నిష్పత్తి = 1 : 2 : 3 : 4
కోణ నిష్పత్తుల మొత్తము = 1 + 2 + 3 + 4 = 10
చతుర్భుజంలోని నాలుగు కోణాల మొత్తము = 360°
∴ మొదటి కోణ పరిమాణము = \(\frac {1}{10}\) × 360° = 36°
రెండవ కోణ పరిమాణము = \(\frac {2}{10}\) × 360° = 72°
మూడవ కోణ పరిమాణము = \(\frac {3}{10}\) × 360° = 108°
నాల్గవ కోణ పరిమాణము = \(\frac {4}{10}\) × 360° = 144°

ప్రశ్న 5.
ABCD ఒక దీర్ఘచతురస్రము AC కర్ణం అయిన ∆ACD లో కోణాలను కనుగొనండి. కారణాలు తెలపండి.
సాధన.

ABCD ఒక దీర్ఘచతురస్రము; AC ఒక కర్ణము.
∆ACD లో \(\angle \mathrm{D}\) = 90° [∵ \(\angle \mathrm{D}\) దీర్ఘచతురస్రపు ఒక కోణము]
\(\angle \mathrm{A}\) + \(\angle \mathrm{C}\) = 90° [∵ \(\angle \mathrm{D}\) = 90° ⇒ \(\angle \mathrm{A}\) + \(\angle \mathrm{C}\) = 180° – 90° = 90°]
\(\angle \mathrm{D}\) లంబకోణము మరియు \(\angle \mathrm{A}\), \(\angle \mathrm{C}\)లు పూరకాలు.

SCERT AP 9th Class Maths Solutions Chapter 7 త్రిభుజాలు Ex 7.3 Textbook Exercise Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 7th Lesson త్రిభుజాలు Exercise 7.3

ప్రశ్న 1.
ఒక సమద్విబాహు త్రిభుజము ABCలో AB = AC, AD అనేది A నుండి BCకి గీసిన లంబము అయిన
(i) BC భుజాన్ని AD సమద్విఖండన చేయునని
(ii) ∠A ని AD కోణ సమద్విఖండన చేయునని చూపండి.
సాధన.

ΔABC లో AB = AC మరియు AD ⊥ BC
i) ΔABD మరియు ΔACD లలో
AB = AC (దత్తాంశం)
∠ADB = ∠ADC (AD ⊥ BC)
AD = AD (ఉమ్మడి భుజము)
∴ ΔABD ≅ ΔACD
(∵ లం.క.భు. నియమము నుండి)
⇒ BD = CD (CPCT)
⇒ AD, BC ను సమద్విఖండన చేయును.

ii) ∠BAD = ∠CAD
(ΔAB, ΔACD ల యొక్క CPCT)
∴ AD అనునది ∠A యొక్క కోణ సమద్విఖండన రేఖ అగును.

ప్రశ్న 2.
ΔABC లో రెండు భుజములు AB, BC మరియు మధ్యగతం AM వరుసగా ΔPQR లో రెండు భుజములు PQ, QRలు మరియు మధ్యగతం PNకు సమానము (పటము చూడండి). అయిన
i) ΔABM ≅ ΔPON
ii) ΔABC ≅ ΔPQR అని చూపండి.

సాధన.
దత్తాంశము నుండి AB = PQ
AM = PN
i) ΔABM మరియు ΔPQN లలో
AB = PQ (దత్తాంశము)
AM = PN (దత్తాంశము)
BM = QN
(∵ BC = QR ⇒ \(\frac {1}{2}\)BC = \(\frac {1}{2}\)QR ⇒ BM = QN)
∴ ΔΑΒΜ ≅ ΔΡQΝ
(∵ భు.భు. భు. నియమం ప్రకారం)

ii) ΔABC మరియు ΔPQR లలో
AB = PQ (దత్తాంశం)
BC = QR (దత్తాంశం)
∠ABC = ∠PQN [∵ ΔABM మరియు ΔPQN ల యొక్క CPCT (i) నుండి]
∴ ΔABC ≅ ΔPQR
(∵ భు.కో.భు. నియమం ప్రకారం)

ప్రశ్న 3.
ΔABC లో BE, CF లు రెండు సమాన లంబములు. లం.క.భు. సర్వసమానత్వ నియమాన్ని ఉపయోగించి AABC సమద్విబాహు త్రిభుజమని చూపండి.

సాధన.
ΔABC లో BE, CF లు సమాన లంబాలు.
ΔBCE మరియు ΔCBF లలో
∠BEC = ∠CFB = 90° (∵ పటం నుండి)
BC = BC (ఉమ్మడి భుజం మరియు కర్ణము)
CF = BE (దత్తాంశము)
∴ ΔBEC ≅ ΔCBE
⇒ ∠EBC = ∠FCB (∵ CPCT)
కాని ఈ కోణాలు ΔABC యొక్క భుజాలైన AC మరియు AB ల అంతర కోణాలు.
⇒ AC = AB

ప్రశ్న 4.
ఒక సమద్విబాహు త్రిభుజము ABC లో AB = AC అయిన ∠B = ∠C అని నిరూపించండి.
(గమనిక : AP ⊥ BC అయ్యేటట్లు APని గీయండి, లం.క.భు. నియమాన్ని ఉపయోగించండి.)
సాధన.

దత్తాంశం : ΔABC ఒక సమద్విబాహు త్రిభుజము మరియు AB = AC.
సారాంశం : ∠B = ∠C
D, BC మధ్య బిందువనుకొనుము.
నిర్మాణం : A, D లను కలుపుము.
ఉపపత్తి : ΔABD మరియు ΔACD లలో
AB = AC (దత్తాంశం)
BD = DC (నిర్మాణము)
AD = AD (ఉమ్మడి భుజము)
∴ ΔABD ≅ ΔACD
(∵ భు.భు.భు. నియమం ప్రకారం)
⇒ ∠B = ∠C [∵ CPCT]

ప్రశ్న 5.
ఒక సమద్విబాహు త్రిభుజము ABCలో AB = AC. AD = AB అగునట్లు భుజము BA ని D బిందువు వద్దకు పొడిగించినారు (పటము చూడండి). ∠BCD ఒక లంబకోణమని చూపండి.

సాధన.

దత్తాంశం : ΔDBC లో; AB = AC; AD = AB
ΔABC లో
∠ABC + ∠ACB = ∠DAC ………. (1)
[∵ బాహ్య కోణము]
ΔACD లో
∠ADC + ∠ACD = ∠BAC …………..(2)
(1) & (2) లను కలుపగా,
∠DAC + ∠BAC = 2∠ACB + 2∠ACD
[∵ ∠ABC = ZACB
∠ADC = ∠ACD]
180° = 2 [∠ACB + ∠ACD]
180° = 2[∠BCD]
∴ ∠BCD = \(\frac{180^{\circ}}{2}\) = 90°
(లేక)
పటం నుండి,
∠2 = x + x = 2x
∠1 = y + y = 2y
∠1 + ∠2 = 2x + 2y
180° = 2(x + y)
∴ x + y = \(\frac{180^{\circ}}{2}\) = 90°

ప్రశ్న 6.
ΔABC ఒక లంబకోణ త్రిభుజము. దీనిలో ∠A = 90° మరియు AB = AC అయిన ∠B = ∠C అని చూపండి.
సాధన.

దత్తాంశం : ΔABC ఒక లంబకోణ త్రిభుజము.
∠A = 90° మరియు AB = AC
సారాంశం: ∠B = ∠C
నిర్మాణం : BC మధ్య బిందువు D ను, A ను కలుపుము.
ఉపపత్తి : ΔADC మరియు ΔADB లలో
AD = AD (ఉమ్మడి భుజం)
AC = AB (దత్తాంశం)
DC = DB (నిర్మాణము)
⇒ ΔADC ≅ ΔADB
⇒ ∠C = ∠B (CPCT)

ప్రశ్న 7.
ఒక సమబాహు త్రిభుజములో ప్రతీ కోణము 60° అని చూపండి.
సాధన.

దత్తాంశం : ΔABC ఒక సమబాహు త్రిభుజము.
మరియు AB = BC = CA
∠A = ∠B (∵ సమాన భుజాలకు ఎదురుగానున్న కోణాలు సమానము)
∠B = ∠C (∵ సమాన భుజాలకు ఎదురుగానున్న కోణాలు సమానము)
⇒ ∠A = ∠B = ∠C = x అనుకొనుము.
∠A + ∠B + ∠C = 180°
⇒ x + x + x = 180°
3x = 180°
⇒ y = \(\frac{180^{\circ}}{3}\) = 60°
∴ సమబాహు త్రిభుజంలో ప్రతీ కోణము 60°.

AP SCERT 9th Class Maths Textbook Solutions Chapter 9 సాంఖ్యక శాస్త్రము InText Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 9th Lesson సాంఖ్యక శాస్త్రము InText Questions

కృత్యం

1. తరగతిలోని విద్యార్థులను నాలుగు బృందాలుగా విభజించి, ఒక్కొక్క బృందమునకు కింద చూపిన దత్తాంశముల సేకరణకు కేటాయించారు. (పేజీ నెం. 195).
(i) మీ తరగతిలోని అందరు విద్యార్థుల బరువులు.
(ii) ఒక్కొక్క విద్యార్థి యొక్క (సోదరులు లేక సోదరిల సంఖ్య) తోబుట్టువుల సంఖ్య,
(iii) గత మాసంలో రోజువారీగా గైరుహాజరయిన వారి సంఖ్య
(iv) తరగతిలో ప్రతి విద్యార్థి యొక్క ఇంటి నుండి పాఠశాల దూరము.

2. మీ తరగతిలోని విద్యార్థుల ఇంటి పేరులో (ఆంగ్లములో) మొదటి అక్షరాలు (Initials) సేకరించండి. అవర్గీకృత పౌనఃపున్య విభాజక పట్టిక తయారుచేసి కింది ప్రశ్నలకు జవాబులివ్వండి. (పేజీ నెం. 197)
(i) ఎక్కువ మంది విద్యార్థుల ఇంటి పేర్ల మొదటి అక్షరం ఏది ?
(ii) ఎంతమంది విద్యార్థుల ఇంటిపేర్ల మొదటి అక్షరం T ?
(iii) ఏ అక్షరం అతి తక్కువ సార్లు ఉపయోగింపబడినది ?
సాధన.
విద్యార్థి కృత్యం.

ఇవి చేయండి

1. కింది వానిలో ఏది ప్రాథమిక, ఏది గౌణ దత్తాంశము? (పేజీ నెం. 195)

ప్రశ్న (i)
2001 నుండి 2010 వరకు మీ పాఠశాలలో నమోదు కాబడిన విద్యార్థుల వివరాలు.
సాధన.
గౌణ దత్తాంశము.

ప్రశ్న (ii)
వ్యాయామ ఉపాధ్యాయుడు నమోదు చేసిన మీ తరగతిలో విద్యార్థుల ఎత్తులు.
సాధన.
ప్రాథమిక దత్తాంశము.

ఆలోచించి, చర్చించి రాయండి

1. అంకగణిత మధ్యమము, మధ్యగతము, బాహుళకము విడివిడిగా ఉపయోగించు సందర్భములను మూడింటిని రాయండి. (పేజీ నెం. 202)
సాధన.
సగటు :
(a) కొంతమంది విద్యార్థులకు, మధ్యాహ్న భోజనంను ఏర్పాటుచేయు సందర్భంలో
(b) తరగతిలోని విద్యార్థుల మార్కులను పోల్చు సందర్భంలో
(c) ఒక నెలలో ఒక వర్తకుడు పొందు రోజు వారీ వేతనంను లెక్కించు సందర్భంలో

మధ్యగతం :
(a) ఒక సంస్థలోని ఉద్యోగుల జీతాలను లెక్కించు సందర్భంలో
(b) ఒక తరగతిలోని బాలురు మరియు బాలికల ఎత్తును కొలుచు సందర్భంలో

బాహుళకము:
(a) ఒక నగరంలో ఎక్కువగా ఉపయోగించు ప్రయాణ సాధనాలను తెలుసుకొను సందర్భంలో
(b) ఒక షూ షాపులో ఎక్కువగా అమ్ముడుపోవు షూ సైజును లెక్కించు సందర్భంలో

2. మీ తరగతిలోని విద్యార్థులను ఎత్తుల ఆధారంగా వర్గాలుగా విభజించండి. (ఉదాహరణకు బాలురు – బాలికలు) మరియు బాహుళకమును కనుగొనండి. (పేజీ నెం. 208)
సాధన.
విద్యార్థి తన తరగతి గదిలో ఉన్న బాలురు – బాలలికల ఎత్తులను తీసుకొని బాహుళకమును కనుగొనండి.

3. చెప్పుల దుకాణదారు చెప్పులు కొనుగోలు చేయునపుడు ఏ కొలత చెప్పులు ఎక్కువగా ఆర్డరు చేస్తాడు ? (పేజీ నెం. 208)
సాధన.
విద్యార్థి తనకు దగ్గరలోగల చెప్పుల దుకాణంకు వెళ్ళి సమాధానం రాబట్టవలెను.

ప్రయత్నించండి (పేజీ నెం . 207)

1. 75, 21, 56, 36, 81, 05, 42 రాశుల మధ్యగతాన్ని కనుగొనండి.
సాధన.
ఇచ్చిన దత్తాంశమును ఆరోహణ క్రమంలో వ్రాయగా 05, 21, 36, 42, 56, 75, 81.
దత్తాంశంలోని అంశాలు = 7 (బేసి సంఖ్య)
\(\frac{\mathrm{n}+1}{2}\) వ పదము = \(\frac{\mathrm{7}+1}{2}\)
\(\frac {8}{2}\) = 4వ పదము
∴ మధ్యగతము = 42

2. ఆరోహణ క్రమములో ఉన్న దత్తాంశం 7, 10, 15, x, y, 27, 30 యొక్క మధ్యగతము 17. ఈ దత్తాంశమునకు 50 అను రాశిని చేర్చగా మధ్యగతము 18 అయినచో X మరియు y లను కనుగొనుము. (పేజీ నెం. 207)
సాధన.
ఆరోహణ క్రమంలో వున్న దత్తాంశము
7, 10, 15, x, y, 27, 30.
దత్తాంశంలోని అంశాల సంఖ్య n = 7 (బేసి సంఖ్య)
∴ మధ్యగతము = \(\frac{\mathrm{n}+1}{2}\) వ పదము = \(\frac{\mathrm{7}+1}{2}\) = \(\frac {8}{2}\) = 4వ పదము
∴ శవ పదము = x = 17 (సమస్య నుండి)
ఇచ్చిన దత్తాంశమునకు 50 అను రాశిని చేర్చిన ఏర్పడు మధ్యగతము 18.
50 ను చేర్చగా ఇచ్చిన దత్తాంశము 7, 10, 15, 17,y, 27, 30, 50
దత్తాంశంలోని అంశాల సంఖ్య = n= 8 (సరి సంఖ్య)
∴ మధ్యగతము = \(\left(\frac{\left(\frac{\mathrm{n}}{2}\right)+\left(\frac{\mathrm{n}}{2}+1\right)}{2}\right)\) వ పదము = \(\left(\frac{\left(\frac{\mathrm{n}}{2}\right)+\left(\frac{\mathrm{n}}{2}+1\right)}{2}\right)\) వ పదము
18 = \(\frac{17+y}{2}\) (సమస్య నుండి)
17 + y = 36 ⇒ y = 36 – 17 = 19

3. కింది దత్తాంశమునకు మధ్యగతము కనుగొనండి.

సాధన.

మధ్యగతము = (\(\frac{\mathrm{n}+1}{2}\)) వ పదము = \(\frac{\mathrm{29}+1}{2}\) = 15 వ పదము
∴ 15వ అంశము = 15 (పట్టిక నుండి)

4. అవర్గీకృత పౌనఃపున్య విభాజనము యొక్క మధ్యగతంను కనుగొనునప్పుడు క్రమంలో వ్రాయవలెను. ఎందుకు ? (పేజీ నెం. 208)
సాధన.
అవర్గీకృత పౌనఃపున్య విభాజనము యొక్క మధ్యగతంను కనుగొనునప్పుడు దత్తాంతంను ఆరోహణ / అవరోహణ క్రమంలో వ్రాయవలెను. ఎందుకనగా ఆ దత్తాంశంను సరిగ్గా సమ భాగముగా విభజించాలి కావున.

ఉదాహరణలు

1. గణిత పరీక్షలో 50 మంది విద్యార్థులు పొందిన మార్కులు ఈ విధంగా ఇవ్వబడ్డాయి.
5, 8, 6, 4, 2, 3, 4, 9, 10, 2, 1, 1, 3, 4, 5, 8, 6, 7, 10, 21, 1, 3, 4, 4, 5, 8, 6, 7, 10, 2, 8, 6, 4, 2, 5, 4, 9, 10, 2, 1, 1, 3, 4, 5 8, 6, 4, 5, 8 (పేజీ నెం. 196)
సాధన.

దత్తాంశమునకు గణన చిహ్నాలు ఉపయోగించి పట్టికలో చూపబడినది. ఒక మార్కును సాధించిన మొత్తం విద్యార్థుల సంఖ్యను ఆ మార్కు యొక్క పౌనఃపున్యం అందురు. ఉదాహరణకు 4 మార్కులు సాధించిన విద్యార్థుల సంఖ్య 9, అంటే 4 మార్కుల యొక్క పౌనఃపున్యము 9. ఈ పట్టికలోని గణన చిహ్నాలు ముడి దత్తాంశములోని రాశులను పోల్చి లెక్కించుటకు ఉపయోగపడతాయి.

పట్టికలోని అన్ని పౌనఃపున్యముల మొత్తము దత్తాంశములోని రాశుల మొత్తమును సూచిస్తుంది. ఈ విధంగా దత్తాంశములోని అన్ని విభిన్న రాశు లను పౌనఃపున్యములతో సూచించు పట్టికను ‘అవర్గీకృత పౌనఃపున్య విభాజన పట్టిక’ లేక ‘రాశుల భారత్వ పట్టిక’ అంటారు.

2. ఒక బుట్టలోని 50 నారింజ పండ విడి విడి బరువులు (గ్రాములలో) కింది ఇవ్వబడ్డాయి. (పేజీ నెం. 197)
35, 45, 56, 50, 30, 110, 95, 40, 70, 100, 60, 80, 85, 60, 52, 95, 98, 35, 47, 45, 105, 90, 30, 50, 75, 95, 85, 80, 35, 45, 40, 50, 60, 65, 55, 45, 30, 90, 115, 65, 60, 40, 100, 55, 75, 110, 85, 95, 55, 50.
సాధన.
దత్తాంశములోని రాశులను ఒక్కసారిగా ప్రదర్శించుటకు, సమగ్రంగా, సులభంగా అర్థం చేసుకొనుటకు అనువుగా రావు లన్నింటిని తరగతులు, 30 – 39, 40 – 49, 50 – 59, ….. 100 – 109, 110 – 109 గా విభజిస్తాం . ఈ చిన్నచిన్న వర్గములను లేదా సమూహములను తరగతులు అంటారు. ఒక్కొక్క తరగతి యొక్క పరిమాణమును తరగతి పొడవు’ లేక ‘తరగతి వెడల్పు’ అంటారు. ఉదాహరణకు తరగతి 30 – 39 లో 30ను ‘దిగువ అవధి’ అని, 39ను ‘ఎగువ అవధి’ అని అంటారు. ఈ తరగతి పొడవు 10 (దిగువ, ఎగువ అవధులతో సహా).

దత్తాంశములోని రాశులను చిన్న చిన్న వర్గములుగా విభజించి పౌనఃపున్యములతో సూచించు పట్టికను ‘వర్గీకృత పౌనఃపున్య విభాజన పట్టిక’ అంటారు. ఇది దత్తాంశమును సమగ్రంగా, సంక్షిప్తంగా ప్రదర్శించి అర్థం చేసుకోవడం సులభతరం చేస్తుంది.

పై పౌనఃపున్య విభాజనములోని తరగతులు ఒకదానిపై ఒకటి అతిపాతం చెందుట లేదు అనగా ఏ విలువ రెండు తరగతులలో పునరావృతం కాదు. ఈ తరగతులను సమ్మిళిత తరగతులు అంటాం.

ఏ దత్తాంశములో అయినా ఎక్కువ తరగతి పొడవుతో తరగతి హద్దులు తక్కువ తరగతులకు లేక తక్కువ తరగతి పొడవుతో తక్కువ తరగతులను ఏర్పాటు చేసుకొనవచ్చును. కానీ తరగతులు మాత్రం ఒకదానిపై ఒకటి అతిపాతం చెందకూడదు. సామాన్యంగా మొదట దత్తాంశపు వ్యాప్తి (వ్యాప్తి = గరిష్ట దత్తాంశపు విలువ – కనిష్ఠ దత్తాంశపు విలువ) ని కనుగొందురు. వ్యాప్తిని ఉపయోగించి తరగతి పొడవు మరియు తరగతుల సంఖ్యను నిర్ణయింతురు. ఉదాహరణకు 30 – 35, 36 – 40, …. గా విభజింపవచ్చును.

పై దత్తాంశంలో ఒక నారింజపండు భారము 39.5 గ్రా. అయినచో ఆ విలువను ఏ తరగతికి చేర్చవలెను? 30 – 39 తరగతిలోనా లేక 40 – 49 తరగతిలోనా ?

ఇటువంటి సందర్భములలో తరగతుల యొక్క నిజ అవధులు లేక హద్దులు సహాయపడతాయి. ఒక తరగతి యొక్క ఎగువ అవధి, తరువాత తరగతి యొక్క దిగువ అవధుల సరాసరిని ఆ తరగతి యొక్క ఎగువ హద్దు అంటారు. అదే విలువ తరువాత తరగతి యొక్క దిగువ హద్దు అవుతుంది. ఇదే విధంగా అన్ని తరగతుల యొక్క హద్దులను రాయవచ్చు. మొదటి తరగతికి ముందు ఒక తరగతి ఊహించుకోవడం ద్వారా మొదటి తరగతి దిగువ హద్దును, అట్లే చివరి తరగతికి తరువాత ఒక తరగతిని ఊహించటం ద్వారా చివరి తరగతి యొక్క ఎగువ హద్దును లెక్కించవచ్చును.

హద్దులు ఏర్పరచిన తరువాత కూడా 39.5 ను ఏ తరగతిలో అనగా 29.5 – 39.5 లేక 39.5 – 49.5 చేర్చవలెననే సంశయము ఏర్పడుతుంది. సాంప్రదాయకంగా తరగతి యొక్క ఎగువహద్దు ఆ తరగతికి చెందదు అని గ్రహించవలెను. కావున 39,5 రాశి 39.5 – 49.5 తరగతికి చెందుతుంది.

30 – 40, 40 – 50, 50 – 60, … తరగతులు ఒక దానిపై ఒకటి అతిపాతం చెందుతాయి. ఈ తరగతులను ‘మినహాయింపు తరగతులు’ అంటారు. సమ్మిళిత తరగతుల హద్దులలో మినహాయింపు తరగతులు ఏర్పడుట గమనించవచ్చు. ఒక తరగతి ఎగువ మరియు దిగువ హద్దుల భేదము ఆ తరగతి అంతరము. కావున 90-99 తరగతి అంతరము 10.

3. సెప్టెంబరు నెలలో ఒక నగరము యొక్క సాపేక్ష అర్థత (శాతములలో) విలువలు కింది విధంగా ఇవ్వబడ్డాయి. (ఎందుకనగా 99.5 – 89.5 = 10) (పేజీ నెం. 199)

(i) 84 – 86, 86 – 88, …… తరగతి అంతరాలతో వర్గీకృత పౌనఃపున్య విభాజనమును నిర్మించండి. .
(ii) దత్తాంశము వ్యాప్తి ఎంత ?
సాధన.
(i) ఇచ్చిన తరగతులతో గణన చిహ్నాల సహాయంతో నిర్మింపబడిన వర్గీకృత పౌనఃపున్య విభాజనము.

(సూచన : దత్తాంశము 90; 90 – 92 తరగతికి 96; 96 – 98 తరగతికి చెందును.)
(ii) దత్తాంశము యొక్క వ్యాప్తి = గరిష్ట విలువ – కనిష్ఠ విలువ
= 99.2 – 84.9 = 14.3

4. ఒక వారము ఒక పట్టణపు వర్షపాతము 4 సెం.మీ., 5 సెం.మీ., 12 సెం.మీ., 3 సెం.మీ., 6 సెం.మీ., 8 సెం.మీ., 0.5 సెం.మీ. అని రికార్డు చేయబడినది. అయిన దినసరి సరాసరి వర్షపాతమెంత? (పేజీ నెం. 203)
సాధన.
వారంలో రోజువారీ వర్షపాతము (సెం.మీ.) = 4.5 సెం.మీ., 5 సెం.మీ., 12 సెం.మీ., 3 సెం.మీ., 6 సెం.మీ., 8 సెం.మీ., 0.5 సెం.మీ.
దత్తాంశములోని రాశుల సంఖ్య n = 7
అంకగణిత మధ్యమము \(\overline{\mathbf{x}}=\frac{\Sigma \mathbf{x}_{\mathbf{i}}}{\mathrm{n}}=\frac{\mathbf{x}_{1}+\mathrm{x}_{2}+\mathrm{x}_{3}+\ldots \ldots \mathrm{x}_{\mathrm{n}}}{\mathrm{n}}\), x₁, x₂, …… x_n రాశులు.
మరియు \(\overline{\mathrm{X}}\) వాటి సగటు = \(\frac{4+5+12+3+6+8+0.5}{7}=\frac{38.5}{7}\) = 5.5 సెం.మీ.

5. 10, 12, 18, 13 P మరియు 17 ల సరాసరి 15 అయిన P విలువను కనుగొనండి. (పేజీ నెం. 204)
సాధన.
సరాసరి \(\overline{\mathbf{x}}=\frac{\Sigma \mathbf{x}_{\mathbf{i}}}{\mathbf{n}}\)
15 = \(\frac{10+12+18+13+P+17}{6}\)
90 = 70 + P
P = 90 – 70 = 20

6. కింది పౌనఃపున్య విభాజనమునకు అంకగణితమధ్యమం కనుగొనండి (పేజీ నెం. 205)

సాధన.

సోపానం – 1 : ప్రతి వరుసలో f_i × x_i కనుగొనుము.
సోపానం – 2 : పౌనఃపున్యముల మొత్తం (Σf_i)
మరియు f_i × x_i లబ్ధముల మొత్తం (Σf_ix_i) లను కనుగొనుము,

సోపానం – 3 : అంకగణితమధ్యమము
\(\overline{\mathrm{X}}\) = \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}=\frac{755}{50}\) = 15.1

7. కింది పౌనఃపున్య విభాజనము యొక్క అంకగణిత మధ్యమం 7.5 అయిన, ‘A’ విలువను కనుగొనండి. (పేజీ నెం. 205)

సాధన.

పౌనఃపున్యముల మొత్తం (Σf_i) = 42 + A
రాశుల మొత్తం f_i × x_i(Σf_ix_i) = 306 + 8A
అంకగణిత మధ్యమం \(\overline{\mathrm{x}}\) = \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\)
ఇచ్చిన విలువ ప్రకారం = 7.5
కావున 7.5 = \(\frac {306 + 8A}{42 + A}\)
306 + 8A = 315 + 7.5 A
8A – 7.5A = 315 – 306
0.5A = 9
A = 18

8. కింది అవర్గీకృత పౌనఃపున్య విభాజనమునకు అంకగణిత మధ్యమము కనుగొనండి. (పేజీ నెం.206)

సాధన.

(i) సాధారణ పద్ధతి :
అవర్గీకృత పౌనఃపున్య విభాజనపు సగటుకు కింది సూత్రాన్ని ఉపయోగించండి.
\(\bar{x}=\frac{\sum_{\mathrm{i}=1}^{7} \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\sum_{\mathrm{i}=1}^{7} \mathrm{f}_{\mathrm{i}}}=\frac{622}{40}\) = 15.55

(ii) విచలన పద్దతి:

ఈ పద్ధతిలో దత్తాంశములోని ఏదైనా ఒకరాశిని ఊహించిన అంకగణిత మధ్యమంగా గుర్తించి అంకగణిత మధ్యమం కనుగొంటారు. ఈ దత్తాంశమునకు ఊహించిన అంకగణిత మధ్యమం A = 16 అనుకొని పట్టికను పూరించగా …..
పౌనఃపున్యముల మొత్తం = 40
విచలనముల f_i × d_i లబ్దాల మొత్తం = – 60 + 42.
Σf_id_i = – 18
అంకగణిత మధ్యమం \(\overline{\mathrm{X}}\) = A + \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{d}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\) = 16 + \(\frac {-18}{40}\)
= 16 – 0.45
= 15.55

9. కింద ఒక రోజు దుకాణదారుడు అమ్మిన పాదరక్షల సైజు నంబర్లు ఇవ్వబడినవి. బాహుళకము కనుగొనండి. 6, 7, 8, 9, 10, 6, 7, 10, 7, 6, 7, 9, 7, 6 (పేజీ నెం. 208)
సాధన.
దత్తాంశ రాశులను ఆరోహణ క్రమంలో రాయగా 6, 6, 6, 6, 7, 7, 7, 7, 7, 8, 9, 9, 10, 10 లేక పౌనఃపున్య విభాజనము రాయగా

ఇచ్చట 7 అను సంఖ్య 5 సార్లు వచ్చింది.
∴ దత్తాంశము యొక్క బాహుళకము = 7.

10. 100 మార్కులకు నిర్వహించిన పరీక్షలో 20 మంది విద్యార్థుల మార్కులు
93, 84, 97, 98, 1000, 78, 86, 100, 85, 92, 55, 91, 90, 75, 94, 83, 60, 81, 95
(a) 91 – 100, 81 – 90 ……… తరగతులతో పౌనఃపున్య విభాజన పట్టిక తయారుచేయండి.
(b) బాహుళక తరగతిని గుర్తించండి. (అత్యధిక పౌనఃపున్యం గల తరగతిని ‘బాహుళక తరగతి’ అంటారు)
(c) మధ్యగతపు తరగతులను గుర్తించండి. (పేజీ నెం. 209)
సాధన.
(a)

(b) గరిష్ఠ పౌనఃపున్యాలు ‘9’ గల తరగతి 91 – 100 కావున ఇదే బాహుళకపు తరగతి.
(c) 20 లో మధ్య మరాశి 10.
దత్తాంశములోని రాశులను ఆరోహణ లేక అవరోహణ క్రమములో ఎట్లు లెక్కించును 10వ రాశి 81 – 90 తరగతిలో గలదు. కావున 81 – 90ను మధ్యగత తరగతి అంటారు.

SCERT AP 9th Class Maths Solutions Chapter 7 త్రిభుజాలు Ex 7.2 Textbook Exercise Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 7th Lesson త్రిభుజాలు Exercise 7.2

ప్రశ్న 1.
సమద్విబాహు త్రిభుజము ABC లో AB = AC. ∠B, ∠Cల కోణ సమద్విఖండన రేఖలు ‘O’ బిందువు వద్ద ఖండించుకొంటాయి. A మరియు O బిందువులను కలపండి.
(i) OB = OC (ii) AO, ∠A కు కోణ సమద్విఖండనరేఖ.

సాధన.
దత్తాంశము :
ΔABC ఒక సమద్విబాహు త్రిభుజము.
AB = AC మరియు ∠B, ∠C ల కోణ సమద్విఖండన రేఖలు ‘O’ వద్ద ఖండించుకొంటాయి.
సారాంశము :
i) OB = OC
ii) AO, ∠A కు కోణ సమద్విఖండన రేఖ
నిర్మాణము :
A మరియు O లను కలపండి.
ఉపపత్తి :
i) OB = OC
∠B = ∠C (సమానభుజాలకు ఎదురుగానున్న కోణాలు సమానం)
\(\frac {1}{2}\)∠B = \(\frac {1}{2}\)∠C (ఇరువైపులా 2 చే భాగించగా)
∠OBC = ∠OCB
⇒ OB = OC (∵ ΔOBC లో సమానకోణాలకు ఎదురుగానున్న భుజాలు)

ii) AAOB మరియు ΔAOC లలో
AB = AC (దత్తాంశము)
BO = CO (నిరూపించబడినది)
∠ABO = ∠ACO (∵ ∠B = ∠C)
∴ ΔAOB ≅ ΔAOC
∠BAO = ∠CAO [∵ ΔAOB మరియు ΔAOC ల యొక్క CPCT)
∴ AO, ∠A కు కోణ సమద్విఖండన రేఖ.

ప్రశ్న 2.
ΔABC లో AD అనేది BC భుజమునకు లంబ సమద్విఖండన రేఖ. (కింది పటాన్ని చూడండి). ΔABC, AB = AC అయ్యేటట్లున్న సమద్విబాహు త్రిభుజమని చూపండి.

సాధన.
ΔABC లో AD ⊥ BC మరియు BD = DC
ΔABD మరియు ΔACD లలో
AD = AD (ఉమ్మడి భుజము)
BD = DC (దత్తాంశము)
∠ADB = ∠ADC (దత్తాంశము)
∴ ΔABD ≅ ΔACD (∵ భు.కో.భు ప్రకారం)
⇒ AB = AC (∵ ΔABD మరియు ΔACD ల యొక్క CPCT)
∴ ΔABC ఒక లంబకోణ త్రిభుజము.

ప్రశ్న 3.
ΔABC ఒక సమద్విబాహు త్రిభుజము. సమాన భుజాలు AC, AB లకు గీసిన లంబాలు వరుసగా BE మరియు CF అయిన ఈ లంబాలు సమానమని చూపండి.

సాధన.
దత్తాంశము నుండి ΔABC ఒక సమద్విబాహు త్రిభుజము.
AC = AB; BD ⊥ AC; CE ⊥ AB
ΔBCD మరియు ΔCBE లలో
∠BDC = ∠CEB = 90° (దత్తాంశం నుండి)
∠BCD = ∠CBE (∵ త్రిభుజంలో సమాన భుజాలకు ఎదురుగా గల కోణాలు సమానం)
BC = BC
∴ ΔBCD ≅ ΔCBE (∵ కో.కో. భు. నియమము)
⇒ BD = CE (CPCT)

ప్రశ్న 4.
ΔABC లో AC, AB భుజాలకు గీసిన లంబాలు BE, CF లు సమానము (పటము చూడండి) అయిన
i) ΔABD ≅ ΔACE
ii) AB = AC అనగా ΔABC ఒక సమద్విబాహు త్రిభుజమని చూపండి.

సాధన.
దత్తాంశం నుండి BD ⊥ AC; CE ⊥ AC
BD = CE
ΔABD మరియు ΔACE లలో
∠ADB = ∠AEC = 90° (దత్తాంశం నుండి)
∠A = ∠A (ఉమ్మడి కోణము)
BD = CE.
∴ ΔABD ≅ ΔACE (∵ కో.కో.భు. నియమం )
⇒ AB = AC (∵ CPCT)

ప్రశ్న 5.
ΔABC, ΔDBC లు ఒకే భుజము BC పై ఉన్న రెండు సమద్విబాహు త్రిభుజములు (పటము చూడండి) అయిన ∠ABD = ∠ACD అని చూపండి.

సాధన.

దత్తాంశం : ΔABC మరియు ΔDBC లు సమద్విబాహు త్రిభుజాలు.
సారాంశము : ∠ABD = ∠ACD
నిర్మాణం : A మరియు D లను కలుపుము.
ఉపపత్తి : ΔABD మరియు ACD లలో
AB = AC (∵ సమద్విబాహు త్రిభుజం యొక్క సమాన భుజాలు)
BD = CD (∵ సమద్విబాహు త్రిభుజం యొక్క సమాన భుజాలు)
AD = AD (∵ ఉమ్మడి భుజము)
∴ ΔABD ≅ ΔACD
(∵ భు.భు.భు. నియమం నుండి)
⇒ ∠ABD = ∠ACD (CPCT)

SCERT AP 9th Class Maths Solutions Chapter 7 త్రిభుజాలు Ex 7.1 Textbook Exercise Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 7th Lesson త్రిభుజాలు Exercise 7.1

ప్రశ్న 1.
చతుర్భుజం ACBD లో, AC = AD మరియు ∠Aకు AB కోణ సమద్విఖండనరేఖ అయిన ΔABC ≅ ΔABD అని చూపండి. BC మరియు BD ల గురించి మీరు ఏమి చెప్పగలరు ?

సాధన.
దత్తాంశము AC = AD
∠BAC = ∠BAD
(∵ ∠A ను AB సమద్విఖండన చేయును)
ΔABC మరియు ΔABD లలో
AC = AD (∵ దత్తాంశము)
∠BAC = ∠BAD (∵ దత్తాంశము)
AB = AB (ఉమ్మడి భుజము)
భు-కో-భు నియమం ప్రకారము
ΔABC = ΔABD
రెండు త్రిభుజాలు సర్వసమానం కావున వాటి అనురూప భుజాలు సమానం.
∴ BC = BD

ప్రశ్న 2.
ABCD చతుర్భుజంలో AD = BC మరియు ∠DAB = ∠CBA అయిన
i) ΔABD ≅ ΔBAC
ii) BD = AC
iii) ∠ABD = ∠BAC అని నిరూపించుము.

సాధన.
i) దత్తాంశం AD = BC మరియు
∠DAB = ∠CBA
ΔABD మరియు ΔBAC లలో
AB = AB (∵ ఉమ్మడి భుజము)
AD = BC (∵ దత్తాంశం)
∠DAB = ∠CBA (∵ దత్తాంశం)
భు-కో-భు నియమం ప్రకారం
ΔABD ≅ ΔBAC
ii) AC = BD (∵ CPCT)
iii) ∠ABD = ∠BAC [∵ CPCT , (i) నుండి]

ప్రశ్న 3.
AD, BCలు సమానము మరియు రేఖాఖండము AB కి లంబములు. అయిన CD రేఖాఖండము AB ని సమద్విఖండన చేయునని చూపుము.

సాధన.
దతాంశం AD = BC; AD ⊥ AB; BC ⊥ AB
ΔBOC మరియు ΔAOD లలో
∠BOC = ∠AOD (∵ శీర్షాభిముఖ కోణములు సమానము)
∠OBC = ∠OAD (∵ లంబకోణము)
BC = AD
కో.కో.భు. నియమం నుండి,
∴ ΔOBC ≅ ΔOAD
∴ OB = OA (∵ CPCT)
∴ AB ని ‘O’ బిందువు సమద్విఖండన చేయును.
OD = OC
∴ CD ని ‘O’ బిందువు సమద్విఖండన చేయును.
⇒ CD రేఖాఖండము AB ని సమద్విఖండన చేయును.

ప్రశ్న 4.
l, m అనే ఒక జత సమాంతర రేఖలు p మరియు q అనే వేరొక జత సమాంతర రేఖలచే ఖండించబడినవి. అయిన ΔABC ≅ ΔCDA అని నిరూపించుము.

సాధన.
దత్తాంశం l // m; p // q
ΔABC మరియు ΔCDA లలో
∠BAC = ∠DCA (∵ ఏకాంతర కోణములు సమానము)
∠ACB = ∠CAD
AC = AC
కో-భు-కో నియమము నుండి
∴ ΔABC ≅ ΔCDA

ప్రశ్న 5.
క్రింది పటంలో AC = AE; AB = AD మరియు ∠BAD = ∠EAC అయిన BC = DE అని నిరూపించుము.

సాధన.
దత్తాంశం AC = AE, AB = AD మరియు
∠BAD = ∠EAC
ΔABC మరియు ΔADE లలో
AB = AD
AC = AE
∠BAD = ∠EAC
భు-కో-భు నియమం నుండి,
∴ ΔABC ≅ ΔADE
⇒ BC = DE (CPCT)

ప్రశ్న 6.
లంబకోణ త్రిభుజము ABC లో లంబకోణము C వద్ద ఉన్నది. కర్ణము AB యొక్క మధ్య బిందువు M. C బిందువును M కు కలిపి DM = CM అగునట్లు D బిందువు వద్దకు పొడిగించినారు. పటంలో చూపినట్లు D బిందువును B బిందువుకు కలిపినారు. అయిన క్రింది వాటిని నిరూపించండి.

i) ΔAMC ≅ ΔBMD
ii) ∠DBC ఒక లంబకోణము
iii) ΔDBC ≅ ΔACB
iv) CM = \(\frac {1}{2}\)AB
సాధన.
దత్తాంశము ∠C = 90°
AB యొక్క మధ్య బిందువు M ;
DM = CM (i.e, DC మధ్య బిందువు M)

i) ΔAMC మరియు ΔBMD లలో
AM = BM (∵ AB మధ్య బిందువు M)
CM = DM (∵ CD మధ్య బిందువు M)
∠AMC = ∠BMD (∵ శీర్షాభిముఖ కోణాలు)
భు-కో-భు నియమం నుండి,
∴ ΔAMC ≅ ΔBMD

ii) ∠MDB = ∠MCA
(ΔAMC మరియు ΔBMD ల CPCT)
కాని ఈ కోణములు ఏకాంతర కోణాలు. అవి DB మరియు AC రేఖలను DC తిర్యగ్రేఖ ఖండించడం వలన ఏర్పడినవి.
∴ DB || AC
మరియు AC ⊥ BC; DB ⊥ BC
∴ ∠DBC ఒక లంబకోణం.

iii) ΔDBC మరియు ΔACB లలో
DB = AC (ΔBMD మరియు ΔAMC ల CPCT)
∠DBC = ∠ACB = 90° (నిరూపించబడినది)
BC = BC (ఉమ్మడి భుజము)
భు-కో-భు నియమము ప్రకారము,
ΔDBC ≅ ΔACB

iv) DC = AB (ΔDBC మరియు ΔACB ల యొక్క CPCT)
\(\frac {1}{2}\)DC = \(\frac {1}{2}\)AB (ఇరువైపులా 2 చే భాగించగా)
CM = \(\frac {1}{2}\)AB

ప్రశ్న 7.
క్రింది పటంలో ABCD ఒక చతురస్రము మరియు ΔAPB ఒక సమబాహు త్రిభుజము అయిన ΔAPD ≅ ΔBPC అని నిరూపించుము.
(సూచన : ΔAPD మరియు ΔBPCలలో \(\overline{\mathrm{AD}}=\overline{\mathrm{BC}}, \overline{\mathrm{AP}}=\overline{\mathrm{BP}}\) మరియు ∠PAD = ∠PBC = 90° – 60° = 30°)

సాధన.
దత్తాంశము □ABCD ఒక చతురస్రము.
ΔAPB ఒక సమబాహు త్రిభుజము.
ΔAPD మరియు ΔBPC లలో
AP = BP (∵ సమబాహు త్రిభుజ భుజాలు)
AD = BC (∵ చతురస్ర భుజములు)
∠PAD = ∠PBC [∵ 90° – 60°]
∴ ΔAPD ≅ ΔBPC (భు.కో.భు. నియమం ద్వారా)

ప్రశ్న 8.
క్రింది పటంలో AB = AC కావున ΔABC ఒక సమద్విబాహు త్రిభుజము BA మరియు \(\overline{\mathrm{CA}}\) లను \(\overline{\mathrm{AQ}}\) = \(\overline{\mathrm{AP}}\) అగునట్లు వరుసగా Q, P బిందువుల వద్దకు పొడిగించిన \(\overline{\mathrm{PB}}\) = \(\overline{\mathrm{QC}}\) అని నిరూపించుము.
(సూచన : ΔAPBమరియు ΔACQలను పోల్చుము)

సాధన.
దత్తాంశం నుండి ΔABC ఒక సమద్విబాహు త్రిభుజము.
AP = AQ
ΔAPB మరియు ΔAQC లలో
AP = AQ (దత్తాంశము)
AB = AC (దత్తాంశము)
∠PAB = ∠QAC (∵ శీర్షాభిముఖ కోణాలు)
∴ ΔAPB = ΔAQC (∵ భు-కో-భు నియమము)
∴ \(\overline{\mathrm{PB}}\) = \(\overline{\mathrm{QC}}\) (ΔAPB మరియు ΔAQC ల యొక్క CPCT)

ప్రశ్న 9.
క్రింది పటంలో ΔABC లో BC మధ్య బిందువు D. DE ⊥ AB, DF ⊥ ACమరియు DE = DF అయిన ΔBED ≅ ΔCFD అని నిరూపించుము.

సాధన.
దత్తాంశము నుండి ΔABC లో BC యొక్క మధ్య బిందువు D.
DF ⊥ AC; DE = DF
DE ⊥ AB
ΔBED మరియు ΔCFD లలో
∠BED = ∠CFD = 90° (దత్తాంశం నుండి)
BD = CD (∵ BC మధ్య బిందువు D)
ED = FD (దత్తాంశము)
∴ ΔBED ≅ ΔCFD (లం-క-భు నియమం ప్రకారం)

ప్రశ్న 10.
ఒక త్రిభుజములో ఒక కోణం యొక్క కోణ సమద్వి ఖండనరేఖ ఎదుటి భుజాన్ని కూడా సమద్విఖండన చేసిన ఆ త్రిభుజము సమద్విబాహు త్రిభుజమని చూపుము.
సాధన.

దత్తాంశం : ΔABC ఒక త్రిభుజము. A యొక్క కోణసమద్విఖండన రేఖ BC ను ఖండించును.
సారాంశం : ΔABC ఒక సమద్విబాహు త్రిభుజము
ఉపపత్తి : ఒక త్రిభుజంలో శీర్షకోణ సమద్విఖండన రేఖ ఎదుటి భుజాన్ని సమాన నిష్పత్తిలో ఖండించును.
∴ \(\frac{A B}{A C}=\frac{B D}{D C}\)
⇒ \(\frac{\mathrm{AB}}{\mathrm{AC}}\) = 1 (:: దత్తాంశము)
⇒ AB = AC
∴ ΔABC ఒక సమద్విబాహు త్రిభుజము.

ప్రశ్న 11.
ఇచ్చిన పటంలో ABC ఒక లంబకోణ త్రిభుజము. లంబకోణము శీర్షము B వద్ద కలదు మరియు ∠BCA = 2∠BAC అయిన కర్ణము AC = 2BC అని చూపుము.

(సూచన : BC = BD అగునట్లు CBని D బిందువు వద్దకు పొడిగించుము).
సాధన.

దత్తాంశము : ΔABC ఒక లంబకోణ త్రిభుజము.
∠B = 90° మరియు ∠BCA = 2∠BAC
సారాంశము : AC = 2BC
నిర్మాణం : CB ను D బిందువు వరకు పొడిగించుము.
BC = BD అగును. A, D లను కలుపుము.
ఉపపత్తి : ΔABC మరియు ΔABD లలో
AB = AB (ఉమ్మడి భుజం)
BC = BD (నిర్మాణము)
∠ABC = ∠ABD (∵ లంబకోణము)
∴ ΔABC ≅ ΔABD
⇒ AC = AD మరియు ∠BAC = ∠BAD = 30°
[∵ CPCT]

ΔACD లో, ∠ACD = ∠ADC = ∠CAD = 60°
∴ ΔACD ఒక సమబాహు త్రిభుజము
⇒ AC = CD = AD
⇒ AC = 2BC (∵ BC మధ్య బిందువు C).

AP SCERT 9th Class Maths Textbook Solutions Chapter 9 సాంఖ్యక శాస్త్రము Ex 9.2 Textbook Exercise Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 9th Lesson సాంఖ్యక శాస్త్రము Exercise 9.2

ప్రశ్న 1.
ఒక సరుకుల రవాణా కార్యాలయంలోని పార్సిక్ష ఇరువులు కింది పట్టికలో ఇవ్వబడ్డాయి. ఒక్కొక్క పార్సిలు యొక్క సరాసరి బరువెంత?

సాధన.

\(\overline{\mathrm{X}}\) = \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}=\frac{17000}{200}=\frac{170}{2}\)
\(\overline{\mathrm{X}}\) = 85
∴ సగటు = 85

ప్రశ్న 2.
ఒక గ్రామములోని ప్రతి కుటుంబములో గల పిల్లల వివరాలు కింది పట్టికలో ఇవ్వబడ్డాయి. ఒక్కొక్క కుటుంబములోని సరాసరి పిల్లల సంఖ్య కనుగొనండి.

సాధన.

\(\overline{\mathrm{X}}\) = \(\frac{\Sigma f_{i} x_{i}}{\Sigma f_{i}}=\frac{144}{84}\)
∴ సగటు = 1.714285

ప్రశ్న 3.
కింది పౌనఃపున్య విభాజనము యొక్క సరాసరి 7.2 అయిన ‘K’ విలువను కనుగొనండి.

సాధన.

Σf_i = 40 + k, Σf_ix_i = 260 + 10k
ఇచ్చిన సగటు \(\overline{\mathrm{X}}\) = 7.2
కాని సగటు \(\overline{\mathrm{X}}\) = \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathbf{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}[latex]
7.2 = [latex]\frac{260+10 k}{40+k}\)
288.0 + 7.2k = 260 + 10k
10k – 7.2k = 288 – 260
2.8k = 28
k = \(\frac {28}{2.8}\) = 10

ప్రశ్న 4.
భారతదేశ జన గణన ప్రకారం గ్రామములు, జనాభా వివరాలు కింది విధంగా ఇవ్వబడ్డాయి. (జనాభా దగ్గర వేలకు సవరించబడినది) ఒక్కొక్క గ్రామం యొక్క సరాసరి జనాభా ఎంత ?

సాధన.

Σf_i = 145 Σf_ix_i = 2571 వేలు
∴ సగటు \(\overline{\mathrm{X}}\) = \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}=\frac{2571}{145}\) = 17.731 వేలు

ప్రశ్న 5.
AFLATOUN అనే సాంఘిక, ఆర్థిక విద్యావిషయక సంస్థ హైదరాబాదు జిల్లాలోని ఉన్నత పాఠశాలల విద్యార్థులచే పొదుపు కార్యక్రమమును ప్రారంభించింది. మండలాలవారీగా ఒక్క నెలలో పొదుపు చేయబడిన మొత్తాలు ఇవ్వబడ్డాయి.

ఒక్కొక్క మండలంలో పాఠశాలవారీ సరాసరి పొదుపు మొత్తమెంత ? జిల్లా మొత్తంమీద పాఠశాల సరాసరి పొదుపు ఎంత ?
సాధన.

Σf_i = 33 Σf_ix_i = 14652
∴ సగటు = \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\)
\(\overline{\mathrm{X}}\) =\(\frac{14652}{33}\) = ₹444

ప్రశ్న 6.
ఒక పాఠశాలలోని 9వ తరగతి బాల బాలికల ఎత్తుల వివరాలు ఈ విధంగా ఉన్నవి.

బాల బాలికల ఎత్తులను పోల్చండి.
సూచన : బాలబాలికల మధ్యగత ఎత్తును కనుగొనండి.]
సాధన.

బాలుర మధ్యగత తరగతి = \(\frac{37+1}{2}=\frac{38}{2}\) = 19 వ అంశము
∴ బాలుర యొక్క ఎత్తు = 147 సెం.మీ.
బాలికల మధ్యగత తరగతి = \(\frac{29+1}{2}=\frac{30}{2}\) = 15వ అంశము
∴ బాలికల యొక్క ఎత్తు = 152 సెం.మీ.

ప్రశ్న 7.
ప్రపంచ క్రికెట్ ఆటగాళ్లలో శతకాలు (100 పరుగులు) చేసిన వారి సంఖ్యలు కింది పట్టికలో ఇవ్వబడ్డాయి.

ఈ దత్తాంశమునకు సరాసరి, మధ్యగతము, బాహుళకములను కనుగొనండి.
సాధన.

N = Σf_i = 139 Σf_ix_i = 1555
సగటు \(\overline{\mathrm{x}}=\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}=\frac{1555}{139}\) = 11.187
మధ్యగతము = (\(\frac {N}{2}\) + 1) వ పదం \(\frac{139+1}{2}=\frac{140}{2}\) = 70వ పదం = 10 బాహుళకము = 5

ప్రశ్న 8.
కొత్త సంవత్సరాది సందర్భముగా ఒక మిఠాయి దుకాణం వారు మిఠాయి పొట్లాలను సిద్ధపరుచుచున్నారు. ఒక్కొక్క మీఠాయి పొట్లాం ధర, సిద్ధపరచిన పొట్లాల సంఖ్యలు కింది పౌనఃపున్య విభాజనములో ఇవ్వబడ్డాయి.

పై దత్తాంశమునకు అంకగణిత మధ్యమము, మధ్యగతము, బాహుళకములు కనుగొనండి.
సాధన.

N = Σf_i = 150 Σf_ix_i = 12000
సగటు = \(\overline{\mathrm{x}}=\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}=\frac{12000}{150}\) = 80
మధ్యగతము = (\(\frac{N}{2}\) మరియు \(\frac{N}{2}\) + 1) ల సగటు = 75 మరియు 76 అంశాల సగటు = 75 బాహుళకం = 50

ప్రశ్న 9.
ముగ్గురు విద్యార్థుల సగటు బరువు 40 కి.గ్రా. వారిలో రంగా బరువు 46 8.గ్రా, మరియు మిగిలిన ఇద్దరు విద్యార్థులు రహీమ్, రేష్మాల బరువులు సమానం అయిన రహీమ్ బరువు ఎంత ?
సాధన.
రంగా బరువు = 46 కి.గ్రా.
రేష్మా బరువు = రహీమ్ బరువు = x కి.గ్రా. అనుకొనుము.
సగటు = విద్యార్ధుల బరువుల మొత్తం / విద్యార్థుల సంఖ్య = 40కి.గ్రా.
∴ 40 = \(\frac {46+x+x}{3}\)
40 × 3 = 46 + 2x
120 – 46 = 2x
2x = 74
∴ x = \(\frac {74}{2}\) = 37
∴ రహీమ్ బరువు = 37 కి.గ్రా.

ప్రశ్న 10.
ఒక ఉన్నత పాఠశాలలోని వివిధ తరగతుల విద్యార్థులు ఒక అనాథశరణాలయంనకు ఇచ్చిన విరాళములు (రూపాయలలో) కింది విధంగా ఉన్నవి.

ఈ వివరాలకు అంకగణిత మధ్యమము, మధ్యగతము, బాహుళకములు కనుగొనండి.
సాధన.

సగటు \(\overline{\mathrm{x}}=\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}=\frac{900}{80}\) = 11.25
మధ్యగతము = (\(\frac{N}{2}\) మరియు \(\frac{N}{2}\) + 1) ల సగటు = \(\frac{80}{2}\), (\(\frac{80}{2}\) + 1) అంశాల సగటు
= 40 మరియు 41 అంశాల సగటు = ₹10
∴ ఈ బాహుళకము = ₹10

ప్రశ్న 11.
నాలుగు సంఖ్యలలో మొదటి రెండింటి సరాసరి 4, మొదటి మూడింటి సరాసరి కి, అన్నింటి సరాసరి 15 మరియు ఆ సంఖ్యలలో ఒకటి 2 అయిన మిగిలిన సంఖ్యలను కనుగొనుము.
సాధన.
సాధారణముగా సగటు = రాశుల మొత్తము / రాశుల సంఖ్య
దత్తాంశము 4 సంఖ్యల సగటు = 15 ⇒ 4 సంఖ్యల మొత్తము = 15 × 4 = 60
మొదటి 3 సంఖ్యల సగటు = 9 ⇒ మొదటి 3 సంఖ్యల మొత్తము = 9 × 3 = 27
మొదటి 2 సంఖ్యల సగటు = 4 ⇒ మొదటి 2 సంఖ్యల సగటు = 4 × 2 = 8
నాల్గవ సంఖ్య = నాలుగు సంఖ్యల మొత్తం-మూడు సంఖ్యల మొత్తం = 60 – 27 = 33
మూడవ సంఖ్య = మూడు సంఖ్యల మొత్తం – రెండు సంఖ్యల మొత్తం = 27 – 8 = 19
రెండవ సంఖ్య = రెండు సంఖ్యల మొత్తం – ఇచ్చిన సంఖ్య = 8 – 2 = 6
∴ మిగిలిన మూడు సంఖ్యలు = 6, 19, 33

SCERT AP 9th Class Maths Solutions Chapter 6 రెండు చరరాశులలో రేఖీయ సమీకరణాలు InText Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 6th Lesson రెండు చరరాశులలో రేఖీయ సమీకరణాలు InText Questions

ఇవి చేయండి

1. కింది రేఖా సమీకరణాలను ax + by + c = 0 రూపంలో రాసి, ప్రతి సందర్భంలోనూ a, b మరియు c విలువలు రాయండి. [పేజీ నెం. 128]
i) 3x + 2y = 9
సాధన.
ఇచ్చిన రేఖ 3x + 2y = 9 ను ax + by + c = 0 రూపంలో వ్రాయగా 3x + 2y – 9 = 0.
∴ a = 3, b = 2, c = – 9

ii) – 2x + 3y = 6
సాధన.
ఇచ్చిన రేఖ – 2x + 3y = 6 ను ax + by + c = 0 రూపంలో వ్రాయగా
– 2x + 3y – 6 = 0 ⇒ 2x – 3y + 6 = 0
∴ a = 2, b = – 3, c = 6

iii) 9x – 5y = 10
సాధన.
ఇచ్చిన రేఖ 9x – 5y = 10 ను ax + by + c = 0 రూపంలో వ్రాయగా 9x – 5y – 10 = 0
∴ a = 9, b = – 5, c = – 10

iv) \(\frac{x}{2}-\frac{y}{3}-5=0\)
సాధన.
ఇచ్చిన రేఖ \(\frac{x}{2}-\frac{y}{3}-5=0\)
⇒ \(\frac{3 x-2 y-30}{6}\) = 0 (2, 3 ల క.సా.గు = 6)
⇒ 3x – 2y – 30 = 0
∴ a = 3, b = – 2, c = – 30

v) 2x = y
సాధన.
ఇచ్చిన రేఖ 2x = y ను ax + by + c = 0 రూపంలో వ్రాయగా 2x – y = 0.
∴ a = 2, b = – 1, c = 0

2. i) కింది సమీకరణాలకు రేఖాచిత్రాలు గీయండి. [పేజీ నెం. 145]
a) x = 2
b) x = – 2
c) x = 4
d) x = – 4
సాధన.

ii) ఈ రేఖాచిత్రాలన్నీ Y- అక్షానికి సమాంతరంగా ఉన్నాయా ?
సాధన.
అవును, ఈ రేఖలన్నీ Y- అక్షానికి సమాంతరంగా వున్నాయి.

iii) ప్రతీ సందర్భంలో రేఖాచిత్రానికి, Y- అక్షానికి మధ్యగల దూరమును కనుగొనుము.
సాధన.

3. i) కింది సమీకరణాలకు రేఖాచిత్రాలను గీయండి. [పేజీ నెం. 145]
a) y = 2
b) y = – 2
c) y = 3
d) y = – 3
సాధన.
ప్రశ్న 1 లో గల గ్రాఫును చూడుము.

ii) ఈ రేఖాచిత్రాలన్నీ X- అక్షానికి సమాంతరంగా ఉన్నాయా ?
సాధన.
అవును, ఈ రేఖలన్నీ X – అక్షంకు సమాంతరంగా ఉన్నాయి.

iii) ప్రతీ సందర్భములో రేఖాచిత్రానికి, X- అక్షానికి మధ్యగల దూరమును కనుగొనుము.
సాధన.

4. 3x – 2y = 5 సమీకరణమునకు 5 సాధనలను కనుగొనుము. [పేజీ నెం. 130]
సాధన.
ఇచ్చిన సమీకరణం 3x – 2y = 5

ప్రయత్నించండి

1. ఒక గ్రాఫ్ పేపరుపై (2, 4) బిందువును గుర్తించుము. ఈ బిందువు గుండా ఒక రేఖను గీచి కింది ప్రశ్నలకు సమాధానమిమ్ము. [పేజీ నెం. 135]
1. ఈ (2, 4) బిందువు గుండా మరొక రేఖను గీయగలవా ?
సాధన.
అవును, (2, 4) బిందువు గుండా మరొక రేఖను గీయగలను.

2. ఇలాంటి ఎన్ని రేఖలను గీయగలము ?
సాధన.
ఇలాంటివి అనంత రేఖలను గీయగలము.

3. (2, 4) బిందువు సాధనగా గల రెండు చరరాశులలో రేఖీయ సమీకరణాలు ఎన్ని ఉన్నాయి ?
సాధన.
(2, 4) బిందువు సాధనగా అనంత రేఖీయ సమీకరణాలు ఉన్నాయి.

2. Y- అక్షం సమీకరణమును కనుగొనుము. [పేజీ నెం. 146]
సాధన.
Y- అక్షంపై గల బిందువులన్నింటికి x – నిరూపకము సున్న.
∴ Y- అక్షం సమీకరణము x = 0.

ఉదాహరణలు

1. సచిన్ మరియు సెహ్వాగ్ కలిసి 137 పరుగులు చేశారు. ఈ సమాచారమును రెండు చరరాశులలో రేఖీయ సమీకరణంగా వ్యక్తపరచండి. [పేజీ నెం. 125]
సాధన.
సచిన్ చేసిన పరుగుల సంఖ్యను ‘x’ మరియు సెహ్వాగ్ చేసిన పరుగుల సంఖ్యను ‘y’ అనుకొనిన
పై దత్తాంశమును సమీకరణ రూపంలో x + y = 137 గా రాయవచ్చు.

2. హేమ వయస్సు, మేరీ వయస్సుకు 4 రెట్లు. ఈ దత్తాంశమునకు సరిపోవు రెండు చరరాశులలో రేఖీయ సమీకరణమును రాయుము. [పేజీ నెం.126]
సాధన.
హేమ వయస్సును ‘x’ సంవత్సరాలు అని, మేరి వయస్సును ‘y’ సంవత్సరాలు అని అనుకొనుము.
అయితే దత్తాంశము ప్రకారము, హేమ వయస్సు = మేరి వయస్సుకు 4 రెట్లు.
అనగా x = 4y ⇒ x – 4y = 0 (ఎలా ?) ఇది ఒక రేఖీయ సమీకరణము అయినది.

3. ఒక సంఖ్య, దానిలోని అంకెలను తారుమారు చేయగా వచ్చే సంఖ్య కంటే 27 ఎక్కువ. సంఖ్యలోని ఒకట్ల, పదుల స్థానములోని అంకెలను వరుసగా x, y అనుకొని ఈ దత్తాంశమునకు సరిపోవు రెండు చరరాశులలో రేఖీయ సమీకరణమును రాయుము. [పేజీ నెం. 126]
సాధన.
ఒకట్ల స్థానములోని అంకె x మరియు పదుల స్థానములోని అంకె y అనుకొనిన ఆ సంఖ్య = 10y + x
సంఖ్యలోని అంకెలను తారుమారు చేయగా వచ్చే సంఖ్య = 10x + y (రెండు అంకెల సంఖ్య యొక్క స్థానవిలువను గుర్తుకు తెచ్చుకోండి).
∴ దత్తాంశము ప్రకారము
సంఖ్య – తారుమారు చేయగా వచ్చే సంఖ్య = 27.
∴ 10y + x – (10x + y) = 27
⇒ 10y + x – 10x – y – 27 = 0
⇒ 9y – 9x – 27 = 0
⇒ y – x – 3 = 0
∴ కావలసిన సమీకరణము x – y + 3 = 0.

4. కింది ప్రతి సమీకరణమును ax + by + c = 0 రూపంలో రాసి a, b మరియు c విలువలను కనుగొనుము. [పేజీ నెం. 126]
i) 3x + 4y = 5
ii) x – 5 = \(\sqrt{3}\)y
iii) 3x = y
iv) \(\frac{x}{2}+\frac{y}{2}=\frac{1}{6}\)
v) 3x – 7 = 0
సాధన.
i) 3x + 4y = 5 ను 3x + 4y – 5 = 0 గా రాయవచ్చు. ఇచ్చట a = 3, b = 4 మరియు c = – 5.
ii) x – 5 = \(\sqrt{3}\)y ని 1.x – \(\sqrt{3}\)y – 5 = 0 గా రాయవచ్చు.
ఇచ్చట a = 1, b = – \(\sqrt{3}\) మరియు c = – 5.
iii) సమీకరణము 3x = y ని 3x – y + 0 = 0 గా రాయవచ్చు. ఇచ్చట a = 3, b = – 1 మరియు c = 0.
iv) ఇచ్చిన సమీకరణము \(\frac{x}{2}+\frac{y}{2}=\frac{1}{6}\)
\(\frac{x}{2}+\frac{y}{2}-\frac{1}{6}\) = 0; a = \(\frac {1}{2}\), b = \(\frac {1}{2}\) మరియు c = \(\frac {-1}{6}\)
v) 3x – 7 = 0 ని 3x + 0. y – 7 = 0 గా రాయవచ్చు.
∴ a = 3, b = 0; c = – 7.

5. ఈ క్రింది ప్రతి సమీకరణము ax + by + c = 0 రూపంలోకి మార్చి a, b మరియు c విలువలను కనుగొనుము. [పేజీ నెం. 127]
i) x = – 5
ii) y = 2
iii) 2x = 3
iv) 5y = – 3
సాధన.

6. 4x + y = 9 సమీకరణమునకు 4 వేరు వేరు సాధనలను కనుగొనుము. (పట్టికలో ఖాళీలను పూరింపుము). [పేజీ నెం. 130]

సాధన.

∴ (0, 9), (\(\frac {9}{4}\), 0), (1, 5) మరియు (- 1, 13) లు కొన్ని సాధనలు.

7. కింది వానిలో ఏవి x + 2y = 4 సమీకరణానికి సాధన అవుతాయి ? (పట్టికలో ఖాళీలను పూరించుము.) [పేజీ నెం. 131]

i) (0, 2)
ii) (2, 0)
iii) (4, 0)
iv) (\(\sqrt{2}\), – 3\(\sqrt{2}\))
v) (1, 1)
vi) (- 2, 3)
సాధన.
ఒక జతను ఇచ్చిన సమీకరణంలో ప్రతిక్షేపించినపుడు LHS = RHS అయిన ఆ జతను ఇచ్చిన సమీకరణం యొక్క సాధన అంటామని మనకు తెలుసు.
ఇచ్చట ఇవ్వబడిన సమీకరణము x + 2y = 4

8. 5x – 7y = k కు x = 3, y = 2 సాధన k అయిన విలువను కనుగొనుము. k విలువతో వచ్చే సమీకరణాన్ని రాయండి. [పేజీ నెం.132]
సాధన.
x = 3, y = 2 సాధన అని ఇవ్వబడింది కనుక 5x – 7y = k అయిన 5 × 3 – 7 × 2 = k
⇒ 15 – 14 = k ⇒ 1 = k :
∴ k = 1
కావలసిన సమీకరణం 5x – 7y = 1.

9. 5x + 3y – 7 = 0 యొక్క సాధన x = 2k + 1 మరియు y = k అయిన ఓ విలువ ఎంత ? [పేజీ నెం. 132]
సాధన.
5x + 3y – 7 = 0 సమీకరణమునకు x = 2k + 1; y = k సాధన ఇవ్వబడింది.
⇒ 5(2k + 1) + 3k – 7 = 0 ⇒ 10k + 5 + 3k – 7 = 0
⇒ 13k – 2 = 0 (ఇది ఒక ఏకచరరాశిలో రేఖీయ సమీకరణము).
⇒ 13k = 2
∴ k = \(\frac {2}{13}\)

10. y – 2x = 4 సమీకరణమునకు రేఖాచిత్రమును గీచి కింది ప్రశ్నలకు సమాధానమిమ్ము. [పేజీ నెం. 135]
i) (2, 8) బిందువు రేఖపై ఉన్నదా ? (2, 8) సమీకరణం యొక్క సాధన అవుతుందా ? (2, 8)ను సమీకరణంలో ప్రతిక్షేపించుట ద్వారా సరిచూడుము.
ii) (4, 2) బిందువు రేఖపై ఉన్నదా ? బీజీయ పద్ధతి ద్వారా (4, 2) సమీకరణానికి సాధన అవుతుందేమో సరిచూడుము.
iii) రేఖాచిత్రము నుంచి మరొక మూడు సాధనలను కనుగొనుము. అదే విధముగా సాధనలు కాని వానిని మూడింటిని కనుగొనుము.
సాధన.
ఇవ్వబడిన సమీకరణము y – 2x = 4 ⇒ y = 2x + 4

A, B మరియు C బిందువులను గ్రాఫ్ మీద గుర్తించి వానిని కలిపిన పటములో చూపించిన విధంగా కలిపితే BC రేఖ వస్తుంది. ఇదియే మనకు కావలసిన y- 2x = 4 యొక్క రేఖాచిత్రము అవుతుంది.

i) (2, 8) బిందువును గ్రాఫ్ పేపరుపై గుర్తించిన BC రేఖపై ఉండడం గమనించవచ్చు.
బీజీయ పద్ధతిలో సరిచూచుట (2, 8) బిందువును సమీకరణంలో ప్రతిక్షేపించిన
LHS = y – 2x = 8 – 2 × 2 = 8 – 4 = 4 = RHS,
కనుక (2, 8) సాధన అవుతుంది.

ii) (4, 2) బిందువును గ్రాఫ్ పేపర్ పై గుర్తించిన అది BC రేఖమీద లేకపోవడాన్ని మీరు గమనించవచ్చు.
బీజీయ పద్దతిలో సరిచూచుట : (4, 2) ను ఇచ్చిన సమీకరణంలో ప్రతిక్షేపిస్తే,
LHS = y – 2x = 2 – 2 × 4 = 2 – 8 = – 6 ≠ RHS
∴ (4, 2) సాధన కాదు.

iii) ఒకరేఖ మీది ఏ బిందువైనా సమీకరణానికి సాధన అవుతుందని మనకు తెలుసు. కనుక రేఖమీద ఏవైనా మూడు బిందువులు తీసుకుంటే అవి సాధనలు అవుతాయి. ఉదాహరణకు (- 4, – 4) …. అదే విధంగా రేఖమీదలేని ఏ బిందువు కూడా సాధన కాదని తెలుసు. కనుక రేఖ మీద లేని ఏవైనా మూడు బిందువులను తీసుకుంటే అవి సాధనలు కావు.
ఉదాహరణకు : (i) (1, 5); ………; ………

11. x – 2y = 3 యొక్క రేఖాచిత్రమును గీయుము. [పేజీ నెం. 136]
రేఖాచిత్రము నుంచి ఈ కింది వానిని కనుగొనుము.
i) x = – 5 అయ్యే విధంగా ఒక సాధన (x, y)
ii) y = 0 అయ్యే విధంగా ఒక సాధన (x, y)
iii) x = 0 అయ్యే విధంగా ఒక సాధన (x, y)
సాధన.
x – 2y = 3 ⇒ y = \(\frac{x-3}{2}\)

గ్రాఫ్ పేపర్ పై A, B, C బిందువులు గుర్తించి వానిని కలిపిన కింది పటములో చూపిన విధంగా రేఖ వస్తుంది. ఈ రేఖయే కావలసిన x – 2y = 3 యొక్క రేఖాచిత్రము అవుతుంది.

i) x = – 5 అయ్యే ఒక సాధన (x, y) ని మనము కనుగొనవలె. అనగా రేఖమీద ఉంటూ దాని x – నిరూపకము ‘- 5′ అయ్యే బిందువును కనుగొనవలె. దీనిని కనుగొనుటకు x = – 5 వద్ద నుంచి Y – అక్షమునకు సమాంతరంగా ఒక రేఖను గీయవలె. అది గ్రాఫ్ ‘P’ వద్ద ఖండిస్తుంది అనుకొనుము. ఈ బిందువు ‘P’ నుంచి X – అక్షానికి సమాంతరంగా రేఖ గీచిన అది Y – అక్షమును – 4 వద్ద ఖండిస్తుంది. (తాకుతుంది).
కనుక P బిందువు నిరూపకాలు = (- 5, – 4)
P(- 5, – 4) బిందువు x – 2y = 3 రేఖపై ఉన్నది కావున అది ఒక సాధన అవుతుంది.

ii) y = 0 అయ్యే విధంగా ఒక సాధన (x, y) ని కనుగొనాలి.
y = 0 కనుక బిందువు (x, 0) అవుతుంది. కావున y = 0 కనుక బిందువు X- అక్షంపై ఉంటూ x – 2y = 3 రేఖాచిత్రము మీద ఉండే బిందువును కనుగొనాలి.
రేఖాచిత్రము నుంచి ఇలాంటి బిందువు (3, 0) అని గమనించగలము.
∴ సాధన = (3, 0).

iii) x = 0 అయ్యే విధంగా ఒక సాధన (x, y) ని కనుగొనవలె.
x = 0 కనుక బిందువు (0, y) అవుతుంది. అనగా బిందువు Y – అక్షంపై ఉంటుంది. అంటే Y – అక్షం పై ఉంటూ x – 2y = 3 గ్రాఫ్ మీద ఉండే బిందువును కనుగొనాలి.
రేఖాచిత్రము నుంచి ఇలాంటి బిందువు (0, \(\frac {-3}{2}\)) అని గుర్తించగలము.
∴ సాధన = (0, \(\frac {-3}{2}\))

12. ఒక పాఠశాలలో 25% బాలికలు, మిగిలినవారు బాలురు. ఈ సమాచారమునకు సరిపోవు రెండు చరరాశులలో రేఖీయ సమీకరణమును రూపొందించి దానికి రేఖాచిత్రము గీయుము. రేఖాచిత్రము నుంచి ఈ కింది ప్రశ్నలకు సమాధానమును రాబట్టుము. [పేజీ నెం. 138]

i) బాలికల సంఖ్య 25 అయిన బాలుర సంఖ్య ఎంత ?
ii) బాలుర సంఖ్య 45 అయిన బాలికల సంఖ్య ఎంత ?
iii) బాలుర సంఖ్యకు మూడు వేరువేరు విలువలను తీసుకొని అనురూపంగా బాలికల సంఖ్యను కనుగొనుము. అదే విధంగా బాలికల సంఖ్యకు మూడు వేరువేరు విలువలను తీసుకొని అనురూపంగా బాలుర సంఖ్యను కనుగొనుము.
సాధన.
బాలికల సంఖ్యను ‘x’ మరియు బాలుర సంఖ్యను ‘y’ అనుకొనిన
మొత్తం విద్యార్థుల సంఖ్య = x + y
ఇచ్చిన దత్తాంశము ప్రకారము బాలికల సంఖ్య మొత్తం విద్యార్థులలో = 25% అంటే,
x = (x + y) లో 25% = (x + y) × \(\frac {25}{100}\) లో (x + y) = \(\frac {1}{4}\) (x + y)
x = \(\frac {1}{4}\)(x + y) ⇒ 4x = x + y ⇒ 3x = y
∴ కావలసిన సమీకరణము 3x = y లేదా 3x – y = 0.

గ్రాఫ్ పై A, B మరియు C బిందువులను గుర్తించి వానిని కలిపిన కింది పటములో చూపిన విధంగా AB రేఖ ఏర్పడుతుంది.
స్కేలు : X-అక్షం : 1 సెం.మీ. = 20 బాలికలు
Y-అక్షం : 1 సెం.మీ. = 20 బాలురు

రేఖాచిత్రము నుండి ఈ కింది వానిని కనుగొనగలము.
i) బాలికల సంఖ్య 25 అయిన బాలుర సంఖ్య 75.
ii) బాలుర సంఖ్య 45 అయిన బాలికల సంఖ్య 15.
iii) బాలుర సంఖ్యకు మీకు నచ్చిన మూడు వేరువేరు సంఖ్యలను తీసుకొని వానికి అనురూపమైన బాలికల సంఖ్యను, అదే విధంగా బాలికల సంఖ్యకు మీకు నచ్చిన మూడు వేరువేరు సంఖ్యలను తీసుకొని వానికి అనురూపమైన బాలుర సంఖ్యను కనుగొనుము. ఇచ్చట గ్రాఫ్ ను, సమీకరణమును పరిశీలించండి. సమీకరణము y = 3x రూపంలో ఉంది మరియు సరళరేఖ మూల బిందువుగుండా పోతుంది. y = mx (m ఏదైనా వాస్తవ సంఖ్య) సమీకరణమునకు రేఖాచిత్రము గీచిన అది మూల బిందువు గుండా పోతుంది అని గమనిస్తారు.

13. కింది ప్రతి రేఖాచిత్రానికి నాలుగు సమీకరణాలు ఇవ్వబడినాయి. వానిలో రేఖాచిత్రాన్ని సూచించు సరియైన సమీకరణమును గుర్తించుము. [పేజీ నెం. 140]
i) సమీకరణాలు :
A) y = x
B) x + y = 0
C) y = 2x
D) 2 + 3y = 7x

ii) సమీకరణాలు :
A) y = x + 2
B) y = x – 2
C) y = – x + 2
D) x + 2y = 6

సాధన.
i) రేఖాచిత్రము (1, – 1) (0, 0) (- 1, 1) బిందువులు ఒకే రేఖ పై ఉండడం మనం గమనించవచ్చు. అనగా ఇవి కావలసిన సమీకరణానికి సాధనలు అవుతాయి. అంటే ఈ బిందువులను కావలసిన సమీకరణంలో ప్రతిక్షేపిస్తే అది తృప్తి చెందుతుంది. మరి ఒక విధంగా చెప్పాలంటే ఈ బిందువులను ఏ సమీకరణంలో ప్రతిక్షేపిస్తే అది తృప్తి చెందుతుందో అదియే కావలసిన సమీకరణము.

(1, – 1) బిందువును మొదటి సమీకరణము y = x లో ప్రతిక్షేపించిన అది తృప్తి చెందదు. కనుక y = x కావలసిన సమీకరణం కాదు. అయితే రెండవ సమీకరణము తృప్తి చెందుతుంది. నిజానికి పై మూడు బిందువులకు ఈ సమీకరణము తృప్తి చెందుతుంది. కనుక x + y = 0 కావలసిన సమీకరణం అవుతుంది.
మిగిలిన రెండు సమీకరణాలలో ఈ బిందువులను ప్రతిక్షేపించినప్పుడు అవి తృప్తి చెందవు. కనుక అవి కావలసిన సమీకరణాలు కావు.

ii) రేఖాచిత్రములో (2, 0), (0, 2) మరియు (- 1, 3) బిందువులు రేఖపై ఉన్నాయి. ఈ బిందువులు మొదటి, రెండవ సమీకరణాలను తృప్తిపరచవు. మూడవ సమీకరణము y = – x + 2 ను తీసుకుందాం. దీనిలో పై బిందువులను ప్రతిక్షేపించినప్పుడు అది తృప్తి చెందుతుంది. కనుక y = – x + 2 కావలసిన సమీకరణం అవుతుంది. ఈ బిందువులు x + 2y = 6 ను తృప్తిపరుస్తాయోమో పరిశీలించుము.

AP SCERT 9th Class Maths Textbook Solutions Chapter 9 సాంఖ్యక శాస్త్రము Ex 9.1 Textbook Exercise Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 9th Lesson సాంఖ్యక శాస్త్రము Exercise 9.1

ప్రశ్న 1.
కింది పౌనఃపున్య విభాజనము నుండి రాశులు, వాని పౌనఃపున్యములు గల పట్టిక తయారుచేయండి.

సాధన.

ప్రశ్న 2.
9వ తరగతిలోని 36 మంది యొక్క రక్తం గ్రూపులు ఈ విధంగా ఉన్నవి.

ఈ దత్తాంశమునకు పౌనఃపున్య విభాజన పట్టికను తయారుచేయండి. అతి సామాన్యమైన గ్రూపు ఏది ? అరుదైన గ్రూపు ఏది ?
సాధన.

పట్టిక నుంచి ‘O’ సామాన్య గ్రూపు మరియు ‘AB’ అరుదైన గ్రూపు.

ప్రశ్న 3.
ఒక్కొక్కసాగికి మూడు నాణెముల చొప్పున 30 సార్లు ఎగురవేసి ఒక్కొక్కసారికి పడిన బొమ్మలను లెక్కించడం కింది విధంగా ఉంది.

దత్తాంశమునకు పౌనఃపున్య విభాజన పట్టిక తయారుచేయండి.
సాధన.

ప్రశ్న 4.
ఒక టి.వి. ఛానల్ వారు ధూమపాన నిషేధముపై SMS (సంక్షిప్త సందేశాలు) అభిప్రాయములను ఆహ్వానించిరి. ఇచ్చిన ఐచ్ఛికములు, A – పూర్తి నిషేధము, B – బహిరంగ ప్రదేశములలో నిషేధము, C – నిషేధము అవసరం లేదు. అని ఇవ్వగా SMS సమాధానములు ఇట్లున్నవి:

దత్తాంశమునకు వర్గీకృత పౌనఃపున్య విభాజనము తయారుచేయండి. సరియైన SMS సమాధానములు ఎన్ని ? వానిలో అధిక సంఖ్యాకుల అభిప్రాయము ఏది ?
సాధన.

మొత్తం వచ్చిన సమాధానములు = 19 + 36 + 10 = 65
అధిక సంఖ్యాకుల అభిప్రాయము = B.

ప్రశ్న 5.
కింది కమ్మీ రేఖాచిత్రము నుండి పౌనఃపున్య విభాజన పట్టికను రాయండి.

సాధన.

ప్రశ్న 6.
కింది పటంలో ఇవ్వబడిన సోపాన రేఖాచిత్రము నుండి పౌనఃపున్య విభాజనమును తయారుచేయండి. రేఖాచిత్రములో ఉపయోగించిన (అక్షములపై) స్కేలును తెల్పండి.

సాధన.
పౌనఃపున్య విభాజన పట్టిక :

స్కేలు : X – అక్షం : 1 సెం.మీ. = 1 తరగతి అంతరం
Y – అక్షం : 1 సెం.మీ. = 10 మంది విద్యార్థులు

ప్రశ్న 7.
75 మార్కులకు రాయబడిన పరీక్షలో 30 మంది విద్యార్థులు సాధించిన మార్కులు ఇవ్వబడ్డాయి.
42, 21, 50, 37, 42, 37, 38, 42, 49, 52, 38, 53, 57, 47, 29, 59, 61, 33, 17, 17, 39, 44, 42, 39, 14, 7, 27, 19, 54,51. ఈ దత్తాంశమునకు సమాన తరగతులతో (0-10, 10-20 ….) పౌనఃపున్య విభాజన పట్టిక తయారుచేయండి.
సాధన.

ప్రశ్న 8.
ఒక వీధిలోని 25 ఇండ్ల యొక్క నెలవారి విద్యుత్ వినియోగపు బిల్లులు (రూపాయలలో) ఇవ్వబడ్డాయి. తరగతి పొడవు రూ. 75 ఉందునట్లుగా ఈ దత్తాంశమునకు పౌనఃపున్య విభాజన పట్టిక తయారుచేయండి.
170, 212,252, 225, 310,712,412, 425, 322, 325, 192, 198, 230, 320,412,530, 602, 724, 370, 402, 317,403, 405, 372,413.
సాధన.
పరిశీలనాంశాలలో కనిష్ఠ విలువ = 170
పరిశీలనాంశాలలో గరిష్ఠ విలువ = 724

ప్రశ్న 9.
ఒక సంస్థవారు తయారుచేసిన కారు బ్యాటరీలలో 40 బ్యాటరీల జీవిత కాలం (సంవత్సరాలలో) కింది విధంగా నమోదు చేసారు.

పై దత్తాంశమునకు మినహాయింపు తరగతులలో పౌనఃపున్య విభాజన పట్టిక తయారుచేయండి. తరగతి అంతరం 0.5 గా తీసుకొని 2-2.5 తరగతితో ప్రారంభించండి.
సాధన.