SCERT AP 9th Class Maths Solutions Chapter 6 రెండు చరరాశులలో రేఖీయ సమీకరణాలు InText Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 6th Lesson రెండు చరరాశులలో రేఖీయ సమీకరణాలు InText Questions
ఇవి చేయండి
1. కింది రేఖా సమీకరణాలను ax + by + c = 0 రూపంలో రాసి, ప్రతి సందర్భంలోనూ a, b మరియు c విలువలు రాయండి. [పేజీ నెం. 128]
i) 3x + 2y = 9
సాధన.
ఇచ్చిన రేఖ 3x + 2y = 9 ను ax + by + c = 0 రూపంలో వ్రాయగా 3x + 2y – 9 = 0.
∴ a = 3, b = 2, c = – 9
ii) – 2x + 3y = 6
సాధన.
ఇచ్చిన రేఖ – 2x + 3y = 6 ను ax + by + c = 0 రూపంలో వ్రాయగా
– 2x + 3y – 6 = 0 ⇒ 2x – 3y + 6 = 0
∴ a = 2, b = – 3, c = 6
iii) 9x – 5y = 10
సాధన.
ఇచ్చిన రేఖ 9x – 5y = 10 ను ax + by + c = 0 రూపంలో వ్రాయగా 9x – 5y – 10 = 0
∴ a = 9, b = – 5, c = – 10
iv) \(\frac{x}{2}-\frac{y}{3}-5=0\)
సాధన.
ఇచ్చిన రేఖ \(\frac{x}{2}-\frac{y}{3}-5=0\)
⇒ \(\frac{3 x-2 y-30}{6}\) = 0 (2, 3 ల క.సా.గు = 6)
⇒ 3x – 2y – 30 = 0
∴ a = 3, b = – 2, c = – 30
v) 2x = y
సాధన.
ఇచ్చిన రేఖ 2x = y ను ax + by + c = 0 రూపంలో వ్రాయగా 2x – y = 0.
∴ a = 2, b = – 1, c = 0
![]()
2. i) కింది సమీకరణాలకు రేఖాచిత్రాలు గీయండి. [పేజీ నెం. 145]
a) x = 2
b) x = – 2
c) x = 4
d) x = – 4
సాధన.
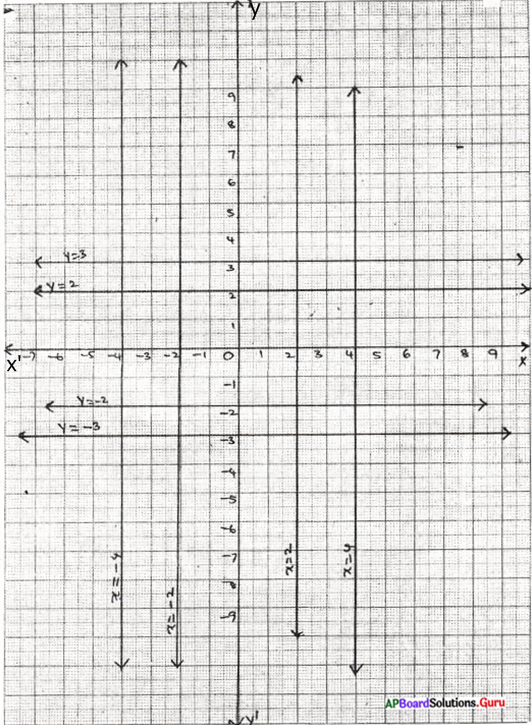
ii) ఈ రేఖాచిత్రాలన్నీ Y- అక్షానికి సమాంతరంగా ఉన్నాయా ?
సాధన.
అవును, ఈ రేఖలన్నీ Y- అక్షానికి సమాంతరంగా వున్నాయి.
iii) ప్రతీ సందర్భంలో రేఖాచిత్రానికి, Y- అక్షానికి మధ్యగల దూరమును కనుగొనుము.
సాధన.
| రేఖాచిత్రము | దూరము | మూల బిందువుకు కుడివైపు / ఎడమవైపు |
| a) x = 2 | 2 యూనిట్లు | కుడివైపు |
| b) x = – 2 | 2 యూనిట్లు | ఎడమవైపు |
| c) x = 4 | 4 యూనిట్లు | కుడివైపు |
| d) x = – 4 | 4 యూనిట్లు | ఎడమవైపు |
3. i) కింది సమీకరణాలకు రేఖాచిత్రాలను గీయండి. [పేజీ నెం. 145]
a) y = 2
b) y = – 2
c) y = 3
d) y = – 3
సాధన.
ప్రశ్న 1 లో గల గ్రాఫును చూడుము.
ii) ఈ రేఖాచిత్రాలన్నీ X- అక్షానికి సమాంతరంగా ఉన్నాయా ?
సాధన.
అవును, ఈ రేఖలన్నీ X – అక్షంకు సమాంతరంగా ఉన్నాయి.
iii) ప్రతీ సందర్భములో రేఖాచిత్రానికి, X- అక్షానికి మధ్యగల దూరమును కనుగొనుము.
సాధన.
| రేఖాచిత్రము | దూరము | మూల బిందువుకు కుడివైపు / ఎడమవైపు |
| a) x = 2 | 2 యూనిట్లు | మూలబిందువుకు పైన |
| b) x = – 2 | 2 యూనిట్లు | మూలబిందువుకు కింద |
| c) x = 4 | 3 యూనిట్లు | మూలబిందువుకు పైన |
| d) x = – 4 | 3 యూనిట్లు | మూలబిందువుకు కింద |
![]()
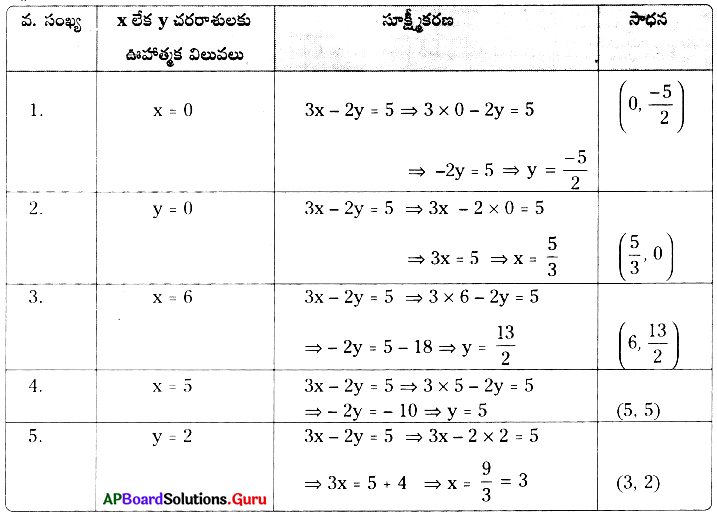
4. 3x – 2y = 5 సమీకరణమునకు 5 సాధనలను కనుగొనుము. [పేజీ నెం. 130]
సాధన.
ఇచ్చిన సమీకరణం 3x – 2y = 5
ప్రయత్నించండి
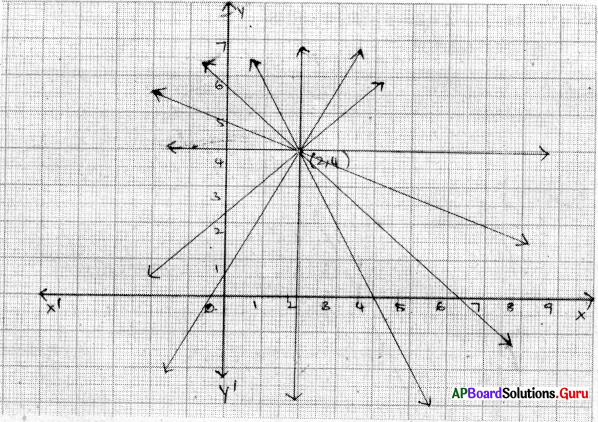
1. ఒక గ్రాఫ్ పేపరుపై (2, 4) బిందువును గుర్తించుము. ఈ బిందువు గుండా ఒక రేఖను గీచి కింది ప్రశ్నలకు సమాధానమిమ్ము. [పేజీ నెం. 135]
1. ఈ (2, 4) బిందువు గుండా మరొక రేఖను గీయగలవా ?
సాధన.
అవును, (2, 4) బిందువు గుండా మరొక రేఖను గీయగలను.
2. ఇలాంటి ఎన్ని రేఖలను గీయగలము ?
సాధన.
ఇలాంటివి అనంత రేఖలను గీయగలము.
3. (2, 4) బిందువు సాధనగా గల రెండు చరరాశులలో రేఖీయ సమీకరణాలు ఎన్ని ఉన్నాయి ?
సాధన.
(2, 4) బిందువు సాధనగా అనంత రేఖీయ సమీకరణాలు ఉన్నాయి.
2. Y- అక్షం సమీకరణమును కనుగొనుము. [పేజీ నెం. 146]
సాధన.
Y- అక్షంపై గల బిందువులన్నింటికి x – నిరూపకము సున్న.
∴ Y- అక్షం సమీకరణము x = 0.
![]()
ఉదాహరణలు
1. సచిన్ మరియు సెహ్వాగ్ కలిసి 137 పరుగులు చేశారు. ఈ సమాచారమును రెండు చరరాశులలో రేఖీయ సమీకరణంగా వ్యక్తపరచండి. [పేజీ నెం. 125]
సాధన.
సచిన్ చేసిన పరుగుల సంఖ్యను ‘x’ మరియు సెహ్వాగ్ చేసిన పరుగుల సంఖ్యను ‘y’ అనుకొనిన
పై దత్తాంశమును సమీకరణ రూపంలో x + y = 137 గా రాయవచ్చు.
2. హేమ వయస్సు, మేరీ వయస్సుకు 4 రెట్లు. ఈ దత్తాంశమునకు సరిపోవు రెండు చరరాశులలో రేఖీయ సమీకరణమును రాయుము. [పేజీ నెం.126]
సాధన.
హేమ వయస్సును ‘x’ సంవత్సరాలు అని, మేరి వయస్సును ‘y’ సంవత్సరాలు అని అనుకొనుము.
అయితే దత్తాంశము ప్రకారము, హేమ వయస్సు = మేరి వయస్సుకు 4 రెట్లు.
అనగా x = 4y ⇒ x – 4y = 0 (ఎలా ?) ఇది ఒక రేఖీయ సమీకరణము అయినది.
3. ఒక సంఖ్య, దానిలోని అంకెలను తారుమారు చేయగా వచ్చే సంఖ్య కంటే 27 ఎక్కువ. సంఖ్యలోని ఒకట్ల, పదుల స్థానములోని అంకెలను వరుసగా x, y అనుకొని ఈ దత్తాంశమునకు సరిపోవు రెండు చరరాశులలో రేఖీయ సమీకరణమును రాయుము. [పేజీ నెం. 126]
సాధన.
ఒకట్ల స్థానములోని అంకె x మరియు పదుల స్థానములోని అంకె y అనుకొనిన ఆ సంఖ్య = 10y + x
సంఖ్యలోని అంకెలను తారుమారు చేయగా వచ్చే సంఖ్య = 10x + y (రెండు అంకెల సంఖ్య యొక్క స్థానవిలువను గుర్తుకు తెచ్చుకోండి).
∴ దత్తాంశము ప్రకారము
సంఖ్య – తారుమారు చేయగా వచ్చే సంఖ్య = 27.
∴ 10y + x – (10x + y) = 27
⇒ 10y + x – 10x – y – 27 = 0
⇒ 9y – 9x – 27 = 0
⇒ y – x – 3 = 0
∴ కావలసిన సమీకరణము x – y + 3 = 0.
4. కింది ప్రతి సమీకరణమును ax + by + c = 0 రూపంలో రాసి a, b మరియు c విలువలను కనుగొనుము. [పేజీ నెం. 126]
i) 3x + 4y = 5
ii) x – 5 = \(\sqrt{3}\)y
iii) 3x = y
iv) \(\frac{x}{2}+\frac{y}{2}=\frac{1}{6}\)
v) 3x – 7 = 0
సాధన.
i) 3x + 4y = 5 ను 3x + 4y – 5 = 0 గా రాయవచ్చు. ఇచ్చట a = 3, b = 4 మరియు c = – 5.
ii) x – 5 = \(\sqrt{3}\)y ని 1.x – \(\sqrt{3}\)y – 5 = 0 గా రాయవచ్చు.
ఇచ్చట a = 1, b = – \(\sqrt{3}\) మరియు c = – 5.
iii) సమీకరణము 3x = y ని 3x – y + 0 = 0 గా రాయవచ్చు. ఇచ్చట a = 3, b = – 1 మరియు c = 0.
iv) ఇచ్చిన సమీకరణము \(\frac{x}{2}+\frac{y}{2}=\frac{1}{6}\)
\(\frac{x}{2}+\frac{y}{2}-\frac{1}{6}\) = 0; a = \(\frac {1}{2}\), b = \(\frac {1}{2}\) మరియు c = \(\frac {-1}{6}\)
v) 3x – 7 = 0 ని 3x + 0. y – 7 = 0 గా రాయవచ్చు.
∴ a = 3, b = 0; c = – 7.
![]()
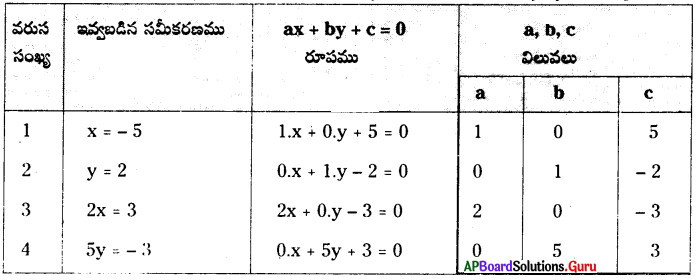
5. ఈ క్రింది ప్రతి సమీకరణము ax + by + c = 0 రూపంలోకి మార్చి a, b మరియు c విలువలను కనుగొనుము. [పేజీ నెం. 127]
i) x = – 5
ii) y = 2
iii) 2x = 3
iv) 5y = – 3
సాధన.
6. 4x + y = 9 సమీకరణమునకు 4 వేరు వేరు సాధనలను కనుగొనుము. (పట్టికలో ఖాళీలను పూరింపుము). [పేజీ నెం. 130]
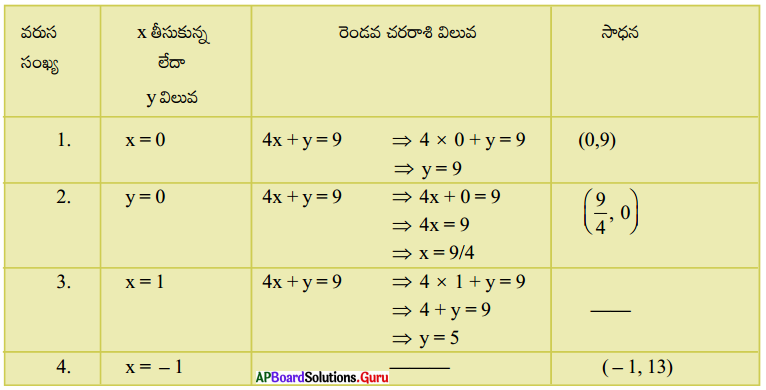
సాధన.
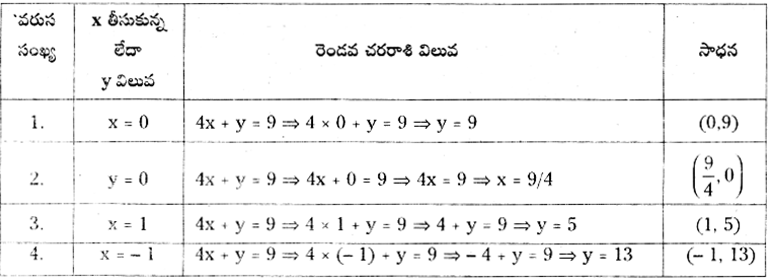
∴ (0, 9), (\(\frac {9}{4}\), 0), (1, 5) మరియు (- 1, 13) లు కొన్ని సాధనలు.
![]()
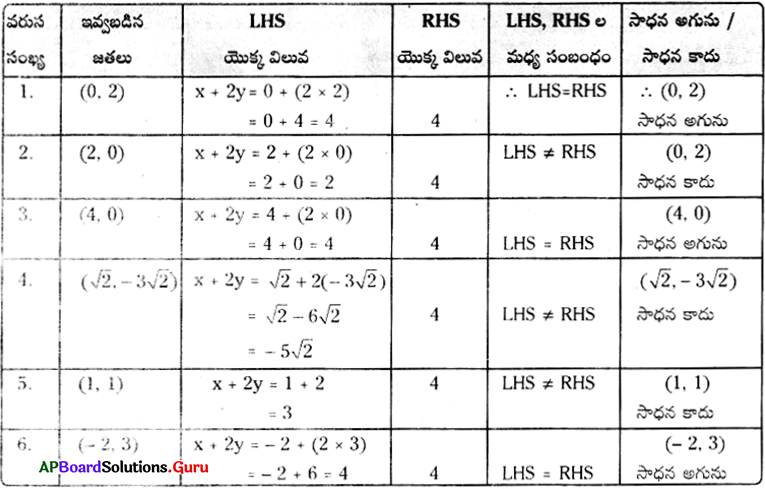
7. కింది వానిలో ఏవి x + 2y = 4 సమీకరణానికి సాధన అవుతాయి ? (పట్టికలో ఖాళీలను పూరించుము.) [పేజీ నెం. 131]
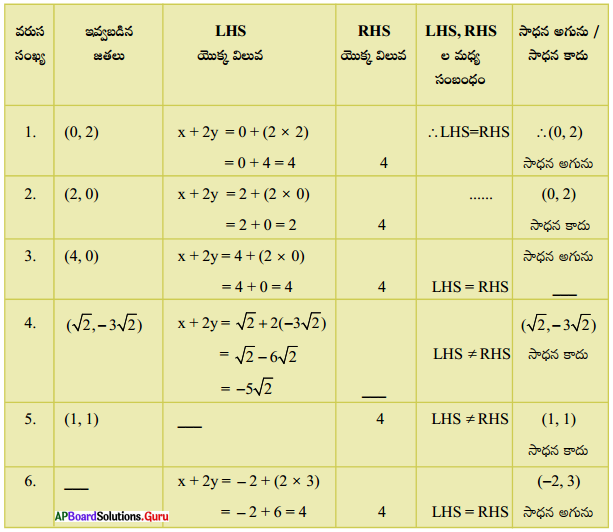
i) (0, 2)
ii) (2, 0)
iii) (4, 0)
iv) (\(\sqrt{2}\), – 3\(\sqrt{2}\))
v) (1, 1)
vi) (- 2, 3)
సాధన.
ఒక జతను ఇచ్చిన సమీకరణంలో ప్రతిక్షేపించినపుడు LHS = RHS అయిన ఆ జతను ఇచ్చిన సమీకరణం యొక్క సాధన అంటామని మనకు తెలుసు.
ఇచ్చట ఇవ్వబడిన సమీకరణము x + 2y = 4
8. 5x – 7y = k కు x = 3, y = 2 సాధన k అయిన విలువను కనుగొనుము. k విలువతో వచ్చే సమీకరణాన్ని రాయండి. [పేజీ నెం.132]
సాధన.
x = 3, y = 2 సాధన అని ఇవ్వబడింది కనుక 5x – 7y = k అయిన 5 × 3 – 7 × 2 = k
⇒ 15 – 14 = k ⇒ 1 = k :
∴ k = 1
కావలసిన సమీకరణం 5x – 7y = 1.
9. 5x + 3y – 7 = 0 యొక్క సాధన x = 2k + 1 మరియు y = k అయిన ఓ విలువ ఎంత ? [పేజీ నెం. 132]
సాధన.
5x + 3y – 7 = 0 సమీకరణమునకు x = 2k + 1; y = k సాధన ఇవ్వబడింది.
⇒ 5(2k + 1) + 3k – 7 = 0 ⇒ 10k + 5 + 3k – 7 = 0
⇒ 13k – 2 = 0 (ఇది ఒక ఏకచరరాశిలో రేఖీయ సమీకరణము).
⇒ 13k = 2
∴ k = \(\frac {2}{13}\)
![]()
10. y – 2x = 4 సమీకరణమునకు రేఖాచిత్రమును గీచి కింది ప్రశ్నలకు సమాధానమిమ్ము. [పేజీ నెం. 135]
i) (2, 8) బిందువు రేఖపై ఉన్నదా ? (2, 8) సమీకరణం యొక్క సాధన అవుతుందా ? (2, 8)ను సమీకరణంలో ప్రతిక్షేపించుట ద్వారా సరిచూడుము.
ii) (4, 2) బిందువు రేఖపై ఉన్నదా ? బీజీయ పద్ధతి ద్వారా (4, 2) సమీకరణానికి సాధన అవుతుందేమో సరిచూడుము.
iii) రేఖాచిత్రము నుంచి మరొక మూడు సాధనలను కనుగొనుము. అదే విధముగా సాధనలు కాని వానిని మూడింటిని కనుగొనుము.
సాధన.
ఇవ్వబడిన సమీకరణము y – 2x = 4 ⇒ y = 2x + 4
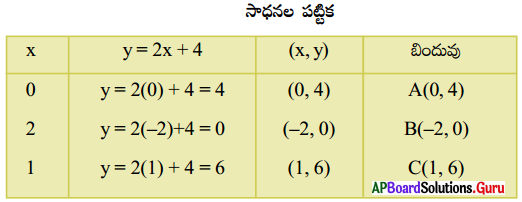
A, B మరియు C బిందువులను గ్రాఫ్ మీద గుర్తించి వానిని కలిపిన పటములో చూపించిన విధంగా కలిపితే BC రేఖ వస్తుంది. ఇదియే మనకు కావలసిన y- 2x = 4 యొక్క రేఖాచిత్రము అవుతుంది.
i) (2, 8) బిందువును గ్రాఫ్ పేపరుపై గుర్తించిన BC రేఖపై ఉండడం గమనించవచ్చు.
బీజీయ పద్ధతిలో సరిచూచుట (2, 8) బిందువును సమీకరణంలో ప్రతిక్షేపించిన
LHS = y – 2x = 8 – 2 × 2 = 8 – 4 = 4 = RHS,
కనుక (2, 8) సాధన అవుతుంది.
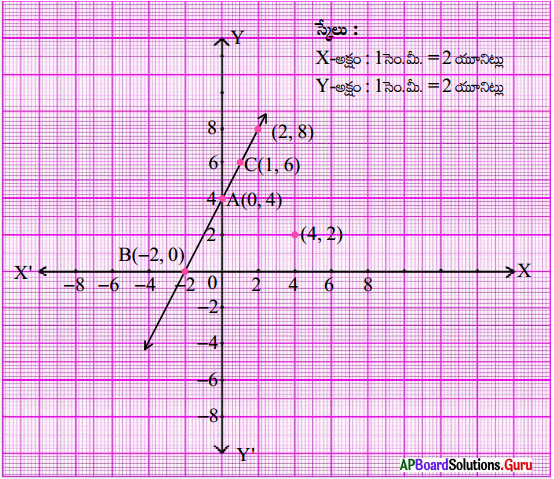
ii) (4, 2) బిందువును గ్రాఫ్ పేపర్ పై గుర్తించిన అది BC రేఖమీద లేకపోవడాన్ని మీరు గమనించవచ్చు.
బీజీయ పద్దతిలో సరిచూచుట : (4, 2) ను ఇచ్చిన సమీకరణంలో ప్రతిక్షేపిస్తే,
LHS = y – 2x = 2 – 2 × 4 = 2 – 8 = – 6 ≠ RHS
∴ (4, 2) సాధన కాదు.
iii) ఒకరేఖ మీది ఏ బిందువైనా సమీకరణానికి సాధన అవుతుందని మనకు తెలుసు. కనుక రేఖమీద ఏవైనా మూడు బిందువులు తీసుకుంటే అవి సాధనలు అవుతాయి. ఉదాహరణకు (- 4, – 4) …. అదే విధంగా రేఖమీదలేని ఏ బిందువు కూడా సాధన కాదని తెలుసు. కనుక రేఖ మీద లేని ఏవైనా మూడు బిందువులను తీసుకుంటే అవి సాధనలు కావు.
ఉదాహరణకు : (i) (1, 5); ………; ………
11. x – 2y = 3 యొక్క రేఖాచిత్రమును గీయుము. [పేజీ నెం. 136]
రేఖాచిత్రము నుంచి ఈ కింది వానిని కనుగొనుము.
i) x = – 5 అయ్యే విధంగా ఒక సాధన (x, y)
ii) y = 0 అయ్యే విధంగా ఒక సాధన (x, y)
iii) x = 0 అయ్యే విధంగా ఒక సాధన (x, y)
సాధన.
x – 2y = 3 ⇒ y = \(\frac{x-3}{2}\)
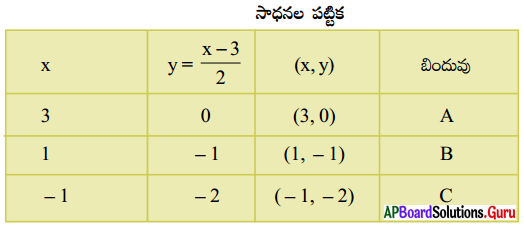
గ్రాఫ్ పేపర్ పై A, B, C బిందువులు గుర్తించి వానిని కలిపిన కింది పటములో చూపిన విధంగా రేఖ వస్తుంది. ఈ రేఖయే కావలసిన x – 2y = 3 యొక్క రేఖాచిత్రము అవుతుంది.
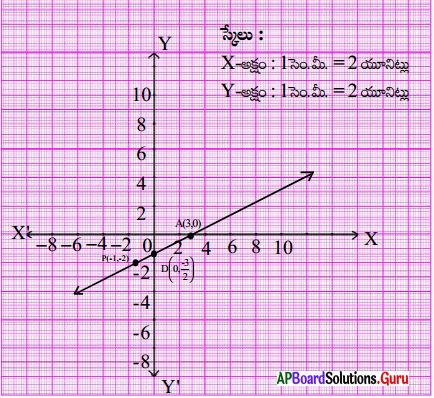
i) x = – 5 అయ్యే ఒక సాధన (x, y) ని మనము కనుగొనవలె. అనగా రేఖమీద ఉంటూ దాని x – నిరూపకము ‘- 5′ అయ్యే బిందువును కనుగొనవలె. దీనిని కనుగొనుటకు x = – 5 వద్ద నుంచి Y – అక్షమునకు సమాంతరంగా ఒక రేఖను గీయవలె. అది గ్రాఫ్ ‘P’ వద్ద ఖండిస్తుంది అనుకొనుము. ఈ బిందువు ‘P’ నుంచి X – అక్షానికి సమాంతరంగా రేఖ గీచిన అది Y – అక్షమును – 4 వద్ద ఖండిస్తుంది. (తాకుతుంది).
కనుక P బిందువు నిరూపకాలు = (- 5, – 4)
P(- 5, – 4) బిందువు x – 2y = 3 రేఖపై ఉన్నది కావున అది ఒక సాధన అవుతుంది.
ii) y = 0 అయ్యే విధంగా ఒక సాధన (x, y) ని కనుగొనాలి.
y = 0 కనుక బిందువు (x, 0) అవుతుంది. కావున y = 0 కనుక బిందువు X- అక్షంపై ఉంటూ x – 2y = 3 రేఖాచిత్రము మీద ఉండే బిందువును కనుగొనాలి.
రేఖాచిత్రము నుంచి ఇలాంటి బిందువు (3, 0) అని గమనించగలము.
∴ సాధన = (3, 0).
iii) x = 0 అయ్యే విధంగా ఒక సాధన (x, y) ని కనుగొనవలె.
x = 0 కనుక బిందువు (0, y) అవుతుంది. అనగా బిందువు Y – అక్షంపై ఉంటుంది. అంటే Y – అక్షం పై ఉంటూ x – 2y = 3 గ్రాఫ్ మీద ఉండే బిందువును కనుగొనాలి.
రేఖాచిత్రము నుంచి ఇలాంటి బిందువు (0, \(\frac {-3}{2}\)) అని గుర్తించగలము.
∴ సాధన = (0, \(\frac {-3}{2}\))
![]()
12. ఒక పాఠశాలలో 25% బాలికలు, మిగిలినవారు బాలురు. ఈ సమాచారమునకు సరిపోవు రెండు చరరాశులలో రేఖీయ సమీకరణమును రూపొందించి దానికి రేఖాచిత్రము గీయుము. రేఖాచిత్రము నుంచి ఈ కింది ప్రశ్నలకు సమాధానమును రాబట్టుము. [పేజీ నెం. 138]

i) బాలికల సంఖ్య 25 అయిన బాలుర సంఖ్య ఎంత ?
ii) బాలుర సంఖ్య 45 అయిన బాలికల సంఖ్య ఎంత ?
iii) బాలుర సంఖ్యకు మూడు వేరువేరు విలువలను తీసుకొని అనురూపంగా బాలికల సంఖ్యను కనుగొనుము. అదే విధంగా బాలికల సంఖ్యకు మూడు వేరువేరు విలువలను తీసుకొని అనురూపంగా బాలుర సంఖ్యను కనుగొనుము.
సాధన.
బాలికల సంఖ్యను ‘x’ మరియు బాలుర సంఖ్యను ‘y’ అనుకొనిన
మొత్తం విద్యార్థుల సంఖ్య = x + y
ఇచ్చిన దత్తాంశము ప్రకారము బాలికల సంఖ్య మొత్తం విద్యార్థులలో = 25% అంటే,
x = (x + y) లో 25% = (x + y) × \(\frac {25}{100}\) లో (x + y) = \(\frac {1}{4}\) (x + y)
x = \(\frac {1}{4}\)(x + y) ⇒ 4x = x + y ⇒ 3x = y
∴ కావలసిన సమీకరణము 3x = y లేదా 3x – y = 0.
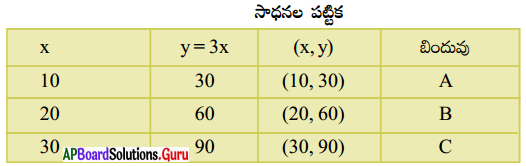
గ్రాఫ్ పై A, B మరియు C బిందువులను గుర్తించి వానిని కలిపిన కింది పటములో చూపిన విధంగా AB రేఖ ఏర్పడుతుంది.
స్కేలు : X-అక్షం : 1 సెం.మీ. = 20 బాలికలు
Y-అక్షం : 1 సెం.మీ. = 20 బాలురు
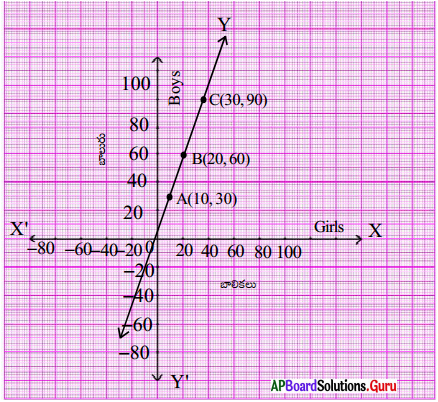
రేఖాచిత్రము నుండి ఈ కింది వానిని కనుగొనగలము.
i) బాలికల సంఖ్య 25 అయిన బాలుర సంఖ్య 75.
ii) బాలుర సంఖ్య 45 అయిన బాలికల సంఖ్య 15.
iii) బాలుర సంఖ్యకు మీకు నచ్చిన మూడు వేరువేరు సంఖ్యలను తీసుకొని వానికి అనురూపమైన బాలికల సంఖ్యను, అదే విధంగా బాలికల సంఖ్యకు మీకు నచ్చిన మూడు వేరువేరు సంఖ్యలను తీసుకొని వానికి అనురూపమైన బాలుర సంఖ్యను కనుగొనుము. ఇచ్చట గ్రాఫ్ ను, సమీకరణమును పరిశీలించండి. సమీకరణము y = 3x రూపంలో ఉంది మరియు సరళరేఖ మూల బిందువుగుండా పోతుంది. y = mx (m ఏదైనా వాస్తవ సంఖ్య) సమీకరణమునకు రేఖాచిత్రము గీచిన అది మూల బిందువు గుండా పోతుంది అని గమనిస్తారు.
![]()
13. కింది ప్రతి రేఖాచిత్రానికి నాలుగు సమీకరణాలు ఇవ్వబడినాయి. వానిలో రేఖాచిత్రాన్ని సూచించు సరియైన సమీకరణమును గుర్తించుము. [పేజీ నెం. 140]
i) సమీకరణాలు :
A) y = x
B) x + y = 0
C) y = 2x
D) 2 + 3y = 7x
ii) సమీకరణాలు :
A) y = x + 2
B) y = x – 2
C) y = – x + 2
D) x + 2y = 6
సాధన.
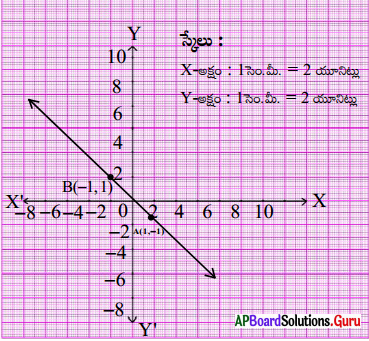
i) రేఖాచిత్రము (1, – 1) (0, 0) (- 1, 1) బిందువులు ఒకే రేఖ పై ఉండడం మనం గమనించవచ్చు. అనగా ఇవి కావలసిన సమీకరణానికి సాధనలు అవుతాయి. అంటే ఈ బిందువులను కావలసిన సమీకరణంలో ప్రతిక్షేపిస్తే అది తృప్తి చెందుతుంది. మరి ఒక విధంగా చెప్పాలంటే ఈ బిందువులను ఏ సమీకరణంలో ప్రతిక్షేపిస్తే అది తృప్తి చెందుతుందో అదియే కావలసిన సమీకరణము.
(1, – 1) బిందువును మొదటి సమీకరణము y = x లో ప్రతిక్షేపించిన అది తృప్తి చెందదు. కనుక y = x కావలసిన సమీకరణం కాదు. అయితే రెండవ సమీకరణము తృప్తి చెందుతుంది. నిజానికి పై మూడు బిందువులకు ఈ సమీకరణము తృప్తి చెందుతుంది. కనుక x + y = 0 కావలసిన సమీకరణం అవుతుంది.
మిగిలిన రెండు సమీకరణాలలో ఈ బిందువులను ప్రతిక్షేపించినప్పుడు అవి తృప్తి చెందవు. కనుక అవి కావలసిన సమీకరణాలు కావు.
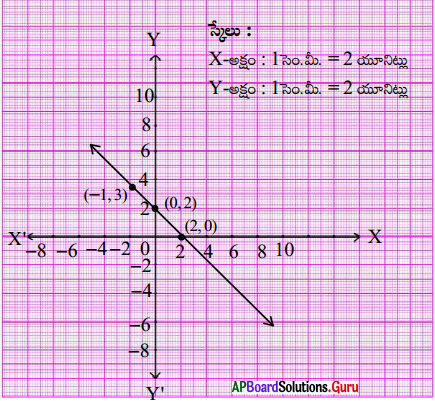
ii) రేఖాచిత్రములో (2, 0), (0, 2) మరియు (- 1, 3) బిందువులు రేఖపై ఉన్నాయి. ఈ బిందువులు మొదటి, రెండవ సమీకరణాలను తృప్తిపరచవు. మూడవ సమీకరణము y = – x + 2 ను తీసుకుందాం. దీనిలో పై బిందువులను ప్రతిక్షేపించినప్పుడు అది తృప్తి చెందుతుంది. కనుక y = – x + 2 కావలసిన సమీకరణం అవుతుంది. ఈ బిందువులు x + 2y = 6 ను తృప్తిపరుస్తాయోమో పరిశీలించుము.