AP SCERT 9th Class Maths Textbook Solutions Chapter 8 చతుర్భుజాలు Ex 8.2 Textbook Exercise Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 8th Lesson చతుర్భుజాలు Exercise 8.2
ప్రశ్న 1.
ABCD ఒక సమాంతర చతుర్భుజము మరియు ABEF ఒక దీర్ఘచతురస్రము అయిన ∆AFD ≅ ∆BEC అని చూపండి.
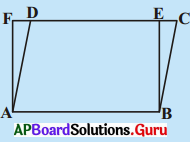
సాధన.
☐ABCD ఒక సమాంతర చతుర్భుజము.
☐ABEF ఒక దీర్ఘచతురస్రము.
∆AFD మరియు ∆BEC లలో
AF = BE (∵ ☐ABEF దీర్ఘచతురస్రపు ఎదుటి భుజాలు)
AD = BC (∵ ☐ABCD సమాంతర చతుర్భుజపు ఎదుటి భుజాలు)
DF = CE (∵ AB = DC = DE + EC
AB = EF = DE + DF)
∴ ∆AFD ≅ ∆BEC (భు. భు. భు నియమం)
![]()
ప్రశ్న 2.
రాంబలో కర్ణాలు దానిని నాలుగు సర్వసమాన త్రిభుజాలుగా విభజిస్తాయని నిరూపించండి.
సాధన.
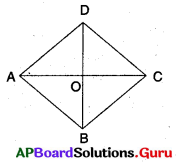
☐ABCD ఒక రాంబస్.
AC మరియు BD లు ‘O’ వద్ద ఖండించుకొనును అనుకొనుము.
∆AOB మరియు ∆COD లలో
\(\angle \mathrm{OAB}=\angle \mathrm{OCD}\) (ఏకాంతర కోణాలు)
AB = CD (రాంబస్ నిర్వచనం)
\(\angle \mathrm{OBA}=\angle \mathrm{ODC}\)……. (1) (ఏకాంతర కోణాలు)
∴ ∆AOB ≅ ∆COD (కో.భు.కో. నియమం)
⇒ AO = OC (CPCT)
మరియు ∆AOD ≅ ∆COD ……… (2) [∵ AO = OC; AD = CD; OD = OD భు.భు.భు. నియమం]
అదే విధముగా,
∆AOD ≅ ∆COB …. (3) అని నిరూపించవచ్చును.
(1), (2) మరియు (3) ల నుండి,
∆AOB ≅ ∆BOC ≅ ∆COD ≅ ∆AOD
∴ రాంబస్ కర్ణాలు రాంబను 4 సర్వసమాన త్రిభుజాలుగా విభజించును.
![]()
ప్రశ్న 3.
ABCD చతుర్భుజములో \(\angle \mathrm{C}\) మరియు \(\angle \mathrm{D}\)ల యొక్క సమద్విఖందన రేఖలు O వద్ద ఖండించుకుంటే \(\angle \mathrm{COD}\) = \(\frac {1}{2}\) (\(\angle \mathrm{A}\) + \(\angle \mathrm{B}\)) అని చూపండి.
సాధన.
