AP Board 9th Class Maths Solutions Chapter 9 సాంఖ్యక శాస్త్రము InText Questions

AP SCERT 9th Class Maths Textbook Solutions Chapter 9 సాంఖ్యక శాస్త్రము InText Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 9th Lesson సాంఖ్యక శాస్త్రము InText Questions

కృత్యం

1. తరగతిలోని విద్యార్థులను నాలుగు బృందాలుగా విభజించి, ఒక్కొక్క బృందమునకు కింద చూపిన దత్తాంశముల సేకరణకు కేటాయించారు. (పేజీ నెం. 195).
(i) మీ తరగతిలోని అందరు విద్యార్థుల బరువులు.
(ii) ఒక్కొక్క విద్యార్థి యొక్క (సోదరులు లేక సోదరిల సంఖ్య) తోబుట్టువుల సంఖ్య,
(iii) గత మాసంలో రోజువారీగా గైరుహాజరయిన వారి సంఖ్య
(iv) తరగతిలో ప్రతి విద్యార్థి యొక్క ఇంటి నుండి పాఠశాల దూరము.

2. మీ తరగతిలోని విద్యార్థుల ఇంటి పేరులో (ఆంగ్లములో) మొదటి అక్షరాలు (Initials) సేకరించండి. అవర్గీకృత పౌనఃపున్య విభాజక పట్టిక తయారుచేసి కింది ప్రశ్నలకు జవాబులివ్వండి. (పేజీ నెం. 197)
(i) ఎక్కువ మంది విద్యార్థుల ఇంటి పేర్ల మొదటి అక్షరం ఏది ?
(ii) ఎంతమంది విద్యార్థుల ఇంటిపేర్ల మొదటి అక్షరం T ?
(iii) ఏ అక్షరం అతి తక్కువ సార్లు ఉపయోగింపబడినది ?
సాధన.
విద్యార్థి కృత్యం.

ఇవి చేయండి

1. కింది వానిలో ఏది ప్రాథమిక, ఏది గౌణ దత్తాంశము? (పేజీ నెం. 195)

ప్రశ్న (i)
2001 నుండి 2010 వరకు మీ పాఠశాలలో నమోదు కాబడిన విద్యార్థుల వివరాలు.
సాధన.
గౌణ దత్తాంశము.

ప్రశ్న (ii)
వ్యాయామ ఉపాధ్యాయుడు నమోదు చేసిన మీ తరగతిలో విద్యార్థుల ఎత్తులు.
సాధన.
ప్రాథమిక దత్తాంశము.

ఆలోచించి, చర్చించి రాయండి

1. అంకగణిత మధ్యమము, మధ్యగతము, బాహుళకము విడివిడిగా ఉపయోగించు సందర్భములను మూడింటిని రాయండి. (పేజీ నెం. 202)
సాధన.
సగటు :
(a) కొంతమంది విద్యార్థులకు, మధ్యాహ్న భోజనంను ఏర్పాటుచేయు సందర్భంలో
(b) తరగతిలోని విద్యార్థుల మార్కులను పోల్చు సందర్భంలో
(c) ఒక నెలలో ఒక వర్తకుడు పొందు రోజు వారీ వేతనంను లెక్కించు సందర్భంలో

మధ్యగతం :
(a) ఒక సంస్థలోని ఉద్యోగుల జీతాలను లెక్కించు సందర్భంలో
(b) ఒక తరగతిలోని బాలురు మరియు బాలికల ఎత్తును కొలుచు సందర్భంలో

బాహుళకము:
(a) ఒక నగరంలో ఎక్కువగా ఉపయోగించు ప్రయాణ సాధనాలను తెలుసుకొను సందర్భంలో
(b) ఒక షూ షాపులో ఎక్కువగా అమ్ముడుపోవు షూ సైజును లెక్కించు సందర్భంలో

2. మీ తరగతిలోని విద్యార్థులను ఎత్తుల ఆధారంగా వర్గాలుగా విభజించండి. (ఉదాహరణకు బాలురు – బాలికలు) మరియు బాహుళకమును కనుగొనండి. (పేజీ నెం. 208)
సాధన.
విద్యార్థి తన తరగతి గదిలో ఉన్న బాలురు – బాలలికల ఎత్తులను తీసుకొని బాహుళకమును కనుగొనండి.

3. చెప్పుల దుకాణదారు చెప్పులు కొనుగోలు చేయునపుడు ఏ కొలత చెప్పులు ఎక్కువగా ఆర్డరు చేస్తాడు ? (పేజీ నెం. 208)
సాధన.
విద్యార్థి తనకు దగ్గరలోగల చెప్పుల దుకాణంకు వెళ్ళి సమాధానం రాబట్టవలెను.

ప్రయత్నించండి (పేజీ నెం . 207)

1. 75, 21, 56, 36, 81, 05, 42 రాశుల మధ్యగతాన్ని కనుగొనండి.
సాధన.
ఇచ్చిన దత్తాంశమును ఆరోహణ క్రమంలో వ్రాయగా 05, 21, 36, 42, 56, 75, 81.
దత్తాంశంలోని అంశాలు = 7 (బేసి సంఖ్య)
\(\frac{\mathrm{n}+1}{2}\) వ పదము = \(\frac{\mathrm{7}+1}{2}\)
\(\frac {8}{2}\) = 4వ పదము
∴ మధ్యగతము = 42

2. ఆరోహణ క్రమములో ఉన్న దత్తాంశం 7, 10, 15, x, y, 27, 30 యొక్క మధ్యగతము 17. ఈ దత్తాంశమునకు 50 అను రాశిని చేర్చగా మధ్యగతము 18 అయినచో X మరియు y లను కనుగొనుము. (పేజీ నెం. 207)
సాధన.
ఆరోహణ క్రమంలో వున్న దత్తాంశము
7, 10, 15, x, y, 27, 30.
దత్తాంశంలోని అంశాల సంఖ్య n = 7 (బేసి సంఖ్య)
∴ మధ్యగతము = \(\frac{\mathrm{n}+1}{2}\) వ పదము = \(\frac{\mathrm{7}+1}{2}\) = \(\frac {8}{2}\) = 4వ పదము
∴ శవ పదము = x = 17 (సమస్య నుండి)
ఇచ్చిన దత్తాంశమునకు 50 అను రాశిని చేర్చిన ఏర్పడు మధ్యగతము 18.
50 ను చేర్చగా ఇచ్చిన దత్తాంశము 7, 10, 15, 17,y, 27, 30, 50
దత్తాంశంలోని అంశాల సంఖ్య = n= 8 (సరి సంఖ్య)
∴ మధ్యగతము = \(\left(\frac{\left(\frac{\mathrm{n}}{2}\right)+\left(\frac{\mathrm{n}}{2}+1\right)}{2}\right)\) వ పదము = \(\left(\frac{\left(\frac{\mathrm{n}}{2}\right)+\left(\frac{\mathrm{n}}{2}+1\right)}{2}\right)\) వ పదము
18 = \(\frac{17+y}{2}\) (సమస్య నుండి)
17 + y = 36 ⇒ y = 36 – 17 = 19

3. కింది దత్తాంశమునకు మధ్యగతము కనుగొనండి.

సాధన.

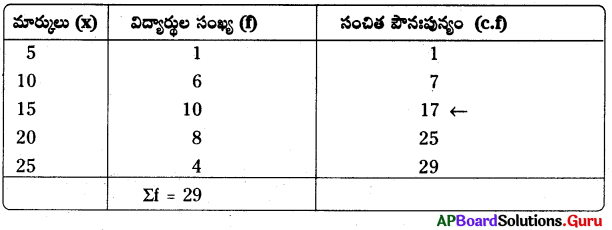
మధ్యగతము = (\(\frac{\mathrm{n}+1}{2}\)) వ పదము = \(\frac{\mathrm{29}+1}{2}\) = 15 వ పదము
∴ 15వ అంశము = 15 (పట్టిక నుండి)

4. అవర్గీకృత పౌనఃపున్య విభాజనము యొక్క మధ్యగతంను కనుగొనునప్పుడు క్రమంలో వ్రాయవలెను. ఎందుకు ? (పేజీ నెం. 208)
సాధన.
అవర్గీకృత పౌనఃపున్య విభాజనము యొక్క మధ్యగతంను కనుగొనునప్పుడు దత్తాంతంను ఆరోహణ / అవరోహణ క్రమంలో వ్రాయవలెను. ఎందుకనగా ఆ దత్తాంశంను సరిగ్గా సమ భాగముగా విభజించాలి కావున.

ఉదాహరణలు

1. గణిత పరీక్షలో 50 మంది విద్యార్థులు పొందిన మార్కులు ఈ విధంగా ఇవ్వబడ్డాయి.
5, 8, 6, 4, 2, 3, 4, 9, 10, 2, 1, 1, 3, 4, 5, 8, 6, 7, 10, 21, 1, 3, 4, 4, 5, 8, 6, 7, 10, 2, 8, 6, 4, 2, 5, 4, 9, 10, 2, 1, 1, 3, 4, 5 8, 6, 4, 5, 8 (పేజీ నెం. 196)
సాధన.

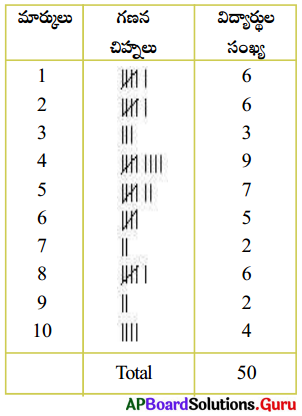
దత్తాంశమునకు గణన చిహ్నాలు ఉపయోగించి పట్టికలో చూపబడినది. ఒక మార్కును సాధించిన మొత్తం విద్యార్థుల సంఖ్యను ఆ మార్కు యొక్క పౌనఃపున్యం అందురు. ఉదాహరణకు 4 మార్కులు సాధించిన విద్యార్థుల సంఖ్య 9, అంటే 4 మార్కుల యొక్క పౌనఃపున్యము 9. ఈ పట్టికలోని గణన చిహ్నాలు ముడి దత్తాంశములోని రాశులను పోల్చి లెక్కించుటకు ఉపయోగపడతాయి.

పట్టికలోని అన్ని పౌనఃపున్యముల మొత్తము దత్తాంశములోని రాశుల మొత్తమును సూచిస్తుంది. ఈ విధంగా దత్తాంశములోని అన్ని విభిన్న రాశు లను పౌనఃపున్యములతో సూచించు పట్టికను ‘అవర్గీకృత పౌనఃపున్య విభాజన పట్టిక’ లేక ‘రాశుల భారత్వ పట్టిక’ అంటారు.

2. ఒక బుట్టలోని 50 నారింజ పండ విడి విడి బరువులు (గ్రాములలో) కింది ఇవ్వబడ్డాయి. (పేజీ నెం. 197)
35, 45, 56, 50, 30, 110, 95, 40, 70, 100, 60, 80, 85, 60, 52, 95, 98, 35, 47, 45, 105, 90, 30, 50, 75, 95, 85, 80, 35, 45, 40, 50, 60, 65, 55, 45, 30, 90, 115, 65, 60, 40, 100, 55, 75, 110, 85, 95, 55, 50.
సాధన.
దత్తాంశములోని రాశులను ఒక్కసారిగా ప్రదర్శించుటకు, సమగ్రంగా, సులభంగా అర్థం చేసుకొనుటకు అనువుగా రావు లన్నింటిని తరగతులు, 30 – 39, 40 – 49, 50 – 59, ….. 100 – 109, 110 – 109 గా విభజిస్తాం . ఈ చిన్నచిన్న వర్గములను లేదా సమూహములను తరగతులు అంటారు. ఒక్కొక్క తరగతి యొక్క పరిమాణమును తరగతి పొడవు’ లేక ‘తరగతి వెడల్పు’ అంటారు. ఉదాహరణకు తరగతి 30 – 39 లో 30ను ‘దిగువ అవధి’ అని, 39ను ‘ఎగువ అవధి’ అని అంటారు. ఈ తరగతి పొడవు 10 (దిగువ, ఎగువ అవధులతో సహా).

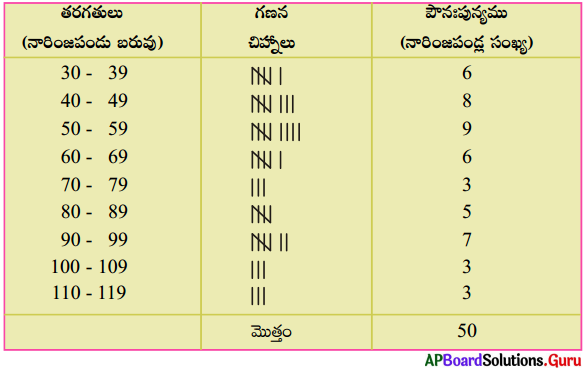
దత్తాంశములోని రాశులను చిన్న చిన్న వర్గములుగా విభజించి పౌనఃపున్యములతో సూచించు పట్టికను ‘వర్గీకృత పౌనఃపున్య విభాజన పట్టిక’ అంటారు. ఇది దత్తాంశమును సమగ్రంగా, సంక్షిప్తంగా ప్రదర్శించి అర్థం చేసుకోవడం సులభతరం చేస్తుంది.

పై పౌనఃపున్య విభాజనములోని తరగతులు ఒకదానిపై ఒకటి అతిపాతం చెందుట లేదు అనగా ఏ విలువ రెండు తరగతులలో పునరావృతం కాదు. ఈ తరగతులను సమ్మిళిత తరగతులు అంటాం.

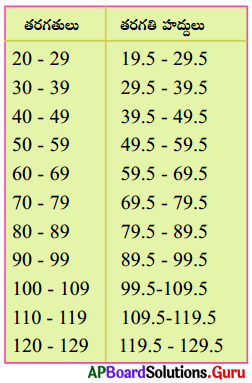
ఏ దత్తాంశములో అయినా ఎక్కువ తరగతి పొడవుతో తరగతి హద్దులు తక్కువ తరగతులకు లేక తక్కువ తరగతి పొడవుతో తక్కువ తరగతులను ఏర్పాటు చేసుకొనవచ్చును. కానీ తరగతులు మాత్రం ఒకదానిపై ఒకటి అతిపాతం చెందకూడదు. సామాన్యంగా మొదట దత్తాంశపు వ్యాప్తి (వ్యాప్తి = గరిష్ట దత్తాంశపు విలువ – కనిష్ఠ దత్తాంశపు విలువ) ని కనుగొందురు. వ్యాప్తిని ఉపయోగించి తరగతి పొడవు మరియు తరగతుల సంఖ్యను నిర్ణయింతురు. ఉదాహరణకు 30 – 35, 36 – 40, …. గా విభజింపవచ్చును.

పై దత్తాంశంలో ఒక నారింజపండు భారము 39.5 గ్రా. అయినచో ఆ విలువను ఏ తరగతికి చేర్చవలెను? 30 – 39 తరగతిలోనా లేక 40 – 49 తరగతిలోనా ?

ఇటువంటి సందర్భములలో తరగతుల యొక్క నిజ అవధులు లేక హద్దులు సహాయపడతాయి. ఒక తరగతి యొక్క ఎగువ అవధి, తరువాత తరగతి యొక్క దిగువ అవధుల సరాసరిని ఆ తరగతి యొక్క ఎగువ హద్దు అంటారు. అదే విలువ తరువాత తరగతి యొక్క దిగువ హద్దు అవుతుంది. ఇదే విధంగా అన్ని తరగతుల యొక్క హద్దులను రాయవచ్చు. మొదటి తరగతికి ముందు ఒక తరగతి ఊహించుకోవడం ద్వారా మొదటి తరగతి దిగువ హద్దును, అట్లే చివరి తరగతికి తరువాత ఒక తరగతిని ఊహించటం ద్వారా చివరి తరగతి యొక్క ఎగువ హద్దును లెక్కించవచ్చును.

హద్దులు ఏర్పరచిన తరువాత కూడా 39.5 ను ఏ తరగతిలో అనగా 29.5 – 39.5 లేక 39.5 – 49.5 చేర్చవలెననే సంశయము ఏర్పడుతుంది. సాంప్రదాయకంగా తరగతి యొక్క ఎగువహద్దు ఆ తరగతికి చెందదు అని గ్రహించవలెను. కావున 39,5 రాశి 39.5 – 49.5 తరగతికి చెందుతుంది.

30 – 40, 40 – 50, 50 – 60, … తరగతులు ఒక దానిపై ఒకటి అతిపాతం చెందుతాయి. ఈ తరగతులను ‘మినహాయింపు తరగతులు’ అంటారు. సమ్మిళిత తరగతుల హద్దులలో మినహాయింపు తరగతులు ఏర్పడుట గమనించవచ్చు. ఒక తరగతి ఎగువ మరియు దిగువ హద్దుల భేదము ఆ తరగతి అంతరము. కావున 90-99 తరగతి అంతరము 10.

3. సెప్టెంబరు నెలలో ఒక నగరము యొక్క సాపేక్ష అర్థత (శాతములలో) విలువలు కింది విధంగా ఇవ్వబడ్డాయి. (ఎందుకనగా 99.5 – 89.5 = 10) (పేజీ నెం. 199)

(i) 84 – 86, 86 – 88, …… తరగతి అంతరాలతో వర్గీకృత పౌనఃపున్య విభాజనమును నిర్మించండి. .
(ii) దత్తాంశము వ్యాప్తి ఎంత ?
సాధన.
(i) ఇచ్చిన తరగతులతో గణన చిహ్నాల సహాయంతో నిర్మింపబడిన వర్గీకృత పౌనఃపున్య విభాజనము.

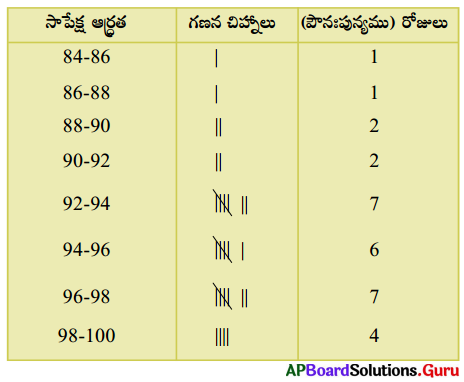
(సూచన : దత్తాంశము 90; 90 – 92 తరగతికి 96; 96 – 98 తరగతికి చెందును.)
(ii) దత్తాంశము యొక్క వ్యాప్తి = గరిష్ట విలువ – కనిష్ఠ విలువ
= 99.2 – 84.9 = 14.3

4. ఒక వారము ఒక పట్టణపు వర్షపాతము 4 సెం.మీ., 5 సెం.మీ., 12 సెం.మీ., 3 సెం.మీ., 6 సెం.మీ., 8 సెం.మీ., 0.5 సెం.మీ. అని రికార్డు చేయబడినది. అయిన దినసరి సరాసరి వర్షపాతమెంత? (పేజీ నెం. 203)
సాధన.
వారంలో రోజువారీ వర్షపాతము (సెం.మీ.) = 4.5 సెం.మీ., 5 సెం.మీ., 12 సెం.మీ., 3 సెం.మీ., 6 సెం.మీ., 8 సెం.మీ., 0.5 సెం.మీ.
దత్తాంశములోని రాశుల సంఖ్య n = 7
అంకగణిత మధ్యమము \(\overline{\mathbf{x}}=\frac{\Sigma \mathbf{x}_{\mathbf{i}}}{\mathrm{n}}=\frac{\mathbf{x}_{1}+\mathrm{x}_{2}+\mathrm{x}_{3}+\ldots \ldots \mathrm{x}_{\mathrm{n}}}{\mathrm{n}}\), x₁, x₂, …… x_n రాశులు.
మరియు \(\overline{\mathrm{X}}\) వాటి సగటు = \(\frac{4+5+12+3+6+8+0.5}{7}=\frac{38.5}{7}\) = 5.5 సెం.మీ.

5. 10, 12, 18, 13 P మరియు 17 ల సరాసరి 15 అయిన P విలువను కనుగొనండి. (పేజీ నెం. 204)
సాధన.
సరాసరి \(\overline{\mathbf{x}}=\frac{\Sigma \mathbf{x}_{\mathbf{i}}}{\mathbf{n}}\)
15 = \(\frac{10+12+18+13+P+17}{6}\)
90 = 70 + P
P = 90 – 70 = 20

6. కింది పౌనఃపున్య విభాజనమునకు అంకగణితమధ్యమం కనుగొనండి (పేజీ నెం. 205)

సాధన.

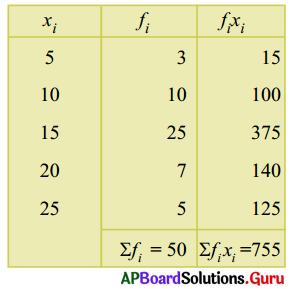
సోపానం – 1 : ప్రతి వరుసలో f_i × x_i కనుగొనుము.
సోపానం – 2 : పౌనఃపున్యముల మొత్తం (Σf_i)
మరియు f_i × x_i లబ్ధముల మొత్తం (Σf_ix_i) లను కనుగొనుము,

సోపానం – 3 : అంకగణితమధ్యమము
\(\overline{\mathrm{X}}\) = \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}=\frac{755}{50}\) = 15.1

7. కింది పౌనఃపున్య విభాజనము యొక్క అంకగణిత మధ్యమం 7.5 అయిన, ‘A’ విలువను కనుగొనండి. (పేజీ నెం. 205)

సాధన.

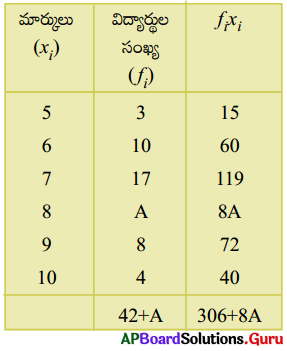
పౌనఃపున్యముల మొత్తం (Σf_i) = 42 + A
రాశుల మొత్తం f_i × x_i(Σf_ix_i) = 306 + 8A
అంకగణిత మధ్యమం \(\overline{\mathrm{x}}\) = \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\)
ఇచ్చిన విలువ ప్రకారం = 7.5
కావున 7.5 = \(\frac {306 + 8A}{42 + A}\)
306 + 8A = 315 + 7.5 A
8A – 7.5A = 315 – 306
0.5A = 9
A = 18

8. కింది అవర్గీకృత పౌనఃపున్య విభాజనమునకు అంకగణిత మధ్యమము కనుగొనండి. (పేజీ నెం.206)

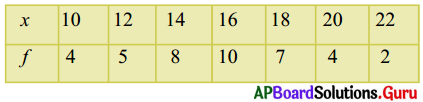
సాధన.

(i) సాధారణ పద్ధతి :
అవర్గీకృత పౌనఃపున్య విభాజనపు సగటుకు కింది సూత్రాన్ని ఉపయోగించండి.
\(\bar{x}=\frac{\sum_{\mathrm{i}=1}^{7} \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\sum_{\mathrm{i}=1}^{7} \mathrm{f}_{\mathrm{i}}}=\frac{622}{40}\) = 15.55

(ii) విచలన పద్దతి:

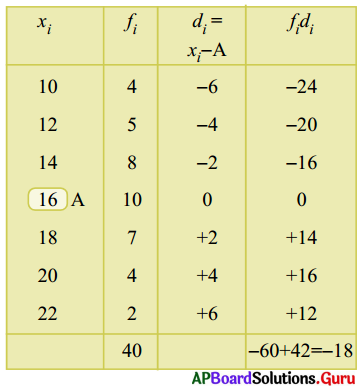
ఈ పద్ధతిలో దత్తాంశములోని ఏదైనా ఒకరాశిని ఊహించిన అంకగణిత మధ్యమంగా గుర్తించి అంకగణిత మధ్యమం కనుగొంటారు. ఈ దత్తాంశమునకు ఊహించిన అంకగణిత మధ్యమం A = 16 అనుకొని పట్టికను పూరించగా …..
పౌనఃపున్యముల మొత్తం = 40
విచలనముల f_i × d_i లబ్దాల మొత్తం = – 60 + 42.
Σf_id_i = – 18
అంకగణిత మధ్యమం \(\overline{\mathrm{X}}\) = A + \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{d}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\) = 16 + \(\frac {-18}{40}\)
= 16 – 0.45
= 15.55

9. కింద ఒక రోజు దుకాణదారుడు అమ్మిన పాదరక్షల సైజు నంబర్లు ఇవ్వబడినవి. బాహుళకము కనుగొనండి. 6, 7, 8, 9, 10, 6, 7, 10, 7, 6, 7, 9, 7, 6 (పేజీ నెం. 208)
సాధన.
దత్తాంశ రాశులను ఆరోహణ క్రమంలో రాయగా 6, 6, 6, 6, 7, 7, 7, 7, 7, 8, 9, 9, 10, 10 లేక పౌనఃపున్య విభాజనము రాయగా

ఇచ్చట 7 అను సంఖ్య 5 సార్లు వచ్చింది.
∴ దత్తాంశము యొక్క బాహుళకము = 7.

10. 100 మార్కులకు నిర్వహించిన పరీక్షలో 20 మంది విద్యార్థుల మార్కులు
93, 84, 97, 98, 1000, 78, 86, 100, 85, 92, 55, 91, 90, 75, 94, 83, 60, 81, 95
(a) 91 – 100, 81 – 90 ……… తరగతులతో పౌనఃపున్య విభాజన పట్టిక తయారుచేయండి.
(b) బాహుళక తరగతిని గుర్తించండి. (అత్యధిక పౌనఃపున్యం గల తరగతిని ‘బాహుళక తరగతి’ అంటారు)
(c) మధ్యగతపు తరగతులను గుర్తించండి. (పేజీ నెం. 209)
సాధన.
(a)

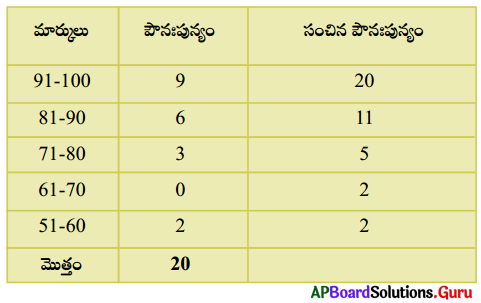
(b) గరిష్ఠ పౌనఃపున్యాలు ‘9’ గల తరగతి 91 – 100 కావున ఇదే బాహుళకపు తరగతి.
(c) 20 లో మధ్య మరాశి 10.
దత్తాంశములోని రాశులను ఆరోహణ లేక అవరోహణ క్రమములో ఎట్లు లెక్కించును 10వ రాశి 81 – 90 తరగతిలో గలదు. కావున 81 – 90ను మధ్యగత తరగతి అంటారు.