Mahesh

AP SCERT 9th Class Maths Textbook Solutions Chapter 9 సాంఖ్యక శాస్త్రము Ex 9.2 Textbook Exercise Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 9th Lesson సాంఖ్యక శాస్త్రము Exercise 9.2

ప్రశ్న 1.
ఒక సరుకుల రవాణా కార్యాలయంలోని పార్సిక్ష ఇరువులు కింది పట్టికలో ఇవ్వబడ్డాయి. ఒక్కొక్క పార్సిలు యొక్క సరాసరి బరువెంత?

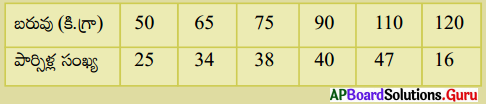
సాధన.

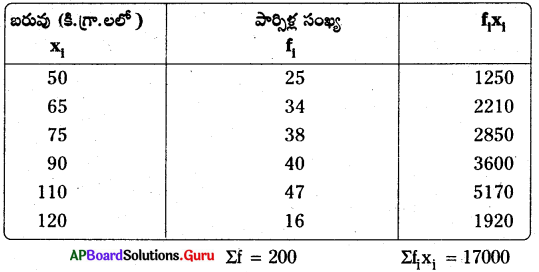
[latex]\overline{\mathrm{X}}[/latex] = [latex]\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}=\frac{17000}{200}=\frac{170}{2}[/latex]
[latex]\overline{\mathrm{X}}[/latex] = 85
∴ సగటు = 85

ప్రశ్న 2.
ఒక గ్రామములోని ప్రతి కుటుంబములో గల పిల్లల వివరాలు కింది పట్టికలో ఇవ్వబడ్డాయి. ఒక్కొక్క కుటుంబములోని సరాసరి పిల్లల సంఖ్య కనుగొనండి.

సాధన.

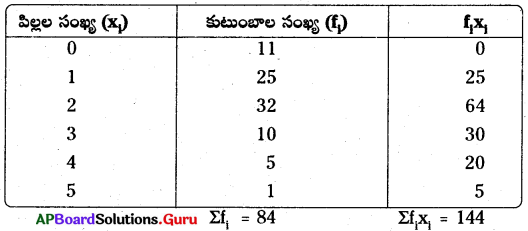
[latex]\overline{\mathrm{X}}[/latex] = [latex]\frac{\Sigma f_{i} x_{i}}{\Sigma f_{i}}=\frac{144}{84}[/latex]
∴ సగటు = 1.714285

ప్రశ్న 3.
కింది పౌనఃపున్య విభాజనము యొక్క సరాసరి 7.2 అయిన ‘K’ విలువను కనుగొనండి.

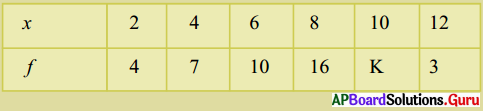
సాధన.

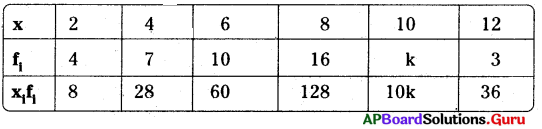
Σf_i = 40 + k, Σf_ix_i = 260 + 10k
ఇచ్చిన సగటు [latex]\overline{\mathrm{X}}[/latex] = 7.2
కాని సగటు [latex]\overline{\mathrm{X}}[/latex] = [latex]\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathbf{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}[latex]
7.2 = [latex]\frac{260+10 k}{40+k}[/latex]
288.0 + 7.2k = 260 + 10k
10k – 7.2k = 288 – 260
2.8k = 28
k = [latex]\frac {28}{2.8}[/latex] = 10

ప్రశ్న 4.
భారతదేశ జన గణన ప్రకారం గ్రామములు, జనాభా వివరాలు కింది విధంగా ఇవ్వబడ్డాయి. (జనాభా దగ్గర వేలకు సవరించబడినది) ఒక్కొక్క గ్రామం యొక్క సరాసరి జనాభా ఎంత ?

సాధన.

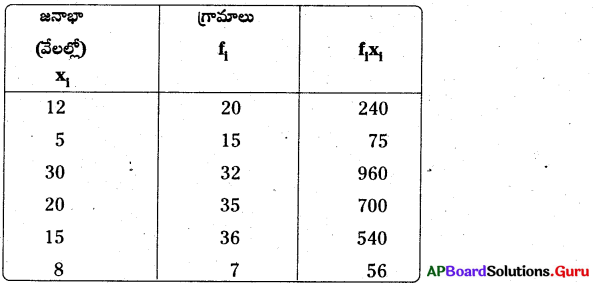
Σf_i = 145 Σf_ix_i = 2571 వేలు
∴ సగటు [latex]\overline{\mathrm{X}}[/latex] = [latex]\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}=\frac{2571}{145}[/latex] = 17.731 వేలు

ప్రశ్న 5.
AFLATOUN అనే సాంఘిక, ఆర్థిక విద్యావిషయక సంస్థ హైదరాబాదు జిల్లాలోని ఉన్నత పాఠశాలల విద్యార్థులచే పొదుపు కార్యక్రమమును ప్రారంభించింది. మండలాలవారీగా ఒక్క నెలలో పొదుపు చేయబడిన మొత్తాలు ఇవ్వబడ్డాయి.

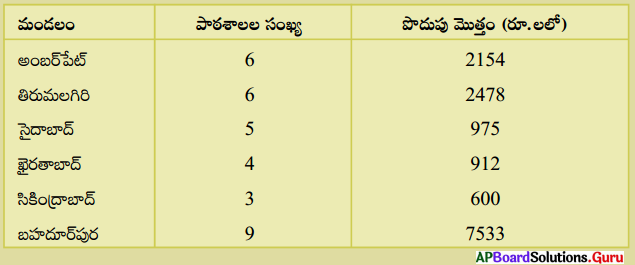
ఒక్కొక్క మండలంలో పాఠశాలవారీ సరాసరి పొదుపు మొత్తమెంత ? జిల్లా మొత్తంమీద పాఠశాల సరాసరి పొదుపు ఎంత ?
సాధన.

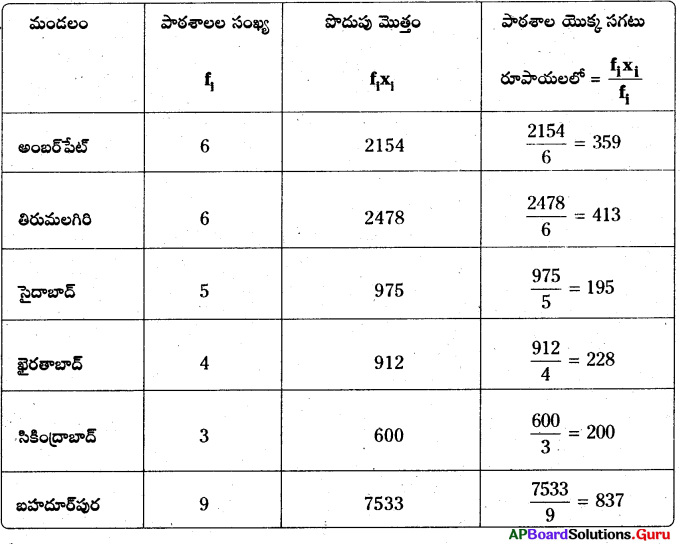
Σf_i = 33 Σf_ix_i = 14652
∴ సగటు = [latex]\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}[/latex]
[latex]\overline{\mathrm{X}}[/latex] =[latex]\frac{14652}{33}[/latex] = ₹444

ప్రశ్న 6.
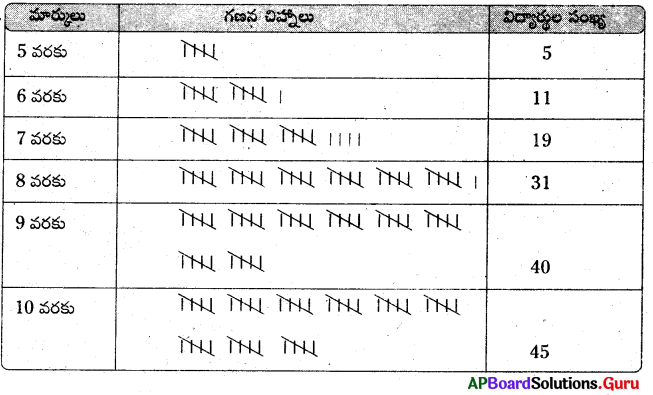
ఒక పాఠశాలలోని 9వ తరగతి బాల బాలికల ఎత్తుల వివరాలు ఈ విధంగా ఉన్నవి.

బాల బాలికల ఎత్తులను పోల్చండి.
సూచన : బాలబాలికల మధ్యగత ఎత్తును కనుగొనండి.]
సాధన.

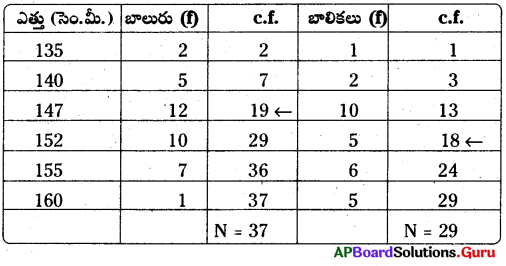
బాలుర మధ్యగత తరగతి = [latex]\frac{37+1}{2}=\frac{38}{2}[/latex] = 19 వ అంశము
∴ బాలుర యొక్క ఎత్తు = 147 సెం.మీ.
బాలికల మధ్యగత తరగతి = [latex]\frac{29+1}{2}=\frac{30}{2}[/latex] = 15వ అంశము
∴ బాలికల యొక్క ఎత్తు = 152 సెం.మీ.

ప్రశ్న 7.
ప్రపంచ క్రికెట్ ఆటగాళ్లలో శతకాలు (100 పరుగులు) చేసిన వారి సంఖ్యలు కింది పట్టికలో ఇవ్వబడ్డాయి.

ఈ దత్తాంశమునకు సరాసరి, మధ్యగతము, బాహుళకములను కనుగొనండి.
సాధన.

N = Σf_i = 139 Σf_ix_i = 1555
సగటు [latex]\overline{\mathrm{x}}=\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}=\frac{1555}{139}[/latex] = 11.187
మధ్యగతము = ([latex]\frac {N}{2}[/latex] + 1) వ పదం [latex]\frac{139+1}{2}=\frac{140}{2}[/latex] = 70వ పదం = 10 బాహుళకము = 5

ప్రశ్న 8.
కొత్త సంవత్సరాది సందర్భముగా ఒక మిఠాయి దుకాణం వారు మిఠాయి పొట్లాలను సిద్ధపరుచుచున్నారు. ఒక్కొక్క మీఠాయి పొట్లాం ధర, సిద్ధపరచిన పొట్లాల సంఖ్యలు కింది పౌనఃపున్య విభాజనములో ఇవ్వబడ్డాయి.

పై దత్తాంశమునకు అంకగణిత మధ్యమము, మధ్యగతము, బాహుళకములు కనుగొనండి.
సాధన.

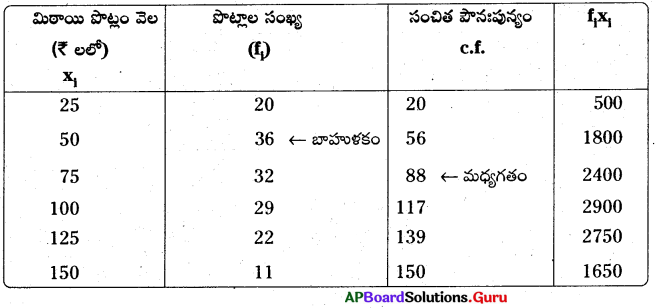
N = Σf_i = 150 Σf_ix_i = 12000
సగటు = [latex]\overline{\mathrm{x}}=\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}=\frac{12000}{150}[/latex] = 80
మధ్యగతము = ([latex]\frac{N}{2}[/latex] మరియు [latex]\frac{N}{2}[/latex] + 1) ల సగటు = 75 మరియు 76 అంశాల సగటు = 75 బాహుళకం = 50

ప్రశ్న 9.
ముగ్గురు విద్యార్థుల సగటు బరువు 40 కి.గ్రా. వారిలో రంగా బరువు 46 8.గ్రా, మరియు మిగిలిన ఇద్దరు విద్యార్థులు రహీమ్, రేష్మాల బరువులు సమానం అయిన రహీమ్ బరువు ఎంత ?
సాధన.
రంగా బరువు = 46 కి.గ్రా.
రేష్మా బరువు = రహీమ్ బరువు = x కి.గ్రా. అనుకొనుము.
సగటు = విద్యార్ధుల బరువుల మొత్తం / విద్యార్థుల సంఖ్య = 40కి.గ్రా.
∴ 40 = [latex]\frac {46+x+x}{3}[/latex]
40 × 3 = 46 + 2x
120 – 46 = 2x
2x = 74
∴ x = [latex]\frac {74}{2}[/latex] = 37
∴ రహీమ్ బరువు = 37 కి.గ్రా.

ప్రశ్న 10.
ఒక ఉన్నత పాఠశాలలోని వివిధ తరగతుల విద్యార్థులు ఒక అనాథశరణాలయంనకు ఇచ్చిన విరాళములు (రూపాయలలో) కింది విధంగా ఉన్నవి.

ఈ వివరాలకు అంకగణిత మధ్యమము, మధ్యగతము, బాహుళకములు కనుగొనండి.
సాధన.

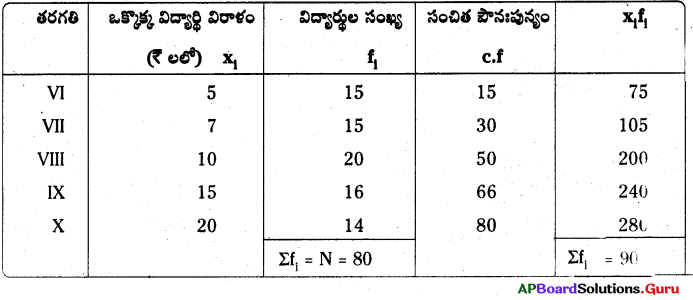
సగటు [latex]\overline{\mathrm{x}}=\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}=\frac{900}{80}[/latex] = 11.25
మధ్యగతము = ([latex]\frac{N}{2}[/latex] మరియు [latex]\frac{N}{2}[/latex] + 1) ల సగటు = [latex]\frac{80}{2}[/latex], ([latex]\frac{80}{2}[/latex] + 1) అంశాల సగటు
= 40 మరియు 41 అంశాల సగటు = ₹10
∴ ఈ బాహుళకము = ₹10

ప్రశ్న 11.
నాలుగు సంఖ్యలలో మొదటి రెండింటి సరాసరి 4, మొదటి మూడింటి సరాసరి కి, అన్నింటి సరాసరి 15 మరియు ఆ సంఖ్యలలో ఒకటి 2 అయిన మిగిలిన సంఖ్యలను కనుగొనుము.
సాధన.
సాధారణముగా సగటు = రాశుల మొత్తము / రాశుల సంఖ్య
దత్తాంశము 4 సంఖ్యల సగటు = 15 ⇒ 4 సంఖ్యల మొత్తము = 15 × 4 = 60
మొదటి 3 సంఖ్యల సగటు = 9 ⇒ మొదటి 3 సంఖ్యల మొత్తము = 9 × 3 = 27
మొదటి 2 సంఖ్యల సగటు = 4 ⇒ మొదటి 2 సంఖ్యల సగటు = 4 × 2 = 8
నాల్గవ సంఖ్య = నాలుగు సంఖ్యల మొత్తం-మూడు సంఖ్యల మొత్తం = 60 – 27 = 33
మూడవ సంఖ్య = మూడు సంఖ్యల మొత్తం – రెండు సంఖ్యల మొత్తం = 27 – 8 = 19
రెండవ సంఖ్య = రెండు సంఖ్యల మొత్తం – ఇచ్చిన సంఖ్య = 8 – 2 = 6
∴ మిగిలిన మూడు సంఖ్యలు = 6, 19, 33

AP SCERT 9th Class Maths Textbook Solutions Chapter 9 సాంఖ్యక శాస్త్రము Ex 9.1 Textbook Exercise Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 9th Lesson సాంఖ్యక శాస్త్రము Exercise 9.1

ప్రశ్న 1.
కింది పౌనఃపున్య విభాజనము నుండి రాశులు, వాని పౌనఃపున్యములు గల పట్టిక తయారుచేయండి.

సాధన.

ప్రశ్న 2.
9వ తరగతిలోని 36 మంది యొక్క రక్తం గ్రూపులు ఈ విధంగా ఉన్నవి.

ఈ దత్తాంశమునకు పౌనఃపున్య విభాజన పట్టికను తయారుచేయండి. అతి సామాన్యమైన గ్రూపు ఏది ? అరుదైన గ్రూపు ఏది ?
సాధన.

పట్టిక నుంచి ‘O’ సామాన్య గ్రూపు మరియు ‘AB’ అరుదైన గ్రూపు.

ప్రశ్న 3.
ఒక్కొక్కసాగికి మూడు నాణెముల చొప్పున 30 సార్లు ఎగురవేసి ఒక్కొక్కసారికి పడిన బొమ్మలను లెక్కించడం కింది విధంగా ఉంది.

దత్తాంశమునకు పౌనఃపున్య విభాజన పట్టిక తయారుచేయండి.
సాధన.

ప్రశ్న 4.
ఒక టి.వి. ఛానల్ వారు ధూమపాన నిషేధముపై SMS (సంక్షిప్త సందేశాలు) అభిప్రాయములను ఆహ్వానించిరి. ఇచ్చిన ఐచ్ఛికములు, A – పూర్తి నిషేధము, B – బహిరంగ ప్రదేశములలో నిషేధము, C – నిషేధము అవసరం లేదు. అని ఇవ్వగా SMS సమాధానములు ఇట్లున్నవి:

దత్తాంశమునకు వర్గీకృత పౌనఃపున్య విభాజనము తయారుచేయండి. సరియైన SMS సమాధానములు ఎన్ని ? వానిలో అధిక సంఖ్యాకుల అభిప్రాయము ఏది ?
సాధన.

మొత్తం వచ్చిన సమాధానములు = 19 + 36 + 10 = 65
అధిక సంఖ్యాకుల అభిప్రాయము = B.

ప్రశ్న 5.
కింది కమ్మీ రేఖాచిత్రము నుండి పౌనఃపున్య విభాజన పట్టికను రాయండి.

సాధన.

ప్రశ్న 6.
కింది పటంలో ఇవ్వబడిన సోపాన రేఖాచిత్రము నుండి పౌనఃపున్య విభాజనమును తయారుచేయండి. రేఖాచిత్రములో ఉపయోగించిన (అక్షములపై) స్కేలును తెల్పండి.

సాధన.
పౌనఃపున్య విభాజన పట్టిక :

తరగతి	విద్యార్థుల సంఖ్య
I	40
II	55
III	65
IV	30
V	15

స్కేలు : X – అక్షం : 1 సెం.మీ. = 1 తరగతి అంతరం
Y – అక్షం : 1 సెం.మీ. = 10 మంది విద్యార్థులు

ప్రశ్న 7.
75 మార్కులకు రాయబడిన పరీక్షలో 30 మంది విద్యార్థులు సాధించిన మార్కులు ఇవ్వబడ్డాయి.
42, 21, 50, 37, 42, 37, 38, 42, 49, 52, 38, 53, 57, 47, 29, 59, 61, 33, 17, 17, 39, 44, 42, 39, 14, 7, 27, 19, 54,51. ఈ దత్తాంశమునకు సమాన తరగతులతో (0-10, 10-20 ….) పౌనఃపున్య విభాజన పట్టిక తయారుచేయండి.
సాధన.

ప్రశ్న 8.
ఒక వీధిలోని 25 ఇండ్ల యొక్క నెలవారి విద్యుత్ వినియోగపు బిల్లులు (రూపాయలలో) ఇవ్వబడ్డాయి. తరగతి పొడవు రూ. 75 ఉందునట్లుగా ఈ దత్తాంశమునకు పౌనఃపున్య విభాజన పట్టిక తయారుచేయండి.
170, 212,252, 225, 310,712,412, 425, 322, 325, 192, 198, 230, 320,412,530, 602, 724, 370, 402, 317,403, 405, 372,413.
సాధన.
పరిశీలనాంశాలలో కనిష్ఠ విలువ = 170
పరిశీలనాంశాలలో గరిష్ఠ విలువ = 724

ప్రశ్న 9.
ఒక సంస్థవారు తయారుచేసిన కారు బ్యాటరీలలో 40 బ్యాటరీల జీవిత కాలం (సంవత్సరాలలో) కింది విధంగా నమోదు చేసారు.

పై దత్తాంశమునకు మినహాయింపు తరగతులలో పౌనఃపున్య విభాజన పట్టిక తయారుచేయండి. తరగతి అంతరం 0.5 గా తీసుకొని 2-2.5 తరగతితో ప్రారంభించండి.
సాధన.

AP SCERT 9th Class Maths Textbook Solutions Chapter 10 ఉపరితల వైశాల్యములు మరియు ఘనపరిమాణములు InText Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 10th Lesson ఉపరితల వైశాల్యములు మరియు ఘనపరిమాణములు InText Questions

ప్రయత్నించండి

1. ‘l’ సెం.మీ. పొడవైన భుజం గల ఒక ఘనమును తీసుకోండి. ముందు కృత్యములో దీర్ఘమనమును కత్తిరించిన విధంగానే చేసి దాని యొక్క ప్రక్కతల వైశాల్యమును, సంపూర్ణతల వైశాల్యమును కనుగొనుము. (పేజీ నెం.216)
సాధన.

‘l’ సెం.మీ. భుజం గల ఒక ఘనమును కత్తిరించి, తెరచిన పైన పటంలో చూపిన విధంగా ఏర్పడును.
పటంలో A, B, C, D, E, F అను ‘l’ భుజంగా గల చతురస్రములు కలవు.
తలాలు A, C, D, F లు ఘనము యొక్క ప్రక్క తలాలను తెలియజేయుచున్నవి.
∴ ఘనపు ప్రక్కతల వైశాల్యము = 4l² చ.యూ.
మొత్తం ఆరు తలాలు కలిసి ఘనమును ఏర్పరచును.
∴ ఘనపు సంపూర్ణతల వైశాల్యము = 6l² చ.యూ.

2. (a) ‘a’భుజముగా గల ఘనము యొక్క ఘనపరిమాణమును కనుక్కోండి. (పేజీ నెం.217)

సాధన.
a భుజముగా గల ఘనము యొక్క ఘనపరిమాణము
V = భుజము³ = a³ ఘ. యూనిట్లు.

(b) అదే విధముగా ఒక ఘనము ఘనపరిమాణం 1000 ఘనపు సెంటీమీటర్లు అయితే దాని యొక్క భుజమును కనుక్కోండి. (పేజీ నెం.217)
సాధన.
ఘనపరిమాణం = V = భుజము³
= 10 × 10 × 10 = 10³
∴ భూజము = 10 సెం.మీ.

3. స్థూపము యొక్క ప్రక్కతల వైశాల్యము మారకుండా దానియొక్క వ్యాసార్ధమును రెట్టింపు చేస్తే దాని ఎత్తులో కలిగే మార్పు ఎంత ? (పేజీ నెం. 225)
సాధన.
మొదటి స్థూపపు వ్యాసార్ధము మరియు ఎత్తులు వరుసగా r మరియు h అనుకొనుము.
ప్రక్కతల వైశాల్యము = 2πrh
స్టూప వ్యాసార్థం రెట్టింపయిన, ప్రక్కతల వైశాల్యములో మార్పు లేకుండా ఉంటే దాని ఎత్తు h₁ అనుకొనుము.
కొత్త ప్రక్కతల వైశాల్యము = 2πrh
= 2π (2r) (h₁)
⇒ 2πrh = 4πrh₁
∴ h₁ = [latex]\frac {2πrh}{4πr}[/latex] = [latex]\frac {1}{2}[/latex]h
∴ ఎత్తు, అసలు ఎత్తులో సగము ఉండును.

4. వాటర్ హీటరు యొక్క స్థూపాకార పైపు యొక్క పొడవు 14 మీటర్లు మరియు వ్యాసము 5 సెం.మీ. అయితే నీటిని వేడిచేసే ఈ హీటరు యొక్క సంపూర్ణతల వైశాల్యమును కనుగొనుము. (పేజీ నెం.225)
సాధన.
వ్యాసార్ధము (r) = వ్యాసము / 2 = [latex]\frac {5}{2}[/latex] = 2.5 సెం.మీ.
పైపు పొడవు = ఎత్తు = 14 మీ.
హీటరు సంపూర్ణతల వైశాల్యము = 2πr (r + h)
= 2 × [latex]\frac {22}{7}[/latex] × 2.5 × (2.5 + 14)
= [latex]\frac {110}{7}[/latex] × 16.5 = [latex]\frac {1815}{7}[/latex]
= 259.29 సెం.మీ.³

5. ‘r’ వ్యాసార్ధము, ‘l’ చాపము పొడవు గల సెక్టరును వృత్తాకార కాగితం నుండి కత్తిరించి శంఖువుగా తయారుచేయుము. శంఖువు యొక్క ప్రక్కతల వైశాల్యం A = πrl ను ఏ విధంగా ఉత్పాదిస్తావో చెప్పుము. (పేజీ నెం. 228)

సాధన.
వ్యాసార్థం ‘r’ మరియు చాపము పొడవు ‘l’ గా గల సెక్టరును వృత్తాకార కాగితం నుండి కత్తిరించి శంఖువుగా మార్చగా వ్యాసార్థం ‘r’, ఏటవాలు ఎత్తు ‘l’ గా మరియు చాపం పొడవు ‘l’ భూ చుట్టుకొలత 2πr గా మారును.
సెక్టరు వైశాల్యము = [latex]\frac {lr}{2}[/latex] = శంఖువు వైశాల్యం

= [latex]\frac {2πrl}{2}[/latex] = శంఖువు ప్రక్కతల వైశాల్యము = πrl

6. గోళం ఉపరితల వైశాల్యాన్ని మీరు ఇంకేదైనా పద్ధతిలో కనుగొనగలరా ? (పేజీ నెం. 235)
సాధన.

గోళం ఉపరితల వైశాల్యానికి సూత్రంను కనుగొనుటకు గోళమును సర్వసమాన పిరమిడ్ యొక్క భూములన్నీ గోళ ఉపరితలాన్ని ఆక్రమిస్తున్నాయని ఊహించిన ఆ పటంపైన చూపబడినట్లుగా ఏర్పడును.
పై పటంలో అటువంటి ఒక పిరమిడను చూపటము జరిగినది. పిరమిడ్ యొక్క వైశాల్యంకు, ఘనపరిమాణంకు గల నిష్పత్తిని తీసుకొనగా,
పిరమిడ్ వైశాల్యం A.
పిరమిడ్ ఘనపరిమాణం V = (1/3) × A × r = (A × r) / 3
∴ పిరమిడ్ యొక్క వైశాల్యం, ఘనపరిమాణాల నిష్పత్తి A/V= A + (A × r) / 3 = (3 × A) / (A × r) = 3 / r
ఆ గోళమును n సర్వసమాన పిరమిడ్లుగా విభజించిన భూమిని అనుకొనుము.
n పిరమిడ్ యొక్క మొత్తం వైశాల్యం = n × A.
అదే విధంగా , పిరమిడ్ యొక్క మొత్తం ఘనపరిమాణము = n × V.
∴ గోళము యొక్క n పిరమిడ్ల యొక్క వైశాల్యాల మొత్తంకు, ఘనపరిమాణాల మొత్తంకు గల నిష్పత్తి = n × A / n × V = A / V
మనకు ముందుగానే A / V = 3 / r అనుకున్నాము
కావున, n × A_{పిరమిడ్} = A_గోళం
n × V_{పిరమిడ్} = V_గోళం (అన్ని పిరమిడ్ల వైశాల్యాలు (లేక) ఘనపరిమాణాలు, వరుసగా గోళము యొక్క ఉపరితల వైశాల్యంకు లేక ఘనపరిమాణంకు సమానము)
పై పరిశీలనల నుండి,

∴ గోళం యొక్క సంపూర్ణ ఉపరితల వైశాల్యం 4πr² అగును.

ఇవి చేయండి

1. 4 సెం.మీ. భుజముగా గల ఘనము యొక్క ప్రక్కతల వైశాల్యమును, సంపూర్ణతల వైశాల్యమును కనుగొనుము. (పేజీ నెం. 216)

సాధన.
భుజము l = 4 సెం.మీ.
∴ ఘనము యొక్క ప్రక్కతల వైశాల్యము = 4l²
= 4 × 4² = 4³ = 64 సెం.మీ².
∴ ఘనము యొక్క సంపూర్ణతల వైశాల్యము
= 6l² = 6 × 4² = 6 × 16 = 96 సెం.మీ².

2. ఒక ఘనము యొక్క భుజమును 50% పెంచితే ఎంత శాతము దాని యొక్క సంపూర్ణతల వైశాల్యము పెరుగుతుంది ? (పేజీ నెం. 216)
సాధన.
ఘనపు భుజము = x యూనిట్లు అనుకొనుము.
ఘనము యొక్క సంపూర్ణతల వైశాల్యము = 6l²
= 6x²చ, యూ.
కొత్త భుజము = x + xలో 50% = x + [latex]\frac {50x}{100}[/latex] = x + [latex]\frac{x}{2}=\frac{3 x}{2}[/latex]
కొత్త సంపూర్ణతల వైశాల్యము = 6l²
= [latex]6\left(\frac{3 x}{2}\right)^{2}=6 \times \frac{9 x^{2}}{4}=\frac{27 x^{2}}{2}[/latex]
వైశాల్యంలో పెరుగుదల = [latex]\frac{27 \mathrm{x}^{2}}{2}[/latex] – 6x²
= [latex]\left(\frac{27-12}{2}\right) x^{2}=\frac{15}{2} x^{2}[/latex]
∴ వైశాల్యంలో పెరుగుదల శాతము
= వైశాల్యంలో పెరుగుదల / అసలు వైశాల్యము × 100

ఇక్కడ x = పెరుగుదల / తగ్గుదల

3. ఒక దీర్ఘఘనం యొక్క పొడవు, వెడల్పు చురియు ఎత్తు విలువలు l = 12 సెం.మీ., b = 10 సెం.మీ. మరియు h= 8 సెం.మీ. అయిన ఆ దీర్ఘఘన ఘనపరిమాణాన్ని కనుగొనండి. (పేజీ నెం. 218)
సాధన.
దీర్ఘఘనపు పొడవు (l) = 12 సెం.మీ., వెడల్పు
(b) = 10 సెం.మీ. మరియు ఎత్తు (b) = 8 సెం.మీ.
ఘనపరిమాణం V = lbh = 12 × 10 × 8
= 960 ఘ. సెం.మీ.

4. భుజం 10 సెం.మీ.గా గల సమఘనము యొక్క ఘనపరిమాణము కనుగొనండి. (పేజీ నెం. 218)
సాధన.
ఘనపరిమాణము V = l³ = 10 × 10 × 10
= 1000 ఘ. సెం.మీ.

5. పటంలో చూపబడిన లంబకోణ సమద్విబాహం త్రిభుజాకార పట్టకము యొక్క ఘనపరిమాణము కనుక్కోండి. (పేజీ నెం. 218)

సాధన.
పట్టక ఘనపరిమాణము = పట్టక భూ వైశాల్యం × ఎత్తు
= [latex]\frac {1}{2}[/latex] × 5 × 5 × 8
= 25 × 4
= 100 ఘ. సెం.మీ.

6. 10 సెం.మీ. భుజము కలిగిన చతురస్రాకార భూమి మరియు 8 సెం.మీ. ఎత్తు కలిగిన పిరమిడ్ యొక్క ఘనపరిమాణము కనుక్కోంది. (పేజీ నెం. 219)
సాధన.
పిరమిడ్ ఘనపరిమాణము
= [latex]\frac {1}{3}[/latex] × భూ వైశాల్యం × ఎత్తు
= [latex]\frac {1}{3}[/latex] × 10 × 10 × 8 = [latex]\frac {800}{3}[/latex] సెం.మీ.³
= 266.67 సెం.మీ³.

7. సమఘనము యొక్క ఘనపరిమాణము 1200 ఘనపు సెంటీమీటర్లు. సమఘనపు ఎత్తుతో సమాన ఎత్తు కలిగిన చతురస్రాకార పిరమిడ్ యొక్క ఘనపరిమాణమును కనుగొనుము. (పేజీ నెం. 219)
సాధన.
చతుర రార పిరమిడ్ యొక్క ఘనపరిమాణం
= [latex]\frac {1}{3}[/latex] × సమఘన ఘనపరిమాణము
= [latex]\frac {1}{3}[/latex] × 1200 = 400 ఘ. సెం.మీ.

8. క్రింది పటములో చూపబడిన స్థూపము యొక్క ప్రక్కతల వైశాల్యంను కనుగొనండి. (పేజీ నెం. 221)

ప్రశ్న (i)
r = x సెం.మీ.; h = yసెం.మీ.
సాధన.
స్థూపపు ప్రక్కతల వైశాల్యం = 2πrh .
= 2πxy సెం.మీ.²

ప్రశ్న (ii)
d = 7 సెం.మీ.; h = 10 సెం.మీ.
సాధన.

స్థూపపు ప్రక్కతల వైశాల్యం = 2πrh
= 2 × [latex]\frac {22}{7}[/latex] × [latex]\frac {7}{2}[/latex] × 10
= 220 సెం.మీ.²

ప్రశ్న (iii)
r = 3 సెం.మీ.; b = 14 సెం.మీ.
సాధన.

స్థూపపు ప్రక్కతల వైశాల్యం = 2πrh
= 2 × [latex]\frac {22}{7}[/latex] × 3 × 14
= 264 సెం.మీ.²

9. ఈ కింది స్థూపముల యొక్క సంపూర్ణతల వైశాల్యమును కనుగొనుము. (పేజీ నెం. 222)

సాధన.
(i) r = 7 సెం.మీ. ; h = 10 సెం.మీ.
స్థూపపు సంపూర్ణతల వైశాల్యము = 2πr (r + h)
= 2 × [latex]\frac {22}{7}[/latex] × 7 (7 + 10)
= 2 × [latex]\frac {22}{7}[/latex] × 7 × 17
= 748 చ.సెం.మీ.

(ii) స్థూపం భూ వైశాల్యం = 250 చ.సెం.మీ. .
h = 7 సెం.మీ. ; πr² = 250 సెం.మీ.
πr² = 250 ⇒ [latex]\frac {22}{7}[/latex] × r² = 250
⇒ r² = 125 × [latex]\frac {7}{11}[/latex]
∴ r = [latex]\sqrt{\frac{875}{11}}[/latex]
r = 8.9 సెం.మీ.
స్థూపపు సంపూర్ణతల వైశాల్యము =
= 2 × [latex]\frac {22}{7}[/latex] × 8.9 (8.9 + 7)
= [latex]\frac{44 \times 8.9 \times 15.9}{7}=\frac{6226.44}{7}[/latex]
= 889.50 (సుమారుగా)

10. ఒక లంబకోణ త్రిభుజాన్ని తీసుకోంది/ కత్తిరించండి. పటంలో చూపినట్లు దానికి ఒక సన్నని వెదురుషుల్లను లంబాకార భుజమును అతికించండి. కర్రయొక్క రెండు వైపులను పట్టుకొని చుట్టూ తిప్పండి. తిప్పేవేగము స్థిరముగా ఉండాలి. మీరు ఏమి గమనించారు? (పేజీ నెం. 229)
సాధన.

ఒక క్రమ వృత్తాకార శంఖువు ఏర్పడుటను గమనించితిని.

11. ఈ కింది క్రమ వృత్తాకార శంఖువు యొక్క ప్రక్కతల వైశాల్యం, సంపూర్ణతల వైశాల్యములను కనుగొనుము. (పేజీ నెం. 229)
సాధన.

OP = 2 సెం.మీ.; OB = 3.5 సెం.మీ.
OP = h = 2 సెం.మీ.
r = OB = 3.5 సెం.మీ.
ప్రక్కతల వైశాల్యము = πrl
కాని l = [latex]\sqrt{\mathrm{r}^{2}+\mathrm{h}^{2}}[/latex]
= [latex]\sqrt{2^{2}+3 \cdot 5^{2}}[/latex]
= [latex]\sqrt{4+12.25}[/latex]
= [latex]\sqrt{16.25}[/latex] = 4.03
వక్రతల వైశాల్యము = [latex]\frac {22}{7}[/latex] × 3.5 × 4.03
= 44.34 సెం.మీ².
సంపూర్ణతల వైశాల్యము = πr (r + l)
= [latex]\frac {22}{7}[/latex] × 3.5(3.5 + 4.03)
= [latex]\frac {22}{7}[/latex] × 3.5 × 7.53 = 82.83 సెం.మీ².

OP = 3.5 సెం.మీ.; AB = 10 సెం.మీ.
r = [latex]\frac {AB}{2}[/latex] = 5 సెం.మీ. ; h = 3.5 సెం.మీ.
l = [latex]\sqrt{\mathrm{r}^{2}+\mathrm{h}^{2}}=\sqrt{5^{2}+3.5^{2}}=\sqrt{25+12.25}[/latex]
వ.త,వై. = πrl = [latex]\frac {22}{7}[/latex] × 5 × 6.10
= 95.90 సెం.మీ².
స.త.వై = πr (r + 1)
= [latex]\frac {22}{7}[/latex] × 5 × (5 + 6.10)
= 174.42 సెం.మీ².

12. ఒక క్రమ వృత్త స్థూపాకార వస్తువులో r వ్యాసార్ధముగా గల గోళం అమర్చబడినది. అయితే
(i) గోళం యొక్క ఉపరితల వైశాల్యం
(ii) స్థూపము యొక్క వక్రతల వైశాల్యం
(iii) (i) మరియు (ii) వైశాల్యముల నిష్పత్తి కనుక్కోండి. (పేజీ నెం. 236)

సాధన.
(i) గోళం వ్యాసార్ధం = స్థూపం వ్యాసార్ధము = r
∴ గోళం యొక్క ఉపరితల వైశాల్యం = 4πr²
(ii) స్థూపం యొక్క వక్రతల వైశాల్యం = 2πr (2r) [∵ h = 2r] = 4πr²
(iii) (i) మరియు (ii) వైశాల్యా ల నిష్పత్తి = 4πr² : 4πr² = 1 : 1

13. ఈ కింది పటముల యొక్క ఉపరితల వైశాల్యములను కనుగొనండి. (పేజీ నెం. 236)

(i)

గోళం ఉపరితల వైశాల్యం = 4πr²
గోళం వ్యాసార్ధం = 7 సెం.మీ.
గోళం ఉపరితల వై = 4 × [latex]\frac {22}{7}[/latex] × 7 × 7 = 616 సెం.మీ².

(ii)

అడ్డగోళ ఉపరితల వైశాల్యము = 2πr² = 2 × [latex]\frac {22}{7}[/latex] × 7 × 7
= 308 సెం.మీ²
స.త.వై = 3πr² = 3 × [latex]\frac {22}{7}[/latex] × 7 × 7 = 462 సెం.మీ²

14. కింది పటంలో చూపబడిన గోళముల యొక్క ఘనపరిమాణములను కనుక్కోంది. (పేజీ నెం. 238)
సాధన.

r = 3 సెం.మీ.
V = [latex]\frac {22}{7}[/latex]πr³ = [latex]\frac {4}{3}[/latex] × [latex]\frac {22}{7}[/latex] × 3 × 3 × 3
= 113.14 సెం.మీ³.

d = 5.4 సెం.మీ.
r = [latex]\frac {d}{2}[/latex] = [latex]\frac {5.4}{2}[/latex] = 2.7 సెం.మీ.
V = [latex]\frac {4}{3}[/latex]πr³ = [latex]\frac {4}{3}[/latex] × [latex]\frac {22}{7}[/latex] × 2.7 × 2.7 × 2.7 = 82.48 సెం.మీ³.

15. 6.3 సెం.మీ. వ్యాసార్థంగా గల గోళ ఘనపరిమాణమును కనుక్కోంది. (పేజీ నెం.238)
సాధన.
గోళ వ్యాసార్ధం r = 6.3 సెం.మీ.
గోళ ఘనపరిమాణము V= [latex]\frac {4}{3}[/latex]πr³ = [latex]\frac {4}{3}[/latex] × [latex]\frac {22}{7}[/latex] × 6.3 × 6.3 × 6.3 = 1047.81 సెం.మీ³.

కృత్యం

1. భూమి, ఎత్తు సమానముగా గల ఘనము, చతురస్రాకార పిరమిడ్లను తీసుకొందాం. (పేజీ నెం. 218)

పిరమిడను ఒక ద్రవముతో నింపి ఆ ద్రవమును ఘనములో పూర్తిగా నింపండి. ఘనము నింపడానికి ఎన్నిసార్లు పిరమిడ్ నుపయోగించాలి ? పరిశీలిస్తే మూడుసార్లు అని తెలుస్తుంది.
దీనిని బట్టి, పిరమిడ్ యొక్క ఘనపరిమాణం
= [latex]\frac {1}{3}[/latex] × క్రమ పట్టకం ఘనపరిమాణం (ఒకే భూమి, ఒకే ఎత్తు)
= [latex]\frac {1}{3}[/latex] × భూవైశాల్యం × ఎత్తు
సూచన : ఒక క్రమ పట్టకము, భూమికి లంబంగా ఉండేలా పక్క తలాలను కల్గి ఉంటుంది. మరియు ఆ పక్క తలాలన్నీ దీర్ఘచతురస్రాలే.

2. ఒక దీర్ఘచతురస్రాకార పలుచని అట్ట లేక కాగితమును తీసుకోండి. ఒక పొడవాటి దళసరి తీగను తీసుకొని పటములో చూపిన విధంగా అతికింపుము. తీగయొక్క రెండు చివరలను పట్టుకొని దీర్ఘచతురస్రాకార అట్టను వేగముగా త్రిప్పండి.

మీరు ఏమి గమనించారు ? కంటికి కనబడిన ఆకృతి ఎమిటి ? దానిని స్థూపముగా మీరు గుర్తించారా ? (పేజీ నెం. 220)

3. సెక్టరును శంఖువుగా మార్చే విధానం (పేజీ నెం. 227)
ఈ కింది సూచనలను పాటిస్తూ పటములో చూపిన విధముగా చేయండి.

(i) పటం (a) చూపిన విధంగా ఒక దళసరి కాగితముపై వృత్తమును గీయండి.
(ii) పటం (b) లో చూపినట్లు సెక్టరు AOB ను కత్తిరించండి.
(iii) పటం (c)లో చూపినట్లు A మరియు B చివరలను
ఒకదానితో ఒకటి తాకేటట్లు నెమ్మదిగా పటములో చూపిన విధముగా కలుషము. A, Bలు ఆధ్యారోహణము కాకూడదు. A, B లును అతికింపుము.
(iv) మీరు పొందిన ఆకృతి యొక్క లక్షణములు ఏమిటి? అది క్రమ వృత్తాకార శంఖువు అవుతుందా ?
‘OA’ మరియు ‘OB’ లను కలిపి శంఖువు తయారుచేసేటప్పుడు OA, OB మరియు చాపము AB ల యొక్క పొడవులలో గమనించిన మార్పులు ఏమిటి?

4. ఒక దళసరి కాగితంపై ఒక వృత్తమును గీయుము. దానిని కత్తిరింపుము. దాని వ్యాసము వెంబడి ఒక తీగను అతికింపుము. తీగ యొక్క రెండు చివరలు పట్టుకొని తిప్పుము. సమవేగముతో తిప్పితే మీరు ఏమి గమనించారు? (పేజీ నెం.235)

ఉదాహరణలు

1. 14 సెం.మీ. పొడవుగల దీర్ఘ చతురస్రాకార కాగితమునకు వెడల్పు వెంబడి రోల్ చేస్తే 20 సెం.మీ. వ్యాసార్థముగా గల స్థూపం ఏర్పడింది. అయిన స్థూపము (పటం 1) యొక్క ఘనపరిమాణము కనుక్కోండి. (π = [latex]\frac {22}{7}[/latex] గా తీసుకొండి.) (పేజీ నెం. 222)
సాధన.
దీర్ఘచతురస్రాకార కాగితమును వెడల్పు వెంబడి రోల్ చేయగా ఏర్పడిన స్థూపము యొక్క ఎత్తు, కాగితపు వెడల్పునకు సమానమవుతుంది. అయితే

స్థూపము యొక్క ఎత్తు h = 14 సెం.మీ.
మరియు వ్యాసార్థం (r) = 20 సెం.మీ.
స్థూపము ఘనపరిమాణము V = πr²h
= [latex]\frac {22}{7}[/latex] × 20 × 20 × 14 = 17600 ఘనపు సెంటీమీటర్లు
స్థూపపు ఘనపరిమాణము = 17600 ఘ, సెం.మీ.

2. ఒక దీర్ఘచతురస్రాకారపు కాగితము 11 సెం.మీ. × 4 సెం.మీ. కొలతలను కల్గియుంది. దానిని అంచులు ఆధ్యారోహణము చెందకుండా ఉండే విధముగా, 4 సెం.మీ. ఎత్తు కల్గిన స్థూపముగా మలిస్తే, స్థూపము యొక్క ఘనపరిమాణమును కనుక్కోండి. (పేజీ నెం. 223)
సాధన.
కాగితము యొక్క పొడవు, స్థూపము యొక్క భూపరిధికి సమానముగా, వెడల్పు ఎత్తునకు సమానముగా ఉంటుంది.

స్థూపపు వ్యాసార్ధము r = మరియు ఎత్తు = h స్టూపపు భూపరిధి = 2πr = 11 సెం.మీ.
2 × [latex]\frac {22}{7}[/latex] × r = 11
r = [latex]\frac {7}{4}[/latex]సెం.మీ.
h = 4 సెం.మీ.
స్టూపపు ఘనపరిమాణం (V) = 2π²h
= [latex]\frac {22}{7}[/latex] × [latex]\frac {7}{4}[/latex] × [latex]\frac {7}{4}[/latex] × 4 = 38.5 ఘనపు సెంటీమీటర్లు.

3. దీర్ఘచతురస్రాకారములో దళసరి కాగితము 14 సెం.మీ. × 18 సెం.మీ. కొలతలు కల్గియుంది. దానిని పొడవు వెంబడి చుట్టూ స్థూపమును తయారుచేసాము. స్థూపమును ఘనముగా (పూర్తిగా నింపబడిన) భావిస్తే దాని యొక్క వ్యాసార్ధమును, సంపూర్ణతల వైశాల్యమును కనుగొనుము. (పేజీ నెం. 223)
సాధన.
స్టూపము యొక్క ఎత్తు = 18 సెం.మీ.
స్థూపము యొక్క భూపరిధి = 44 సెం.మీ.
2πr = 44 సెం.మీ.
r = [latex]\frac{44}{2 \times \pi}=\frac{44 \times 7}{2 \times 22}[/latex] = 7 సెం.మీ.
సంపూర్ణతల వైశాల్యం = 2πr(r + h)
= 2 × [latex]\frac {22}{7}[/latex] × 7(7 + 18)
= 1100 చ.సెం.మీ.

4. 5 మి.మీ. మందము కల్గిన వృత్తాకార ప్లేటులను ఒకదానిపై మరొకటి పేర్చి స్థూపముగా ఏర్పరిస్తే, దాని యొక్క పక్కతల వైశాల్యము 462 చ.సెం.మీ. స్థూపమును ఏర్పరిచేందుకు కావలసిన వృత్తాకార ప్లేటుల సంఖ్య ఎంత ? ప్లేటు యొక్క వ్యాసార్థమును 2. 3.5 సెం.మీ.గా తీసుకోండి. (పేజీ నెం. 224)
సాధన.
వృత్తాకార ప్లేటు యొక్క మందం = 5 మి.మీ.
= [latex]\frac {5}{10}[/latex] సెం.మీ. = 0.5 సెం.మీ.
ప్లేటు యొక్క వ్యాసార్ధము = 3.5 సెం.మీ.
స్థూపము యొక్క పక్కతల వైశాల్యము = 462 చ. సెం.మీ.
∴ 2πrh = 462 ………… (i)
స్థూపము ఏర్పాటుకు అవసరమయ్యే ప్లేటుల సంఖ్య x అనుకొనుము.
∴ స్థూపము యొక్క ఎత్తు = h = ప్లేటు యొక్క మందం × ప్లేటుల సంఖ్య = 0.5x
∴ 2πrh = 2 × [latex]\frac {22}{7}[/latex] × 3.5 × 0.5x ……. (ii)
(i) మరియు (ii) సమీకరణముల నుండి,
2 × [latex]\frac {22}{7}[/latex] × 3.5 × 9.5x = 462
∴ x = [latex]\frac{462 \times 7}{2 \times 22 \times 3.5 \times 0.5}[/latex] = 42 ప్లేట్లు.

5. ఒక గుల్ల లోహపు స్థూపము యొక్క బాహ్య వ్యాసార్ధము 8 సెం.మీ. మరియు ఎత్తు 10 సెం.మీ. మరియు సంపూర్ణతల వైశాల్యము . 338 π చ.సెం.మీ. గుల్ల లోహపు స్థూపము యొక్క మందమును కనుక్కోండి. (పేజీ నెం. 224)
సాధన.

బాహ్య వ్యాసార్ధము = R = 8 సెం.మీ.
అంతర వ్యాసార్ధము = r
ఎత్తు = 10 సెం.మీ.
సంపూర్ణతల వైశాల్యము = 338 π చ.సెం.మీ.
కాని సంపూర్ణతల వైశాల్యము = బయటి స్థూపము యొక్క పక్కతల వైశాల్యం (CSA) + లోపల యున్న స్థూపము యొక్క ప్రక్కతల వైశాల్యం (CSA) + 2 × భూ వైశాల్యము (కంకణము)
= 2πRh + 2πrh + 2π(R² – r²)
= 2π(Rh + rh + R² – r²)
∴ 2π(Rh + rh + R² – r²) = 338π
Rh + rh + R² – r² = 169
⇒ (10 × 8) + (r × 10) + 8² – r² = 100
⇒ r² – 10r + 25 = 0
⇒ (r – 5)² = 0
∴ r = 5
∴ లోహపు స్థూపము యొక్క మందం = R – r = (8 – 5) సెం.మీ. = 3 సెం.మీ.

6. ఒక మొక్కజొన్న కంకి శంఖువు ఆకారములో ఉంది. వెదల్పు ఎక్కువగాయున్న ప్రాంతపు వ్యాసార్థము 1.4 సెం.మీ. మరియు ఎత్తు (పొడవు) 12 సెం.మీ. ప్రతి చ. సెం.మీ. ప్రాంతములో సుమారుగా 4 జొన్న గింజలుంటే మొత్తము ఎన్ని గింజలుంటాయి? (పేజీ నెం.230)
సాధన.

ఇక్కడ l = [latex]\sqrt{r^{2}+h^{2}}[/latex]
= [latex]\sqrt{(1.4)^{2}+(12)^{2}}[/latex] సెం.మీ.
= [latex]\sqrt{145.96}[/latex] = 12.08 సెం.మీ. (సుమారుగా)
మొక్కజొన్న కంకి వక్రతల వైశాల్యం = πrl
= [latex]\frac {22}{7}[/latex] × 1.4 × 12.08 చ.సెం.మీ.
= 53.15 చ.సెం.మీ.
= 53.2 చ. సెం.మీ. (సుమారుగా)
మొక్కజొన్న కంకిలో 1 చ.సెం.మీ. వైశాల్యములో గల జొన్న గింజల సంఖ్య = 4
∴ మొక్క జొన్న కంకి ప్రక్కతల వైశాల్యములో గల మొత్తము జొన్న గింజల సంఖ్య = 53.2 × 4 = 212.8 = 213 (సుమారుగా),
అందుచే మొక్కజొన్న కంకి సుమారుగా 213 గింజలుంటాయి.

7. 5.6 సెం.మీ. భూవ్యాసార్ధము మరియు 158,4 చ.సెం.మీ. ప్రక్కతల వైశాల్యము గల శంఖువు యొక్క ఏటవాలు ఎత్తు మరియు శంఖువు ఎత్తులను కనుగొనుము. (పేజీ నెం. 231)
సాధన.
భూ వ్యాసార్ధము = 5.6 సెం.మీ.
ఎత్తు = h, ఏటవాలు ఎత్తు = l
వక్రతల వైశాల్యము = πrl = 158.4 చ.సెం.మీ.
⇒ [latex]\frac {22}{7}[/latex] × 5.6 × l = 158.4
⇒ l = [latex]\frac{158.4 \times 7}{22 \times 5.6}=\frac{18}{2}[/latex] = 9 సెం.మీ.
l² = r² + h² అని మనకు తెలుసు
h² = l² – r²= 9² – (5.6)²
= 81 – 31.36 = 49.64
h = [latex]\sqrt{49.64}[/latex]
h = 7.05 సెం.మీ. (సుమారుగా)

8. ఒక గుడారం స్థూపముపై శంఖువు వలె ఉంది. శంఖువు యొక్క వ్యాసము స్థూపము భూవ్యాసము 24 మీటర్లకు సమానముగా యుంది. స్థూపము యొక్క ఎత్తు 11 మీ. మరియు శంఖువు యొక్క ఎత్తు 5 మీటర్లు, గుడారము తయారుచేయడానికి కావలసిన గుడ్డ చదరపు మీటరుకు ₹10 చొప్పున మొత్తము ఎంత ఖర్చవుతుంది ? (పేజీ నెం.231)
సాధన.
స్థూపపు భూవ్యాసము = శంఖువు వ్యాసం = 24 మీ.
∴ భూవ్యాసార్ధము = 12 మీ.
స్థూపము య్కొ ఎత్తు = 11 మీ. = h₁
శంఖము యొక్క ఎత్తు = 5 మీ. = h₂
శంఖము యొక్క ఏటవాటు ఎత్తు ‘l’ అనుకొందాం.
l = GD = [latex]\sqrt{r^{2}+h^{2}}=\sqrt{12^{2}+5^{2}}[/latex] = 13 మీ.

కావలసిన గుడ్డ వైశాల్యము = స్థూపము యొక్క ప్రక్కతల వైశాల్యం + శంఖువు ప్రక్కతల వైశాల్యం
= 2πrh₁ + πrl
= πr (2h₁ + l)
= [latex]\frac {22}{7}[/latex] × 12(2 × 11 + 13) చ.మీ.
= [latex]\frac{22 \times 12}{7}[/latex] × 35 చ.మీ. = 22 × 60 చ.మీ. = 1320 చ.మీ.
గుడ్డ యొక్క వెల = ₹ 10 చదరపు మీటరుకు
∴ గుడ్డ యొక్క మొత్తం ఖరీదు = వెల × గుడ్డ యొక్క వైశాల్యం
= ₹10 × 1320 = ₹13,200

9. సైన్యము తన బేనొక్యాంప్ కొరకు శంఖువు ఆకారములో ఎత్తు 3 మీ. మరియు భూవ్యాసము 8 మీ.గా యున్న గుదారమును ఏర్పాటుచేసిన
(i) గుదారం తయారుచేయడానికి కావలసిన బట్ట యొక్క వెల చ.మీ.నకు ₹70 అయిన మొత్తము ఖర్చు ఎంత?
(ii) ప్రతి వ్యక్తికి 3.5 ఘనపు మీటర్ల గాలి కావలసి యుంటే గుడారములో కూర్చోగల వ్యక్తుల సంఖ్య ఎంత ? (పేజీ నెం. 232)
సాధన.

గుడారం యొక్క వ్యాసం = 8 మీ.
r = [latex]\frac{d}{2}=\frac{8}{2}[/latex] = 4మీ.
ఎత్తు = 3 మీ.
ఏటవాలు ఎత్తు (l) = [latex]\sqrt{\mathrm{h}^{2}+\mathrm{r}^{2}}[/latex]
= [latex]\sqrt{\mathrm{3}^{2}+\mathrm{4}^{2}}[/latex] = [latex]\sqrt{25}[/latex] = 5 మీ.
∴ గుడారం యొక్క ప్రక్కతల వైశాల్యం = πrl
= [latex]\frac {22}{7}[/latex] × 4 × 5 = [latex]\frac {440}{7}[/latex] చ.మీ.
శంఖువు ఘనపరిమాణం = [latex]\frac {1}{3}[/latex]πr²h
= [latex]\frac {1}{3}[/latex] × [latex]\frac {22}{7}[/latex] × 4 × 4 × 3
= [latex]\frac {352}{7}[/latex] ఘనపు మీటర్లు
(i) గుదారం తయారీకి కావలసిన గుడ్డ ఖరీదు
= ప్రక్కతల వైశాల్యం × యూనిట్ల
= [latex]\frac {440}{7}[/latex] × 70 = ₹4400

(ii) గుడారంలో కూర్చోగల వ్యక్తుల సంఖ్య = శంఖాకార గుడారం ఘనపరిమాణం / ప్రతి వ్యక్తికి కావల్సిన గాలి ఘనపరిమాణం
= [latex]\frac{352}{7} \div 3.5=\frac{352}{7} \times \frac{1}{3.5}[/latex] – 14.36
= 14 మంది వ్యక్తులు (సుమారుగా)

10. గోళం ఉపరితల వైశాల్యం = 154 చ.సెం.మీ. అయిన దాని వ్యాసార్ధమును కనుగొనుము. (పేజీ నెం. 238)
సాధన.
గోళం ఉపరితల వైశాల్యం = 4πr²
4πr² = 154 ⇒ 4 × [latex]\frac {22}{7}[/latex] × r² = 154
⇒ r² = [latex]\frac{154 \times 7}{4 \times 22}=\frac{7^{2}}{2^{2}}[/latex]
⇒ r = [latex]\frac {7}{2}[/latex] = 3.5 సెం.మీ.

11. ఒక అర్ధగోళాకారపు గిన్నె రాతితో తయారుచేయబడి 5 సెం.మీ. మందం కల్గియుంది. దాని లోపలి వ్యాసార్థం 35 సెం.మీ. అయిన గిన్నె యొక్క సంపూర్ణతల వైశాల్యంను కనుగొనుము. (పేజీ నెం. 239)
సాధన.
వెలుపలి వ్యాసార్ధం R, లోపలి వ్యాసార్థం ‘r’.
మందం 5 సెం.మీ. అనుకొందాం.
∴ R = (r + 5) సెం.మీ. = (35 + 5) సెం.మీ.
= 40 సెం.మీ.

సంపూర్ణతల వైశాల్యం = బయటి ఉపరితల వైశాల్యం + లోపలి ఉపరితల వైశాల్యం + కంకణ వైశాల్యం
= 2πR² + 2πr² + π(R² – r²)
= π(2R² + 2r² + R² – r²)
= [latex]\frac {22}{7}[/latex](3R² + r²) = [latex]\frac {22}{7}[/latex] (3 × 40² + 35²) చ.సెం.మీ.
= [latex]\frac{6025 \times 22}{7}[/latex] చ.సెం.మీ.
= 18935.71 చ.సెం.మీ. (సుమారుగా)

12. అర్ధగోళాకారపు పై కప్పు కల్గిన ఒక భవనం (పటములో చూపిన విధంగా) నకు రంగు వేయాలి. పై కప్పు యొక్క భూపరిధి 17.6 మీ. ఆయిన 10 చ.సెం.మీ. వకు రంగు వేయుటకు 5 రూపాయలు చొప్పున భవనంనకు రంగువేయడానికి ఎంత ఖర్చు అవుతుంది? (పేజీ నెం. 299)
సాధన.

భవనంలోని వృత్తాకార ఉపరితల వైశాల్యంనకు మాత్రమే రంగు వేయాలి కనుక అర్ధగోళం యొక్క ప్రక్కతల వైశాల్యం కనుగొనాలి. పైకప్పు యొక్క భూపరిధి = 17.6 మీ.
∴ 17.6 = 2πr
అందుచే పై కప్పు యొక్క వ్యాసార్ధం = 17.6 × [latex]\frac{7}{2 \times 22}[/latex] మీ. = 2.8 మీ.
పై కప్పు యొక్క ప్రక్కతల వైశాల్యం = 2πr²
= 2 × [latex]\frac {22}{7}[/latex] × 2.8 × 28 చ.మీ.
= 49.28 చ.మీ.
100 చ.సెం.మీ. ప్రాంతమునకు రంగువేయడానికి అయ్యేఖర్చు = ₹ 5
∴ 1 చ.మీ. ప్రాంతమునకు రంగు వేయడానికి అయ్యే ఖర్చు = ₹500
∴ రంగు వేయడానికి అయ్యే మొత్తం ఖర్చు = 500 × 49.28 = ₹24640

13. ఒక సర్కస్ లో మోటార్ సైకిలిస్టు ఒక గుల్ల గోళాకార ఆకృతిలో విన్యాసములు చేయుచున్నాడు. గుల్ల గోళము యొక్క వ్యాసం 7 మీ, సైకిలిస్టు విన్యాసంలో తిరిగేందుకు అవకాశము ఉండే ప్రాంత వైశాల్యము ఎంత ? (పేజీ నెం. 240)
సాధన.
గోళం వ్యాసం = 7 మీ., వ్యాసార్ధం = 3.5 మీ.
అందుచే విన్యాసకుడు తిరగగలిగే ప్రాంత వైశాల్యం గోళం యొక్క ఉపరితల వైశాల్యంనకు సమానం.
4πr² = 4 × [latex]\frac {22}{7}[/latex] × 3.5 × 3.5 చ.మీ. = 154 చ.మీ.

14. షాటి ఫుటనకు ఉపయోగించే లోహపు గోళం యొక్క వ్యాసార్థం 4.9 సెం.మీ. లోహం యొక్క సాంద్రత 7.8 గ్రా. ఘనపు సెం.మీ. అయిన షాట్‌పుట్ యొక్క ద్రవ్యరాశి కనుగొనుము. (పేజీ నెం. 240)
సాధన.
షాట్ పుట్ లోహపు గోళము కనుక దాని ద్రవ్యరాశి గోళము యొక్క ఘనపరిమాణం మరియు సాంద్రతల లబ్ధమునకు సమానము. అందుచే మనము గోళము యొక్క ఘనపరిమాణమును కనుగొనాలి.
ఇప్పుడు గోళం ఘనపరిమాణం = [latex]\frac {4}{3}[/latex]πr³
= [latex]\frac {4}{3}[/latex] × [latex]\frac {22}{7}[/latex] × 4.9 × 4.9 × 4.9 ఘ. సెం.మీ.
= 493 ఘ. సెం.మీ. (సమారుగా)
1 ఘనపు సెంటీ మీటరు లోహం యొక్క ద్రవ్యరాశి = 7.8 గ్రా.
అందుచే షాట్‌పుట్ యొక్క ద్రవ్యరాశి = 7.8 × 493 గ్రాములు = 3845.44 గ్రా. = 3.85 కి.గ్రా. (సుమారుగా)

15. ఒక అర్ధగోళాకారపు గిన్నె యొక్క వ్యాసార్ధం 3.5 సెం.మీ. దానిలో నింపగలిగే నీటి ఘనపరిమాణం ఎంత? (పేజీ నెం. 240)
సాధన.
గిన్నెలోని నీటి ఘనపరిమాణం = అర్ధగోళం ఘనపరిమాణం
= [latex]\frac {4}{3}[/latex] × [latex]\frac {22}{7}[/latex] × 3.5 × 3.5 × 3.5 ఘు. సెం.మీ.
= 89.8 ఘన సెం.మీ. (సమారుగా)

AP SCERT 9th Class Maths Textbook Solutions Chapter 10 ఉపరితల వైశాల్యములు మరియు ఘనపరిమాణములు Ex 10.4 Textbook Exercise Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 10th Lesson ఉపరితల వైశాల్యములు మరియు ఘనపరిమాణములు Exercise 10.4

ప్రశ్న 1.
ఒక గోళపు వ్యాసార్థం 2.5 సెం.మీ. అయిన దాని ఉపరితల వైశాల్యం, ఘనపరిమాణం ఎంత ?
సాధన.
గోళపు వ్యాసార్ధము, r = 3.5 సెం.మీ.
ఉపరితల వైశాల్యం = 4πr² = 4 × [latex]\frac {22}{7}[/latex] × 3.5 × 3.5
= 4 × 22 × 0.5 × 3.5 = 154 సెం.మీ².
ఘనపరిమాణము = [latex]\frac {4}{3}[/latex]πr³
= [latex]\frac {4}{3}[/latex] × [latex]\frac {22}{7}[/latex] × 3.5 × 3.5 × 3.5
= [latex]\frac{4 \times 22 \times 0.5 \times 12.25}{3}[/latex]
= 179.666 సెం.మీ.³
= 179.7 సెం.మీ.³

ప్రశ్న 2.
ఒక గోళం ఉపరితల వైశాల్యం 1018[latex]\frac {2}{7}[/latex] చ.సెం.మీ. అయిన దాని ఘనపరిమాణం ఎంత ?
సాధన.
గోళపు ఉపరితల వైశాల్యము = 4πr²
= 1018[latex]\frac {2}{7}[/latex] సెం.మీ².
4πr² = [latex]\frac {7128}{7}[/latex]
r² = [latex]\frac{7128 \times 7}{7 \times 4 \times 22}[/latex]
r² = 81
r = [latex]\sqrt{81}[/latex] = 9 సెం.మీ.
∴ గోళపు ఘనపరిమాణము = [latex]\frac {4}{3}[/latex]πr³
= [latex]\frac {4}{3}[/latex] × [latex]\frac {22}{7}[/latex] × 9 × 9 × 9
= [latex]\frac {21384}{7}[/latex] = 3054.857 సెం.మీ.³
= 3054.86 సెం.మీ³.

ప్రశ్న 3.
గ్లోబులో భూమధ్యరేఖ పొడవు 44 సెం.మీ. అయిన దాని ఉపరితల వైశాల్యం ఎంత?
సాధన.
గ్లోబు యొక్క భూమధ్యరేఖ పొడవు
2πr = 44 సెం.మీ.
2 × [latex]\frac {22}{7}[/latex] × r = 44
∴ r = [latex]\frac{44 \times 7}{2 \times 22}[/latex] = 7 సెం.మీ.
∴ ఉపరితల వైశాల్యము = 4πr²
= 4 × [latex]\frac {22}{7}[/latex] × 7 × 7
= 4 × 22 × 7 = 616 సెం.మీ².

ప్రశ్న 4.
ఒక గోళాకారపు బంతి యొక్క వ్యాసం 21 సెం.మీ. .. ఇటువంటి 5 బంతులను తయారుచేయడానికి కావలసిన పదార్ద పరిమాణం ఎంత?
సాధన.
గోళాకార బంతి యొక్క వ్యాసము ‘d’ = 21 సెం.మీ,
వ్యాసార్ధము ‘r’ = [latex]\frac {d}{2}[/latex] = [latex]\frac {21}{2}[/latex] = 10.5 సెం.మీ.
ఒక బంతి యొక్క ఉపరితల వైశాల్యము = 4πr²
= 4 × [latex]\frac {22}{7}[/latex] × 10.5 × 10.5
= 88 × 1.5 × 10.5 = 1386 సెం.మీ².
∴ అటువంటి 5 బంతులకు అవసరమైన పదార్థ పరిమాణము = 5 × 1386 = 6930 సెం.మీ².

ప్రశ్న 5.
రెండు గోళముల వ్యాసార్ధముల నిష్పత్తి 2 : 3. అయిన వాటి ఉపరితల వైశాల్యాలు మరియు ఘన పరిమాణముల నిష్పత్తిని కనుగొనుము.
సాధన.
వ్యాసార్థాల నిష్పత్తి = r₁ : r₂ = 2 : 3
ఉపరితల వైశాల్యాల నిష్పత్తి
= [latex]4 \pi r_{1}^{2}: 4 \pi r_{2}^{2}=r_{1}^{2}: r_{2}^{2}[/latex]
= 2² : 3² = 4 : 9
ఘనపరిమాణాల నిష్పత్తి = [latex]\frac{4}{3} \pi r_{1}^{3}: \frac{4}{3} \pi r_{2}^{3}=r_{1}^{3}: r_{2}^{3}[/latex]
= 2³ : 3³ = 8 : 27

ప్రశ్న 6.
10 సెం.మీ. వ్యాసార్ధముగా గల అర్ధగోళం యొక్క సంపూర్ణతల వైశాల్యంను కనుగొనుము. (π = 3.14 గా తీసుకొనుము)
సాధన.
అర్ధగోళపు వ్యాసార్ధము = 10 సెం.మీ.
అర్ధగోళ సంపూర్ణతల వైశాల్యము = 3πr²
= 3 × 3.14 × 10 × 10 = 9.42 × 100
= 942 సెం.మీ².

ప్రశ్న 7.
ఒక గోళాకార బెలూన్ యొక్క వ్యాసం 14 సెం.మీ. నుండి 28 సెం.మీ. వరకు పెరిగే విధంగా గాలి నింపబడింది. ఈ రెండు సందర్భములలో గల ఉపరితల వైశాల్యముల నిష్పత్తిని కనుగొనుము.
సాధన.
బెలూన్ యొక్క వ్యాసం, d = 14 సెం.మీ.
బెలూన్ వ్యాసార్థం, r = [latex]\frac {d}{2}[/latex] = [latex]\frac {14}{2}[/latex] = 7 సెం.మీ.
∴ ఉపరితల వైశాల్యం = 4πr² = 4 × [latex]\frac {22}{7}[/latex] × 7 × 7
= 88 × 7 = 616 సెం.మీ.²
గాలిని నింపినపుడు బెలూన్ వ్యాసము = 28 సెం.మీ.,
వ్యాసార్ధము = [latex]\frac {d}{2}[/latex] = [latex]\frac {28}{2}[/latex] = 14 సెం.మీ.
ఉపరితల వైశాల్యము = 4πr²
= 4 × [latex]\frac {22}{7}[/latex] × 14 × 14
= 88 × 28 = 2464 సెం.మీ².
వైశాల్యాల నిష్పత్తి = 616 : 2464
= 1 : 4
(లేదా)
అసలు వ్యాసార్ధము = [latex]\frac {14}{2}[/latex] = 7 సెం.మీ.
పెరిగిన వ్యాసార్ధము = [latex]\frac {28}{2}[/latex] = 14 సెం.మీ.
వైశాల్యాల నిష్పత్తి = [latex]\mathrm{r}_{1}^{2}: \mathrm{r}_{2}^{2}=7^{2}: 14^{2}[/latex]
= 7 × 7 : 14 × 14 = 1 : 4

ప్రశ్న 8.
0.25 సెం.మీ. మందం కల ఇత్తడితో ఒక అర్ధగోళాకార గిన్నెను తయారుచేశారు. గిన్నె లోపలి వ్యాసార్ధం 5 సెం.మీ. అయిన గిన్నె యొక్క ఉపరితల వైశాల్యం మరియు లోపలితల వైశాల్యంనకు గల నిష్పత్తిని కనుగొనండి.
సాధన.
అర్ధవృత్తపు లోపలి వ్యాసార్ధము = ‘r’ = 5 సెం.మీ.
అర్ధవృత్తపు బయటి వ్యాసార్ధము ‘R’ = లోపలి వ్యాసార్థం + మందం
= (5 + 0.25) సెం.మీ. = 5.25 సెం.మీ.
వైశాల్యాల నిష్పత్తి = 3πR² : 3πr²
= R² : r²
= (5.25)² : 5²
= 27.5625 : 25
= 1.1025 : 1
= 11025 : 10000
= 441 : 400
(గమనిక : వ్యాసార్ధంను వ్యాసంగా తీసుకున్న టెస్టుక్ జవాబును పొందవచ్చును)

ప్రశ్న 9.
ఒక సీసపు బంతి యొక్క వ్యాసం 21 సెం.మీ. దానిని తయారు చేయడానికి ఉపయోగించే సీసం యొక్క సాంద్రత 11.34 గ్రా. సెం.మీ³. అయిన బంతి యొక్క బరువు ఎంత ?
సాధన.
బంతి వ్యాసము = 2.1 సెం.మీ.
వ్యాసార్ధము, r = [latex]\frac {d}{2}[/latex] = [latex]\frac {2.1}{2}[/latex] = 1.05 సెం.మీ.
బంతి ఘనపరిమాణము ‘V’ = [latex]\frac {4}{3}[/latex]πr³
= [latex]\frac {4}{3}[/latex] × [latex]\frac {22}{7}[/latex] × 1.05³ = [latex]\frac {101.87}{21}[/latex]
సీసపు సాంద్రత = 11.34 గ్రా|| సెం.మీ³
బంతి బరువు = ఘనపరిమాణము × సాంద్రత
= 4.851 × 11.34
= 55.010 గ్రా||లు

ప్రశ్న 10.
ఒక స్థూపాకార లోహము యొక్క వ్యాసం 5 సెం.మీ. మరియు ఎత్తు 3[latex]\frac {1}{3}[/latex] సెం.మీ. దానిని కరిగించి ఒక గోళముగా తయారుచేస్తే దాని యొక్క వ్యాసం ఎంత ?
సాధన.
స్థూపపు వ్యాసము ‘d’ = 5 సెం.మీ.
వ్యాసార్ధము, r = [latex]\frac {d}{2}[/latex] = [latex]\frac {5}{2}[/latex] = 25 సెం.మీ.
సూపపు ఎత్తు, h = 3[latex]\frac {1}{3}[/latex] = [latex]\frac {10}{3}[/latex]సెం.మీ.
స్థూపపు ఘనపరిమాణం
= πr²h = [latex]\frac {22}{7}[/latex] × 2.5 × 2.5 × [latex]\frac {10}{3}[/latex]
దత్తాంశము నుండి స్థూపమును కరిగించి గోళముగా పోతపోసిరి.
∴ స్థూపపు ఘనపరిమాణం = గోళపు ఘనపరిమాణం
[latex]\frac {4}{3}[/latex]πr³ = [latex]\frac {22}{7}[/latex] × 2.5 × 2.5 × [latex]\frac {10}{3}[/latex] (∴ r గోళపు వ్యాసార్ధము)
∴ r³ = [latex]\frac {3}{4}[/latex] × 2.5 × 2.5 × [latex]\frac {10}{3}[/latex]
r³ = 2.5³
∴ r = 2.5 సెం.మీ.
గోళపు వ్యాసము, d = 2r
= 2 × 2.5 = 5 సెం.మీ.

ప్రశ్న 11.
10.5 సెం.మీ. వ్యాసము గల అర్ధగోళాకారపు గిన్నెలో నింపగల పాల యొక్క సామర్థ్యం ఎంత ?
సాధన.
అర్ధగోళాకారపు గిన్నె వ్యాసము = 10.5 సెం.మీ.
అర్ధగోళాకారపు గిన్నె వ్యాసార్ధం
= [latex]\frac {d}{2}[/latex] = [latex]\frac {10.5}{2}[/latex] = 5.25 సెం.మీ.
గిన్నెలో పట్టు పాల పరిమాణము = గిన్నె ఘనపరిమాణం
= [latex]\frac {2}{3}[/latex]πr³
= [latex]\frac {2}{3}[/latex] × [latex]\frac {22}{7}[/latex] × 5.25 × 5.25 × 5.25
= 303.1875 సెం.మీ³.
= [latex]\frac {303.1875}{1000}[/latex]లీ. = 0303లీ.

ప్రశ్న 12.
ఒక అర్ధగోళాకార గిన్నె యొక్క వ్యాసం 9 సెం.మీ. గిన్నెలోగల ద్రవమును 3 సెం.మీ. వ్యాసం మరియు 3 సెం.మీ. ఎత్తుగల స్థూపాకారపు సీసాలలో నింపుతూ ఉంటే నిండుగా ఉన్న గిన్నెలోని ద్రవమును ఎన్ని సీసాలలో నింపవచ్చు ?
సాధన.
అర్ధగోళాకారపు గిన్నె వ్యాసము d = 9 సెం.మీ.
∴ ఆర్ధగోళాకారపు గిన్నె వ్యాసార్ధము,
r = [latex]\frac {d}{2}[/latex] = [latex]\frac {9}{2}[/latex] = 4.5 సెం.మీ.
ద్రవపు ఘనపరిమాణం = గిన్నె ఘనపరిమాణము
= [latex]\frac {2}{3}[/latex]πr³
= [latex]\frac {2}{3}[/latex] × [latex]\frac {22}{7}[/latex] × 4.5 × 4.5 × 4.5
స్థూపాకారపు సీసా వ్యాసము d = 3 సెం.మీ,
⇒ స్థూపాకారపు సీసా వ్యాసార్ధం
r = [latex]\frac {d}{2}[/latex] = [latex]\frac {3.0}{2}[/latex] = 1.5 సెం.మీ.
సీసా ఎత్తు, h = 3 సెం.మీ.
కావలసిన సీసాల సంఖ్య = n అనుకొనుము.
n సీసాల మొత్తం ఘనపరిమాణము = n . πr²h
ఈ ఘనపరిమాణం గిన్నెలోని ద్రవపు ఘనపరిమాణంకు సమానము.
n . [latex]\frac {22}{7}[/latex] × 1.5 × 1.5 × 3
= [latex]\frac {2}{3}[/latex] × [latex]\frac {22}{7}[/latex] × 4.5 × 4.5 × 4.5
∴ n = [latex]\frac{2}{3} \times \frac{20.25}{1.5}[/latex] = 9
∴ కావలసిన సీసాల సంఖ్య = 9

AP SCERT 9th Class Maths Textbook Solutions Chapter 10 ఉపరితల వైశాల్యములు మరియు ఘనపరిమాణములు Ex 10.3 Textbook Exercise Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 10th Lesson ఉపరితల వైశాల్యములు మరియు ఘనపరిమాణములు Exercise 10.3

ప్రశ్న 1.
శంఖువు భూ వైశాల్యం 38.5 చ.సెం.మీ. మన పరిమాణం 77 మ. సెం.మీ. అయిన దాని యొక్క ఎత్తును కనుగొనుము.
సాధన.
శంఖువు యొక్క భూ వైశాల్యం, πr² = 38.5 సెం.మీ².
శంఖువు యొక్క ఘనపరిమాణం V = [latex]\frac {1}{3}[/latex]πr²h = 77

∴ శంఖువు యొక్క ఎత్తు = 6 సెం.మీ.

ప్రశ్న 2.
శంఖువు ఘనపరిమాణం 462 ఘనపు మీటర్లు. భూ వ్యాసార్థం 7 మీటర్లు అయిన దాని ఎత్తును కనుగొనుము.
సాధన.
శంఖువు ఘనపరిమాణం V = [latex]\frac {1}{3}[/latex]πr²h = 462 ఘ॥మీ.
వ్యాసార్ధము ‘r’ = 7 మీ.
ఎత్తు = h అనుకొనుము.
[latex]\frac {1}{3}[/latex] × [latex]\frac {22}{7}[/latex] × 7 × 7 × h = 462
h = [latex]\frac{462 \times 3}{22 \times 7}[/latex] = 9
∴ ఎత్తు = 9 మీ.

ప్రశ్న 3.
ఒక శంఖువు ప్రక్కతల వైశాల్యం 308 చ.సెం.మీ. మరియు ఏటవాలు ఎత్తు 14 సెం.మీ. అయిన
(i) భూ వ్యాసార్ధం (ii) శంఖువు యొక్క సంపూర్ణతల వైశాల్యం కనుక్కోండి.
సాధన.
శంఖువు ప్రక్కతల వైశాల్యం , πrl = 308 చ. సెం.మీ.
ఏటవాలు ఎత్తు, l = 14 సెం.మీ.
(i) πrl = 308 చ. సెం.మీ. ; l = 14 సెం.మీ.
[latex]\frac {22}{7}[/latex] × r × 14 = 308
⇒ r = [latex]\frac {308}{44}[/latex] = 7 సెం.మీ.

(ii) శంఖుపు సంపూర్ణతల వైశాల్యం = πr (r + l)
[latex]\frac {22}{7}[/latex] × 7 × (7 + 14)
= 22 × 21 = 462 సెం.మీ².

ప్రశ్న 4.
చ.సెం.మీ.కు 25 పైసల వంతున ఒక శంఖువు యొక్క సంపూర్ణతల వైశాల్యమంతటికి రంగువేయటానికి అయ్యే ఖర్చు ₹176 అయిన, ఏటవాలు ఎత్తు 25 సెం.మీ. అయినప్పుడు దాని ఘనపరిమాణం కనుక్కోండి.
సాధన.
శంఖువు యొక్క ఏటవాలు ఎత్తు, l = 25 సెం.మీ.
25 పైసల వంతున చ.సెం.మీ.కు ఆగు ఖర్చు = ₹ 176
∴ శంఖువు యొక్క సంపుర్ణతల వైశాల్యం
= [latex]\frac {176}{25}[/latex] × 100 = 176 × 4 = 704 సెం.మీ².
శంఖువు యొక్క సంపూర్ణతల వైశాల్యం = πr(r + l)
= 704సెం.మీ²
కాబట్టి [latex]\frac {22}{7}[/latex]r(r + 25) = 704
r(r + 25) = [latex]\frac{704 \times 7}{22}[/latex] = 224
r² + 25r = 224
⇒ r² + 25r – 224 = 0
⇒ r² + 32r – 7r – 224 = 0
⇒ r(r +32) – 7 (r + 32) = 0
⇒ (r + 32) (r – 7) = 0
⇒ r = 7
h = [latex]\sqrt{l^{2}-\mathrm{r}^{2}}[/latex]
= [latex]\sqrt{25^{2}-7^{2}}=\sqrt{625-49}[/latex]
= [latex]\sqrt{576}[/latex]
= 24 సెం.మీ.
∴ శంఖువు యొక్క ఘనపరిమాణం = [latex]\frac {1}{3}[/latex]πr²h
= [latex]\frac {1}{3}[/latex] × [latex]\frac {22}{7}[/latex] × 7 × 7 × 24
= 22 × 7 × 8 = 1232 సెం.మీ³.

ప్రశ్న 5.
15 సెం.మీ. వ్యాసార్ధం గల ఒక వృత్తాకార దళసరి కాగితం నుండి 216° సెక్టరు కోణం గల సెక్టరును కత్తిరించి దాని అంచులతో యున్న వ్యాసార్థములను వంచి శంఖువుగా మలిస్తే దాని యొక్క ఘనపరిమాణం ఎంత?
సాధన.
సెక్బారు యొక్క వ్యాసార్థం, ‘r’ = 15 సెం.మీ.
సెక్బారు కోణము, ‘x’ = 216°
∴ సెక్బారు పొడవు (l) = [latex]\frac {x}{360}[/latex] × 2πr
= [latex]\frac {216}{360}[/latex] × 2πr = [latex]\frac {3}{5}[/latex] (2πr)
శంఖువు యొక్క చుట్టుకొలత = చాపము పొడవు శంఖువు యొక్క 2πr = వృత్తం యొక్క శంఖువు యొక్క వ్యాసార్థం ‘r’ = [latex]\frac {3}{5}[/latex] × 15 = 9
వృత్త వ్యాసార్ధము, ‘r’ = శంఖువు యొక్క ఏటవాలు ఎత్తు (l) = 9 సెం.మీ.
∴ శంఖువు ఎత్తు (h) = [latex]\sqrt{l^{2}-\mathrm{r}^{2}}[/latex]
= [latex]\sqrt{15^{2}-9^{2}}=\sqrt{225-81}[/latex]
= [latex]\sqrt{144}[/latex] = 12 సెం.మీ.
∴ శంఖువు ఘనపరిమాణము = [latex]\frac {1}{3}[/latex] πr²h
= [latex]\frac {1}{3}[/latex] × [latex]\frac {22}{7}[/latex] × 9 × 9 × 12
= 1018.285 ఘ. సెం.మీ.
= 1018.3 ఘ. సెం.మీ. (సుమారుగా)

ప్రశ్న 6.
ఒక గుదారం యొక్క ఎత్తు 9 మీ. దాని యొక్క వ్యాసం 24 మీ. అయిన దాని ఏటవాలు ఎత్తు ఎంత ? గుదారంను తయారుచేయడానికి కావలసిన గుడ్డ వెల చ.మీ. ₹14 అయిన మొత్తం గుడ్డ వెల ఎంత ?
సాధన.
శంఖు ఆకారపు ‘టెంట్ ఎత్తు ‘h’ = 9 మీ.
భూ వ్యాసము = 24 మీ.
భూ వ్యాసార్ధము ‘r’ = [latex]\frac{d}{2}=\frac{24}{2}[/latex] = 12 మీ.
కాన్వాసు ఖరీదు = ₹14 చ.మీ.కు
శంఖువు వక్రతల వైశాల్యము = πrl
l = [latex]\sqrt{\mathrm{r}^{2}+\mathrm{h}^{2}}[/latex]
= [latex]\sqrt{12^{2}+9^{2}}=\sqrt{144+81}[/latex]
= [latex]\sqrt{225}[/latex] = 15 మీ.
∴ వక్రతల వైశాల్యం = πrl = [latex]\frac {22}{7}[/latex] × 12 × 15
చ.మీ.కు ₹14 చొప్పున అయిన ఖర్చు
= 14 × [latex]\frac {22}{7}[/latex] × 12 × 15 = ₹7920

ప్రశ్న 7.
శంఖువు యొక్క ప్రకృతల వైశాల్యం 1159[latex]\frac {5}{9}[/latex] చ.సెం.మీ. దాని యొక్క భూవైశాల్యం 254[latex]\frac {4}{7}[/latex] చ.సెం.మీ. అయిన . దాని ఘనపరిమాణాన్ని కనుగొనుము.
సాధన.
శంఖువు వక్రతల వైశాల్యం = πrl
= 1159[latex]\frac {5}{7}[/latex] చ. సెం.మీ.
శంఖువు భూ వైశాల్యము = πr² = 254[latex]\frac {4}{7}[/latex] చ.సెం.మీ.
[latex]\frac {22}{7}[/latex] × r² = [latex]\frac {1782}{7}[/latex]
∴ r² = [latex]\frac{1782}{7} \times \frac{7}{22}=\frac{1782}{22}[/latex] = 81
= 178 x 7 – 1782 = 81
⇒ [latex]\sqrt{81}[/latex] = 9 సెం.మీ.

πrl = [latex]\frac {8118}{7}[/latex] చ.మీ. కావున

ప్రశ్న 8.
ఒక గుడారం 4.8 మీ. ఎత్తుగల స్థూపాకారంగా ఉంది. దానిపై 4.5 మీ. భూవ్యాసార్థం, కేంద్రం నుండి 10.8 మీ. ఎత్తు ఉండే విధముగా ఒక శంఖువు అమర్చబడి ఉంది. అయిన గుడారము తయారు చేయుటకు కావలసిన గుడ్డ వైశాల్యం ఎంత?
సాధన.

స్థూపపు వ్యాసార్ధం, l = 4.5 మీ.
స్థూపపు ఎత్తు = h = 4.8 మీ.
∴ స్థూపపు వక్రతల వైశాల్యం = 2πrh
= 2 × [latex]\frac {22}{7}[/latex] × 4.5 × 48
= 135.771 మీ².
శంఖువు వ్యాసార్ధం ‘r’ = స్థూపపు వ్యాసార్ధం = 4.5 మీ.
శంఖువు ఎత్తు ‘h’ = 10.8 – 4.8 = 6 మీ.
∴ శంఖువు ఏటవాలు ఎత్తు
l = [latex]\sqrt{r^{2}+h^{2}}=\sqrt{4.5^{2}+6^{2}}[/latex]
= [latex]\sqrt{20.25+36}=\sqrt{56.25}[/latex] = 7.5 మీ.
∴ శంఖువు వక్రతల వైశాల్యం = πrl
= [latex]\frac {22}{7}[/latex] × 4.5 × 7.5
= [latex]\frac {742.5}{7}[/latex] = 106.071 మీ².
∴ కావలసిన కాన్వాసు గుడ్డ పరిమాణం = స్థూపపు వక్రతలవైశాల్యం + శంఖువు వక్రతలవైశాల్యం
= 135.771 + 106.071
= 241.842 మీ².

ప్రశ్న 9.
8 మీటర్ల ఎత్తు, 6 మీటర్ల భూవ్యాసార్థం కలిగిన శంఖువు ఆకృతి గుదారం తయారుచేయుటకు 3 మీ. వెడల్పు కలిగిన టార్పలిన్ గుడ్డ ఎంత పొడవును కలిగియుండాలి ? (మార్జినను, వృథా అయ్యే గుద్దను కూడా పరిగణనలోకి తీసుకొంటే సుమారుగా 20 సెం.మీ. పొడవు గల టార్పలిన్ అదనంగా వినియోగమవుతుంది). (π = 3.14)
సాధన.
శంఖువు వ్యాసార్ధము, r = 6 మీ.
శంఖువు ఎత్తు, h = 8మీ.
∴ ఏటవాలు ఎత్తు l = [latex]\sqrt{\mathrm{r}^{2}+\mathrm{h}^{2}}[/latex]
= [latex]\sqrt{\mathrm{6}^{2}+\mathrm{8}^{2}}[/latex]
= [latex]\sqrt{36+64}=\sqrt{100}[/latex]
=10 మీ.
∴ శంఖువు వక్రతల వైశాల్యం = πrl = 3.14 × 6 × 10
= 188.4 మీ².
టార్పలిన్ పొడవు = l అనుకొనుము.
∴ టార్పలిన్ వైశాల్యము, lb = 188.4 + 0.6
= 189 మీ².
⇒ 3l = 189
⇒ l = [latex]\frac {189}{3}[/latex] = 63 మీ.

ప్రశ్న 10.
ఒక జోకర్ యొక్క టోపి 7 సెం.మీ. వ్యాసార్ధము మరియు 27 సెం.మీ. ఎత్తు కలిగిన క్రమ వృత్త శంఖువు ఆకారంలో ఉంది. అటువంటి 10 టోపీలను తయారు చేయడానికి ఎంత వైశాల్యం గల బట్ట అవసరం?
సాధన.
శంఖువు వ్యాసార్ధము, r = 7 సెం.మీ.
శంఖువు ఎత్తు, h = 27 సెం.మీ.
∴ శంఖువు ఏటవాలు ఎత్తు (l)
= [latex]\sqrt{\mathrm{r}^{2}+\mathrm{h}^{2}}=\sqrt{7^{2}+27^{2}}[/latex]
= [latex]\sqrt{49+729}=\sqrt{778}[/latex]
∴ శంఖువు వక్రతల వైశాల్యం = πrl
= [latex]\frac {22}{7}[/latex] × 7 × [latex]\sqrt{778}[/latex] = 22 × [latex]\sqrt{778}[/latex]
∴ 10 టోపీలకు అవసరమైన బట్ట వైశాల్యం = 10 × 22 × [latex]\sqrt{778}[/latex]
= 6136,383 సెం.మీ².

ప్రశ్న 11.
పటములో చూపిన విధముగా ఒక శంఖువు ఆకృతిలో ఉన్న పాత్ర భూవ్యాసం 5.2 మీ. మరియు ఏటవాలు ఎత్తు 6.8 మీ. కలిగి ఉంది. దానిలో నీరు నిమిషానికి 1.8 ఘనపు మీటర్ల చొప్పున నింపబడుతుంది. అయితే పాత్రను నింపడానికి పట్టేకాలం ఎంత ?

సాధన.
పటం నుండి శంఖువు వ్యాసము = 5.2 మీ.
దాని వ్యాసార్ధము ‘r’ = [latex]\frac {5.2}{2}[/latex] = 26 మీ.
శంఖువు ఎత్తు = h = 6.8 మీ
∴ శంఖువు ఘనపరిమాణం = [latex]\frac {1}{3}[/latex] πr²h
= [latex]\frac {1}{3}[/latex] × [latex]\frac {1}{3}[/latex] × 2.6 × 2.6 × 6.8 = [latex]\frac {1011.296}{21}[/latex] = 48.156 మీ³.
ఒక సెకనులో పంపు ద్వారా ప్రవహించు నీటి పరిమాణం = 1.8మీ³.
∴ కావలసిన సమయం = మొత్తం ఘనపరిమాణం / 1.8
= [latex]\frac {48.156}{1.8}[/latex] = 26.753 = 27 ని॥లు.

ప్రశ్న 12.
రెండు సరూప శంఖువుల యొక్క ఘనపరిమాణములు 121 మరియు 96, ఘనపు యూనిట్లు శంఖువులలో ఒకదాని ప్రక్కతల వైశాల్యం 157 చదరపు యూనిట్లు. అయిన రెండవ దాని ప్రక్కతల వైశాల్యం ఎంత ?
సాధన.
రెండు సరూప శంఖువుల యొక్క ఘనపరిమాణాల నిష్పత్తి = 12π : 96π
= 1 : 8
= (1)³ : (2)³
= 1 : 2
∴ ఆ సరూప శంఖువుల ప్రక్కతల వైశాల్యాల నిష్పత్తి
= (1)² : (2)²
= 1 : 4
మొదటి శంఖువు ప్రక్కతల వైశాల్యము = 15π చ||యూ
∴ 1 భాగము = 15π అయిన
4 భాగాలు = 4 × 15π = 60π
∴ రెండవ శంఖువు ప్రక్కతల వైశాల్యము = 60π

AP SCERT 9th Class Maths Textbook Solutions Chapter 10 ఉపరితల వైశాల్యములు మరియు ఘనపరిమాణములు Ex 10.2 Textbook Exercise Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 10th Lesson ఉపరితల వైశాల్యములు మరియు ఘనపరిమాణములు Exercise 10.2

ప్రశ్న 1.
రెండు వైపులా మూయబడిన స్థూపాకారపు ట్యాంకు యొక్క ఎత్తు 1.4 మీటర్లు మరియు దాని భూవ్యాసార్ధము 56 సెం.మీ.గా యుండి లోహరేకుతో చేయబడియుంది. దీని సంపూర్ణతల వైశాల్యం ఎంత?
సాధన.
ట్యాంకు యొక్క భూ వ్యాసార్ధము ‘r’ = 56 సెం.మీ.
= [latex]\frac {56}{100}[/latex] మీ. = 0.56 మీ
ట్యాంకు యొక్క ఎత్తు h = 1.4 మీ.
ట్యాంకు యొక్క సంపూర్ణతల వైశాల్యం = 2πr (r + h)
లోహరేకు యొక వైశాల్యం = 2πr (r + h)
= 2 × [latex]\frac {22}{7}[/latex] × 0.56 × (0.56 + 1.4)
= 2 × 22 × 0.08 × 1.96
= 6.8992 మీ²
= 6.90 మీ²

ప్రశ్న 2.
స్థూపము యొక్క ఘనపరిమాణము 308 ఘనపు సెంటి మీటర్లు, ఎత్తు 8 సెం.మీ. అయిన దాని ప్రక్కతల వైశాల్యమును, సంపూర్ణతల వైశాల్యమును కనుగొనుము.
సాధన.
స్థూపము యొక్క ఘనపరిమాణం V = πr²h
= 308 సెం.మీ³
స్థూపము యొక్క ఎత్తు h = 8 సెం.మీ.
∴ 308 = [latex]\frac {22}{7}[/latex] . r² × 8
∴ r² = 308 × [latex]\frac {7}{22}[/latex] × [latex]\frac {1}{8}[/latex]
r² = 12.25
∴ r = [latex]\sqrt{12.25}[/latex] = 3.5 సెం.మీ.
ప్రక్కతల వైశాల్యం = 2πrh
= 2 × [latex]\frac {22}{7}[/latex] × 3.5 × 8 = 176 సెం.మీ.²
సంపూర్ణతల వైశాల్యం = 2πr (r + h)
= 2 × [latex]\frac {22}{7}[/latex] × 3.5 (3.5 + 8)
= 2 × 22 × 0.5 × 11.5 = 253 సెం.మీ.²

ప్రశ్న 3.
ఒక లోహపు దీర్ఘఘనము 22 సెం.మీ. × 15 సెం.మీ. × 7.5 సెం.మీ. కొలతలను కలిగియుంది. దానిని కరిగించి 14 సెం.మీ. ఎత్తుగల ఒక స్థూపముగా చేసిన దాని వ్యాసార్ధము ఎంత ?
సాధన.
లోహపు దీర్ఘఘనము యొక్క కొలతలు = 22 సెం.మీ. × 15 సెం.మీ. × 7.5 సెం.మీ.
స్థూపము యొక్క ఎత్తు, h = 14 సెం.మీ.
స్థూపముగా చేసిన దీర్ఘఘనము యొక్క ఘనపరిమాణం = స్థూపము యొక్క ఘనపరిమాణం
⇒ lbh = πr²h
⇒ 22 × 15 × 7.5 = [latex]\frac {22}{7}[/latex] × r² × 14
⇒ r² = [latex]\frac{22 \times 15 \times 7.5 \times 7}{14 \times 22}[/latex]
⇒ r² = 7.5 × 7.5 ⇒ r = 7.5 సెం.మీ.

ప్రశ్న 4.
ఒక నీటితొట్టి స్థూపాకారముగా ఉంటూ 616 లీటర్ల సామర్థ్యమును కలిగియుంది. ట్యాంకు వ్యాసం 5.6 మీటర్లు అయిన ట్యాంకు ఎత్తును కనుగొనుము.
సాధన.
స్థూపము యొక్క ఘనపరిమాణము, V = πr²h = 616 లీ.
ట్యాంకు యొక్క వ్యాసం = 5.6 మీ.
వ్యాసార్ధం, r = [latex]\frac{d}{2}=\frac{5.6}{2}[/latex] = 28 మీ.
ఎత్తు = h అనుకొనుము.
∴ πr²h = 616
[latex]\frac {22}{7}[/latex] × 2.8 × 28 × h = 616
h = [latex]\frac{616 \times 7}{22 \times 2.8 \times 2.8}[/latex] = 25
∴ ఎత్తు = 25 మీ.

ప్రశ్న 5.
ఒక లోహపు గొట్టం యొక్క పొడవు 77 సెం.మీ. దాని మధ్యచ్ఛేద అంతర వ్యాసం 4 సెం.మీ. మరియు బాహ్య వ్యాసం 4 సెం.మీ. (పటం చూడండి). అయిన ఈ క్రింది వానిని కనుగొనండి.

(i) లోపలి ప్రక్కతల వైశాల్యము
(ii) బాహ్య ప్రక్కతల వైశాల్యము
(iii) సంపూర్ణతల వైశాల్యమును కనుగొనండి.
సాధన.
(i) లోపలి ప్రక్కతల వైశాల్యము :
పైపు యొక్క ఎత్తు = 77 సెం.మీ.
లోపలి వ్యాసం = 4 సెం.మీ.
లోపలి వ్యాసార్ధం = [latex]\frac{d}{2}=\frac{4}{2}[/latex] = 2 సెం.మీ.
∴ లోపలి ప్రక్కతల వైశాల్యం = 2πrh
= 2 × [latex]\frac {22}{7}[/latex] × 2 × 77
= 88 × 11 = 968 సెం.మీ.²

(ii) బాహ్యప్రక్కతల వైశాల్యము :
బాహ్య వ్యాసం = 4.4 సెం.మీ.
∴ బాహ్య వ్యాసార్ధం r = [latex]\frac{d}{2}=\frac{4.4}{2}[/latex] = 22 సెం.మీ.
పైపు యొక్క ఎత్తు = h = 77 సెం.మీ.
∴ బాహ్య ప్రక్కతల వైశాల్యం = 2πrh
= 2 × [latex]\frac {22}{7}[/latex] × 2.2 × 77
= 96.8 × 11
= 1064.8 సెం.మీ.²

(iii) సంపూర్ణతల వైశాల్యము :
సంపూర్ణతల వైశాల్యము = లోపలి ప్రక్కతల వైశాల్యము + బాహ్య ప్రక్కతల వైశాల్యము
= 968 + 1064.8
= 2032.8 సెం.మీ².

ప్రశ్న 6.
ఒక భవనము చుట్టూ 16 స్థూపాకార స్తంభములున్నవి. ప్రతి స్థూపాకార స్తంభము 56 సెం.మీ. వ్యాసము మరియు 35 మీ. ఎత్తులను కలిగియుంది. స్తంభముల ప్రక్కతల వైశాల్యమునకు రంగు వేసేందుకు చ.మీ.కు ₹ 5.50 వంతున ఎంత ఖర్చు అవుతుంది ?
సాధన.
స్థూపాకార స్తంభము యొక్క వ్యాసము = 56 సెం.మీ.
వ్యా సార్థము , r = [latex]\frac{d}{2}=\frac{56}{2}[/latex] = 28 సెం.మీ.
= [latex]\frac {28}{100}[/latex] మీ. = 0.28 మీ.
స్తంభము యొక్క ఎత్తు, h = 35 మీ.
మొత్తం స్తంభముల సంఖ్య = 16
రంగు వేసేందుకు ఒక చ.మీ.కు
అగు ఖర్చు = ₹5.50
ఒక స్తంభము యొక్క ప్రక్కతల వైశాల్యము = 2πrh
= 2 × [latex]\frac {22}{7}[/latex] × 0.28 × 35
= 2 × 22 × 0.04 × 35
= 61.6 మీ².
∴ 16 స్థూపాకార ప్తంభముల ప్రక్కతల వైశాల్యం
= 16 × 61.6
= 985.6 మీ.²
16 స్తంభములకు రంగు వేసేందుకు ఒక చ.మీ.కు
₹ 5.5 చొప్పున అగు ఖర్చు = 985.6 × 5.5
= ₹5420.8

ప్రశ్న 7.
ఒక రోడ్డు రోలరు యొక్క వ్యాసము 84 సెం.మీ., పొడవు 120 సెం.మీ. ఒక ఆటస్థలమును చదును చేయుటకు 500 సంపూర్ణ భ్రమణములు చేయవలసి ఉంది. అయితే ఆటస్థల వైశాల్యమును చ.మీ.లలో కనుగొనండి.
సాధన.
రోడ్డు రోలరు యొక్క వ్యాసము = 84 సెం.మీ.
వ్యాసార్థం = [latex]\frac {84}{2}[/latex] = 42 సెం.మీ.
= [latex]\frac {42}{100}[/latex] మీ. = 0.42 మీ.
రోడ్డు రోలరు యొక్క పొడవు = 120 సెం.మీ.
= [latex]\frac {120}{100}[/latex] = 1.2 మీ.
ఆట స్థలమును చదునుచేయుటకు 500 సంపూర్ణ భ్రమణములు చేయవలసియుంది.
కాబట్టి 500 × రోలరు యొక్క ప్రక్కతల వైశాల్యము = ఆటస్థలం యొక్క వైశాల్యము
∴ ఆటస్థలం యొక్క వైశాల్యము = 500 × 2πrh
= 500 × 2 × [latex]\frac {22}{7}[/latex] × 0.42 × 1.2 = 1584 మీ²

ప్రశ్న 8.
వృత్తాకార బావి యొక్క లోపలి వ్యాసము 3.5 మీ., లోతు 10 మీ. అయిన (i) లోపలి ప్రక్కతల వైశాల్యము (ii) ప్రక్కతలాలను ప్లాస్టరింగ్ చేయుటకు చ.మీ.కు 40 రూపాయల వంతున ఎంత ఖర్చు అవుతుంది ?
సాధన.
వృత్తాకార బావి యొక్క లోపలి వ్యాసము d = 3.5మీ.
వ్యాసార్ధము, r = [latex]\frac{d}{2}=\frac{3.5}{2}[/latex] = 1.75 మీ.
బావి యొక్క లోతు (h) – 10 మీ.
(i) లోపలి ప్రక్కతల వైశాల్యము = 2πrh
= 2 × [latex]\frac {22}{7}[/latex] × 1.75 × 10
= 110 మీ²

(ii) ప్లాస్టరింగ్ చేయుటకు చ.మీ.కు ₹ 40 చొప్పున
అగు ఖర్చు = 110 × 40
= ₹4400

9.

ప్రశ్న (i)
ఒక స్థూపాకార పెట్రోలు ట్యాంకు భూవ్యాసం 4.2 మీ., ఎత్తు 4.5 మీ. అయిన ట్యాంకు యొక్క సంపూర్ణతల వైశాల్యమును కనుక్కోంది.
సాధన.
స్థూపాకార ట్యాంకు యొక్క వ్యాసము ‘d’ = 4.2 మీ.
వ్యాసార్ధము, r = [latex]\frac{d}{2}=\frac{4.2}{2}[/latex] = 21 మీ.
ట్యాంకు యొక్క ఎత్తు 5 = 4.5 మీ.
ట్యాంకు యొక్క సంపూర్ణతల వైశాల్యము
= 2πr (r + h)
= 2 × [latex]\frac {22}{7}[/latex] × 21 (2.1 + 4.5)
= 2 × 22 × 0.3 × 6.6 = 87.12 మీ.²

ప్రశ్న (ii)
ట్యాంకును తయారుచేసేందుకు వాడిన స్టీలులో [latex]\frac {1}{12}[/latex] వ వంతు వృథా అయిన ఎంత పరిమాణపు స్టీలును ఉపయోగించారో లెక్కించుము.
సాధన.
వృథా అయిన స్టీలు పరిమాణం = [latex]\frac {1}{12}[/latex]
ట్యాంకును తయారుచేసేందుకు వాడిన స్టీలు
= 1 – [latex]\frac {1}{12}[/latex] = [latex]\frac {11}{12}[/latex]
మొత్తం స్టీలు పరిమాణం = x మీ² అనుకొనుము.
[latex]\frac {11}{12}[/latex]x = 87.12 మీ.²
∴ x = 87.12 × [latex]\frac {12}{11}[/latex] = 95.04 మీ.²

ప్రశ్న 10.
ఒక వైపు మూయబడి స్థూపాకార ద్రమ్ యొక్క లోపలి వ్యాసార్ధము 28 సెం.మీ., ఎత్తు 21 మీ. అయిన ఆ ద్రమ్ లో నిల్వ చేయగల నీటి సామర్థ్యమును లీటర్లలో తెల్పుము. (1 లీటరు = 1000 ఘనపు సెంటీమీటర్లు)
సాధన.
స్థూపాకార డ్రమ్ యొక్క లోపలి వ్యాసార్ధము ‘r’ = 28 సెం.మీ.
ఎత్తు, h = 2.1 మీ. = 2.1 × 100 = 210 సెం.మీ.
డ్రమ్ యొక్క ఘనపరిమాణము = πr²h
= [latex]\frac {22}{7}[/latex] × 28 × 28 × 210
= 22 × 4 × 28 × 210 = 517440 ఘ. సెం.మీ.
= [latex]\frac {517440}{1000}[/latex] లీ. = 517.44 లీ.

ప్రశ్న 11.
ఒక స్థూపాకార వస్తువు యొక్క ప్రక్కతల వైశాల్యము 1760 చ.సెం.మీ. మరియు దాని ఘనపరిమాణము 12320 ఘనపు సెంటీమీటర్లు అయిన దాని ఎత్తును కనుగొనుము.
సాధన.
స్థూపాకార వస్తువు యొక్క ప్రక్కతల వైశాల్యము = 2πrh
= 1760 సెం.మీ.²
స్థూపాకార వస్తువు యొక్క ఘనపరిమాణం = πr²h
= 12320 సెం.మీ.³
ఎత్తు = h అనుకొనుము.
ఘనపరిమాణం / ప్రక్కతల వైశాల్యం = [latex]\frac{\pi r^{2} h}{2 \pi r h}=\frac{12320}{1760}[/latex]
⇒ [latex]\frac {r}{2}[/latex] = 7
∴ r = 7 × 2 = 14 సెం.మీ.
2πrh = 1760 సెం.మీ.²
2 × [latex]\frac {22}{7}[/latex] × 14h = 1760 సెం.మీ.
h = [latex]\frac{1760 \times 7}{2 \times 22 \times 14}[/latex] = 20 సెం.మీ.
∴ స్థూపాకార వస్తువు యొక్క ఎత్తు = 20 సెం.మీ.

AP SCERT 9th Class Maths Textbook Solutions Chapter 10 ఉపరితల వైశాల్యములు మరియు ఘనపరిమాణములు Ex 10.1 Textbook Exercise Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 10th Lesson ఉపరితల వైశాల్యములు మరియు ఘనపరిమాణములు Exercise 10.1

1. ఈ కింది క్రమ పట్టకము యొక్క ప్రక్కతల వైశాల్యము మరియు సంపూర్ణతల వైశాల్యములను కనుగొనండి.

ప్రశ్న (i)

సాధన.
ప్రక్కతల వైశాల్యము = 4l²
= 4 × 4² = 64 సెం.మీ².
సంపూర్ణతల వైశాల్యము = 6l²
= 6 × 4² = 96 సెం.మీ².

ప్రశ్న (ii)

సాధన.
ప్రక్కతల వైశాల్యము = 2h (l + b)
= 2 × 5 (8 + 6)
= 10 × 14 = 140 సెం.మీ².
పంపూర్ణతల వైశాల్యము = 2 (lb+ bh + lh)
= 2(8 × 6 + 6 × 5 + 8 × 5)
= 2 (48 + 30 + 40)
= 236 సెం.మీ².

ప్రశ్న 2.
ఒక సమఘనము యొక్క సంపూర్ణతల వైశాల్యం 1350 చదరపు మీటర్లు. అయిన దాని ఘనపరిమాణమును కనుగొనుము.
సాధన.
ఘనము యొక్క సంపూర్ణతల వైశాల్యము 6l² = 1350
l² = [latex]\frac {1350}{6}[/latex]
l² = 225
l = [latex]\sqrt{225}[/latex] = 15 మీ.
ఘనము యొక్క ఘనపరిమాణము = l³
= 15 × 15 × 15 = 3375 మీ³.

ప్రశ్న 3.
పొదవు 12మీ., వెడల్పు 10 మీ. మరియు 7.5 మీ. ఎత్తు కలిగిన గది యొక్క నాలుగు గోడల వైశాల్యమును కనుగొనండి. (ద్వారములు లేదా కిటికీలు లేని గదిగా ఊహించండి).
సాధన.
గది యొక్క పొడవు = 12 మీ.
గది యొక్క వెడల్పు = 10 మీ.
గది యొక్క ఎత్తు = 7.5 మీ.
నాలుగు గోడల వైశాల్యం A = 2h (l + b)
= 2 × 7.5 (12 + 10)
= 15 × 22 = 330 మీ²

ప్రశ్న 4.
ఒక దీర్ఘఘనము యొక్క ఘనపరిమాణం 1200 ఘనపు సెంటీమీటర్లు, దాని యొక్క పొడవు 15 సెం.మీ., వెడల్పు 10 సెం.మీ. అయిన ఎత్తును కనుగొనుము.
సాధన.
దీర్ఘఘనం యొక్క పొడవు, l = 15 సెం.మీ.
దీర్ఘఘనం యొక్క వెడల్పు, b = 10 సెం.మీ.
దీర్ఘఘనం యొక్క ఘనపరిమాణం, V = lbh
= 1200 సెం.మీ³.
ఎత్తు = h ఆనుకొనుము.
∴ 15 × 10 × h = 1200
∴ h = [latex]\frac{1200}{15 \times 10}[/latex] = 8 సెం.మీ.

5. ఒక పెట్టి యొక్క సంపూర్ణతల వైశాల్యము కింది సందర్భాలలో ఏ విధముగా మారుతుంది ? మాటలలో వ్యక్తపరచండి. ప్రతీ కొలత 3 సార్లు పెరిగినప్పుడు . పెట్టె సంపూర్ణతల వైశాల్యం ఏ విధంగా ఉంటుందో కనుగొనండి.

ప్రశ్న (i)
ప్రతీ కొలత రెట్టింపు చేసినప్పుడు
సాధన.
అసలు కొలతలు వరుసగా
పొడవు = l యూనిట్లు
వెడల్పు = b యూనిట్లు
ఎత్తు = 7 యూనిట్లు
సంపూర్ణతల వైశాల్యం = 2 (lb+ bh + lh)
ప్రతీ కొలతను రెట్టింపు చేసినపుడు
పొడవు = 2l, వెడల్పు = 2b, ఎత్తు = 2h
సంపూర్ణతల వైశాల్యము
= 2(2l . 2b + 2b . 2h + 2l . 2h)
= 2 (4lb + 4bh + 4lh)
= 4 × [2 (lb+ bh + lh)]
= 4 × అసలు సంపూర్ణతల వైశాల్యం
∴ సంపూర్ణతల వైశాల్యం 4 రెట్లు పెరుగును.

ప్రశ్న (ii)
ప్రతీ కొలతను మూడు రెట్లు చేసినప్పుడు
సాధన.
పెట్టి యొక్క అసలు మరియు మారిన కొలతలు వరుసగా l, b, h మరియు 3l, 3b, 3h అనుకొనుము.
అసలు సంపూర్ణతల వైశాల్యం = 2 (lb + bh + lh)
మారిన సంపూర్ణతల వైశాల్యం
= 2 (3l . 3b + 3b . 3h + 3l . 3h)
= 2 (9lb + 9bh + 9lh)
= 9 × [2(lb + bh + lh)]
= 9 × (అసలు సం.త.వై.)
సంపూర్ణతల వైశాల్యం 9 రెట్లుగా పెరిగినది.

పెట్టె యొక్క ప్రతీ కొలత n సార్లు పెరిగినపుడు :
పొడవు = nl, వెడల్పు = nb, ఎత్తు = nh
సంపూర్ణతల వైశాల్యం = 2 (nl . nb + nb . nh + nh . nl)
= 2 (n²lb + n²bh + n²lh)
= n² [2 (lb + bh + lh)]
∴ సంపూర్ణతల వైశాల్యం n² రెట్లు పెరుగును.

ప్రశ్న 6.
ఒక పట్టకపు భూమి త్రిభుజాకారములో ఉండి భుజం కొలతలు వరుసగా 8 సెం.మీ., 4 సెం.మీ., 5 సెం.మీ. కలిగియుండి దాని యొక్క ఎత్తు 10 సెం.మీ. అయిన పట్టకము యొక్క ఘనపరిమాణము ఎంత?
సాధన.
పట్టకము యొక్క ఘనపరిమాణం = భూ వైశాల్యం × ఎత్తు
త్రిభుజాకారంలో ఉన్న భూమి యొక్క కొలతలు వరుసగా 3 సెం.మీ., 4 సెం.మీ., 5 సెం.మీ.
∴ వైశాల్యం = s (s – a) (s – b) (s – c)
s = [latex]\frac{a+b+c}{2}=\frac{3+4+5}{2}[/latex] = 6
వైశాల్యం = [latex]\sqrt{6(6-3)(6-4)(6-5)}[/latex]
= [latex]\sqrt{6 \times 3 \times 2 \times 1}[/latex]
= 6 సెం.మీ.²
∴ పట్టకం యొక్క ఘనపరిమాణం
= భూ వైశాల్యం × ఎత్తు = 6 × 10 = 60 సెం.మీ.³
(లేదా)
త్రిభుజము యొక్క కొలతలు 3 సెం.మీ., 4 సెం.మీ., మరియు 5 సెం.మీ. అయిన లంబకోణ త్రిభుజం.
∴ త్రిభుజం యొక్క వైశాల్యం
= [latex]\frac {1}{2}[/latex]bh = [latex]\frac {1}{2}[/latex] × 3 × 4 = 6 సెం.మీ.²
పట్టకం యొక్క ఘనపరిమాణం
= భూ వైశాల్యం × ఎత్తు
= 6 × 10 = 60 సెం.మీ.³

ప్రశ్న 7.
ఒక క్రమ చతురస్రాకార పిరమిడ్ యొక్క భూ చుట్టుకొలత 16 మీటర్లు, ఎత్తు 3 మీటర్లు అయిన దాని ఘనపరిమాణమును కనుగొనుము.
సాధన.
పిరమిడ్ భూ చుట్టుకొలత = 16మీ.
పిరమిడ్ యొక్క ఎత్తు.= 3 మీ.
పిరమిడ్ యొక్క ఘనపరిమాణం = [latex]\frac {1}{3}[/latex] × (భూ వైశాల్యం × ఎత్తు)
= [latex]\frac {1}{3}[/latex] × 4 × 4 × 3 = 16 మీ.³
[4 × భుజం = 16 ∴ భుజము = 4 మీ. వైశాల్యం = s² = 4 × 4]

ప్రశ్న 8.
ఒలింపిక్స్ లోని ఈతకొలను 50 మీటర్ల పొడవు, 25 మీటర్ల వెడల్పు మరియు 3 మీటర్ల లోతుగల దీర్ఘఘనాకృతిలోయుంది. అది ఎన్ని లీటర్ల నీటిని నింపే సామర్థ్యము కలిగి ఉంది ?
సాధన.
దీర్ఘఘనాకృతిలో ఉన్న ఈతకొలను యొక్క
పొడవు = 50 మీ. , వెడల్పు = 25 మీ. , లోతు = 3 మీ.
∴ ఈతకొలను యొక్క ఘనపరిమాణము
V = lbh
V = 50 × 25 × 3 = 3750 మీ.³
∴ ఈత కొలను 37,50 లీటర్ల నీటిని నింపే సామర్థ్యము కలిగి ఉంది. [∵ 1 మీ³. = 1లీ.]

AP SCERT 9th Class Maths Textbook Solutions Chapter 11 వైశాల్యాలు InText Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 11th Lesson వైశాల్యాలు InText Questions

ఆలోచించి, చర్చించి రాయండి

1. 1 సెం.మీ. ప్రమాణము 5 మీ. లను సూచిస్తే, 6 చదరపు సెం.మీ. వైశాల్యము దేనిని సూచిస్తుంది ? (పేజీ నెం. 247)
సాధన.
1 సెం.మీ. = 5 మీ.
1 సెం.మీ.² = 1 సెం.మీ. × 1 సెం.మీ. = 5 మీ. × 5 మీ. = 25 చ.మీ.
∴ 6 చ.సెం.మీ. = 6 × 25 చ.మీ. = 150 చ.మీ.

2. 1 చ.మీ. = 100² చ.సెం.మీ. అని రజని అన్నది. నీవు ఏకీభవిస్తావా ? వివరించుము. (పేజీ నెం. 247)
సాధన.
1 చ.మీ. = 100 చ.సెం.మీ. కావున రజనీతో నేను ఏకీభవిస్తాను.

2. కింది పటాలలో ఏవి ఒకే భూమి, ఒకే సమాంతర రేఖల మధ్య ఉన్నాయి ? ఇటువంటి సందర్భములో భూమి (ఉమ్మడి భుజం) ని, రెండు సమాంతర రేఖలను తెలపండి. (పేజీ నెం. 249)

సాధన.
(a) పటం (a) లో ∆PCD మరియు ☐ABCD లు ఒకే భూమి CD మరియు ఒకే సమాంతర రేఖలు AB మరియు , CD ల మధ్యన కలవు.
(b) పటం (b) లో ☐PQRS మరియు ☐MNSRలు ఒకే భూమి SR పై గలవు. కాని ఒకే సమాంతర రేఖల మధ్యన లేవు.
(c) పటం (c) లో ∆TRQ మరియు ☐PQRS లు ఒకే భూమి QR పై మరియు ఒకే జత సమాంతర రేఖలు PS మరియు QRల మధ్యన గలవు.
(d) పటం (d) లో ∆APD మరియు ☐ABCD లు ఒకే భూమి AD మరియు ఒకే జత సమాంతర రేఖలు AD మరియు BC ల మధ్యన గలవు.
(e) పటం (e) లో ఇచ్చిన నియమము పాటించబడ లేదు.

3. రెందు త్రిభుజాలు ABC మరియు DBCలను ఒకే భూమి మరియు ఒకే సమాంతర రేఖల మధ్య ఉండునట్లు (పటంలో చూపిన విధంగా) గీయండి. AC మరియు BDU ఖండన బిందువుకు P లని పేరు పెట్టండి. CE || BA మరియు BF || CD లను AD రేఖపై E మరియు F లు ఉన్నట్లు గీయండి. (∆PAB) వైశాల్యము = (∆PDC) వైశాల్యములని మీరు చూపగలరా ?

సూచన: (ఈ రెండు త్రిభుజాలు సర్వసమానాలు కానప్పటికీ సమాన వైశాల్యములు కలిగి ఉన్నాయి.) (పేజీ నెం. 254)
సాధన.
☐ABCE వైశాల్యము = 2 × ∆ABC [∵ ∆ABC మరియు ☐ABCE లు ఒకే భూమి BC పై మరియు ఒకే జత సమాంతర రేఖలు BC మరియు AE ల మధ్యన గలవు]
⇒ ∆ABC = [latex]\frac {1}{2}[/latex]☐ABCE ……. (1)
అదే విధముగా ☐BCDF = 2 × ∆BCD (∵ ∆BCD మరియు ☐BCDE లు ఒకే భూమి BC మరియు ఒకే జత సమాంతర రేఖలు BC మరియు DEల మధ్యన గలవు.)
∴ ∆BCD = [latex]\frac {1}{2}[/latex]☐BCDF ……….. (2)
కాని ☐ABCE = ☐BCDF [∵ ☐ABCE మరియు ☐BCDF లు ఒకే భూమి BC మరియు ఒకే జత సమాంతర రేఖలు BC మరియు FE లపై కలవు]
(1) మరియు (2) ల నుండి , ∆ABC = ∆BCD
∆PAB + ∆PBC = ∆PBC + ∆PDC
⇒ ∆PAB = ∆PDC నిరూపించబడినది.

4. లంబకోణ త్రిభుజము ABCE A లంబకోణం. BC, CA మరియు AB లపై వరుసగా BCED, ACFG మరియు ABMN అనే చతురస్రాలు గీయబడ్డాయి. రేఖాఖందం AX ⊥ DE, BCని Y వద్ద, DE ని X వద్ద ఖండించింది. AD, AE లు కలుపబడ్డాయి. అదే విధంగా BF, CM లు కలుపబడ్డాయి. (పటంలో చూడండి). అయితే కింద వానిని నిరూపించండి. (పేజీ నెం. 258)

ప్రశ్న (i)
∆MBC ≅ ∆ABD
సాధన.
∆MBC మరియు ∆ABD లలో
MB = AB [∵ చతురస్ర భుజములు)
BC = BC [∵ ఉమ్మడి భుజము]
[latex]\angle \mathrm{MBC}=\angle \mathrm{ABD}[/latex] [∵ [latex]\angle \mathrm{MBC}=\angle \mathrm{ABD}[/latex] = 90° + [latex]\angle \mathrm{ABC}[/latex]]
∴ ∆MBC ≅ ∆ABD (భు.కో.భు. నియమం ప్రకారం)

ప్రశ్న (ii)
(BYXD) వై॥ = 2 (∆MBC) వై॥
సాధన.
☐BYXD మరియు ∆ABD లు ఒకే భూమి BD మరియు రెండు సమాంతర రేఖలు BD, AX ల మధ్య కలవు కావున.
∴ ☐BYXD = 2 ∆ABD = 2 ∆MBC [∵ (i) నుండి]
∴ (BYXD)వై॥ = 2 (∆MBC)వై॥

ప్రశ్న (iii)
(BYXD) వై॥ = (ABMN) వై॥
సాధన.
(ABMN) వై॥ = 2 × (∆MBC) వై॥ [∵ ☐ABMN, ∆MBC లు ఒకే భూమి MB మరియు సమాంతర రేఖలు MB, NC ల మధ్య కలవు]
∴ ☐ABMN = ☐BYXD [(ii) నుండి]

ప్రశ్న (iv)
∆FCB = ∆ACE
సాధన.
∆FCB మరియు ∆ACE లలో
CB = CE (∵ ఒకే చతురస్రపు భుజాలు)
FC = AC (∵ ఒకే చతురస్రపు భుజాలు)
[latex]\angle \mathrm{FCE}=\angle \mathrm{ACE}[/latex] (∵ [latex]\angle \mathrm{FCE}=\angle \mathrm{ACE}[/latex] = 90° + [latex]\angle \mathrm{ACB}[/latex])
∴ ∆FCB ≅ ∆ACE (భు. కో.భు. నియమం)

ప్రశ్న (v)
(CYXE) వై॥ = 2 (FCB) వై॥
సాధన.
☐CYXE మరియు ∆ACE లు ఒకే భూమి CE మరియు రెండు సమాంతర రేఖలు CE మరియు XYల మధ్యన గలవు.
∴ ☐CYXE = 2 × ∆ACE = 2 × ∆FCB [(iv) నుండి]

ప్రశ్న (vi)
(CYXE) వై॥ = (ACFG) వై॥
సాధన.
☐CYXE = 2 × ∆FCB [(v) నుండి]
= ☐ACFG [∵ ☐ACFG మరియు ∆FCB లు ఒకే భూమి CF మరియు ఒకే జత సమాంతర రేఖలు CF మరియు AGల మధ్యన కలవు.]

ప్రశ్న (vii)
(BCED) వై॥ = (ABMN) వై|| + (ACFG) వై॥
సాధన.
☐BCED = ☐BYXD + ☐CYXE (పటం నుండి)
= ☐ABMN + ☐ACFG [∵ ☐BYXD = ☐ABMN (iii) నుండి ☐CYXE = ☐ACFG (vi) నుండి] నిరూపించబడినది. ఫలితం (vii) ను మాటలలో రాయండి.
సాధన.
“ఒక లంబకోణ త్రిభుజంలో కర్ణము మీది వర్గము, మిగిలిన రెండు భుజాల మీది వర్గాల మొత్తమునకు సమానము” దీనినే పైథాగరస్ సిద్ధాంతము అంటారు.

కృత్యం

1.


ఒక ఉల్లిపొర కాగితం (ట్రేసింగ్ పేపర్) పై రెండు జతల త్రిభుజాలను పటంలో చూపినట్లు గీయండి. త్రిభుజాలు I, II లను ఒకదానిపై ఒకటి పూర్తిగా ఏకీభవించునట్లు ఉంచండి. త్రిభుజాలు III మరియు IV లు ఒకే భూమి, ఒకే ఎత్తును కలిగిన ఒక సమద్విబాహు త్రిభుజము మరియు ఒక లంబకోణ త్రిభుజము. III మరియు IV పటాలు ఒకదానితో మరొకటి పూర్తిగా ఏకీభవించలేదు. I, II పటాలు ఒకదానితో మరొకటి పూర్తిగా ఏకీభవించినారు. కావున ఇవి సర్వసమాన పటాలు మరియు వీటి వైశాల్యాలు సమానము. ఎందుకనగా అవి ఆక్రమించిన ప్రదేశం సమానము. III, IV పటాలు ఒకదానితో మరొకటి ఏకీభవించలేదు. కనుక అవి సర్వసమాన పటాలుకావు.

వీటి వైశాల్యాలు సమానమేనా ?
పటం (V) ను పరిశీలిస్తే ఈ పటాలు సర్వసమానం కానప్పటికీ, ఇవి సమాన వైశాల్యం కలిగి ఉన్నాయి. (ఈ పటాలను కాగితాలతో కత్తిరించి మరియు త్రిభుజ వైశాల్య సూత్రం ద్వారా కనుగొని చూడండి) అందుచే III మరియు IV పటాలు సర్వసమాన పటాలుకానప్పటికీ, సమాన వైశాల్యాలు గల పటాలు అయినవి. (పేజీ నెం. 245)

2. ఒక గ్రాఫ్ కాగితముపై రెండు సమాంతర చతుర్భుజాలు ABCD మరియు PQCD లను పటంలో చూపిన విధంగా గీయాలి.

ఈ రెండు సమాంతర చతుర్భుజాలు ఒకే భూమి DC పైన మరియు ఒకే సమాంతర రేఖలు PB మరియు DCల మధ్య ఉన్నాయి. దీనిలో DCQA పట భాగము రెండు సమాంతర చతుర్భుజాలలో ఉమ్మడి భాగమని స్పష్టమౌతున్నది. కావున మనము ∆DAP మరియు ∆CBQలు ఒకే వైశాల్యం కలిగి ఉంటాయని చెప్పగలిగితే అప్పుడు (PQCD) వైశాల్యము = (ABCD) వైశాల్యము అవుతుంది. (పేజీ నెం. 250)

3. పటంలో చూపిన విధంగా ఒక జత త్రిభుజాలను ఒకే భూమి లేదా సమాన భూములు, ఒకే సమాంతర రేఖల మధ్య గ్రాఫ్ కాగితంపై గీయండి.
∆ABC మరియు ∆DBC లు అనేవి రెండు త్రిభుజాలు ఒకే భూమి BC పైన, ఒకే సమాంతర రేఖలు BC, AD ల మధ్య ఉన్నాయి.
ADని ఇరువైపులా పొడిగించుము మరియు CE || AB, BF || CDలను గీయండి. ఇప్పుడు సమాంతర చతుర్భుజాలు AECB మరియు FDCB లు ఒకే భూమి BC మరియు ఒకే సమాంతర రేఖలు BC మరియు EF ల మధ్య ఉన్నాయి. కావున (AECB) వై॥ = (FDCB) వై॥ (ఎలా ?)

దీని నుండి మనకు (∆ABC) వై॥ = [latex]\frac {1}{2}[/latex] (సమాంతర చతుర్భుజం AFCB) వై॥ …………… (i)
మరియు (∆DBC) వై॥ = [latex]\frac {1}{2}[/latex] (సమాంతర చతుర్భుజం FDCB) వై॥ అగును …….. (ii)
(i), (ii) నుండి, దీని నుండి (∆ABC) వై॥ = (∆DBC) వై॥ అని చెప్పవచ్చు.
మనం ∆ABC మరియు ∆DBCల వైశాల్యాలను ముందు కృత్యములో చెప్పినట్లుగా చదరాలను లెక్కించు పద్ధతి ద్వారా గణించి వైశాల్యములు ఎలా సమానం అవుతాయో సరిచూడవచ్చు. (పేజీ నెం. 254)

సిద్ధాంతాలు

1. ఒకే భూమి మరియు ఒకే సమాంతర రేఖల మధ్యగల సమాంతర చతుర్భుణాల వైశాల్యాలు సమానము. (పేజీ నెం. 250)
సాధన.
ఉపపత్తి : ABCD మరియు PQCD అనే రెండు సమాంతర చతుర్భుజాలు ఒకే భూమి DC మరియు రెండు సమాంతర రేఖలు DC మరియు PB ల మధ్య ఉన్నాయనుకుందాం. ∆DAP మరియు ∆CBQలలో

PD || CQ మరియు PB తిర్యగ్రేఖ వలన [latex]\angle \mathrm{DPA}=\angle \mathrm{CQB}[/latex] మరియు AD || CB మరియు PB తిర్యగ్రేఖవలన [latex]\angle \mathrm{DAP}=\angle \mathrm{CBQ}[/latex] ఇలాగే PQCD సమాంతర చతుర్భుజమైనందున PD = QC అగును. ఇందుచే ∆DAP, ∆CBQ లు రెండు సర్వసమాన త్రిభుజాలు మరియు వాటి వైశాల్యాలు సమానము.
కావున (PQCD) వై॥ = (AQCD) వై॥ + (DAP)వై॥ = (AQCD)వై॥ + (CBQ)వై॥ = (ABCD)వై॥ అగును.
గ్రాఫ్ కాగితములపై గీచిన సమాంతర చతుర్భుజాలలో చదరాల సంఖ్యను లెక్కించి ఫలితాన్ని సరిచూడవచ్చును.

రెండు సమాంతర చతుర్భుజాల వైశాల్యాలు సమానంగా ఉండడానికి అవి ఒకే సమాంతర రేఖల మధ్య ఉన్ననూ, ఒకే భూమిపై ఉండనవసరం లేదని రేష్మా వాదించింది. దానికి సమాన భూమి ఉంటే సరిపోతుందని అన్నది. ఆమె వాదన అవగాహన కొరకు పైపటము పరిశీలిద్దాము.
AB = A₁B₁ అయిన A₁B₁C₁D₁ సమాంతర చతుర్భుజాన్ని ABCD సమాంతర చతుర్భుజముపై ఏకీభవించునట్లు ఉంచితే A శీర్షం A₁ పైన B శీర్షం B₁ పైన వచ్చాయి. అదే విధంగా [latex]\overline{\mathrm{C}_{1} \mathrm{D}_{1}}[/latex],CD పై ఏకీభవించింది. కావున వీటి వైశాల్యాలు సమానమైనాయి.

2. రెండు త్రిభుజాలు ఒకే భూమి (లేదా సమాన భూములు) మరియు ఒకే వైశాల్యాలు కలిగి ఉంటే అవి ఒకే సమాంతర రేఖల మధ్య ఉంటాయి. (పేజీ నెం. 255)

పటం పరిశీలించండి. BC భుజం పైన గల త్రిభుజాలు ఏవి ? ∆ABC, ∆DBC త్రిభుజాల ఎత్తులు ఏవి ?
ఒకే భూమిని కలిగి, వైశాల్యాలు సమానం అయితే, వాటి ఎత్తులు ఎలా ఉంటాయి ? A, Dలు సరేఖీయాలేనా ?

ఉదాహరణలు

1. ABCD ఒక సమాంతర చతుర్భుజము ABEF ఒక దీర్ఘచతురస్రము DG, AB పైకి గీచిన లంబము అయిన
(i) (ABCD) వై॥ = (ABEF) వై॥
(ii) (ABCD) వై॥ = AB × DG అని చూపండి. (పేజీ నెం. 251)
సాధన.

(i) దీర్ఘచతురస్రము కూడా ఒక సమాంతర చతుర్భుజమే.
∴ (ABCD) వై॥ = (ABEF) వై॥ ………. (1) (ఒకే భూమి, ఒకే సమాంతర రేఖల మధ్య ఉండే రెండు సమాంతర చతుర్భుజాలు)

(ii) (ABCD) వై॥ = (ABEF) వై॥ (∴ (1) నుండి)
= AB × BE (∵ ABEF దీర్ఘచతురస్రం కావున)
= AB × DG
(∵ DG ⊥ AB మరియు DG = BE)
అందుచే (ABCD) వై॥ = AB × DG అయినది.
పై ఫలితము బట్టి మనము “సమాంతర చతుర్భుజ వైశాల్యము. దాని భూమి (ఏదైనా ఒక భుజము) మరియు దానిపైకి గీయబడిన లంబాల పొడవుల లబ్దానికి సమానము” అని చెప్పవచ్చు.

2. త్రిభుజము ABC మరియు సమాంతర చతుర్భుజము ABEF లు ఒకే భూమి AB మరియు ఒకే సమాంతర రేఖలు AB మరియు EF ల మధ్య ఉంటే (∆ABC) వై॥ = [latex]\frac {1}{2}[/latex](ABEF) వై॥ అని చూపండి. (పేజీ నెం. 251)
సాధన.
BH || AC అగునట్లు B గుండా ఒక రేఖను గీస్తే అది పొడిగించిన FE ని H వద్ద ఖండించింది.
∴ ABHC ఒక సమాంతర చతుర్భుజము.

BC కర్ణము దీనిని రెండు సర్వసమాన త్రిభుజాలుగా విభజించింది. కావున
(∆ABC) వై॥ = (∆BCH) వై॥
= [latex]\frac {1}{2}[/latex](ABHC) వై॥
కాని సమాంతర చతుర్భుజాలు ABHC మరియు ABEF లు ఒకే భూమి AB పైన AB || EF సమాంతరరేఖల మధ్య ఉన్నాయి. కావున (∆BHC) వై॥ = (ABEF) వై॥ అందువలన
(∆ABC) వై॥ = [latex]\frac {1}{2}[/latex](ABEF) వైశాల్యం అయినది.
దీని నుండి మనం “ఒకే భూమి, ఒకే సమాంతర రేఖల మధ్యన ఒక త్రిభుజము, సమాంతర చతుర్భుజము ఉంటే, త్రిభుజ వైశాల్యము, సమాంతర చతుర్భుజం వైశాల్యములో సగము ఉంటుంది” అని చెప్పవచ్చును.

3. ఒక రాంబిలో కర్ణాలు 12 సెం.మీ. మరియు 16 సెం.మీ. దాని ఆసన్న భుజాల మధ్య బిందువులను వరుస క్రమములో కలుపగా ఏర్పడే పటము యొక్క వైశాల్యము ఎంత ? (పేజీ నెం. 251)
సాధన.
ABCD రాంబస్ యొక్క భుజాలు AB, BC, CD మరియు DA ల మధ్య బిందువులు M, N, O మరియు Pలను వరుసలో కలుపగా ఏర్పడిన పటము MNOP.

ఏర్పడిన MNOPఏ ఆకారంలో ఉంది ? ఎందుకు ? PN కలిపితే PN || AB మరియు PN || DC అవుతాయి (ఎలా ?) ఒకే భూమి, ఒకే సమాంతర రేఖల మధ్య ఒక త్రిభుజము, సమాంతర చతుర్భుజము ఉంటే త్రిభుజ వైశాల్యం, సమాంతర చతుర్భుజ వైశాల్యంలో సగం ఉంటుందని మీకు తెలుసు.

పై ఫలితాన్ని బట్టి సమాంతరచతుర్భుజము ABNP మరియు త్రిభుజము MNP లు ఒకే భూమి PN పైన, ఒకే సమాంతరాలు PN మరియు AB ల మధ్య ఉన్నాయి.

∆MNP వై॥ = [latex]\frac {1}{2}[/latex]ABPNవై॥ ……………… (i)
ఇదే విధముగా ∆PONవై॥ = [latex]\frac {1}{2}[/latex]PNCDవై॥ ……………..(ii)
మరియు రాంబస్ వైశాల్యము = [latex]\frac {1}{2}[/latex] × d₁d₂ కావున (i), (ii), (iii) లను బట్టి
(MNOP) వై॥ = (∆MNP) వై॥ + (∆PON) వై॥
= [latex]\frac {1}{2}[/latex](ABNP) వై॥ + [latex]\frac {1}{2}[/latex](ABCD) వై॥
= [latex]\frac {1}{2}[/latex](రాంబస్ ABCD) వై॥
= [latex]\frac {1}{2}[/latex]([latex]\frac {1}{2}[/latex] × 12 × 16) = 48 చ. సెం.మీ.

4. ఒక త్రిభుజాన్ని దాని మధ్యగతము సమాన వైశాల్యాలు గల రెండు త్రిభుజాలుగా విభజిస్తుందని చూపండి. (పేజీ నెం. 255)
సాధన.

త్రిభుజము ABC లో AD మధ్యగతం అనుకోండి. ∆ABD మరియు ∆ADC లకు ఒకే ఉమ్మడి శీర్షం. దీని భూములు BD మరియు DCలు సమానము. AE ⊥ BC గీయండి.
ఇప్పుడు, (∆ABD) = [latex]\frac {1}{2}[/latex] × భూమి BD × ∆ADB యొక్క ఎత్తు
= [latex]\frac {1}{2}[/latex] × BD × AE
= [latex]\frac {1}{2}[/latex] × DC × AE (∵ BD = DC)
= [latex]\frac {1}{2}[/latex] × భూమి DC × ∆ACD యొక్క ఎత్తు
= ∆ACD వై॥
కావున (∆ABD) వై॥ = (∆ACD) వై అయినది.

5. కింది పటంలో ABCD ఒక చతుర్భుజం. AC ఒక కర్ణము, DE || AC మరియు BC ని పొడిగించగా అది E వద్ద ఖండించింది. అయిన (ABCD) వై॥ = (∆ABE) వై॥ అని చూపండి. (పేజీ నెం. 256)
సాధన.

(ABCD) వై॥ = (∆ABC) వై॥ + (∆DAC) వై॥
∆DAC మరియు ∆EAC లు ఒకే భూమి [latex]\overline{\mathrm{AC}}[/latex]
మరియు ఒకే సమాంతరాలు DE || AC మధ్యగలవు.
(∆DAC) వై॥ = (∆EAC) వై॥ (ఎందుకు ?)
సమాన వైశాల్యాల పటాలను ఇరువైపులా కలుపగా
(∆DAC) వై॥ + (∆ABC) వై॥
= (∆EAC) వై॥ + (∆ABC) వై॥
కావున (ABCD) వై॥ = (∆ABE) వై॥

6. కింది పటంలో AP || BQ || CR. (∆AQC) వై॥ = (∆PBR) వై॥ అని చూపండి. (పేజీ నెం. 258)
సాధన.

∆ABQ మరియు ∆PBQ లు ఒకే భూమి BQ మరియు ఒకే సమాంతర రేఖలు AP || BQల మధ్య ఉన్నాయి.
కావున (∆ABQ) వై॥ = (∆PBQ) వై॥ …………. (1)
ఇదే విధంగా (∆CQB) వై॥ = (∆RQB) వై॥
(ఒకే భూమి BQ మరియు BQ || CR) …….. (2)
(1), (2) ఫలితాలను కలుపగా
(∆ABQ) వై॥ + (∆CQB) వై॥ = (∆PBQ) వై॥ + (∆RQB) వై॥
అందుచే ∆AQC వై॥ = ∆PBR వై॥ అయినది.

AP SCERT 9th Class Maths Textbook Solutions Chapter 11 వైశాల్యాలు Ex 11.3 Textbook Exercise Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 11th Lesson వైశాల్యాలు Exercise 11.3

1. ∆ABC లో (పటం చూడండి), మధ్యగతరేఖ AD యొక్క మధ్యబిందువు E అయిన

ప్రశ్న (i)
∆ABE వై|| = ∆ACE వై||
సాధన.
∆ABC లో, AD మధ్యగతము.
∴ ∆ABD = ∆ACD ………..(1)
(∵ ఒక త్రిభుజంలోని మధ్యగతము దానిని రెండు సమాన త్రిభుజాలుగా విభజించును)
అదే విధంగా ∆ABD లో BE మధ్యగతము
∴ ∆ABE = ∆BED = [latex]\frac {1}{2}[/latex]∆ABD ……….. (2)
అదే విధంగా ∆ACD లో CE మధ్యగతము
∴ ∆ACE = ∆CDE = [latex]\frac {1}{2}[/latex]∆ACD ……. (3)
(1), (2) మరియు (3) ల నుండి;
∆ABE = ∆ACE అని నిరూపించబడినది.
(లేక)
∆ABD = ∆ACD
[∵ ∆ABC లో AD మధ్యగతము)
[latex]\frac {1}{2}[/latex]∆ABD = [latex]\frac {1}{2}[/latex]∆ACD [2చే భాగించగా]
∆ABE = ∆AEC [∵ ∆ABD కు BE మధ్యగతము]
[∆ACD కు CE మధ్యగతము]

ప్రశ్న (ii)
∆ABE వై|| = [latex]\frac {1}{4}[/latex](∆ABC) వై||
సాధన.
∆ABE = [latex]\frac {1}{2}[/latex]∆ABD
[(i) నుండి; ∆ABD యొక్క మధ్యగతం BE]
∆ABE = [latex]\frac {1}{2}[/latex] [[latex]\frac {1}{2}[/latex]∆ABC]
[∵ ∆ABC యొక్క మధ్యగతము AD]
= [latex]\frac {1}{4}[/latex]∆ABC
అని నిరూపించబడినది.

ప్రశ్న 2.
సమాంతర చతుర్భుజములో కర్ణాలు, దానిని సమాన వైశాల్యం గల నాలుగు త్రిభుజాలుగా విభజిస్తాయని చూపండి.
సాధన.
☐ABCD ఒక సమాంతర చతుర్భుజము.
కర్ణాలు AC మరియు BD లు ‘O’ వద్ద ఖండించు కుంటాయి.
∆ABC మరియు ☐ABCDలు ఒకే భూమి AB మరియు ఒకే సమాంతరాలు AB మరియు CDల మధ్యన కలవు.

∴ ∆ABC = [latex]\frac {1}{2}[/latex] ☐ABCD
∆ABC లో; BO మధ్యగతము
[∵ AC, BD కర్ణాల మధ్య ఖండన బిందువు O]
∴ ∆AOB ≅ ∆BOC …….. (1)
[∵ ఒక త్రిభుజంలో మధ్యగతము ఆ త్రిభుజంను సమాన వైశాల్యాలు గల రెండు త్రిభుజాలుగా విభజించును]
అదే విధంగా ∆ABD మరియు ☐ABCD లు ఒకే భూమి AB మరియు రెండు సమాంతరాలు AB, CDల మధ్యన కలవు.
∴ ∆ABD = [latex]\frac {1}{2}[/latex]☐ABCD
మరియు ∆AOB = ∆AOD …… (2)
[∵ ∆ABD యొక్క మధ్యగతము AO]
(1) మరియు (2)ల నుండి,
∆AOB = ∆BOC = ∆AOD
అదే విధముగా ∆AOD = ∆COD
[∵ ∆ACD మధ్య గత రేఖ OD]
∴ ∆AOB = ∆BOC = ∆COD = ∆AOD
అని నిరూపించబడినది.

ప్రశ్న 3.
పటంలో త్రిభుజాలు ∆ABC మరియు ∆ABD ఒకే భూమి AB పైన ఉన్నాయి. CD రేఖాఖండం [latex]\overline{\mathrm{AB}}[/latex] ని O వద్ద సమద్విఖండన చేస్తే (∆ABC) వై॥ = (∆ABD) వై॥ అని చూపండి.

సాధన.
పటం నుండి ∆AOC మరియు ∆BOD లలో
OA = OB [∵ దత్తాంశము]
OC = OD
[latex]\angle \mathrm{AOC}=\angle \mathrm{BOD}[/latex] (శీర్షాభిముఖ కోణాలు]
∴ ∆AOC ≅ ∆BOD (భు.కో.భు. నియమం)
ఆ విధంగా AC = BD (CPCT)
[latex]\angle \mathrm{OAC}=\angle \mathrm{OBD}[/latex] (CPCT)
కాని AC, BDల యొక్క ఏకాంతర కోణాలు
∴ AC // BD
అదే విధంగా AC = BD మరియు AC // BD;
☐ABCD ఒక సమాంతర చతుర్భుజము.
☐ABCD యొక్క కర్ణము AB
⇒ ∆ABC ≅ ∆ABD (∵ ఒక సమాంతర చతుర్భుజమును కర్ణము రెండు సర్వ సమాన త్రిభుజాలుగా విభజించును)
∴ (∆ABC) వైశాల్యము = (∆ABD) వైశాల్యము

4. పటంలో చూపిన విధంగా ∆ABC లో D, E, F లు వరుసగా భుజాలు BC, CA మరియు AB యొక్క మధ్య బిందువులు అయిన కింది వానిని నిరూపించండి.

ప్రశ్న (i)
BDEF ఒక సమాంతర చతుర్భుజము
సాధన.
∆ABC లో D, E మరియు F లు భుజాల మధ్య బిందువులు.
∴ EF// BC
EF = [latex]\frac {1}{2}[/latex]BC
FD // AC
FD = [latex]\frac {1}{2}[/latex]AC
ED // AB
ED = [latex]\frac {1}{2}[/latex]AB [∵ ఒక త్రిభుజపు రెండు భుజాల మధ్య బిందువులను కలుపగా ఆ రేఖాఖండం మూడవ భుజంకు సమాంతరము మరియు దానిలో సగముండును.]
∴ ☐BDEFలో
BD = EF (∵ BC మధ్య బిందువు D మరియు [latex]\frac {1}{2}[/latex]BC = EF]
DE = BF
∴ ☐BDEF ఒక సమాంతర చతుర్భుజము.

ప్రశ్న (ii)
(∆DEF) వై || = [latex]\frac {1}{4}[/latex](∆ABC) వై ||
సాధన.
☐BDEFఒక సమాంతర చతుర్భుజం ((i) నుండి) కావున ∆BDF = ∆DEF
అదే విధముగా ☐CDFE; ☐AEDF లు సమాంతర చతుర్భూజాలు.
∴ ∆DEF = ∆CDE = ∆AEF
∴ ∆ABC = ∆AEF + ∆BDF + ∆CDF + ∆DEF = 4∆DEF
⇒ ∆DEF = [latex]\frac {1}{4}[/latex]∆ABC

ప్రశ్న (iii)
(BDEF) వై || = [latex]\frac {1}{2}[/latex](∆ABC) వై ||.
సాధన.
☐BDEF = 2∆DEF ……….. (1)
((ii) నుండి)
∆ABC = 4 ∆DEF ………… (2)
((ii) నుండి)
(1) మరియు (2) నుండి,
∆ABC = 2 (2∆DEF) = 2 ☐BDEF అని నిరూపించబడినది.

ప్రశ్న 5.
పటంలో చూపిన విధంగా ∆ABCలో D మరియు E బిందువులు వరుసగా AB, AC భుజాల పై గల బిందువులు మరియు (∆DBC) వై॥ = (∆EBC) వై॥ అయిన DE // BC అని చూపండి.

సాధన.
∆DBC = ∆EBC
రెండు త్రిభుజాలు ఒకే భూమి BC మరియు ఒకే జత సమాంతర రేఖలు BC మరియు DE ల మధ్యన కలవు. కావున వాటి వైశాల్యాలు సమానము.
∴ BC // DE.

ప్రశ్న 6.
కింది పటంలో BC కు సమాంతరంగా A గుండా XY అనే రేఖ గీయబడింది. BE || CA మరియు CF || BA లను గీస్తే అవి XY ను E మరియు Fల వద్ద వరుసగా ఖండిస్తే (∆ABE) వై॥ = (∆ACF) వై॥ అని చూపండి.

సాధన.
దత్తాంశం XY//BC; BE//CA; CF//BA
చతుర్భుజం ABCF లో AB//CF మరియు BC//AF
కావున ☐ABCF ఒక సమాంతర చతుర్భుజము.
☐ABCE మరియు ☐ACBE లలో
∆ABC = ∆ACE …….. (1);
∆ABC = ∆ABE ……. (2) [∵ ఒక సమాంతర చతుర్భుజమును కర్ణము రెండు సరూప త్రిభుజములుగా విభజించును]
∴ ∆ACF = ∆ABE [(1) మరియు (2) ల నుండి] నిరూపించబడినది.

ప్రశ్న 7.
కింది పటంలో ABCD ట్రెపీజియంలో AB//DC కర్ణాలు AC మరియు BD లు ‘O’ వద్ద ఖండించుకున్నాయి.
(∆AOD) వై|| = (∆BOX) వై॥ అని చూపండి.

సాధన.
దత్తాంశం AB // CD
∆ADC మరియు ∆BCD లు ఒకే భూమి మరియు ఒకే సమాంతరాలు AB మరియు CDల మధ్యన కలవు.
AB // CD.
∴ ∆ADC = ∆BCD
⇒ ∆ADC – ∆COD = ∆BCD – ∆COD
⇒ ∆AOD = ∆BOC (పటం నుండి)

8. కింది పటంలో ABCDE ఒక పంచభుజి. B గుండా ACకు సమాంతరంగా గీచిన రేఖ, పొడిగించిన DCని F వద్ద ఖండించిన కింది వానిని నిరూపించుము.

ప్రశ్న (i)
(∆ACB) వై॥ = (∆ACF) వై ॥
సాధన.
ABCDE ఒక పంచభుజి మరియు AC//BF
∆ACB మరియు ∆ACF లు ఒకే భూమి AC మరియు ఒకే సమాంతరాలు AC//BF ల మధ్యన కలవు.
∴ ∆ACB = ∆ACF

ప్రశ్న (ii)
(AEDF) వై ॥ = (ABCDE) వై ॥

సాధన.
☐AEDF = ☐AEDC + ∆ACF
= ☐DAEDC + ∆ABC
[∵ ∆ACF = ∆ACB]
= (ABCDE) వై॥ నిరూపించబడినది

ప్రశ్న 9.
కిందీ పటంలో ∆RAS వై॥ = ∆RBS వై॥ మరియు ∆QRB వై॥ = ∆PAS పై॥ అయిన చతుర్భుజాలు PQRS మరియు RSBA లు రెండునూ ట్రెపీజియమ్ ని చూపండి.

సాధన.
∆RAS = ∆RBS ……. (1)
రెండు త్రిభుజాలు ఒకే భూమి RS మరియు ఒకే జత సమాంతర రేఖలు RS మరియు AB ల మధ్యన కలవు. కాబట్టి వాటి వైశాల్యాలు సమానము. మరియు RS//AB
∴ ☐ABRS చతుర్భుజం నందు AB//RS.
∴ ☐ABRS (లేదా) ☐RSBA ఒక ట్రెపీజియమ్
∆QRB = ∆PAS (దత్తాంశం)
⇒ ∆QRB – ∆RBS = ∆PAS – ∆RAS
[(1) నుండి ∆RBS = ∆RAS]
⇒ ∆QRS = ∆PRS.
ఈ త్రిభుజాలు ఒకే భూమి RS పై మరియు RS మరియు PQల మధ్యన కలవు. కావున వాటి వైశాల్యాలు సమానము, PQ//RS.
PQRS చతుర్భుజంలో PQ//RS. కావున ☐PQRS ట్రెపీజియము.

ప్రశ్న 10.
ఒక గ్రామంలో రామయ్య అనే వ్యక్తికి చతుర్భుజాకారంలో ఖాళీ స్థలం కలదు. ఆ గ్రామ పంచాయితీలో పాఠశాల నిర్మాణానికి అతని స్థలంలో ఒక మూలలో కొంత భాగం కావల్సివచ్చింది. ఆయన స్థలాన్ని ఇవ్వడానికి అంగీకరిస్తూ, దానికి బదులుగా అంతే వైశాల్యం గల స్థలాన్ని పొందితే ఏ విధంగా ఆ స్థలం వస్తుందో వివరించండి. (స్థలం యొక్క చిత్తు పటం గీయండి.)
సాధన.

పటం నుండి ☐ABCD రామయ్య పొలం అనుకొనుము.
∆MCD లో పాఠశాల నిర్మాణము జరుగును.
M, BC మధ్య బిందువు
☐ABCD ≅ ∆ADE
BD కర్ణంను గీయుము.
C గుండా BD కి సమాంతర రేఖను గీయుము. అది BC ని E వద్ద ఖండించును.
D, Eలను కలుపుము. ∆ADE మనకు కావలసిన త్రిభుజము.
పరిశీలన:
∆CED మరియు ∆CEBలు ఒకే భూమి CE మరియు ఒక జత సమాంతరాలు CE, DB ల మధ్యన ఉన్నవి.

∴ ∆CED = ∆CEB (పటం నుండి)
∆CEM + ∆CMD = ∆CEM + ∆BME
∴ ∆CMD = ∆BME
∴ ∆ADE = ☐ABCD

AP SCERT 9th Class Maths Textbook Solutions Chapter 11 వైశాల్యాలు Ex 11.2 Textbook Exercise Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 11th Lesson వైశాల్యాలు Exercise 11.2

ప్రశ్న 1.
ABCD సమాంతర చతుర్భుజ వైశాల్యము 36 చ.సెం.మీ. AB = 4.2 సెం.మీ. అయిన ABEF సమాంతర చతుర్భుజము కనుగొనుము.

సాధన.
☐ABCD వైశాల్యము = 36 చ.సెం.మీ.
AB = 4.2 సెం.మీ.
36 = 4.2 × h
⇒ h = [latex]\frac {36}{4.2}[/latex]
☐ABCD మరియు ☐ABEF లు ఒకే భూమి మరియు ఒకే జత సమాంతరాల మధ్యన గలవు. కావున
∴ ☐ABCD వై|| = ☐ABEF వై||
☐ABEF వై|| = భూమి × ఎత్తు = AB × ఎత్తు
∴ ఎత్తు = [latex]\frac {36}{4.2}[/latex] = 8.571 సెం.మీ.

ప్రశ్న 2.
ABCD ఒక సమాంతర చతుర్భుజము. DC భుజము పైకి గీయబడిన లంబము AE మరియు AD భుజము పైకి గీయబడిన లంబము CF. AB = 10 సెం.మీ., AE = 8 సెం.మీ. మరియు CF = 12 సెం.మీ. అయిన AD కొలత కనుగొనుము

సాధన.
సమాంతర చతుర్భుజపు వైశాల్యము = భూమి × ఎత్తు
AB × AE = AD × CF
⇒ 10 × 8 = 12 × AD
⇒ AD = [latex]\frac{10 \times 8}{12}[/latex] = 6.666………….
∴ AD = 6.7 సెం.మీ.

ప్రశ్న 3.
ABCD ఒక సమాంతర చతుర్భుజములో AB, BC, CD మరియు AD భుజాల మధ్య బిందువులు వరుసగా E, F, G మరియు H లు అయిన (EFGH) వై|| = [latex]\frac {1}{2}[/latex](ABCD) వై|| అని చూపుము.

సాధన.
☐ABCD ఒక సమాంతర చతుర్భుజము.
E, F, G మరియు H లు సమాంతర చతుర్భుజము యొక్క భుజాల మధ్య బిందువులు, E మరియు Gలను కలుపుము.
∆EFG మరియు ☐EBCGలు ఒకే భూమి EG మరియు సమాంతరాలు EG మరియు BC ల మధ్యన కలవు.
∴ ∆EFG = [latex]\frac {1}{2}[/latex] ☐EBCG …….. (1)
అదే విధంగా,
∆EHG = [latex]\frac {1}{2}[/latex] ☐EGDA ……….. (2)
(1) మరియు (2) ల నుండి,
∆EFG + ∆EHG = [latex]\frac {1}{2}[/latex] ☐EBCG + [latex]\frac {1}{2}[/latex] ☐EGDA
☐EFGH = [latex]\frac {1}{2}[/latex] [☐EBCG + ☐EGDA]
☐EFGH = [latex]\frac {1}{2}[/latex] [☐ABCD] నిరూపించబడినది.

ప్రశ్న 4.
∆APM, ∆DPO, ∆OCN మరియు ∆MNBలను ఒకచోట చేర్చితే ఏ రకమైన చతుచ్భుజం వస్తుంది?
సాధన.

☐ABCD ఒక రాంబస్.
M, N, O, Pలు భుజాల మధ్య బిందువులు.
ఈ మధ్య బిందువులను కలుపగా ∆APM, ∆DPO, ∆OCN మరియు ∆MNB లు ఏర్పడినవి.
వీటిలో షేడ్ ప్రాంతం కలిగిన పటం ఏర్పడును.

ప్రశ్న 5.
ABCD సమాంతర చతుర్భుజములో P మరియు Q అను రెండు బిందువులు వరుసగా DC మరియు ADలపై ఉంటే (∆APB) వై॥ = (∆BQC) వై॥ అని చూపండి.

సాధన.
∆APB మరియు ☐ABCDలు ఒకే భూమి AB మరియు రెండు సమాంతరాలు AB మరియు CDల మధ్యన కలదు.
∴ ∆APB = [latex]\frac {1}{2}[/latex] ☐ABCD ……… (1)
అదే విధంగా ∆BCQ మరియు ☐BCDA లు ఒకే భూమి BC మరియు సమాంతరాలు BC, AD ల మధ్యన గలవు.
∴ ∆BCQ = [latex]\frac {1}{2}[/latex] ☐BCDA ……..(2)
కాని ☐ABCD మరియు ☐BCDA లు సమాంతరాలు.
∴ ∆APB = ∆BCQ[(1) మరియు (2) ల నుండి]

6. ABCD సమాంతర చతుర్భుజము అంతరములో P అనేది ఒక బిందువు అయిన కింది వానిని నిరూపించండి.

ప్రశ్న (i)
(∆APB) వై|| + (∆PCD) వై|| = [latex]\frac {1}{2}[/latex](ABCD) వై||

సాధన.
☐ABCD ఒక సమాంతర చతుర్భుజము.
P ఒక సమాంతర చతుర్భుజము యొక్క అంతర బిందువు AB కి సమాంతరంగా P గుండా ఒక [latex]\overline{\mathrm{XY}}[/latex] రేఖను గీయుము.
∆APB = [latex]\frac {1}{2}[/latex]☐AXYB ……. (1)
[∵ ∆APB, ☐AXYB లు ఒకే భూమి ABమరియు AB, XY సమాంతర రేఖల మధ్యన కలవు]
మరియు ∆PCD = [latex]\frac {1}{2}[/latex]☐CDXY …….. (2)
[∵ ∆PCD; ☐CDXYలు ఒకే భూమి CD మరియు సమాంతరాలు CD మరియు XY ల మధ్యన కలవు]
(1) మరియు (2) లను కలపగా
∆APB + ∆PCD = [latex]\frac {1}{2}[/latex]☐AXYB + [latex]\frac {1}{2}[/latex]☐CDXY
= [latex]\frac {1}{2}[/latex] [☐AXYB + ☐CDXY] [పటం నుండి]
= [latex]\frac {1}{2}[/latex] ☐ABCD

ప్రశ్న (ii)
(∆APD) వై|| + (∆PBC) వై॥ = (∆APB) వై॥ + (∆PCD) వై॥
(సూచన : AB కి సమాంతరముగా P నుండి ఒక రేఖను గీయుము).
సాధన.
LM // AD ను నిర్మించుము.
∆APD + ∆PBC = [latex]\frac {1}{2}[/latex] ☐AMLD + [latex]\frac {1}{2}[/latex]BMLC
= [latex]\frac {1}{2}[/latex] [☐AMLD + ☐BMLC)
= [latex]\frac {1}{2}[/latex] ☐ABCD = ∆APB + ∆PCD [(i) నుండి] అని నిరూపించబడినది.
[∵ ∆APD, ☐AMLD లు ఒకే భూమి AD మరియు సమాంతరాలు AD మరియు LM ల మధ్యన కలవు]

ప్రశ్న 7.
ట్రెపీజియం యొక్క వైశాల్యము దాని సమాంతర భుజాల మొత్తాన్ని వాటి మధ్య దూరంతో గుణించగా వచ్చే లబ్ధంలో సగము ఉంటుందని నిరూపించండి.
సాధన.

☐ABCDఒక ట్రెపీజియం;
AB//CD మరియు DE ⊥ AB
☐ABCD = ∆ABC + ∆ADC
= [latex]\frac {1}{2}[/latex]AB × DE + [latex]\frac {1}{2}[/latex]DC × DE
[∵ ∆ = [latex]\frac {1}{2}[/latex] × భూమి × ఎత్తు]
= [latex]\frac {1}{2}[/latex] × DE (AB + DC) అని నిరూపించబడినది.

8. PQRS మరియు ABRS అనేవి రెండు సమాంతర చతుర్భుజాలు. BR భుజముపై X అనేది ఒక బిందువు. అయిన

ప్రశ్న (i)
(PQRS) వై|| = (ABRS) వై ||
సాధన.
☐PQRS మరియు ☐ABRSలు ఒకే భూమి SR మరియు సమాంతర భుజాలు SR మరియు PB ల మధ్యన గలవు.
∴ ☐PQRS వై|| = ☐ABRS వై||

ప్రశ్న (ii)
(∆AXS) వై|| = [latex]\frac {1}{2}[/latex](PQRS) వై||
సాధన.
(1) నుండి ☐PQRS = ☐ABRS
☐ABRS మరియు ∆AXS లు ఒకే భూమి AS మరియు AS, BR అను సమాంతరాల మధ్యన కలవు.
∴ ∆AXS = [latex]\frac {1}{2}[/latex]☐ABRS
= [latex]\frac {1}{2}[/latex]☐PQRS ((1) నుండి) నిరూపించబడినది.

ప్రశ్న 9.
ఒక రైతుకు పటంలో చూపినట్లు PQRS సమాంతర చతుర్భుజు ఆకారములో పొలము ఉన్నది. RS భుజముపై మధ్యబిందువు A నుండి P, Q బిందువులను కలిపారు. పొలము ఎన్ని భాగాలుగా విభజింపబడినది ? ఏ భాగాలు ఏ ఆకారములో ఉన్నాయి ? రైతు తన పొలములో వరి మరియు వేరుశెనగ పంటను సమాన భాగాలలో వేయాలనుకుంటే, ఏ విధంగా వేస్తాడు ? కారణాలు తెలపండి.

సాధన.
పటం నుండి ∆APQ, ☐PQRSలు ఒకే భూవిం PQ
మరియు సమాంతరాలు PQ, SR ల మధ్యన కలవు.
∴ ∆APQ = [latex]\frac {1}{2}[/latex]☐PQRS
⇒ ☐PQRS – ∆APQ = [latex]\frac {1}{2}[/latex]☐PQRS
⇒ [latex]\frac {1}{2}[/latex]☐PQRS = ∆ASP + ∆ARQ
∴ రైతు తన వేరుశనగ పంటను ∆APQ ప్రాంతంలో వేస్తాడు.
రైతు తన వరి పంటను ∆ARQ ప్రాంతంలోనూ, వేరుశెనగ పంటను ∆ASP ప్రాంతంలోను పండిస్తాడు.

ప్రశ్న 10.
రాంబస్ యొక్క వైశాల్యము, దాని కర్ణముల లబ్దములో సగం ఉంటుందని నిరూపించండి.
సాధన.

☐ABCD ఒక రాంబస్.
d₁ మరియు d₂ కర్ణాలు ‘O’ వద్ద ఖండించుకుంటాయి.
d₁ ⊥ d₂ కావున

AP SCERT 9th Class Maths Textbook Solutions Chapter 11 వైశాల్యాలు Ex 11.1 Textbook Exercise Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 11th Lesson వైశాల్యాలు Exercise 11.1

ప్రశ్న 1.
∆ABC లో [latex]\angle \mathrm{ABC}[/latex] = 90°, AD = DC, AB = 12 సెం.మీ. మరియు BC = 6.5 సెం.మీ. అయిన ∆ADB వైశాల్యము కనుగొనండి.

సాధన.
∆ADB = [latex]\frac {1}{2}[/latex] ∆ABC (∵ ∆ABC లో AD మధ్యగతము)
= [latex]\frac {1}{2}[/latex][[latex]\frac {1}{2}[/latex]AB × BC)
= [latex]\frac {1}{2}[/latex] × 12 × 6.5 = 19.5 చ. సెం.మీ.

ప్రశ్న 2.
PARS చతుర్భుజములో [latex]\angle \mathrm{QPS}=\angle \mathrm{SQR}[/latex] = 90°, PQ = 12 సెం.మీ., PS = 9 సెం.మీ., QR = 8 సెం.మీ. మరియు SR = 17 సెం.మీ. అయిన PQRS వైశాల్యం కనుగొనండి. (సూచన : PQRSలో రెండు భాగాలున్నాయి రెండు భాగాలున్నాయి.

సాధన.
∆QPS వైశాల్యము
= [latex]\frac {1}{2}[/latex] × భూమి × ఎత్తు
= [latex]\frac {1}{2}[/latex] × 9 x 12 = 54 చ.సెం.మీ.
∆QPS లో Q² = PQ² + PS²
QS = [latex]\sqrt{12^{2}+9^{2}}=\sqrt{144+81}[/latex]
= [latex]\sqrt{225}[/latex] = 15
∴ ∆QSR వైశాల్యము = [latex]\frac {1}{2}[/latex] × భూమి × ఎత్తు
= [latex]\frac {1}{2}[/latex] × 15 × 8 = 60 చ. సెం.మీ.
☐PQRS = ∆QPS + ∆QSR
= 54 + 60 = 114 చ.సెం.మీ.

ప్రశ్న 3.
కింది పటములో ADCE ఒక దీర్ఘచతురస్రము అయిన ABCD ట్రెపీజియం వైశాల్యము కనుగొనండి. (సూచన : ABCD లో రెండు భాగాలున్నాయి)

సాధన.
ట్రెపీజియం వైశాల్యము
= [latex]\frac {1}{2}[/latex] (సమాంతర భుజాల మొత్తం) × (ఎత్తు)
(A) = [latex]\frac {1}{2}[/latex] (a + b) h
పటం నుండి, a = 3 + 3 = 6 సెం.మీ. .
b = 3 సెం.మీ. (∵ దీర్ఘచతురస్రపు ఎదుటి భుజాలు)
h = 8 సెం.మీ.
∴ A = [latex]\frac {1}{2}[/latex](6 + 3) × 8 = 36 చ.సెం.మీ.

ప్రశ్న 4.
ABCD ఒక సమాంతర చతుర్భుజము. కర్ణములు AC మరియు BD లు ‘O’ వద్ద ఖండించుకున్నాయి. (∆AOD) వై|| = (∆BOC) వై|| అని నిరూపించండి. (సూచన : సర్వసమాన పటాలు సమాన వైశాల్యాలు కలిగి ఉంటాయి.)

సాధన.
☐ABCD ఒక సమాంతర చతుర్భుజము.
కర్ణాలు AC మరియు BD లు ‘O’ వద్ద ఖండించుకుంటాయి.
∆AOD మరియు ∆BOC లలో
AD = BC [∵ //^gm యొక్క ఎదుటి భుజాలు]
AO = OC [∵ కర్ణాలు సమద్విఖండన చేసుకొనును]
OD = OB
∴ ∆AOD ≅ ∆BOC (భు.భు.భు. నియమం ప్రకారం)
∴ ∆AOD = ∆BOC (సమాన వైశాల్యాలు గల త్రిభుజాలు)

AP SCERT 9th Class Maths Textbook Solutions Chapter 12 వృత్తాలు InText Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 12th Lesson వృత్తాలు InText Questions

ఇవి చేయండి

1. పటములో వృత్తం A నకు సర్వసమానంగా ఉన్న వృత్తాలను గుర్తించండి. (పేజీ నెం. 262)

సాధన.
వృత్తం A నకు సర్వసమానంగా ఉన్న వృత్తం ‘E’.

2. వృత్తాల యొక్క ఏ కొలత వాటిని సర్వసమానం చేస్తుంది? (పేజీ నెం. 262)
సాధన.
వృత్తాల యొక్క వ్యాసార్ధములు వాటిని సర్వసమానం చేస్తుంది.

ప్రయత్నించండి

1. ‘O’ కేంద్రంగా కల వృత్తంలో AB ఒక జ్యా మరియు ‘M’ జ్యా మధ్య బిందువు. అయినా [latex]\overline{\mathrm{OM}}[/latex], AB కి అంబింగా ఉండునని నిరూపించండి. (సూచన : OA, OB లను కలిపి ∆OAM మరియు ∆OBM లను పోల్చండి.) (పేజీ నెం. 267)

సాధన.

‘O’ వృత్త కేంద్రము.
AB ఒక జ్యా, M, AB పై మధ్య బిందువు.
A, B లను ‘O’ తో కలుపుము.
∆OMA మరియు ∆OMB లలో
OA = OB (వ్యాసార్ధాలు )
OM = OM (ఉమ్మడి భుజం)
MA = MB (దత్తాంశము)
∴ ∆OMA ≅ ∆OMB
(భు. భు.భు. సర్వసమాన ధర్మం )
∴ [latex]\angle \mathrm{OMA}=\angle \mathrm{OMB}[/latex] (C.P.C.T).
కాని [latex]\angle \mathrm{OMA}[/latex] మరియు [latex]\angle \mathrm{OMB}[/latex] లు రేఖీయ ద్వయం
∴ [latex]\angle \mathrm{OMA}=\angle \mathrm{OMB}[/latex] = 90°
i.e., OM ⊥ AB.

2. మూడు బిందువులు సరేఖీయాలైన, వాటి గుండా పోయేట్లు గీయగల వృత్తాలెన్ని? ఒక రేఖపై ఏవేని మూడు బిందువులను తీసుకొని వాటి గుండా పోయేటట్లు వృత్తాలను గీయడానికి ప్రయత్నించండి. (పేజీ నెం. 268)
సాధన.
మూడు బిందువులు సరేఖీయాలైన వాటి గుండాపోవు వృత్తంను గీయలేము.

3. పటంలో ‘O’ వృత్త కేంద్రం మరియు AB = CD; OM మరియు ON లు వరుసగా [latex]\overline{\mathrm{AB}}[/latex] మరియు [latex]\overline{\mathrm{CD}}[/latex]లకు కేంద్రం నుండి గీచిన లంబాలు. అయిన OM = ON అని నిరూపించండి. (పేజీ నెం. 269)

సాధన.
‘O’ వృత్త కేంద్రము మరియు AB = CD జ్యాలు.
OM ⊥ AB; ON ⊥ CD
∆OMB మరియు ∆ONC లలో
OB = OC [∵ వ్యాసార్ధాలు]
BM = CN (∵ [latex]\frac {1}{2}[/latex]AB = [latex]\frac {1}{2}[/latex]CD)
[latex]\angle \mathrm{OMB}=\angle \mathrm{ONC}[/latex] [∵ ప్రతి కోణం 90°]
∴ ∆OMB ≅ ∆ONC (లం. క.భు. సర్వసమాన నియమం ప్రకారం )
OM = ON (C.P.C.T)

కృత్యం

1. ఈ క్రింది కృత్యాన్ని చేద్దాం. కాగితంపై ఒక బిందువును . గుర్తించండి. ఈ బిందువును కేంద్రంగా తీసుకొని ఏదేని వ్యాసార్ధంతో ఒక పృత్తాన్ని గీయండి. ఇదే కేంద్రంతో వ్యాసార్ధాన్ని పెంచి లేదా తగ్గించి మరికొన్ని వృత్తాలను గీయండి. ఈ కృత్యం ద్వారా గీచిన వృత్తాలను ఏమని పిలుస్తారు ? (పేజీ నెం. 261)

ఒకే కేంద్రం గల వృత్తాలను ఏకకేంద్ర వృత్తాలు అంటారు.

2. ఒక పలుచని గుండ్రని కాగితం (వృత్తాకార కాగితం) తీసుకొని, దానిని సగానికి (మధ్యకు) మడచి తెరవండి. మరలా మరొక సగానికి మడచి తెరవండి. ఇదే విధంగా అనేకసార్లు తిరిగి చేయండి. చివరికి తెరిచి చూస్తే మీరేమి గమనిస్తారు ? (పేజీ నెం. 262)

3. ఒక గ్రుండని (వృత్తాకార) కాగితాన్ని తీసుకోండి. వృత్త అంచులు ఏకీభవించునట్లు ఏదేని ఒక వ్యాసం వెంట మడవండి. మడతను తెరచి ఇంకొక వ్యాసం వెంబడి మడవండి. మడతను తెరచి చూసిన రెండు వ్యాసాలు కేంద్రం ‘O’ వద్ద ఖండించుకొనుటను గమనిస్తాం. రెండు జతల శీర్షాభిముఖ కోణాలు ఏర్పడుతాయి. ఇవి సమానం, వ్యాసం చివరి బిందువుల A, B, C మరియు D అని పేర్లు పెట్టండి.

జ్యాలు [latex]\overline{\mathrm{AC}}, \overline{\mathrm{BC}}, \overline{\mathrm{BD}}[/latex] మరియు [latex]\overline{\mathrm{AD}}[/latex]లను గీయండి.
నాలుగు వృత్తఖండాలు 1, 2, 3 మరియు 4 లను కత్తిరించండి. ఈ ఖండాలను జతలుగా ఒకదానిపై మరొకటి ఉంచిన (1, 3) మరియు (2, 4) జతలు అంచులు ఏకీభవిస్తాయి. అంటే [latex]\overline{\mathrm{AD}}=\overline{\mathrm{BC}}[/latex] మరియు [latex]\overline{\mathrm{AC}}=\overline{\mathrm{BD}}[/latex] అవుతాయా ?
ఒక ప్రత్యేక సందర్భములో పై ధర్మాన్ని పరిశీలించారు. ఇదే విషయాన్ని వేర్వేరు కొలతలుగల సమాన కోణాలు తీసుకొని సరిచూసిన జ్యాలు సమానమగును. కింది సిద్ధాంతము ద్వారా గమనించగలం. (పేజీ నెం. 265)

4. వృత్తాకారంలోగల ఒక కాగితాన్ని తీసుకొని దాని కేంద్రం ‘O’ ను గుర్తించండి. వృత్తం యొక్క కొంత భాగాన్ని మడచి తిరిగి తెరవండి. ఏర్పడిన మడత జ్యా ABను సూచిస్తుందనుకోండి. ఇంకొక మడత వృత్త కేంద్రం మరియు జ్యా మధ్య బిందువు గుండా పోయేటట్లు కాగితాన్ని మరల మడవండి. ఇప్పుడు మడతల మధ్య ఏర్పడిన కోణాలను కొలవండి, అవి లంబకోణాలు.

“కాబట్టి వృత్తకేంద్రం నుండి జ్యాను సమద్విఖండన చేసే రేఖ జ్యూకు లంబంగా ఉంటుంది” అని పరికల్పన చేయవచ్చు. (పేజీ నెం. 267)

5. వృత్తం దానిని సగానికి మధ్యలో మడవండి. ఇప్పుడు ఆర్ధవృత్త చాపపు అంచు దగ్గరయుంచి మడత విప్పిన మీకు రెండు సర్వసమాన జ్యాల మడతలు వచ్చును. వాటిని [latex]\overline{\mathrm{AB}}[/latex] మరియు [latex]\overline{\mathrm{CD}}[/latex] లుగా గుర్తించండి కేంద్రాన్ని ‘O’ గా గుర్తించండి. కేంద్రం ‘O’ నుండి ప్రతి జ్యాకు లంబపు మడత పెట్టండి. విభాగిని ఉపయోగించి వృత్తకేంద్రం నుండి జ్యాలకు గల లంబ దూరాలను పోల్చండి.

ఈ కృత్యాన్ని వృత్తం మడత ద్వారా సమాన జ్యాలు ఏర్పరుస్తూ అనేకసార్లు మరలా చేయండి. మీ పరిశీలనలను . ఒక పరికల్పనగా తెల్పండి. సర్వసమాన జ్యాలు వృత్త కేంద్రం నుండి సమాన దూరంలో ఉంటాయి. (పేజీ నెం. 269)

6. పటంలో చతుర్పులు తీరాలు A, B C మరియు Dలు ఒకే వృత్తం పైన గలవు. ఇటువంటి చతుర్భుజాలు ABCD లను మూడింటిని గీసి చతుర్భుజ కోణాలను కొలచి పట్టికను నింపండి.

పట్టిక నుండి నీవు ఏమి చెప్పగలవు ? (పేజీ నెం. 275)

సిద్ధాంతాలు

1. ఒక వృత్తంలోని రెండు జ్యాలు సమానమైతే అవి కేంద్రం వద్ద ఏర్పరచే కోణాలు సమానం. (పేజీ నెం. 265)
సాధన.
దత్తాంశం : ‘O’ కేంద్రంగా గల వృత్తంలో [latex]\overline{\mathrm{AB}}[/latex] మరియు [latex]\overline{\mathrm{CD}}[/latex] లు రెండు సమాన జ్యాలు. అవి కేంద్రం వద్ద ఏర్పరచిన కోణాలు [latex]\angle \mathrm{AOB}[/latex] మరియు [latex]\angle \mathrm{AOB}[/latex].
సారాంశం: [latex]\angle \mathrm{AOB}[/latex] = [latex]\angle \mathrm{COD}[/latex]
నిర్మాణం : వృత్త కేంద్రాన్ని జ్యాల యొక్క అంత్య బిందువులతో కలుపుము. ఇప్పుడు ∆AOB మరియు ∆COD లు ఏర్పడతాయి.
నిరూపణ:

∆AOB మరియు ∆COD లలో
AB = CD (దత్తాంశం)
OA = OC (ఒకే వృత్త వ్యాసార్ధాలు)
OB = OD (ఒకే వృత్త వ్యాసార్ధాలు)
కావున ∆AOB ≅ ∆COD (భు.భు.భు. నియమం)
కావున ∆AOB ≅ ∆COD (సర్వసమాన త్రిభుజపు అనురూప కోణాలు)

2. ఒక వృత్తంలోని జ్యాలు కేంద్రం వద్ద చేసే కోణాలు సమానమైన ఆ జ్యాలు సమానం.

ఇది ఇంతకు ముందు చెప్పబడిన సిద్ధాంతం యొక్క విపర్యయం ఇచ్చిన ప్రకారం
[latex]\angle \mathrm{PQR} \cong \angle \mathrm{MQN}[/latex]
అని తీసుకుంటే [latex]\angle \mathrm{PQR} ≡ \angle \mathrm{MQN}[/latex] అని మీరు గమనించగలరు. (పేజీ నెం. 266)

3. ఒక చాపము ఒక వృత్తకేంద్రం వద్ద ఏర్పరచుకోణం, ఆ చాపం మిగిలిన వృత్తంపై ఏదేని బిందువు వద్ద ఏర్పరిచే కోణానికి రెట్టింపు ఉంటుంది. (పేజీ నెం. 272)

సాధన.
‘O’ అనునది వృత్తకేంద్రం.
చాపము [latex]\overparen{\mathrm{PQ}}[/latex] కేంద్రం వద్ద ఏర్పరచు కోణం [latex]\angle \mathrm{POQ}[/latex].
Rఅనునది ([latex]\overparen{\mathrm{PQ}}[/latex] పై లేనట్టి) మిగిలిన వృత్తం మీద ఏదేని ఒక బిందువు.
నిరూపణ : ఇక్కడ (i) [latex]\overparen{\mathrm{PQ}}[/latex] ఒక అల్ప చాపం,
(ii) [latex]\overparen{\mathrm{PQ}}[/latex] ఒక అర్ధవృత్తం మరియు
(iii) [latex]\overparen{\mathrm{PQ}}[/latex] ఒక అధిక చాపం అయ్యే మూడు సందర్భాలు కలవు.
R బిందువును ‘O’ కలిపి S బిందువు దాకా పొడిగించడం ద్వారా నిరూపణను మొదలు పెడదాం. (అన్ని సందర్భాలలోనూ) అన్ని సందర్భాలలోను ∆ROP లో
OP = OR (ఒకే వృత్త వ్యాసార్ధాలు)
∴ [latex]\angle \mathrm{ORP}=\angle \mathrm{OPR}[/latex] (సమద్విబాహు త్రిభుజంలో సమాన భుజాలకు ఎదురుగా ఉండే కోణాలు సమానం).
[latex]\angle \mathrm{POS}[/latex] కోణము ∆ROP కు బాహ్య కోణం (నిర్మాణం)
[latex]\angle \mathrm{POS}=\angle \mathrm{ORP}+\angle \mathrm{OPR}[/latex] లేదా 2[latex]\angle \mathrm{OPR}[/latex] ……. (1)
(∵ బాహ్యకోణం అంతరాభిముఖ కోణాల మొత్తానికి సమానం)

ఇదే విధంగా ∆ROQ
[latex]\angle \mathrm{SOQ}=\angle \mathrm{ORQ}+\angle \mathrm{OQR}[/latex] లేదా 2[latex]\angle \mathrm{ORQ}[/latex] …….. (2)
(∵ బాహ్యకోణం అంతరాభిముఖ కోణాల మొత్తానికి సమానం)
(1) మరియు (2) ల నుండి,
[latex]\angle \mathrm{POS}+\angle \mathrm{SOQ}=2(\angle \mathrm{ORP}+\angle \mathrm{ORQ})[/latex]
అంటే ఇది [latex]\angle \mathrm{POQ}=2 \angle \mathrm{QRP}[/latex] తో సమానం ……….. (3)
కావున “ఒక చాపము వృత్త కేంద్రం వద్ద ఏర్పరచు కోణం, ఆ చాపం మిగిలిన వృత్తంపై ఏదేని బిందువు వద్ద ఏర్పరచే కోణానికి రెట్టింపు ఉంటుంది” అనే సిద్ధాంతం నిరూపించడమైనది.

4. రెండు బిందువులను కలిపే రేఖాఖండం (ఆ రేఖాఖండానికి ఒకే వైపునగల) ఏవేని రెండు వేర్వేరు బిందువుల మధ్య ఏర్పరచు కోణాలు సమానం అయితే ఆ బిందువులన్నీ ఒకే వృత్తంపై ఉంటాయి. అంటే అవి చక్రీయాలు అవుతాయి. ఈ ఫలితం యొక్క సత్య విలువను కింది విధంగా పరిశీలించవచ్చు. (పేజీ నెం. 274)
సాధన.
దత్తాంశం : ఏవేని రెండు బిందువులు A, B లను కలుపు రేఖాఖండం [latex]\overline{\mathrm{AB}}[/latex] నకు ఒకే వైపున గల రెండు బిందువులు C మరియు Dల వద్ద [latex]\overline{\mathrm{AB}}[/latex] చేయు కోణాలు [latex]\angle \mathrm{ACB}[/latex] మరియు [latex]\angle \mathrm{ADB}[/latex] లు సమానమని ఈయబడినవి.

సారాంశం : A, B, C మరియు D లు ఒకే వృత్తం పైన బిందువులు అనగా చక్రీయ బిందువులు.
నిర్మాణం : సరేఖీయాలు కాని మూడు బిందువులు A, B మరియు Cల గుండాపోయేట్లు ఒక వృత్తాన్ని గీయండి.
నిరూపణ : [latex]\angle \mathrm{ACB}=\angle \mathrm{ADB}[/latex] అగునట్లుగా D = ‘D’ బిందువు వృత్తంపైన లేనట్లైతే

వృత్తంపై E లేదా ‘E’ అనే బిందువు, AD లేదా ADని పొడిగించినప్పుడు ఖండన బిందువుగా వ్యవస్థితం అవుతుంది. అంటే A, B, C మరియు E లు ఒక వృత్తంపై ఉంటాయి కనుక
[latex]\angle \mathrm{ACB}=\angle \mathrm{AEB}[/latex] (ఎందువలన ?)
కానీ [latex]\angle \mathrm{ACB}=\angle \mathrm{ADB}[/latex] అని ఈయబడినది.
కాబట్టి [latex]\angle \mathrm{AEB}=\angle \mathrm{ADB}[/latex]
ఇది E మరియు Dలు ఏకీభవిస్తే తప్ప సాధ్యం కాదు. (ఎందువలన ?)
కావున E కూడా Dతో ఏకీభవిస్తుంది.

5. చక్రీయ చతుర్భుజంలోని ఎదుటి కోణాల జతలు సంపూరకాలు. (పేజీ నెం. 276)
సాధన.
దత్తాంశము : ABCD ఒక చక్రీయ చతుర్భుజం,

6. ఒక చతుర్భుజంలో ఏ రెండు ఎదుటి కోణాల మొత్తం అయినా 180° అయితే అది చక్రీయ చతుర్భుజం అవుతుంది. (పేజీ నెం. 277)
సాధన.
దత్తాంశం :

చతుర్భుజం ABCD లో
[latex]\angle \mathrm{ABC}+\angle \mathrm{ADC}[/latex] = 180°
[latex]\angle \mathrm{DAB}+\angle \mathrm{BCD}[/latex] = 180°
సారాంశం : ABCD ఒక చక్రీయ చతుర్భుజం.
నిర్మాణం : సరేఖీయాలు కానీ బిందువులు A, B మరియు Cల గుండా ఒక వృత్తాన్ని గీయండి. వృత్తం D ద్వారా పోయినట్లైతే A, B, C, D ల చక్రీయాలు కావున సిద్ధాంతము నిరూపించినట్లే.
ఈ వృత్తం D బిందువు ద్వారా పోనట్లైతే ఆ వృత్తం [latex]\overline{\mathrm{CD}}[/latex] ను లేదా [latex]\overline{\mathrm{CD}}[/latex] ను పొడిగించినప్పుడు D వద్ద ఖండిస్తుంది. [latex]\overline{\mathrm{AE}}[/latex] ను గీయండి.

నిరూపణ : ABCE ఒక చక్రీయ చతుర్భుజం (నిర్మాణం)
[latex]\angle \mathrm{AEC}+\angle \mathrm{ABC}[/latex] = 180° (చక్రీయ చతుర్భుజంలో ఎదుటి కోణాల మొత్తం)
కాని [latex]\angle \mathrm{ABC}+\angle \mathrm{ADC}[/latex] = 180° (దత్తాంశం)
[latex]\angle \mathrm{AEC}+\angle \mathrm{ABC}=\angle \mathrm{ABC}+\angle \mathrm{ADC}[/latex]
కానీ ఈ కోణాలలో ఒకటి ∆ADE యొక్క అంతరకోణం మరియు రెండవది బాహ్యకోణం. త్రిభుజ బాహ్య కోణం ఎల్లప్పుడూ దాని అంతరాభి. ముఖ కోణాల కన్నా ఎక్కువ అని మనకు తెలుసు.
∴ [latex]\angle \mathrm{AEC}=\angle \mathrm{ADC}[/latex] అనునది ఒక విరుద్దత.
అంటే A, B మరియు Cల ద్వారా గీచిన వృత్తం D ద్వారా పోవట్లేదనే మన కల్పన అసత్యం. A, B మరియు C ల ద్వారా గీచిన వృత్తం D ద్వారా కూడా పోవును. A, B, C మరియు Dలు ఒకే వృత్తంపైని బిందువులు అంటే ABCD ఒక చక్రీయ చతుర్భుజం.

ఉదాహరణలు

1. AB = 5 సెం.మీ.; [latex]\angle \mathrm{B}[/latex] = 75° మరియు BC = 7 సెం.మీ. లుగా గల ∆ABC యొక్క పరిషృత్తాన్ని గీయండి. (పేజీ నెం. 268)
సాధన.

AB = 5 సెం.మీ. పొడవుగల రేఖాఖండాన్ని గీయండి. [latex]\angle \mathrm{B}[/latex] = 75° ఉండునట్లు B వద్ద కోణకిరణం BX ను నిర్మించండి. B కేంద్రంగా 7 సెం.మీ. వ్యాసార్ధంతో ఒక చాపరేఖను గీయండి. చాపరేఖ [latex]\overrightarrow{\mathrm{BX}}[/latex] ను C వద్ద ఖండించును. C మరియు A లను కలపగా ∆ABC ఏర్పడుతుంది. [latex]\overline{\mathrm{AB}}[/latex] మరియు [latex]\overline{\mathrm{BC}}[/latex] లకు లంది సమద్విఖండన రేఖలు [latex]\overline{\mathrm{PQ}}[/latex] మరియు [latex]\overline{\mathrm{RS}}[/latex] లను గీయండి. [latex]\overline{\mathrm{PQ}}[/latex] మరియు [latex]\overline{\mathrm{RS}}[/latex] ల ఖండన బిందువు ‘O’. ఇప్పుడు ‘O’ ను కేంద్రంగా మరియు OA ను వ్యాసార్ధంగా ఒక వృత్తాన్ని గీయండి. B మరియు C బిందువుల ద్వారా కూడా పోతుంది. ఇదియే కావలసిన పరివృత్తం.

2. పటంలో ‘O’ వృత్త కేంద్రం అయిన CD పొడవును కనుక్కోండి. (పేజీ నెం. 269)

సాధన.
∆AOB మరియు ∆COD లలో
OA = OC (ఎందువలన?)
CB = OD (ఎందువలన ?)
[latex]\angle \mathrm{AOB}=\angle \mathrm{COD}[/latex]
∆AOB ≅ ∆COD
AB = CD (సర్వసమాన త్రిభుజముల సర్వసమాన భాగాలు)
AB = 5 సెం.మీ. కావున CD = 5 సెం.మీ.

3. పక్క పటంలో ‘O’ కేంద్రంగా రెండు ఏక కేంద్ర వృత్తాలు కలవు. పెద్ద వృత్తం యొక్క జ్యా AD చిన్న వృత్తాన్ని B మరియు Cల వద్ద అందిస్తుంది. అయిన AB = CD అని చూపండి. (పేజీ నెం. 269)

దత్తాంశం : ‘O’ కేంద్రంగా కల ఏక కేంద్ర వృత్తాలలో పెద్ద వృత్తం యొక్క జ్యా [latex]\overline{\mathrm{AD}}[/latex] చిన్న వృత్తాన్ని B మరియు Cల వద్ద ఖండిస్తోంది.
సారాంశం : AB = CD
నిర్మాణం: [latex]\overline{\mathrm{AD}}[/latex]కు లంబంగా [latex]\overline{\mathrm{OE}}[/latex] ను గీయుము.
నిరూపణ : ‘O’ కేంద్రంగా గల పెద్ద వృత్తానికి AD ఒక జ్యా మరియు [latex]\overline{\mathrm{OE}}[/latex], [latex]\overline{\mathrm{AD}}[/latex] కి లంబము.
∵ [latex]\overline{\mathrm{AD}}[/latex] ను [latex]\overline{\mathrm{OE}}[/latex] సమద్విఖండన చేస్తుంది (కేంద్రం నుండి జ్యాకు గీచిన లంబం, జ్యాను సమద్విఖండన చేస్తుంది.
∴ AE = ED ……….. (i)
‘O’ కేంద్రంగా గల చిన్న వృత్తానికి [latex]\overline{\mathrm{BC}}[/latex] ఒక జ్యా మరియు [latex]\overline{\mathrm{AD}}[/latex] కు [latex]\overline{\mathrm{OE}}[/latex] లంబం.
∵ [latex]\overline{\mathrm{BC}}[/latex] కు [latex]\overline{\mathrm{OE}}[/latex] సమద్విఖండన చేస్తుంది. (పై సిద్ధాంతం నుండి)
∴ BE = CE …….. (ii)
సమీకరణం (ii) ను (i) నుండి తీసివేయగా,
AE – BE = ED – EC
AB = CD

4. ‘O’ అనునది వృత్త కేంద్రం. PQ ఒక వ్యాసము. అయిన 2PRQ = 90° అని నిరూపించుము. (లేదా) అర్ధవృత్తంలోని కోణం లంబకోణమని చూపండి. (పేజీ నెం. 273)
నిరూపణ:

‘O’ కేంద్రంగా గల వృత్తంలో PQ ఒక వ్యాసం అని ఈయబడినది. [latex]\angle \mathrm{PRQ}[/latex] = 180° (సరళరేఖపై ఏదేని బిందువు వద్ద కోణం 180°)
మరియు [latex]\angle \mathrm{POQ}[/latex] = 2[latex]\angle \mathrm{PRQ}[/latex] (ఒక చాపం వృత్త కేంద్రం వద్ద ఏర్పరిచే కోణం, ఆ చాపం మిగిలిన వృత్తంపై ఏదేని బిందువు వద్ద ఏర్పరచే కోణానికి రెట్టింపు).
[latex]\angle \mathrm{PRQ}[/latex] = [latex]\frac {180°}{2}[/latex] = 90°

5. కింది పటంలో x° విలువను కనుగొనండి. (పేజీ వెం. 273)

సాధన.
[latex]\angle \mathrm{ACB}[/latex] = 40° కావున
సిద్ధాంతం ప్రకారం, AB చాపం కేంద్రం వద్ద చేయుకోణం.
[latex]\angle \mathrm{AOB}[/latex] = 2[latex]\angle \mathrm{ACB}[/latex] = 2 × 40° = 80°
x° + [latex]\angle \mathrm{AOB}[/latex] = 360°
కాబట్టి x° = 360° – 80° = 280°

6. పటంలో [latex]\angle \mathrm{A}[/latex] = 120° అయిన [latex]\angle \mathrm{C}[/latex]ను కనుగొనుము. (పేజీ నెం. 276)

సాధన.
ABCD ఒక చక్రీయ చతుర్భుజం
కావున [latex]\angle \mathrm{A}+\angle \mathrm{C}[/latex] = 180°
120° + [latex]\angle \mathrm{C}[/latex] = 180°
కావున [latex]\angle \mathrm{C}[/latex] = 180° – 120° = 60°

7. పటంలో [latex]\overline{\mathrm{AB}}[/latex] వృత్తం యొక్క ఒక వ్యాసము. జ్యా [latex]\overline{\mathrm{CD}}[/latex] వృత్త వ్యాసార్ధానికి సమానం. [latex]\overline{\mathrm{AC}}[/latex] మరియు [latex]\overline{\mathrm{BD}}[/latex] లు పొడిగించగా అవి E బిందువు వద్ద ఖండించుకొనును. అయిన [latex]\angle \mathrm{AEB}[/latex] = 60° అని చూపండి. (పేజీ నెం. 277)
సాధన.

OC, OD మరియు BC లను కలపండి.
∆ODC ఒక సమబాహు త్రిభుజము (ఎందువలన?)
[latex]\angle \mathrm{COD}[/latex] = 60°
ఇప్పుడు [latex]\angle \mathrm{CBD}[/latex] = [latex]\frac {1}{2}[/latex][latex]\angle \mathrm{COD}[/latex] (ఎందువలన ?)
దీని నుండి [latex]\angle \mathrm{CBD}[/latex] = 30°
మరల [latex]\angle \mathrm{ACB}[/latex] = 90° (ఎందువలన ?)
కావున [latex]\angle \mathrm{BCE}[/latex] = 180° – [latex]\angle \mathrm{ACB}[/latex] = 90°
దీని నుండి [latex]\angle \mathrm{CEB}[/latex] = 90° – 30° = 60°,
అంటే [latex]\angle \mathrm{AEB}[/latex] = 60°