AP Board 9th Class Maths Solutions Chapter 10 ఉపరితల వైశాల్యములు మరియు ఘనపరిమాణములు InText Questions

AP SCERT 9th Class Maths Textbook Solutions Chapter 10 ఉపరితల వైశాల్యములు మరియు ఘనపరిమాణములు InText Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 10th Lesson ఉపరితల వైశాల్యములు మరియు ఘనపరిమాణములు InText Questions

ప్రయత్నించండి

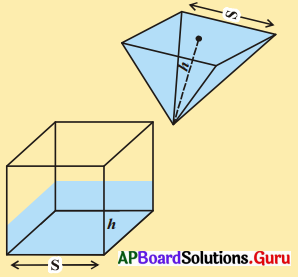
1. ‘l’ సెం.మీ. పొడవైన భుజం గల ఒక ఘనమును తీసుకోండి. ముందు కృత్యములో దీర్ఘమనమును కత్తిరించిన విధంగానే చేసి దాని యొక్క ప్రక్కతల వైశాల్యమును, సంపూర్ణతల వైశాల్యమును కనుగొనుము. (పేజీ నెం.216)
సాధన.

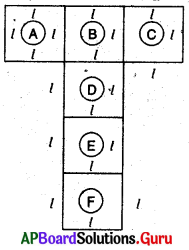
‘l’ సెం.మీ. భుజం గల ఒక ఘనమును కత్తిరించి, తెరచిన పైన పటంలో చూపిన విధంగా ఏర్పడును.
పటంలో A, B, C, D, E, F అను ‘l’ భుజంగా గల చతురస్రములు కలవు.
తలాలు A, C, D, F లు ఘనము యొక్క ప్రక్క తలాలను తెలియజేయుచున్నవి.
∴ ఘనపు ప్రక్కతల వైశాల్యము = 4l² చ.యూ.
మొత్తం ఆరు తలాలు కలిసి ఘనమును ఏర్పరచును.
∴ ఘనపు సంపూర్ణతల వైశాల్యము = 6l² చ.యూ.

2. (a) ‘a’భుజముగా గల ఘనము యొక్క ఘనపరిమాణమును కనుక్కోండి. (పేజీ నెం.217)

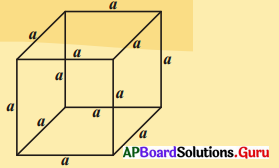
సాధన.
a భుజముగా గల ఘనము యొక్క ఘనపరిమాణము
V = భుజము³ = a³ ఘ. యూనిట్లు.

(b) అదే విధముగా ఒక ఘనము ఘనపరిమాణం 1000 ఘనపు సెంటీమీటర్లు అయితే దాని యొక్క భుజమును కనుక్కోండి. (పేజీ నెం.217)
సాధన.
ఘనపరిమాణం = V = భుజము³
= 10 × 10 × 10 = 10³
∴ భూజము = 10 సెం.మీ.

3. స్థూపము యొక్క ప్రక్కతల వైశాల్యము మారకుండా దానియొక్క వ్యాసార్ధమును రెట్టింపు చేస్తే దాని ఎత్తులో కలిగే మార్పు ఎంత ? (పేజీ నెం. 225)
సాధన.
మొదటి స్థూపపు వ్యాసార్ధము మరియు ఎత్తులు వరుసగా r మరియు h అనుకొనుము.
ప్రక్కతల వైశాల్యము = 2πrh
స్టూప వ్యాసార్థం రెట్టింపయిన, ప్రక్కతల వైశాల్యములో మార్పు లేకుండా ఉంటే దాని ఎత్తు h₁ అనుకొనుము.
కొత్త ప్రక్కతల వైశాల్యము = 2πrh
= 2π (2r) (h₁)
⇒ 2πrh = 4πrh₁
∴ h₁ = \(\frac {2πrh}{4πr}\) = \(\frac {1}{2}\)h
∴ ఎత్తు, అసలు ఎత్తులో సగము ఉండును.

4. వాటర్ హీటరు యొక్క స్థూపాకార పైపు యొక్క పొడవు 14 మీటర్లు మరియు వ్యాసము 5 సెం.మీ. అయితే నీటిని వేడిచేసే ఈ హీటరు యొక్క సంపూర్ణతల వైశాల్యమును కనుగొనుము. (పేజీ నెం.225)
సాధన.
వ్యాసార్ధము (r) = వ్యాసము / 2 = \(\frac {5}{2}\) = 2.5 సెం.మీ.
పైపు పొడవు = ఎత్తు = 14 మీ.
హీటరు సంపూర్ణతల వైశాల్యము = 2πr (r + h)
= 2 × \(\frac {22}{7}\) × 2.5 × (2.5 + 14)
= \(\frac {110}{7}\) × 16.5 = \(\frac {1815}{7}\)
= 259.29 సెం.మీ.³

5. ‘r’ వ్యాసార్ధము, ‘l’ చాపము పొడవు గల సెక్టరును వృత్తాకార కాగితం నుండి కత్తిరించి శంఖువుగా తయారుచేయుము. శంఖువు యొక్క ప్రక్కతల వైశాల్యం A = πrl ను ఏ విధంగా ఉత్పాదిస్తావో చెప్పుము. (పేజీ నెం. 228)

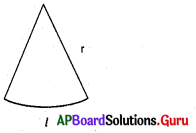
సాధన.
వ్యాసార్థం ‘r’ మరియు చాపము పొడవు ‘l’ గా గల సెక్టరును వృత్తాకార కాగితం నుండి కత్తిరించి శంఖువుగా మార్చగా వ్యాసార్థం ‘r’, ఏటవాలు ఎత్తు ‘l’ గా మరియు చాపం పొడవు ‘l’ భూ చుట్టుకొలత 2πr గా మారును.
సెక్టరు వైశాల్యము = \(\frac {lr}{2}\) = శంఖువు వైశాల్యం

= \(\frac {2πrl}{2}\) = శంఖువు ప్రక్కతల వైశాల్యము = πrl

6. గోళం ఉపరితల వైశాల్యాన్ని మీరు ఇంకేదైనా పద్ధతిలో కనుగొనగలరా ? (పేజీ నెం. 235)
సాధన.

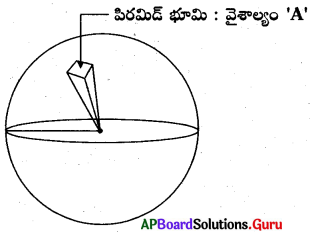
గోళం ఉపరితల వైశాల్యానికి సూత్రంను కనుగొనుటకు గోళమును సర్వసమాన పిరమిడ్ యొక్క భూములన్నీ గోళ ఉపరితలాన్ని ఆక్రమిస్తున్నాయని ఊహించిన ఆ పటంపైన చూపబడినట్లుగా ఏర్పడును.
పై పటంలో అటువంటి ఒక పిరమిడను చూపటము జరిగినది. పిరమిడ్ యొక్క వైశాల్యంకు, ఘనపరిమాణంకు గల నిష్పత్తిని తీసుకొనగా,
పిరమిడ్ వైశాల్యం A.
పిరమిడ్ ఘనపరిమాణం V = (1/3) × A × r = (A × r) / 3
∴ పిరమిడ్ యొక్క వైశాల్యం, ఘనపరిమాణాల నిష్పత్తి A/V= A + (A × r) / 3 = (3 × A) / (A × r) = 3 / r
ఆ గోళమును n సర్వసమాన పిరమిడ్లుగా విభజించిన భూమిని అనుకొనుము.
n పిరమిడ్ యొక్క మొత్తం వైశాల్యం = n × A.
అదే విధంగా , పిరమిడ్ యొక్క మొత్తం ఘనపరిమాణము = n × V.
∴ గోళము యొక్క n పిరమిడ్ల యొక్క వైశాల్యాల మొత్తంకు, ఘనపరిమాణాల మొత్తంకు గల నిష్పత్తి = n × A / n × V = A / V
మనకు ముందుగానే A / V = 3 / r అనుకున్నాము
కావున, n × A_{పిరమిడ్} = A_గోళం
n × V_{పిరమిడ్} = V_గోళం (అన్ని పిరమిడ్ల వైశాల్యాలు (లేక) ఘనపరిమాణాలు, వరుసగా గోళము యొక్క ఉపరితల వైశాల్యంకు లేక ఘనపరిమాణంకు సమానము)
పై పరిశీలనల నుండి,

∴ గోళం యొక్క సంపూర్ణ ఉపరితల వైశాల్యం 4πr² అగును.

ఇవి చేయండి

1. 4 సెం.మీ. భుజముగా గల ఘనము యొక్క ప్రక్కతల వైశాల్యమును, సంపూర్ణతల వైశాల్యమును కనుగొనుము. (పేజీ నెం. 216)

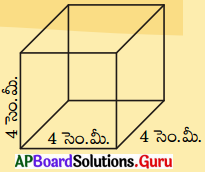
సాధన.
భుజము l = 4 సెం.మీ.
∴ ఘనము యొక్క ప్రక్కతల వైశాల్యము = 4l²
= 4 × 4² = 4³ = 64 సెం.మీ².
∴ ఘనము యొక్క సంపూర్ణతల వైశాల్యము
= 6l² = 6 × 4² = 6 × 16 = 96 సెం.మీ².

2. ఒక ఘనము యొక్క భుజమును 50% పెంచితే ఎంత శాతము దాని యొక్క సంపూర్ణతల వైశాల్యము పెరుగుతుంది ? (పేజీ నెం. 216)
సాధన.
ఘనపు భుజము = x యూనిట్లు అనుకొనుము.
ఘనము యొక్క సంపూర్ణతల వైశాల్యము = 6l²
= 6x²చ, యూ.
కొత్త భుజము = x + xలో 50% = x + \(\frac {50x}{100}\) = x + \(\frac{x}{2}=\frac{3 x}{2}\)
కొత్త సంపూర్ణతల వైశాల్యము = 6l²
= \(6\left(\frac{3 x}{2}\right)^{2}=6 \times \frac{9 x^{2}}{4}=\frac{27 x^{2}}{2}\)
వైశాల్యంలో పెరుగుదల = \(\frac{27 \mathrm{x}^{2}}{2}\) – 6x²
= \(\left(\frac{27-12}{2}\right) x^{2}=\frac{15}{2} x^{2}\)
∴ వైశాల్యంలో పెరుగుదల శాతము
= వైశాల్యంలో పెరుగుదల / అసలు వైశాల్యము × 100

ఇక్కడ x = పెరుగుదల / తగ్గుదల

3. ఒక దీర్ఘఘనం యొక్క పొడవు, వెడల్పు చురియు ఎత్తు విలువలు l = 12 సెం.మీ., b = 10 సెం.మీ. మరియు h= 8 సెం.మీ. అయిన ఆ దీర్ఘఘన ఘనపరిమాణాన్ని కనుగొనండి. (పేజీ నెం. 218)
సాధన.
దీర్ఘఘనపు పొడవు (l) = 12 సెం.మీ., వెడల్పు
(b) = 10 సెం.మీ. మరియు ఎత్తు (b) = 8 సెం.మీ.
ఘనపరిమాణం V = lbh = 12 × 10 × 8
= 960 ఘ. సెం.మీ.

4. భుజం 10 సెం.మీ.గా గల సమఘనము యొక్క ఘనపరిమాణము కనుగొనండి. (పేజీ నెం. 218)
సాధన.
ఘనపరిమాణము V = l³ = 10 × 10 × 10
= 1000 ఘ. సెం.మీ.

5. పటంలో చూపబడిన లంబకోణ సమద్విబాహం త్రిభుజాకార పట్టకము యొక్క ఘనపరిమాణము కనుక్కోండి. (పేజీ నెం. 218)

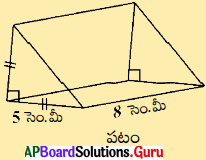
సాధన.
పట్టక ఘనపరిమాణము = పట్టక భూ వైశాల్యం × ఎత్తు
= \(\frac {1}{2}\) × 5 × 5 × 8
= 25 × 4
= 100 ఘ. సెం.మీ.

6. 10 సెం.మీ. భుజము కలిగిన చతురస్రాకార భూమి మరియు 8 సెం.మీ. ఎత్తు కలిగిన పిరమిడ్ యొక్క ఘనపరిమాణము కనుక్కోంది. (పేజీ నెం. 219)
సాధన.
పిరమిడ్ ఘనపరిమాణము
= \(\frac {1}{3}\) × భూ వైశాల్యం × ఎత్తు
= \(\frac {1}{3}\) × 10 × 10 × 8 = \(\frac {800}{3}\) సెం.మీ.³
= 266.67 సెం.మీ³.

7. సమఘనము యొక్క ఘనపరిమాణము 1200 ఘనపు సెంటీమీటర్లు. సమఘనపు ఎత్తుతో సమాన ఎత్తు కలిగిన చతురస్రాకార పిరమిడ్ యొక్క ఘనపరిమాణమును కనుగొనుము. (పేజీ నెం. 219)
సాధన.
చతుర రార పిరమిడ్ యొక్క ఘనపరిమాణం
= \(\frac {1}{3}\) × సమఘన ఘనపరిమాణము
= \(\frac {1}{3}\) × 1200 = 400 ఘ. సెం.మీ.

8. క్రింది పటములో చూపబడిన స్థూపము యొక్క ప్రక్కతల వైశాల్యంను కనుగొనండి. (పేజీ నెం. 221)

ప్రశ్న (i)
r = x సెం.మీ.; h = yసెం.మీ.
సాధన.
స్థూపపు ప్రక్కతల వైశాల్యం = 2πrh .
= 2πxy సెం.మీ.²

ప్రశ్న (ii)
d = 7 సెం.మీ.; h = 10 సెం.మీ.
సాధన.

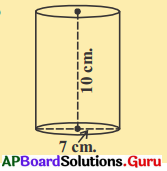
స్థూపపు ప్రక్కతల వైశాల్యం = 2πrh
= 2 × \(\frac {22}{7}\) × \(\frac {7}{2}\) × 10
= 220 సెం.మీ.²

ప్రశ్న (iii)
r = 3 సెం.మీ.; b = 14 సెం.మీ.
సాధన.

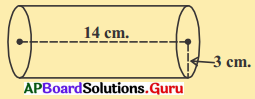
స్థూపపు ప్రక్కతల వైశాల్యం = 2πrh
= 2 × \(\frac {22}{7}\) × 3 × 14
= 264 సెం.మీ.²

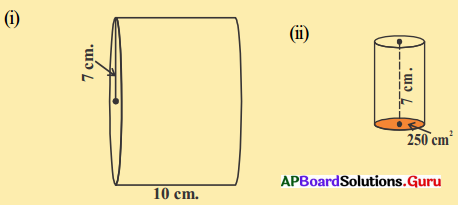
9. ఈ కింది స్థూపముల యొక్క సంపూర్ణతల వైశాల్యమును కనుగొనుము. (పేజీ నెం. 222)

సాధన.
(i) r = 7 సెం.మీ. ; h = 10 సెం.మీ.
స్థూపపు సంపూర్ణతల వైశాల్యము = 2πr (r + h)
= 2 × \(\frac {22}{7}\) × 7 (7 + 10)
= 2 × \(\frac {22}{7}\) × 7 × 17
= 748 చ.సెం.మీ.

(ii) స్థూపం భూ వైశాల్యం = 250 చ.సెం.మీ. .
h = 7 సెం.మీ. ; πr² = 250 సెం.మీ.
πr² = 250 ⇒ \(\frac {22}{7}\) × r² = 250
⇒ r² = 125 × \(\frac {7}{11}\)
∴ r = \(\sqrt{\frac{875}{11}}\)
r = 8.9 సెం.మీ.
స్థూపపు సంపూర్ణతల వైశాల్యము =
= 2 × \(\frac {22}{7}\) × 8.9 (8.9 + 7)
= \(\frac{44 \times 8.9 \times 15.9}{7}=\frac{6226.44}{7}\)
= 889.50 (సుమారుగా)

10. ఒక లంబకోణ త్రిభుజాన్ని తీసుకోంది/ కత్తిరించండి. పటంలో చూపినట్లు దానికి ఒక సన్నని వెదురుషుల్లను లంబాకార భుజమును అతికించండి. కర్రయొక్క రెండు వైపులను పట్టుకొని చుట్టూ తిప్పండి. తిప్పేవేగము స్థిరముగా ఉండాలి. మీరు ఏమి గమనించారు? (పేజీ నెం. 229)
సాధన.

ఒక క్రమ వృత్తాకార శంఖువు ఏర్పడుటను గమనించితిని.

11. ఈ కింది క్రమ వృత్తాకార శంఖువు యొక్క ప్రక్కతల వైశాల్యం, సంపూర్ణతల వైశాల్యములను కనుగొనుము. (పేజీ నెం. 229)
సాధన.

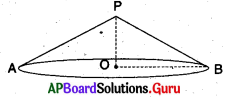
OP = 2 సెం.మీ.; OB = 3.5 సెం.మీ.
OP = h = 2 సెం.మీ.
r = OB = 3.5 సెం.మీ.
ప్రక్కతల వైశాల్యము = πrl
కాని l = \(\sqrt{\mathrm{r}^{2}+\mathrm{h}^{2}}\)
= \(\sqrt{2^{2}+3 \cdot 5^{2}}\)
= \(\sqrt{4+12.25}\)
= \(\sqrt{16.25}\) = 4.03
వక్రతల వైశాల్యము = \(\frac {22}{7}\) × 3.5 × 4.03
= 44.34 సెం.మీ².
సంపూర్ణతల వైశాల్యము = πr (r + l)
= \(\frac {22}{7}\) × 3.5(3.5 + 4.03)
= \(\frac {22}{7}\) × 3.5 × 7.53 = 82.83 సెం.మీ².

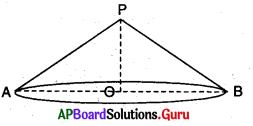
OP = 3.5 సెం.మీ.; AB = 10 సెం.మీ.
r = \(\frac {AB}{2}\) = 5 సెం.మీ. ; h = 3.5 సెం.మీ.
l = \(\sqrt{\mathrm{r}^{2}+\mathrm{h}^{2}}=\sqrt{5^{2}+3.5^{2}}=\sqrt{25+12.25}\)
వ.త,వై. = πrl = \(\frac {22}{7}\) × 5 × 6.10
= 95.90 సెం.మీ².
స.త.వై = πr (r + 1)
= \(\frac {22}{7}\) × 5 × (5 + 6.10)
= 174.42 సెం.మీ².

12. ఒక క్రమ వృత్త స్థూపాకార వస్తువులో r వ్యాసార్ధముగా గల గోళం అమర్చబడినది. అయితే
(i) గోళం యొక్క ఉపరితల వైశాల్యం
(ii) స్థూపము యొక్క వక్రతల వైశాల్యం
(iii) (i) మరియు (ii) వైశాల్యముల నిష్పత్తి కనుక్కోండి. (పేజీ నెం. 236)

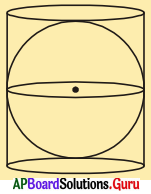
సాధన.
(i) గోళం వ్యాసార్ధం = స్థూపం వ్యాసార్ధము = r
∴ గోళం యొక్క ఉపరితల వైశాల్యం = 4πr²
(ii) స్థూపం యొక్క వక్రతల వైశాల్యం = 2πr (2r) [∵ h = 2r] = 4πr²
(iii) (i) మరియు (ii) వైశాల్యా ల నిష్పత్తి = 4πr² : 4πr² = 1 : 1

13. ఈ కింది పటముల యొక్క ఉపరితల వైశాల్యములను కనుగొనండి. (పేజీ నెం. 236)

(i)

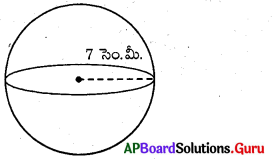
గోళం ఉపరితల వైశాల్యం = 4πr²
గోళం వ్యాసార్ధం = 7 సెం.మీ.
గోళం ఉపరితల వై = 4 × \(\frac {22}{7}\) × 7 × 7 = 616 సెం.మీ².

(ii)

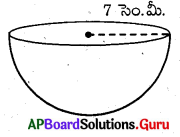
అడ్డగోళ ఉపరితల వైశాల్యము = 2πr² = 2 × \(\frac {22}{7}\) × 7 × 7
= 308 సెం.మీ²
స.త.వై = 3πr² = 3 × \(\frac {22}{7}\) × 7 × 7 = 462 సెం.మీ²

14. కింది పటంలో చూపబడిన గోళముల యొక్క ఘనపరిమాణములను కనుక్కోంది. (పేజీ నెం. 238)
సాధన.

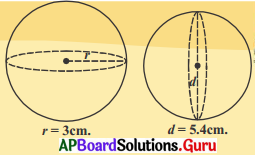
r = 3 సెం.మీ.
V = \(\frac {22}{7}\)πr³ = \(\frac {4}{3}\) × \(\frac {22}{7}\) × 3 × 3 × 3
= 113.14 సెం.మీ³.

d = 5.4 సెం.మీ.
r = \(\frac {d}{2}\) = \(\frac {5.4}{2}\) = 2.7 సెం.మీ.
V = \(\frac {4}{3}\)πr³ = \(\frac {4}{3}\) × \(\frac {22}{7}\) × 2.7 × 2.7 × 2.7 = 82.48 సెం.మీ³.

15. 6.3 సెం.మీ. వ్యాసార్థంగా గల గోళ ఘనపరిమాణమును కనుక్కోంది. (పేజీ నెం.238)
సాధన.
గోళ వ్యాసార్ధం r = 6.3 సెం.మీ.
గోళ ఘనపరిమాణము V= \(\frac {4}{3}\)πr³ = \(\frac {4}{3}\) × \(\frac {22}{7}\) × 6.3 × 6.3 × 6.3 = 1047.81 సెం.మీ³.

కృత్యం

1. భూమి, ఎత్తు సమానముగా గల ఘనము, చతురస్రాకార పిరమిడ్లను తీసుకొందాం. (పేజీ నెం. 218)

పిరమిడను ఒక ద్రవముతో నింపి ఆ ద్రవమును ఘనములో పూర్తిగా నింపండి. ఘనము నింపడానికి ఎన్నిసార్లు పిరమిడ్ నుపయోగించాలి ? పరిశీలిస్తే మూడుసార్లు అని తెలుస్తుంది.
దీనిని బట్టి, పిరమిడ్ యొక్క ఘనపరిమాణం
= \(\frac {1}{3}\) × క్రమ పట్టకం ఘనపరిమాణం (ఒకే భూమి, ఒకే ఎత్తు)
= \(\frac {1}{3}\) × భూవైశాల్యం × ఎత్తు
సూచన : ఒక క్రమ పట్టకము, భూమికి లంబంగా ఉండేలా పక్క తలాలను కల్గి ఉంటుంది. మరియు ఆ పక్క తలాలన్నీ దీర్ఘచతురస్రాలే.

2. ఒక దీర్ఘచతురస్రాకార పలుచని అట్ట లేక కాగితమును తీసుకోండి. ఒక పొడవాటి దళసరి తీగను తీసుకొని పటములో చూపిన విధంగా అతికింపుము. తీగయొక్క రెండు చివరలను పట్టుకొని దీర్ఘచతురస్రాకార అట్టను వేగముగా త్రిప్పండి.

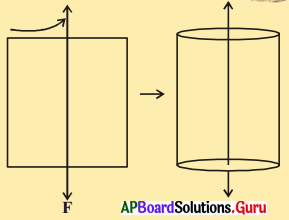
మీరు ఏమి గమనించారు ? కంటికి కనబడిన ఆకృతి ఎమిటి ? దానిని స్థూపముగా మీరు గుర్తించారా ? (పేజీ నెం. 220)

3. సెక్టరును శంఖువుగా మార్చే విధానం (పేజీ నెం. 227)
ఈ కింది సూచనలను పాటిస్తూ పటములో చూపిన విధముగా చేయండి.

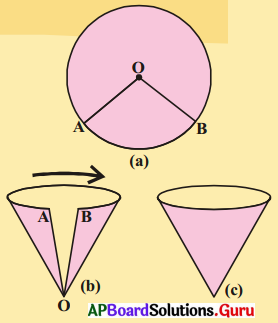
(i) పటం (a) చూపిన విధంగా ఒక దళసరి కాగితముపై వృత్తమును గీయండి.
(ii) పటం (b) లో చూపినట్లు సెక్టరు AOB ను కత్తిరించండి.
(iii) పటం (c)లో చూపినట్లు A మరియు B చివరలను
ఒకదానితో ఒకటి తాకేటట్లు నెమ్మదిగా పటములో చూపిన విధముగా కలుషము. A, Bలు ఆధ్యారోహణము కాకూడదు. A, B లును అతికింపుము.
(iv) మీరు పొందిన ఆకృతి యొక్క లక్షణములు ఏమిటి? అది క్రమ వృత్తాకార శంఖువు అవుతుందా ?
‘OA’ మరియు ‘OB’ లను కలిపి శంఖువు తయారుచేసేటప్పుడు OA, OB మరియు చాపము AB ల యొక్క పొడవులలో గమనించిన మార్పులు ఏమిటి?

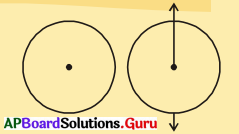
4. ఒక దళసరి కాగితంపై ఒక వృత్తమును గీయుము. దానిని కత్తిరింపుము. దాని వ్యాసము వెంబడి ఒక తీగను అతికింపుము. తీగ యొక్క రెండు చివరలు పట్టుకొని తిప్పుము. సమవేగముతో తిప్పితే మీరు ఏమి గమనించారు? (పేజీ నెం.235)

ఉదాహరణలు

1. 14 సెం.మీ. పొడవుగల దీర్ఘ చతురస్రాకార కాగితమునకు వెడల్పు వెంబడి రోల్ చేస్తే 20 సెం.మీ. వ్యాసార్థముగా గల స్థూపం ఏర్పడింది. అయిన స్థూపము (పటం 1) యొక్క ఘనపరిమాణము కనుక్కోండి. (π = \(\frac {22}{7}\) గా తీసుకొండి.) (పేజీ నెం. 222)
సాధన.
దీర్ఘచతురస్రాకార కాగితమును వెడల్పు వెంబడి రోల్ చేయగా ఏర్పడిన స్థూపము యొక్క ఎత్తు, కాగితపు వెడల్పునకు సమానమవుతుంది. అయితే

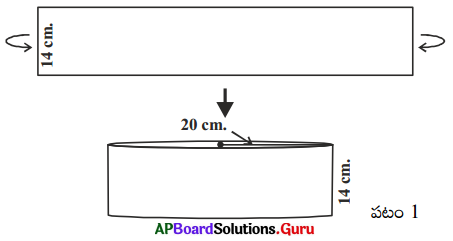
స్థూపము యొక్క ఎత్తు h = 14 సెం.మీ.
మరియు వ్యాసార్థం (r) = 20 సెం.మీ.
స్థూపము ఘనపరిమాణము V = πr²h
= \(\frac {22}{7}\) × 20 × 20 × 14 = 17600 ఘనపు సెంటీమీటర్లు
స్థూపపు ఘనపరిమాణము = 17600 ఘ, సెం.మీ.

2. ఒక దీర్ఘచతురస్రాకారపు కాగితము 11 సెం.మీ. × 4 సెం.మీ. కొలతలను కల్గియుంది. దానిని అంచులు ఆధ్యారోహణము చెందకుండా ఉండే విధముగా, 4 సెం.మీ. ఎత్తు కల్గిన స్థూపముగా మలిస్తే, స్థూపము యొక్క ఘనపరిమాణమును కనుక్కోండి. (పేజీ నెం. 223)
సాధన.
కాగితము యొక్క పొడవు, స్థూపము యొక్క భూపరిధికి సమానముగా, వెడల్పు ఎత్తునకు సమానముగా ఉంటుంది.

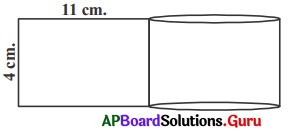
స్థూపపు వ్యాసార్ధము r = మరియు ఎత్తు = h స్టూపపు భూపరిధి = 2πr = 11 సెం.మీ.
2 × \(\frac {22}{7}\) × r = 11
r = \(\frac {7}{4}\)సెం.మీ.
h = 4 సెం.మీ.
స్టూపపు ఘనపరిమాణం (V) = 2π²h
= \(\frac {22}{7}\) × \(\frac {7}{4}\) × \(\frac {7}{4}\) × 4 = 38.5 ఘనపు సెంటీమీటర్లు.

3. దీర్ఘచతురస్రాకారములో దళసరి కాగితము 14 సెం.మీ. × 18 సెం.మీ. కొలతలు కల్గియుంది. దానిని పొడవు వెంబడి చుట్టూ స్థూపమును తయారుచేసాము. స్థూపమును ఘనముగా (పూర్తిగా నింపబడిన) భావిస్తే దాని యొక్క వ్యాసార్ధమును, సంపూర్ణతల వైశాల్యమును కనుగొనుము. (పేజీ నెం. 223)
సాధన.
స్టూపము యొక్క ఎత్తు = 18 సెం.మీ.
స్థూపము యొక్క భూపరిధి = 44 సెం.మీ.
2πr = 44 సెం.మీ.
r = \(\frac{44}{2 \times \pi}=\frac{44 \times 7}{2 \times 22}\) = 7 సెం.మీ.
సంపూర్ణతల వైశాల్యం = 2πr(r + h)
= 2 × \(\frac {22}{7}\) × 7(7 + 18)
= 1100 చ.సెం.మీ.

4. 5 మి.మీ. మందము కల్గిన వృత్తాకార ప్లేటులను ఒకదానిపై మరొకటి పేర్చి స్థూపముగా ఏర్పరిస్తే, దాని యొక్క పక్కతల వైశాల్యము 462 చ.సెం.మీ. స్థూపమును ఏర్పరిచేందుకు కావలసిన వృత్తాకార ప్లేటుల సంఖ్య ఎంత ? ప్లేటు యొక్క వ్యాసార్థమును 2. 3.5 సెం.మీ.గా తీసుకోండి. (పేజీ నెం. 224)
సాధన.
వృత్తాకార ప్లేటు యొక్క మందం = 5 మి.మీ.
= \(\frac {5}{10}\) సెం.మీ. = 0.5 సెం.మీ.
ప్లేటు యొక్క వ్యాసార్ధము = 3.5 సెం.మీ.
స్థూపము యొక్క పక్కతల వైశాల్యము = 462 చ. సెం.మీ.
∴ 2πrh = 462 ………… (i)
స్థూపము ఏర్పాటుకు అవసరమయ్యే ప్లేటుల సంఖ్య x అనుకొనుము.
∴ స్థూపము యొక్క ఎత్తు = h = ప్లేటు యొక్క మందం × ప్లేటుల సంఖ్య = 0.5x
∴ 2πrh = 2 × \(\frac {22}{7}\) × 3.5 × 0.5x ……. (ii)
(i) మరియు (ii) సమీకరణముల నుండి,
2 × \(\frac {22}{7}\) × 3.5 × 9.5x = 462
∴ x = \(\frac{462 \times 7}{2 \times 22 \times 3.5 \times 0.5}\) = 42 ప్లేట్లు.

5. ఒక గుల్ల లోహపు స్థూపము యొక్క బాహ్య వ్యాసార్ధము 8 సెం.మీ. మరియు ఎత్తు 10 సెం.మీ. మరియు సంపూర్ణతల వైశాల్యము . 338 π చ.సెం.మీ. గుల్ల లోహపు స్థూపము యొక్క మందమును కనుక్కోండి. (పేజీ నెం. 224)
సాధన.

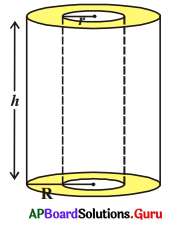
బాహ్య వ్యాసార్ధము = R = 8 సెం.మీ.
అంతర వ్యాసార్ధము = r
ఎత్తు = 10 సెం.మీ.
సంపూర్ణతల వైశాల్యము = 338 π చ.సెం.మీ.
కాని సంపూర్ణతల వైశాల్యము = బయటి స్థూపము యొక్క పక్కతల వైశాల్యం (CSA) + లోపల యున్న స్థూపము యొక్క ప్రక్కతల వైశాల్యం (CSA) + 2 × భూ వైశాల్యము (కంకణము)
= 2πRh + 2πrh + 2π(R² – r²)
= 2π(Rh + rh + R² – r²)
∴ 2π(Rh + rh + R² – r²) = 338π
Rh + rh + R² – r² = 169
⇒ (10 × 8) + (r × 10) + 8² – r² = 100
⇒ r² – 10r + 25 = 0
⇒ (r – 5)² = 0
∴ r = 5
∴ లోహపు స్థూపము యొక్క మందం = R – r = (8 – 5) సెం.మీ. = 3 సెం.మీ.

6. ఒక మొక్కజొన్న కంకి శంఖువు ఆకారములో ఉంది. వెదల్పు ఎక్కువగాయున్న ప్రాంతపు వ్యాసార్థము 1.4 సెం.మీ. మరియు ఎత్తు (పొడవు) 12 సెం.మీ. ప్రతి చ. సెం.మీ. ప్రాంతములో సుమారుగా 4 జొన్న గింజలుంటే మొత్తము ఎన్ని గింజలుంటాయి? (పేజీ నెం.230)
సాధన.

ఇక్కడ l = \(\sqrt{r^{2}+h^{2}}\)
= \(\sqrt{(1.4)^{2}+(12)^{2}}\) సెం.మీ.
= \(\sqrt{145.96}\) = 12.08 సెం.మీ. (సుమారుగా)
మొక్కజొన్న కంకి వక్రతల వైశాల్యం = πrl
= \(\frac {22}{7}\) × 1.4 × 12.08 చ.సెం.మీ.
= 53.15 చ.సెం.మీ.
= 53.2 చ. సెం.మీ. (సుమారుగా)
మొక్కజొన్న కంకిలో 1 చ.సెం.మీ. వైశాల్యములో గల జొన్న గింజల సంఖ్య = 4
∴ మొక్క జొన్న కంకి ప్రక్కతల వైశాల్యములో గల మొత్తము జొన్న గింజల సంఖ్య = 53.2 × 4 = 212.8 = 213 (సుమారుగా),
అందుచే మొక్కజొన్న కంకి సుమారుగా 213 గింజలుంటాయి.

7. 5.6 సెం.మీ. భూవ్యాసార్ధము మరియు 158,4 చ.సెం.మీ. ప్రక్కతల వైశాల్యము గల శంఖువు యొక్క ఏటవాలు ఎత్తు మరియు శంఖువు ఎత్తులను కనుగొనుము. (పేజీ నెం. 231)
సాధన.
భూ వ్యాసార్ధము = 5.6 సెం.మీ.
ఎత్తు = h, ఏటవాలు ఎత్తు = l
వక్రతల వైశాల్యము = πrl = 158.4 చ.సెం.మీ.
⇒ \(\frac {22}{7}\) × 5.6 × l = 158.4
⇒ l = \(\frac{158.4 \times 7}{22 \times 5.6}=\frac{18}{2}\) = 9 సెం.మీ.
l² = r² + h² అని మనకు తెలుసు
h² = l² – r²= 9² – (5.6)²
= 81 – 31.36 = 49.64
h = \(\sqrt{49.64}\)
h = 7.05 సెం.మీ. (సుమారుగా)

8. ఒక గుడారం స్థూపముపై శంఖువు వలె ఉంది. శంఖువు యొక్క వ్యాసము స్థూపము భూవ్యాసము 24 మీటర్లకు సమానముగా యుంది. స్థూపము యొక్క ఎత్తు 11 మీ. మరియు శంఖువు యొక్క ఎత్తు 5 మీటర్లు, గుడారము తయారుచేయడానికి కావలసిన గుడ్డ చదరపు మీటరుకు ₹10 చొప్పున మొత్తము ఎంత ఖర్చవుతుంది ? (పేజీ నెం.231)
సాధన.
స్థూపపు భూవ్యాసము = శంఖువు వ్యాసం = 24 మీ.
∴ భూవ్యాసార్ధము = 12 మీ.
స్థూపము య్కొ ఎత్తు = 11 మీ. = h₁
శంఖము యొక్క ఎత్తు = 5 మీ. = h₂
శంఖము యొక్క ఏటవాటు ఎత్తు ‘l’ అనుకొందాం.
l = GD = \(\sqrt{r^{2}+h^{2}}=\sqrt{12^{2}+5^{2}}\) = 13 మీ.

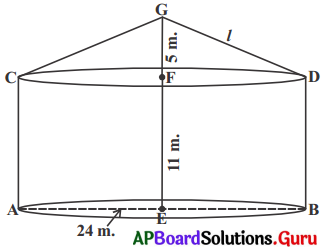
కావలసిన గుడ్డ వైశాల్యము = స్థూపము యొక్క ప్రక్కతల వైశాల్యం + శంఖువు ప్రక్కతల వైశాల్యం
= 2πrh₁ + πrl
= πr (2h₁ + l)
= \(\frac {22}{7}\) × 12(2 × 11 + 13) చ.మీ.
= \(\frac{22 \times 12}{7}\) × 35 చ.మీ. = 22 × 60 చ.మీ. = 1320 చ.మీ.
గుడ్డ యొక్క వెల = ₹ 10 చదరపు మీటరుకు
∴ గుడ్డ యొక్క మొత్తం ఖరీదు = వెల × గుడ్డ యొక్క వైశాల్యం
= ₹10 × 1320 = ₹13,200

9. సైన్యము తన బేనొక్యాంప్ కొరకు శంఖువు ఆకారములో ఎత్తు 3 మీ. మరియు భూవ్యాసము 8 మీ.గా యున్న గుదారమును ఏర్పాటుచేసిన
(i) గుదారం తయారుచేయడానికి కావలసిన బట్ట యొక్క వెల చ.మీ.నకు ₹70 అయిన మొత్తము ఖర్చు ఎంత?
(ii) ప్రతి వ్యక్తికి 3.5 ఘనపు మీటర్ల గాలి కావలసి యుంటే గుడారములో కూర్చోగల వ్యక్తుల సంఖ్య ఎంత ? (పేజీ నెం. 232)
సాధన.

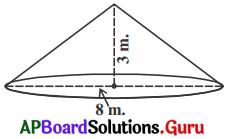
గుడారం యొక్క వ్యాసం = 8 మీ.
r = \(\frac{d}{2}=\frac{8}{2}\) = 4మీ.
ఎత్తు = 3 మీ.
ఏటవాలు ఎత్తు (l) = \(\sqrt{\mathrm{h}^{2}+\mathrm{r}^{2}}\)
= \(\sqrt{\mathrm{3}^{2}+\mathrm{4}^{2}}\) = \(\sqrt{25}\) = 5 మీ.
∴ గుడారం యొక్క ప్రక్కతల వైశాల్యం = πrl
= \(\frac {22}{7}\) × 4 × 5 = \(\frac {440}{7}\) చ.మీ.
శంఖువు ఘనపరిమాణం = \(\frac {1}{3}\)πr²h
= \(\frac {1}{3}\) × \(\frac {22}{7}\) × 4 × 4 × 3
= \(\frac {352}{7}\) ఘనపు మీటర్లు
(i) గుదారం తయారీకి కావలసిన గుడ్డ ఖరీదు
= ప్రక్కతల వైశాల్యం × యూనిట్ల
= \(\frac {440}{7}\) × 70 = ₹4400

(ii) గుడారంలో కూర్చోగల వ్యక్తుల సంఖ్య = శంఖాకార గుడారం ఘనపరిమాణం / ప్రతి వ్యక్తికి కావల్సిన గాలి ఘనపరిమాణం
= \(\frac{352}{7} \div 3.5=\frac{352}{7} \times \frac{1}{3.5}\) – 14.36
= 14 మంది వ్యక్తులు (సుమారుగా)

10. గోళం ఉపరితల వైశాల్యం = 154 చ.సెం.మీ. అయిన దాని వ్యాసార్ధమును కనుగొనుము. (పేజీ నెం. 238)
సాధన.
గోళం ఉపరితల వైశాల్యం = 4πr²
4πr² = 154 ⇒ 4 × \(\frac {22}{7}\) × r² = 154
⇒ r² = \(\frac{154 \times 7}{4 \times 22}=\frac{7^{2}}{2^{2}}\)
⇒ r = \(\frac {7}{2}\) = 3.5 సెం.మీ.

11. ఒక అర్ధగోళాకారపు గిన్నె రాతితో తయారుచేయబడి 5 సెం.మీ. మందం కల్గియుంది. దాని లోపలి వ్యాసార్థం 35 సెం.మీ. అయిన గిన్నె యొక్క సంపూర్ణతల వైశాల్యంను కనుగొనుము. (పేజీ నెం. 239)
సాధన.
వెలుపలి వ్యాసార్ధం R, లోపలి వ్యాసార్థం ‘r’.
మందం 5 సెం.మీ. అనుకొందాం.
∴ R = (r + 5) సెం.మీ. = (35 + 5) సెం.మీ.
= 40 సెం.మీ.

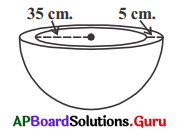
సంపూర్ణతల వైశాల్యం = బయటి ఉపరితల వైశాల్యం + లోపలి ఉపరితల వైశాల్యం + కంకణ వైశాల్యం
= 2πR² + 2πr² + π(R² – r²)
= π(2R² + 2r² + R² – r²)
= \(\frac {22}{7}\)(3R² + r²) = \(\frac {22}{7}\) (3 × 40² + 35²) చ.సెం.మీ.
= \(\frac{6025 \times 22}{7}\) చ.సెం.మీ.
= 18935.71 చ.సెం.మీ. (సుమారుగా)

12. అర్ధగోళాకారపు పై కప్పు కల్గిన ఒక భవనం (పటములో చూపిన విధంగా) నకు రంగు వేయాలి. పై కప్పు యొక్క భూపరిధి 17.6 మీ. ఆయిన 10 చ.సెం.మీ. వకు రంగు వేయుటకు 5 రూపాయలు చొప్పున భవనంనకు రంగువేయడానికి ఎంత ఖర్చు అవుతుంది? (పేజీ నెం. 299)
సాధన.

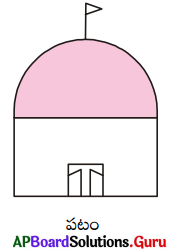
భవనంలోని వృత్తాకార ఉపరితల వైశాల్యంనకు మాత్రమే రంగు వేయాలి కనుక అర్ధగోళం యొక్క ప్రక్కతల వైశాల్యం కనుగొనాలి. పైకప్పు యొక్క భూపరిధి = 17.6 మీ.
∴ 17.6 = 2πr
అందుచే పై కప్పు యొక్క వ్యాసార్ధం = 17.6 × \(\frac{7}{2 \times 22}\) మీ. = 2.8 మీ.
పై కప్పు యొక్క ప్రక్కతల వైశాల్యం = 2πr²
= 2 × \(\frac {22}{7}\) × 2.8 × 28 చ.మీ.
= 49.28 చ.మీ.
100 చ.సెం.మీ. ప్రాంతమునకు రంగువేయడానికి అయ్యేఖర్చు = ₹ 5
∴ 1 చ.మీ. ప్రాంతమునకు రంగు వేయడానికి అయ్యే ఖర్చు = ₹500
∴ రంగు వేయడానికి అయ్యే మొత్తం ఖర్చు = 500 × 49.28 = ₹24640

13. ఒక సర్కస్ లో మోటార్ సైకిలిస్టు ఒక గుల్ల గోళాకార ఆకృతిలో విన్యాసములు చేయుచున్నాడు. గుల్ల గోళము యొక్క వ్యాసం 7 మీ, సైకిలిస్టు విన్యాసంలో తిరిగేందుకు అవకాశము ఉండే ప్రాంత వైశాల్యము ఎంత ? (పేజీ నెం. 240)
సాధన.
గోళం వ్యాసం = 7 మీ., వ్యాసార్ధం = 3.5 మీ.
అందుచే విన్యాసకుడు తిరగగలిగే ప్రాంత వైశాల్యం గోళం యొక్క ఉపరితల వైశాల్యంనకు సమానం.
4πr² = 4 × \(\frac {22}{7}\) × 3.5 × 3.5 చ.మీ. = 154 చ.మీ.

14. షాటి ఫుటనకు ఉపయోగించే లోహపు గోళం యొక్క వ్యాసార్థం 4.9 సెం.మీ. లోహం యొక్క సాంద్రత 7.8 గ్రా. ఘనపు సెం.మీ. అయిన షాట్‌పుట్ యొక్క ద్రవ్యరాశి కనుగొనుము. (పేజీ నెం. 240)
సాధన.
షాట్ పుట్ లోహపు గోళము కనుక దాని ద్రవ్యరాశి గోళము యొక్క ఘనపరిమాణం మరియు సాంద్రతల లబ్ధమునకు సమానము. అందుచే మనము గోళము యొక్క ఘనపరిమాణమును కనుగొనాలి.
ఇప్పుడు గోళం ఘనపరిమాణం = \(\frac {4}{3}\)πr³
= \(\frac {4}{3}\) × \(\frac {22}{7}\) × 4.9 × 4.9 × 4.9 ఘ. సెం.మీ.
= 493 ఘ. సెం.మీ. (సమారుగా)
1 ఘనపు సెంటీ మీటరు లోహం యొక్క ద్రవ్యరాశి = 7.8 గ్రా.
అందుచే షాట్‌పుట్ యొక్క ద్రవ్యరాశి = 7.8 × 493 గ్రాములు = 3845.44 గ్రా. = 3.85 కి.గ్రా. (సుమారుగా)

15. ఒక అర్ధగోళాకారపు గిన్నె యొక్క వ్యాసార్ధం 3.5 సెం.మీ. దానిలో నింపగలిగే నీటి ఘనపరిమాణం ఎంత? (పేజీ నెం. 240)
సాధన.
గిన్నెలోని నీటి ఘనపరిమాణం = అర్ధగోళం ఘనపరిమాణం
= \(\frac {4}{3}\) × \(\frac {22}{7}\) × 3.5 × 3.5 × 3.5 ఘు. సెం.మీ.
= 89.8 ఘన సెం.మీ. (సమారుగా)