AP Board 9th Class Maths Solutions Chapter 11 వైశాల్యాలు InText Questions

AP SCERT 9th Class Maths Textbook Solutions Chapter 11 వైశాల్యాలు InText Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 11th Lesson వైశాల్యాలు InText Questions

ఆలోచించి, చర్చించి రాయండి

1. 1 సెం.మీ. ప్రమాణము 5 మీ. లను సూచిస్తే, 6 చదరపు సెం.మీ. వైశాల్యము దేనిని సూచిస్తుంది ? (పేజీ నెం. 247)
సాధన.
1 సెం.మీ. = 5 మీ.
1 సెం.మీ.² = 1 సెం.మీ. × 1 సెం.మీ. = 5 మీ. × 5 మీ. = 25 చ.మీ.
∴ 6 చ.సెం.మీ. = 6 × 25 చ.మీ. = 150 చ.మీ.

2. 1 చ.మీ. = 100² చ.సెం.మీ. అని రజని అన్నది. నీవు ఏకీభవిస్తావా ? వివరించుము. (పేజీ నెం. 247)
సాధన.
1 చ.మీ. = 100 చ.సెం.మీ. కావున రజనీతో నేను ఏకీభవిస్తాను.

2. కింది పటాలలో ఏవి ఒకే భూమి, ఒకే సమాంతర రేఖల మధ్య ఉన్నాయి ? ఇటువంటి సందర్భములో భూమి (ఉమ్మడి భుజం) ని, రెండు సమాంతర రేఖలను తెలపండి. (పేజీ నెం. 249)

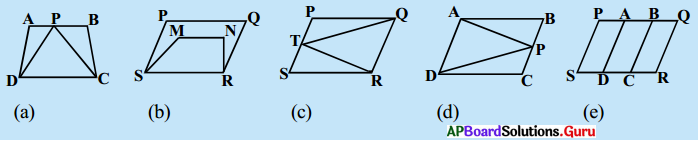
సాధన.
(a) పటం (a) లో ∆PCD మరియు ☐ABCD లు ఒకే భూమి CD మరియు ఒకే సమాంతర రేఖలు AB మరియు , CD ల మధ్యన కలవు.
(b) పటం (b) లో ☐PQRS మరియు ☐MNSRలు ఒకే భూమి SR పై గలవు. కాని ఒకే సమాంతర రేఖల మధ్యన లేవు.
(c) పటం (c) లో ∆TRQ మరియు ☐PQRS లు ఒకే భూమి QR పై మరియు ఒకే జత సమాంతర రేఖలు PS మరియు QRల మధ్యన గలవు.
(d) పటం (d) లో ∆APD మరియు ☐ABCD లు ఒకే భూమి AD మరియు ఒకే జత సమాంతర రేఖలు AD మరియు BC ల మధ్యన గలవు.
(e) పటం (e) లో ఇచ్చిన నియమము పాటించబడ లేదు.

3. రెందు త్రిభుజాలు ABC మరియు DBCలను ఒకే భూమి మరియు ఒకే సమాంతర రేఖల మధ్య ఉండునట్లు (పటంలో చూపిన విధంగా) గీయండి. AC మరియు BDU ఖండన బిందువుకు P లని పేరు పెట్టండి. CE || BA మరియు BF || CD లను AD రేఖపై E మరియు F లు ఉన్నట్లు గీయండి. (∆PAB) వైశాల్యము = (∆PDC) వైశాల్యములని మీరు చూపగలరా ?

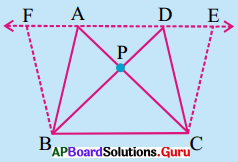
సూచన: (ఈ రెండు త్రిభుజాలు సర్వసమానాలు కానప్పటికీ సమాన వైశాల్యములు కలిగి ఉన్నాయి.) (పేజీ నెం. 254)
సాధన.
☐ABCE వైశాల్యము = 2 × ∆ABC [∵ ∆ABC మరియు ☐ABCE లు ఒకే భూమి BC పై మరియు ఒకే జత సమాంతర రేఖలు BC మరియు AE ల మధ్యన గలవు]
⇒ ∆ABC = \(\frac {1}{2}\)☐ABCE ……. (1)
అదే విధముగా ☐BCDF = 2 × ∆BCD (∵ ∆BCD మరియు ☐BCDE లు ఒకే భూమి BC మరియు ఒకే జత సమాంతర రేఖలు BC మరియు DEల మధ్యన గలవు.)
∴ ∆BCD = \(\frac {1}{2}\)☐BCDF ……….. (2)
కాని ☐ABCE = ☐BCDF [∵ ☐ABCE మరియు ☐BCDF లు ఒకే భూమి BC మరియు ఒకే జత సమాంతర రేఖలు BC మరియు FE లపై కలవు]
(1) మరియు (2) ల నుండి , ∆ABC = ∆BCD
∆PAB + ∆PBC = ∆PBC + ∆PDC
⇒ ∆PAB = ∆PDC నిరూపించబడినది.

4. లంబకోణ త్రిభుజము ABCE A లంబకోణం. BC, CA మరియు AB లపై వరుసగా BCED, ACFG మరియు ABMN అనే చతురస్రాలు గీయబడ్డాయి. రేఖాఖందం AX ⊥ DE, BCని Y వద్ద, DE ని X వద్ద ఖండించింది. AD, AE లు కలుపబడ్డాయి. అదే విధంగా BF, CM లు కలుపబడ్డాయి. (పటంలో చూడండి). అయితే కింద వానిని నిరూపించండి. (పేజీ నెం. 258)

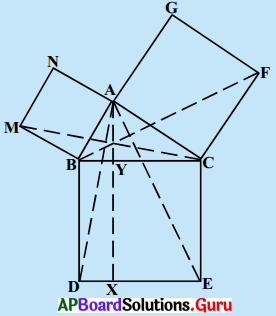
ప్రశ్న (i)
∆MBC ≅ ∆ABD
సాధన.
∆MBC మరియు ∆ABD లలో
MB = AB [∵ చతురస్ర భుజములు)
BC = BC [∵ ఉమ్మడి భుజము]
\(\angle \mathrm{MBC}=\angle \mathrm{ABD}\) [∵ \(\angle \mathrm{MBC}=\angle \mathrm{ABD}\) = 90° + \(\angle \mathrm{ABC}\)]
∴ ∆MBC ≅ ∆ABD (భు.కో.భు. నియమం ప్రకారం)

ప్రశ్న (ii)
(BYXD) వై॥ = 2 (∆MBC) వై॥
సాధన.
☐BYXD మరియు ∆ABD లు ఒకే భూమి BD మరియు రెండు సమాంతర రేఖలు BD, AX ల మధ్య కలవు కావున.
∴ ☐BYXD = 2 ∆ABD = 2 ∆MBC [∵ (i) నుండి]
∴ (BYXD)వై॥ = 2 (∆MBC)వై॥

ప్రశ్న (iii)
(BYXD) వై॥ = (ABMN) వై॥
సాధన.
(ABMN) వై॥ = 2 × (∆MBC) వై॥ [∵ ☐ABMN, ∆MBC లు ఒకే భూమి MB మరియు సమాంతర రేఖలు MB, NC ల మధ్య కలవు]
∴ ☐ABMN = ☐BYXD [(ii) నుండి]

ప్రశ్న (iv)
∆FCB = ∆ACE
సాధన.
∆FCB మరియు ∆ACE లలో
CB = CE (∵ ఒకే చతురస్రపు భుజాలు)
FC = AC (∵ ఒకే చతురస్రపు భుజాలు)
\(\angle \mathrm{FCE}=\angle \mathrm{ACE}\) (∵ \(\angle \mathrm{FCE}=\angle \mathrm{ACE}\) = 90° + \(\angle \mathrm{ACB}\))
∴ ∆FCB ≅ ∆ACE (భు. కో.భు. నియమం)

ప్రశ్న (v)
(CYXE) వై॥ = 2 (FCB) వై॥
సాధన.
☐CYXE మరియు ∆ACE లు ఒకే భూమి CE మరియు రెండు సమాంతర రేఖలు CE మరియు XYల మధ్యన గలవు.
∴ ☐CYXE = 2 × ∆ACE = 2 × ∆FCB [(iv) నుండి]

ప్రశ్న (vi)
(CYXE) వై॥ = (ACFG) వై॥
సాధన.
☐CYXE = 2 × ∆FCB [(v) నుండి]
= ☐ACFG [∵ ☐ACFG మరియు ∆FCB లు ఒకే భూమి CF మరియు ఒకే జత సమాంతర రేఖలు CF మరియు AGల మధ్యన కలవు.]

ప్రశ్న (vii)
(BCED) వై॥ = (ABMN) వై|| + (ACFG) వై॥
సాధన.
☐BCED = ☐BYXD + ☐CYXE (పటం నుండి)
= ☐ABMN + ☐ACFG [∵ ☐BYXD = ☐ABMN (iii) నుండి ☐CYXE = ☐ACFG (vi) నుండి] నిరూపించబడినది. ఫలితం (vii) ను మాటలలో రాయండి.
సాధన.
“ఒక లంబకోణ త్రిభుజంలో కర్ణము మీది వర్గము, మిగిలిన రెండు భుజాల మీది వర్గాల మొత్తమునకు సమానము” దీనినే పైథాగరస్ సిద్ధాంతము అంటారు.

కృత్యం

1.


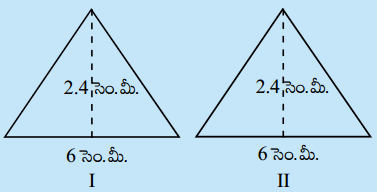
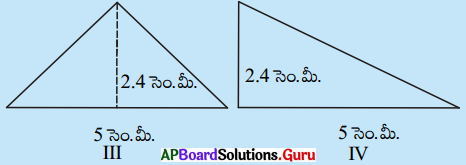
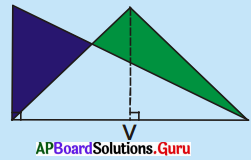
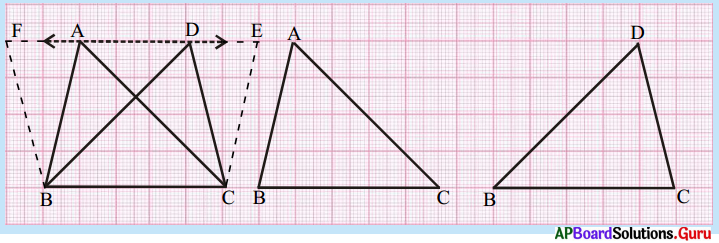
ఒక ఉల్లిపొర కాగితం (ట్రేసింగ్ పేపర్) పై రెండు జతల త్రిభుజాలను పటంలో చూపినట్లు గీయండి. త్రిభుజాలు I, II లను ఒకదానిపై ఒకటి పూర్తిగా ఏకీభవించునట్లు ఉంచండి. త్రిభుజాలు III మరియు IV లు ఒకే భూమి, ఒకే ఎత్తును కలిగిన ఒక సమద్విబాహు త్రిభుజము మరియు ఒక లంబకోణ త్రిభుజము. III మరియు IV పటాలు ఒకదానితో మరొకటి పూర్తిగా ఏకీభవించలేదు. I, II పటాలు ఒకదానితో మరొకటి పూర్తిగా ఏకీభవించినారు. కావున ఇవి సర్వసమాన పటాలు మరియు వీటి వైశాల్యాలు సమానము. ఎందుకనగా అవి ఆక్రమించిన ప్రదేశం సమానము. III, IV పటాలు ఒకదానితో మరొకటి ఏకీభవించలేదు. కనుక అవి సర్వసమాన పటాలుకావు.

వీటి వైశాల్యాలు సమానమేనా ?
పటం (V) ను పరిశీలిస్తే ఈ పటాలు సర్వసమానం కానప్పటికీ, ఇవి సమాన వైశాల్యం కలిగి ఉన్నాయి. (ఈ పటాలను కాగితాలతో కత్తిరించి మరియు త్రిభుజ వైశాల్య సూత్రం ద్వారా కనుగొని చూడండి) అందుచే III మరియు IV పటాలు సర్వసమాన పటాలుకానప్పటికీ, సమాన వైశాల్యాలు గల పటాలు అయినవి. (పేజీ నెం. 245)

2. ఒక గ్రాఫ్ కాగితముపై రెండు సమాంతర చతుర్భుజాలు ABCD మరియు PQCD లను పటంలో చూపిన విధంగా గీయాలి.

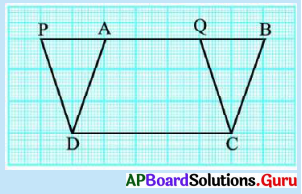
ఈ రెండు సమాంతర చతుర్భుజాలు ఒకే భూమి DC పైన మరియు ఒకే సమాంతర రేఖలు PB మరియు DCల మధ్య ఉన్నాయి. దీనిలో DCQA పట భాగము రెండు సమాంతర చతుర్భుజాలలో ఉమ్మడి భాగమని స్పష్టమౌతున్నది. కావున మనము ∆DAP మరియు ∆CBQలు ఒకే వైశాల్యం కలిగి ఉంటాయని చెప్పగలిగితే అప్పుడు (PQCD) వైశాల్యము = (ABCD) వైశాల్యము అవుతుంది. (పేజీ నెం. 250)

3. పటంలో చూపిన విధంగా ఒక జత త్రిభుజాలను ఒకే భూమి లేదా సమాన భూములు, ఒకే సమాంతర రేఖల మధ్య గ్రాఫ్ కాగితంపై గీయండి.
∆ABC మరియు ∆DBC లు అనేవి రెండు త్రిభుజాలు ఒకే భూమి BC పైన, ఒకే సమాంతర రేఖలు BC, AD ల మధ్య ఉన్నాయి.
ADని ఇరువైపులా పొడిగించుము మరియు CE || AB, BF || CDలను గీయండి. ఇప్పుడు సమాంతర చతుర్భుజాలు AECB మరియు FDCB లు ఒకే భూమి BC మరియు ఒకే సమాంతర రేఖలు BC మరియు EF ల మధ్య ఉన్నాయి. కావున (AECB) వై॥ = (FDCB) వై॥ (ఎలా ?)

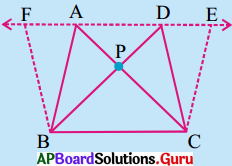
దీని నుండి మనకు (∆ABC) వై॥ = \(\frac {1}{2}\) (సమాంతర చతుర్భుజం AFCB) వై॥ …………… (i)
మరియు (∆DBC) వై॥ = \(\frac {1}{2}\) (సమాంతర చతుర్భుజం FDCB) వై॥ అగును …….. (ii)
(i), (ii) నుండి, దీని నుండి (∆ABC) వై॥ = (∆DBC) వై॥ అని చెప్పవచ్చు.
మనం ∆ABC మరియు ∆DBCల వైశాల్యాలను ముందు కృత్యములో చెప్పినట్లుగా చదరాలను లెక్కించు పద్ధతి ద్వారా గణించి వైశాల్యములు ఎలా సమానం అవుతాయో సరిచూడవచ్చు. (పేజీ నెం. 254)

సిద్ధాంతాలు

1. ఒకే భూమి మరియు ఒకే సమాంతర రేఖల మధ్యగల సమాంతర చతుర్భుణాల వైశాల్యాలు సమానము. (పేజీ నెం. 250)
సాధన.
ఉపపత్తి : ABCD మరియు PQCD అనే రెండు సమాంతర చతుర్భుజాలు ఒకే భూమి DC మరియు రెండు సమాంతర రేఖలు DC మరియు PB ల మధ్య ఉన్నాయనుకుందాం. ∆DAP మరియు ∆CBQలలో

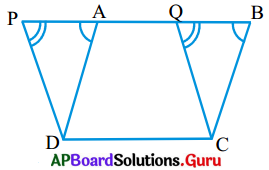
PD || CQ మరియు PB తిర్యగ్రేఖ వలన \(\angle \mathrm{DPA}=\angle \mathrm{CQB}\) మరియు AD || CB మరియు PB తిర్యగ్రేఖవలన \(\angle \mathrm{DAP}=\angle \mathrm{CBQ}\) ఇలాగే PQCD సమాంతర చతుర్భుజమైనందున PD = QC అగును. ఇందుచే ∆DAP, ∆CBQ లు రెండు సర్వసమాన త్రిభుజాలు మరియు వాటి వైశాల్యాలు సమానము.
కావున (PQCD) వై॥ = (AQCD) వై॥ + (DAP)వై॥ = (AQCD)వై॥ + (CBQ)వై॥ = (ABCD)వై॥ అగును.
గ్రాఫ్ కాగితములపై గీచిన సమాంతర చతుర్భుజాలలో చదరాల సంఖ్యను లెక్కించి ఫలితాన్ని సరిచూడవచ్చును.

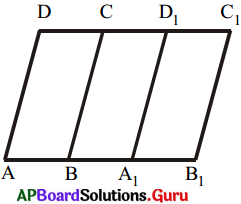
రెండు సమాంతర చతుర్భుజాల వైశాల్యాలు సమానంగా ఉండడానికి అవి ఒకే సమాంతర రేఖల మధ్య ఉన్ననూ, ఒకే భూమిపై ఉండనవసరం లేదని రేష్మా వాదించింది. దానికి సమాన భూమి ఉంటే సరిపోతుందని అన్నది. ఆమె వాదన అవగాహన కొరకు పైపటము పరిశీలిద్దాము.
AB = A₁B₁ అయిన A₁B₁C₁D₁ సమాంతర చతుర్భుజాన్ని ABCD సమాంతర చతుర్భుజముపై ఏకీభవించునట్లు ఉంచితే A శీర్షం A₁ పైన B శీర్షం B₁ పైన వచ్చాయి. అదే విధంగా \(\overline{\mathrm{C}_{1} \mathrm{D}_{1}}\),CD పై ఏకీభవించింది. కావున వీటి వైశాల్యాలు సమానమైనాయి.

2. రెండు త్రిభుజాలు ఒకే భూమి (లేదా సమాన భూములు) మరియు ఒకే వైశాల్యాలు కలిగి ఉంటే అవి ఒకే సమాంతర రేఖల మధ్య ఉంటాయి. (పేజీ నెం. 255)

పటం పరిశీలించండి. BC భుజం పైన గల త్రిభుజాలు ఏవి ? ∆ABC, ∆DBC త్రిభుజాల ఎత్తులు ఏవి ?
ఒకే భూమిని కలిగి, వైశాల్యాలు సమానం అయితే, వాటి ఎత్తులు ఎలా ఉంటాయి ? A, Dలు సరేఖీయాలేనా ?

ఉదాహరణలు

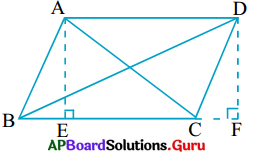
1. ABCD ఒక సమాంతర చతుర్భుజము ABEF ఒక దీర్ఘచతురస్రము DG, AB పైకి గీచిన లంబము అయిన
(i) (ABCD) వై॥ = (ABEF) వై॥
(ii) (ABCD) వై॥ = AB × DG అని చూపండి. (పేజీ నెం. 251)
సాధన.

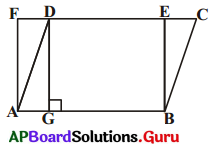
(i) దీర్ఘచతురస్రము కూడా ఒక సమాంతర చతుర్భుజమే.
∴ (ABCD) వై॥ = (ABEF) వై॥ ………. (1) (ఒకే భూమి, ఒకే సమాంతర రేఖల మధ్య ఉండే రెండు సమాంతర చతుర్భుజాలు)

(ii) (ABCD) వై॥ = (ABEF) వై॥ (∴ (1) నుండి)
= AB × BE (∵ ABEF దీర్ఘచతురస్రం కావున)
= AB × DG
(∵ DG ⊥ AB మరియు DG = BE)
అందుచే (ABCD) వై॥ = AB × DG అయినది.
పై ఫలితము బట్టి మనము “సమాంతర చతుర్భుజ వైశాల్యము. దాని భూమి (ఏదైనా ఒక భుజము) మరియు దానిపైకి గీయబడిన లంబాల పొడవుల లబ్దానికి సమానము” అని చెప్పవచ్చు.

2. త్రిభుజము ABC మరియు సమాంతర చతుర్భుజము ABEF లు ఒకే భూమి AB మరియు ఒకే సమాంతర రేఖలు AB మరియు EF ల మధ్య ఉంటే (∆ABC) వై॥ = \(\frac {1}{2}\)(ABEF) వై॥ అని చూపండి. (పేజీ నెం. 251)
సాధన.
BH || AC అగునట్లు B గుండా ఒక రేఖను గీస్తే అది పొడిగించిన FE ని H వద్ద ఖండించింది.
∴ ABHC ఒక సమాంతర చతుర్భుజము.

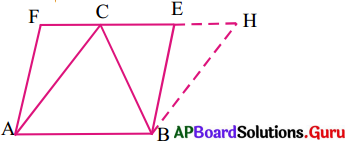
BC కర్ణము దీనిని రెండు సర్వసమాన త్రిభుజాలుగా విభజించింది. కావున
(∆ABC) వై॥ = (∆BCH) వై॥
= \(\frac {1}{2}\)(ABHC) వై॥
కాని సమాంతర చతుర్భుజాలు ABHC మరియు ABEF లు ఒకే భూమి AB పైన AB || EF సమాంతరరేఖల మధ్య ఉన్నాయి. కావున (∆BHC) వై॥ = (ABEF) వై॥ అందువలన
(∆ABC) వై॥ = \(\frac {1}{2}\)(ABEF) వైశాల్యం అయినది.
దీని నుండి మనం “ఒకే భూమి, ఒకే సమాంతర రేఖల మధ్యన ఒక త్రిభుజము, సమాంతర చతుర్భుజము ఉంటే, త్రిభుజ వైశాల్యము, సమాంతర చతుర్భుజం వైశాల్యములో సగము ఉంటుంది” అని చెప్పవచ్చును.

3. ఒక రాంబిలో కర్ణాలు 12 సెం.మీ. మరియు 16 సెం.మీ. దాని ఆసన్న భుజాల మధ్య బిందువులను వరుస క్రమములో కలుపగా ఏర్పడే పటము యొక్క వైశాల్యము ఎంత ? (పేజీ నెం. 251)
సాధన.
ABCD రాంబస్ యొక్క భుజాలు AB, BC, CD మరియు DA ల మధ్య బిందువులు M, N, O మరియు Pలను వరుసలో కలుపగా ఏర్పడిన పటము MNOP.

ఏర్పడిన MNOPఏ ఆకారంలో ఉంది ? ఎందుకు ? PN కలిపితే PN || AB మరియు PN || DC అవుతాయి (ఎలా ?) ఒకే భూమి, ఒకే సమాంతర రేఖల మధ్య ఒక త్రిభుజము, సమాంతర చతుర్భుజము ఉంటే త్రిభుజ వైశాల్యం, సమాంతర చతుర్భుజ వైశాల్యంలో సగం ఉంటుందని మీకు తెలుసు.

పై ఫలితాన్ని బట్టి సమాంతరచతుర్భుజము ABNP మరియు త్రిభుజము MNP లు ఒకే భూమి PN పైన, ఒకే సమాంతరాలు PN మరియు AB ల మధ్య ఉన్నాయి.

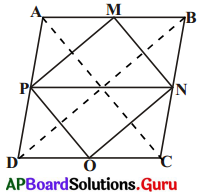
∆MNP వై॥ = \(\frac {1}{2}\)ABPNవై॥ ……………… (i)
ఇదే విధముగా ∆PONవై॥ = \(\frac {1}{2}\)PNCDవై॥ ……………..(ii)
మరియు రాంబస్ వైశాల్యము = \(\frac {1}{2}\) × d₁d₂ కావున (i), (ii), (iii) లను బట్టి
(MNOP) వై॥ = (∆MNP) వై॥ + (∆PON) వై॥
= \(\frac {1}{2}\)(ABNP) వై॥ + \(\frac {1}{2}\)(ABCD) వై॥
= \(\frac {1}{2}\)(రాంబస్ ABCD) వై॥
= \(\frac {1}{2}\)(\(\frac {1}{2}\) × 12 × 16) = 48 చ. సెం.మీ.

4. ఒక త్రిభుజాన్ని దాని మధ్యగతము సమాన వైశాల్యాలు గల రెండు త్రిభుజాలుగా విభజిస్తుందని చూపండి. (పేజీ నెం. 255)
సాధన.

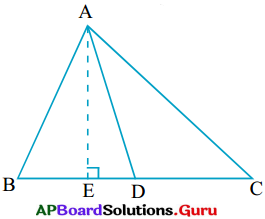
త్రిభుజము ABC లో AD మధ్యగతం అనుకోండి. ∆ABD మరియు ∆ADC లకు ఒకే ఉమ్మడి శీర్షం. దీని భూములు BD మరియు DCలు సమానము. AE ⊥ BC గీయండి.
ఇప్పుడు, (∆ABD) = \(\frac {1}{2}\) × భూమి BD × ∆ADB యొక్క ఎత్తు
= \(\frac {1}{2}\) × BD × AE
= \(\frac {1}{2}\) × DC × AE (∵ BD = DC)
= \(\frac {1}{2}\) × భూమి DC × ∆ACD యొక్క ఎత్తు
= ∆ACD వై॥
కావున (∆ABD) వై॥ = (∆ACD) వై అయినది.

5. కింది పటంలో ABCD ఒక చతుర్భుజం. AC ఒక కర్ణము, DE || AC మరియు BC ని పొడిగించగా అది E వద్ద ఖండించింది. అయిన (ABCD) వై॥ = (∆ABE) వై॥ అని చూపండి. (పేజీ నెం. 256)
సాధన.

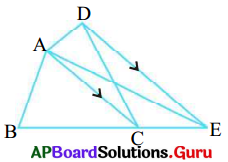
(ABCD) వై॥ = (∆ABC) వై॥ + (∆DAC) వై॥
∆DAC మరియు ∆EAC లు ఒకే భూమి \(\overline{\mathrm{AC}}\)
మరియు ఒకే సమాంతరాలు DE || AC మధ్యగలవు.
(∆DAC) వై॥ = (∆EAC) వై॥ (ఎందుకు ?)
సమాన వైశాల్యాల పటాలను ఇరువైపులా కలుపగా
(∆DAC) వై॥ + (∆ABC) వై॥
= (∆EAC) వై॥ + (∆ABC) వై॥
కావున (ABCD) వై॥ = (∆ABE) వై॥

6. కింది పటంలో AP || BQ || CR. (∆AQC) వై॥ = (∆PBR) వై॥ అని చూపండి. (పేజీ నెం. 258)
సాధన.

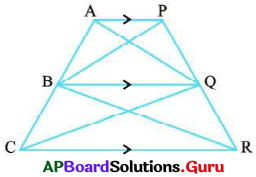
∆ABQ మరియు ∆PBQ లు ఒకే భూమి BQ మరియు ఒకే సమాంతర రేఖలు AP || BQల మధ్య ఉన్నాయి.
కావున (∆ABQ) వై॥ = (∆PBQ) వై॥ …………. (1)
ఇదే విధంగా (∆CQB) వై॥ = (∆RQB) వై॥
(ఒకే భూమి BQ మరియు BQ || CR) …….. (2)
(1), (2) ఫలితాలను కలుపగా
(∆ABQ) వై॥ + (∆CQB) వై॥ = (∆PBQ) వై॥ + (∆RQB) వై॥
అందుచే ∆AQC వై॥ = ∆PBR వై॥ అయినది.