AP SCERT 9th Class Maths Textbook Solutions Chapter 12 వృత్తాలు InText Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 12th Lesson వృత్తాలు InText Questions
ఇవి చేయండి
1. పటములో వృత్తం A నకు సర్వసమానంగా ఉన్న వృత్తాలను గుర్తించండి. (పేజీ నెం. 262)

సాధన.
వృత్తం A నకు సర్వసమానంగా ఉన్న వృత్తం ‘E’.
![]()
2. వృత్తాల యొక్క ఏ కొలత వాటిని సర్వసమానం చేస్తుంది? (పేజీ నెం. 262)
సాధన.
వృత్తాల యొక్క వ్యాసార్ధములు వాటిని సర్వసమానం చేస్తుంది.
ప్రయత్నించండి
1. ‘O’ కేంద్రంగా కల వృత్తంలో AB ఒక జ్యా మరియు ‘M’ జ్యా మధ్య బిందువు. అయినా \(\overline{\mathrm{OM}}\), AB కి అంబింగా ఉండునని నిరూపించండి. (సూచన : OA, OB లను కలిపి ∆OAM మరియు ∆OBM లను పోల్చండి.) (పేజీ నెం. 267)
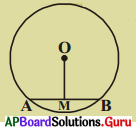
సాధన.
‘O’ వృత్త కేంద్రము.
AB ఒక జ్యా, M, AB పై మధ్య బిందువు.
A, B లను ‘O’ తో కలుపుము.
∆OMA మరియు ∆OMB లలో
OA = OB (వ్యాసార్ధాలు )
OM = OM (ఉమ్మడి భుజం)
MA = MB (దత్తాంశము)
∴ ∆OMA ≅ ∆OMB
(భు. భు.భు. సర్వసమాన ధర్మం )
∴ \(\angle \mathrm{OMA}=\angle \mathrm{OMB}\) (C.P.C.T).
కాని \(\angle \mathrm{OMA}\) మరియు \(\angle \mathrm{OMB}\) లు రేఖీయ ద్వయం
∴ \(\angle \mathrm{OMA}=\angle \mathrm{OMB}\) = 90°
i.e., OM ⊥ AB.
2. మూడు బిందువులు సరేఖీయాలైన, వాటి గుండా పోయేట్లు గీయగల వృత్తాలెన్ని? ఒక రేఖపై ఏవేని మూడు బిందువులను తీసుకొని వాటి గుండా పోయేటట్లు వృత్తాలను గీయడానికి ప్రయత్నించండి. (పేజీ నెం. 268)
సాధన.
మూడు బిందువులు సరేఖీయాలైన వాటి గుండాపోవు వృత్తంను గీయలేము.
![]()
3. పటంలో ‘O’ వృత్త కేంద్రం మరియు AB = CD; OM మరియు ON లు వరుసగా \(\overline{\mathrm{AB}}\) మరియు \(\overline{\mathrm{CD}}\)లకు కేంద్రం నుండి గీచిన లంబాలు. అయిన OM = ON అని నిరూపించండి. (పేజీ నెం. 269)
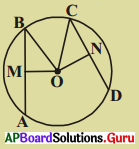
సాధన.
‘O’ వృత్త కేంద్రము మరియు AB = CD జ్యాలు.
OM ⊥ AB; ON ⊥ CD
∆OMB మరియు ∆ONC లలో
OB = OC [∵ వ్యాసార్ధాలు]
BM = CN (∵ \(\frac {1}{2}\)AB = \(\frac {1}{2}\)CD)
\(\angle \mathrm{OMB}=\angle \mathrm{ONC}\) [∵ ప్రతి కోణం 90°]
∴ ∆OMB ≅ ∆ONC (లం. క.భు. సర్వసమాన నియమం ప్రకారం )
OM = ON (C.P.C.T)
కృత్యం
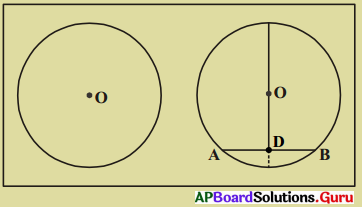
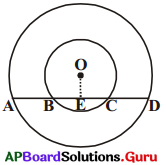
1. ఈ క్రింది కృత్యాన్ని చేద్దాం. కాగితంపై ఒక బిందువును . గుర్తించండి. ఈ బిందువును కేంద్రంగా తీసుకొని ఏదేని వ్యాసార్ధంతో ఒక పృత్తాన్ని గీయండి. ఇదే కేంద్రంతో వ్యాసార్ధాన్ని పెంచి లేదా తగ్గించి మరికొన్ని వృత్తాలను గీయండి. ఈ కృత్యం ద్వారా గీచిన వృత్తాలను ఏమని పిలుస్తారు ? (పేజీ నెం. 261)

ఒకే కేంద్రం గల వృత్తాలను ఏకకేంద్ర వృత్తాలు అంటారు.
2. ఒక పలుచని గుండ్రని కాగితం (వృత్తాకార కాగితం) తీసుకొని, దానిని సగానికి (మధ్యకు) మడచి తెరవండి. మరలా మరొక సగానికి మడచి తెరవండి. ఇదే విధంగా అనేకసార్లు తిరిగి చేయండి. చివరికి తెరిచి చూస్తే మీరేమి గమనిస్తారు ? (పేజీ నెం. 262)
![]()
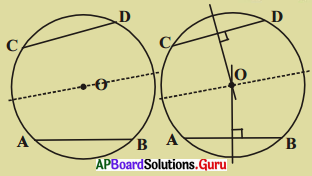
3. ఒక గ్రుండని (వృత్తాకార) కాగితాన్ని తీసుకోండి. వృత్త అంచులు ఏకీభవించునట్లు ఏదేని ఒక వ్యాసం వెంట మడవండి. మడతను తెరచి ఇంకొక వ్యాసం వెంబడి మడవండి. మడతను తెరచి చూసిన రెండు వ్యాసాలు కేంద్రం ‘O’ వద్ద ఖండించుకొనుటను గమనిస్తాం. రెండు జతల శీర్షాభిముఖ కోణాలు ఏర్పడుతాయి. ఇవి సమానం, వ్యాసం చివరి బిందువుల A, B, C మరియు D అని పేర్లు పెట్టండి.
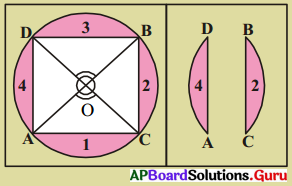
జ్యాలు \(\overline{\mathrm{AC}}, \overline{\mathrm{BC}}, \overline{\mathrm{BD}}\) మరియు \(\overline{\mathrm{AD}}\)లను గీయండి.
నాలుగు వృత్తఖండాలు 1, 2, 3 మరియు 4 లను కత్తిరించండి. ఈ ఖండాలను జతలుగా ఒకదానిపై మరొకటి ఉంచిన (1, 3) మరియు (2, 4) జతలు అంచులు ఏకీభవిస్తాయి. అంటే \(\overline{\mathrm{AD}}=\overline{\mathrm{BC}}\) మరియు \(\overline{\mathrm{AC}}=\overline{\mathrm{BD}}\) అవుతాయా ?
ఒక ప్రత్యేక సందర్భములో పై ధర్మాన్ని పరిశీలించారు. ఇదే విషయాన్ని వేర్వేరు కొలతలుగల సమాన కోణాలు తీసుకొని సరిచూసిన జ్యాలు సమానమగును. కింది సిద్ధాంతము ద్వారా గమనించగలం. (పేజీ నెం. 265)
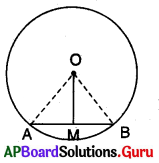
4. వృత్తాకారంలోగల ఒక కాగితాన్ని తీసుకొని దాని కేంద్రం ‘O’ ను గుర్తించండి. వృత్తం యొక్క కొంత భాగాన్ని మడచి తిరిగి తెరవండి. ఏర్పడిన మడత జ్యా ABను సూచిస్తుందనుకోండి. ఇంకొక మడత వృత్త కేంద్రం మరియు జ్యా మధ్య బిందువు గుండా పోయేటట్లు కాగితాన్ని మరల మడవండి. ఇప్పుడు మడతల మధ్య ఏర్పడిన కోణాలను కొలవండి, అవి లంబకోణాలు.
“కాబట్టి వృత్తకేంద్రం నుండి జ్యాను సమద్విఖండన చేసే రేఖ జ్యూకు లంబంగా ఉంటుంది” అని పరికల్పన చేయవచ్చు. (పేజీ నెం. 267)
5. వృత్తం దానిని సగానికి మధ్యలో మడవండి. ఇప్పుడు ఆర్ధవృత్త చాపపు అంచు దగ్గరయుంచి మడత విప్పిన మీకు రెండు సర్వసమాన జ్యాల మడతలు వచ్చును. వాటిని \(\overline{\mathrm{AB}}\) మరియు \(\overline{\mathrm{CD}}\) లుగా గుర్తించండి కేంద్రాన్ని ‘O’ గా గుర్తించండి. కేంద్రం ‘O’ నుండి ప్రతి జ్యాకు లంబపు మడత పెట్టండి. విభాగిని ఉపయోగించి వృత్తకేంద్రం నుండి జ్యాలకు గల లంబ దూరాలను పోల్చండి.
ఈ కృత్యాన్ని వృత్తం మడత ద్వారా సమాన జ్యాలు ఏర్పరుస్తూ అనేకసార్లు మరలా చేయండి. మీ పరిశీలనలను . ఒక పరికల్పనగా తెల్పండి. సర్వసమాన జ్యాలు వృత్త కేంద్రం నుండి సమాన దూరంలో ఉంటాయి. (పేజీ నెం. 269)
![]()
6. పటంలో చతుర్పులు తీరాలు A, B C మరియు Dలు ఒకే వృత్తం పైన గలవు. ఇటువంటి చతుర్భుజాలు ABCD లను మూడింటిని గీసి చతుర్భుజ కోణాలను కొలచి పట్టికను నింపండి.
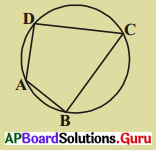
పట్టిక నుండి నీవు ఏమి చెప్పగలవు ? (పేజీ నెం. 275)
సిద్ధాంతాలు
1. ఒక వృత్తంలోని రెండు జ్యాలు సమానమైతే అవి కేంద్రం వద్ద ఏర్పరచే కోణాలు సమానం. (పేజీ నెం. 265)
సాధన.
దత్తాంశం : ‘O’ కేంద్రంగా గల వృత్తంలో \(\overline{\mathrm{AB}}\) మరియు \(\overline{\mathrm{CD}}\) లు రెండు సమాన జ్యాలు. అవి కేంద్రం వద్ద ఏర్పరచిన కోణాలు \(\angle \mathrm{AOB}\) మరియు \(\angle \mathrm{AOB}\).
సారాంశం: \(\angle \mathrm{AOB}\) = \(\angle \mathrm{COD}\)
నిర్మాణం : వృత్త కేంద్రాన్ని జ్యాల యొక్క అంత్య బిందువులతో కలుపుము. ఇప్పుడు ∆AOB మరియు ∆COD లు ఏర్పడతాయి.
నిరూపణ:
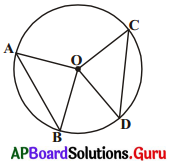
∆AOB మరియు ∆COD లలో
AB = CD (దత్తాంశం)
OA = OC (ఒకే వృత్త వ్యాసార్ధాలు)
OB = OD (ఒకే వృత్త వ్యాసార్ధాలు)
కావున ∆AOB ≅ ∆COD (భు.భు.భు. నియమం)
కావున ∆AOB ≅ ∆COD (సర్వసమాన త్రిభుజపు అనురూప కోణాలు)
2. ఒక వృత్తంలోని జ్యాలు కేంద్రం వద్ద చేసే కోణాలు సమానమైన ఆ జ్యాలు సమానం.
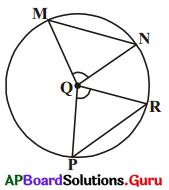
ఇది ఇంతకు ముందు చెప్పబడిన సిద్ధాంతం యొక్క విపర్యయం ఇచ్చిన ప్రకారం
\(\angle \mathrm{PQR} \cong \angle \mathrm{MQN}\)
అని తీసుకుంటే \(\angle \mathrm{PQR} ≡ \angle \mathrm{MQN}\) అని మీరు గమనించగలరు. (పేజీ నెం. 266)
3. ఒక చాపము ఒక వృత్తకేంద్రం వద్ద ఏర్పరచుకోణం, ఆ చాపం మిగిలిన వృత్తంపై ఏదేని బిందువు వద్ద ఏర్పరిచే కోణానికి రెట్టింపు ఉంటుంది. (పేజీ నెం. 272)
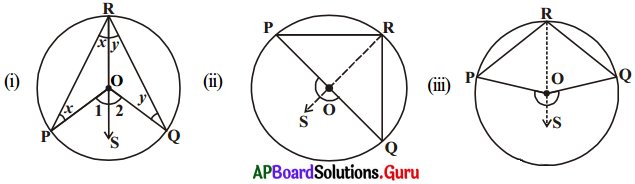
సాధన.
‘O’ అనునది వృత్తకేంద్రం.
చాపము \(\overparen{\mathrm{PQ}}\) కేంద్రం వద్ద ఏర్పరచు కోణం \(\angle \mathrm{POQ}\).
Rఅనునది (\(\overparen{\mathrm{PQ}}\) పై లేనట్టి) మిగిలిన వృత్తం మీద ఏదేని ఒక బిందువు.
నిరూపణ : ఇక్కడ (i) \(\overparen{\mathrm{PQ}}\) ఒక అల్ప చాపం,
(ii) \(\overparen{\mathrm{PQ}}\) ఒక అర్ధవృత్తం మరియు
(iii) \(\overparen{\mathrm{PQ}}\) ఒక అధిక చాపం అయ్యే మూడు సందర్భాలు కలవు.
R బిందువును ‘O’ కలిపి S బిందువు దాకా పొడిగించడం ద్వారా నిరూపణను మొదలు పెడదాం. (అన్ని సందర్భాలలోనూ) అన్ని సందర్భాలలోను ∆ROP లో
OP = OR (ఒకే వృత్త వ్యాసార్ధాలు)
∴ \(\angle \mathrm{ORP}=\angle \mathrm{OPR}\) (సమద్విబాహు త్రిభుజంలో సమాన భుజాలకు ఎదురుగా ఉండే కోణాలు సమానం).
\(\angle \mathrm{POS}\) కోణము ∆ROP కు బాహ్య కోణం (నిర్మాణం)
\(\angle \mathrm{POS}=\angle \mathrm{ORP}+\angle \mathrm{OPR}\) లేదా 2\(\angle \mathrm{OPR}\) ……. (1)
(∵ బాహ్యకోణం అంతరాభిముఖ కోణాల మొత్తానికి సమానం)
ఇదే విధంగా ∆ROQ
\(\angle \mathrm{SOQ}=\angle \mathrm{ORQ}+\angle \mathrm{OQR}\) లేదా 2\(\angle \mathrm{ORQ}\) …….. (2)
(∵ బాహ్యకోణం అంతరాభిముఖ కోణాల మొత్తానికి సమానం)
(1) మరియు (2) ల నుండి,
\(\angle \mathrm{POS}+\angle \mathrm{SOQ}=2(\angle \mathrm{ORP}+\angle \mathrm{ORQ})\)
అంటే ఇది \(\angle \mathrm{POQ}=2 \angle \mathrm{QRP}\) తో సమానం ……….. (3)
కావున “ఒక చాపము వృత్త కేంద్రం వద్ద ఏర్పరచు కోణం, ఆ చాపం మిగిలిన వృత్తంపై ఏదేని బిందువు వద్ద ఏర్పరచే కోణానికి రెట్టింపు ఉంటుంది” అనే సిద్ధాంతం నిరూపించడమైనది.

![]()
4. రెండు బిందువులను కలిపే రేఖాఖండం (ఆ రేఖాఖండానికి ఒకే వైపునగల) ఏవేని రెండు వేర్వేరు బిందువుల మధ్య ఏర్పరచు కోణాలు సమానం అయితే ఆ బిందువులన్నీ ఒకే వృత్తంపై ఉంటాయి. అంటే అవి చక్రీయాలు అవుతాయి. ఈ ఫలితం యొక్క సత్య విలువను కింది విధంగా పరిశీలించవచ్చు. (పేజీ నెం. 274)
సాధన.
దత్తాంశం : ఏవేని రెండు బిందువులు A, B లను కలుపు రేఖాఖండం \(\overline{\mathrm{AB}}\) నకు ఒకే వైపున గల రెండు బిందువులు C మరియు Dల వద్ద \(\overline{\mathrm{AB}}\) చేయు కోణాలు \(\angle \mathrm{ACB}\) మరియు \(\angle \mathrm{ADB}\) లు సమానమని ఈయబడినవి.
సారాంశం : A, B, C మరియు D లు ఒకే వృత్తం పైన బిందువులు అనగా చక్రీయ బిందువులు.
నిర్మాణం : సరేఖీయాలు కాని మూడు బిందువులు A, B మరియు Cల గుండాపోయేట్లు ఒక వృత్తాన్ని గీయండి.
నిరూపణ : \(\angle \mathrm{ACB}=\angle \mathrm{ADB}\) అగునట్లుగా D = ‘D’ బిందువు వృత్తంపైన లేనట్లైతే
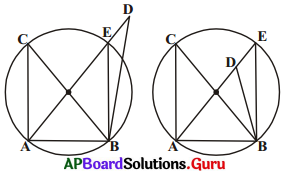
వృత్తంపై E లేదా ‘E’ అనే బిందువు, AD లేదా ADని పొడిగించినప్పుడు ఖండన బిందువుగా వ్యవస్థితం అవుతుంది. అంటే A, B, C మరియు E లు ఒక వృత్తంపై ఉంటాయి కనుక
\(\angle \mathrm{ACB}=\angle \mathrm{AEB}\) (ఎందువలన ?)
కానీ \(\angle \mathrm{ACB}=\angle \mathrm{ADB}\) అని ఈయబడినది.
కాబట్టి \(\angle \mathrm{AEB}=\angle \mathrm{ADB}\)
ఇది E మరియు Dలు ఏకీభవిస్తే తప్ప సాధ్యం కాదు. (ఎందువలన ?)
కావున E కూడా Dతో ఏకీభవిస్తుంది.
5. చక్రీయ చతుర్భుజంలోని ఎదుటి కోణాల జతలు సంపూరకాలు. (పేజీ నెం. 276)
సాధన.
దత్తాంశము : ABCD ఒక చక్రీయ చతుర్భుజం,
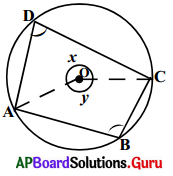
6. ఒక చతుర్భుజంలో ఏ రెండు ఎదుటి కోణాల మొత్తం అయినా 180° అయితే అది చక్రీయ చతుర్భుజం అవుతుంది. (పేజీ నెం. 277)
సాధన.
దత్తాంశం :
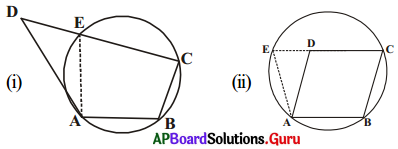
చతుర్భుజం ABCD లో
\(\angle \mathrm{ABC}+\angle \mathrm{ADC}\) = 180°
\(\angle \mathrm{DAB}+\angle \mathrm{BCD}\) = 180°
సారాంశం : ABCD ఒక చక్రీయ చతుర్భుజం.
నిర్మాణం : సరేఖీయాలు కానీ బిందువులు A, B మరియు Cల గుండా ఒక వృత్తాన్ని గీయండి. వృత్తం D ద్వారా పోయినట్లైతే A, B, C, D ల చక్రీయాలు కావున సిద్ధాంతము నిరూపించినట్లే.
ఈ వృత్తం D బిందువు ద్వారా పోనట్లైతే ఆ వృత్తం \(\overline{\mathrm{CD}}\) ను లేదా \(\overline{\mathrm{CD}}\) ను పొడిగించినప్పుడు D వద్ద ఖండిస్తుంది. \(\overline{\mathrm{AE}}\) ను గీయండి.
నిరూపణ : ABCE ఒక చక్రీయ చతుర్భుజం (నిర్మాణం)
\(\angle \mathrm{AEC}+\angle \mathrm{ABC}\) = 180° (చక్రీయ చతుర్భుజంలో ఎదుటి కోణాల మొత్తం)
కాని \(\angle \mathrm{ABC}+\angle \mathrm{ADC}\) = 180° (దత్తాంశం)
\(\angle \mathrm{AEC}+\angle \mathrm{ABC}=\angle \mathrm{ABC}+\angle \mathrm{ADC}\)
కానీ ఈ కోణాలలో ఒకటి ∆ADE యొక్క అంతరకోణం మరియు రెండవది బాహ్యకోణం. త్రిభుజ బాహ్య కోణం ఎల్లప్పుడూ దాని అంతరాభి. ముఖ కోణాల కన్నా ఎక్కువ అని మనకు తెలుసు.
∴ \(\angle \mathrm{AEC}=\angle \mathrm{ADC}\) అనునది ఒక విరుద్దత.
అంటే A, B మరియు Cల ద్వారా గీచిన వృత్తం D ద్వారా పోవట్లేదనే మన కల్పన అసత్యం. A, B మరియు C ల ద్వారా గీచిన వృత్తం D ద్వారా కూడా పోవును. A, B, C మరియు Dలు ఒకే వృత్తంపైని బిందువులు అంటే ABCD ఒక చక్రీయ చతుర్భుజం.
![]()
ఉదాహరణలు
1. AB = 5 సెం.మీ.; \(\angle \mathrm{B}\) = 75° మరియు BC = 7 సెం.మీ. లుగా గల ∆ABC యొక్క పరిషృత్తాన్ని గీయండి. (పేజీ నెం. 268)
సాధన.
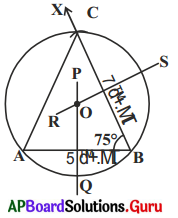
AB = 5 సెం.మీ. పొడవుగల రేఖాఖండాన్ని గీయండి. \(\angle \mathrm{B}\) = 75° ఉండునట్లు B వద్ద కోణకిరణం BX ను నిర్మించండి. B కేంద్రంగా 7 సెం.మీ. వ్యాసార్ధంతో ఒక చాపరేఖను గీయండి. చాపరేఖ \(\overrightarrow{\mathrm{BX}}\) ను C వద్ద ఖండించును. C మరియు A లను కలపగా ∆ABC ఏర్పడుతుంది. \(\overline{\mathrm{AB}}\) మరియు \(\overline{\mathrm{BC}}\) లకు లంది సమద్విఖండన రేఖలు \(\overline{\mathrm{PQ}}\) మరియు \(\overline{\mathrm{RS}}\) లను గీయండి. \(\overline{\mathrm{PQ}}\) మరియు \(\overline{\mathrm{RS}}\) ల ఖండన బిందువు ‘O’. ఇప్పుడు ‘O’ ను కేంద్రంగా మరియు OA ను వ్యాసార్ధంగా ఒక వృత్తాన్ని గీయండి. B మరియు C బిందువుల ద్వారా కూడా పోతుంది. ఇదియే కావలసిన పరివృత్తం.
2. పటంలో ‘O’ వృత్త కేంద్రం అయిన CD పొడవును కనుక్కోండి. (పేజీ నెం. 269)
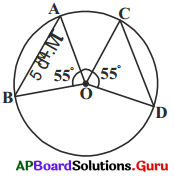
సాధన.
∆AOB మరియు ∆COD లలో
OA = OC (ఎందువలన?)
CB = OD (ఎందువలన ?)
\(\angle \mathrm{AOB}=\angle \mathrm{COD}\)
∆AOB ≅ ∆COD
AB = CD (సర్వసమాన త్రిభుజముల సర్వసమాన భాగాలు)
AB = 5 సెం.మీ. కావున CD = 5 సెం.మీ.
![]()
3. పక్క పటంలో ‘O’ కేంద్రంగా రెండు ఏక కేంద్ర వృత్తాలు కలవు. పెద్ద వృత్తం యొక్క జ్యా AD చిన్న వృత్తాన్ని B మరియు Cల వద్ద అందిస్తుంది. అయిన AB = CD అని చూపండి. (పేజీ నెం. 269)
దత్తాంశం : ‘O’ కేంద్రంగా కల ఏక కేంద్ర వృత్తాలలో పెద్ద వృత్తం యొక్క జ్యా \(\overline{\mathrm{AD}}\) చిన్న వృత్తాన్ని B మరియు Cల వద్ద ఖండిస్తోంది.
సారాంశం : AB = CD
నిర్మాణం: \(\overline{\mathrm{AD}}\)కు లంబంగా \(\overline{\mathrm{OE}}\) ను గీయుము.
నిరూపణ : ‘O’ కేంద్రంగా గల పెద్ద వృత్తానికి AD ఒక జ్యా మరియు \(\overline{\mathrm{OE}}\), \(\overline{\mathrm{AD}}\) కి లంబము.
∵ \(\overline{\mathrm{AD}}\) ను \(\overline{\mathrm{OE}}\) సమద్విఖండన చేస్తుంది (కేంద్రం నుండి జ్యాకు గీచిన లంబం, జ్యాను సమద్విఖండన చేస్తుంది.
∴ AE = ED ……….. (i)
‘O’ కేంద్రంగా గల చిన్న వృత్తానికి \(\overline{\mathrm{BC}}\) ఒక జ్యా మరియు \(\overline{\mathrm{AD}}\) కు \(\overline{\mathrm{OE}}\) లంబం.
∵ \(\overline{\mathrm{BC}}\) కు \(\overline{\mathrm{OE}}\) సమద్విఖండన చేస్తుంది. (పై సిద్ధాంతం నుండి)
∴ BE = CE …….. (ii)
సమీకరణం (ii) ను (i) నుండి తీసివేయగా,
AE – BE = ED – EC
AB = CD
4. ‘O’ అనునది వృత్త కేంద్రం. PQ ఒక వ్యాసము. అయిన 2PRQ = 90° అని నిరూపించుము. (లేదా) అర్ధవృత్తంలోని కోణం లంబకోణమని చూపండి. (పేజీ నెం. 273)
నిరూపణ:
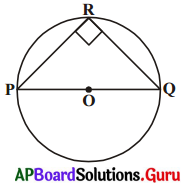
‘O’ కేంద్రంగా గల వృత్తంలో PQ ఒక వ్యాసం అని ఈయబడినది. \(\angle \mathrm{PRQ}\) = 180° (సరళరేఖపై ఏదేని బిందువు వద్ద కోణం 180°)
మరియు \(\angle \mathrm{POQ}\) = 2\(\angle \mathrm{PRQ}\) (ఒక చాపం వృత్త కేంద్రం వద్ద ఏర్పరిచే కోణం, ఆ చాపం మిగిలిన వృత్తంపై ఏదేని బిందువు వద్ద ఏర్పరచే కోణానికి రెట్టింపు).
\(\angle \mathrm{PRQ}\) = \(\frac {180°}{2}\) = 90°
![]()
5. కింది పటంలో x° విలువను కనుగొనండి. (పేజీ వెం. 273)
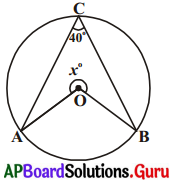
సాధన.
\(\angle \mathrm{ACB}\) = 40° కావున
సిద్ధాంతం ప్రకారం, AB చాపం కేంద్రం వద్ద చేయుకోణం.
\(\angle \mathrm{AOB}\) = 2\(\angle \mathrm{ACB}\) = 2 × 40° = 80°
x° + \(\angle \mathrm{AOB}\) = 360°
కాబట్టి x° = 360° – 80° = 280°
6. పటంలో \(\angle \mathrm{A}\) = 120° అయిన \(\angle \mathrm{C}\)ను కనుగొనుము. (పేజీ నెం. 276)
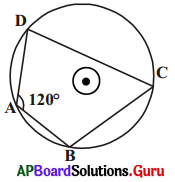
సాధన.
ABCD ఒక చక్రీయ చతుర్భుజం
కావున \(\angle \mathrm{A}+\angle \mathrm{C}\) = 180°
120° + \(\angle \mathrm{C}\) = 180°
కావున \(\angle \mathrm{C}\) = 180° – 120° = 60°
![]()
7. పటంలో \(\overline{\mathrm{AB}}\) వృత్తం యొక్క ఒక వ్యాసము. జ్యా \(\overline{\mathrm{CD}}\) వృత్త వ్యాసార్ధానికి సమానం. \(\overline{\mathrm{AC}}\) మరియు \(\overline{\mathrm{BD}}\) లు పొడిగించగా అవి E బిందువు వద్ద ఖండించుకొనును. అయిన \(\angle \mathrm{AEB}\) = 60° అని చూపండి. (పేజీ నెం. 277)
సాధన.
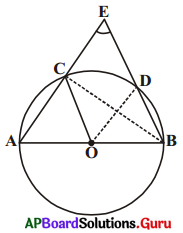
OC, OD మరియు BC లను కలపండి.
∆ODC ఒక సమబాహు త్రిభుజము (ఎందువలన?)
\(\angle \mathrm{COD}\) = 60°
ఇప్పుడు \(\angle \mathrm{CBD}\) = \(\frac {1}{2}\)\(\angle \mathrm{COD}\) (ఎందువలన ?)
దీని నుండి \(\angle \mathrm{CBD}\) = 30°
మరల \(\angle \mathrm{ACB}\) = 90° (ఎందువలన ?)
కావున \(\angle \mathrm{BCE}\) = 180° – \(\angle \mathrm{ACB}\) = 90°
దీని నుండి \(\angle \mathrm{CEB}\) = 90° – 30° = 60°,
అంటే \(\angle \mathrm{AEB}\) = 60°