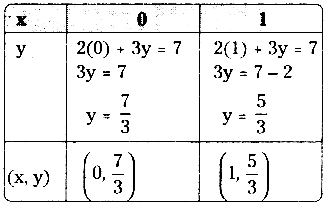SCERT AP 9th Class Maths Solutions Chapter 6 రెండు చరరాశులలో రేఖీయ సమీకరణాలు Ex 6.4 Textbook Exercise Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 6th Lesson రెండు చరరాశులలో రేఖీయ సమీకరణాలు Exercise 6.4
ప్రశ్న 1.
ఈ కింది సమీకరణాలను
a) సంఖ్యారేఖపై సూచించండి మరియు
b) కార్టీజియన్ తలముపై సూచించండి. (గ్రాఫ్ గీయండి)
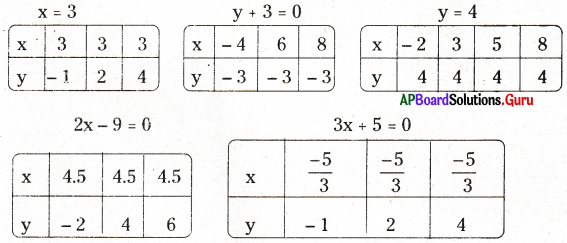
i) x = 3
ii) y + 3 = 0
iii) y = 4
iv) 2x – 9 = 0
v) 3x + 5 = 0
సాధన.
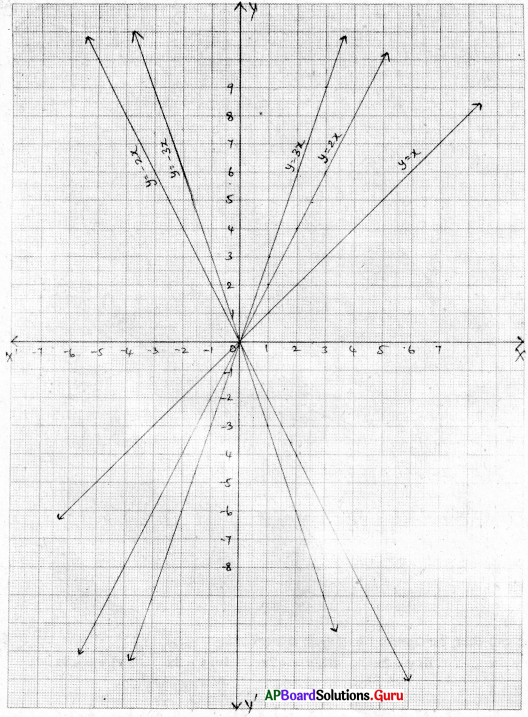
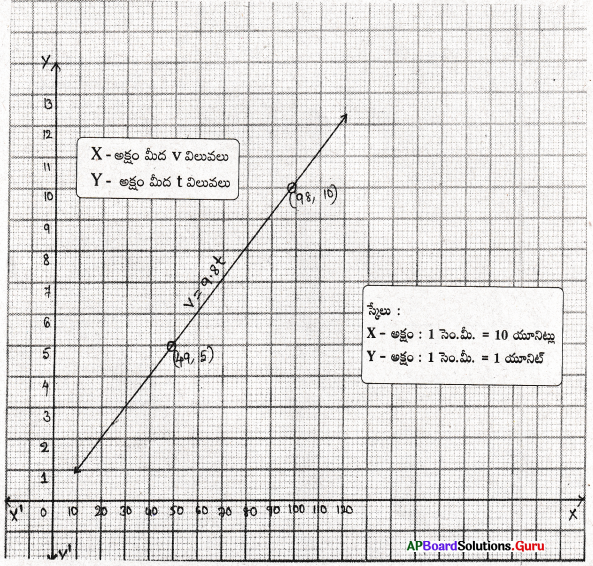
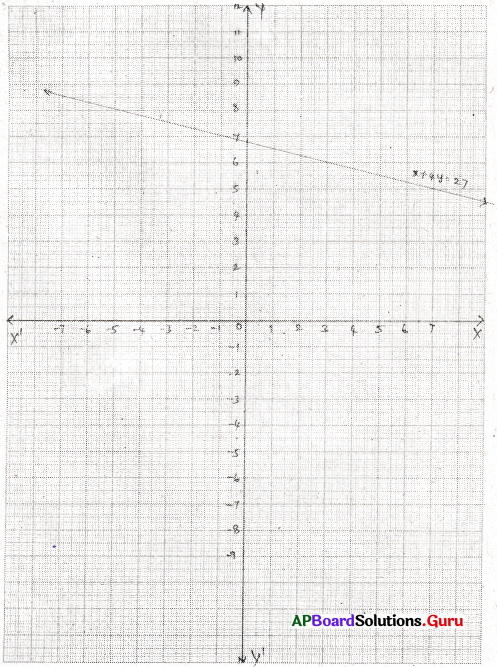
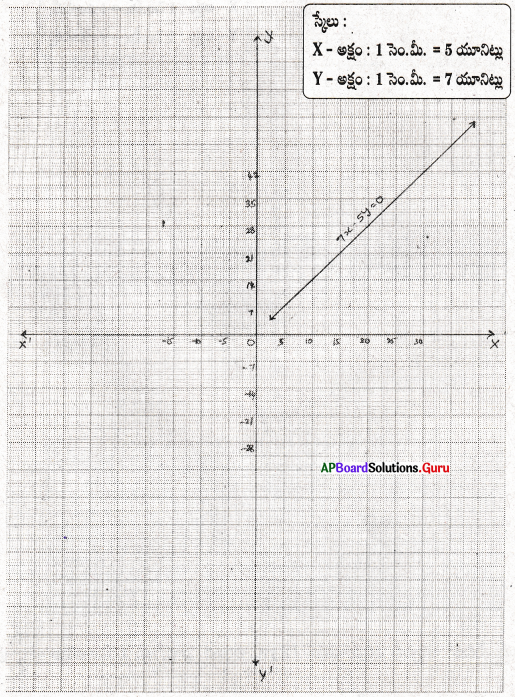
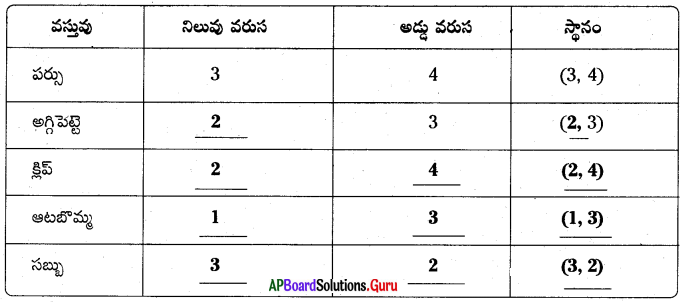
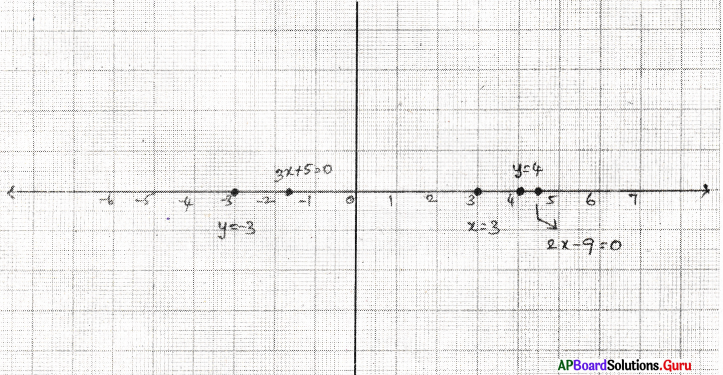
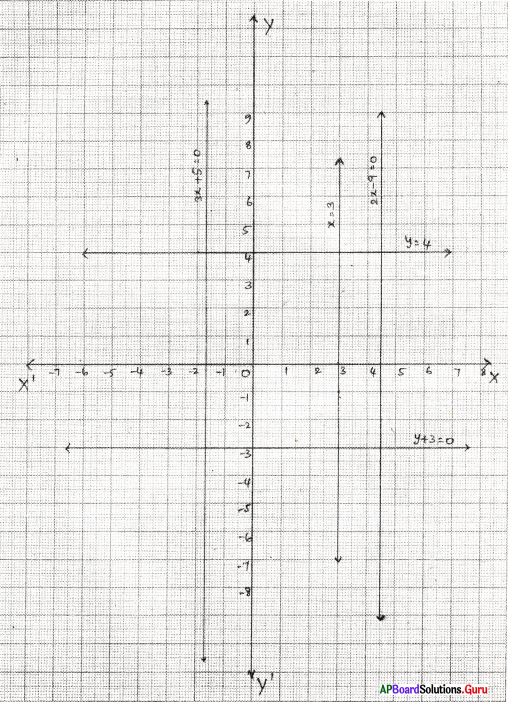
i) x = 3 రేఖ, Y- అక్షంకు సమాంతరంగా ‘3’ యూనిట్ల దూరంలో, మూలబిందువుకు కుడి వైపున ఉండును.
ii) y + 3 = 0
⇒ y = – 3 రేఖ, X- అక్షంకు సమాంతరంగా ‘3’ యూనిట్ల దూరంలో, మూలబిందువుకు ఎడమ వైపున ఉండును.
iii) y = 4 రేఖ, X- అక్షంకు సమాంతరంగా ‘4’ యూనిట్ల దూరములో, మూలబిందువుకు పైన ఉంటుంది.
iv) 2x – 9 = 0
⇒ x = [latex]\frac {9}{2}[/latex] = 4.5 రేఖ, Y- అక్షంకు సమాంతరంగా 4.5 యూనిట్ల దూరములో, మూలబిందువుకు కుడి వైపున ఉండును.
v) 3x + 5 = 0
⇒ 3x = – 5
⇒ x = [latex]\frac {-5}{3}[/latex] రేఖ, Y- అక్షంకు సమాంతరంగా [latex]\frac {5}{3}[/latex] యూనిట్ల దూరములో మూలబిందువుకు ఎడమ వైపున ఉండును.
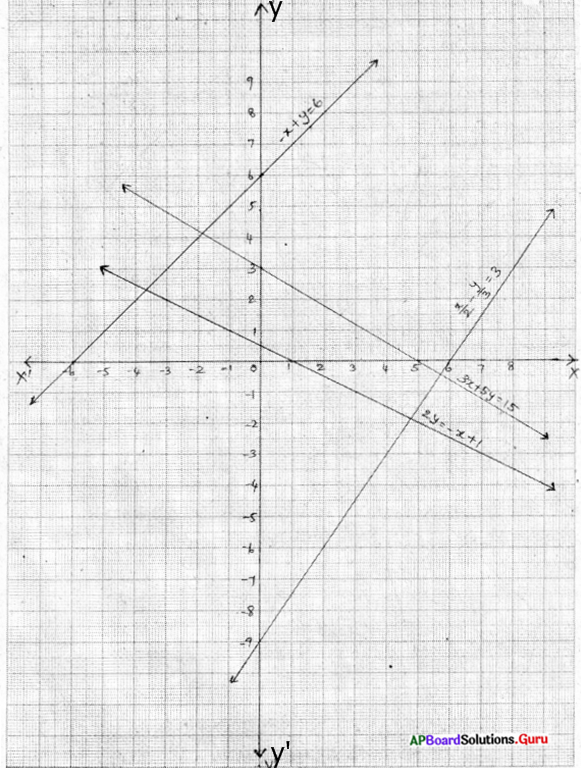
![]()
ప్రశ్న 2.
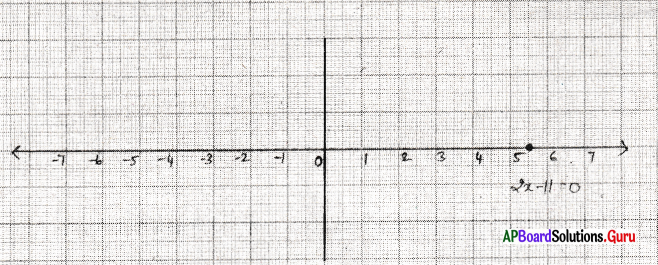
2x – 11 = 0 ను
i) ఏక చరరాశిలో రేఖీయ సమీకరణంగా భావించి
ii) రెండు చరరాశులలో రేఖీయ సమీకరణంగా భావించి జ్యామితీయ రూపంలో వ్యక్తపరచండి. (గ్రాఫ్ గీయండి.)
సాధన.
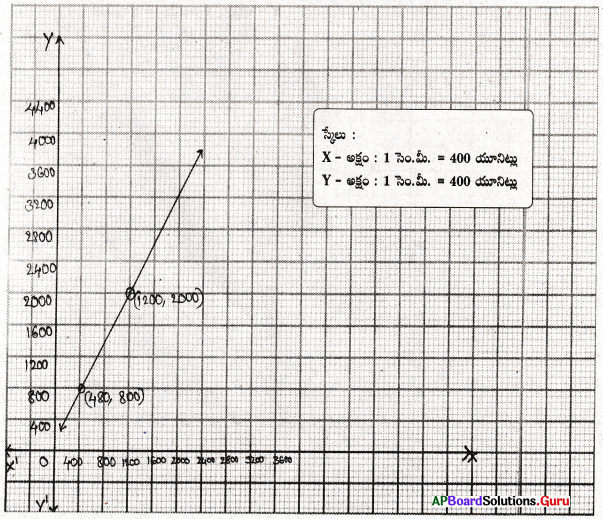
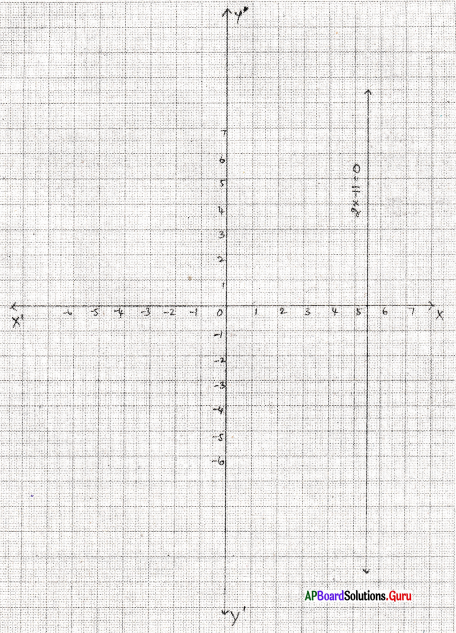
ఇచ్చిన సమీకరణము 2x – 11 = 0
| x | 5.5 | 5.5 | 5.5 |
| y | – 3 | 1 | 5 |
ప్రశ్న 3.
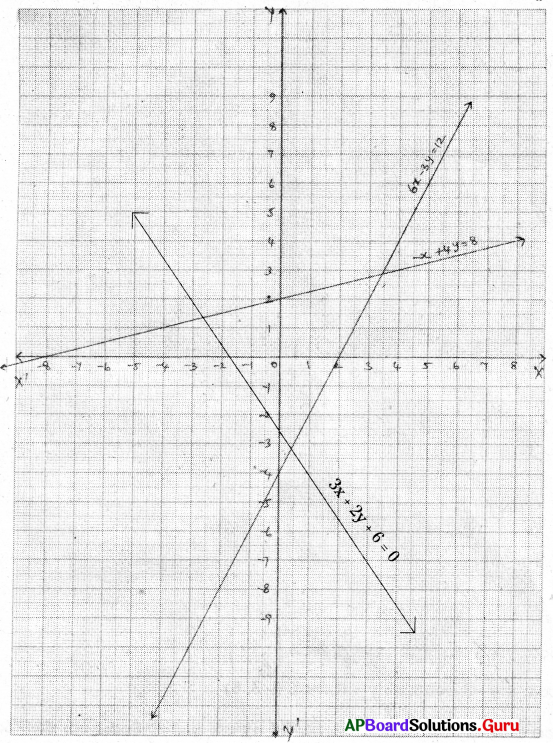
3x + 2 = 8x – 8ను సాధించి సాధనను
i) సంఖ్యారేఖపై
ii) కార్టిజియన్ తలముపై సూచించాలి.
సాధన.
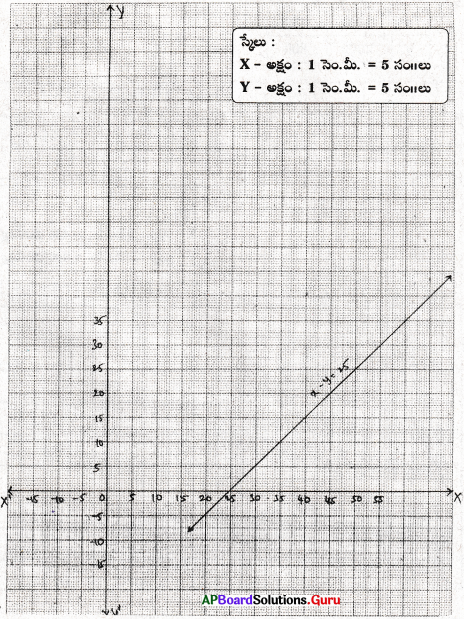
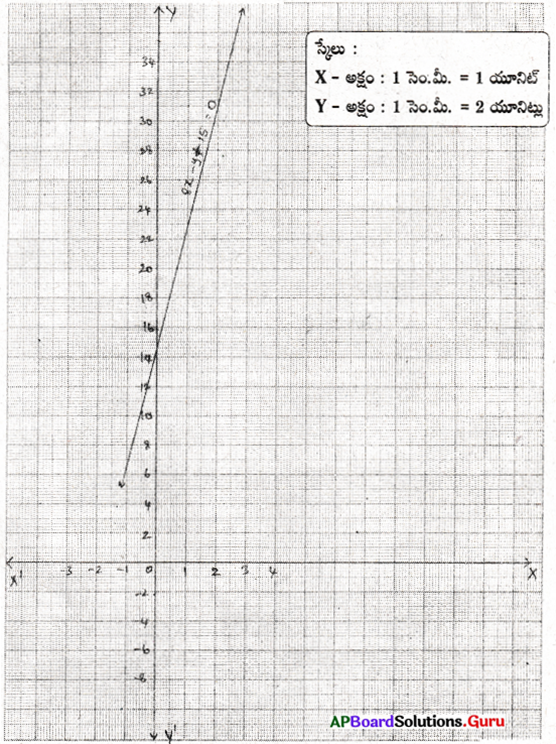
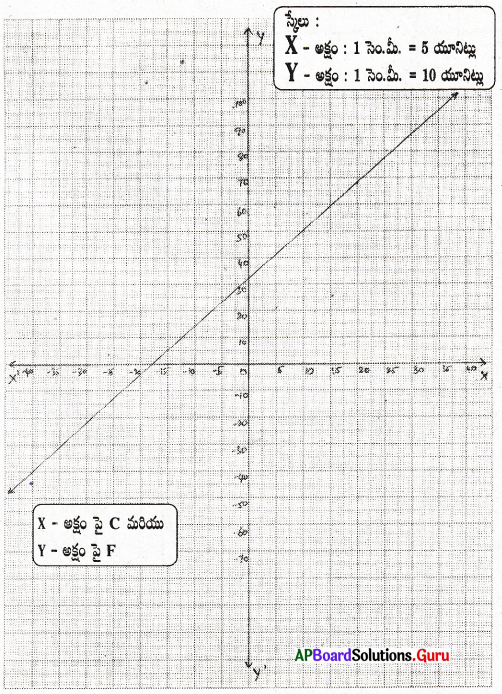
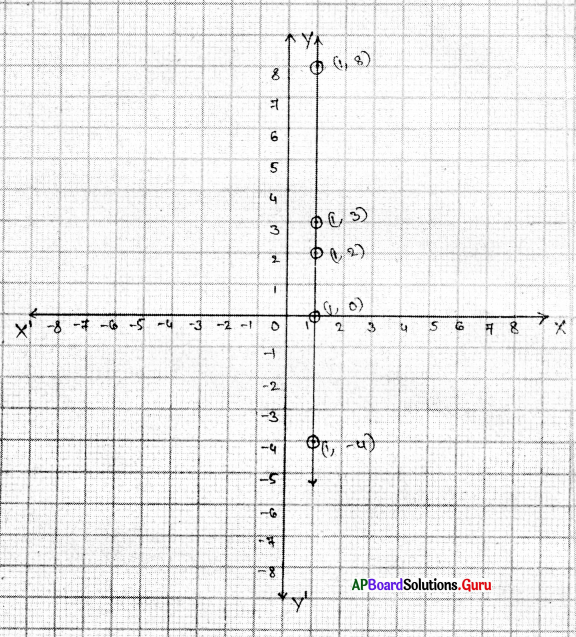
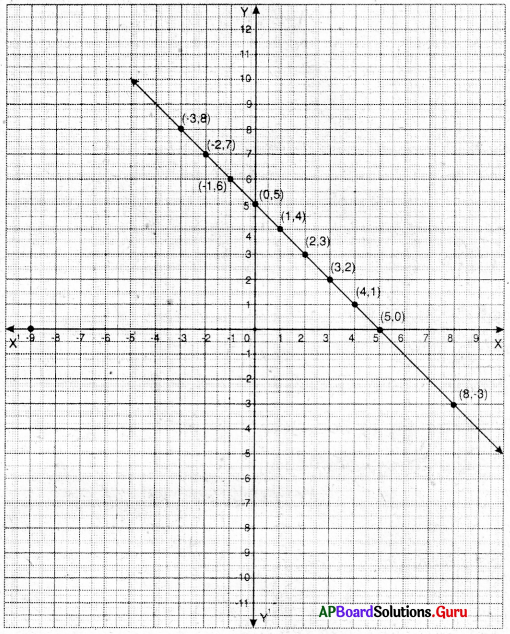
ఇచ్చిన సమీకరణము 3x + 2 = 8x – 8
3x – 8x = – 8 – 2
– 5x = – 10
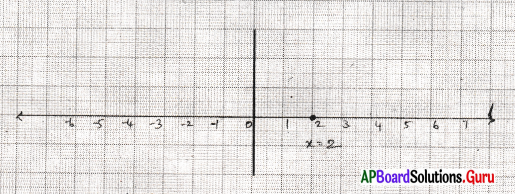
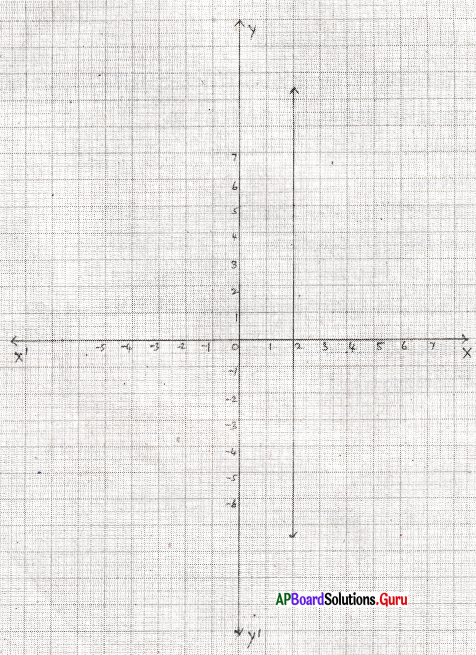
x = [latex]\frac {-10}{-5}[/latex] = 2
| x | 2 | 2 | 2 |
| y | 5 | 6 | – 4 |
![]()
ప్రశ్న 4.
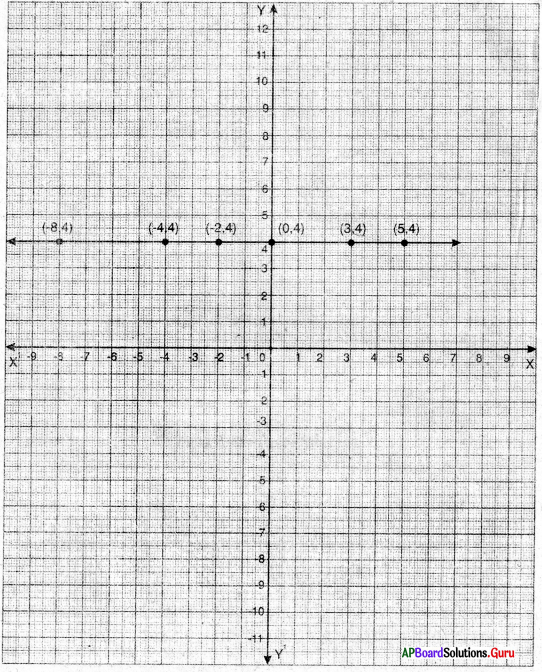
కింది బిందువుల గుండా పోతూ X- అక్షానికి సమాంతరంగా ఉండే సరళరేఖల సమీకరణాలను కనుగొనుము.
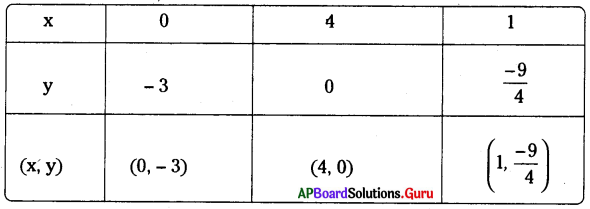
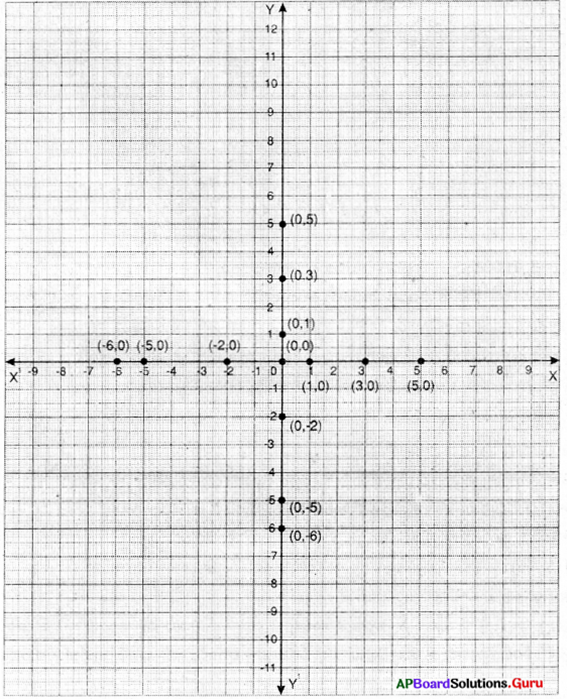
i) (0, – 3)
ii) (0, 4)
iii) (2, – 5)
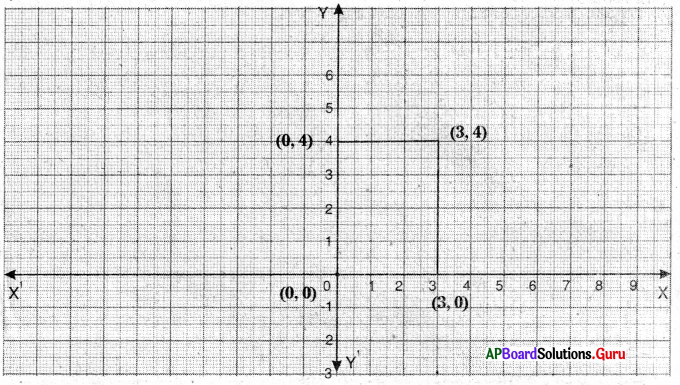
iv) (3, 4)
సాధన.
i) ఇచ్చిన బిందువు (0, – 3)
X- అక్షంనకు సమాంతరంగా వుండు రేఖా సమీకరణం y = k
∴ కావలసిన రేఖా సమీకరణం y = – 3 (లేక) y + 3 = 0.
ii) ఇచ్చిన బిందువు (0, 4)
X- అక్షంనకు సమాంతరంగా వుండు రేఖా సమీకరణం y = k
∴ కావలసిన రేఖా సమీకరణం y = 4 (లేక) y – 4 = 0.
iii) ఇచ్చిన బిందువు (2, – 5)
X- అక్షంనకు సమాంతరంగా వుండు రేఖా సమీకరణం y = k
∴ కావలసిన రేఖా సమీకరణం y = – 5 (లేక) y + 5 = 0.
iv) ఇచ్చిన బిందువు (3, 4)
X- అక్షంనకు సమాంతరంగా వుండు రేఖా సమీకరణం y = k
∴ కావలసిన రేఖా సమీకరణం y = 4 (లేక) y – 4 = 0.
ప్రశ్న 5.
కింది బిందువుల గుండా పోతూ Y- అక్షానికి సమాంతరంగా ఉండే సరళరేఖల సమీకరణాలను కనుగొనుము.
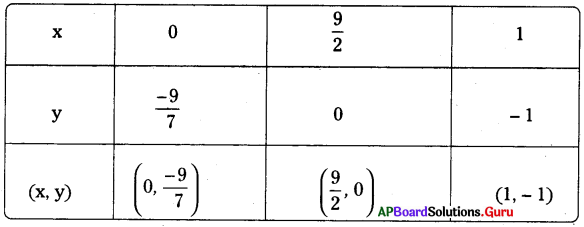
(i) (- 4, 0)
(ii) (2, 0)
(iii) (3, 5)
(iv) (- 4, – 3)
సాధన.
Y- అక్షంకు సమాంతరంగా వుండు రేఖా సమీకరణం x = k
∴ కావలసిన సమీకరణములు
i) (-4, 0) గుండా పోతే ఏర్పడు రేఖా సమీకరణం x = – 4 (లేదా) x + 4 = 0
i) (2, 0) గుండా పోతే ఏర్పడు రేఖా సమీకరణం x = 2 (లేదా) x – 2 = 0
iii) (3, 5) గుండా పోతే ఏర్పడు రేఖా సమీకరణం x = 3 (లేదా) x – 3 = 0
iv) (- 4, – 3) గుండా పోతే ఏర్పడు రేఖా సమీకరణం x = – 4 (లేదా) x + 4 = 0
ప్రశ్న 6.
ఏవైనా మూడు సరళరేఖల సమీకరణాలను రాయుము.
i) X- అక్షానికి సమాంతరంగా ఉండే
సాధన.
y = 3
y = – 4
y = 6
ii) Y- అక్షానికి సమాంతరంగా ఉండే
సాధన.
x = – 2
x = 3
x = 4