SCERT AP 9th Class Maths Solutions Chapter 6 రెండు చరరాశులలో రేఖీయ సమీకరణాలు Ex 6.3 Textbook Exercise Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 6th Lesson రెండు చరరాశులలో రేఖీయ సమీకరణాలు Exercise 6.3
ప్రశ్న 1.
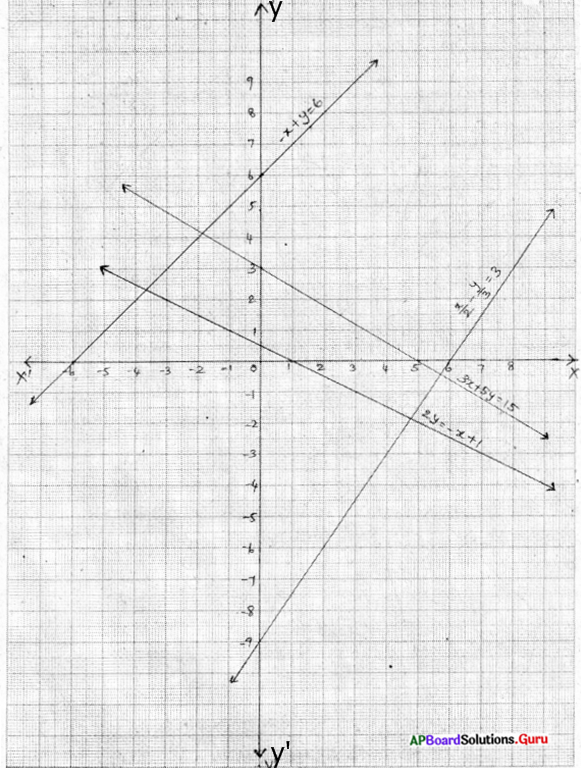
కింది వాని యొక్క రేఖా చిత్రాలను గీయుము.
i) 2y = -x + 1
ii) -x + y = 6
iii) 3x + 5y = 15
iv) \(\frac{x}{2}-\frac{y}{3}\) = 3
సాధన.
i) 2y = -x + 1
⇒ x + 2y = 1
| x | 1 | 3 |
| y | 0 | -1 |
| (x, y) | (1, 0) | (3, -1) |
ii) -x + y = 6
| x | 0 | -6 |
| y | 6 | 0 |
| (x, y) | (0, 6) | (-6, 0) |
iii) 3x + 5y = 15
| x | 0 | 5 |
| y | 3 | 0 |
| (x, y) | (0, 3) | (5, 0) |
iv) \(\frac{x}{2}-\frac{y}{3}\) = 3
⇒ \(\frac{3 x-2 y}{6}\) = 3
⇒ 3x – 2y = 18
| x | 0 | 6 |
| y | -9 | 0 |
| (x, y) | (0, -9) | (6, 0) |
![]()
ప్రశ్న 2.
కింది వాని యొక్క రేఖాచిత్రాలను గీసి, ప్రశ్నలకు సమాధానమిమ్ము.
i) y = x
ii) y = 2x
iii) y = – 2x ,
iv) y = 3x
v) y = – 3x
సాధన.
i) y = x
| x | 1 | 2 |
| y | 1 | 2 |
| (x, y) | (1, 1) | (2, 2) |
ii) y = 2x
| x | 1 | 2 |
| y | 2 | 4 |
iii) y = – 2x
| x | 1 | 2 |
| y | – 2 | – 4 |
iv) y = 3x
| x | 1 | 2 |
| y | 3 | 6 |
v) y = – 3x
| x | 1 | 2 |
| y | -3 | -6 |
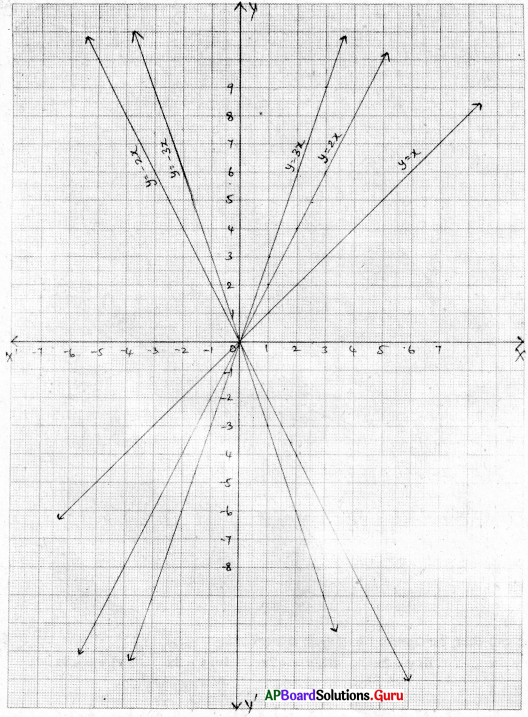
i) ఇవన్నీ y = mx (m ఏదైనా వాస్తవ సంఖ్య) రూపంలో ఉన్నాయా ?
సాధన.
అవును. ఇవన్నీ y = mx రూపంలో వున్నాయి.
ii) వీని రేఖాచిత్రాలన్నీ మూలబిందువు గుండా పోతున్నాయా ?
సాధన.
అవును. వీటి రేఖాచిత్రాలన్నీ మూలబిందువు గుండా పోతున్నాయి.
iii) ఈ రేఖాచిత్రాలు ఆధారంగా నీవేమి నిర్ధారించగలవు ?
సాధన.
y = mx రూపంలో ఉన్న రేఖలన్నీ మూలబిందువు గుండా పోతాయని నిర్ధారించవచ్చు.
![]()
ప్రశ్న 3.
2x + 3y = 11 యొక్క రేఖాచిత్రాన్ని గీయుము. దీని నుండి x = 1 అయిన y విలువ ఎంత ? కనుగొనుము.
సాధన.
| x | 1 | 4 |
| y | 3 | 1 |
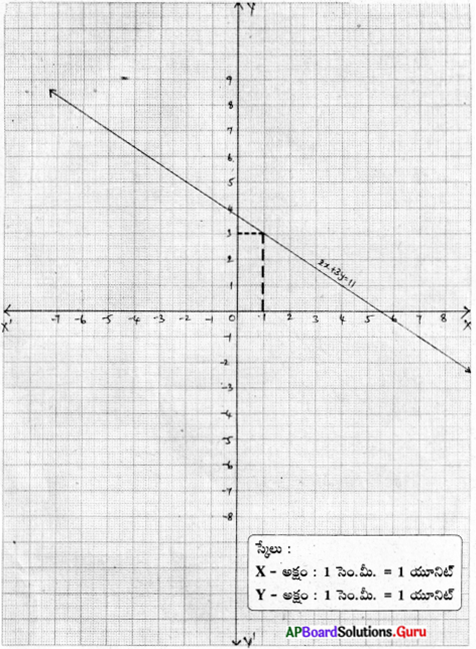
గ్రాఫ్ నుండి, x = 1 అయిన y = 3.
ప్రశ్న 4.
y – x = 2 యొక్క రేఖాచిత్రాన్ని గీయుము. దీని నుంచి
i) x = 4 అయినప్పుడు y విలువను
ii) y = -3 అయినప్పుడు x విలువను కనుగొనుము.
సాధన.
ఇచ్చిన సమీకరణము y – x = 2 లేదా – x + y = 2
| x | 0 | – 2 |
| y | 2 | 0 |
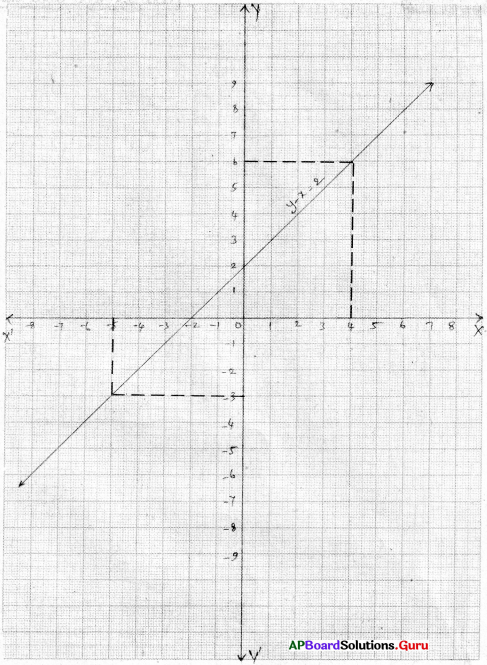
గ్రాఫు నుండి
i) x = 4 అయితే y = 6
ii) y = – 3 అయిన x = – 5
![]()
ప్రశ్న 5.
2x + 3y = 12 యొక్క రేఖాచిత్రం గీయుము. దీని నుండి
(i) y – నిరూపకము 3 అయ్యే విధంగా
(ii) x – నిరూపకము – 3 అయ్యే విధంగా సాధనలను కనుగొనండి.
సాధన.
ఇచ్చిన సమీకరణము 2x + 3y = 12
| x | 0 | 6 |
| y | 4 | 0 |
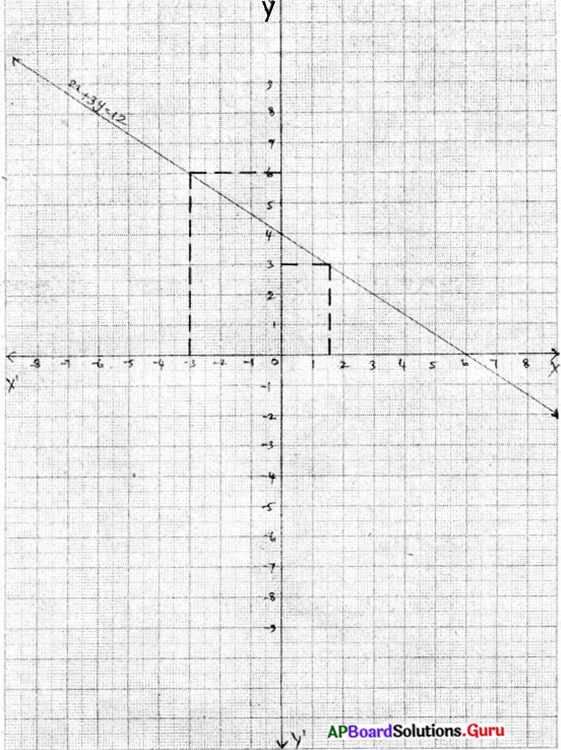
i) గ్రాఫు నుండి, y = 3 అయినపుడు x = \(\frac {3}{2}\); సాధన (\(\frac {3}{2}\), 3)
ii) గ్రాఫు నుండి, x = – 3 అయినపుడు y = 6; సాధన (-3, 6)
ప్రశ్న 6.
కింది సమీకరణాల రేఖాచిత్రాలను గీయండి. ఇది నిరూపక అక్షాలను ఖండించే బిందువులను కనుగొనండి.
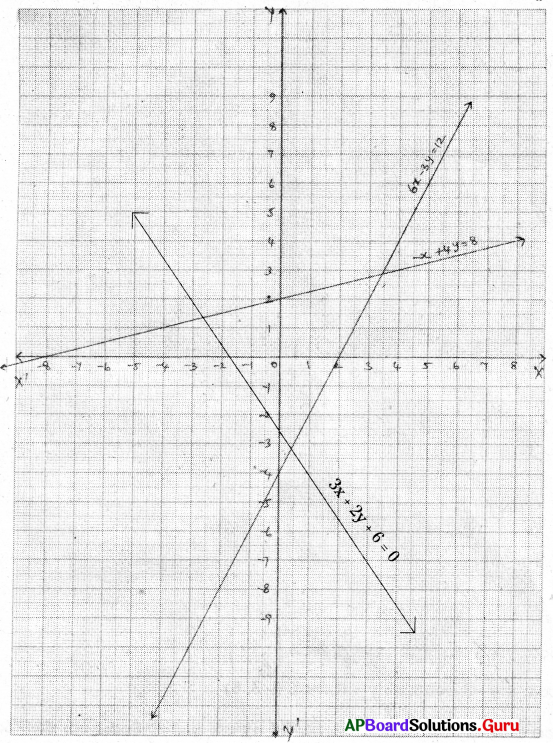
i) 6x – 3y = 12
సాధన.
ఇచ్చిన సమీకరణం 6x – 3y = 12
| x | 0 | 2 |
| y | – 4 | 0 |
గ్రాఫు నుండి ఇచ్చిన రేఖ X – అక్షంను (2, 0) వద్ద మరియు Y – అక్షంను (0, – 4) వద్ద ఖండించును.
ii) -x+ 4y = 8
సాధన.
ఇచ్చిన సమీకరణం – x + 4y = 8
| x | 0 | – 8 |
| y | 2 | 0 |
గ్రాఫు నుండి ఇచ్చిన రేఖ X – అక్షంను (-8, 0) వద్ద మరియు Y – అక్షంను (0, 2) వద్ద ఖండించును.
iii) 3x + 2y + 6 = 0
సాధన.
ఇచ్చిన సమీకరణం 3x + 2y + 6 = 0
| x | 0 | – 2 |
| y | – 3 | 0 |
గ్రాఫు నుండి ఇచ్చిన రేఖ X – అక్షంను (-2, 0) వద్ద మరియు Y – అక్షంను (0, – 3) వద్ద ఖండించును.
![]()
ప్రశ్న 7.
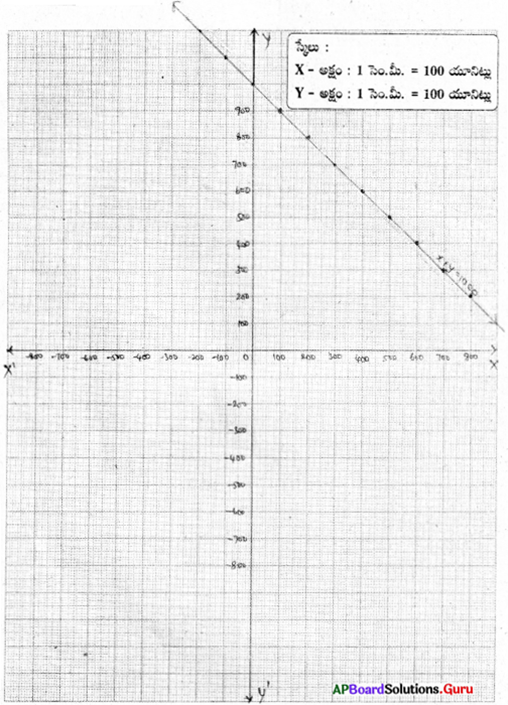
రజియా మరియు ప్రీతి ఒక పాఠశాలలో 9వ తరగతి చదువుచున్నారు. వీరు సహజ విపత్తులు సంభవించినప్పుడు బాధితులకు సహాయం చేయుట కొరకు ఏర్పాటు చేసిన ప్రధానమంత్రి సహాయనిధికి ₹ 1000 ఇచ్చారు. ఈ సమాచారమునకు సరిపడు సమీకరణమును రూపొందించి దానికి రేఖాచిత్రమును గీయుము.
సాధన.
రజియా P.M.R.F కు ఇచ్చిన విరాళము = ₹ x అనుకొనుము.
ప్రీతి P.M.R.F కు ఇచ్చిన విరాళము = ₹ y అనుకొనుము.
లెక్క ప్రకారము x + y = 1000
| x + y = 1000 | ||
| x | 200 | 300 |
| y | 800 | 700 |
ప్రశ్న 8.
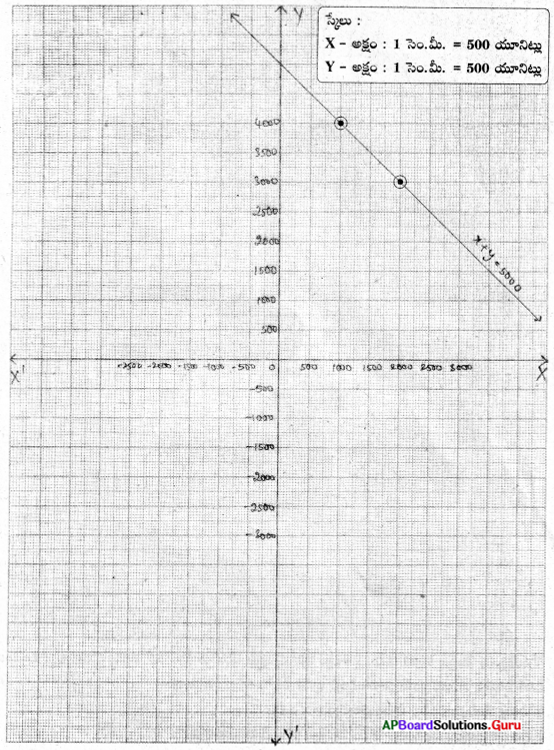
గోపయ్య తన మొత్తం 5000 చ.మీ. వైశాల్యం కలిగిన రెండు వేరువేరు పొలాలలో వరిని, గోధుమలను పండించాడు. దీనికి సరిపడు సమీకరణంను రూపొందించి దానికి రేఖాచిత్రమును గీయుము.
సాధన.
గోపయ్య వరిని పండించిన పొలం వైశాల్యం = x చ.మీ.
మరియు గోధుమను పండించిన పొలం వైశాల్యం = y చ.మీ. అనుకొనుము.
∴ లెక్క ప్రకారము x + y = 5000
| x + y = 5000 | ||
| x | 1000 | 2000 |
| y | 4000 | 3000 |
ప్రశ్న 9.
6 కి.గ్రా. ద్రవ్యరాశి గల వస్తువుపై బలాన్ని ప్రయోగించినప్పుడు అది పొందిన త్వరణము, ప్రయోగించిన బలానికి అనులోమానుపాతంలో ఉంటుంది. ఈ పరిశీలనకు సరిపడు సమీకరణమును రాసి, దానికి రేఖాచిత్రమును గీయుము.
సాధన.
వస్తువు ద్రవ్యరాశి = m = 6 kg; ప్రయోగించబడిన బలం = F, త్వరణము = a అయిన
లెక్క ప్రకారము, వస్తువుపై ప్రయోగించిన బలం, త్వరణానికి అనులోమానుపాతంలో ఉంటుంది.
∴ f ∝ a ⇒ f = m · a ⇒ f = 6a
| f = 6a | ||
| a | 2 | 3 |
| f | 12 | 18 |
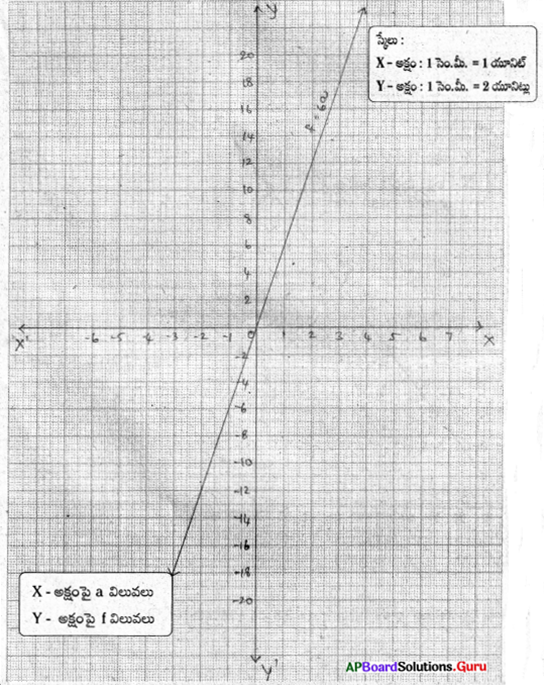
![]()
ప్రశ్న 10.
ఒక పర్వతము మీద నుంచి ఒక రాయి కింద పడుతూ ఉంది. దాని యొక్క వేగము v = 9.8t. (t = కాలము) దీనికి అనుగుణమైన రేఖాచిత్రమును గీచి, దాని నుండి ‘4’ సెకండ్ల సమయంలో దాని వేగమెంతో కనుగొనుము.
సాధన.
రాయి యొక్క వేగము v, రాయి ప్రయాణించిన కాలము = t
రాయి వేగము, కాలములకు మధ్యగల సంబంధము = v = 9.8t
| v = 9.8 t | ||
| v | 49 | 98 |
| t | 5 | 10 |
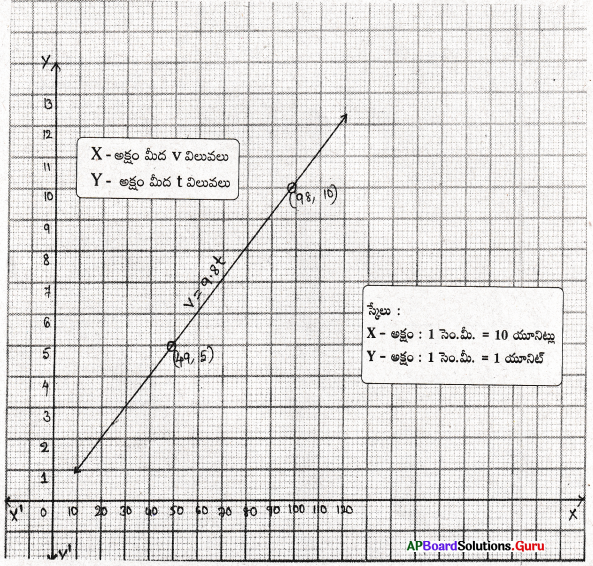
4 సెకండ్ల సమయములో రాయి వేగము = v = 9.8 × 4 = 39.2 మీ/సె2.
ప్రశ్న 11.
ఒక ఎలక్షన్లో 60% ఓటర్లు తమ ఓటు హక్కును వినియోగించుకొనినారు. దీనికి సరిపడు రేఖాచిత్రము గీచి, దాని నుంచి కింది వానిని కనుగొనుము.
i) 1200 ఓటర్లు మాత్రమే తమ ఓటు హక్కును వినియోగించుకొన్న మొత్తం ఓటర్లు ఎంత మంది ?
ii) మొత్తం ఓటర్ల సంఖ్య 800 అయిన ఓటు హక్కును వినియోగించుకున్నవారెందరు?
[సూచన : ఓటు హక్కు వినియోగించుకున్న వారి సంఖ్య ‘x’ మరియు మొత్తం ఓటర్ల సంఖ్య ‘y’ అనుకొనిన x = 60% y]
సాధన.
మొత్తం ఓటర్ల సంఖ్య = y అనుకొనుము.
ఓటు హక్కును వినియోగించుకున్న ఓటర్ల సంఖ్య = x అనుకొనుము.
లెక్క ప్రకారం, x = yలో 60%
| x | 1200 | 480 |
| y | 2000 | 800 |
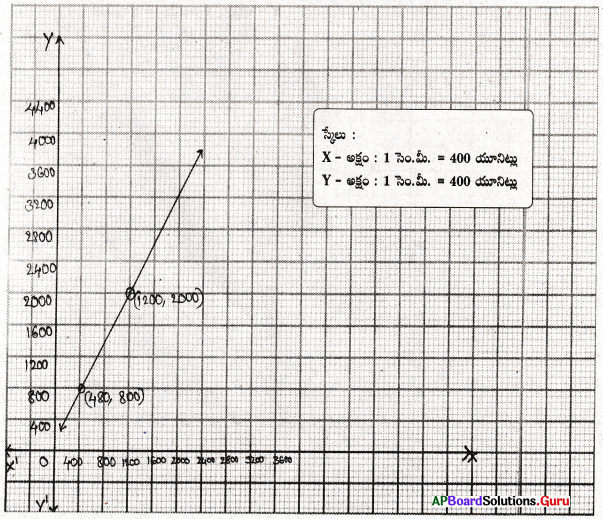
i) గ్రాఫ్ నుంచి x = 1200 అయిన మొత్తం ఓటర్ల సంఖ్య y = 2000.
ii) గ్రాఫ్ నుంచి y = 800 అయిన మొత్తం ఓటర్ల సంఖ్య x = 480.
![]()
ప్రశ్న 12.
రూప పుట్టినప్పుడు ఆమె తండ్రి వయస్సు 25 సం॥లు. ఈ దత్తాంశమునకు సరిపోవు సమీకరణమును రాసి దాని రేఖాచిత్రము గీసి దాని నుంచి ఈ కింది వానిని కనుగొనుము.
i) రూపకు 25 సం॥ల వయస్సు ఉన్నప్పుడు ఆమె తండ్రి వయస్సు.
ii) రూప తండ్రికి 40 సం॥ల వయస్సు ఉన్నప్పుడు రూప వయస్సు.
సాధన.
రూప తండ్రి వయస్సు = x సం॥ అనుకొనుము.
రూప వయస్సు = 9 సం॥లు
లెక్క ప్రకారం , x – y = 25 సం॥లు
| x | 40 | 50 |
| y | 15 | 25 |
గ్రాఫ్ నుండి,
i) రూపకు 25 సం॥లు ఉన్నప్పుడు ఆమె తండ్రి వయస్సు 50 సం॥లు.
ii) రూప తండ్రికి 40 సం॥లు ఉన్నప్పుడు ఆమె వయస్సు 15 సం॥లు.
ప్రశ్న 13.
ఒక ఆటో మొదటి గంట ప్రయాణానికి ₹ 15, తరువాత ప్రతీ గంట ప్రయాణానికి ₹ 8లు వసూలు చేయును. x కి.మీ. దూరానికి చెల్లించిన మొత్తం సొమ్ము ‘y’ అనుకొని ఈ సమాచారమునకు సరిపడు సమీకరణమును రాసి దానికి రేఖాచిత్రము గీయుము. రేఖాచిత్రము నుంచి చెల్లించిన మొత్తము ₹ 55 అయితే ప్రయోగించిన దూరమును మరియు 7 గంటలు ప్రయాణిస్తే చెల్లించవలసిన మొత్తమును కనుగొనుము.
సాధన.
మొదటి గంట ప్రయాణానికి అగు ఛార్జీ = ₹ 15
మొదటి గంట తర్వాత ప్రతీ గంటకు అగు ఛార్జీ = ₹ 8
x కి.మీ. దూరముకు చెల్లించిన సొమ్ము = ₹ y
లెక్క ప్రకారం y = 15 + 8x
∴ 8x – y + 15 = 0
| x | 2 | 1 |
| y | 31 | 23 |
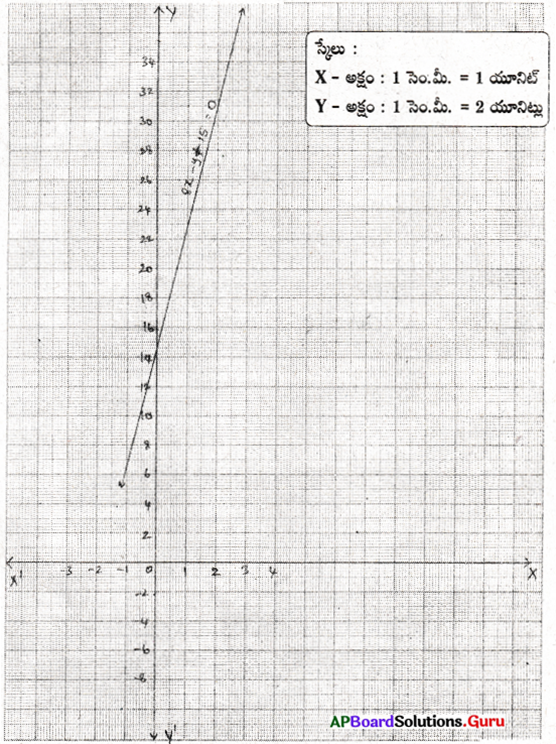
i) y = 55 అయితే x = 5 అగును.
ii) x = 7 అయిన y = 71 అగును.
![]()
ప్రశ్న 14.
పుస్తకాలను అద్దెకిచ్చే ఒక లైబ్రరీ మొదటి మూడు రోజులకు ఒక స్థిర మొత్తాన్ని ఆ తరువాత ప్రతి రోజుకు కొంత అదనపు మొత్తాన్ని వసూలు చేస్తుంది. జాన్ ఒక పుస్తకాన్ని 7 రోజులు ఉంచుకొని ₹ 27 లు చెల్లించాడు. మొదటి మూడు రోజుల స్థిర మొత్తాన్ని ₹ x మరియు ఆ తరువాత ప్రతీ రోజుకూ అదనంగా చెల్లించే మొత్తాన్ని ₹ y అనుకొని చెల్లించే స్థిరమొత్తము ₹ 7అయిన ప్రతీరోజూ అదనంగా చెల్లించే మొత్తాన్ని మరియు ప్రతీరోజూ అదనంగా చెల్లించే మొత్తము ₹ 4 అయిన మొదటి మూడు రోజులకు చెల్లించవలసిన స్థిరమొత్తమును కనుగొనుము.
సాధన.
జాన్ ఒక పుస్తకాన్ని 7 రోజులు ఉంచుకొని చెల్లించిన మొత్తం సొమ్ము ₹ 27
మొదటి మూడు రోజులకు అగు మొత్తము = ₹ x (స్థిరము)
చివరి నాలుగు రోజులకు అగు మొత్తము = ₹ 4y (అదనంగా ప్రతీరోజూ అగు ఖర్చు ₹ y)
లెక్క ప్రకారం x + 4y = 27
| x | 3 | 11 | 7 |
| y | 6 | 4 | 5 |
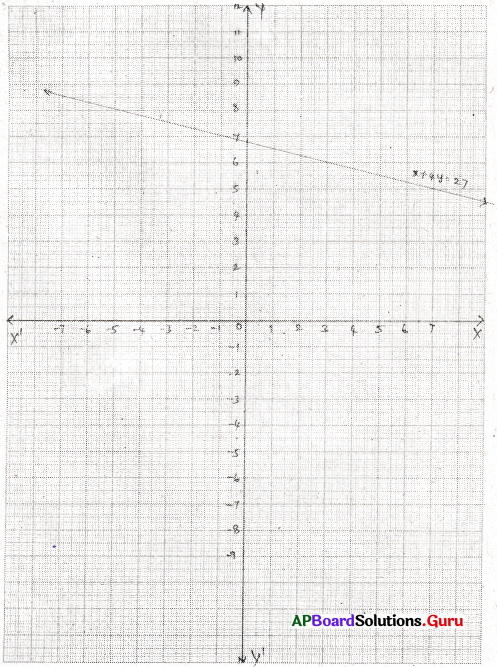
x = 7 అయినపుడు y = 5.
y = 4 అయినపుడు x = 11.
ప్రశ్న 15.
హైదరాబాద్ రైల్వేస్టేషన్లో ఒక కారును నిలిపి ఉంచినందుకు మొదటి రెండు గంటలకు ₹ 50 ఆ తరువాత ప్రతి గంటకు ₹ 10 లు చెల్లించవలెను. ఈ సమాచారమునకు సరిపడు సమీకరణమును రాసి, రేఖాచిత్రమును గీయుము. దాని నుంచి కింది వానిని కనుగొనుము.
i) 3 గం॥లు కారును ఉంచిన చెల్లించిన మొత్తము
ii) 6 గం॥లు కారును ఉంచిన చెల్లించిన మొత్తము
iii) రేఖ చెల్లించిన మొత్తము ₹ 80 అయిన ఆమె ఎన్ని గంటలు కారును నిలిపి ఉంచింది ?
సాధన.
చెల్లించిన మొత్తము సొమ్ము = ₹ y
మొదటి రెండు గంటలకు చెల్లించవలసిన సొమ్ము = ₹ 50.
ఒక గంటకు ₹ 10 ల చొప్పున x గంటలకు చెల్లించవలసిన మొత్తం సొమ్ము y = 50 + (x – 2) 10
⇒ y = 50 + 10 x – 20 ⇒ y = 10x + 30
∴ లెక్క ప్రకారం y = 10x + 30
| x | 3 | 5 | 6 |
| y | 60 | 80 | 90 |
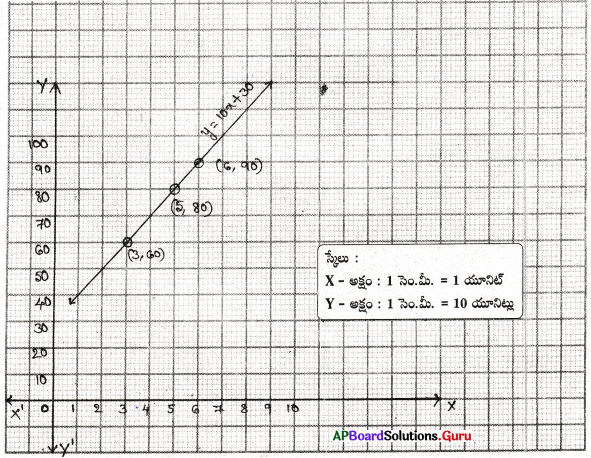
i) మూడు గంటలకు చెల్లించవలసిన సొమ్ము = 50 + 10 × 1 = ₹ 60
ii) ఆరు గంటలకు చెల్లించవలసిన సొమ్ము = 50 + 10 × 4 = 50 + 40 = ₹ 90
iii) రేఖ తన కారును 5 గంటలు ఉంచినది.
![]()
ప్రశ్న 16.
సమీరా కారును 60 కి.మీ./గంట స్థిర వేగముతో నడుపుతుంది. దూరము – కాలము రేఖాచిత్రము గీసి, దాని నుంచి ఈ కింది సమయాలలో సమీరా ప్రయాణించిన దూరమును కనుగొనుము.
i) 1\(\frac {1}{2}\) గంట
ii) 2 గంటలు
iii) 3\(\frac {1}{2}\) గంటలు
సాధన.
కారు వేగము = 60 కి.మీ./గం.
ప్రయాణానికి తీసుకున్న సమయము = x గంటలు
ప్రయాణించిన దూరము = y గంటలు
లెక్క ప్రకారం, 60x = y ⇒ 60x – y = 0
| x | 2 | 4 | 5 |
| y | 120 | 240 | 300 |
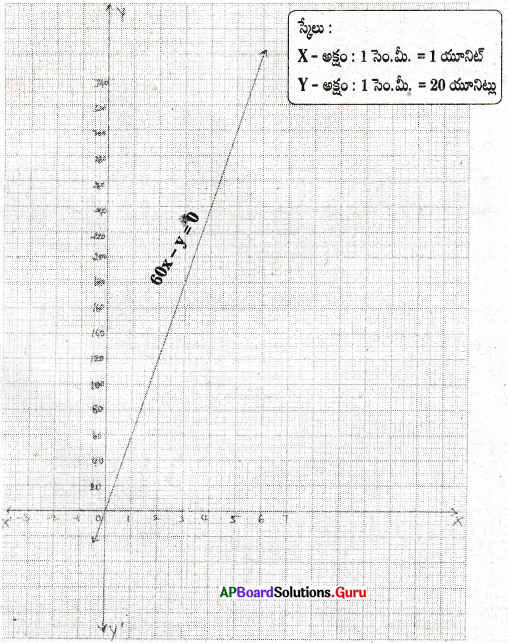
i) 1\(\frac {1}{2}\) గంటలలో కారు ప్రయాణించిన దూరము = 90 కి.మీ.
ii) 2 గంటలలో కారు ప్రయాణించిన దూరము = 120 కి.మీ.
iii) 3\(\frac {1}{2}\) గంటలలో కారు ప్రయాణించిన దూరము = 210 కి.మీ.
ప్రశ్న 17.
నీటిలో హైడ్రోజన్ మరియు ఆక్సిజన్ అణుభారాల నిష్పత్తి 1 : 8. అయిన ఈ సమాచారాన్ని తెలియజేయు సమీకరణమును రూపొందించి దానికి రేఖాచిత్రం గీసి, దీని నుండి ఆక్సిజన్ పరిమాణము 12గ్రా॥ అయిన హైడ్రోజన్ పరిమాణమును, హైడ్రోజన్ పరిమాణము, \(\frac {3}{2}\)గ్రా॥ అయినప్పుడు ఆక్సిజన్ పరిమాణమును కనుగొనుము.
(సూచన : హైడ్రోజన్ మరియు ఆక్సిజన్ పరిమాణాలను వరుసగా ‘x’, ‘y’ అనుకొనిన x : y = 1 : 8 ⇒ 8x = y)
సాధన.
నీటిలో హైడ్రోజన్ పరిమాణము = x గ్రా. అనుకొనుము.
ఆక్సిజన్ పరిమాణము = y గ్రా. అనుకొనుము.
నీటిలో హైడ్రోజన్, ఆక్సిజన్ నిష్పత్తి = 1 : 8
లెక్క ప్రకారం, 8x = y ⇒ 8x – y = 0
| x | 1 | 2 | 4 | 5 |
| y | 8 | 16 | 32 | 40 |
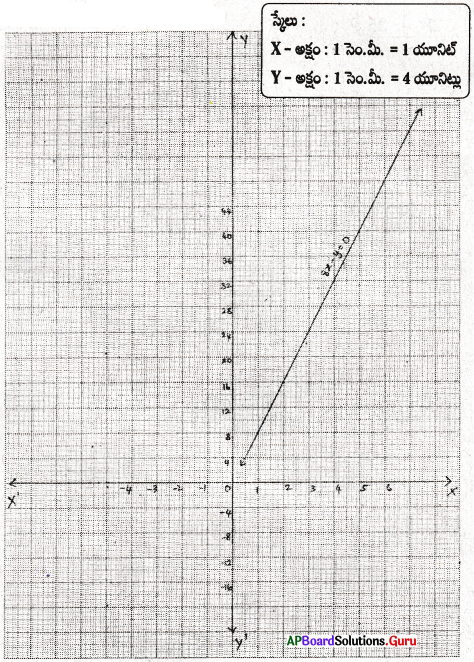
గ్రాఫ్ నుండి, నీటిలో ఆక్సిజన్ పరిమాణము 12 గ్రా. అయిన హైడ్రోజన్ పరిమాణము = \(\frac {3}{2}\) గ్రా.
నీటిలో హైడ్రోజన్ పరిమాణము \(\frac {3}{2}\) గ్రా. అయిన ఆక్సిజన్ పరిమాణము = 12 గ్రా.లు
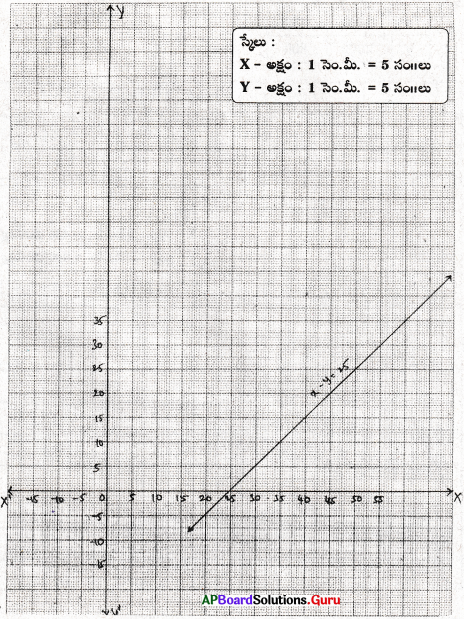
ప్రశ్న 18.
28 లీటర్ల పాలు, నీళ్ల మిశ్రమములో వాని నిష్పత్తి 5 : 2 అయిన మిశ్రమమునకు, పాలకు మధ్యగల సంబంధంను తెలియజేయు సమీకరణమును రూపొందించి దానికి రేఖాచిత్రము గీయుము. దాని నుంచి పై మిశ్రమములో పాల పరిమాణమును కనుగొనుము.
(సూచన : మిశ్రమమునకు, పాలకు మధ్యగల నిష్పత్తి = 5 + 2 : 5 = 7 : 5)
సాధన.
మిశ్రమములో గల పాల పరిమాణం = x లి॥ అనుకొనుము.
మిశ్రమము యొక్క పరిమాణము = y లీ॥ అనుకొనుము.
మిశ్రమములో పాలు మరియు నీళ్ల నిష్పత్తి = 5 : 2
నిష్పత్తిలోని పదాల మొత్తము = 5 + 2 = 7
∴ పాల పరిమాణము ‘x’ = \(\frac {5}{7}\)y లీ.
⇒ 7x = 5y ⇒ 7x – 5y = 0
| x | 10 | 20 | 25 |
| y | 14 | 28 | 35 |
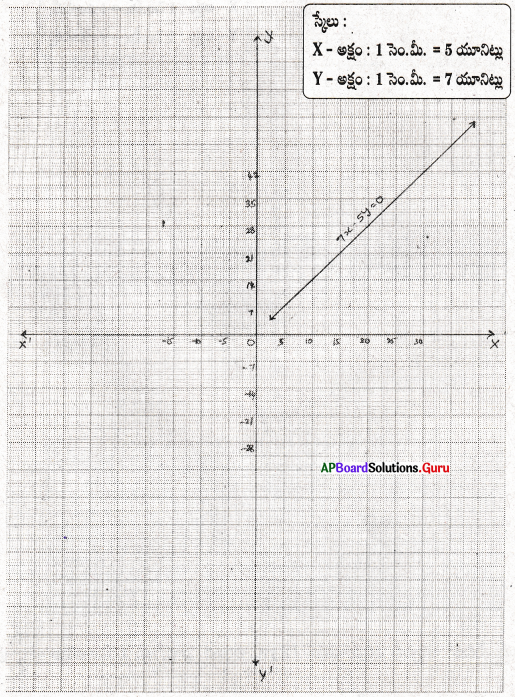
గ్రాఫ్ నుండి, మిశ్రమములోని పాల పరిమాణము = 20 లీటర్లు.
![]()
ప్రశ్న 19.
అమెరికా, కెనడా దేశాలలో ఉష్ణోగ్రతను ఫారన్ హీట్ మానంలో కొలుస్తారు. అయితే ఇండియా లాంటి దేశాలలో సెల్సియస్ మానంలో కొలుస్తారు. ఫారన్ హీట మానానికి, సెల్సియస్మనానికి మధ్య గల సంబంధం కింది సమీకరణం తెలియజేస్తుంది.
F= (\(\frac {9}{5}\))C + 32
i) సెల్సియస్ డిగ్రీలను X – అక్షం మీద, ఫారన్ హీట్ డిగ్రీలను Y – అక్షం మీద తీసుకొని పై సమీకరణానికి రేఖాచిత్రము గీయుము.
ii) 30°C కి సమానమైన ఫారన్ హీట్ మానంలోని ఉష్ణోగ్రతలను కనుగొనుము.
iii) 95°F కు సమానమైన సెల్సియసమానంలోని ఉష్ణోగ్రతను కనుగొనుము.
iv) సెల్సియసమానములోనూ, ఫారన్ హీట్ మానంలోనూ ఒకే సంఖ్యా విలువలు కలిగి ఉండే ఉష్ణోగ్రత ఏమైనా ఉందా ? దాని విలువను కనుగొనుము.
సాధన.
i) ఫారన్ హీట్ మానానికి, సెల్సియస్మనానికి మధ్యగల సంబంధము F = \(\frac {9}{5}\)C + 32
| C | 20 | 30 | 35 | – 40 |
| F | 68 | 86 | 95 | – 40 |
C = 20 అయిన F = \(\frac {9}{5}\) × 20 + 32 = 68
C = 30 అయిన F = \(\frac {9}{5}\) × 30 + 32 = 86
C = 35 అయిన F = \(\frac {9}{5}\) × 35 + 32 = 95
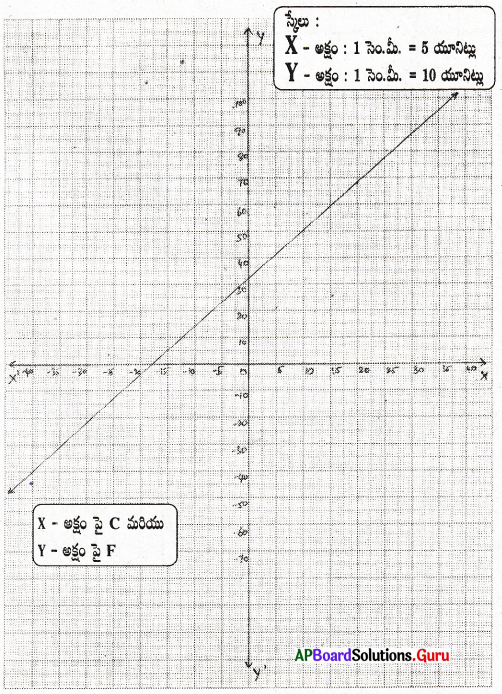
గ్రాఫు నుండి,
ii) 30° C = 86° F
iii) 95° F = 35° C
iv) C = – 40 అయిన F = – 40